偏差値の使い方 (+ 偏差値の求め方)
「偏差値」というワードは
どちらかというと
社会では忌み嫌われる部類に入りますね
なんとなく頭でっかちで、
つまらないというイメージが
ついてまわるからでしょうか
悪いイメージがつく理由は簡単ですね
例えば、
空手なら白帯(無級)から黄帯・・・黒帯(初段以上)、
将棋にも〇級~9段、
相撲にも幕下~横綱、
そろばんにも、スイミングスクールにも、
職場にも、その他色々なことに
上達具合といいますか
自分のレベルを表す「階級」制度がありますね。
これらの階級の存在意義で
最も重要なものは
「自分の現在地を客観的に確認すること」であったり
「向上心を煽る(あおる)」ということだと思います。
ですがこれらは
自分が望んで入った世界での話です。
対して
「学力偏差値」は望んでいなくても
小学、中学の義務教育制度がある以上
勝手に番付されてしまいますね。
どんなことでも勝手に土俵に乗せられて、
勝手に番付されたら
嫌な気分になるのも仕方ないのかなと感じます。
そして、
社会に出ると
勉強成績が良くなかった人でも
出世していきますので
(∵その職での成績がすべて)、
反作用として
学生時代の「偏差値」というワードを
悪く言うのでしょうね。
親子中学では
偏差値は「悪いもの」でも
逆に「全て」でもありませんが…
皆さまは「中学宿題をしよう」ではなく、
「中学勉強を頑張ろう」
「難関高校を目指そう」という
人たちだと思います
それは「自分で土俵に上った」
ということですので、
「偏差値」を「自分の階級」として
現在地を確認するための目印として
利用していきましょうね。
言うまでもありませんが
土俵に上がっていない友達に
偏差値の話題はタブー
ということにもなりますね。
イメージ
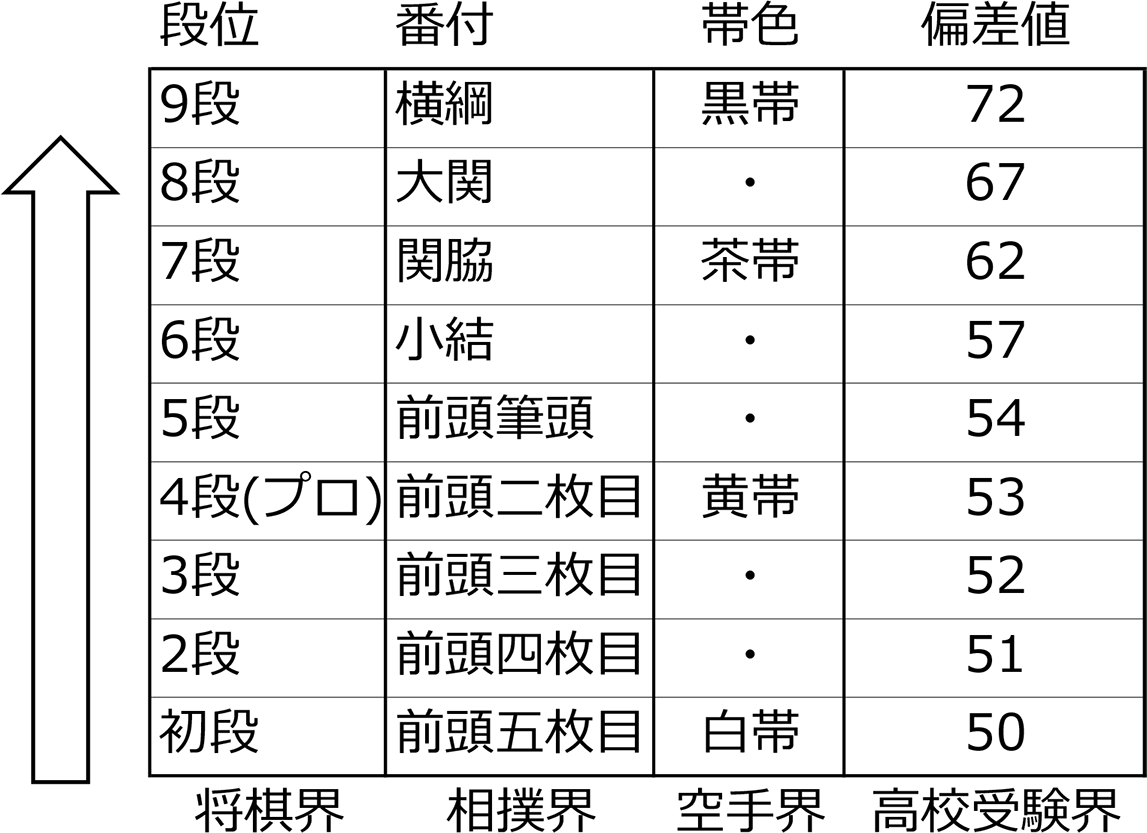
皆様の番付(偏差値)が上がりますように!!
話が前後しますが
偏差値とは
→50を真ん中として、50からどれくらい離れているかという値ですね
自分の「平均点」からわかること→平均点との差
自分の「偏差値」からわかること→全体での位置
偏差値を求める必要性
必要なデータ…全員のそれぞれの点数
よって、
みんなの点数などは知り得ようがないので
求めることはできませんし
自分で求めようとする必要もありませんね
(自分で求めて、自分で偏差値65相当か・・・
と思うより
全国模試を受けて、
「あなたは現在偏差値62です!」
と言われた方がパリッとしますね
詰将棋をして
自分は初段相当かぁ・・・
よりも連盟などに「あなたは1級!」
と言われるほうがパリッとしますよね
自分を強く信じていても
他者の言葉なりにパリッとさせられることは
多々ありますね!)
【 偏差値の求め方 】
念のため
もし全員の点数が分かっている場合の求め方です
①全員のデータ
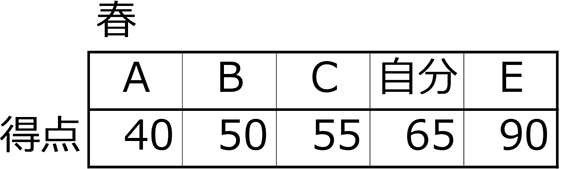
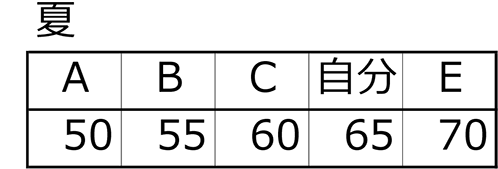
だったとします
②平均点
春の平均点=\(\frac{40+50+55+65+90}{5人}\)=60点
夏の平均点=\(\frac{50+55+60+65+70}{5人}\)=60点


③偏差 =「平均点との差」
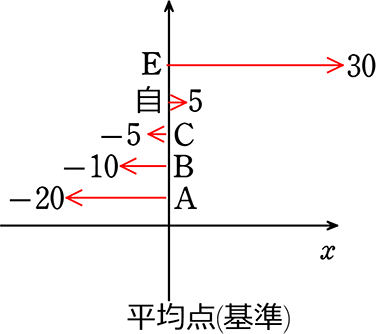
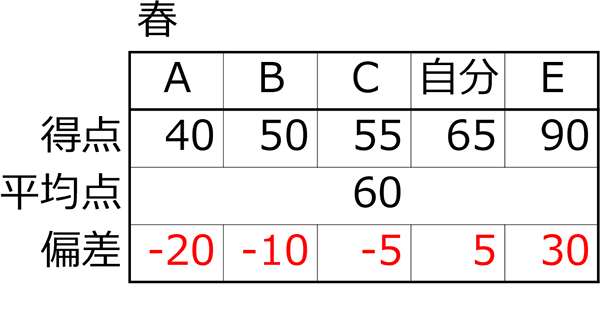
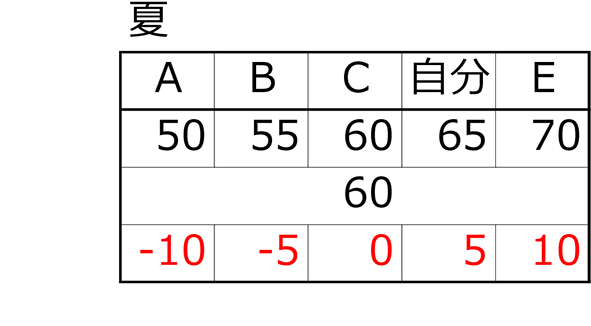
④偏差の2乗 (距離という線を、2乗して正方形の面積にする感じでしょうか)

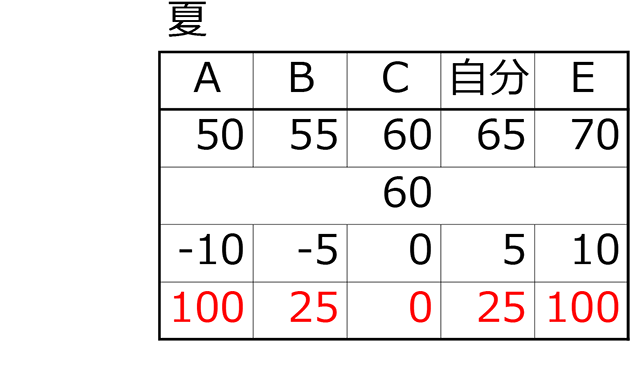
⑤分散 =「(偏差の2乗)の平均」
大~小ある面積の平均という感じでしょうか
春の分散=\(\frac{400+100+25+25+900}{5人}\) =290
夏の分散 =\(\frac{100+25+0+25+100}{5人}\) =50


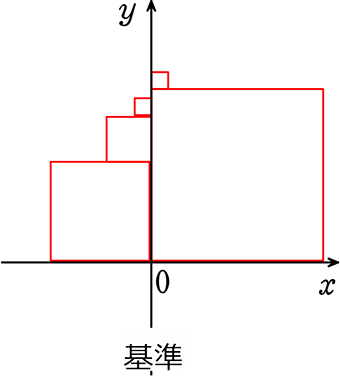
イメージ

春の方が「散らばっている」イメージでしょうか
⑥標準偏差 =「分散のプラスの方の平方根」
1辺の長さに戻す感じでしょうか
x2=290 → x=\(\sqrt{290}\)=17.02939 (3年:2乗のとり方)
x2=50 → x=\(\sqrt{50}\)=7.072068


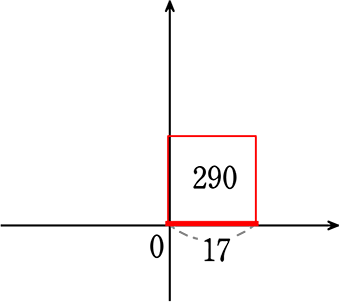
今後は この「17」が春の基準になります
全員のふり幅の基準となりますが、
わざわざ2乗して また戻す意味がわからない、
ふり幅なら「偏差」の絶対値を全て足して5人で割ったものでよいのでは?
と感じますね
基準=\(\frac{20+10+5+5+30}{5人}\)=14でもよいのでは?と

→これを「平均偏差」と言って「基準」になれるのですが
日本では偏差値を求める場合「標準偏差」の方を採用しているのです
(重さのg、長さのmは
世界が、人が作った「基準」で納得がいきますが
「標準偏差」という「基準」は
いわば「部署レベル」の「基準」です。
ですが
納得がいかなくても従うしかないのです
「標準」≒ある範囲内でのの基準
たとえば
納得のいかない計算式で求められた基準でも、今後はその「課税標準額」を基準に税額を求めていくのと同じですね
⑦個人の偏差値=\(\frac{偏差}{標準偏差}\)×10+50
まず\(\frac{偏差}{標準偏差}\)は標準偏差の1化ですね (1年:割合の意味)

→ 「偏差」たちの位置関係がはっきりしていきますね
・位置関係はわかったけど、見にくいなぁ
→「10」を掛けよう (\(\frac{偏差}{標準偏差}\)×10+50)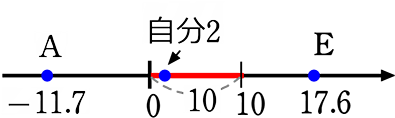
→もし「100」を掛けようなら、「%」ですね
Eは標準偏差の176%の場所にいる
・マイナスもイメージが湧かないなぁ
→「50」足そう (\(\frac{偏差}{標準偏差}\)×10+50)



同じ点数65点、平均60点でも偏差値が違いますね!
夏のテストの方が難しいテストだったということかな・・・
Eさんがガクッと落ちたり
Aさんが頑張ったり
「標準偏差」(基準)の幅が春より小さくなったからですね















