| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平方根 | (2) 式の展開・因数分解 | (3) 二次方程式 |
二次方程式
ア 二次方程式の必要性と解の意味
この単元で言う 「二次方程式」とは、正確には、
「1元二次方程式」ですね ( 〇元〇次の意味)
すなわち、
ax2+bx+c=0 や ax2+bx(a, b, c は定数、a≠0)のような方程式ですね (一元 = 使用する「文字」の種類が1種類 )
たとえば、
4x2+8x+3=0 のような形ですね
| → | 使っている文字は「x」の1種類(一元)ですね |
| → | 右辺を全て「移項」して「0」にしたとき、左辺で最も次数の高い項が、「2次」ですね |
そして、
「一次方程式」同様、「x」が「x2」であっても
「xの値を求めたい!」というものが「二次方程式」であって、
そのまま「二次方程式の必要性」ということになりますね!
基本的に「方程式」は、「移項」や「等式の性質」を駆使して、
左辺を「x」だけの形( x = 〇〇 )にすれば、〇〇が「解」ですね
「二次方程式」の解き方は、
・「移項」
・「等式の性質」のほかに
・「平方根の考え方」
・「因数分解」
・「解の公式」
・できれば「平方完成」
が新たな「武器」として必要なだけですね!
イ 因数分解や平方の形に変形することによる二次方程式の解法
それでは実際に二次方程式を解いていきましょう
〈 武器① 〉平方根の求め方を利用
x2 = 9 A. x = ±3 でしたね
左辺の「x2 」を「x」にするためには、
機械的に右辺全体に「±√ 」を付けるだけでしたね!
これをもう少ししっかり言うと、
『左辺が、丸々2乗されている 場合、
右辺全体に ±√を付けるだけ』 となりますね (平方根の掘り下げ利用)
《 例 》
・x2 = 16 → 左辺丸々2乗の形 → ∴ x = ±\(\small{\sqrt{16}}\) = ±4
・c2 = a2+b2 → 左辺丸々2乗の形 → ∴ c = \(±\small{\sqrt{a^2+b^2}}\)
| ・ | x2-25 = 0 → x2 = 25 → 左辺丸々2乗の形 → ∴ x = ±\(\small{\sqrt{25}}\) = ±5 |
| ・ | (x+3)2 = 36 → 左辺丸々2乗の形 ←(カッコ)を「1文字」と見れますね → x+3=±\(\small{\sqrt{36}}\) → x+3 = ±6 → x=-3±6 → ∴ x = 3または x = -9 |
| ・ | (x+2)2-2=5 → (x+2)2 = 7 → 左辺丸々2乗の形
→ x+2 = ±\(\small{\sqrt{7}}\) → ∴ x = -2±\(\small{\sqrt{7}}\) |
| ・ | 9(x-3)2 = 4 → (x-3)2 = \(\large{\frac{4}{9}}\) → 左辺丸々2乗の形 → x-3 = ±\(\small{\sqrt{\large{\frac{4}{9}}}}\) → x = 3±\(\large{\frac{2}{3}}\) → ∴ x = \(\large{\frac{11}{3}}\), x = \(\large{\frac{7}{3}}\)
または、 |
| ・ | x(x+2)=6 → x2+2x = 6 → x2 = -2x+6 → ダメですね(右辺にxを含む項があってはいけませんね!)
→ 左辺丸々2乗の形 にできない → 平方根の求め方を利用できない → 他の解き方 → 後で出てきますのでその時にお話しますね |
| ⇒ | x(x+2) = 0 → 両辺をxで割ると → x+2 = 0 → x = -2 ??
『ダメですね!』 xは「未知数」ですから、-1かも3かも-0.5かも「0」かも・・・まだわかりませんね! |
〈武器②〉因数分解を利用
例えば、 6( ) という「
2・3・( ) ですね!(もう皆様は(カッコ)の中の数字や文字に惑わされることなく
(カッコ)を「1文字」と見れますものね!)
これで、6( )という「1つの項」は、「2の倍数」であり「3の倍数」であり「( )の倍数」あることは確定で、
あとは( )しだいで全てが確定しますね!
では、 6( )
( ) = 0 とわかりますね
ではでは、 ( )( ) = 0 なら、前の( )が0か、 後の( )が0か、
または
両方とも0 のいずれかということがわかりますね!
そして、( )( )の形は… 文字を含んだ数字を因数分解した後の形と同じですね
ex) (x+2)(x-3)
これを利用して、二次方程式を解いていきます
《 例 》 方程式を解きましょう
・ x2+10x+9 = -15
→ ① 右辺は必ず「0」にします
x2+10x+24 = 0
→ ② 左辺を因数分解します
(x+4)(x+6) = 0
| → | この式は、(x+4)が「0」のとき、または、(x+6)が「0」のとき成立しますね! |
→ ③ よって、
x+4
x+6
A. x = -4, x = -6 となります!
確認のため、x = -4, x = -6 を x2+10x+24 = 0に代入してみますね
x = -4 のとき (-4)2+10(-4)+24 = 0
→ 16-40+24 = 0
→ 0 = 0 OK
x = -6 のとき (-6)2+10(-6)+24 = 0
→ 36-60+24 = 0
→ 0 = 0 OKですね!
・ x2-3x = 0
→ (x)(x-3) = 0
→ x(x-3) = 0 A. x = 0, x = 3
→ 「この式が成立するためには、(x) = 0 のとき、または(x-3) = 0のとき」
という理屈が理解できれば、今後は
すなわち、
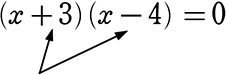 という形になれば
という形になれば
セットの数字の「符号を逆にしたもの」が、解ですね!
A. x = -3, x = 4
・ x2-8x+16 = 0
→ (x-4)2 = 0 A. x = 4
・ (x+3)2 = 36
→ x2+6x+9-36 = 0
→ x2+6x-27 = 0
→ (x+9)(x-3) = 0 A. x = -9, x = 3
…ですが…「平方根の求め方の利用」で1度求めていますね!
左辺丸々2乗の形 → x+3 = ±\(\small{\sqrt{36 }}\) でしたね!
→ x=-3±6 → x=-9, 3
・ x2-25 = 0
→ x2 = 25
→ 左辺丸々2乗の形 → x = ±5
または
→ 因数分解で、(x-5)(x+5) = 0
→ x = ±5
これは どちらも同じくらいの労力ですね
二次方程式は、8割方「因数分解を利用」で求めますので、
ついつい「平方根の求め方の利用」を忘れて、ひと手間かけてしまいますね
ですが、よく言えば、「因数分解利用」さえできれば「平方根利用」は
ど忘れしていても大丈夫!ということですね

因数分解利用で、右辺を「0」にする理由
「右辺を0にする」に納得がいかない場合のみ お読みくださいね
右辺が「0」ではない x2+10x+9 = -15 を同様に進めてみると…
(x+9)(x+1) = -15
考えられる、 整数の ( )( ) = -15 は…
(-1)(15) = -15 (1)(-15) = -15
(-15)(1) = -15 (15)(-1) = -15
(-3)(5) = -15 (-5)(3) = -15
(-5)(3) = -15 (5)(-3) = -15
整数に限定しなければ、無限にありますね
例えば、(-1)(15) = -15 の場合 x+9 = -1, x+1 = 15 の場合のみ成立
→ x = -10, x = 14 となりますね
しかし、x = -10を x2+10x+9 = -15 に代入すると
(-10)2+10(-10)+9 = -15
9 = -15?
x = 14 を x2+10x+9 = -15 に代入すると
(14)2+10(14)+9 = -15
345 = -15? 成立しませんね!
どうして、右辺が「0」の時のみ成立するのでしょうか?
x2+10x+9 = -15 を右辺を「0」にして、
x2+10x+24 = 0 で右辺の「0」を「y」としてグラフを描くと
y = x2+10x+24 →
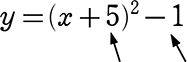
頂点の座標(-5, -1)

「0」をyとする → 原点の座標は(0, 0)
x2+10x+24 = 0 の解は
→ (x+4)(x+6) = 0 で
x = -4, x = -6
すなわち、y = 0 のときの xの値ですね
すなわち、x座標との「交点」ですね
では、x2+10x+9 = -15 で右辺の「-15」を「y」としてのグラフを描くと
y = x2+10x+9 → y = (x+5)2-16
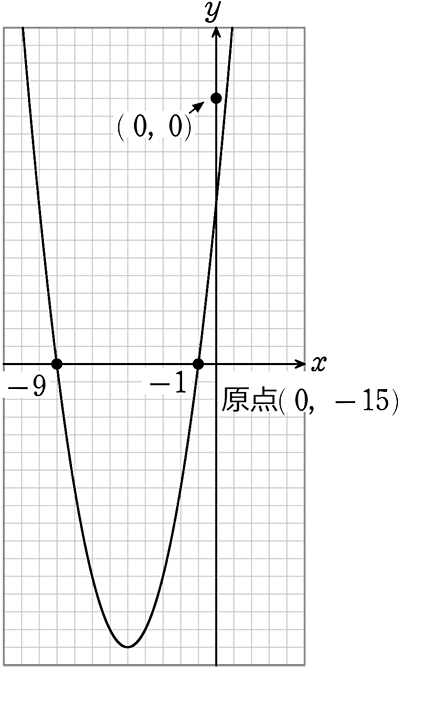
「-15」をyとする → 原点の座標は(0, -15)
x2+10x+9 = -15 のx切片は
→ (x+9)(x+1) = -15 で
x = -9, x = -1
すなわち、y = -15 のときの xの値
すなわち、x座標との「交点」ですね
以上より、「右辺を0にする」とは「原点を(0, 0)にする」ということですね
数学の基準は (0, 0) ですよね!
→ 右辺が「自由 (0, 自由)」では、曲線とx軸の交点は無限にありますね
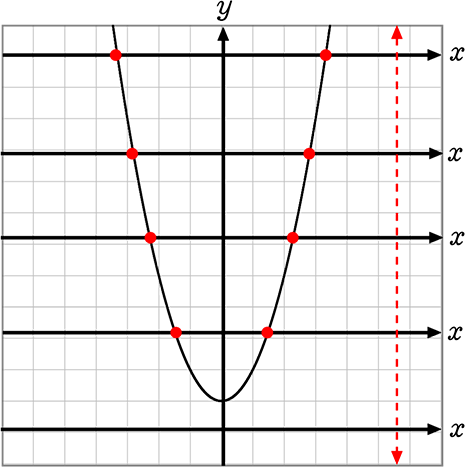
というわけで、因数分解を利用して二次方程式を解く場合には、
基準を(0, 0)にしてくださいね、すなわち、「右辺を0」にしてくださいね!
( ).png)
クリック・タップで答え (反応が遅い場合があります)
( )sp.png)
クリック・タップで答え (反応が遅い場合があります)

二次方程式の解の書き方
まず、ここまでで分かったことは、
二次方程式の解は、基本「2つ 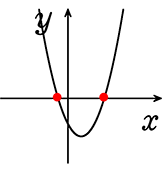 」あるということでしょうか
」あるということでしょうか
他にも、2つの解の値が全く同じで、結果「ただ1つ  」に見える「重解」、
」に見える「重解」、
解のない「解なし 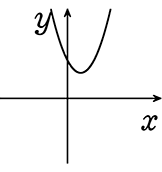 」の3種類となりますね
」の3種類となりますね
y = x2+x-2 (2次関数)
↓
(0) = x2+x-2 (2次方程式)
→ 2次方程式の解は、2次関数でいう y = 0 のときの xの値ですね
そして、本題の「解答の書き方」ですが、何気に色々ありますね
あまりこだわるところではありませんが…
例えば、
・次の方程式を解きましょう
x2-5x+6 = 0
(x-2)(x-3) = 0
① A. x = 2 または x = 3
② A. x = 2, x = 3
③ A. x = 2, 3
④ A. x = 2 と x = 3
⑤ A. 2, 3
どれが正しい解の書き方なのでしょうか?
→ 1番正確な表現は ①ですね

①の「x = 2またはx = 3」ですね!
④の「2と3」は・・・
このように無理やり重複部分をつくって、
「2と3ならいつでもOKなんでしょ、x2-5x+6 = 0 の x2のx には2を入れて、
-5x の x には3を入れたら、0にならないんだけど!なんて言われたらたまりませんね!
→ 同時使用性はありません!
「または」が1番無難ですね!
②の「 ,」も、③の「 ,」も、一般社会では「と」「や」に当たりますが、
数学のこの場面では、暗黙の了解で「または」の意味ですね
「または」も一般社会と数学界では、捉え方が異なりますね!
| ・ | 一般社会の「または」→ 一方を選んだら他方を否定 |
| ・ | 数学界の「または」→ 一方を選んでも他方を否定しない |
湖の女神様:「あなたの落とした斧は、この金の斧ですか?または、この銀の斧ですか?」
きこり:「銀の斧です、金の斧は私のものではありません」
湖の女神様:「よろしい」
湖の女神様:「あなたの落とした斧は、この金の斧ですか?または、この銀の斧ですか?」
数学者:「銀の斧です、そして金の斧も私のです」
湖の女神様:「『または』と言ったでしょ! どっちかでしょ!」
数学者:「『または』と言ったでしょ!だから両方OKでしょ!」
⑤の A. 2, 3 は危険ですね
これは、「xの値を求めましょう」ならマルかもしれませんが、
「方程式を解きましょう」では、必ず「x = 」を付けてくださいね!
「無難」「暗黙の了解」「危険」など、はっきりしない言い回しが
多くなりましたが、実際はっきりしていないのです
結局、
| ① | A. x = 2 または x = 3 (正確だけど、あまり見かけない) |
| ② | A. x = 2, x = 3 (教科書でよく使われている) |
| ③ | A. x = 2, 3 (普段よく使う) |
| ④ | A. x = 2 と x = 3 (あまり見かけないし危険) |
| ⑤ | A. 2, 3 (OUT!) |
というわけで、
テストでは②
家では③ でよいのではと思います
A. x = 2±\(\small{\sqrt{3}}\) などは、
A. x = 2+\(\small{\sqrt{3}}\), x = 2-\(\small{\sqrt{3}}\) としなくても
A. x = 2±\(\small{\sqrt{3}}\) でOKなんですよね…
ウ 解の公式を用いた二次方程式の解法
〈武器③〉解の公式を利用
明らかに整数では因数分解できない二次方程式がありますね
そういう場合は、「解の公式」というものに当てはめれば、解が出ます!

解の公式
ax2+bx+c = 0の解は
x = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\)
最初、憶えるのは大変ですが、憶えてしまえば安心ですね
今までの、「平方根を利用した求め方」や「因数分解を利用した求め方」
もカバーしているのですから
《 例 》
・ x2 = 36 → x =±\(\small{\sqrt{36}}\)
「平方根を利用した求め方」であっと言う間ですが、あえて「解の公式」で
→ x2-36 = 0 右辺は「因数分解を利用」同様「0」にします。式を、ax2+bx+c = 0 の形にする
→ x = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\) aとはx2の係数、bとはxの係数、cとは定数項
x = \(\large{\frac{-(0)±\sqrt{(0)^2-4・1・(-36)}}{2(1)}}\) a = 1, b = 0, c =-36 を当てはめた
→ x = \(\large{\frac{±\sqrt{4・36}}{2}}\) = \(\large{\frac{±2・6}{2}}\) =±6
A. x = ±6
・ (x+3)2 = 36 → x+3 =±\(\small{\sqrt{36}}\)
「平方根を利用した求め方」であっと言う間ですが、これも試しに
| → | x2+6x-27 = 0 … 「展開」「移項」で、ax2+bx+c = 0 の形に |
→ x = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\)
= \(\large{\frac{-6±\sqrt{36-4\ \cdot \ (-27)}}{2}}\)
= \(\large{\frac{-6±\sqrt{36+108}}{2}}\)
= \(\large{\frac{-6±\sqrt{144}}{2}}\)
= \(\large{\frac{-6±12}{2}}\)
= -3±6 A. x = -9, 3
・ x2+8x+15 = 0 →(x+3)(x+5) = 0
| → | 「因数分解を利用した求め方」であっと言う間ですが、これも試しに |
→ x = \(\large{\frac{-8±\sqrt{64-60}}{2}}\)
= \(\large{\frac{-8±\sqrt{4}}{2}}\)
= -4±1 A. x = -5, x = -3
→ 逆を言えば、きれいな解が出た時は、
因数分解 (x+5)(x+3) = 0 できていた ということですね
・ 4x2-4x-3 = 0 →(2x+1)(2x-3) = 0
| → | 「因数分解を利用した求め方」であっと言う間ですが、これも試しに |
→ x = \(\large{\frac{4±\sqrt{16-4・4・(-3)}}{8}}\)
= \(\large{\frac{4±\sqrt{16+48}}{8}}\)
= \(\large{\frac{4±\sqrt{64}}{8}}\)
= \(\large{\frac{4±8}{8}}\)
= \(\large{\frac{1±2}{2}}\) A. x = \(\large{\frac{3}{2}}\), -\(\large{\frac{1}{2}}\)
・ x2-4x+2 = 0 → -2×(-1)、-2+(-1) = -3・・・ウーン
| → | 明らかに「きれいに因数分解できない」ですね → √ が出ますね! |
→ 「解の公式」の本当の出番ですね!
→ x = \(\large{\frac{4±\sqrt{16-4・1・2}}{2}}\)
= \(\large{\frac{4±\sqrt{8}}{2}}\)
= \(\large{\frac{4±2\sqrt{2}}{2}}\)
= 2±\(\small{\sqrt{2}}\) A. x = 2±\(\small{\sqrt{2}}\)
・ 4x2+8x-5 = 0
| → | きれいに因数分解できそうなできなさそうな… → 解の公式! |
→ x = \(\large{\frac{-8±\sqrt{64-4・4・(-5)}}{8}}\)
= \(\large{\frac{-8±\sqrt{64+80}}{8}}\)
= \(\large{\frac{-8±\sqrt{144}}{8}}\)
= \(\large{\frac{-8±12}{8}}\)
= \(\large{\frac{-2±3}{2}}\) A. x = -\(\large{\frac{5}{2}}\),\(\large{\frac{1}{2}}\)
〈おまけ武器④〉平方完成利用
・平方完成とは
平方完成とは、
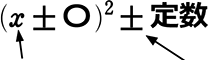
係数がない 見た目(展開しないと)、x1 の項がない
の形にすることですね
例えば
(x+1)2は展開すると、x2+2x+1ですね
逆に、x2+2x+1を因数分解すると (x+1)2ですね
では、x2+2xを因数分解すると、x(x+2)ですね
ですが「平方完成」は
おつりが出てもいいから (x±定数)2の形にしようというものです
おつりは 自由な数字で清算してOKです。
x2+2x = (x+1)2-1 ← -1がお釣り清算分 となります
確かに、(x+1)2-1を展開すると x2+2x+1-1 で帳尻が合っていますね!
「平方完成」の利用場面は、この後お話しする
| ・ | 「二次方程式を解く武器」であったり |
| ・ | 「解の公式の作り方」であったり、 |
| ・ | 高校数学では「二次関数の頂点の座標を求める場合」に必要となりますね |
ex)
y = x2+2x-3 のグラフの頂点を求めましょう(高校)
(平方完成すると)
y = (x+1)2-4
∴ 頂点(-1, -4)となります (一次関数の平行移動と同じ考え方ですね)
(因数分解すると)
y = (x-1)(x+3)
∴ x軸との交点は(1, 0) (-3, 0)となります
(x = 0 を代入すると)
y = (0)2+2(0)-3 = -3
∴ y軸との交点は(0,-3)となります
グラフにすると
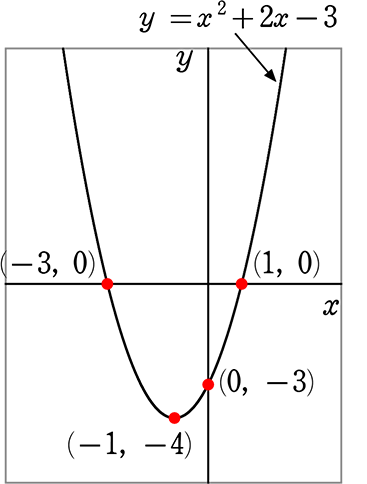
中学の二次関数は、必ず原点(0, 0)を通る「y = ax2」までですね!
それでは本題に戻りまして
平方完成 〔 (x±〇)2の形なのに帳尻があっている〕してみましょう

①「xの項の半分を用意」して、②「暗算で展開して、増えてしまったものを引いて帳尻合わせ」 ですね


では、「二次方程式の解法」に「平方完成」を利用してみましょう
《 例 》
4x2+8x-5 = 0 (上の問題と同じものです)
x2+2x-\(\large{\frac{5}{4}}\) = 0 x2の係数4で両辺を割った (x2の係数を「1」にした)
x2+2x = \(\large{\frac{5}{4}}\) 定数項は右辺に移項しておく
(x+1)2-1=\(\large{\frac{5}{4}}\) (x±数)2の形にして、そして数合わせ
ex) (x+1)2を展開すると、x2+2x+1←「+1」が元より増えてしまった部分
(x+1)2 = \(\large{\frac{5}{4}}\)+1 新たに発生した定数項「-1」も右辺に移項した
(x+1)2 = \(\large{\frac{9}{4}}\) 「平方完成」完成!(本来は(x+1)2-\(\large{\frac{9}{4}}\) = 0が完成形)
→ 「平方根の求め方利用」が使える形! (左辺丸々2乗 → 右辺丸々に±√)
x+1 = ±\(\small{\sqrt{\large{\frac{9}{4}}}}\)
x = ±\(\large{\frac{3}{2}}\)-1 √ の前出しと、移項
∴ x = -\(\large{\frac{5}{2}}\), x = \(\large{\frac{1}{2}}\)
《 例 》
x2-4x+2 = 0 (2つ前の問題 解に√ が残る問題でも試しますね)
(x-2)2-4 = -2 +2の移項、x2-4xの平方完成(-4が数合わせ)
(x-2)2 = 2 左辺丸々2乗の形に!
x-2 = ±\(\small{\sqrt{2}}\)
x = 2±\(\small{\sqrt{2}}\)
A. x = 2±\(\small{\sqrt{2}}\) ← 同じですね!
以上のように、4つの武器
「平方根の求め方を利用」「因数分解を利用」「解の公式」「平方完成利用」で
全ての 二次方程式の計算問題が解けますね!
「解の公式」は、「万能」ではありますが、「面倒」ですね
→ 最終手段的な方法といえますね
ex) 10mmのボルトは10mmのスパナで回したい、
万能なモンキーレンチはできれば使いたくない という感じでしょうか…
(女子にはわかりにくい例えですいません!)
おまけの〈武器④〉平方完成利用は、「解の公式」さえしっかり使うことができれば、不要となりますが、
絶対必須となりますのでマスターしてしまいましょうね!

解の公式の作り方
解の公式は、 ax2+bx+c = 0 の式を何とか x =(左辺がxだけ)の式にするということですね!
ですが
① x = にすると、右辺にx2が残る →
| ② | x(x±数字)にすると、最後xかxを含む項で両辺を割らなければならない → 「0」かもしれない未知数xで両辺を割ってはいけない→× |
| ③ | 左辺をx2だけにして、平方根の求め方利用したい→右辺にxが残っている → ×!ですがおしい! |
| ④ | 左辺を「丸々2乗」の形にして、平方根の求め方 → 〇!→「平方完成」の技が必要ということですね! |
もちろん今までの「移項」「等式の性質」も必要ですね
では
● ax2+bx+c = 0
▼ 3x2+5x+1 = 0
まずは「平方完成」の準備として
x2 の係数で両辺を割って
x2の係数を「1」にします
● x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{c}{a}}\) = 0
▼ x2+\(\large{\frac{5}{3}}\)x+\(\large{\frac{1}{3}}\) = 0
定数項はどんどん右辺に移項します
● x2+\(\large{\frac{b}{a}}\)x = -\(\large{\frac{c}{a}}\)
▼ x2+\(\large{\frac{5}{3}}\)x = -\(\large{\frac{1}{3}}\)
左辺を「平方完成」します
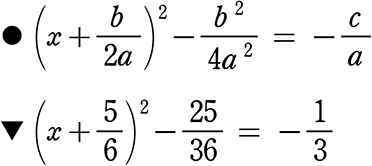
新たにできた定数項も右辺に
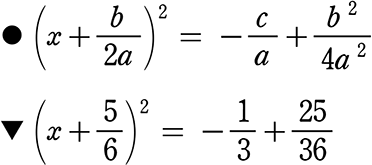
右辺を通分、計算しておきますか
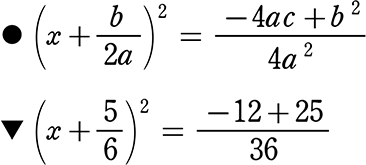
左辺丸々2乗の形になったので、
右辺丸々に±√ を付けます
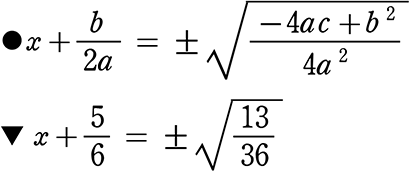
右辺の√ の前出し
● x+\(\large{\frac{b}{2a}}\) = \(\large{\frac{±\sqrt{b^2-4ac}}{2a}}\)
▼ x+\(\large{\frac{5}{6}}\) = \(\large{\frac{±\sqrt{13}}{6}}\)
左辺の残りの定数項も移行します
● x = \(\large{\frac{±\sqrt{b^2-4ac}}{2a}}\)-\(\large{\frac{b}{2a}}\)
▼ x=\(\large{\frac{±\sqrt{13}}{6}}\)-\(\large{\frac{5}{6}}\)
整理計算
● x = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\) //
▼ x = \(\large{\frac{-5±\sqrt{13}}{6}}\) //
「平方完成」を使わない方法として
x2+\(\large{\frac{b}{a}}\)x = -\(\large{\frac{c}{a}}\) や
x2+\(\large{\frac{5}{3}}\)x = -\(\large{\frac{1}{3}}\) の段階で、次に「平方完成」という時に
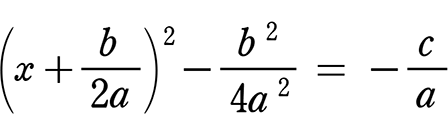
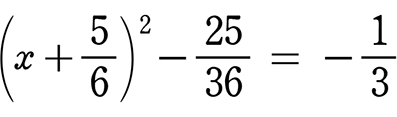 とせずに
とせずに
x の係数の「半分を2乗したもの」をあらかじめ両辺に足す という方法もありますね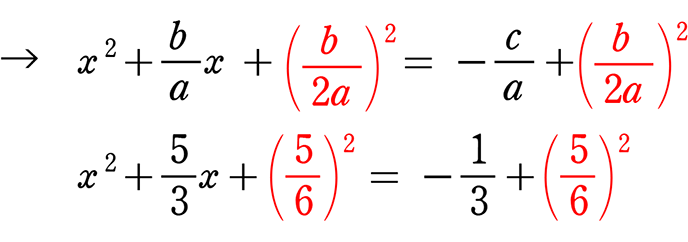
→ x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{b^2}{4a^2}}\) = -\(\large{\frac{c}{a}}\)+\(\large{\frac{b^2}{4a^2}}\)
x2+\(\large{\frac{5}{3}}\)x+\(\large{\frac{25}{36}}\) = -\(\large{\frac{1}{3}}\)+\(\large{\frac{25}{36}}\)
→ 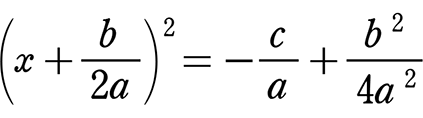 (左辺はただの因数分解という意味に)
(左辺はただの因数分解という意味に)
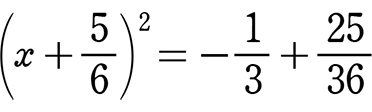 (左辺はただの因数分解という意味に)
(左辺はただの因数分解という意味に)
・
・
・
このようにもできますが、これはただの「平方完成」の先取りというだけで
考え方はほとんど「平方完成利用」と同じですね!
→ 店員さん「502円です」
と言われて、1000円を出して
店員さん「498円のおつりです」と言った瞬間に
「あっ!2円あります」とするのか
店員さん「502円です」
と言われて、あらかじめ
1002円出して500円のおつりをいただくのか
の違いですね
① 判別式D
判別式は、二次方程式ax2+bx+c = 0 の解が
① 2個 なのか
② 1個 なのか(重解)
③ 解なし
なのかを
リトマス紙のようなものでしょうか
ax2+bx+c = 0 において
判別式 D = b2-4ac
・b2-4ac>0 のとき 解は「2つ」
・b2-4ac = 0 のとき 解は「1つ」
・b2-4ac<0 のとき 解は「なし」
D:discriminant:判別
「b2-4ac 」…どこかで見ましたね
x = \(\large{\frac{-b±\sqrt{\color{red}{ b^2-4ac}}}{2a}}\)
解の公式の√部分の中身ですね
これで判別式Dの仕組みがわかりますね
| → | b2-4ac が「プラス」なら、√ の前の±が生きるので → 解が2つですね |
| → | b2-4ac が「0」なら、√ の前の±の意味がなくなるので → 解が1つですね |
| → | b2-4ac が「マイナス」なら、√ の中がマイナス!→ そんな実数はない →解なしですね |
《 例 》
解の個数を調べましょう
・3x2+4x+1 = 0
D = b2-4ac = 16-4・3・1 = 4 >0 ∴ 2つ
・2x2-7x-5 = 0
D = 49-4・2・(-5) = 89 >0 ∴ 2つ
・4x2+12x+9 = 0
D = 144-4・4・9 = 0 ∴ 1つ
・x2+4x+5 = 0
D = 16-4・1・5 = -4 <0 ∴ 解なし
《 例 1》
方程式x2+2ax+4 = 0 がただ一つの解を持つとき、
aの値を求めましょう
→ 「ただ一つの解」 → 判別式D = 0 のとき
D = b2-4ac = (2a)2-4・1・4 = 4a2-16
→ 4a2-16 が 0 のとき重解!
→ a2-4 = 0
→ (a-2)(a+2) = 0
A. a = -2, a = 2
《 例 2》
方程式 3x2-4x-a = 0 がただ一つの解を持つとき、
aの値を求めましょう
→ 「ただ一つの解」 → 判別式D = 0 のとき
D = (-4)2-4・3・(-a) = 16+12a
→ 16+12a = 0 のとき重解 → a =-\(\large{\frac{4}{3}}\)
〈簡略版判別式D/4〉
ax2+(偶数b)x+c = 0 の場合
D = b2-4acより少し楽な「判別式\(\large{\frac{D}{4}}\)」が使えますね
判別式 D/4 = (\(\large{\frac{b}{2}}\))2-ac
簡単に言うと
偶数bなら
D/4 = (半b)2-ac
使えると少し早く少し楽ですが、 D = b2-4ac だけでも十分といえます
《 例 》 解の個数を調べましょう
・ 3x2+4x+1 = 0
D/4 = (4の半分)2-ac = (2)2-3・1 = 1 >0 ∴ 2つ
・4x2+12x+9
D/4 = (6)2-4・9 = 36-36 = 0 ∴ 1つ
《 例 1’》 《 例 1》と同じ問題です
方程式x2+2ax+4 = 0 がただ一つの解を持つとき、aの値を求めましょう
D/4 = (bの半分の)2-ac = a2-1・4 = a2-4 = (a+2)(a-2) が0のとき重解
→ (a+2)(a-2) = 0
A. a = -2, a = 2 ←同じですね

D/4 が成り立つ理由 (簡易版 解の公式)
なぜ、D/4が成り立つのでしょうか?
| → | 偶数b のときで、解の公式をつくってみればわかりますね! |
| → | 偶数b ということは、式は |
ax2+2bx+c=0 の時ですね。では
ax2+(2b)x+c = 0 (平方完成の準備として
x2+\(\large{\frac{(2b)}{a}}\)x+\(\large{\frac{c}{a}}\) = 0 x2の係数を1にした)
x2+\(\large{\frac{(2b)}{a}}\)x = -\(\large{\frac{c}{a}}\) (定数項はどんどん右辺に移項)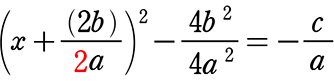 (平方完成した)
(平方完成した)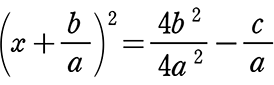 (約分+定数項の移項)
(約分+定数項の移項)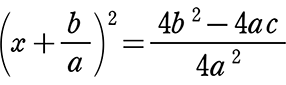 (右辺を通分しておいた)
(右辺を通分しておいた)
x+\(\large{\frac{b}{a}}\) = ±\(\small{\sqrt{\large{\frac{4b^2-4ac}{4a^2}}}}\) (左辺丸々2乗の形→右辺丸々に±√)
x = -\(\large{\frac{b}{a}}\)±\(\small{\sqrt{\large{\frac{4b^2-4ac}{4a^2}}}}\) (定数項は移項)
x = -\(\large{\frac{b}{a}}\)±\(\small{\sqrt{\large{\frac{4(b^2-ac)}{4a^2}}}}\) (このあたりが
x = -\(\large{\frac{b}{a}}\)±\(\small{\sqrt{\large{\frac{b^2-ac}{a^2}}}}\) D/4の名前の由来でしょうか)
x = -\(\large{\frac{b}{a}}\)±\(\large{\frac{\sqrt{b^2-ac}}{a}}\) (√の前出し)
x = \(\large{\frac{-b±\sqrt{b^2-ac}}{a}}\) (簡易版 解の公式 完成)
→ 2bで出発したのにb になっていますね
通常版と区別するために
x = \(\large{\frac{-b\color{red}{′ }±\sqrt{b\color{red}{′ \ }^2-ac}}{a}}\) としたりしますが
x = \(\large{\frac{-(半b)±\sqrt{(半b)^2-ac}}{a}}\) で十分ですね
というわけで、
簡易版判別式 D/4=(半b)2-ac も成り立ちますね
まとめ
| 通常版 | 簡易版 (偶数b のとき) |
||
| 解の公式 | x=\(\boldsymbol{\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}}\) | ⇒ | x=\(\boldsymbol{\large{\frac{-(半b)±\sqrt{(半b)^2-ac}}{a}}}\)
(数字がなくなった) |
| 判別式 | D=b2-4ac | ⇒ | D/4=(半b)2-ac |
ですが、まずは通常版を完璧に身につける!ですね
《 例 》
5x2-6x-18=0 について
① 解の公式(通常版)で解きましょう
x = \(\large{\frac{-(-6)±\sqrt{(-6)^2-4(5)(-18)}}{2(5)}}\)
= \(\large{\frac{6±\sqrt{36+360}}{10}}\)
= \(\large{\frac{6±\sqrt{396}}{10}}\)
= \(\large{\frac{6±\sqrt{9\ \cdot \ 4\ \cdot \ 11}}{10}}\)
= \(\large{\frac{6±6\sqrt{11}}{10}}\)
= \(\large{\frac{3±3\sqrt{11}}{5}}\)
② 簡易版で解きましょう (5x2-6x-18=0)
x = \(\large{\frac{-(-3)±\sqrt{(-3)^2-(5)(-18)}}{5}}\)
= \(\large{\frac{3±\sqrt{9+90}}{5}}\)
= \(\large{\frac{3±\sqrt{99}}{5}}\)
= \(\large{\frac{3±\sqrt{9\ \cdot \ 11}}{5}}\)
= \(\large{\frac{3±3\sqrt{11}}{5}}\)
| ③ | 解は何個でしょうか (①②から解は2つと分かりますが確認のため) |
(5x2-6x-18=0)
D = (-6)2-4(5)(-18)
= 36+360
= 396 >0 ∴ 2個
④ 簡易版で何個でしょうか (5x2-6x-18=0)
D/4 = (-3)2-(5)(-18)
= 9+90
= 99 >0 ∴ 2個 (396の\(\large{\frac{1}{4}}\)になっている)
《 例 》
x2+3x-18=0 を簡易版で解きましょう
→ もちろん 奇数b にも対応していますが…
x = \(\large{\frac{-(1.5)±\sqrt{(1.5)^2-(1)(-18)}}{1}}\)
= -1.5±\(\small{\sqrt{2.25+18}}\)
= -1.5±\(\small{\sqrt{20.25}}\)
= -1.5±4.5
= -6, 3
| → | △.5の2乗や、小数(分数)の「前出し」を考えさせられる |
| ⇒ | 使い勝手が悪いですね → それなら通常版! |
② 解と係数の関係
x2+bx+c = 0 の2つの解が α、β であるならば、
x2+bx+c = 0 は (x-α)(x-β) = 0 と因数分解できる といえるはずですね
(x-α)(x-β) = 0 を展開すると
x2-(α+β)x+αβ = 0 = x2+bx+c
…ということは、それぞれの係数を対応させると
| -(α+β)=b → α+β=-b → 「2つの解を足したものは-b」 |
・αβ=c → 「2つの解を掛けたものはc」
実際の数字で確認すると
x2+5x+6 → (x+3)(x+2) = 0 → α = -3、β = -2
| ・ | α+β = -3+(-2) = -5 = 確かに「-b」 ですね |
| ・ | αβ = -3×(-2) = 6 = 確かに「c」 ですね |
当たり前と言えば当たり前ですね
《 例 》
・x2+3x-2 = 0 の解を α、βとするとき、 α+β、 αβの値を求めましょう
A. α+β = -3、 αβ = -2
→ 因数分解をして、解を求める作業が不要ですね!
・x2+5x+3 = 0 の解を α、βとするとき、 α+β、αβの値を求めましょう
A. α+β = -5、 αβ = 3
せっかくですので、もう少し、全部をカバーさせますね
(↓x2の前にaがある)
ax2+bx+c = 0 は両辺をaで割って → x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{c}{a}}\) = 0 とできますね
x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{c}{a}}\) = 0 の2つの解が α、β であるならば、
x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{c}{a}}\) = 0 は (x-α)(x-β) = 0 と因数分解できることになりますね
(x-α)(x-β) = 0 を展開すると
x2-(α+β)x+αβ = 0 = x2+\(\large{\frac{b}{a}}\)x+\(\large{\frac{c}{a}}\)
ということは、それぞれの係数を対応させると
| ・ | -(α+β)=\(\large{\frac{b}{a}}\) → α+β=-\(\large{\frac{b}{a}}\) →「2つの解を足したものは -\(\large{\frac{b}{a}}\) |
・αβ=\(\large{\frac{c}{a}}\) →「2つの解を掛けたものは \(\large{\frac{c}{a}}\)」
これでx2 の係数が「1」でなくてもOK、全てをカバーしていますね!
上のx2(1x2)の、
α+β = -b は -\(\large{\frac{b}{a}}\) = -\(\large{\frac{b}{1}}\) = -bだったのですね!
αβ = c は \(\large{\frac{c}{a}}\) = \(\large{\frac{c}{1}}\) = c だったのですね!

解と係数の関係
x2+bx+c = 0 の2つの解を α、β とすると
・ α+β = -b
・ αβ = c
ax2+bx+c = 0 の2つの解を α、β とすると
・ α+β = -\(\large{\frac{b}{a}}\)
・ αβ = \(\large{\frac{c}{a}}\)
( 上に、\(\large{\frac{}{a}}\) をつけただけ)
《 例 》
| ・ | 3x2-8x+5 = 0 の解を α、βとするとき、 α+β、 αβの値を求めましょう |
α+β = -\(\large{\frac{b}{a}}\) = \(\large{\frac{8}{3}}\)
αβ = \(\large{\frac{c}{a}}\) = \(\large{\frac{5}{3}}\)
| ・ | 3x2+5x+1 = 0 の解を α、βとするとき、 α+β、 αβの値を求めましょう |
α+β = -\(\large{\frac{b}{a}}\) = -\(\large{\frac{5}{3}}\)
αβ = \(\large{\frac{c}{a}}\) = \(\large{\frac{1}{3}}\)
《 例 》
3x2+5x+1 = 0 の解を α、βとするとき、以下の値を求めましょう
(1) α2+β2
| → | この手の問題は、まず α+β、 αβを求めておきましょうね |
α+β = -\(\large{\frac{5}{3}}\)、 αβ = \(\large{\frac{1}{3}}\)
| → | α2+β2 =(α+β)2-2αβ と変形できますね |
∴ (-\(\large{\frac{5}{3}}\))2-2(\(\large{\frac{1}{3}}\)) =\(\large{\frac{25}{9}}\)-\(\large{\frac{2}{3}}\) = \(\large{\frac{25-6}{9}}\)=\(\large{\frac{19}{9}}\)
(2) α3+β3
| → | 工夫してみると
α3+β3 = (α+β)(α2+β2)-αβ2-βα2 |
→ あとは今まで求めたα+β, αβ, α2+β2の値を代入するだけ
∴ (α+β)(α2+β2)-αβ(α+β) = (-\(\large{\frac{5}{3}}\))(\(\large{\frac{19}{9}}\))-(\(\large{\frac{1}{3}}\))(-\(\large{\frac{5}{3}}\))
=-\(\large{\frac{95}{27}}\)+\(\large{\frac{5}{9}}\) = \(\large{\frac{-95+15}{27}}\)
=-\(\large{\frac{80}{27}}\)
この手の問題は、どうすれば、α+β、αβ、で構成された式に変形できるのかがミソ(展開したり(α+β)2の形にしてみたり)ですね
もちろん 3x2+5x+1 = 0 の2つの解を実際に求めて、
代入ミチミチ計算でも同じ値が出るはずですが…ちょっと…いやすぎですね
③ 応用計算問題
《 例 》
方程式 3x2-(2a-5)x-3a-1 = 0の解の1つが2であるとき、
aの値と、もう一つの解を求めましょう
| → | xに1つ目の解「2」を代入すれば、与式はaしか残らないのがわかりますね |
→ aがわかるはず
3(2)2-(2a-5)(2)-3a-1 = 0
12-4a+10-3a-1 = 0
-7a = -21
∴ a = 3
| → | 与式にa = 3 を代入すれば → ただの二次方程式 |
→ もう一つの解がわかるはず
3x2-〔2(3)-5〕x-3(3)-1 = 0
3x2-x-10 = 0 ←たすき掛けが厳しいなら、解の公式で
(3x+5)(x-2) = 0
∴ x = -\(\large{\frac{5}{3}}\) ←新たに判明した解
x = 2 ←問題文からすでに分かっていた解
A. a = 3 , x =-\(\large{\frac{5}{3}}\)
《 例 》
方程式ax(x+1)+b(x+1)(x+2)+c(x+2)(x+3) = 0 の解が「0」と「1」のとき、a:b:c を求めましょう
| → | よくわからないので、解っている値をどんどん代入してみる |
・与式のxに0を代入してみると
0+2b+6c = 0 → b+3c = 0 → 1b = -3c …①
∴ b:c = \(\large{\frac{1}{1}}\):-\(\large{\frac{1}{3}}\) = 3:-1 …(1)
( =で繋がった式を、比にする)
→ あとは、a:b (a、bだけの式) か a:c(a、cだけの式) がわかれば a:b:c とつながるな
・与式のxにもう一つの解「1」を代入してみると
2a+6b+12c = 0 → a+3b+6c = 0 …②
→ ②に①を代入すれば、②はaとcだけの式になるな
a+3(-3c)+6c = 0 → a-3c = 0 → a = 3c
∴ a:c = \(\large{\frac{1}{1}}\):\(\large{\frac{1}{3}}\) = 3:1…(2)
→ (1)と(2)をつなげるには
どちらにも使われているcの数字を合わす ですね
b:c = 3:-1
c:a = 1:3 = -1:-3
∴ b:c:a = 3:-1:-3
A. a:b:c = -3:3:-1 (または3:-3:1)
《 例 》
方程式x2+ax+b = 0 の解が x = 5しか持たない(重解)とき、a、bの値を求めましょう
| → | 解が2つなら → (x+1)(x+2) = 0 のような形 |
→ 解が1つ → (x+1)2 のような形 ですね
よって、x = 5 なので、 (x-5)2 = 0 の形ですね
これを展開すると、 x2-10x+25 = 0
係数を対応させて
A. a = -10、 b = 25
《 例 》
方程式x2-6x+a = 0 の解が1つしかない(重解)とき、a の値を求めましょう
→ 平方完成すれば、 (x+1)2 = 0 のような形になるはずですね
(x-3)2-9+a = 0
(x-3)2 = -a+9
→ この右辺の「-a+9」 が「0」になればよいということですね
-a+9 = 0 → a = 9 A. a = 9
(別解)
判別式D/4 = (半b)2-ac = 0の時、重解ですね
→ (-3)2-1・a = 0 → 9-a = 0 A. a = 9
《 例 》
方程式x2-ax+12 = 0 が正の整数解をもつとき、 aの値を全て求めましょう
→ 「正」の「整数解」になるような因数分解の形は
(x-整数)(x-整数) = 0 のような形
cf) (x+整数)(x+整数) = 0 は「負」の「整数解」ですね
→ 掛けて「12」になるような2数は…
① (x-1)(x-12) = 0 → x2-13x+12
② (x-2)(x-6) = 0 → x2-8x+12
③ (x-3)(x-4) = 0 → x2-7x+12
係数を対応させて… A, a = 7, 8, 13
《 例 》
方程式x2-a2x+138 = 0 の2つの解が、ともに正の整数になるような正の整数a の値を求めましょう
→ ① (x-2)(x-69) = 0 → x2-71x+138 = 0
→ ② (x-3)(x-46) = 0 → x2-49x+138 = 0
→ ③ (x-6)(x-23) = 0 → x2-29x+138 = 0
↑23は素数なのでここまで
a2 = 71 → a = ±\(\small{\sqrt{71}}\)
a2 = 49 → a = ±7
a2 = 29 → a = ±\(\small{\sqrt{29}}\)
→ aは正の整数(という条件)より A. a = 7
〔 式の値 〕
《 例 》
2次方程式 x2+2x-2=0 の負の解をa とするとき、2a2-3a+1 の値を求めよ
・ x=\(\large{\frac{-2±\sqrt{4+8}}{2}}\) =\(\large{\frac{-2±\sqrt{4\ \cdot \ 3}}{2}}\) =-1±\(\small{\sqrt{3}}\)
∴ 負の解a は、-1-\(\small{\sqrt{3}}\)
→ この後の代入作業がいつも嫌になりますね → 何かいい方法はないかな…
(方法① α+β, αβ の利用(解と係数の関係))
今回の問題では使えませんね ← α+β, αβの型に変形できない。解も1つしか使わない。
(方法② 「=0」の利用)
例えば、x2+2x-2=0 の解が 1なら、1を代入すれば左辺は0になるということ、 解が2なら、2を代入すれば左辺が0になるということ、 解がa なら、a を代入すれば左辺は0になるということ、
→ そして、解a を代入した瞬間の形 a2+2a-2=0 これを利用したい!
→ 2a2-3a+1
=a2+a2+2a+2a-7a-2-2+5
=a2+2a-2+a2+2a-2-7a+5 ←強引に a2+2a-2=0 が利用できるように変形した
=0+0-7a+5 =-7a+5
∴ これにaの値を代入して、 -7(-1-\(\small{\sqrt{3}}\))+5 =7+7\(\small{\sqrt{3}}\)+5 =12+7\(\small{\sqrt{3}}\)
(方法③ 次数減らし)
②同様、解がa を代入すれば左辺は0になるということ、
→ そして、解a を代入した瞬間の形→ a2+2a-2=0 → a2=-2a+2 → a2 =(実は) -2a+2
∴ 2a2-3a+1
=2(-2a+2)-3a+1
=-4a+4-3a+1
=-7a+5 ←2次式を1次にできた
∴ -7(-1-\(\small{\sqrt{3}}\))+5 = 7+7\(\small{\sqrt{3}}\)+5 = 12+7\(\small{\sqrt{3}}\)
(方法④ せめて因数分解)
2a2-3a+1 =(2a )(a ) =(2a-1)(a-1)
∴ {2(-1-\(\small{\sqrt{3}}\))-1}{(-1-\(\small{\sqrt{3}}\))-1}
=(-2-2\(\small{\sqrt{3}}\)-1)(-2-\(\small{\sqrt{3}}\))
=(-3-2\(\small{\sqrt{3}}\))(-2-\(\small{\sqrt{3}}\))
=(3+2\(\small{\sqrt{3}}\))(2+\(\small{\sqrt{3}}\))
=6+3\(\small{\sqrt{3}}\)+4\(\small{\sqrt{3}}\)+6
=12+7\(\small{\sqrt{3}}\) ←今回はそんなに楽にならなかった
(方法⑤ 最悪でも直接代入がありますね)
2a2-3a+1
=2(-1-\(\small{\sqrt{3}}\))2-3(-1-\(\small{\sqrt{3}}\))+1
=2(1+2\(\small{\sqrt{3}}\)+3)+3+3\(\small{\sqrt{3}}\)+1
=8+4\(\small{\sqrt{3}}\)+3\(\small{\sqrt{3}}\)+4
=12+7\(\small{\sqrt{3}}\)
エ 二次方程式の活用
二次方程式を利用する具体的な問題ですね
→ 正確には「利用」というより、式を立ててみて、xを求めるべく計算していたら2乗の形が発生した → 結果、二次方程式の文章問題だった。ということですね
→ 問題を読んだ時に、これは1次方程式の問題なのか、連立方程式の問題なのか、2次方程式の問題なのかを分かる必要はないですね → ただ文章を数字と文字で表してみた → 結果、~方程式の問題だった
整数
《 例 》
連続する3つの整数があります。最小の数の平方の3倍は 最大の数の3倍から
中央の数の平方の2倍を引いたものに等しいとき、3つの整数を求めましょう
| → | 連続する3つの整数を、 n, n+1, n+2 とおく (n-1, n, n+1)でも何でも可) |
→ 文章を式にすると
3n2 = 3(n+2)-2(n+1)2 あとはn について解くだけですね
3n2 = 3n+6-2n2-4n-2
5n2+n-4 = 0
(5n-4)(n+1) = 0
∴ n = \(\large{\frac{4}{5}}\), -1
3つの数は整数より、n = -1 条件に合わない解は、ばっさり切ってOKです
n = -1を n, n+1, n+2 に代入して A. -1, 0, 1
図形
《 例 》
縦が横より5cm長い長方形があります。縦の長さを3cm短くして、
横の長さを 2倍すると、元の長方形より面積が20cm2 増加しました
元の長方形の縦と横の長さを求めましょう
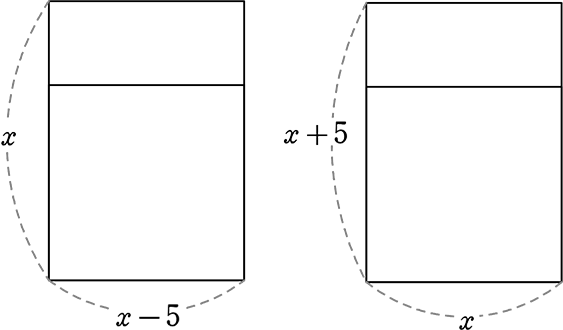
どちらでもOKです 右図でいきますね
(新しい長方形)-(元の正方形) = 20cm2
→ 元の長方形の横をxとする
・新しい長方形の面積 = (x+5-3)・2x = (x+2)・2x = 2x2+4x
・元の長方形の面積 = (x+5)・x = x2+5x
→ 2x2+4x-(x2+5x) =20
x2-x-20 = 0
(x-5)(x+4) = 0 ∴ x = -4, 5
x>0 より ←図形の長さにマイナスはない
x = 5 A. 縦10cm 横5cm
cf問題) これは何%増加したということでしょうか?
\(\large{\frac{長方形の面積}{元の正方形の面積}}\) = \(\large{\frac{50}{25}}\) = 2 →200%増(2倍)
割合
《 例 》
商品Aはx%値上げをすると、売り上げ個数が\(\large{\frac{1}{3}}\)%減少します
売り上げ金額を12%増やすには 何%値上げすればよいでしょうか (x<100)
(値段問題の考え方)
| → | 変動幅しかないので計算できませんね
|
→ 合計金額 = 1個の金額×合計個数 = ab円
(イメージ)
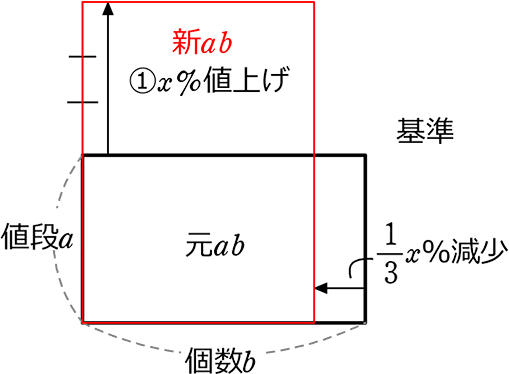
これで面積のように
考えることができますね
→ 新ab- 元ab =1.12 ではダメですね! 右辺が「割合」ですので
→ \(\large{\frac{新ab}{元ab}}\) = 1.12 ですね!
または、新ab = 1.12(元ab)
・新ab = a(1+x)×b(1-\(\large{\frac{x}{3}}\))
・元ab = そのままab
方程式は、 \(\large{\frac{a(1+x)×b(1-\large{\frac{x}{3}})}{ab}}\) = 1.12
(または、元を1.12倍すれば新より
1.12ab=\(\large{\frac{a(1+x)×b(1-\large{\frac{x}{3}})}{ab}}\))
(1+x)(1-\(\large{\frac{x}{3}}\)) = 1.12 約分をした
(1+x)(3-x) = 3.36 両辺×3
3-x+3x-x2 = 3.36 左辺展開
x2-2x = -0.36 両辺×-1、 移項
(x-1)2 = 1-0.36 = 0.64 平方完成
x-1 = ±\(\small{\sqrt{0.64}}\) = ±0.8
x = 1±0.8
∴ x = 1.8, x = 0.2 → x = 180, 20(%)
x<100 より x = 20
A. 20%値上げすればよい (個数は\(\large{\frac{20}{3}}\)%減)
| ・ | 答を書く前に、
過去の○○をxにしたのか、未来の○○をxにしたのか再度確認ですね |
| ・ | 売り上げ個数 → 合計個数
売り上げ金額 → 合計金額 |
《 例 》
AB間の距離は20km、s君はAからBへ、t君はBからAへ、同時に出発しました
2人がすれ違ってからt君は1時間20分後にAに着きました
s君の速度が4km/時のとき、出発からすれ違うまでの時間を求めましょう
→ まずは図ですね
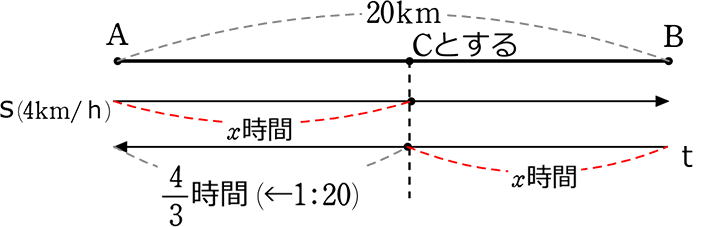
・全体が解っているのは距離20kmですから
→ 理想は 距離AC+距離CB = 20km でしょうか
・すれ違うまでの時間(SがCに着くまでの時間)をxとしてみますね
→ 距離AC = Sの速さ×時間x = 4x
・ACの距離が解ったので(4x)、tの速さが解りますね
→ tの速さ = 距離AC÷t のCA間の時間 = \(\large{\frac{4x}{\large{\frac{4}{3}}}}\) =\(\large{\frac{12x}{4}}\) = 3x
⇒ 距離BC = tの速さ×時間x = 3x×x = 3x2
∴ AC+BC = 4x+3x2 = 20
3x2+4x-20 = 0
(3x+10)(x-2) = 0
∴ x = -\(\large{\frac{10}{3}}\), 2
x>0より (時間はプラス) x = 2
A. 2時間
落下
《 例 》
井戸に石を落とすと、2秒後に水音がしました。井戸の深さを求めましょう
石はx秒後に5x2m落ちるとし、音の速さは340m/秒秒とします
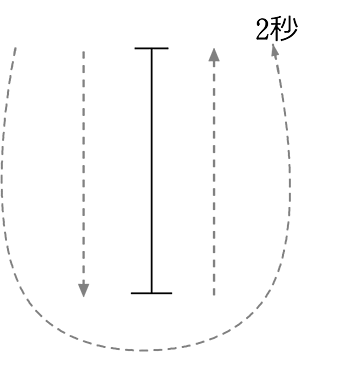
→ 「石」が水面に着いたとたんに、
「石」が「音」に変身して戻ってくる
イメージ
または、
石自体が急激にスピードupするイメージ
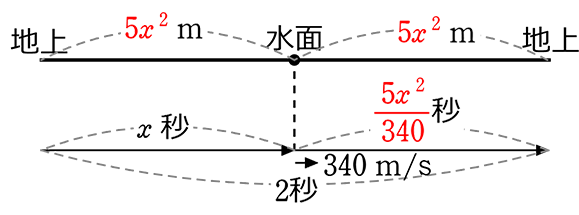
時間+時間 = 2秒 が理想でしょうか
→ ex. 水面までの時間が2秒なら → 距離は5(2)2=20mだ
水面までの時間が3秒なら → 距離は5(3)2=45mだ
水面までの時間がx秒なら → 距離は5(x)2=5x2mだ
←(問題文の5x2 は「距離」です「速さ」ではありません)
・水面までの時間 = x秒 (往路)
・戻る時間 = 距離÷速さ = \(\large{\frac{5x^2}{340}}\) 秒 (復路)
∴ x+\(\large{\frac{5x^2}{340}}\) = 2
5x2+340x-680 = 0
x2+68x-136 = 0
x = \(\large{\frac{-68±\sqrt{4624-4・(-136)}}{2}}\)
= -68±\(\large{\frac{\sqrt{5168}}{2}}\)
= \(\large{\frac{-68±4\sqrt{323}}{2}}\)
= -34±2\(\small{\sqrt{323}}\)
x>0 より(時間はプラス) x = -34+2\(\small{\sqrt{323}}\) 秒
∴ 水面までの距離 は… 5x2に-34+2\(\small{\sqrt{323}}\)を代入して
→ 5(-34+2\(\small{\sqrt{323}}\))2
= 5(1156-136\(\small{\sqrt{323}}\)+1292)
= 5(2448-136\(\small{\sqrt{323}}\))
= 680(18-\(\small{\sqrt{323}}\))
A. 680(18-\(\small{\sqrt{323}}\)) m
食塩水
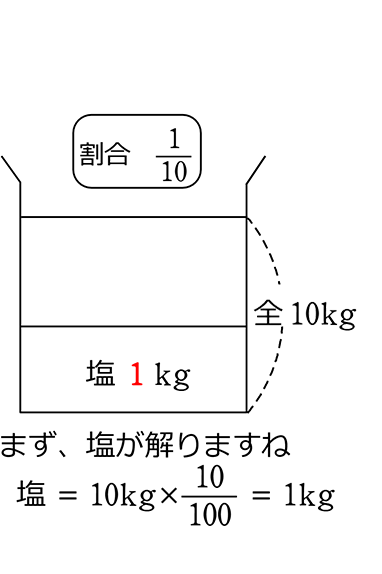
《 例 》
10%の食塩水10kgから、いくらかをくみ出し、それと同量の「水」を足し、
さらに最初にくみ出した量の2倍をくみ出し、それと同量の「水」を足すと
7.2%になりました。最初にくみ出した水は何kgでしょう
移り変わりを略図で表すと (食塩水問題の考え方)
→ 1つ前と変わらないものを青
→ 1つ前と変わるものを赤にしますね
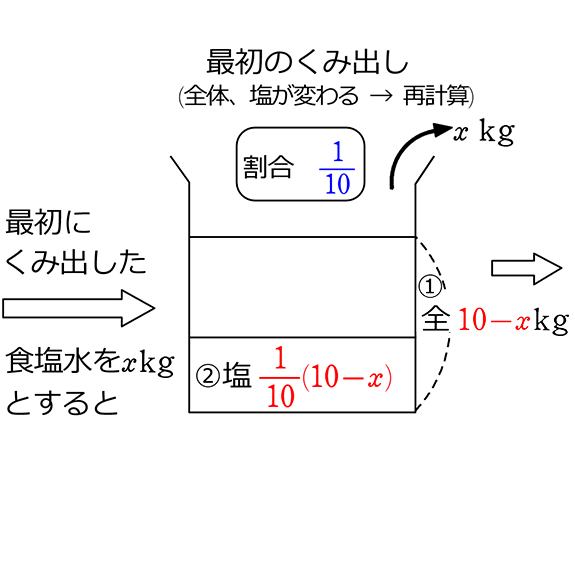
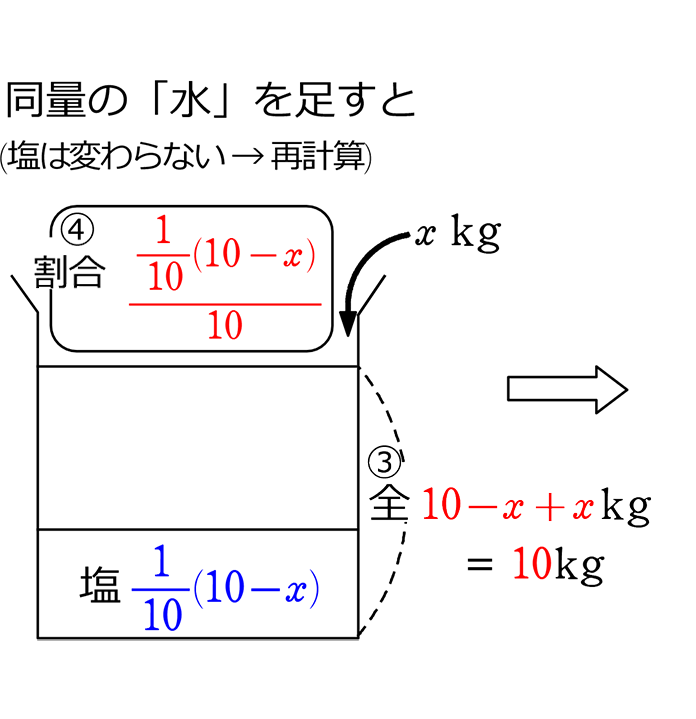
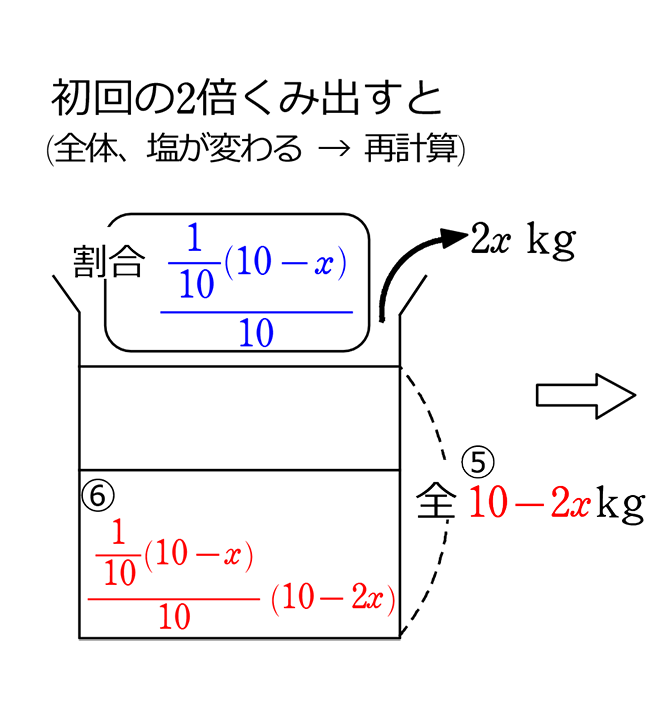
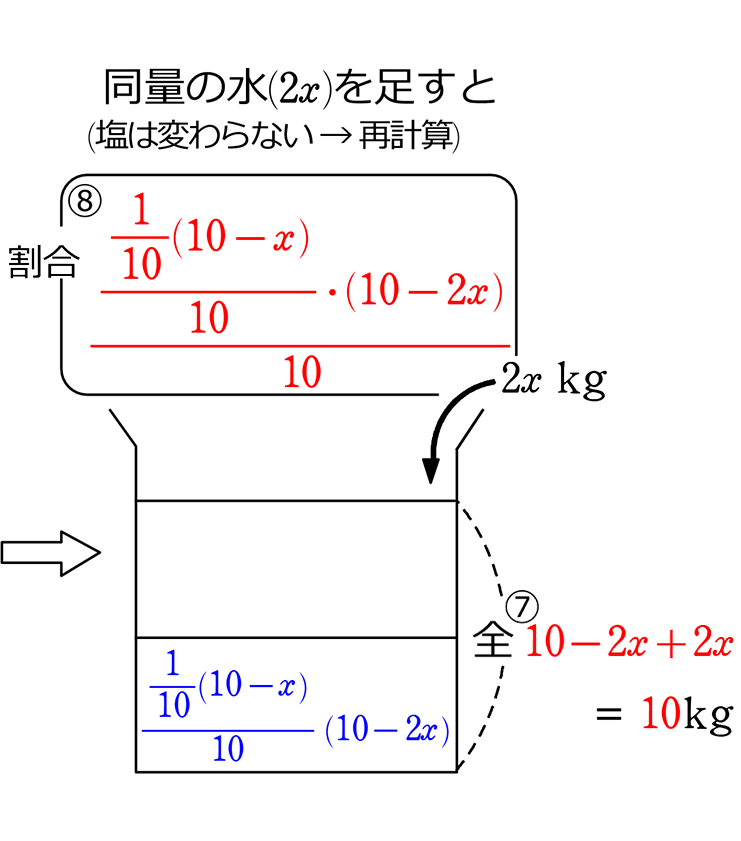
最後の割合が7.2%と言っていますね
最後の割合=\(\large{\frac{7.2}{100}}\)
→ \(\large{\frac{\large{\frac{\large{\frac{1}{10}}(10-x)}{10}}\ \cdot \ (10-2x)}{10}}\)=\(\large{\frac{7.2}{100}}\) これを解くと
(10-x)(10-2x)=72 両辺×1000
100-30x-2x2-72=0 展開、移項
x2-15x+14=0 両辺÷(-2)、整理
(x-14)(x-1)=0 因数分解
∴ x=1, 14
0<x<5 より 2xkgの汲み出しは 0kg~10kgでしかできない 0<2x<10 → 0<x<5
A. 1kg
今回は塩や割合を
何を何で割ったか、かけたか、を分かりやすいように、
そのままの値で行いましたが
普段はその都度簡単な形にしてOKですね
\(\large{\frac{\large{\frac{1}{10}}(10-x)}{10}}\) → \(\large{\frac{1}{100}}\)(10-x) など
方程式の文章問題は
| ・ | 図を書いて、イメージですね |
| ・ | 順を追ってつぶしていく (いきなり最終式が出ることは少ないですね) |
| ・ | 文字が入って複雑な項も、惑わされずにこれは「距離」、これは「塩」、これは「割合」など思い込む (信じる!) ですね |
その他の問題は、「問題集」で!!















