| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 関数 |
| ア | 事象と関数 y=ax2 |
|---|---|
| イ | 関数 y=ax2の特徴 |
| ・ | 各部名称 |
| ・ | y=ax 2 のグラフ |
| ・ | 実は全ての放物線は相似 |
| ・ | 比例定数 a |
| ① | 変域 |
| ② | 変化の割合 |
| ③ | 一次関数との交点 |
| ・ | 関数の原型 |
| ④ | 一次関数との接点 |
| ウ | 関数 y=ax2を用いた具体的な事象の説明 |
| ① | 具体的な事象 |
| ・ | 「加速・減速」の放物線 |
| ・ | 停止距離 |
| ・ | 「風圧」の放物線 |
| ・ | パスカルとは |
| ・ | 空気抵抗とは |
| ・ | 「ふりこの紐」の長さの放物線 |
| ・ | 「ダイヤモンドの価格」の放物線 |
| ・ | 世界最大のダイヤ原石は3106ctだった |
| ・ | 「動く点がつくる面積」の放物線 |
| ・ | 「動く図形がつくる面積」の放物線 |
| ② | グラフ操作問題 |
| ・ | 相似と放物線 |
| ・ | 正方形と放物線 |
| ・ | 正三角形と放物線 |
| ・ | 平行四辺形と放物線 |
| ・ | 面積と放物線 |
| ・ | (座標上の2点間の距離) |
| エ | いろいろな事象と関数 |
| ・ | 円運動の関数 |
| ・ | 段階料金の関数 |
関数
ア 事象と関数 y=ax2
関数とは、x の値が決まれば、y の値が「ただ1つ決まる」
1年では、『比例』を学びましたね ← 原点(0, 0)を通る一次関数
・基本形 y = ax
・aのことを 比例定数
・グラフは (0, 0)を通る直線

と、『反比例』
・基本形 y=\(\large{\frac{a}{x}}\) (xy =a)
・aのことを 比例定数
・グラフは 双曲線

2年では、『一次関数』
・基本形 y = ax+b
・aのことを 変化の割合や、傾き
・グラフは 直線
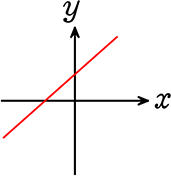
そして、3年では『関数y = ax2 』
・基本形 y = ax2
・aのことを、比例定数
・グラフは、頂点が(0, 0)の放物線
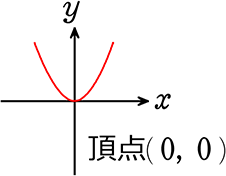
を学んでいきますね
ちなみに、高校では『二次関数』
・基本形 y = ax2+bx+c
・aのことを 比例定数
・グラフは 放物線
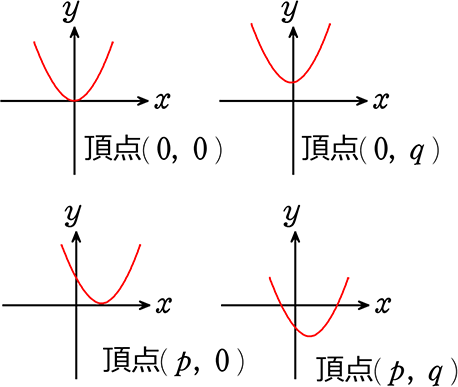
を学ぶことになりますね
ということは、今から学ぶ『関数y = ax2 』は「二次関数の1場面」、
「必ず頂点が(0, 0)な二次関数」ということができますね!
『一次関数』が、(0, 0)を通れば『比例』という個別名称があるのに、
『二次関数』の頂点が、(0, 0)のときは『関数y = ax2 』……個別名称とは
言い難いですが、個別名称がないのでこれがそのまま個別名称です
では、どのような現象のとき このようなグラフが発生するのでしょうか?
ex) 1辺xcmの正方形とその面積ycm2の関係を見ると




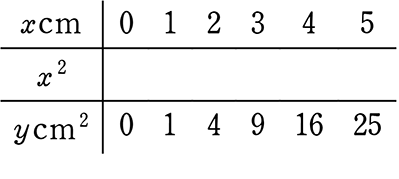

→ 上はy = 1x2 ですね
このようなときも、『yはx2 に比例する』といいます
そして「yはx2 に比例する」と言えば、数式の基本形は『y = ax2』となりますね
yはx2 の1倍 → y = 1x2 →「1」は書かないので → y = x2 ですね!
cf) yはx2 の2倍 → y = 2x2 ですね
ex) 球が斜面を転がり始めてから、x秒間に転がる距離ymの関係
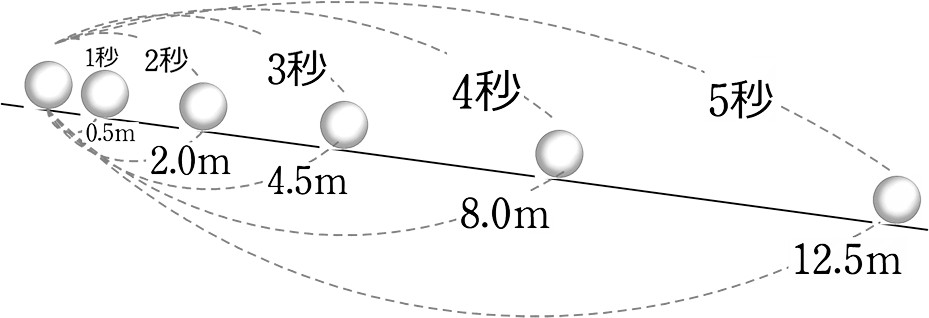


→ yはいつもx2の半分ですね、「yはx2に比例」していますね!

クリック・タップで答え (反応が遅い場合があります)
イ 関数y=ax2の特徴
各部名称
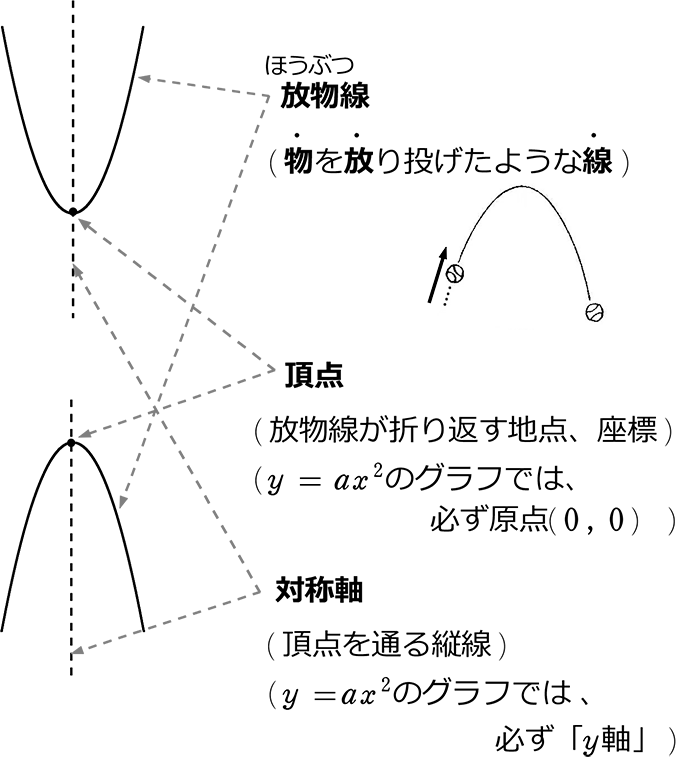
y=ax2 のグラフ
「グラフを描け」という問題は、定期テストでしか出ませんが、1度描いてみますね
《 例 》
y = x2 、y = 2x2 、y = -2x2 、y = \(\large{\frac{1}{2}}\)x2、y = -\(\large{\frac{1}{2}}\)x2 のグラフを描きましょう

① それぞれの式で
「x = 1のとき、yは…」
「x = 2のとき、yは…」
という点を2、3個かきこむ
② 対称軸(y軸)の反対側に
同様の点を書き込む
(代入作業の省略)
③ 各点を手書きで
適当に滑らかに結ぶ
完成です!
(点の結び方がカクカクさえして
いなければ、マル!ですね)

〔 関数y = ax2 のグラフの特徴 〕
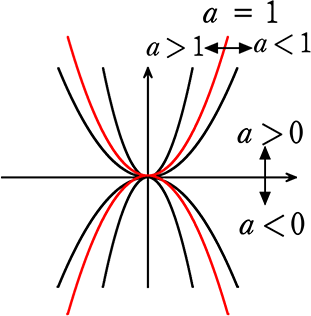
① 頂点は、必ず「原点(0, 0)」
② 対称軸(y軸)について対称な曲線 (= 左右対称)
③ a>0のとき、下に
a<0のとき、上に凸 (= 下開き)
④ aが大きいほど開きが小さい (= 細長くなる) (= aが開き具合を決める)
⑤ y = ax2 のグラフと y = -ax2 のグラフは、x軸について対称
⑥ グラフの上端(y=-ax2では下端)付近では曲線が直線に見えるが
あくまで曲線である (= 直線部分はない)

実は放物線は全て相似
〔全くの余談です〕
「相似」ということは、形が同じということですね
y = \(\large{\frac{1}{2}}\)x2のグラフも、y = x2のグラフも、y = 2x2のグラフも、
その他全てのy = ax2 のグラフも…同じ形…?
開き具合が違うのに・・・
ですが、ちゃんと「相似」なのです!
〔証明〕
1目盛りの「価値」が異なる方眼用紙に、y = \(\large{\frac{1}{2}}\)x2、y = x2、y = 2x2を描いてみますね

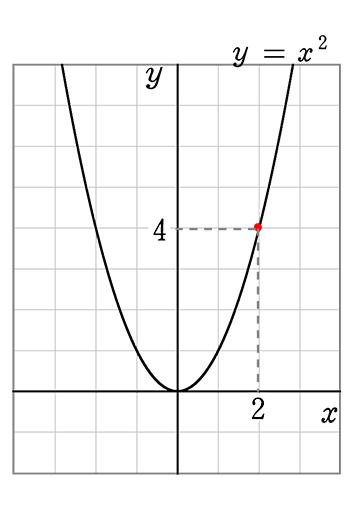
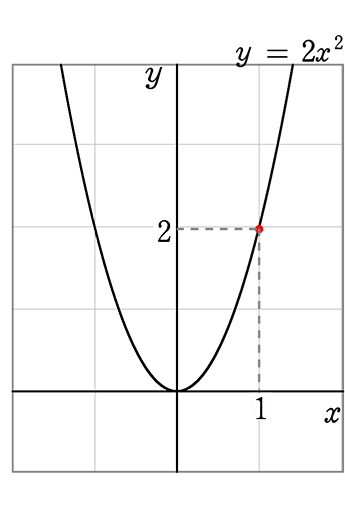
→ 升目の価値を無視すれば、全く同じ形の放物線ですね!
イメージ的には、y = \(\large{\frac{1}{2}}\)x2を見ている位置から、
2倍の望遠鏡で y = x2 を見れば、y = \(\large{\frac{1}{2}}\)x2 と同じ大きさ、形に見える
4倍の望遠鏡で y = 2x2 を見れば、y = \(\large{\frac{1}{2}}\)x2 と同じ大きさ、形に見える
感じでしょうか
そして、基準が同じ方眼用紙に3つを描けば
升目が縮まる分、放物線が細くなるものも
升目が広まる分、放物線が開くものが出てくるということですね!
どのような
戻りまして、
y =ax2 のグラフを目盛りから描くことは、習い始めだけですね!
今後、問題を解く上で必要と思われるのは、
自分なりの「略グラフ」を持つということだと思います
例えば、y = x2 なら
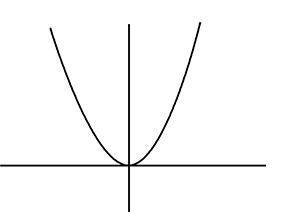
y = \(\large{\frac{1}{2}}\)x2 なら
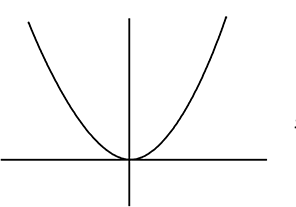
y = 2x2 なら
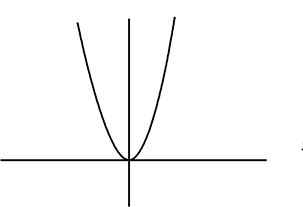
というふうに、「自分なりの略グラフ」を持つこと、すぐ描けること、が大事になっていきますね!
比例定数 a
比例 y = ax の「a」は、「比例定数」
一次関数 y = ax+b の「a」は、「変化の割合」「傾き」
関数 y = ax2 の「a」は「比例定数」 と言いましたね!
比例の「a」も 関数 y = ax2 の「a」も「比例定数」
ということは、2つの「a」は同じ意味なのでしょうか?
→ 同じ意味です!
ただ、結果が変わってきますね
・比例 y = ax の aはxに対する「比例定数」
∴ 必ず「直線」→ 「 = 傾き具合」を表す
・関数 y = ax2 の aはx2 に対する「比例定数」
∴ 必ず「放物線」→ 「曲線の開き具合」
ということですね!

「比例のa、一次関数のa」と「関数y = ax2 のa」は同じ意味、作用ですが、( xが一つ多い分) 結果が異なる
・比例y = axの「a」、一次関数y = ax+b の「a」→ 「直線の傾き具合」
・関数 y = ax2 の「a」→ 「放物線の開き具合」 を表す
◎ 結果が違う → 別物と考えるべき
《 例 》
関数y = ax2 のグラフが点( 3 , 6 )を通るとき、aの値を求めましょう
→ 代入するだけで文字がaだけになりますね
6 = a・32 → 9a = 6 → a = \(\large{\frac{6}{9}}\)
∴ a = \(\large{\frac{2}{3}}\)
① 変域
1年の比例の変域、2年の一次関数の変域と全く同じ考え方でOKですね!
ただ一つ気をつける点は、曲線であるために「yがはみ出る?
(両端のxの値に対応するyの値が、必ずしもそのままyの範囲ではない」ことがある。)
ということですが、
範囲を求めるときは、「簡単でいいから略図を書く」それさえ実行すれば
なんということはないですね!
《 例 》
関数y = \(\large{\frac{1}{2}}\)x2で、xの変域が次の場合、yの最大値と最小値を求めましょう
(1) x≦-2
→ 略図ですね
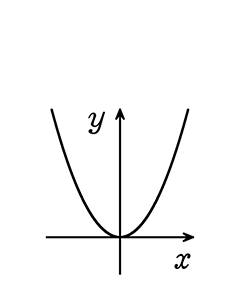
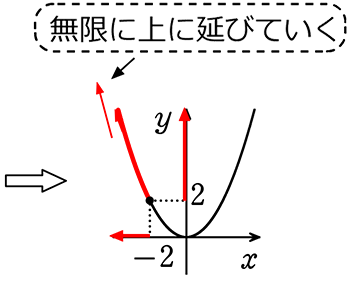
あとはyの目盛りを読んで
∴ 最大値 無限ですね
すなわち、最大値 なし
最小値2
(2) -4≦x≦2
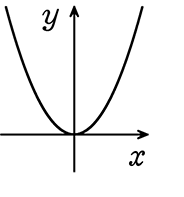

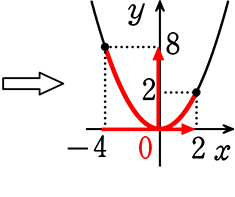
∴ 最大値 8
最小値 0
↑2ではないですよ~
↑x = -4、x = 2の「代入だけでは出てこない部分」も略図ですぐ判明ですね!
(3) x ≧-2
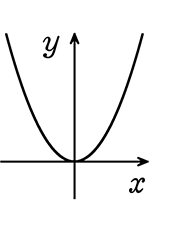

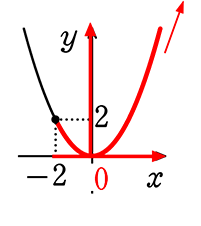
∴ 最大値 なし
最小値 0
《 例 》
関数y = -\(\large{\frac{1}{2}}\)x2で、xの変域が次の場合、yの最大値と最小値を求めましょう
(1) x≧-2
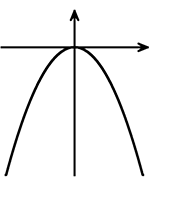

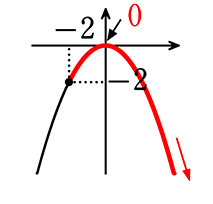
∴ 最大値 0
最小値 なし
《 例 》
関数y = \(\large{\frac{1}{2}}\)x2で、xの変域が次の場合、yの変域を求めましょう
(1) -4≦x≦-2
→ 略図ですね
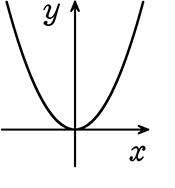
 ∴2≦y≦8
∴2≦y≦8
(2) -4≦x≦2
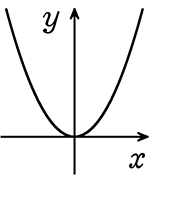

2≦y≦8ではないですね
→ yが取り得る範囲は…

0≦y≦8 ですね!
頭の中でグラフがイメージできるまでは必ず略図を描いてくださいね!
xの変域(範囲)が、対称軸(=y軸)をまたぐ(-〇≦x≦+〇)のときは特に!
(3) -2≦x≦4
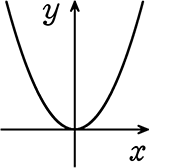
 ∴ 0≦y≦8
∴ 0≦y≦8
(4) 2≦x≦4
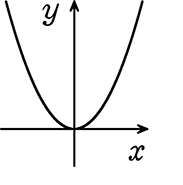
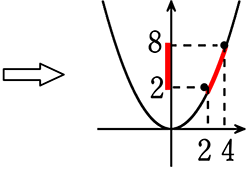 ∴ 2≦y≦8
∴ 2≦y≦8
《 例 》
関数y = ax2 で、xの変域が -1≦x≦2のとき、yの変域は-1≦y≦0であった、
このとき、aの値を求めましょう
→ yの変域が -1≦y≦0 ということは、
高校で学ぶ y = ax2+bx+cであれば、

中学の関数 y = ax2は、必ず「頂点が(0, 0)」なので、
yが「-1」の値をとりうるグラフは
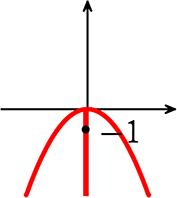
というわけで、適当に上に凸なグラフを描いて
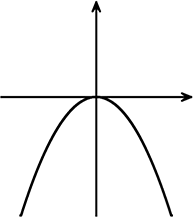
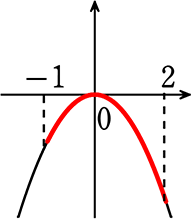

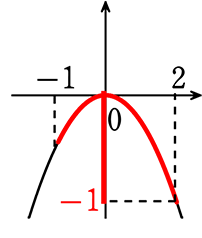
∴ y = ax2 に点(2, -1)を代入して
-1 = 4a → a = -\(\large{\frac{1}{4}}\)
② 変化の割合
一次関数で「変化の割合」といえば「a」、
すなわち、「直線」の「傾き具合」でしたね
直線であれば、どこの2点をとっても「傾き具合」は同じ、一定ですが
放物線に直線部分はありませんので、2点の取り方によって
「様々な傾き具合がある」ということになります

どの2点を結ぶ直線も
違う傾きですね!
イメージ的には・・・
短距離ランナーを2秒間隔で連写撮影すると
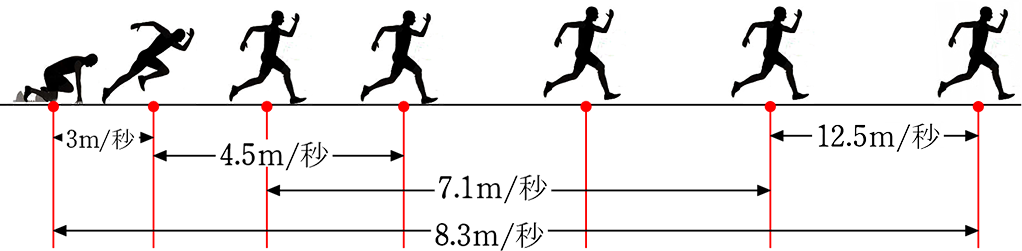
どの2点間も「(2点間の)平均速度 ( = \(\large{\frac{距離}{時間}}\) = \(\large{\frac{yの増加量}{xの増加量}}\))」が違いますね
加速
というわけで、放物線の「変化の割合」は「2点」必要ということになります
( 1点だけで求める「瞬間時速」は高校で!)
そして、2点を取り出して、それらを結んだものは当然「直線」ですね!
すなわち、その2点だけに通用する一次関数の「傾き」を求めるということですね
【 確認 】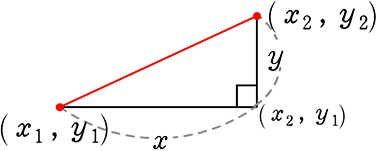
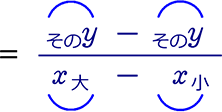
※ このaは、2点間の直線の傾き(変化の割合)の「a」であって、
関数y= ax2 の比例定数「a」ではない
ということは言うまでもありませんね!
《 例 》
関数y = \(\large{\frac{1}{4}}\)x2で、xの値が -4から 2まで増加するとき、変化の割合を求めましょう
→ x = -4のとき(式に代入して)yは4、x = 2のときyは1
→ すなわち2点の座標は (-4, 4) (2, 1)
→ 傾きa = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{1-4}{2-(-4)}}\) = \(\large{\frac{-3}{6}}\) = -\(\large{\frac{1}{2}}\) // 
同じく、xの値が2から4まで増加するとき、変化の割合を求めましょう
→ 結局 (2, 1) (4, 4)の2点を通る直線の傾きと同じことですね
→ 傾きa = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{4-1}{4-2}}\) = \(\large{\frac{3}{2}}\) // 
《 例 》
関数 y = ax2で、xの値が x1から x2まで増加するとき、変化の割合を求めましょう
→ 上と全く同じ問題ですが、全て文字ですね
= \(\large{\frac{yの増加量}{xの増加量}}\)
= \(\large{\frac{ax_2^2-ax_1^2}{x_2-x_1}}\)
= \(\large{\frac{a(x_2^2-x_1^2)}{(x_2-x_1)}}\) ←因数分解できる

= a(x2+x1)
余談公式
関数 y = ax2 上で
2点を結ぶ直線の傾き = a(x2+x1)
→ aはy=ax2 のa
( y = ax+b 上の2点には使えません)
《 先ほどと同問 》
関数 y = \(\large{\frac{1}{4}}\)x2で、xの値が-4から2まで増加するとき、変化の割合を求めましょう
→ 関数 y = ax2 上の2点を結ぶ直線の傾き = a(x2+x1) = \(\large{\frac{1}{4}}\)(2-4)
= -\(\large{\frac{1}{2}}\) // ←確かに同じ答えですね
→ ですが!全くの余談公式です、テストで2点間の傾きを求めることは
1テストあたり、あっても2、3問ですので
2点を結ぶ直線の傾き

で十分ですね!
・曲線の開き具合の「a」 (y = ax2 の「a」) なのか
・直線の傾き具合の「a」 (y = ax+b の「a」) なのか
完全に混乱しなくなってから、使った方がよいのかなと思います
《 例 》
2つの関数 y = ax2 と y = -3x+2 において、xの値が2から4まで増加するときの変化の割合が等しいとき、aの値を求めましょう

→ 放物線上の2点を結んだ線の傾きが、
「(一次関数の傾きである) -3」と同じ
(平行か重なっている状態)
∴ \(\large{\frac{yの増加量}{xの増加量}}\) = -3 より
→\(\large{\frac{16a-4a}{4-2}}\) = -3
\(\large{\frac{12a}{2}}\) = -3
6a = -3
a = -\(\large{\frac{1}{2}}\) //
③ 一次関数との交点
一次関数どうしの交点、すなわち、直線と直線の交点は連立方程式で求めましたね!
放物線と直線の交点も全く同様、連立方程式です!
《 例 》
関数y = 2x2 と y = x+1のグラフの交点の座標を求めましょう
→ 連立方程式ですね、「ひっ算方式」でも「代入方式」でもどちらでもOKですね
\(\small{\begin{cases}
y = 2x^2 \\
y = x+1
\end{cases}}\)
(ひっ算方式)
y = 2x2
-) y = x+1
0 = 2x2-x-1
(2x+1)(x-1) = 0
∴ x = -\(\large{\frac{1}{2}}\), 1
(代入方式)
y = x+1のyに、(y=)2x2を代入して
2x2 = x+1
→ 以下ひっ算方式と同様に
x = -\(\large{\frac{1}{2}}\), 1
ひっ算方式も代入方式も意味は同じでしたね!
→ 解答スペースが少なくて済む分、
今後 親子中学では「代入方式」でいきますね!
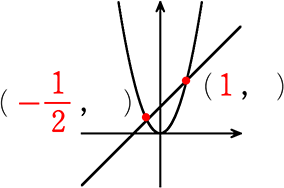
2点のx座標が確定!
→ あとは、y = 2x2 か y = x+1に x = -\(\large{\frac{1}{2}}\), 1を代入してy座標ですね
計算しやすい方で!どちらでもOKです、y = 2x2に代入しますね
・y = 2(-\(\large{\frac{1}{2}}\))2 = \(\large{\frac{1}{2}}\)
・y = 2(1)2 = 2
∴ (\(-\large{\frac{1}{2}}\), \(\large{\frac{1}{2}}\)) (1, 2)
引き算、足し算がない分 シンプルですね
今後 親子中学では「y = ax2に代入」でいきますね!

関数の原型
| 点(p, q) を通る1次関数 | ||
|---|---|---|
| 原型 | 移項型 | (結果) 基本形 |
| (y-q) = a(x-p) | y = a(x-p)+q | (p, q) が (0, 0) なら y = a(x-0)+0 y = ax 比例 の「基本形」\(!\) |
| (p, q) が (0, q) なら y = a(x-0)+q y = ax+q 1次関数 の「基本形」\(!\) |
||
| 頂点(p, q) な2次関数 | ||
| 原型 | 移項型 | (結果) 基本形 |
| (y-q) = a(x-p)2 | y = a(x-p)2+q | (p, q) が (0, 0) なら y = a(x-0)2+0 y = a(x)2 関数y = ax2 の「基本形」\(!\) |
では、逆に
● y = ax はどのような直線?
→ y = a(x) → y = a(x-0)+0 ∴ (0, 0)を通る、傾きaの直線
● y = ax+b はどのような直線?
→ y = a(x)+b → y = a(x-0)+b ∴ (0, b)を通る、傾きaの直線
● y = ax2 はどのような放物線?
→ y = a(x)2 → y = a(x-0)2+0 ∴ (0, 0)を頂点とする、開き具合aの放物線
〔 以下全くの余談です(高校課程) 〕
● y = ax2+bx+c はどのような放物線?
① 平方完成で頂点が分かりましたね( 平方完成の作り方)
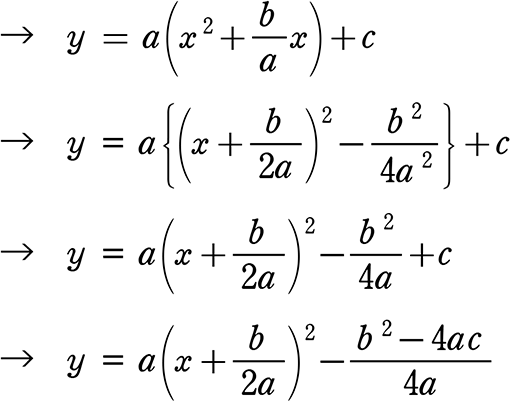
∴ 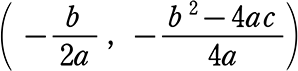 を頂点とする、開き具合aの放物線
を頂点とする、開き具合aの放物線
さらに、
② yが0のときのxの値がx切片でしたね → 因数分解でx軸との交点が分かる
→ (0) = ax2+bx+c → 解はx = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\)なので
y = ax2+bx+c は 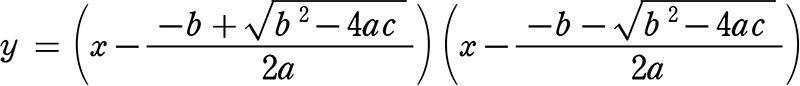 と因数分解できるということ
と因数分解できるということ
∴ x軸上の2点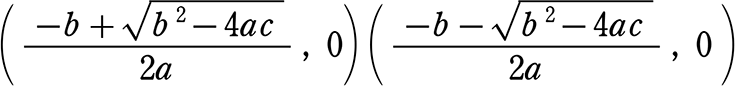 を通り
を通り
かつ①より、頂点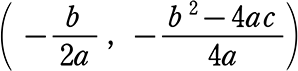 の放物線
の放物線
《 例 》
y = x2+2x-8 のグラフを描いて、必要データを書き込みましょう
(① 平方完成で頂点)
y = (x2+2x)-8 → y = (x+1)2-1-8 → y = (x+1)2-9
∴ 頂点(-1, -9)
(② 因数分解でx切片)
y = x2+2x-8
= (x+4)(x-2)
∴ x切片 (-4, 0) (2, 0)
二次方程式 0 = x2+2x-8
の解は、 ↑yが「0」のとき、
すなわち、x切片だったのですね!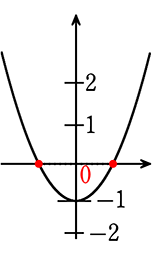
x軸上の点
⇒ yが「0」のときのxの値
(③ xに0を代入でy切片)
y = x2+2x-8
→y = 02+2・0-8 = -8
∴ y切片(0, -8)
①②③よりグラフは
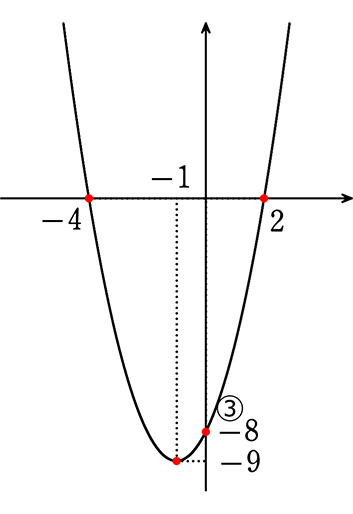
←二次関数の基本データになります
文字だけの式 y = ax2+bx+c ではとんでもなく難しそうでしたが、
実際の数式で行うと…それほど難しくはなさそうですね!
④ 一次関数との接点
「接点」…接する点ですね
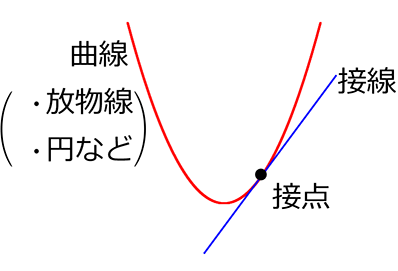

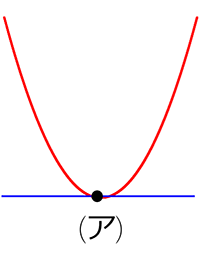
まず、y = ax2 は放物線という(全部分)曲線ですので、直線部分はありませんね
そして、一次関数y = ax+bは直線ですので、その2つが接する部分は
「面」ではなく、必ず「
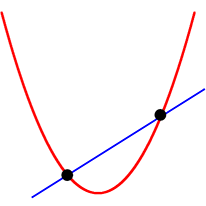
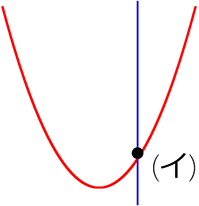
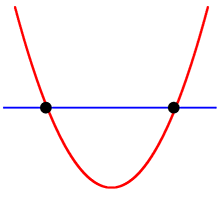
これら3つは直線が曲線を
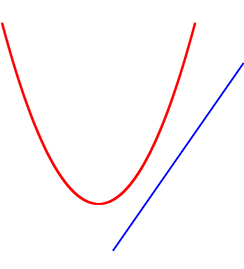
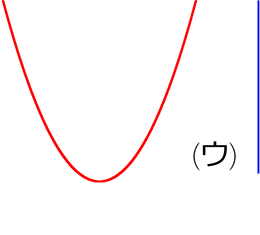
これは接していないので、当然「接点」はありませんね
よって、曲線と直線の「接点」は
① 「ただの交点」ではなく、またがない交点=「接する点」
② あっても1つ
となりますね
そして
(ア)は y=a の直線ですので、一次関数ではないですね
…「関数」とはxの値が決まれば、yの値がただ1つ決まる関係
→ y=a は … xの値に関係なくyは一定の数字(定数)
→ 「接線」ではあるが、惜しいかな「一次関数」と「二次関数」の「接線」
とは言い難いですね
(イ)は x=0 の直線ですので、「あっても1つ」の「1つ」ではありますが
・「接点」ではなく、またいでいるので「ただの交点」
・しかも直線 x=0 は一次関数ではない
(ウ)は実はいずれグラフの上の方で「交わり」ますので、(イ)になりますね
よって、一次関数 y=ax+b は90°の縦線や180°の横線ではなく、
必ず「傾き」というものがありますので
結局のところ 関数 y=ax2 と一次関数 y=ax+b の交点は
① 2点で交わる
② 1点で交わる
③ 交わらない
の3つにしか分類できないということになりますね!
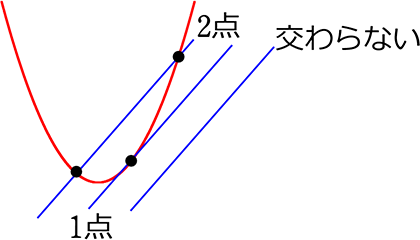
すなわち、y = ax2 とy = ax+b の交点(共通解)が「1つ」であれば
それは「接点」ということにまりますね
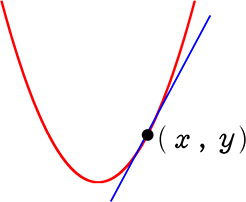
→交点が1つ
= 共通x座標が1つ、共通y座標も1つ
《 例 》
2つの関数の交点の座標を求めましょう
さらに、(確認のため)判別式Dでxの解( = 交点のx座標)の個数を確認しましょう
( 判別式D)
(1) y = x2 と y = 2x+3
● 交点のx座標 = 共通x座標 → x2 = 2x+3 ←今後は「ひっ算方式」ではなく「代入方式」でいきますね
→ x2-2x-3 = 0 → (x-3)(x+1) = 0
∴ x = 3, -1 → 交点の座標は(3, ?)(-1, ?)
交点のy座標 = 共通y座標 → y = x2 の方に x = 3, -1を順次代入
↑今後は「一次関数」ではなく「y = ax2」の方に代入でいきますね
・ y = x2 → y = (3)2 → y = 9 ∴ (3, 9)
・ y = x2 → y = (-1)2 → y =1 ∴ (-1, 1)
ちなみにグラフは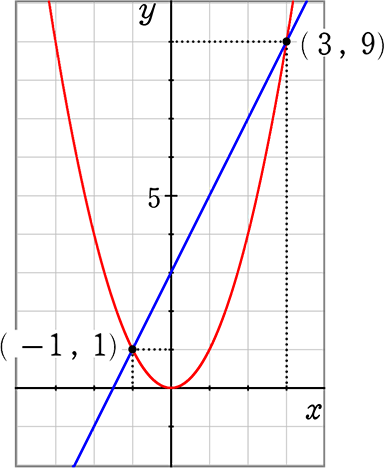
● 二次方程式x2 = 2x+3 → x2-2x-3 = 0を判別式Dで検査すると
D/4 = (bの半分)2-ac = \(\left(\large{\frac{-2}{2}}\right )^2\)-1・(-3) = 1+3 = 4
∴ D>0(Dの値は0より大きい) → xの解は2つ (= x座標が2つ = 交点が2つ)
(確かに2つありましたものね!)
(2) y = x2 と y = 2x-1
● 交点のx座標→ x2-2x+1 = 0 → (x-1)2 = 0 ∴ (1, ?)
交点のy座標→ y = (1)2 → y = 1 ∴ (1, 1)
● D/4 = 1-1 = 0
∴ D = 0 → xの解は1つ( = x座標が1つ = 交点が1つ)
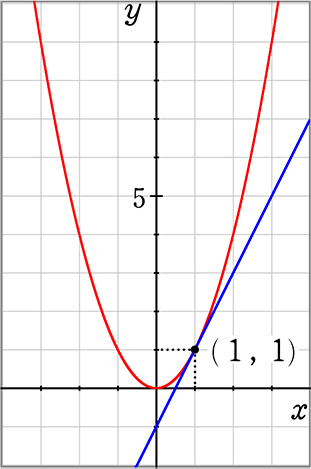
(3) y = x2 と y = 2x-2
● 交点のx座標→ x2-2x+2 = 0 → きれいに因数分解できなさそう
解の公式 → x = \(\large{\frac{-b±\sqrt{b^2-4ac}}{2a}}\) = \(\large{\frac{2±\sqrt{4-8}}{2}}\) = \(\large{\frac{2±\sqrt{\color{red}{-}4}}{2}}\)
∴ √ の中がマイナス → そんな実数は存在しない → 解なし → 共通解なし →交点なし
交点のy座標→ 当然なし
ちなみに、平方完成方式でxを求めてみると
x2-2x+2 = 0 → (x-1)2-1+2 = 0 → (x-1)2 = -1
(x-1)2 = -1をよく見ると…「左辺を丸々2乗したら、-1?」
→ 2乗してマイナスになる実数なんてないですね! ∴ 解なし
● D = 4-8 = -8
∴ D<0 → xの解はない( = 共通x座標がない = 交点がない)
実は先の「解の公式」の中で b2-4ac を計算しているので同等な(不要な)作業ではありましたが、念のためでした
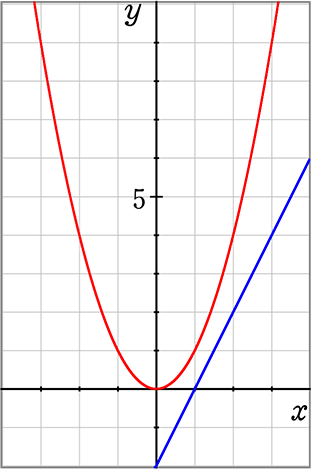
以上3つのグラフを並べておきますね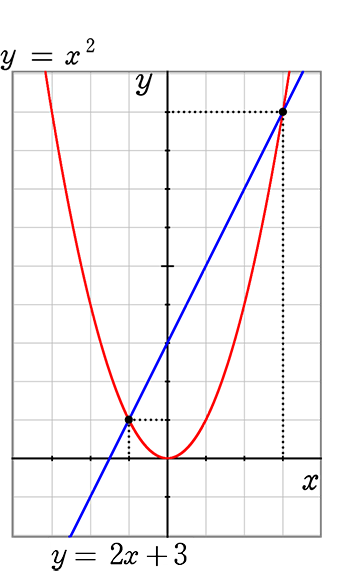
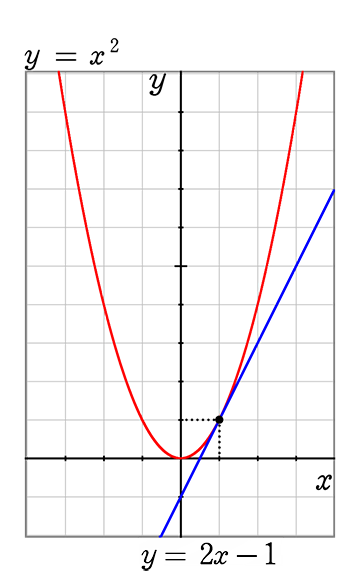
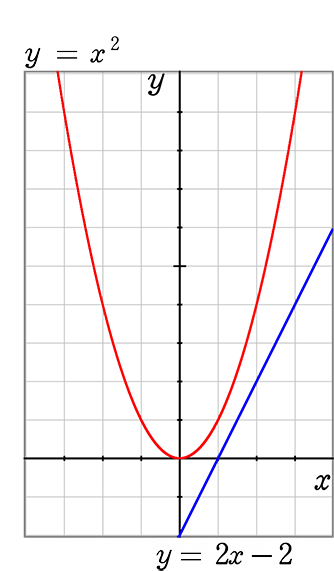
《 例 》
放物線y = \(\large{\frac{1}{2}}\)x2と直線 y = mx-2がただ1つの共有点をもつようなmを求めましょう。ただしmは正の数とします
→ 2つの線の交点のx座標が「ただ一つ」ということは
D = 0 になればよいということですね
・\(\large{\frac{1}{2}}\)x2 = mx-2 → (Dの検査は必ず右辺を0にする) → \(\large{\frac{1}{2}}\)x2-mx+2 = 0 → x2-2mx+4 = 0
・D/4 が 0 → m2-4 = 0 → m = -2, 2
→ m>0の指定より A. m = 2
cf. m>0の指定がなければ、答は m=- 2, 2 の2つですね
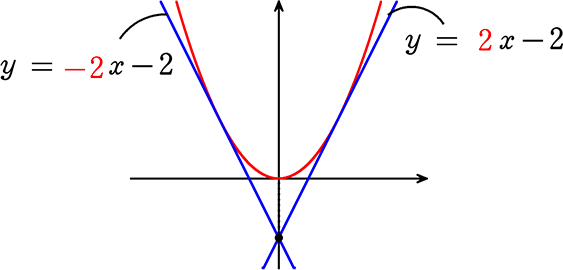
確かに
どちらも接線ですね!
《 例 》
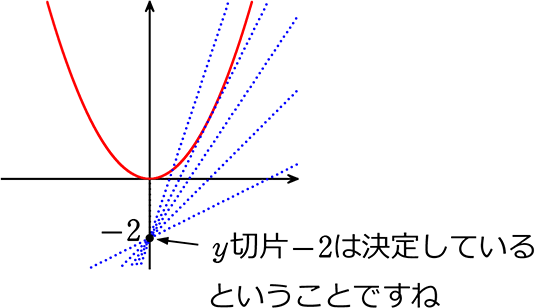
放物線y = \(\large{\frac{1}{2}}\)x2と直線 y = 2x+mが ただ1つの共有点をもつようなmを求めましょう
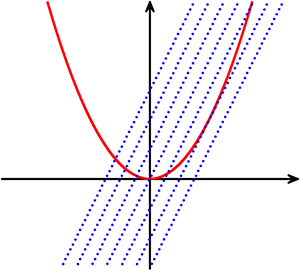
傾き2は決定しているということですね
→ 上と同様に D = 0 になればよいということですね
\(\large{\frac{1}{2}}\)x2 = 2x+m → x2-4x-2m = 0
D/4 = 0 → 4-(-2m) = 0 → 2m = -4
A. m = -2
ウ 関数 y=ax2を用いた具体的な事象の説明
① 具体的な事象
【 加速・減速 】
まずは、「距離」「時間」「速さ」の関係をイメージしてみましょう
最高時速90km( 90km/60分 = 1.5km/分 = 25m/秒 ←「25m毎秒」と読めばよいと思います)の電車が、
A駅→B駅間(3km)を
「静止」→「加速」→「一定走行(等速)90km/時」→「減速」→「停止(静止)」
を行う場合のグラフを考えてみますね
x軸を「時間」、y軸を「距離」とすると…
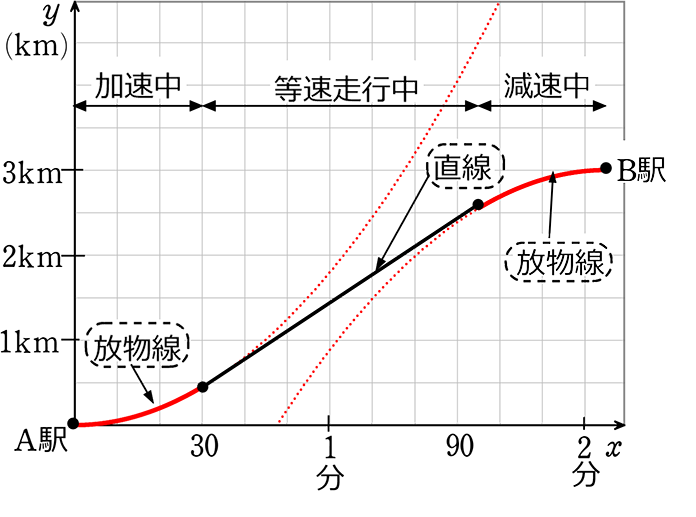
(イメージ)
・加速中、減速中は
→ 二次関数(放物線)
・等速走行中は
→ 一次関数(直線)
身体が後に持っていかれる
= 加速中
身体が前に持っていかれる
= 減速中
ふんばらなくてもよい
= 等速走行中
x軸を「時間」、y軸を「速さ」にすると…
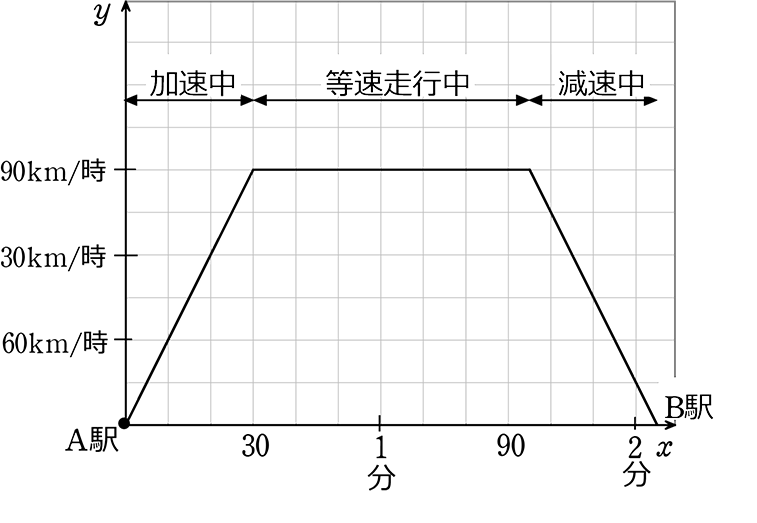
← このグラフは問題では
ほとんど出てきません
簡単なイメージは
こんな感じですね
実際、静止状態からいきなり速さ90km/時になったら…
…大けがでは済まないですね
足元の床が急に90km/時で動き出したら…あっという間に転ばされて、
あっという間に車両の後ろ壁が90km/時で衝突してきますね
ここでは、おおよそ
・加速中、減速中は → 放物線(二次関数)
・等速走行中は → 直線(一次関数)
というイメージだけ持っていただければ 十分かと思います
《 例 》
ある斜面を球が転がるとき、進んだ距離をy、時間をxとすると
yはx2 に比例します、今4秒後に24m進みました。
(1) yをxの式で表しましょう
→ 「yはx2 に比例する」というフレーズが出れば
y = 〇x2 すなわち開き具合は分からないが「頂点(0, 0)の放物線」
すなわち、y = ax2という基本形が確定ということですね (~は~に比例する)
→ y = ax2 に x = 4, y = 24を代入してaを求めるだけですね
y = ax2 → 24 = 16a → a = \(\large{\frac{24}{16}}\) = \(\large{\frac{3}{2}}\)
∴ y = \(\large{\frac{3}{2}}\)x2
(2) 転がり始めてから2秒後から4秒後の「距離」を求めましょう
・ 2秒後の距離 → y = \(\large{\frac{3}{2}}\)x2 に、x = 2(秒)を代入 → y = 6(m)
・ 4秒後の距離 → y = \(\large{\frac{3}{2}}\)x2に、 = 4(秒)を代入 → y = 24(m)
∴ 24-6 = 18 A.(2秒後から4秒後に進んだ距離は) 18m
(3) 2秒後から4秒後間の「平均の速さ」を求めましょう
→ 4秒-2秒の「2秒間」で、「18m」進んでいるので
18÷2 = 9 A.9m/秒
(4) 転がり始めてから2秒後から4秒後間の「変化の割合」を求めましょう
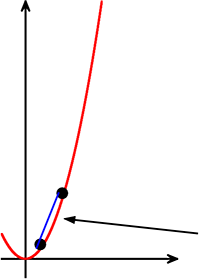 この2点間にだけ通用する「直線」の傾きですね
この2点間にだけ通用する「直線」の傾きですね
変化の割合 = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{24-6}{4-2}}\) = \(\large{\frac{18}{2}}\) = 9
A. 9 ←直線y = 9x+b の「9」
→ 当然、2秒後から4秒後間の「平均の速さ」と同じ「9」ですね
《 例 》
A君は自転車で4m/秒(14.4km/時)の速さで、バス停で停車中のバスを追い抜きました。 A君が追い抜いてから5秒後にバスが y = \(\large{\frac{1}{4}}\)x2の加速感で走り出しました。バスは何秒後にA君に追いつくでしょうか
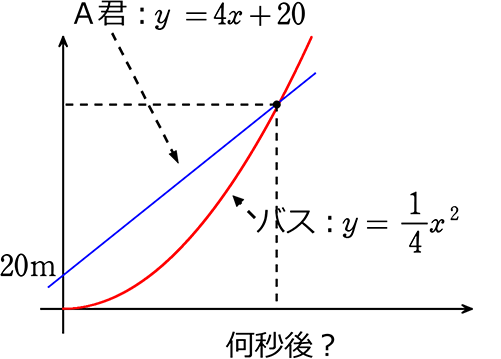
→ バスの走り出しを基準にすると、
A君はすでに20m(4m/秒×5秒)先に
いますね
→ あとは交点を求めるだけですね
\(\large{\frac{1}{4}}\)x2 = 4x+20 → x2-16x-80 = 0 → (x-20)(x+4) = 0
∴ x = -4, 20 x>0より x = 20
A. 20秒後
《 例 》
ある中学校の体育祭の男女混合リレーの1場面で
Aさんが4m/秒で走ってきました。次走者のB君はトップスピードになるまでは
y = 2x2で加速できます
Aさんが何m後方に達したときに走りだせばロスのないバトンパスができる
でしょうか
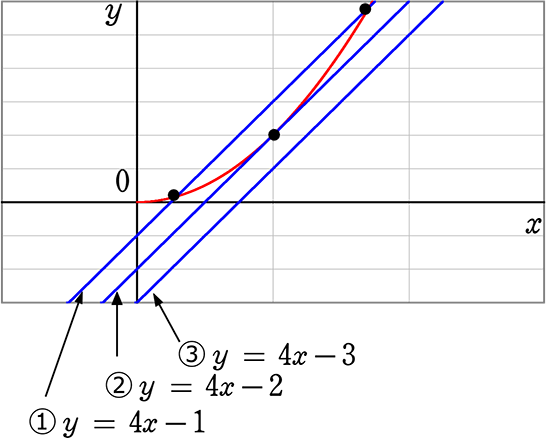
①1m後方の時に走り出すと、ロスがありますね
③3m後方の時に走り出すと、AさんばB君に追いつけずバトンパスができませんね
②2m後方の時に走り出すと、両者とも(その瞬間での)最高速度→ロスなしですね
→ グラフで判明してしまいましたが、ロスのないバトンパスは
直線が放物線の接線のときですね
すなわち、y = 2x2 と y = 4x+bの接線の式の「b」を求めればよいですね
→ 接線であるためには、「交点が1つ」であればよい でしたね!
2x2 = 4x+b → 2x2-4x-b = 0
D/4 = 0 → 4-(-2b) = 0 → 2b = -4 → b = -2
∴ 直線y = 4x+bがy = 2x2 の接線になるためには、b = -2
A. B君は、Aさんが2m後方に来た時に(全開で)走り出せばよい
《 例 》
ブレーキが効き始めてから車が止まるまでに進む距離を 制動距離といいます。
制動距離ymは、時速xkmで走っているとき、
yはxの2乗に比例することがわかっています
(1-a) 時速80kmで走っている「乗用車」がブレーキをかけ、
止まるまでに54m進みました。yをxの式で表しましょう
→ xが「時間」ではなく「速さ」ですね
ですが、そのx(速さ)が「yはxの2乗に比例する」と問題文が言うのですから、
そのままま当てはめていきましょう
→ 「yはxの2乗に比例する」というフレーズがあれば
y = ax2 ですね
54 = (80)2a → 6400a = 54 → a = \(\large{\frac{54}{6400}}\) → a = \(\large{\frac{27}{3200}}\)
∴ y = \(\large{\frac{27}{3200}}\)x2
(1-b) この「乗用車」が時速40kmで走っていた場合の制動距離は?
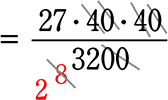
A. 13.5m
(2-a) 時速80kmで走っている「大型トラック」がブレーキをかけ、
止まるまでに84m進みました。yをxの式で表しましょう
→ 同様に y = ax2 ですね
84 = (80)2a → 6400a = 84 → a = \(\large{\frac{84}{6400}}\) → a = \(\large{\frac{42}{3200}}\) = \(\large{\frac{21}{1600}}\)
∴ y = \(\large{\frac{21}{1600}}\)x2
(2-b) この「大型トラック」が時速40kmで走っていた場合の制動距離は?
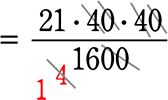
A. 21m
同じ時速40kmでも、乗用車より大型トラックの方が 制動距離が長い = 重いものは止まりにくい

停止距離
実際の「停止距離」は、「空走距離」+「制動距離」となりますね
「空走距離」とは、「止まろう!」と思ってブレーキ操作を始めて、
実際にブレーキが利き始めるまでの距離ですね
(この間はブレーキは全く効いていません)
自転車ならば、ブレーキレバーを握り始めてブレーキシュー( = ブレーキゴム)がリムに当たるまでの時間、この間は操作はしていますが全くブレーキが効いていませんね
この間(反射時間)は0.1秒位ですが、0.1秒でもいく分かは進んでしまっているということですね
乗用車では、操作が多い分(アクセルペダルから足を外して、
ブレーキペダルに足を乗せ換える)、反射時間は0.5秒くらいになってしまいますね
ということは、
時速80kmの空走距離は、
80km/時×0.5秒 → 1333m/分×0.5秒 → 22m/秒×0.5秒
∴ 11mも進んでしまっていますね、そこから「制動距離」25mを足すと36m!
「危ない!止まりたい!」と思ってから36mもかかりますね
35m先に人影を発見しても止まり切れないということですね
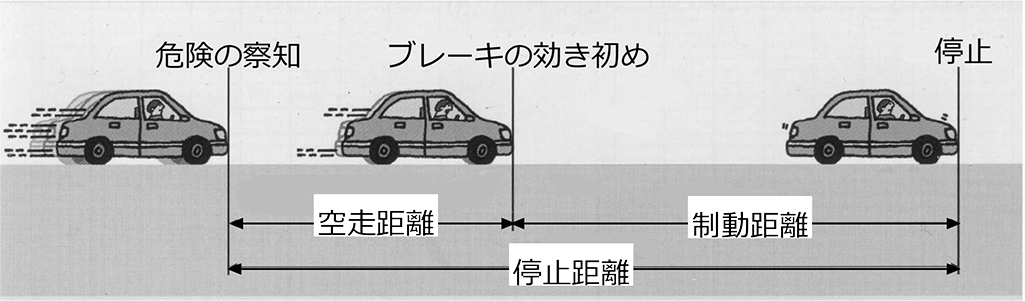
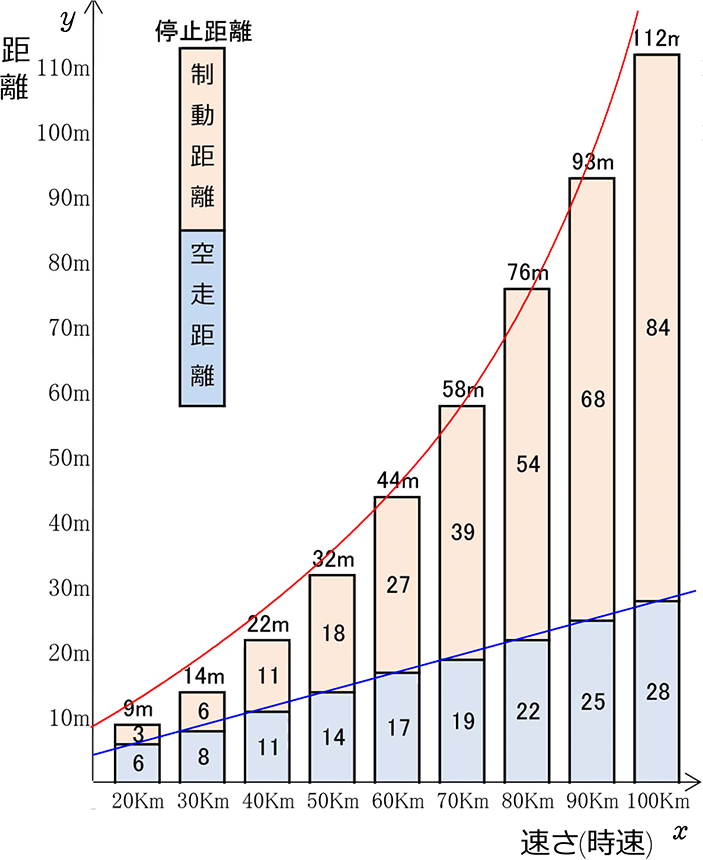
確かにおよそ
減速中(制動距離)は
放物線
y = ax2
等速走行中(空走距離)は
直線
y = ax
になっていますね!
《 例 》
乗用車の空走距離ymは、時速xkmで走っているとき、
yはxに比例します
(1) 時速80kmで走っている「乗用車」がブレーキをかけようと思ってから
ブレーキが効き始めるまでに22m進みました。(空走距離ですね)
yをxの式で表しましょう
→ 「yはxに比例する」というフレーズ → y = ax
80 = 22a → a = \(\large{\frac{80}{22}}\) = \(\large{\frac{40}{11}}\)
∴ y = \(\large{\frac{40}{11}}\)x
(2) 「乗用車」の制動距離yは速さxとの関係において
y = \(\large{\frac{27}{3200}}\)x2 とわかっています
時速60kmのときの「
→ 空走距離 y = \(\large{\frac{40}{11}}\)x …(1)より
空走距離 y = \(\large{\frac{40}{11}}\)・60 = \(\large{\frac{2400}{11}}\) (≒22m)

∴ 停止距離 = 空走距離+制動距離 ≒ 22+30 ≒ 52m
A. およそ52m
( テストで出る場合は歯切れのよい数字になると思います)

動いている物体が重ければ重いほど、
そして 摩擦が少なければ少ないほど
制動距離は長くなりますね
同じ乗用車ならタイヤが太ければ太いほど、
地面との摩擦が大きくなるので
制動距離は短くなりますね
海を16ノット(時速30km )で行く「石油満載タンカー」は
危険を察知してから「全速後進(逆スクリュー)(=フルブレーキ)」をしても、
停止するまでに4kmもかかりますね
→ 重いし、スクリューと海水との摩擦が
タイヤとアスファルトほどの摩擦がないですからね!
【 風圧 】
《 例 》
風の風速をxm/秒、その風が物体にかける風圧をyパスカルとすると、
yはxの2乗に比例することが知られています
(1) 今、風速5m/s(秒)のとき、物体にかかる風圧は12.5パスカルでした
yをxの式で表しましょう
h (hour) → 時間
m (minute) → 分
s (second) → 秒
→ 見慣れない単位が出てきても、もう「単純作業」ということは分かってきましたね
→ 「yはxの2乗に比例」というフレーズ → y = ax2の形
→ 判明している y, x の値を代入してaを求める
12.5 = (5)2a → 25a = 12.5 → a = \(\large{\frac{12.5}{25}}\) = \(\large{\frac{125}{250}}\) = \(\large{\frac{5}{10}}\) = \(\large{\frac{1}{2}}\)
∴ y = \(\large{\frac{1}{2}}\)x2
(2) 風速60m/s (←室戸台風最大瞬間風速)のとき、物体が受ける風圧は?
y = \(\large{\frac{1}{2}}\)x2 → y = \(\large{\frac{1\cdot60\cdot60}{2}}\) = 1800 A. 1800パスカル

圧力の単位 パスカル
具体的な場面での二次関数の利用問題では、見慣れない単位が出てきても
ほとんど yは○○、 xは△△ と言ってくれていると思いますので
それほど、見慣れない単位に対して構える必要はないのですが、折角ですので
Pa「パスカル」・・・圧力の単位ですね
1Pa = 1N/m2 (1m2あたり1ニュートン)
1N = 地球上で100gの物体にはたらく重力
∴ 結局は
1N → 100g
1Pa = 100g/m2(= 1g/100cm2←10cm四方 = 0.01g/cm2←1cm四方
イメージ的には1Paは…
・大の字に寝転がって(身体の前表面を1m2と思って)、
大きいページの新聞紙(1枚約30g)を3枚を体にまんべんなく乗せたくらいの圧力
・指を除いた手のひら(100cm2 = 10cm四方と思って)に、1円玉(1枚1g)を乗せて
点ではなく、手のひら全体で支えているとイメージする感じ
とにかく 1Pa位なら十分立ち向かえますね!

では、上の例題の室戸台風の風速60m/s、1800パスカルはどのくらい?
→ 1800パスカル = 1800 00g/m2= 180kg/m2!
恐ろしいパワーですね・・・
天気予報では「ヘクトパスカル」ということばをよく聞きますね
1hPa(1ヘクトパスカル) = 100Pa
そして、海抜0m地点は・・・ 1気圧ですね
1気圧
= 1013 hPa
= 1013 00 Pa = 1013 00 00g/m2
≒ 約10t/m2 !!
≒ 100kg/100cm2 ←10cm四方
大の字に寝転がったう上に、100kgの人間が片足つま先立ちで何人も乗っているようなものですか…
私たちが深海魚に対して「そんな高圧の中でよく生きていられるな」と思っているように
宇宙人は人間に対して「そんな高圧の中でよく生きていられるな」と
思っているかもしれませんね
人間は、深海魚、深海生物ならぬ 深空気生物ですね!
人間
深海魚
《 例 》
風力発電機において、ローター径をxm、
発電量をykwとすると
yはx2に比例することが知られています
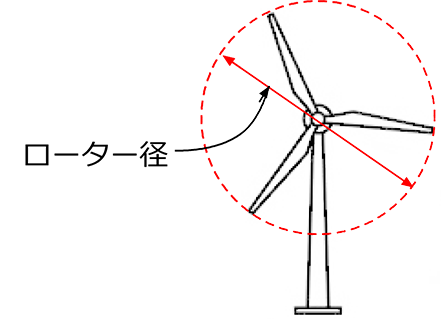
(1) 今、ローター径が40mのとき、発電量は500kwでした
yをxの式で表しましょう
y = ax2 → 500 = (40)2a → 1600a = 500 → a = \(\large{\frac{5}{16}}\)
∴ y = \(\large{\frac{5}{16}}\)x2
(2) ローター径を2倍にすると、発電量は何倍?
→ ローター径が2倍ということは、80m
y = \(\large{\frac{5}{16}}\)・802 = \(\large{\frac{5\cdot80\cdot80}{16}}\) = 5・400 = 2000kw
∴ 2000kw÷500kw = 4 A. 4倍
半径で考えても同じ結果です ∵ 相似比の2乗 = 面積比
その代わり(1)ではローター半径20m、500kwで式を立ててくださいね
直径で式を立てたら直径を当てはめる、半径で式を立てたら半径を当てはめる!
ちなみに
風速をxm/s、発電量をykwとすると
「yはxの3乗に比例」しますね
→ y = ax3
同様に与えられた数値を代入するだけですが、中学の範囲ではないですね!
《 例 》
・ある風力発電機は、風速5m/s(x)のとき発電量は250kw(y)でした
yはx3に比例することが知られています。yをxの式で表しましょう
→ y = ax3 → 250 = (5)3・a → a = \(\large{\frac{250}{5\cdot5\cdot5}}\) = \(\large{\frac{10}{5}}\) = 2
∴ y = 2x3
・風速10m/sのとき、発電量は?
→ y = 2x3 = 2・103 = 2000
∴ 2000kw

空気抵抗
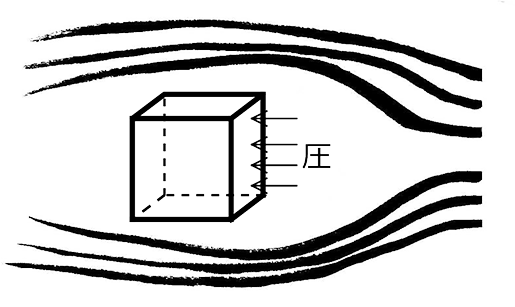
この図はどういう状況なのでしょうか?
① 静止している物体に、風が当たっている
② 静止してる空気中(無風状態)に、物体が動いている
③ 風もあるし、物体も動いている
どれも正解です!
(言葉は変になりますが) 「状況は違えど状況は同じですね」
物体は静止(0m/s)、空気は10m/s → 10m/s相当の圧を受けている
物体は10m/s、空気は静止(0m/s) → 10m/s相当の圧を受けている
物体は10m/s、空気は10m/sの向かい風 → 20m/s相当の圧を受けている
物体は10m/s、空気は10m/sの追い風 → 圧を受けていない
例えばスカイダイビングですと、
飛行機から飛び降りた瞬間から10秒位は、地球の引力によって
どんどんスピードが上がりますが、スピードが上がれば上がるほど
上の理由により、身体に受けるパスカル数も相乗的に大きくなりますね
そして、引力より風圧の方が大きくなれば、上に上がるということに
なるのですが、上に上がるということは→スピードが落ちる→風圧が小さくなる
→引力の方が大きくなる→また落ちる・・・ということで、
つり合った状態がやってきますね!
その点に到達したら、後は「等速落下」であるということですね
この速度を「終端速度」と言います。
終端速度は、物体の「重さ」や「形」で異なってきますが、地球の大気中で
ある限り、全ての物体がそれぞれ「終端速度」を持ちますね
スカイダイビングでは、「大の字」に飛び降りた場合 およそ8秒ほどで
終端速度200km/時に達しますね
200km/時に達した後は「等速」、それ以上は速くなりません!
等速ということは屋根・壁のない新幹線に乗っている事と
変わりはありませんので、
①高い所にいるという恐怖 ②地面が近づいてくるという恐怖
③体が1Gの加速感を感じる恐怖
(G:重力加速度:gravitationl acceleration)
のうち、
少なくとも③の「体が1Gの加速感を感じる恐怖」は無くなっているはずですね
垂直落下でさえ終端速度があるのですから、
斜面を転がる球にも当然終端速度がありますね
ですが、中学数学の「転がる球」「動く球」系の問題では、
「空気抵抗」などあらゆる摩擦、抵抗は無いものとして考えていきます
問題文に「但し書き(ex . 空気抵抗は無視する など)」がなくても、
「いつまでも加速」、「いつまでも運動し続ける」でOKです!
《 例 》
ふりこのひもの長さym、ふりこが左右の1往復にかかる時間をx秒とすると
yはxの2乗に比例することが知られています
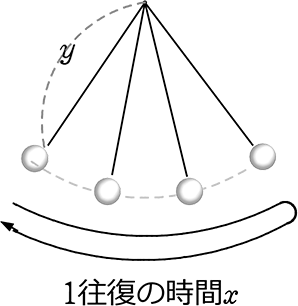
(1) 今、ボンボン時計のふりこの長さが1mのとき、
1往復にかかる時間は2秒でした。
yをxの式で表しましょう
→ 「yはx2の2乗に比例する」 → y = ax2
∴ 1= 22・a → a = \(\large{\frac{1}{4}}\)
∴ y = \(\large{\frac{1}{4}}\)x2
(2) ふりこの長さを90cmにすると1往復にかかる時間は?
\(\small{\sqrt{2}}\) = 1.4、\(\small{\sqrt{5}}\) = 2.2として求めましょう
→ 90cm = 0.9m (立てた式がm → 代入する値もmに!)
yに0.9を代入してxを求めると
0.9 = \(\large{\frac{1}{4}}\)・x2 → x2= 3.6
x>0より x = \(\small{\sqrt{3.6}}\) = \(\small{\sqrt{\large{\frac{36}{10}}}}\) = \(\large{\frac{\sqrt{36}}{\sqrt{10}}}\) = \(\large{\frac{6}{\sqrt{10}}}\) = \(\large{\frac{6\sqrt{10}}{10}}\) = \(\large{\frac{3\sqrt{10}}{5}}\) = \(\large{\frac{3\cdot\sqrt{2}\cdot\sqrt{5}}{5}}\) = \(\large{\frac{3×1.4×2.2}{5}}\) = 1.848
A.1.848秒
(3) 1往復にかかる時間が1秒のときふりこの長さは?
→ xに1を代入してyを求めると
y = \(\large{\frac{1}{4}}\) ・12 = \(\large{\frac{1}{4}}\) = 0.25 A. 0.25m (25cm)
中学数学では空気抵抗を無視(= 真空)しますので、ふりこのおもりが
鉄球であろうとピンポン玉であろうと y = \(\large{\frac{1}{4}}\)x2 の関係ですね
真空中(= 空気がない)では当然空気抵抗がないので
パチンコ玉も羽毛も同じ速さで、「ストーン!」と落下しますね
【 実証 】
教科書と2cm四方の紙辺を 1m位の高さから同時に落とすと…
当然教科書が先に落ちますね、(紙辺はヒラヒラと落ちますね)

教科書の上に紙辺を置いて、落とすと…
同じ速さで落ちますね
紙辺に「空気抵抗」がないからですね
《 例 》
ダイヤモンドの重さをxct(カラット)、価格をy円とすると
yは(およそ)xの2乗に比例することが知られています
(1) 今、重さが1ctのとき、価格は70万円でした。
yをxの式で表しましょう
→ 「yはxの2乗に比例」 → y = ax2 の形
∴ 70万 = 12・a → a = 70万
A. y = 70万x2
(2) 0.3ctのダイヤモンドの価格は?
→ y = 70万・0.32 = 700000・0.09 = 7000×9 = 63000
A. 63000円

カラットとは輝き具合とかではなく、「重さ」ですね
1ct = 0.2g
世界最大のダイヤ原石カリナン(すごいダイヤには名前が付けられる)は
3106ct(621.2g)でした

その後 カリナンは9つに分割され、
きれいにカット仕上げされていますね
そのうちもっとも大きなものが「カリナンⅠ世」530ct(106g)
9つのいずれもイギリス王室、王族所有ですね
カリナンⅠ世を先の関数にあてはめてみると・・・
y = 70万・5302 = 19663000万 ≒ 1966億円!?
人が決める「価値」というものは、何に対してもそうですが
理解が難しいですね
【 動く点 】
《 例 》
図のように、点P, 点Qは同時に頂点Bを
出発し ともに秒速2cmでAB, BC上を
動きます。
点P, Qが出発してからx秒後の
△PBQの面積をycm2として
yをxの式で表しましょう

→ x秒後のBQの距離は、 2xcm(= 底辺)
→ x秒後の正三角形の高さは、PからBQへの垂線
垂線とBQの交点をhとすると x秒後の高さは・・・

PH = \(\large{\frac{\sqrt{3}}{2}}\)・2x = \(\small{\sqrt{3}}\)x cm(= 高さ)
(正三角形の高さ)
(1斜辺あたりの「高さ」「底辺」)
∴ y = \(\large{\frac{1}{2}}\)・底辺・高さ = \(\large{\frac{1}{2}}\)・2x・\(\small{\sqrt{3}}\)x A. y = \(\small{\sqrt{3}}\)x2
PH = \(\large{\frac{\sqrt{3}}{2}}\)・2x の部分が??な場合は
2x:PH = 1:\(\large{\frac{\sqrt{3}}{2}}\) → PH = \(\large{\frac{\sqrt{3}}{2}}\)・2x = \(\small{\sqrt{3}}\)x でも もちろんOKですね
《 例 》
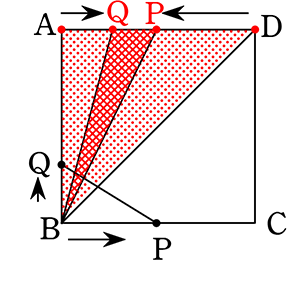
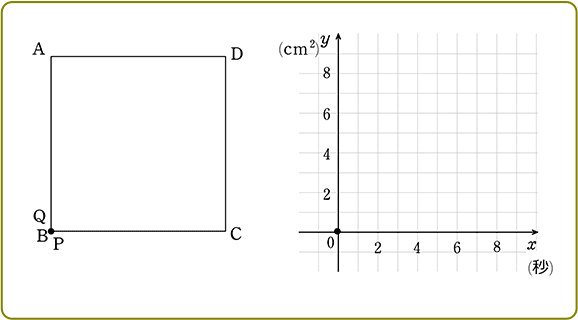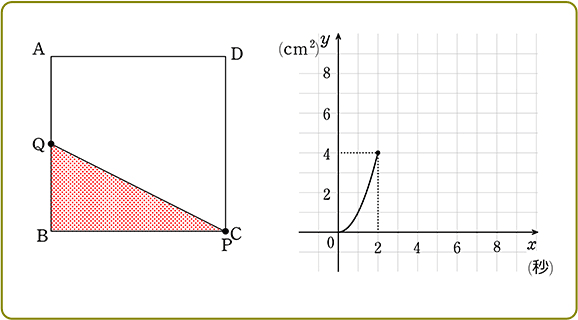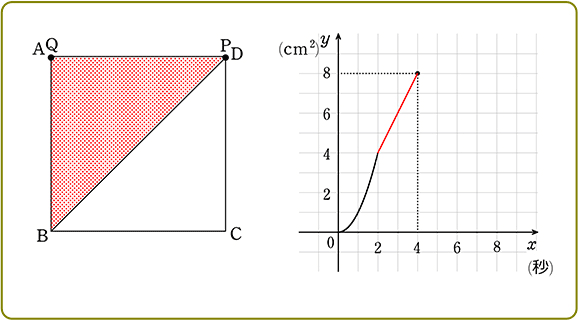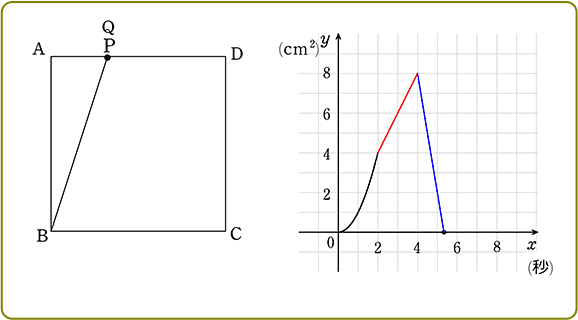
1辺の長さが4cmの正方形ABCDの辺上を動く2点P, Qがあります
点Bを同時に出発して、点Pは毎秒2cmの速さで矢印の方向に、
点Qは毎秒1cmの速さで矢印の方向に進むとき、
x秒後の△BPQの面積をycm2とします

(1) yをxの式で表しましょう
→ 確認として、2点PQの速さが違いますね
→ 簡単にシミレーションしましょう (早い方Pを自分としますね)
Pが2秒でCに到着したときQはまだABの真ん中
Pが4秒でDに到着したときQはやっと点A
P, QがそれぞれD, Aを出発して、Pが\(\large{\frac{1}{3}}\) 秒で\(\large{\frac{2}{3}}\)ADの地点でQと合流
→ ターニングポイントは3つしかなく、しかもPだけを基準に考えられますね
(問題によっては、Pが方向を変えていない間に
Qの方向が変わる(ターニングポイント)こともあります
→ 簡単な図を書き込んでイメージ化
①(0<x≦2秒のとき)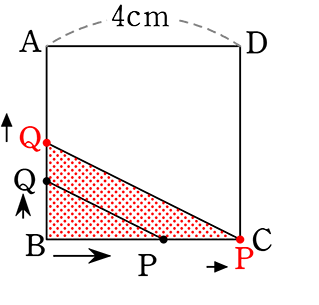
②(2≦x≦4秒のとき)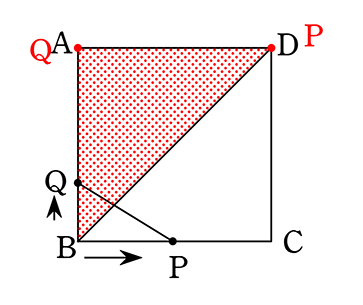
③(4≦x≦5\(\large{\frac{1}{3}}\) 秒のとき)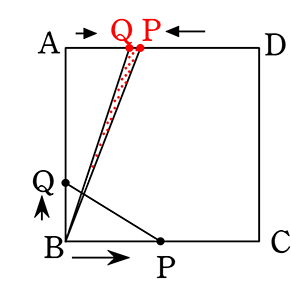
①と②の間がイメージしにくいなら、さらに途中イメージを描いてみる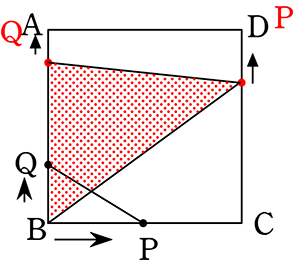
(0<x≦2秒 のとき)
→ (点BPQが作る三角形において、どこを底辺、どこを高さとみなすかは自由です)
(BPを底辺、BQを高さとしてみますね)
BPの距離(長さ) = 2x cm ←距離 = 速さ×時間 = 2cm/秒×x秒)
(2秒で点Cに到着することがわかりますね)
BQの距離(高さ) = 1x cm ←距離 = 速さ×時間 = 1cm/秒×x秒)
∴ 三角形の面積 y = \(\large{\frac{1}{2}}\) ・2x・1x = x2
(2≦x≦4秒 のとき)
→ 今度はBQを底辺としてみますね
→ すると点PがCD間を動いている間は高さはずっと「4」ですね
( 底辺が大きくなっていくので、完全な等積変形ではないですが、考え方は使えますね )
∴ 三角形の面積 y = \(\large{\frac{1}{2}}\) ・1x・4 = 2x
(4≦x≦\(\large{\frac{1}{3}}\) 秒のとき)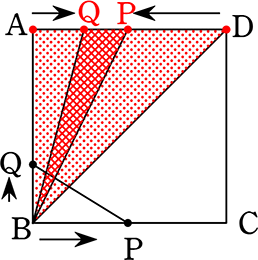
→ 今度はADの辺を底辺としてみると、
ⅰ) △BPQ = \(\large{\frac{1}{2}}\)・PQ・4 = \(\large{\frac{1}{2}}\)・(AD-PD-AQ)・高さ4
他にも
ⅱ) △BPQ = △BAD-Pの速さが3cm/秒の△BDP(QはAで停止)と考えても同じことですね ←(3つの速さのうちの「相対速さ」)
ⅰ) y = \(\large{\frac{1}{2}}\)・{4-(2x-8)-(1x-4)}・4 = (12-2x-x+4)・2 = (-3x+16)・2 = -6x+32 (動点Pの位置表現)
ⅱ) y = △BAD-△BDP = 8-△BDP
= 8-\(\large{\frac{1}{2}}\) ・4・3(x-4) = 8-6x+24 = -6x+32
A. y = x2 (0<x≦2のとき)
y = 2x (2≦x≦4のとき)
y = -6x+32 (4≦x≦\(\large{\frac{16}{5}}\) のとき)
●高さが変わる、変わらなくなる、底辺が変わる、変わらなくなる
( = ターニングポイント)で、面積yの式が変わりますね
●高さも底辺も『両方変化するとき』は両方xを含むので → x2 が発生 → 放物線
高さか底辺か『いずれかしか変化しないとき』は、
片方しかxを含まないので → ただのx が発生 → 直線
●イメージ内で早い方を基準に2点を動かしてみて、ターニングポイントを
把握することがポイントですね!
(2) (1)で求めた関数をグラフに書き込みましょう

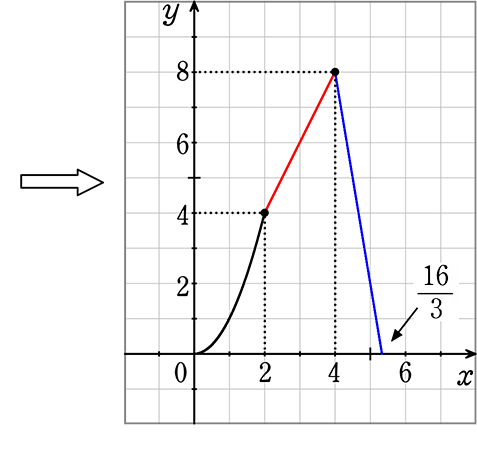
ここで、(1)の4≦x≦\(\large{\frac{16}{5}}\)のときの関数を求める場合の (x-4)をxで求めていたら
→ y = △BAD-△BAQ-△BDP = 8-△BAQ-△BDP
= 8-\(\large{\frac{1}{2}}\)・4・x -\(\large{\frac{1}{2}}\)・4・2x = 8-2x-4x = -6x+8 となりますね
この式でグラフを描くと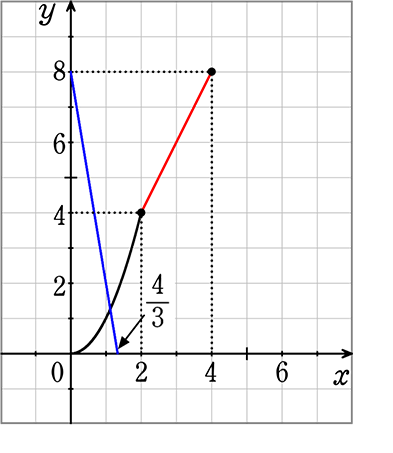
Bが出発点ではなく、
AやDが出発点(基準)ということ
になってしまいますね
面積的には正しいのですが、時間の流れ的におかしいということですね!
よって、
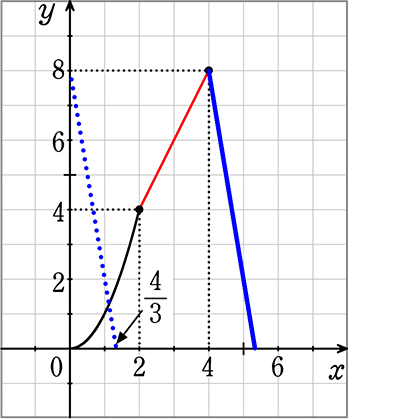
(0, 0)と思っていた基準は、
実はB(0, 0)から見れば(4, 0)である
ので、(0, 0)にそろえるべく(4-4, 0)
xを(x-4)で計算していく
ということですね
( 直線の平行移動)
(3) y = 3 となるxの値を求めましょう
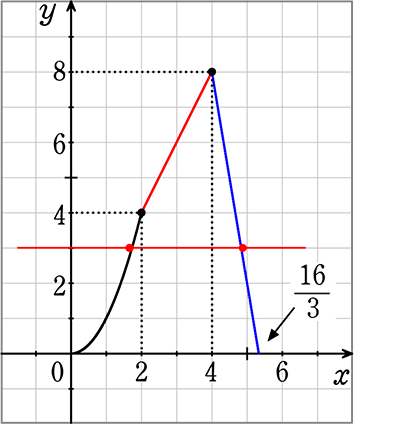
せっかくグラフがあるのですから
グラフを少し利用できますね
赤横線が3cm2ですね
→ y = x2上 と y = -6x+32上に
ありますね
・y = x2 → 3 = x2 → x = ±\(\small{\sqrt{3}}\) → x>0より x = \(\small{\sqrt{3}}\)
・y = -6x+32 → 3 = -6x+32 → 6x = 29 → x = \(\large{\frac{29}{6}}\)
・確認のため、y=2x でも試すと、 → 3 = 2x → x = \(\large{\frac{3}{2}}\)ですが、
y=2x のときの変域は(2≦x≦4)ですので、x=\(\large{\frac{3}{2}}\)は「不適」ですね!
∴ x = \(\small{\sqrt{3}}\) 、x = \(\large{\frac{29}{6}}\) のとき
【 重なる図形 】
《 例 》
図のような台形ABCDと長方形EFGHが点CFで接して並んでいます

長方形を固定し、台形を矢印の方向に点Cと点Gが重なるまでスライドします
FCの距離をxcm、重なった部分の面積をycm2としたとき
yをxの式で表しましょう
→ まずは、台形がどのような台形か分析ですね
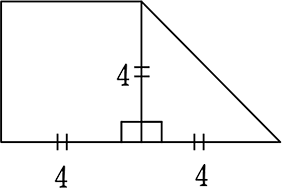
→ 正方形+直角二等辺三角形ですね
→ ①ターニングポイントは、DがEに重なるまで → 直角二等辺三角形の拡大

→ ②その後は、台形の幅が広くなっていく ですね

(0≦x≦4のとき)
y = \(\large{\frac{1}{2}}\)・x・x = \(\large{\frac{1}{2}}\)x2
(4≦x≦8のとき)

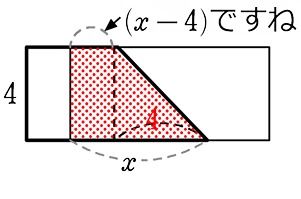
y = 台形の面積
= \(\large{\frac{1}{2}}\)(上+下)(高さ)
= \(\large{\frac{1}{2}}\){(x-4)+x}(4)
= \(\large{\frac{1}{2}}\)・(2x-4)・4 = 4x-8
y = \(\large{\frac{1}{2}}\)x2 (0≦x≦4のとき)
A. y = 4x-8 (4≦x≦8のとき)
《 例 》
先ほどとほぼ同じ問題になりますが・・・
図のような台形ABCDと長方形EFGHが点CFで接して並んでいます
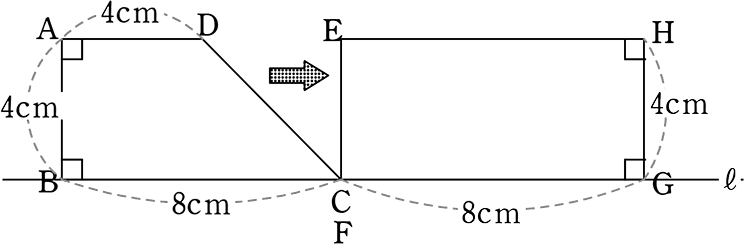
長方形を固定し、台形が矢印の方向に2cm/秒の速さで
点Cと点Gが重なるまでスライドします
x秒後の重なった部分の面積をy cm2としたとき
yをxの式で表しましょう
→ xが「距離」から「時間」になりましたが
時間を、2cm秒×時間にすれば結局「距離」ですね
→ ターニングポイント、2秒(2cm/秒×2秒 = 4cm)までは直角二等辺三角形
その後、台形の幅が広くなっていく ですね


(0≦x≦2 のとき)
y = \(\large{\frac{1}{2}}\) ・2x・2x = 2x2
(2≦x≦4 のとき)
y = 台形の面積
= \(\large{\frac{1}{2}}\)(上+下)(高さ)
= \(\large{\frac{1}{2}}\){(2x-4)+2x}(4)
= \(\large{\frac{1}{2}}\)・(4x-4)・4
= 8x-8
y = 2x2 (0≦x≦2のとき)
A. y= 8x-8 (2≦x≦4のとき)
(2) 面積が16cm2となるのは、動き始めから何秒後でしょう
→ 適当にyに16を代入してみると…
・y = 2x2 → 16 = 2x2 → x2 = 8 → x = 2\(\small{\sqrt{2}}\)
∴ xの値が、0≦x≦2 に収まっていないので OUT!
・y = 8x-8 → 16 = 8x-8 → 8x = 24 → x = 3
∴ xの値が、2≦x≦4 に収まっているのでSAFE!
A. 3秒後
② グラフ操作問題
【 相似 】
《 例 》
関数y = ax2のグラフ上に、2点A(-3, 9)、B(b, b2) がある
2点A、Bを通る直線がx軸と交わる点をCとする
AB:BC = 2:1であるとき bの値を求めましょう
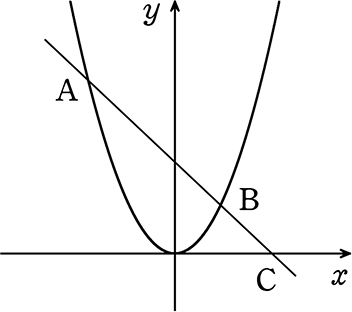
→ データを書き込んでみると
y = ax2 は1点が判れば 式がわかるので
→ 9 = (-3)2a → 9a = 9 → a = 1 ∴ y = x2
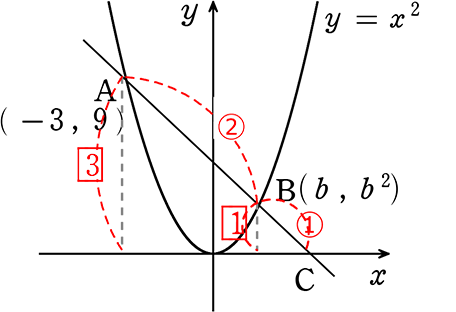
→ 「山型」の「L型」の利用ですね
b2:9 = 1:3 → 3b2 = 9
b = ±\(\small{\sqrt{3}}\)
b>0より ∴ b = \(\small{\sqrt{3}}\)
( 相似「A型、L型、H型」)
《 例 》
図の①はy = x2、②はy = ax2 (a>1)のグラフである
今、直線③が①、②、y軸と図のようにA、B、C、D、Eで交わっている
Aのx座標は-1、AB:BC:CD = 1:2:3 である

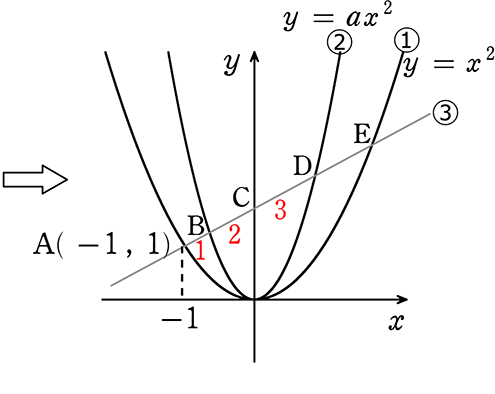
(1) aの値を求めましょう
→ B, C, D のそれぞれの「x座標」は比から求められますね
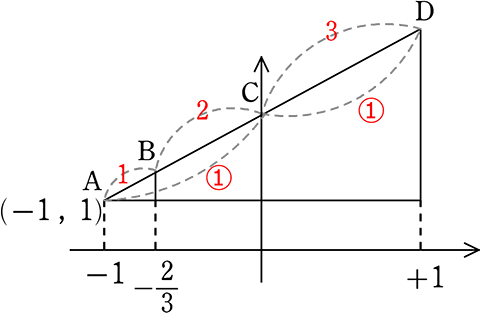
AB:BC = 1:2ということは
BはACを3つに分けた内の2つ
∴ Bのx座標は -\(\large{\frac{2}{3}}\)
∴ Bの座標は、B(-\(\large{\frac{2}{3}}\), \(\large{\frac{4}{9}}\)a)
↑y = ax2に-\(\large{\frac{2}{3}}\)を代入したものが
y座標ですね
AB:BC:CD = 1:2:3ということは
AC:CD = 1:1 ←Cは中点
∴ Dのx座標 1
∴ Dの座標は、D(1, a)
文字が残りながらも(x座標、y座標)が解りましたので、あとは「相似」の
「山型、L型」を利用してy座標ですね
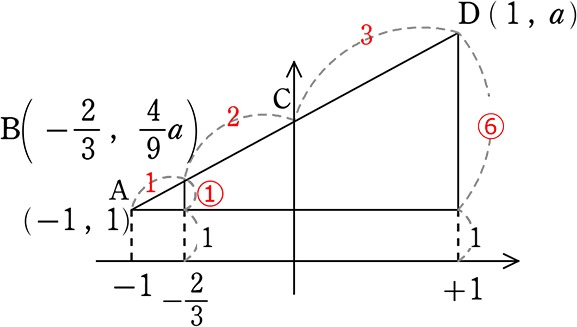
→ \(\large{\frac{4}{9}}\)a-1:a-1 = ①:⑥
\(\large{\frac{4}{9}}\)aはx軸からの距離ですが、三角形の内部の実線部分には不要
なので「-1」
(L型は台形に使えない)
①・(a-1) = ⑥・(\(\large{\frac{4}{9}}\)a-1) → 3a-3 = 8a-18 → -5a = -15
A. a = 3
(2) Eの座標を求めましょう
→ A、B、C、Dの座標が全て数字で判明したのであとは自由自在ですね
2点から直線③の式を求め、y = x2 との交点を求めますね
きれいな数字の A(-1, 1)と D(1, 3)でいきますね
直線y = \(\large{\frac{3-1}{1+1}}\)(x+1)+1 = \(\large{\frac{2}{2}}\)(x+1)+1 = x+1+1 = x+2
∴ 直線③は y = x+2
交点は
\(\small{\begin{cases}
y = x^2 \scriptsize{…①}\\
y = x+2 \scriptsize{…②}
\end{cases}}\)
→ x2 = x+2 → x2-x-2 = 0 → (x-2)(x+1) = 0
∴ x = -1, 2 ←この-1は交点Aのx座標ですね
x>0より x座標は(2, )
y座標 → y = (2)2 = 4
A. E(2, 4)
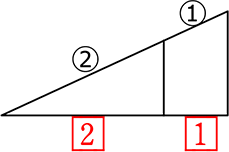
そのまま使えますね(H型)
→ 1つでもx座標がわかっていいれば、他も判るということですね
●x座標がわかれば、文字が残ることもありますが、y座標が判る
(元の y = 〇x2 にx座標を代入するだけですね)
●y座標の文字は、「山型」の「L型」を利用ですね
【 正方形 】
《 例 》
図のように正方形(各辺がx軸、y軸に平行)なとき、Aの座標を求めましょう
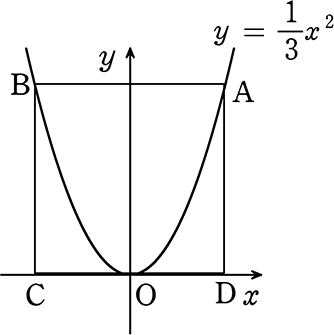
→ Aのx座標を(t, )とおくと・・・
y座標は、y = \(\large{\frac{1}{3}}\)x2に x = tを代入して\(\large{\frac{1}{3}}\)t2 → A(t, \(\large{\frac{1}{3}}\)t2)
ということはDの座標は、D(t, 0)
→ 正方形より、AD = CD = 2OD
AD = 2OD → \(\large{\frac{1}{3}}\)t2 = 2t → t2-6t = 0 → t(t-6) = 0
∴ t = 0, 6 t>0より t = 6
↑0のときも確かに AD = 2ODですが、
「距離」がないので正方形とはいえないということですね
こんなものはありませんね!
これは(0, 0)
という「点」ですね
t = 6と判明しましたので、y座標も数字でわかりますね
y座標 = \(\large{\frac{1}{3}}\)t2 = \(\large{\frac{1}{3}}\)(6)2 = 12
A. A(6, 12)
《 例 》
図のように正方形があるとき、Aの座標を求めましょう
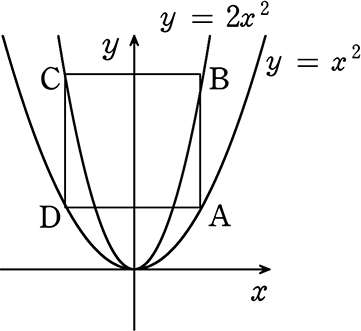
→ Aのx座標をtとおくと・・・
A(t, t2)
B(t, 2t2)
D(-t, t2)
↑Aをtとおく決まりはありません、BでもDでもCでもOKです
→ 正方形より、DA = AB
2t = 2t2-t2 → t2-2t = 0 → t(t-2) = 0
∴ t = 0, 2 t>0より t = 2
∴ A(t, t2) に t = 2を代入して
A. A(2, 4)
《 例 》
図のグラフは、y = ax2 、 y = a
図形ABCDは正方形、
点A、Cはy = ax2 上の点である
正方形の面積が100のとき、aの値を求めましょう
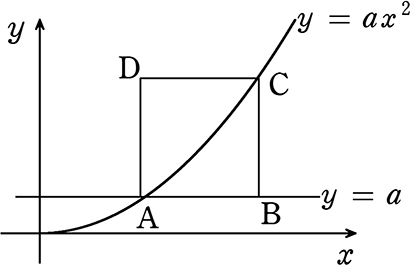
→ 正方形の面積が100ということは、1辺は 10 ですね
→ y = ax2とy =aの交点が求められるかチャレンジですね
ア) 先のようにAのx座標を(t, )としてもよいですし
イ) 今までのように、「交点は連立方程式」でもよいですね
イ)の方が単純ですが、ア)でいってみますね
x座標を(t, )とすると、y座標は・・・
y = ax2から (t, at2) とも表せられるし
y = aから (t, a) とも表せますね
y座標は共通(交点)であるから at2 = a → t2 = 1 → t = ±1
t>0 より t = 1 ∴ A(1, a)
→ A(1, a)より・・・
B(11, a)
C(11, a+10)
と表すことができますね
→ C(11, a+10)は y = ax2 上の点より、代入するとaだけの式になって
aが求められそうですね
a+10 = a(11)2 → a+10 = 121a → 120a = 10
A. a = \(\large{\frac{1}{12}}\)
●正方形の問題は、正方形は「縦 = 横」
●各座標を文字が混ざりながらでも決めてあげれば、「縦 = 横」を
利用して、文字をつぶしていけますね
【 正三角形 】
《 例 》
関数y = ax2 のグラフとy = 4が2点A, Bで交わり、
三角形OABは正三角形になっています
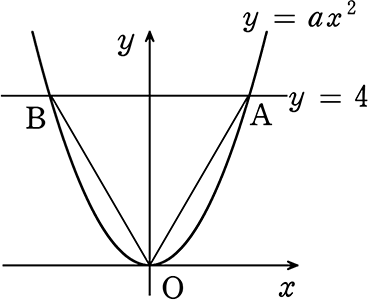
(1) 点Aの座標を求めましょう
→ 正三角形ということは、その半分は「サブローキュー」ですね

t:4 = 1:\(\small{\sqrt{3}}\)
\(\small{\sqrt{3}}\)t = 4
t = \(\large{\frac{4}{\sqrt{3}}}\)
∴ A(\(\large{\frac{4\sqrt{3}}{3}}\), 4)
(2) aの値を求めましょう
→ 判明した座標を代入するだけですね
y = ax2 → 4 = a(\(\large{\frac{4\sqrt{3}}{3}}\))2 → 4 = a・\(\large{\frac{16・3}{9}}\) → 12 = 16a
A. a = \(\large{\frac{3}{4}}\)
(3) 点Bを通り、△OABを2等分する直線の式を求めましょう

→ ということは、
ア) BとAOの中点を通ればよい または
イ) Bを通り傾きがAOと垂直であればよい または
ウ) 図形の性質から単独で傾きを求める どれでもOKですね
考え方ア)
中点m = (\(\large{\frac{x_1+x_2}{2}}\), \(\large{\frac{y_1+y_2}{2}}\)) = (\(\large{\frac{\large{\frac{4\sqrt{3}}{3}}+3}{2}}\), \(\large{\frac{4+0}{2}}\)) = (\(\large{\frac{4\sqrt{3}}{6}}\), 2) = (\(\large{\frac{2\sqrt{3}}{3}}\), 2)
2点 B(-\(\large{\frac{4\sqrt{3}}{3}}\), 4)、m(\(\large{\frac{2\sqrt{3}}{3}}\), 2) を通る直線の式は
\(\small{\begin{cases}
4 = -\large{\frac{4\sqrt{3}}{3}}\small{a+b} \\
2 = \large{\frac{2\sqrt{3}}{3}}\small{a+b}
\end{cases}}\)
12 = -4\(\small{\sqrt{3}}\)a+3b
-) 6 = 2\(\small{\sqrt{3}}\)a +3b
6 = -6\(\small{\sqrt{3}}\)a
∴ a = -\(\large{\frac{\sqrt{3}}{3}}\) , b = \(\large{\frac{8}{3}}\)
∴ y = -\(\large{\frac{\sqrt{3}}{3}}\)x+\(\large{\frac{8}{3}}\)
考え方イ) Bを通り傾きがAOと垂直であればよい
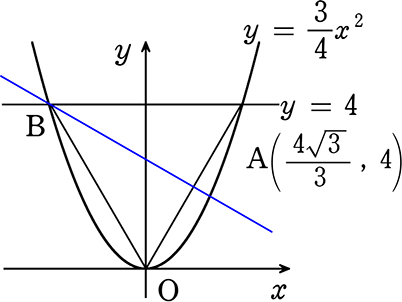
→ AOの傾き = \(\large{\frac{4-0}{\large{\frac{4\small{\sqrt{3}}}{3}}-0}}\) = \(\large{\frac{12}{4\sqrt{3}}}\) = \(\large{\frac{3}{\sqrt{3}}}\) = \(\large{\frac{3\sqrt{3}}{3}}\) = \(\small{\sqrt{3}}\)
→ 傾き\(\small{\sqrt{3}}\)に垂直な傾き = -\(\large{\frac{1}{\small{\sqrt{3}}}}\) = -\(\large{\frac{\sqrt{3}}{3}}\)
(垂直な傾き:2年一次関数)
→ y = -\(\large{\frac{\sqrt{3}}{3}}\)x+b が点B(-\(\large{\frac{4\sqrt{3}}{3}}\), 4) を通るので
4 = -\(\large{\frac{\sqrt{3}}{3}}\)・(\(\large{\frac{-4\sqrt{3}}{3}}\))+b → 4 = \(\large{\frac{12}{9}}\)+b → b = 4-\(\large{\frac{4}{3}}\) = \(\large{\frac{8}{3}}\)
∴ y = -\(\large{\frac{\sqrt{3}}{3}}\)x+\(\large{\frac{8}{3}}\)
考え方ウ) 図形の性質から単独で傾きを求める
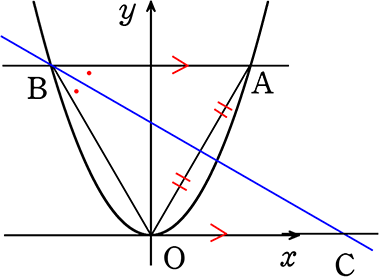
正三角形の1辺AOの中点と頂点Bを通るということは
直線は∠ABOの二等分線
∴ ∠ABC = ∠OCB = 30° (錯角)
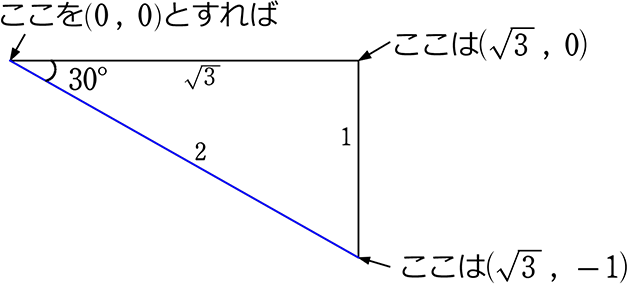
青線の傾き = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{-1-0}{\sqrt{3}-0}}\) = \(\large{\frac{-1}{\sqrt{3}}}\) = -\(\large{\frac{\sqrt{3}}{3}}\)
後は イ)と同様に進めて・・・
y = -\(\large{\frac{\sqrt{3}}{3}}\)x+\(\large{\frac{8}{3}}\) ですね
問題集の解答例と違っていても答が同じであれば、
「考え方」は間違っていないということですね
その上で、問題集の「違う解き方」を理解しようとすれば
さらに「力」がつくということですね!
《 例 》
図のように正三角形の頂点A, Bを y = x2 上におき、
辺BCをy軸と平行になるようすると 重心Gがy軸上にありました
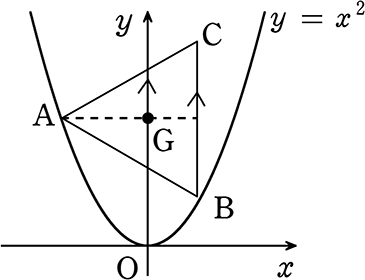
(1) 頂点Bのx座標をtとして 頂点Aの座標を求めましょう
→ B座標はB(t, t2)
→ BCとAGの延長の交点をDとすると
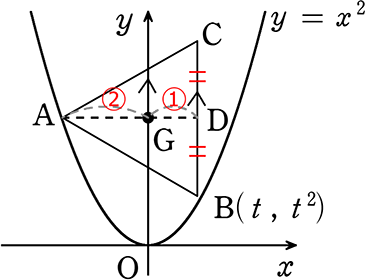
Dの座標は・・・D(t, ?)
Aの座標は・・・GがADの重心より AG:GD = 2:1( 重心)
∴ A(-2t, ?)
AはDと違ってy = x2上の点であるから
x座標が解れば y座標もわかる
x座標-2tをy = x2 に代入して
∴ A(-2t, 4t2)
(2) tの値を求めましょう
→ Dの座標は・・・Aと同じ高さなので、 D(t, 4t2)
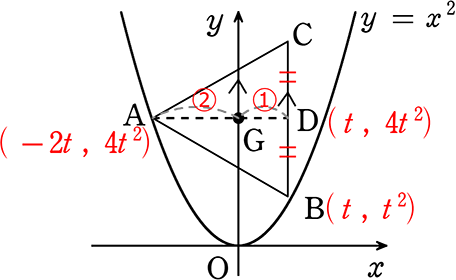
→ AD:DB = \(\small{\sqrt{3}}\):1 = 3t:3t2 → 3\(\small{\sqrt{3}}\)t2 = 3t → \(\small{\sqrt{3}}\)t2-t = 0 → t(\(\small{\sqrt{3}}\)t-1) = 0
∴ t = 0, \(\large{\frac{1}{\sqrt{3}}}\) t>0より A. t = \(\large{\frac{\sqrt{3}}{3}}\)
(3) Cの座標を求めましょう
→ B(t, t2) 、D(t, 4t2)より DB = 3t2
DB = DC より BC間は6t2
∴ C(t, t2+6t2) = (t, 7t2)
これに t = \(\large{\frac{\sqrt{3}}{3}}\) を代入して
C(\(\large{\frac{\sqrt{3}}{3}}\), 7・\(\large{\frac{3}{9}}\))
∴ C(\(\large{\frac{\sqrt{3}}{3}}\), \(\large{\frac{7}{3}}\))
【 平行四辺形 】
《 例 》
図のようにy = 2x2 上に2点A、Bをとり
Bを通りx軸に平行な直線とy軸との交点をCとします
Aを通りx軸に平行な直線と放物線との交点をDとします
△ABCはBCを斜辺とする直角二等辺三角形であった

(1) 点Aのx座標を求めましょう
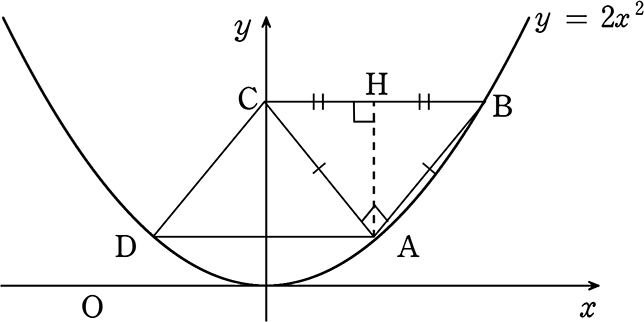
→ 点Aのx座標を(t, )とすると、A(t, 2t2)
後は点Bの座標をtで表して、直角二等辺三角形の性質を用いたら解けそうですね
問題により図が正確でない場合がありますので、
イメージのため正確な直角二等辺三角形を書いてみると
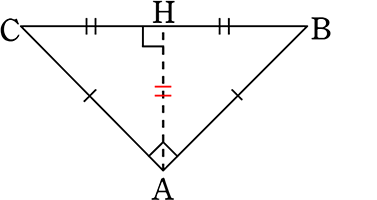
AHも = CH でしたね
∴ CH = BH = AH
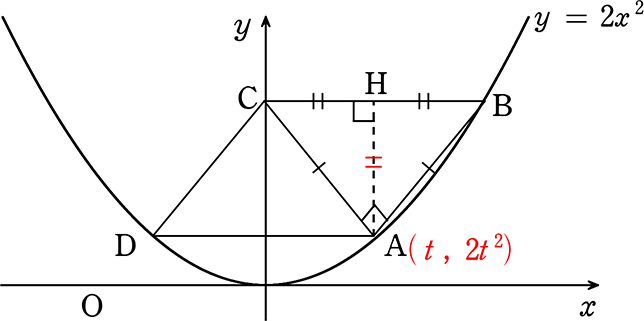
→ Hのx座標は(t, )、 CH = HBより CB = 2CH
∴ B(2t, ) → y = 2x2 に代入して → B(2t, 8t2)
ということは H(t, 8t2)
∴ AH:BH = 1:1 = 6t2:t → 6t2 = t → 6t2-t = 0 → t(6t-1) = 0
∴ t = 0, \(\large{\frac{1}{6}}\) t>0より t = \(\large{\frac{1}{6}}\)
∴A(\(\large{\frac{1}{6}}\), \(\large{\frac{1}{18}}\))
(2) 原点Oを通る直線が、四角形ABCDの面積を2等分するように
直線の式を求めましょう
→ まずは四角形ABCDがどのような四角形か ですね
ADとy軸の交点をEとすると
AE = DE (線対称)
∴ DA = CB …①
AC = DC (線対称)
∴ CD = AB …②
①②より対辺がそれぞれ等しいので四角形ABCDは平行四辺形
( 平行四辺形の条件)
証明方法は他にもたくさんありそうですね
→ 平行四辺形系(平行四辺形・ひし形・長方形・正方形)を2分するには、
平行四辺形の2つの対角線の交点(1つの対角線の中点)を通ればよかったですね
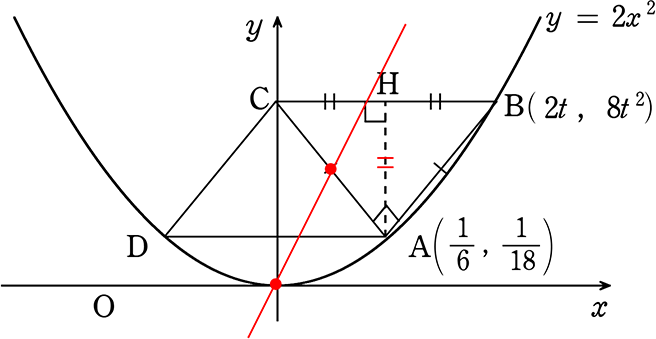
よって、ACの中点を通ればよいということですね
A(\(\large{\frac{1}{6}}\), \(\large{\frac{1}{18}}\))、C(0, \(\large{\frac{2}{9}}\))
→ ACの中点の座標
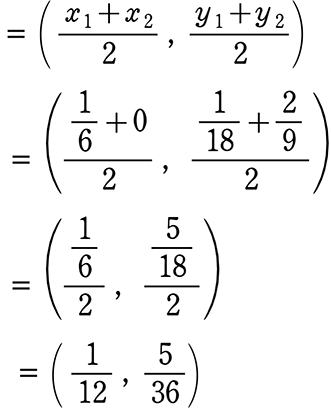
→ 原点と(\(\large{\frac{1}{12}}\), \(\large{\frac{5}{36}}\))を通る式は・・・ y = axに代入して
(原点を通るのでy = axで十分ですね、原点以外なら y = ax+b)
\(\large{\frac{5}{36}}\) = \(\large{\frac{1}{12}}\)a → 5 = 3a → a = \(\large{\frac{5}{3}}\)
∴ y = \(\large{\frac{5}{3}}\)x
【 面積 】
《 例 》
図のように2点A、B、を通る直線①と、
2点A、Bをとおり原点を頂点とする放物線②があります
B(-2, 2)、Cは直線のy切片、AC:BC = 2:1であるとき
次の問いに答えましょう
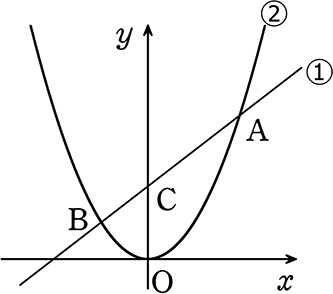
(1) △ABOの面積を求めましょう
→ 判っているデータを書き込むと
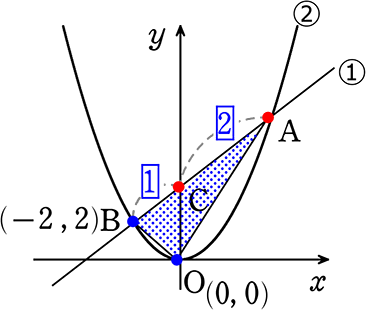
→ あとは●の座標さえわかれば「底辺共有2三角形」より
面積がわかりますね ( 底辺共有2三角形)
→ AC:BC = 2:1より、Aのx座標がわかりますね
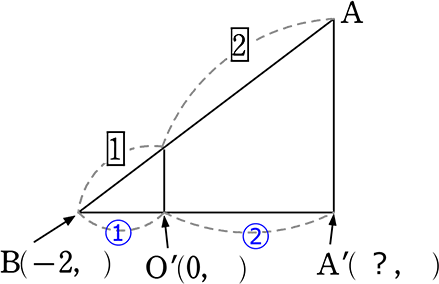
相似の「山型」の「 型」利用でしたね
型」利用でしたね
→ 反対側 = 水平方向 = x軸の比も1:2
∴ BOの
∴ A’O’ = 4 ∴ A(4, )
→ その前に、②の放物線の1点(-2, 2)が判っているので、放物線の式が解る
y = ax2 → 2 = a(-2)2 → 2 = 4a → a = \(\large{\frac{1}{2}}\)
∴ ②の放物線は y = \(\large{\frac{1}{2}}\)x2
∴ Aの座標は y = \(\large{\frac{1}{2}}\)x2 → y = \(\large{\frac{1}{2}}\)(4)2 → y = 8 ∴ A(4, 8)
→ あとはCですね、2点が判明したので「直線の式」がわかる、
「直線の式」がわかれば、そのy切片も求められる ですね
B(-2, 2) A(4, 8)より
\(\small{\begin{cases}
2 = -2a+b \\
8 = 4a+b
\end{cases}}\) これを解いて a= 1、b = 4
∴ ①の直線は y = x+4
∴ y切片であるCは C(0, 4)
→ 4座標が判明しましたので、「底辺共有2三角形」より
△ABO = \(\large{\frac{底辺×(合計高さ)}{2}}\) = \(\large{\frac{CO×(ABの水平距離)}{2}}\) = \(\large{\frac{4\cdot(2+4)}{2}}\) = 12 A. △ABO = 12
(2) △ABOをy軸を軸にして回転させた立体の体積を求めましょう
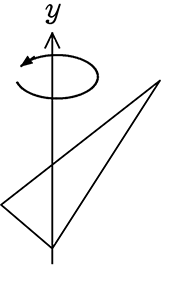
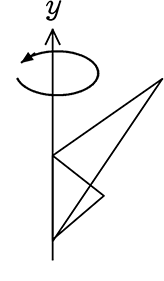
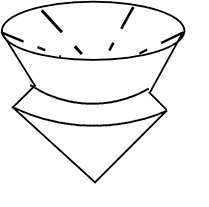
こんな感じの立体でしょうか
大円錐A-不要円錐+中円錐B-不要円錐+ …ですね
円錐だけの式になりましたね
(途中でちょん切られた台形錐?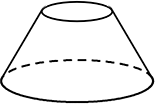
を一発で求める公式はありません)
→ 上から順に分析しますね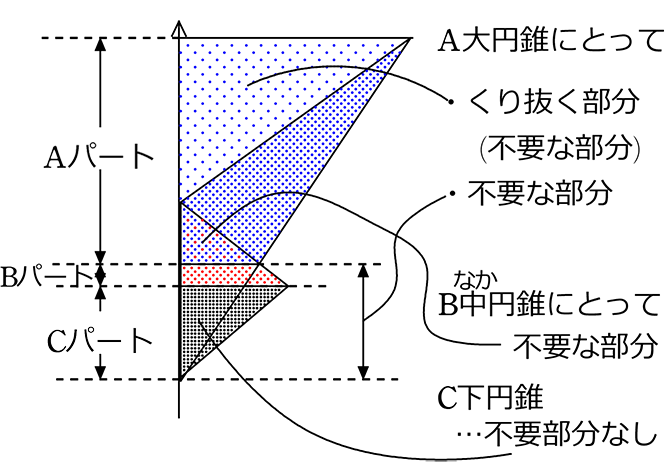
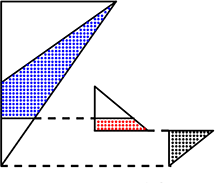
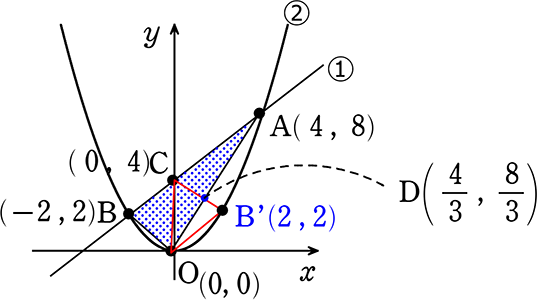
2直線の交点も必要ですね、Dとします
\(\small{\begin{cases}
・AOの直線 y=2x \\
・CB’の直線 y=-x+4
\end{cases}}\)
を解いて ∴ D(\(\large{\frac{4}{3}}\), \(\large{\frac{8}{3}}\))
それでは 分析図と座標を確認しながら…

体積 = Aパート+Bパート+Cパート

= \(\large{\frac{1600π}{81}}\)+\(\large{\frac{152π}{81}}\)+\(\large{\frac{216π}{81}}\)
= \(\large{\frac{1968π}{81}}\)
= \(\large{\frac{656π}{27}}\)
A. (体積は) \(\large{\frac{656}{27}}\)π
《 例 》
図のように、y = x2 のグラフ上に2点A、Bがあり、それぞれのx座標は
-2と3であった、放物線上をAからO、Bと動く点をPとする場合
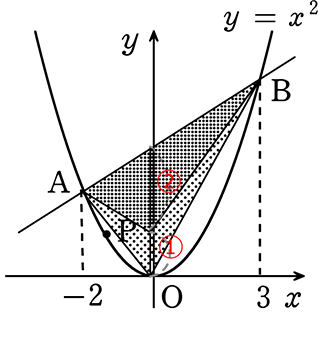
△PABの面積が△OABの面積の\(\large{\frac{2}{3}}\) になるとき、点Pの座標を求めましょう
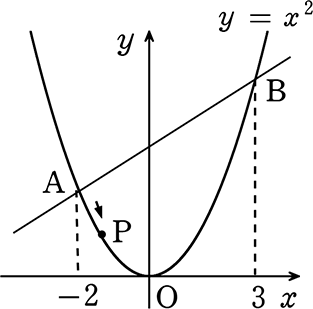
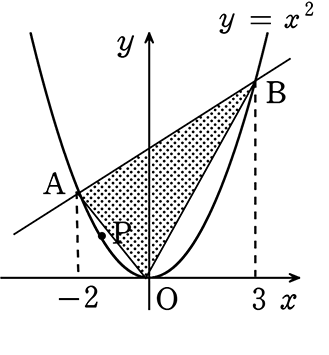
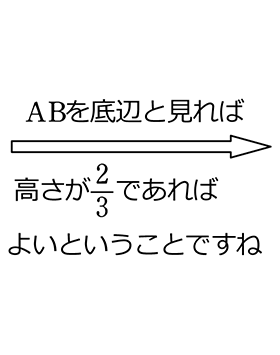
ということは、「頂点の平行移動」 = 「等積変形」ですね
( ここで言う 「高さ」とは正確には「高さにあたるもの」ですね!)
面積を\(\large{\frac{2}{3}}\)にする点Pは 2回ありますね
黒線ABの式を求めて
↓
青線は、傾きは同じで
y切片が黒線の\(\large{\frac{1}{3}}\)の式 原点基準なら
↓
青線と放物線の交点が必要
→ Aの座標 (-2, )が y = x2 上 → y = 4 ∴ A(-2, 4)
Bの座標 (3, )が y = x2 上 → y = 9 ∴ B(3, 9)
→ 2点A, Bを通る黒線の式
y = \(\large{\frac{9-4}{3+2}}\)(x+2)+4 = 1(x+2)+4 = x+6 ∴ y = x+6
→ 青線の式
∴ y = x+2
→ 青線と放物線の交点
\(\small{\begin{cases}
・y = x^2 \\
・y = x+2
\end{cases}}\)
x2 = x+2 → x2-x-2 = 0 → (x-2)(x+1) = 0
∴ x = -1, 2 ∴ P(-1, )と(2, )
y = x2 に代入して
A. P(-1, 1) または (2, 4)
《 例 》
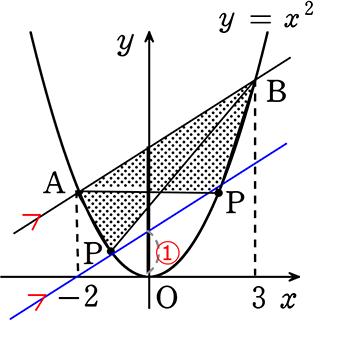
図のように、関数y = ax2 のグラフ上に4点A, B, C, Dがあります
A(-4, 4)、Bのx座標は2、Cのx座標は6、AB//CDのとき
△ABC:△ACD = 1: である
→ AB//CDであるから ABとCDは「底辺にあたるもの」と見れますね
ということは、△CABも△ACDも高さは共通(同じ)ということですね!
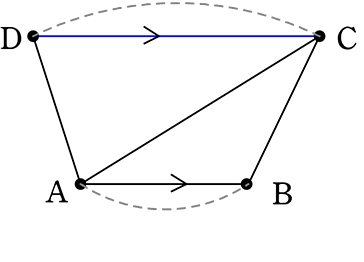
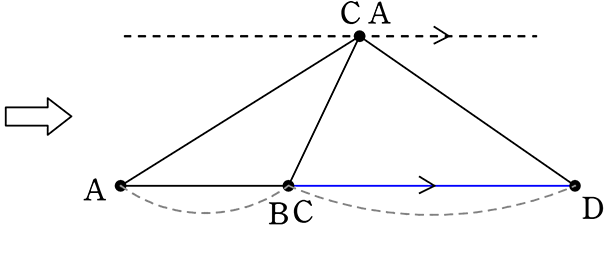
→ 高さが同じということは…底辺の長さの比が そのまま面積比ですね
すなわち AB:DC = △ABC:△ACD
(高さにあたるもの、底辺にあたるもの)
→ あとは AB、CD、長さを求めるために 各座標を求める ですね
順次求めるだけですね

・y = ax2 が通る点が1つでもいいから完全に判っている → y = ax2 が判明
A(-4, 1)を代入してaを求めると … 4 = 16a → a = \(\large{\frac{1}{4}}\)
∴ y = \(\large{\frac{1}{4}}\)x2
・B、C、の座標は x座標が判っているので y = \(\large{\frac{1}{4}}\)x2 に代入するでけですね
B → y = \(\large{\frac{1}{4}}\)(2)2 ∴ B(2, 1)
C → y = \(\large{\frac{1}{4}}\)(6)2 = 9 ∴ C(6, 9)
・直線DCの式は ABと同じ傾(a)き そして C(6, 9)を通る
ABの傾き = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{1-4}{2-(-4)}}\) = \(\large{\frac{-3}{6}}\) = -\(\large{\frac{1}{2}}\)
∴ 平行である直線DCは y = -\(\large{\frac{1}{2}}\)x+b これに判明しているCを入れて
9 = -\(\large{\frac{1}{2}}\)(6)+b → b = 9+3 = 12
∴ 直線DCは y = -\(\large{\frac{1}{2}}\)x+12
・直線DCと放物線の交点が Dの座標
\(\small{\begin{cases}
y = \large{\frac{1}{4}}\small{x^2} \\
y = -\large{\frac{1}{2}}\small{x+12}
\end{cases}}\)
→ \(\large{\frac{1}{4}}\)x2 = -\(\large{\frac{1}{2}}\)x+12 → x2+2x-48 = 0 → (x+8)(x-6) = 0
∴ x = -8, 6 (6, )は点Cですね → ∴ Dが(-8, )
D(-8, )を y = \(\large{\frac{1}{4}}\)x2 に代入して y(座標)を求めると
y = \(\large{\frac{1}{4}}\)(-8)2 = \(\large{\frac{-8\cdot-8}{4}}\) = 16 ∴ D(-8, 16)
・AB = \(\small{\sqrt{(横方向)^2+(縦方向)^2}}\) ←ただの三平方の定理ですね

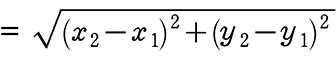
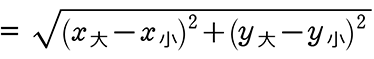
←(x小-x大) でも構いませんが(同じことなので)、
(右にある点)-(左にある点)、
(上にある点)-(下にある点)
と いうふうに自分ルールを決めた方が間違いが少なくなるかと思います
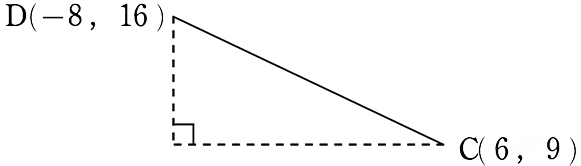
= \(\small{\sqrt{(2+4)^2+(16-9)^2}}\) = \(\small{\sqrt{196+49}}\) = \(\small{\sqrt{245}}\) = 7\(\small{\sqrt{5}}\)
∴ △ABC:△ACD = AB:DC = 3\(\small{\sqrt{5}}\):7\(\small{\sqrt{5}}\) = 3:7 = 1:\(\large{\frac{7}{3}}\)
∴ ( は) \(\large{\frac{7}{3}}\)
→ 後半はただの「作業」でしたね

座標上の2点間の距離
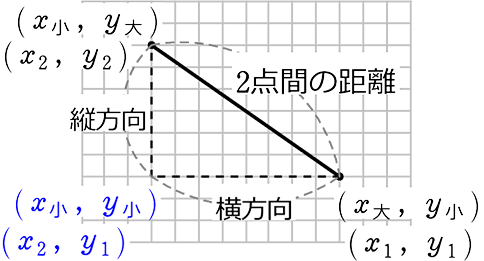
2点間の距離 = 斜辺の長さ

意味さえわかれば「公式」というほどではないですね
よって、どれで理解してもOKですが、おすすめは
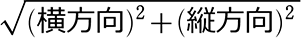
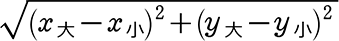
今後、教科書では(x1, y1)、(x2, y2)・・・という表現が増えていきますね
エ いろいろな事象と関数(これまでの関数以外)
円運動系
「時計」「観覧車」など
《 例 》
高さ60cmの時計の分針が30分を出発してから
x分後の分針の先端の高さをycmとする
(1) 0≦x≦120 の範囲で xとyの関係をグラフに表しましょう
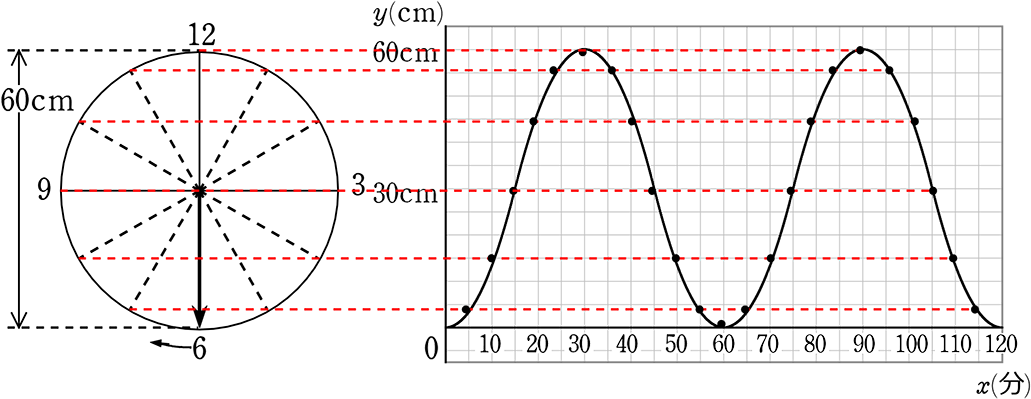
(2) 5分後の高さを求めましょう
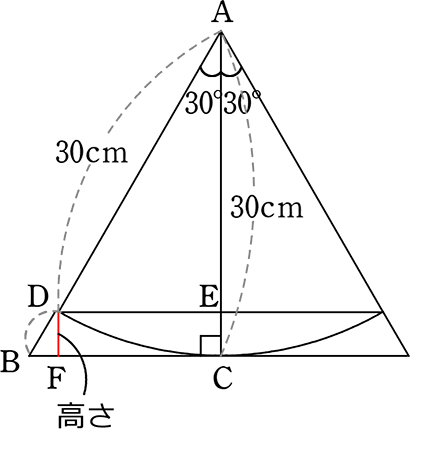
AE:AD30cm = \(\small{\sqrt{3}}\):2
→ 2AE = 30\(\small{\sqrt{3}}\) cm
∴ AE = 15\(\small{\sqrt{3}}\) cm
「山型」の「H型」より
AD:DB = AE:EC
30:DB = 15\(\small{\sqrt{3}}\):30-15\(\small{\sqrt{3}}\)
→ 15\(\small{\sqrt{3}}\)DB = 900-450\(\small{\sqrt{3}}\)
∴ DB = \(\large{\frac{900-450\sqrt{3}}{15\sqrt{3}}}\) = \(\large{\frac{60-30\sqrt{3}}{\sqrt{3}}}\) = \(\large{\frac{60\sqrt{3}-90}{3}}\) = 20\(\small{\sqrt{3}}\)-30
DB:DF = 2:\(\small{\sqrt{3}}\) → (20\(\small{\sqrt{3}}\)-30):DF = 2:\(\small{\sqrt{3}}\) → 2DF = 60-30\(\small{\sqrt{3}}\) → DF = 30-15\(\small{\sqrt{3}}\)
A. 30-15\(\small{\sqrt{3}}\) cm (≒4.02cm)
(3) 10分後の高さを求めましょう
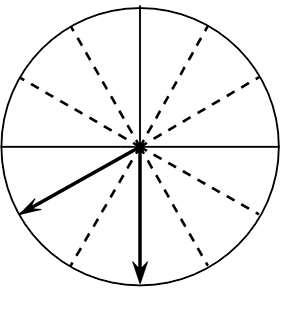
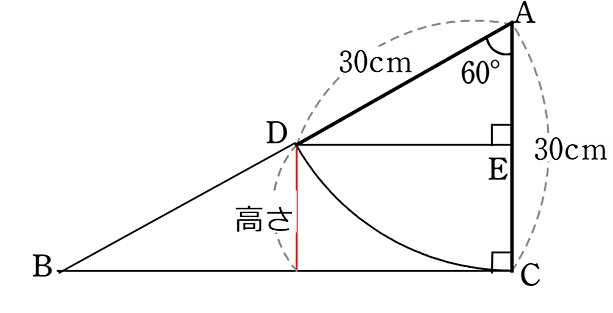
→ ECが高さということですね
AE:AD30cm = 1:2 → 2AE = 30cm
∴ AE = 15cm
∴ EC = 30-15 = 15cm A. 15cm
料金系
「電車・バス・タクシー料金」「宅配料金」「駐車料金」「四捨五入」など区切段階的なもの
《 例 》
あるタクシー会社の料金設定は、下の表のようになっています。
このタクシーにxm乗車したときの運賃をy円とします
乗車距離3kmまでのxとyの関係をグラフに表しましょう
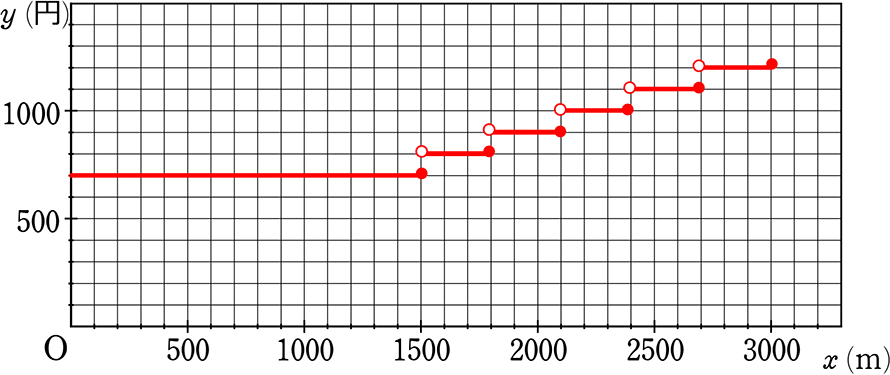
このような「階段状」のグラフでも
「xの値が決まれば、yの値がただ一つ決まる」ので「関数」といえますね
→ 「yはxの関数」と言えますが
逆の「xはyの関数」とは言えなさそうですね
《 例 》
xを小数第一位で四捨五入した数値をyとします。
(1) 0≦x≦5の変域でグラフに表しましょう
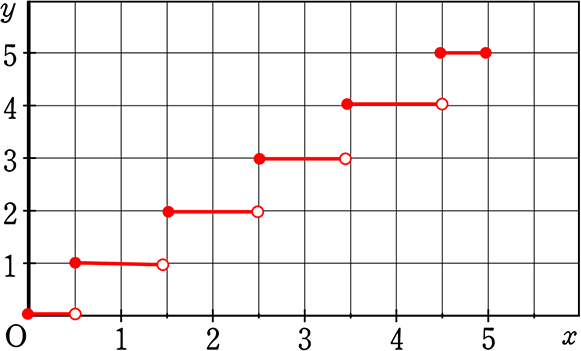
(2) x= 2.49 のとき yの値を求めましょう
→ グラフより y = 2
または 2.49を小数第一位で四捨五入すると 2.0
A. y = 2
お疲れ様でした!
その他の問題は、「問題集」で !!















