| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 図形の相似 | (2) 円周角・中心角 | (3) 三平方の定理 |
| ア | 円周角と中心角の関係の意味と証明 |
|---|---|
| a | 今までの円の性質の再確認 |
| ・ | 内心 |
| ・ | 外心 |
| ・ | 重心 |
| ① | 円周角の定理 |
| ・ | 円周角の定理から派生する定理 |
| ・ | 例題問題 円周角の定理を利用して色々な角度を求めてみる |
| ・ | ここまでの各定理の証明 |
| → | 接点までの距離は等しいという証明 |
| → | 円周角の定理の証明 |
| → | 弧と円周角の定理の証明 |
| ② | 円周角の定理の逆 とその証明 |
| ・ | 内接四角形の対角の和は180° |
| ③ | 内接円、外接円の性質の利用 |
| ・ | 三角形の内接円の半径の利用 |
| ・ | 頂点の角度と円周の関係 |
| ・ | 内接円を持つ四角形の対辺の関係 |
| イ | 円周角と中心角の関係の活用 |
| ① | 接弦定理 |
| ・ | 接弦定理の証明 |
| ・ | 接弦定理の逆 |
| ② | 方べき |
| ・ | 方べきの定理の証明 |
| ③ | 方べきの定理の逆 |
| ・ | 方べきの定理の逆の証明 |
| ④ | その他余談 |
| a | 2つの円の位置関係 |
| b | 2つの円の共通接線の本数 |
| c | トレミーの定理 |
| d | チェバの定理・メネラウスの定理 |
| ・ | メネラウスの定理 |
円周角・中心角
ア 円周角と中心角の関係の意味と証明
「円」には不思議な現象と言いますか、当たり前の現象と言いますか
たくさんの「定理(武器)」がありますね
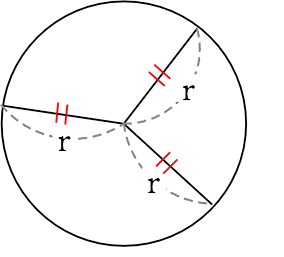
『半径 r は、どこも同じ長さ』
あたりまえすぎるのか、 他の図形と合わさると
見逃してしまうことがありますね
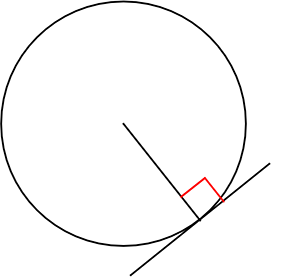
『接線は半径と直角』
(証明)
点と線の最短距離は直角より
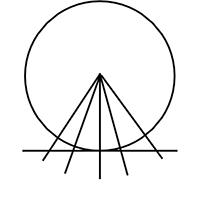
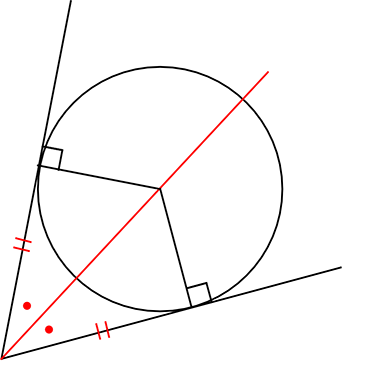
『角の二等分線は円の中心の集まり』
『接点までの距離は等しい』
「接線は半径と直角」
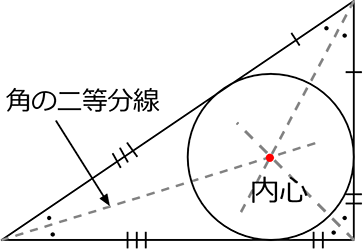
『それぞれは角の二等分線』
⇔『交点が内心』
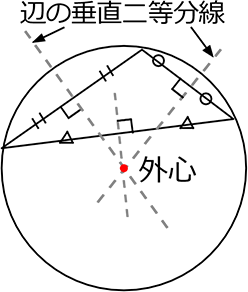
『それぞれは辺の垂直二等分線』
⇔『交点が外心』
cf.
四角形は「必ず」ではないですね → まれに外接円がある
→ まれに外接円がある

三角形5心
【 重心 】
対辺の中点への線 (中線)-1a.png)
中線の交点 ⇔ 重心
『重心に支点をおくと
バランスがとれる』
性質
| 重心 | | ① 中線は2:1 ② 面積6等分 |
① 2:1 とは
-1b.png)
中点連結定理 より
FE//BC、 FE:BC = 1:2
平行線と線分の比の定理より
BG:GE = 2:1
CG:GF = 2:1
同様にFDを結べば
AG:GD = 2:1
(ついでに)
-1c.png)
平行がいっぱいある
対辺がそれぞれ平行より
AFDE、BDEF、CEFD は、
平行四辺形
② 面積6等分 とは
-2a.png)
BCを底辺と見て、高さGが等しいので
① = ②
ADを底辺と見て、高さCが等しいので
(AG:GD = 2:1より)
④③:② = 2:1
ACを底辺と見て、高さGが等しいので
③ = ④
∴ ① = ② = ③ = ④
グルっと1周すれば、
① = ② = ③ = ④ = ⑤ = ⑥
cf.
三角形五心として、「内心」「外心」「重心」「
ありますが、「傍心」「垂心」の2つは中学では不要ですね
それでは、新たな分野へ
中学数学の「円の性質」で最も大事なものと思われる3つのうちの
1つ目「円周角の定理」ですね!
① 円周角の定理
まずは各部名称です


【 円周角 の定理 】

① a = \(\large{\frac{1}{2}}\)b (b = 2a)
(同じ弧に対する)
→ 円周角は中心角の半分
→ 中心角は円周角の2倍
( と
と は同じ向き。
は同じ向き。 と
と 、
、 と
と ではない ですね)
ではない ですね)

② 同じ弧に対する円周角は全て等しい
(∠a = ∠b = ∠c = ∠d = ∠e)
cf.
イメージするときは
「同じ弧に対する~」→「同じ弦に対する~」
でもよいと思います
厳密には「同じ弧に対する~」です
1つの円に対する「弧AB」「弦AB」は1つですが
逆の
1つの「弧AB」「弦AB」に対する円は-3a.png)
→ 弧ABに対する円は「1つに決まる」
→ 弦ABに対する円は「無数に考えられる」
これだけです!
「円周角の定理」に付随するものとして

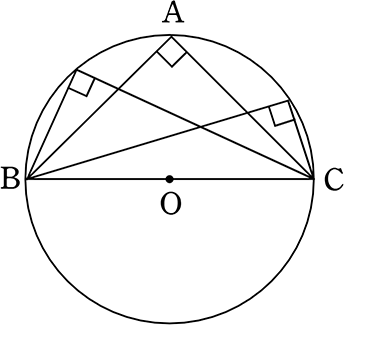
円周角が90°
(\(\small{\stackrel{ \Large \frown }{ BC }}\) は半円の弧)
(∠BOC = 180°)
→ 弧BCに対する中心角BOCは180°と考えれば
円周角BACはその半分 → 90°ですね
念のため
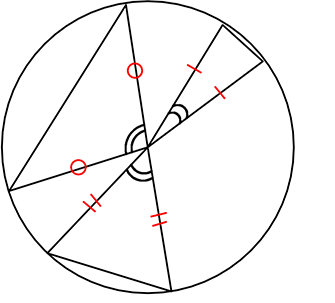
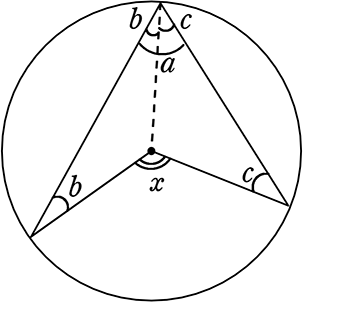
中心角を含む三角形は、 二等辺三角形
( 当然 2辺はどちらも半径だから)
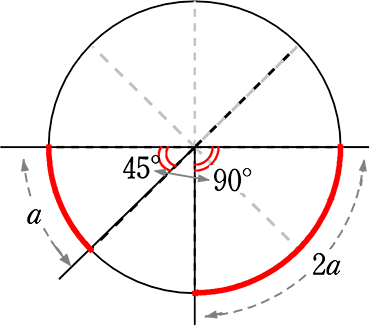
【 定義 】
弧の長さと中心角は比例する
32.png) ということは
ということは
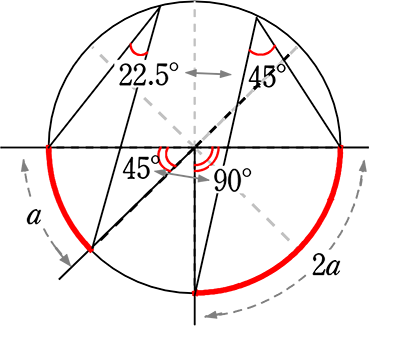
弧の長さと
中心角と
円周角 も比例する
(当然と言えば当然ですね)
不思議なような…当たり前なような…定理ばかりですね

クリック・タップで答え (反応が遅い場合があります)
これは、公式のように憶えてもよいですね
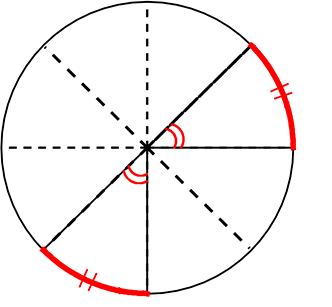
《 例 》
円周を8等分した点です x, y, z の角度を求めましょう
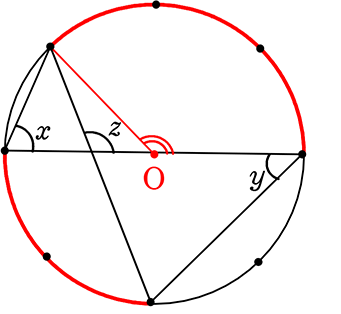
→1コマあたりの中心角は
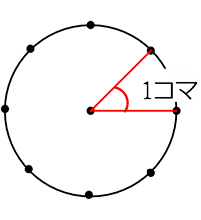
360°÷8 = 45°

xは3コマ分の中心角の半分(=円周角)
→ x = \(\large{\frac{1}{2}}\)(3×45°) = \(\large{\frac{135°}{2}}\) = 67.5°
同様に、yは2コマ分の中心角の半分
→ y = \(\large{\frac{1}{2}}\)(2×45°) = \(\large{\frac{90°}{2}}\) = 45°

同じ弧より 円周角も等しいので
図のような場所もy
∴ zは外角より (スリッパより)
z = x+y = 67.5+45 = 112.5°
《 例 》
図のようなとき、AB:CD を求めましょう
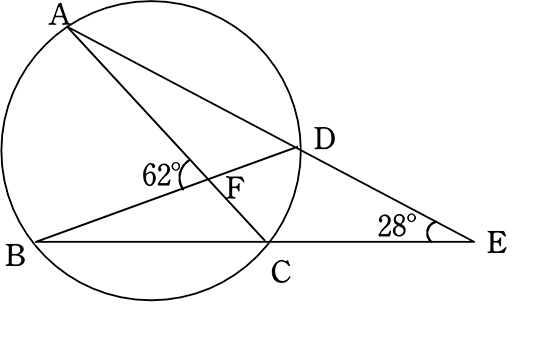
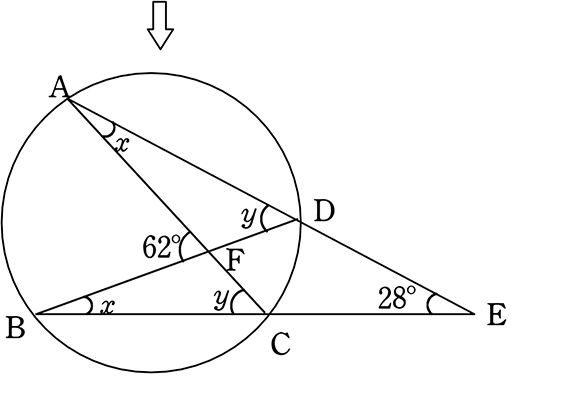
図のようにx, y (同じ弧に対する円周角)
とすると
∠AFB = x+y = 62°(スリッパ)
∠ACB = 28°+x = y (スリッパ)
この連立方程式を解くと
x = 17°
y = 45°
∴ 円周角と弧(弦)の⾧さは比例するので
AB:CD = y:x = 45:17
それでは念のため余談程度で十分だと思われますが、
これまでの円に関する各定理の『証明』です
(円の定理に関する証明は全て、「余談」として見てくださいね!
定理(武器)を使って、「値」を求める問題がほとんどですので!
ですが…「原理」を納得することも大切ですので、できる限り証明していきますね!)
『 接点までの距離は等しい 』
円の外にある1点から引いた2本の接線の⾧さは等しい?
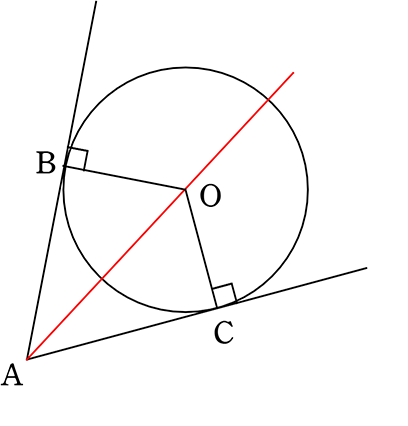
(証明)
△ABOと△ACOにおいて
・△ABOと△ACOは直角三角形 (∠B=∠C=∠R)
・BO = CO (円の半径)
・AO = AO (共通)
∴ 直角三角形の「斜辺と他の1辺が等しい」ので
△ABO ≡ △ACO
∴ AB = AC
『 円周角 の定理 』の証明

a = \(\large{\frac{1}{2}}\)b

同じ弧に対する円周角は全て等しい

点Pが(\(\small{\stackrel{ \Large \frown }{ AB }}\)を除いた部分を、AからBに動くとき
∠APBが常に∠AOBの半分であることを証明すれば、
①、②同時に証明したことになりますね
(証明)
→ 3つの場合分けとなります
(ⅰ) Oが∠APBの内部にある場合

図のように
∠OPA = a とすると
OP = OA (共に半径) より
△OAPは二等辺三角形なので
∴ ∠OPA = ∠OAP = a
POの延長と弧ABの交点をCとする
∠AOC = ∠OPA+∠OAP (外角)
= a+a = 2a
同様に、
∠OPB = b とすると
∠BOC = 2b
∴ ∠APB = a+b
∠AOB = 2a+2b = 2(a+b)
∴ ∠APB = \(\large{\frac{1}{2}}\)∠AOB //
(ⅱ) Oが∠APBの辺上にある場合

△OPBは二等辺三角形 (OP=OB=半径)
∴ ∠OPB = ∠OBP
∠AOBは△OPBの外角 (スリッパ)
∴ ∠APB = \(\large{\frac{1}{2}}\)∠AOB //
(ⅲ) Oが∠APBの外部にある場合

POの延⾧と円の交点をCとする
△OPBは二等辺三角形
∴ ∠BOC = 2a (△OPBのスリッパ)
△OPAは二等辺三角形
∴ ∠AOC = 2b (△OPAのスリッパ)
∠APB = b-a …①
∠AOB = 2b-2a = 2(b-a) …②
∴ ①②より
∠APB = \(\large{\frac{1}{2}}\)∠AOB //
∴ (ⅰ)(ⅱ)(ⅲ)より
① 円周角 = \(\large{\frac{1}{2}}\)中心角
② 同じ弧に対する円周角は全て等しい
すべて「スリッパ」だけで証明できましたね
『弧と円周角 の定理』の証明
弧の長さが等しい


(証明)
手順:弧が同じ → 中心角が同じ → 円周角が同じ
∠APB = \(\large{\frac{1}{2}}\)∠AOB …①
∠CQD = \(\large{\frac{1}{2}}\)∠COD …②
弧の⾧さが等しいとき中心角は等しいので
∠AOB = ∠COD …③
①②③より ∠APB = ∠CQD
(逆の証明)
手順:円周角が同じ → 中心角が同じ → 弧が同じ
(省略しますね)
中心角が等しいとき弧の⾧さは等しいので
∴ \(\small{\stackrel{ \Large \frown }{ AB }}\) = \(\small{\stackrel{ \Large \frown }{ CD }}\)
② 円周角の定理の逆

2点P,Qが直線ABについて
同じ側にあり、
かつ ∠APB = ∠AQB
(↑弧ABは同じである より便利そう)
(証明) 余談として見てOKです
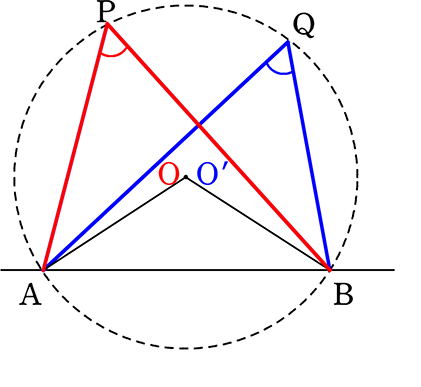
(流れ)
△APBの外接円と△AQBの外接円が
①同じ大きさ
②同じ中心 と言えればよい
△APBに対する △AOB と
△AQBに対する △AO’B が合同なら
→ OとO’が一致
△AOB△AO’Bが二等辺三角形より
(半径にあたるので) → 円の大きさが同じ
∴ 4点は同一円周上
(証明)
円Oを △PABの外接円とすると、OP = OA = OBである
円O’を △QABの外接円とすると、O’Q = O’A = O’Bである
△OABと△AO’Bにおいて
∠AOB = ∠AO’B (仮定より∠P=∠Q、ともにその中心角)
△OABは二等辺三角形 (OA = OBより)
△O’ABも二等辺三角形 (O’A = O’Bより)
二等辺三角形の底角は等しいので
∠OAB = ∠OBA
同様に
∠O’AB= ∠O’BA
△OABと△O’ABの頂角が等しいので
∠OAB = ∠O’AB ∠OBA = ∠O’BA …①
AB = AB (仮定より共通) …②
①②より 「1組の辺とその両端の角が等しい」ので
△OAB ≡ △O’AB
∴ 中心の位置が等しく、半径も等しい(OA=OB=OP=O’A=O’B = O’Q)
ので、2つの外接円が一致する
よって、2点P、Q が直線ABについて同じ側にあり、
かつ ∠APB = ∠AQB ならば 4点P,A,B,Q は1つの円周上にある //
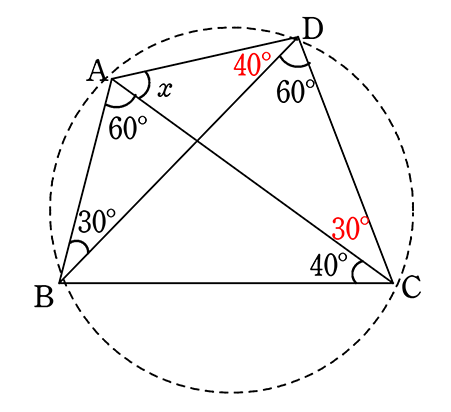
《例》
xを求めましょう
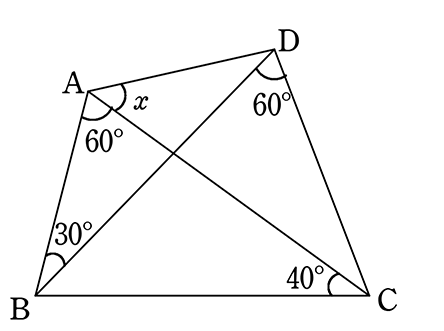
BC共通
∠BAC = ∠BDC
∴ 4点ABCDは同一円周上にある
↑これさえ分かれば!!
∴ AB共通の円周角 ∠ACB = ∠ADB = 40°
AD共通の円周角 ∠ABD = ∠ACD = 30°
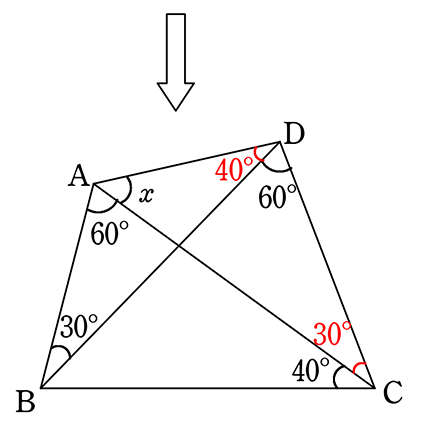
△ACDの内角180°より
x = 180-(40+60+30) = 50°
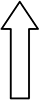
円周角がイメージしにくい場合は
円を書いて下さいね!

→ 色々な方向から円周角が見れるように!
ですね
内接四角形の対角の和は180°
では、2点P、Qが直線ABについて同じ側に「ない」場合の性質です
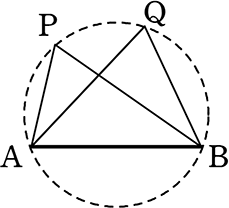
←(今まで)
PQが同じ側
【 内接四角形の対角の和は180°】

4点が同一円周上にある
(四角形が円に内接する)
(a+b = 180°)
(+α)→ a = c (向かい合う内角の外角に等しい)
一言で
「内接四角形」
(∠PAQ+∠PBQ も180° のはずですね)
(原理)
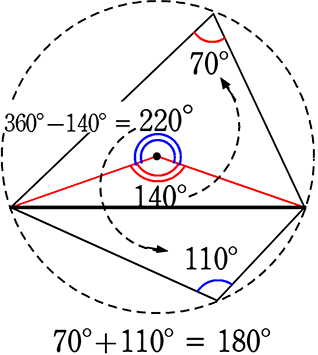
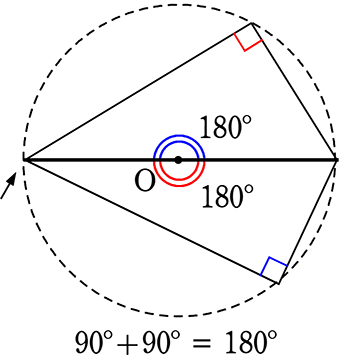

(証明)
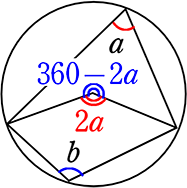
a の中心角 = 2a
逆中心角 = 360°-2a = b の中心角
b の円周角 = \(\large{\frac{360°-2a}{2}}\) = 180°-a
→ a+b = a+(180°-a) = 180°
(イメージ)

2つの中心角の合計は必ず360°
2つの円周角の合計は、その半分 → 180°
〔 a = c の証明 〕
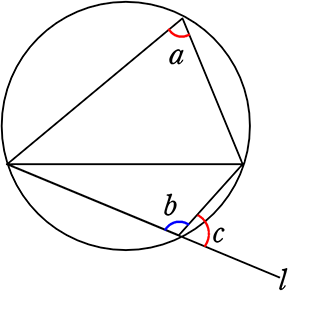
・bは内接四角形(  )から見れば、180°-a
)から見れば、180°-a
→ b = 180°-a → a = 180°-b
・bは直線 l (  )から見れば、180°-c
)から見れば、180°-c
→ b = 180°-c → c = 180°-b
∴ a = c (どちらも右辺が同じ)
(三角形の外角(スリッパ)と同じような考え方ですね)

③ 内接円、外接円の性質の利用
・ 三角形の内接円の半径の利用
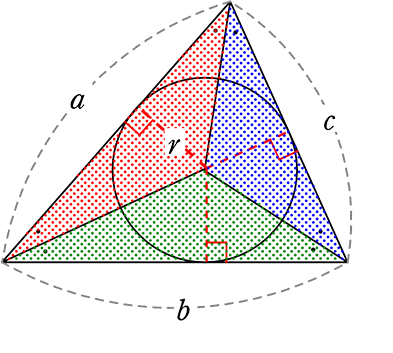
 の面積 =
の面積 =  +
+  +
+ 
= \(\large{\frac{1}{2}}\)ar+\(\large{\frac{1}{2}}\)br+\(\large{\frac{1}{2}}\)cr
= \(\left(\large{\frac{ar+br+cr}{2}}\right )\)
(半径がうまい具合に 「高さ」になる)
《 例 》
図のようなとき面積が 84cm2でした内接円の半径は?
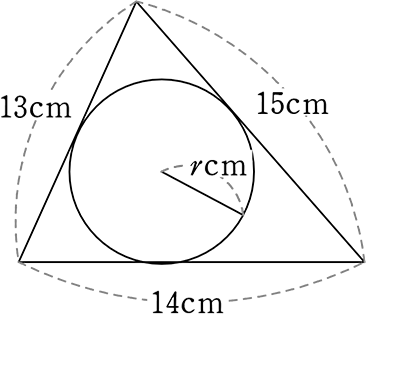
| S | = | \(\large{\frac{13r+14r+15r}{2}}\) |
| = | \(\large{\frac{42r}{2}}\) |
→ 21r = 84 より
r = 4 cm
《 例 》
x を求めましょう
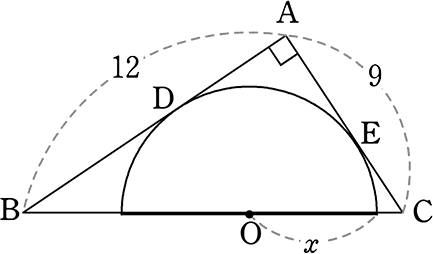
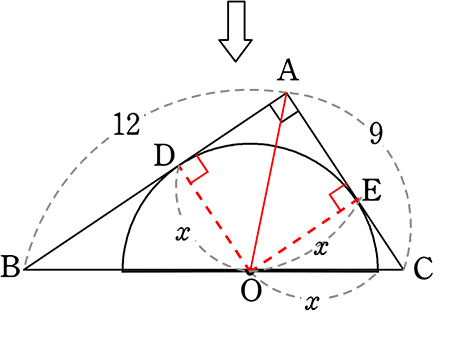
補助線AO, OD, OEを引くと
半径より△OABの高さも
△OCAの高さも xですね
| → △ABC | = | △OAB+△OAC |
| \(\large{\frac{12×9}{2}}\) | = | \(\large{\frac{12x}{2}}\) + \(\large{\frac{9x}{2}}\) |
| 108 | = | 21x |
| 7x | = | 36 |
| x | = | \(\large{\frac{36}{7}}\) |
ちなみに、この次の過程「三平方の定理」で出てきます
「代表的な直角三角形」の1つ「5・4・3 の直角三角形」の内接円の半径rは…
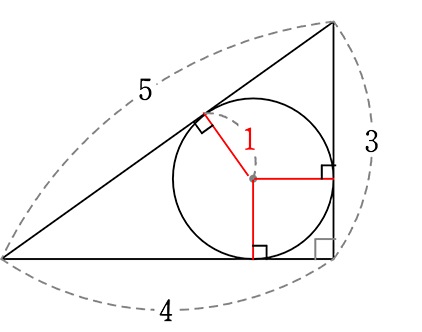
「5, 4, 3 の直角三角形」の
内接円の半径は「1」
上の問題は「5, 4, 3 の三角形」ではありますが、内接円ではないですね
(当たり前ですが)
外接円を描くと
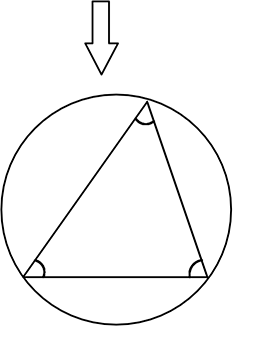
各頂点は「円周角」と言える
《 例 》
次の三角形の外接円の半径を求めましょう

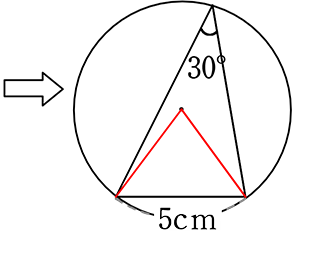
外接円を描くと30°は「円周角」に!
中心角は60°とわかりますね
頂角60°の二等辺三角形 = 正三角形
∴ 半径は 5cm //
頂点の角度と円周の関係
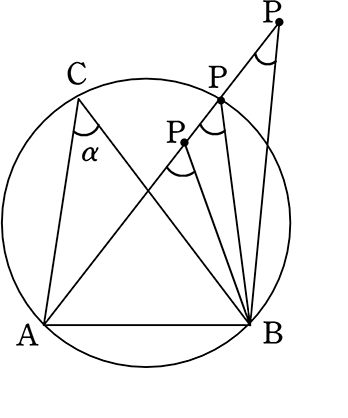
Pは 円周上 にある
Pは 円の内部 にある
Pは 円の外部 にある
証明として、正三角形で底辺の⾧さが同じならば、頂上の角度が
「鈍くなれば、高さが低くなる」「鋭くなれば、高くなる」と
本能的にイメージできるのですが…
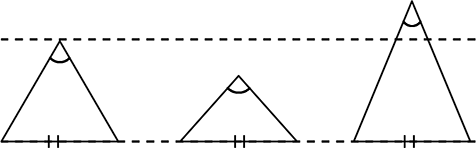
これでは、数学的証明にならないみたいですね…
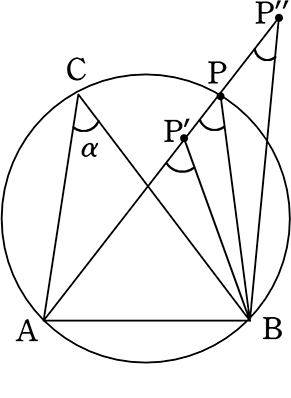
Pは 円の内部 にある
(証明)
内部の点をP’とし、AP’の延⾧と円の交点をPとする
∠AP’Bは△P’PBの∠PP’Bの外角であるから
∠AP’B = ∠APB+∠PBP’
∴ ∠AP’B >∠APB …①
∠APBに何かを足さないと∠AP’Bになれない
→ ∠AP’Bの方が大きいという理論
∠APB = α (円周角の定理) …②
∴ ①②より ∠AP’B>α
∠APB>α
(証明)
点Pが円の内部にないと仮定すると、
点Pは、「円周上」、または「円の外側」にあるかのいずれかである
円周上であれば ∠APB = α、円の外側であれば ∠APB<α となって、
仮定「∠APB>α」 に矛盾する
∴ Pは「円の内部」になければならない (転換法という証明法ですね)
Pは 円の外部 にある
も同様の証明方法となりますので省略しますね
内接円を持つ四角形の対辺の関係
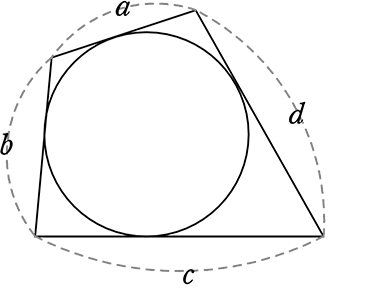
四角形に内接円がある
(対辺 + 対辺 = 対辺 + 対辺)
(証明)
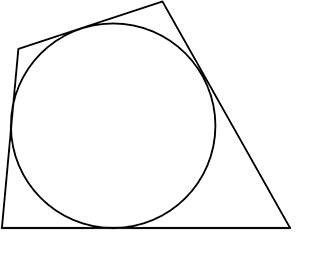
この図は が「4つ」でできている
が「4つ」でできている

接線が「8つ」集まったものと見れますね
ということは
→ 接点までの距離は等しいので
s=s, t=t, u=u, v=v
この4式を足し合わせると
s+t+u+v = s+t+u+v →
∴ 対辺+対辺 = 対辺+対辺 //
《 例 》
図のようなとき、線分CQの長さを求めましょう
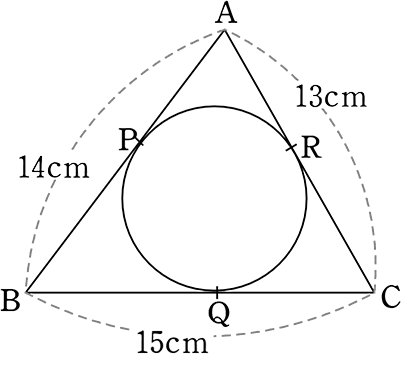
→ CQを xとすると、CRもx
→ AR = AP、BQ = BP より (接点までの距離は等しい)
AR+BQ (=AP+BP) = 14
(13-x)+(15-x) = 14
-2x = -14
x = 7 A. CQ = 7cm
《 例 》
図のような台形に円が内接している時、台形の面積を求めましょう
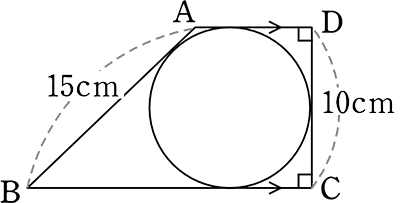
→ 「AD+BC = AB+DC」より
(内接円を持つ四角形
AD+BC = 15+10 = 25
| ∴ 台形の面積 | = | \(\large{\frac{1}{2}}\)(上+下)(高さ) |
| = | \(\large{\frac{1}{2}}\)・25・10 | |
| = | 125 cm2 // |
イ 円周角と中心角の関係の活用
① 接弦定理
中学数学の「円の性質」で最も大事なものと思われる3つのうちの
2つ目「接弦定理」ですね!
現在の公立中学では課程から外れているかもしれませんが
私立中学では必ず学んでいるはずです

接弦定理

・ ∠b = ∠a
・ ∠t = ∠s
(弦BCと接線がつくる∠bは
弧BCの円周角∠aに等しい)
「形」で理解してしまえば十分ですね↓
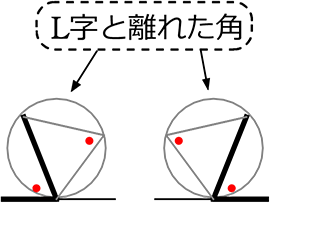
接線と弦のなす角が
離れた角と同じという定理
《 例 》
図のようなとき、xを求めましょう
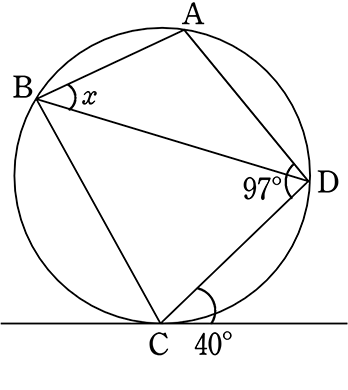

① ∠DBC = 40° (接弦定理)
② ∠ABC+∠ADC = 180°
(内接四角形の対角の和は180°)
∴ (x+40)+97 = 180 → x = 43° //
《 例 》
図のようなとき、xを求めましょう
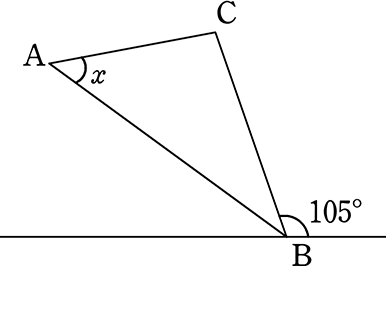
→ A. xは不明!

外接円を書いてみると…
直線は点Bの接線ではない!
→ 「接弦定理」は使えない
接弦定理の証明
それでは、「接弦定理」自体を証明しましょう
…という問題は見たことがありませんが、「納得」するために「原理」として
証明していきますね
「円周角の定理の証明」同様、『場合分け証明』になります
〔 ∠ABCが90°の場合 〕
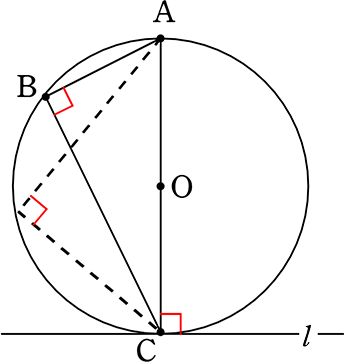
∠ABCが90°のとき、ACは直径 (円周角が90° ⇔ 直径より)
∴ OCは半径
OC ⊥ l (半径と接線は垂直に交わる より)
∠ACl = 90°
∠ABC = 90°(仮定より)
∴ ∠ACl = ∠ABC
外角の定理
ここで次に備えて、「外角の定理(スリッパの定理)」を再度
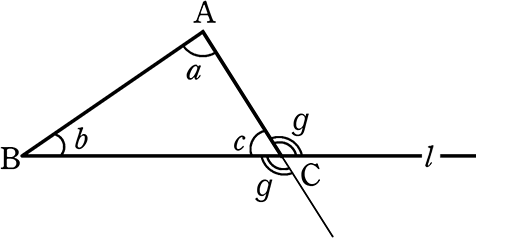
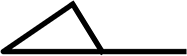 横から見たスリッパ?
横から見たスリッパ?
外角 g = a+b
(証明)
・「三角形の内角」180°から見て c = 180°-(a+b) …①
・「直線」(Bl) 180°から見て c = 180°- g …②
①=②(c = c)より
180°-(a+b) = 180°- g
-a-b = -g
g = a+b //
「三角形の内角の和」も「直線」も、「どちらも」180°ということを、
うまく利用してしていますね! 実は数学ではよく使う手法です
ex)

2つは正方形です
すると ∠a = ∠c となりますね!
・ a = 90°-b
・ c = 90°-b
∴ a = c
| → | 「どちらも」90°をうまく利用していますね |
接弦定理の証明に戻りまして、
〔 ∠ABCが鋭角の場合〕

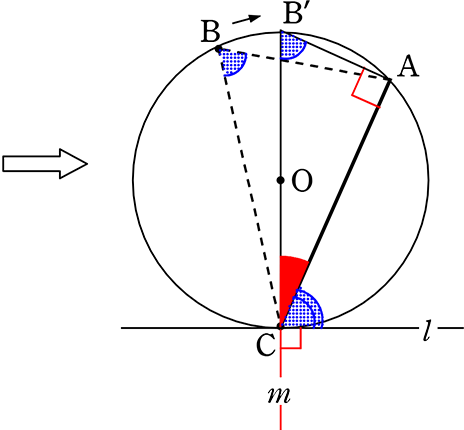
CAをそのままに、BCがOを通るように点Bを動かすと
→ ∠B = ∠B’ (円周角の定理)
→ ∠A = 90° (BCが直径
・三角形の「内角」から見て
 = 180°-90°-
= 180°-90°-  →
→  = 180°-90°-
= 180°-90°- 
・「直線(直径を延長した直線)」B’m から見て
 = 180°-90°-
= 180°-90°-  →
→  = 180°-90°-
= 180°-90°- 
→ どちらも 180°-90°- 
∴  =
= 
〔 ∠ABCが鈍角の場合 〕

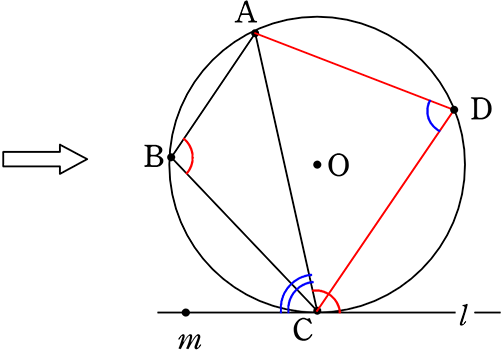
点Bのある\(\small{\stackrel{ \Large \frown }{ AC }}\)の反対側の\(\small{\stackrel{ \Large \frown }{ AC }}\)に、適当な点Dをとると…
∠D= 180°-∠ABC (内接四角形の対角の和は180°)
∠ABCは鈍角(仮定)であるから
∴ ∠D は鋭角
「鋭角の場合の証明」より、∠D= ∠ACm
∴ ①内接四角形から見て、 ∠ABC = 180°-∠D = 180°-∠ACm (置き換えただけ)
②直線mlから見て、 ∠ACl = 180°-∠ACm
∴ ∠B = ∠ACl //
《 例 》
図のようなとき、x を求めましょう
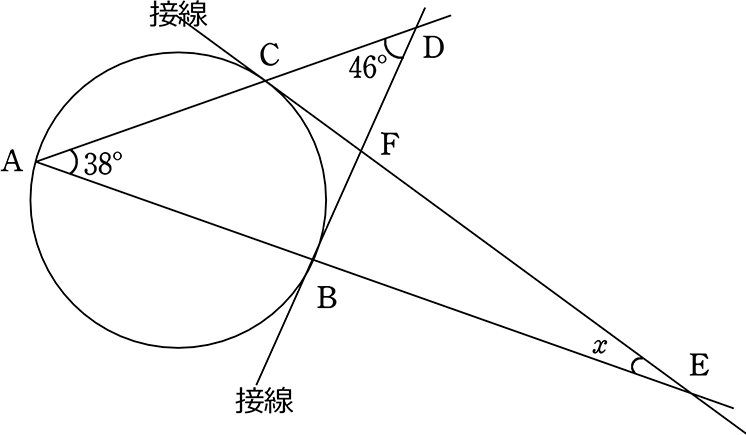
→ CBを結ぶと…
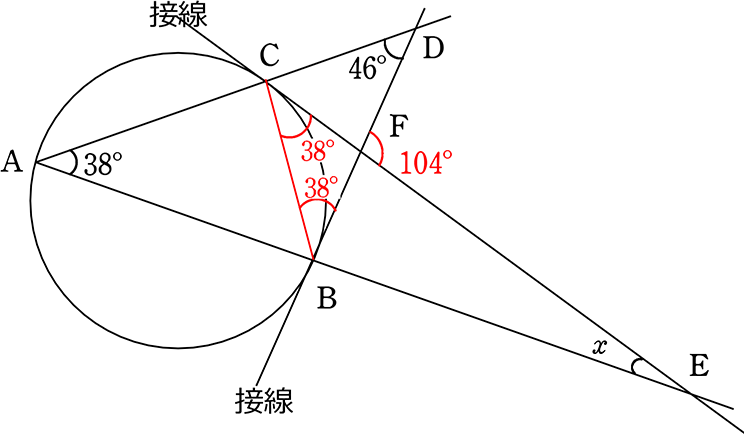
→ ∠DBC = 38° (接弦定理)
→ ∠ECB = 38° (接弦定理)
∴ ∠CFB = ∠DFE (対頂角) = 180°-38°-38° = 104°
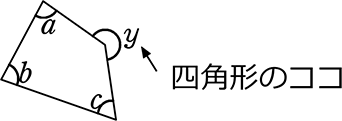
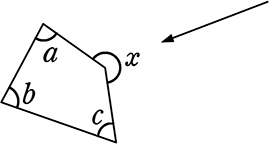
は y = a+b+c (  凹四角形でもOKでしたね)
凹四角形でもOKでしたね)
∴ 104 = 46+38+x
∴ x = 20° //
他にも色々道がありそうですね
∠DCF = 104-46 = 58° (外角の定理)
∠DCFは△CAEの外角
∴ 38+x = 58 → ∴ x = 20° //
どんな方法でも解ければOK!
接弦定理の逆
完全な余談ですね
結果だけで十分ですね!
「あの2つの∠が同じ

【 接弦定理の逆 】
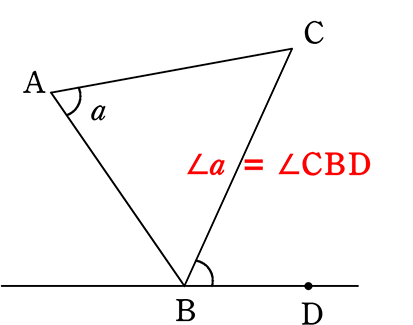

(正確には)
AとDが直線BCに関して反対側にあり、∠a = ∠CBD
接弦定理の逆の証明
念のため証明しますね


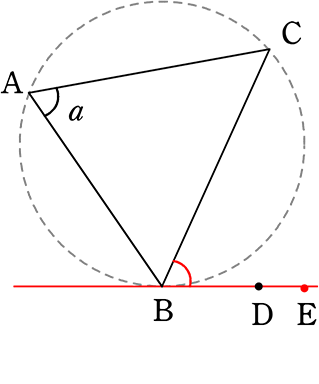
(証明)
△ABCの外接円の接点Bの接線上に、BCに関してAと反対側に点Eをとると、
∠a = ∠CBE (接弦定理より)
∠a = ∠CBD (仮定より)
∴ ∠CBE = ∠CBD となり、
さらにDEはBCの関して同じ側にあるので、B, D, E, は「一直線上」である
∴ BDは三角形ABCの外接円の接線である //
「接線である」ということに価値があるのであって、
「3点は同一円周上にある」ということには全く価値がありませんね
なぜなら、三角形の各頂点は必ず同一円周上にあるからですね
(=どんな三角形でも必ず外接円が描ける)
「同一円周上にある」で価値があるのは「4点(四角形)」の場合ですね!
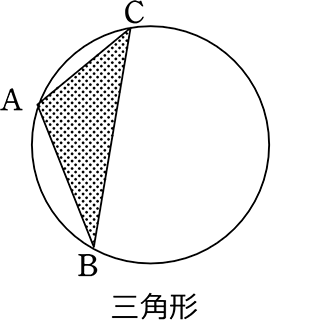
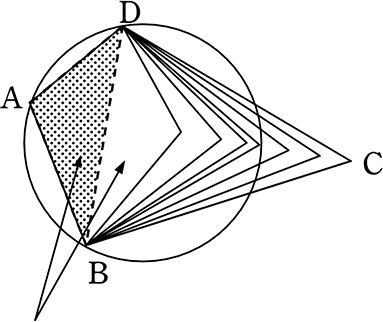
四角形を構成するのは2つの三角形
→ 1つはどの3点を選んでも
「同一円周上(外接円を書ける)」
問題はもう一つの三角形の最後の1点C!
- 思い出 -
娘と何かの問題を解いていた時に…
.png) 「まずは適当に外接円、書いてみるじゃん」
「まずは適当に外接円、書いてみるじゃん」

「…外接円て手書きで書くと何気に難しいよな~」
「じゃあ、そっちもプリントに書き込んでみて!」
![]()

.png) 「・・・」
「・・・」
![]() 「・・・」
「・・・」
.png) 「・・・うッ、うまいね・・・」
「・・・うッ、うまいね・・・」
![]() 「・・・」
「・・・」
cf. バランスイメージ
② 方べき
中学数学の「円の性質」で最も大事なものと思われる3つのうちの最後「方べき」ですね!
「ほうべき」…何か変な名前ですね
名前の由来は分かりませんが
おそらく、
「方」→「平面図形」、
「べき」→「べき乗」≒「累乗」
よって、イメージとして「平面図形」が「累乗」みたいな形になる…感じでしょうか
・・・こだわる部分ではないですね!
3パターンありますが、言っていることは皆同じと言えますね!

方べきの定理
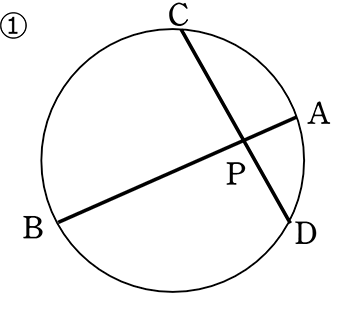
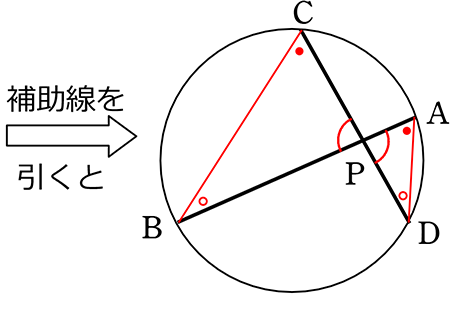
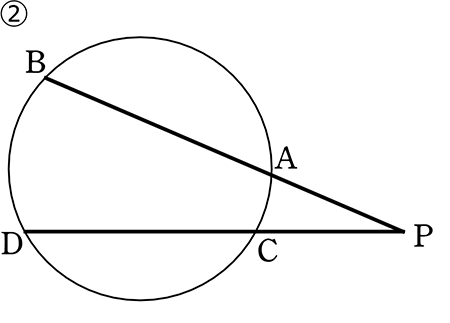
「2角が等しい」
・円周角の定理
・円周角の定理
・または対頂角
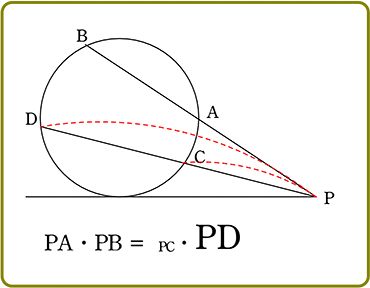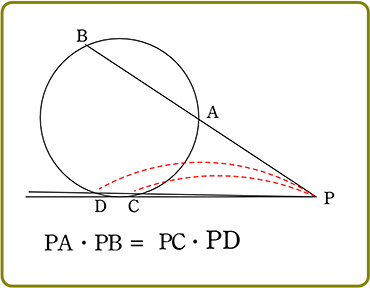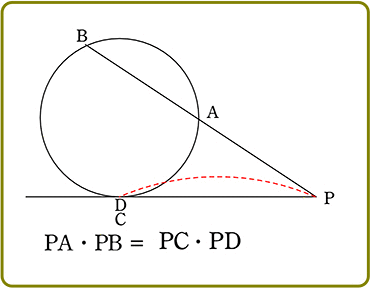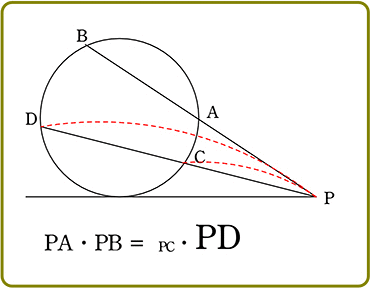
(基本形) △PAD ∽ △PCB
↓
(中間形) PA:PC = PD:PB
↓ (↑他にもたくさんありますね
↓ 「相似ならなんでもよい」)
↓ (もちろん分数形でもOK!)
(最終形) PA・PB = PC・PD
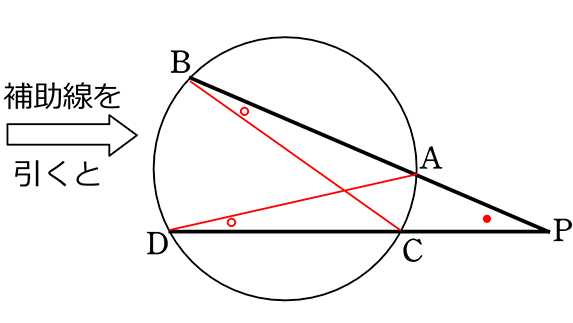
「2角が等しい」
・円周角の定理
・共通角
(基本形) △PDA ∽ △PBC
↓
(中間形) PA:PC = PD:PB
↓
(最終形) PA・PB = PC・PD
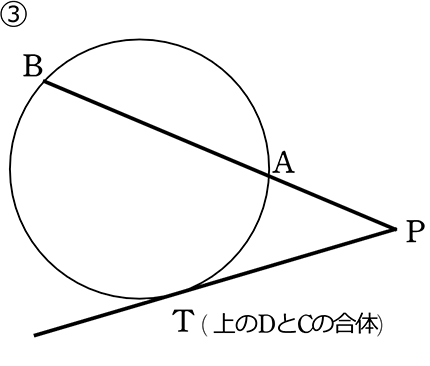

「2角が等しい」
・接弦定理
・共通角
(基本形) △PTA ∽ △PBT
↓
(中間形) PA:
↓
(最終形) PT2 = PB・PA
「基本形」さえ見つけ出せれば、「中間形」「最終形」はおのずと導けますね!
よって、中学数学では「基本形」を見つけ出して「対応する辺」が
どれとどれか(折りたたんだら対応が一致(山型になる)) というイメージさえあれば十分です!
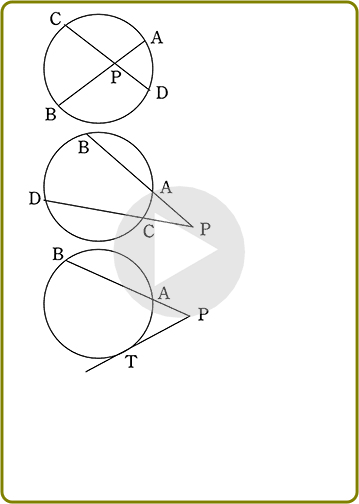
な3イメージで「方べき」は安心ですね
高校数学では「最終形」までを公式のように憶えていれば、幾分か早く問題を
解けると思いますが…それでも「基本形」までで、または
「折りたたんだら山形 (そして、 型や
型や 型を当てはめる)」というイメージがあれば「中間形」までで十分かなと思います。
型を当てはめる)」というイメージがあれば「中間形」までで十分かなと思います。



方べきの定理の証明
証明は…したも同然ではありますが 念のため
(2つの三角形が相似であるといえればよいだけ)
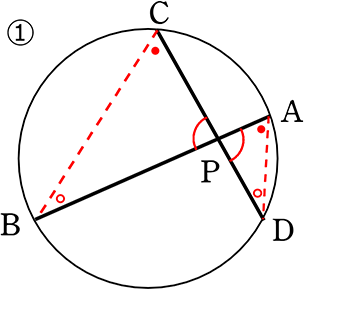
2本の弦AB、CDが、円周上にない点Pで交わる
(証明)
△PADと△PCBにおいて
∠PAD = ∠PCB ( 円周角の定理 )
∠PDA = ∠PBC ( 円周角の定理 )
(∠APD = ∠CPB 対頂角 でもOK)
「2組の角がそれぞれ等しい」ので
△PAD∽△PCB (基本形)
∴ PA:PC = PD:PB (中間形)
| ∴ | PA・PB = PC・PD (最終形) (比の計算) |
∴ 2本の弦AB、CDが、円周上にない点Pで交わる
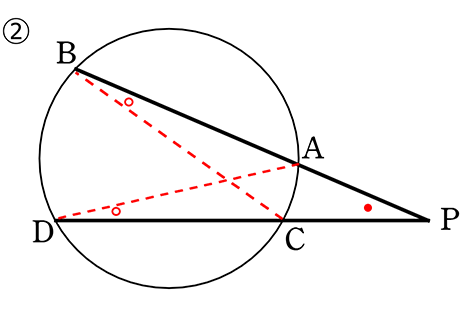
2本の弦AB、CDそれぞれの延長が、円周上にない点Pで交わる
(証明)
△PDAと△PBCにおいて
∠PDA = ∠PBC ( 円周角の定理 )
∠DPA = ∠BPC ( 共通 )
「2組の角がそれぞれ等しい」ので
△PDA∽△PBC (基本形)
∴ PA:PC = PD:PB (中間形)
∴ PA:PB = PC:PD (最終形)
∴ 2本の弦AB、CDそれぞれの延長が、円周上にない点Pで交わる
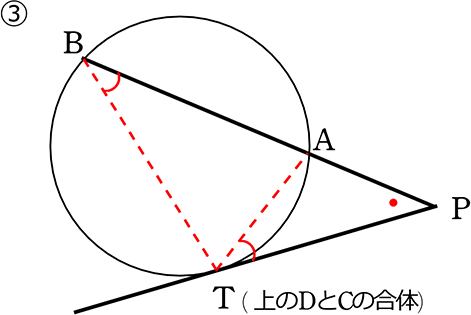
円の外部の点Pから引いた接線の接点をT、
Pを通り円と2点で交わる直線との交点をA, Bとする
(証明)
△PTAと△PBTにおいて
∠PTA = ∠PBT ( 接弦定理 )
∠APT = ∠TPB ( 共通 )
「2組の角がそれぞれ等しい」ので
△PTA∽△PBT (基本形)
∴ PA:PT = PT:PB (中間形)
∴ PA:PB = PT2 (最終形)
∴ 円の外部の点Pから引いた接線の接点をT、Pを通り円と2点で交わる直線との交点をA, Bとする
《 例 》
図のようなとき、x, y を求めましょう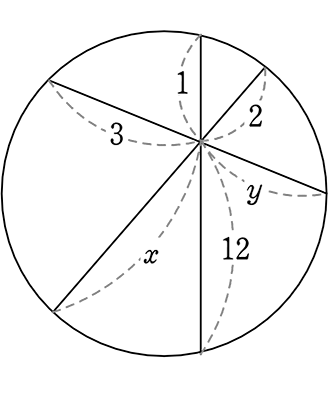
→ 相似な2つを見つけるだけですね
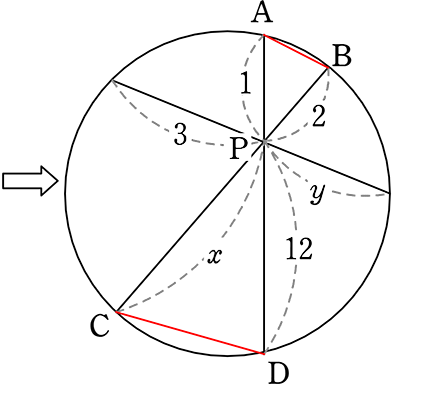

→ 1:x = 2:12 (中間形)
(1:2=x:12, \(\large{\frac{x}{12}}\)=\(\large{\frac{1}{2}}\)
なんでもOKでしたね)
→ 2x = 12 (最終形)
→ x = 6 //
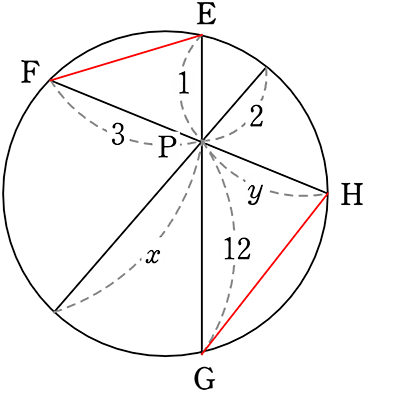

1:y = 3:12
3y = 12
y = 4 //
《 例 》
四角形DBCEが円に内接するとき、xを求めましょう
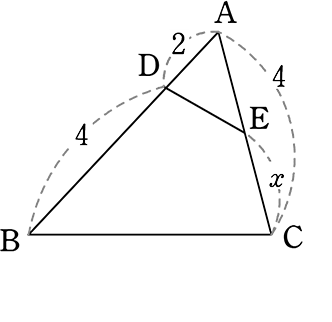
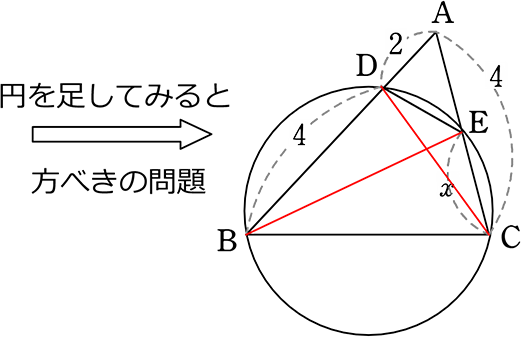
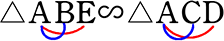
| → (4-x):2 | = | 6:4 |
| 16-4x | = | 12 |
| 4x | = | 4 |
| x | = | 1 // |
③ 方べきの定理の逆
「接弦定理の逆」同様、完全な余談ですね
結果だけで十分ですね!
「2つの三角が 裏返し で相似
ですが、念のため
方べきの定理の逆の証明
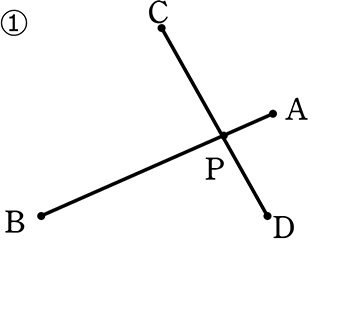
線分ABとCDが、点Pで交わり、
PA・PB = PC・PD

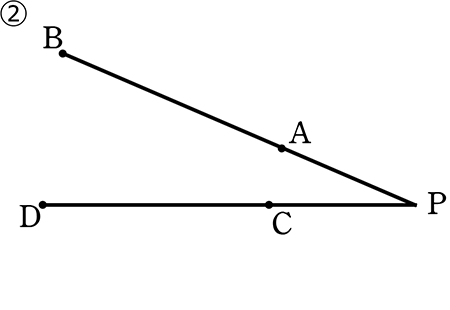
線分ABとCD、それぞれの延⾧線が、
点Pで交わり、PA・PB = PC・PD

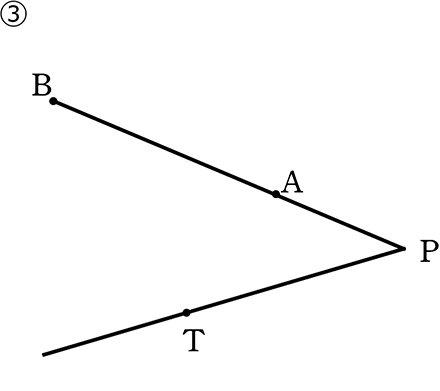
線分ABの延⾧線が、
線分AB上にない点Tを通る直線と、
点Pで交わり、
PA・PB = PT2
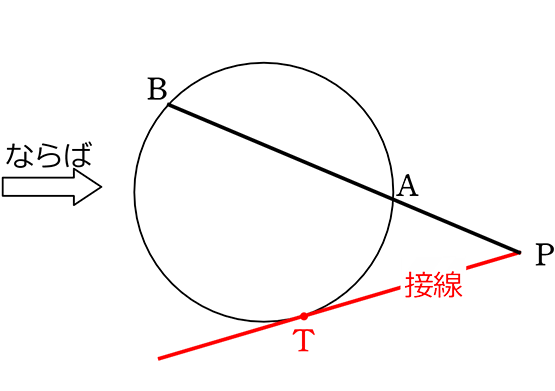
点Tでの接線
(①の証明)
仮定 PA・PB = PC・PD → (変形しておく) PA:PC = PD:PB
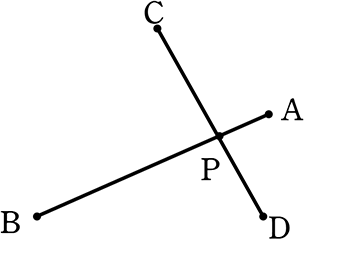

△PADと△PCBにおいて
∠APD = ∠CPB (対頂角)
PA:PC = PD:PB (仮定の変形)
∴ 「2組の辺の比と その間の角がそれぞれ等しい」ので
△PAD∽△PCB
∴ ∠PAD = ∠PCB かつ A , C はBDに関して同じ側にあるので
「円周角の逆の定理  」より
」より
4点 A , B , C , D は同一円周上にある //
(②の証明)
仮定 PA・PB = PC・PD → (変形しておく) PA:PC = PD:PB
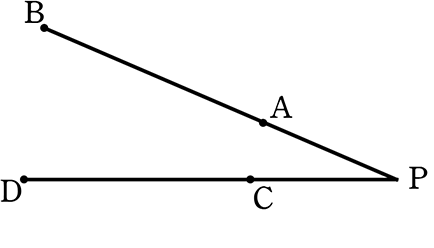
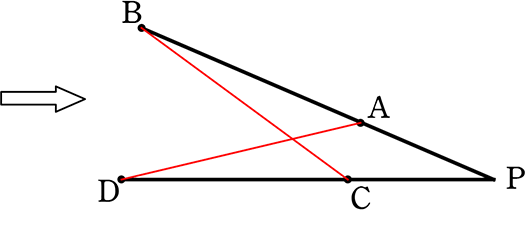
△PADと△PCBにおいて
∠DPA = ∠BPC (共通)
PA:PC = PD:PB (仮定より)
∴ 「2組の辺の比とその間の角がそれぞれ等しい」ので
△PAD∽△PCB
∴ ∠PDA = ∠PBC かつ B , D はACに関して同じ側にあるので
「円周角の逆の定理」より4点 A , B , C , D は同一円周上にある //
(③の証明)
仮定 PA・PB = PT2 → (変形しておく) PA:PT = PT:PB
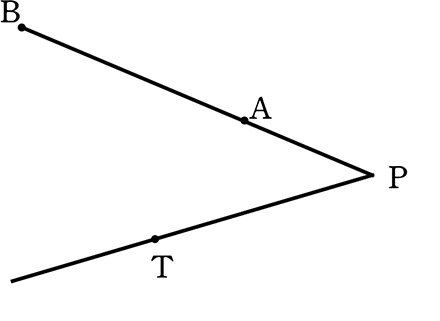
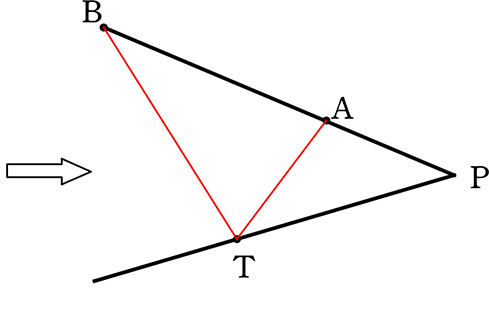
△PTAと△PBTにおいて
∠TPA = ∠BPT (共通)
PA:PT = PT:PB (仮定より)
∴ 「2組の辺の比とその間の角がそれぞれ等しい」ので
△PTA∽△PBT
∴ ∠PTA = ∠PBT より「接弦定理の逆」より
P とB が直線AT に関して反対側にあり、 ∠PBT = ∠PTA
PTは3点 A , B , T を通る円の 点Tでの接線 //
以上、円に関する性質でした!
これらの「武器」と次の過程で学ぶ「三平方の定理」があれば
中学数学の円に関する問題で解けないものはないですね!
お疲れ様でした!
その他の問題は、「問題集」で !!
④ その他余談
これ以降のお話は完全な余談です
将来出会った時に「何これ!」より「なんか見たことある」の方が少しはいいのかなという意味合いだけのお話です
サラッと見でOKです!
a. 2つの円の位置関係
2つの円の位置関係は、
それぞれの「半径」と、「中心間の距離」の関係で5つに分類できますね
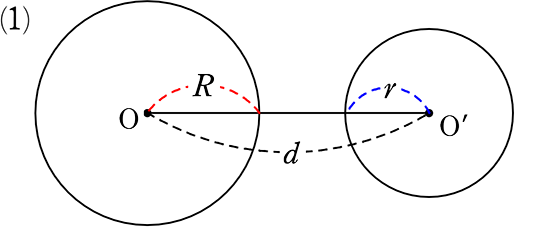
R+r < d
ex. ( 3+2 < 7 )
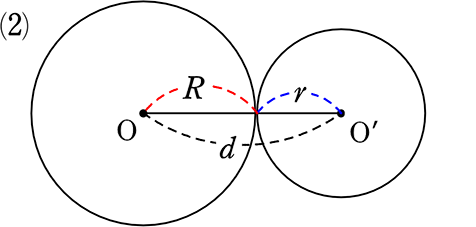
R+r = d
( 3+2 = 5 )
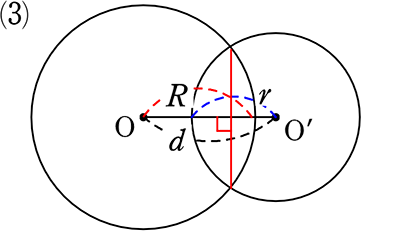
R-r < d < R+r
( 3-2 < 4 < 3+2 )
( 共通弦 ⊥ OO’)
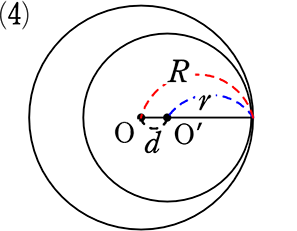
R-r = d
( 3-2 = 1 )
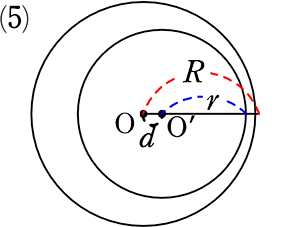
R-r = d
( 3-2 > 0.5 )
当たり前と言えば当たり前ですが、
(3) (4) (5) あたりになると…「ンッ!」となりますね!
b. 2つの円の共通接線の本数

離れた円

接した円

2点で重なった円
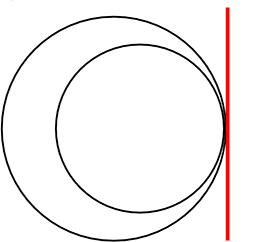
内部で接した円
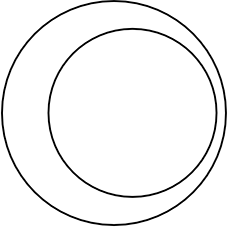
内部で接しない円
c. トレミーの定理
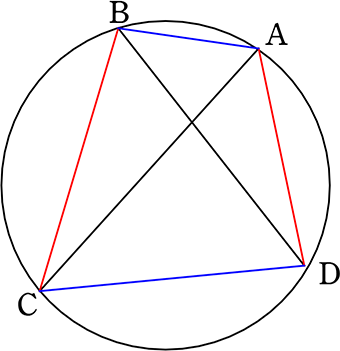
四角形が円に内接
(上×下) + (左×右)= 対角線×対角線
《 例 》
図のようなとき、xを求めましょう

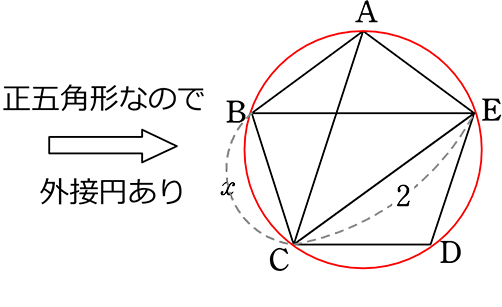
→ AC = BE = CE = 2 (正五角形より)
AB = BC = CD = DE = EA = x (正五角形より)
→ 四角形ABCEで
AB・CE+BC・AE = AC・BE (トレミーの定理)
x・2+x・x = 2・2
x2+2x = 4
(x+1)2 = 5
x = ±\(\small{\sqrt{5}}\)-1
x>0より
x = \(\small{\sqrt{5}}\)-1 //
d. チェバの定理・メネラウスの定理
〔 チェバの定理 〕
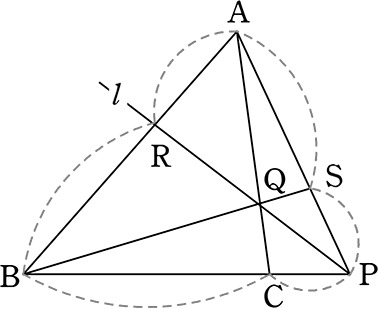
3直線 AC, BS, PR が1点で交わる
〔 メネラウスの定理 〕
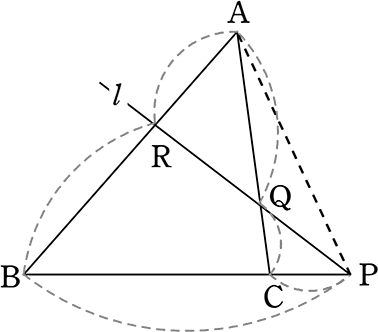
3点 P, Q, R, が一直線上
【 イメージ 】
予備前提イメージとして…何も乗っていない「天秤」はつり合っていますね
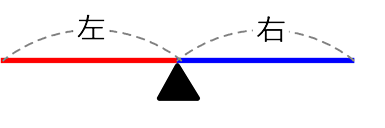
左 = 右 ですね、少し変形すると
\(\large{\frac{左}{右}}\) = 1 や \(\large{\frac{右}{左}}\) = 1 ですね
イメージ
| ① | つり合う = 左右が同じ、または両者どうしで割ると「1」 |
| ② | つり合う = 支点(▲)が1点に決まる |
↑もう、「現象」「摂理」ですね、「意味」など考えるだけ無駄ですね
【 チェバのイメージ 】
チェバの図は3つの「天秤」からできているとイメージできますね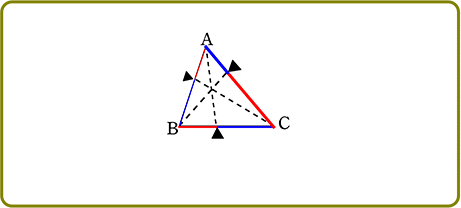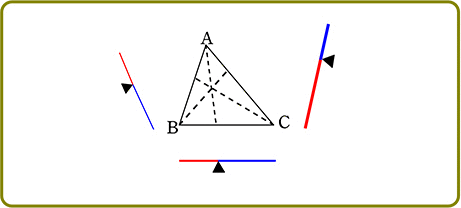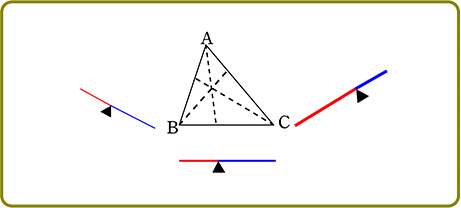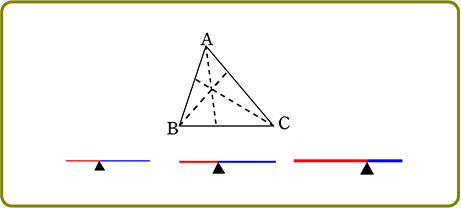
そして、それぞれを下図のよう
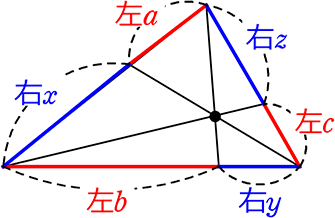 にすると
にすると
現象として、黒丸の動きをボーっと見てくださいね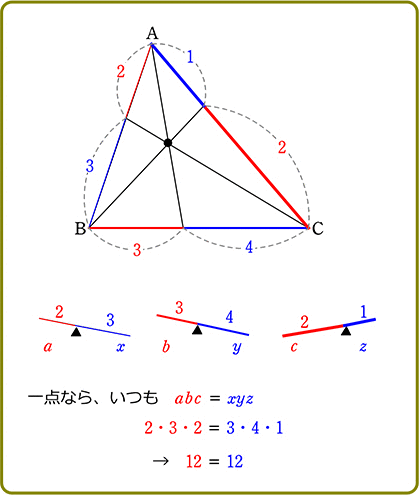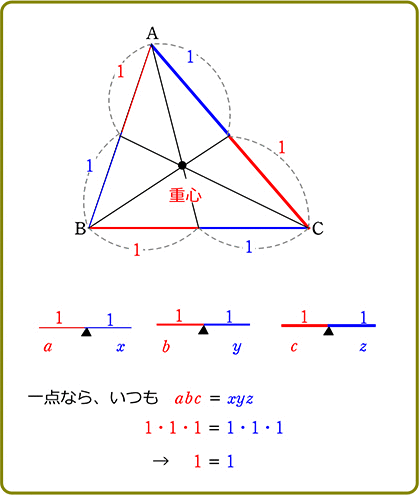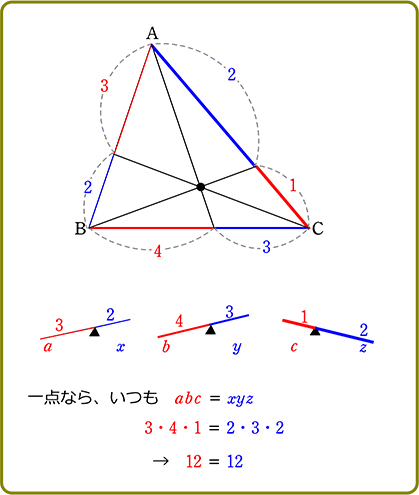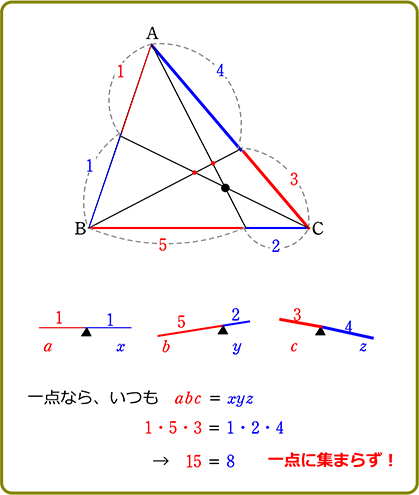
よって
→ 左×左×左 = 右×右×右
かっこよく言えば
\(\large{\frac{左\cdot左\cdot左}{右\cdot右\cdot右}}\) = 1 \(\large{\frac{右\cdot右\cdot右}{左\cdot左\cdot左}}\) = 1 \(\large{\frac{左}{右}}\)・\(\large{\frac{左}{右}}\)・\(\large{\frac{左}{右}}\) = 1 \(\large{\frac{右}{左}}\)・\(\large{\frac{右}{左}}\)・\(\large{\frac{右}{左}}\) = 1
などになっていきますね
結局チェバって何が言いたいの?
→ 左×左×左 = 右×右×右
天秤の支点(▲)が1点で決まるように、交点(●)が1点で決まる「現象」
意味など考えると疲れますね!「現象」です!
《 例 》
AG:GB を求めましょう

チェバ(左のかたまり=右のかたまり)より
AG×1×2 = GB×2×1
2AG = 2GB
AG = GB (=でつながるものを比にする)
A. AG:GB = 1:1
(別解:チェバを使わない)
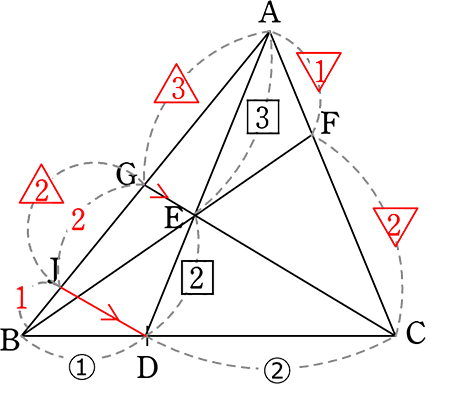
・DからCGに平行なDJを引く
△ADJの「山」より
→ AE:ED = AG:GJ = 3:2
△BGCの「山」より
→ BD:DC = BJ:JG = 1:2
・比の統一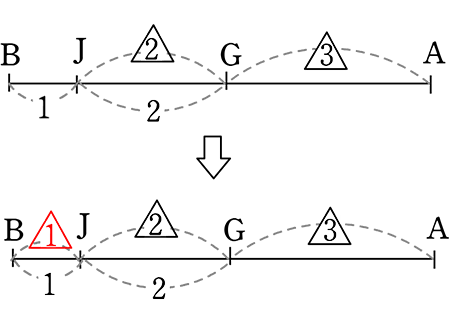
∴ AG:GB = 3:3 = 1:1
(研究)
それでは、三角形の
「チェバ」を知っていないと解けないのでしょうか?
「補助線」では解けないのでしょうか?
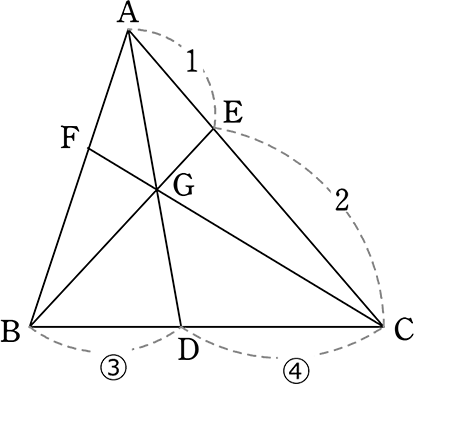
(チェバなら)
AF・3・2 = FB・4・1
6AF = 4FB (=でつながるものを比にする)
AF:FB = \(\large{\frac{1}{6}}\):\(\large{\frac{1}{4}}\) = 4:6 = 2:3
→ あっという間ですね
(補助線なら)
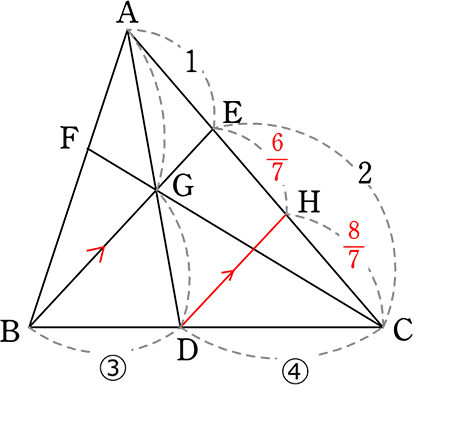
△CBEの「山」より
CH:HE = 4:3
比の統一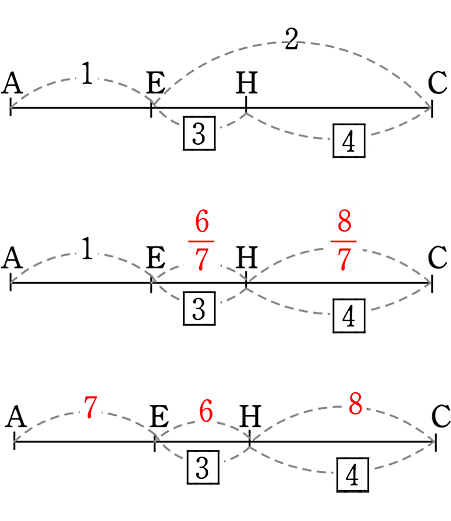
△ADHの「山」より
AG:GD = 1:\(\large{\frac{6}{7}}\) = 7:6
あとは先の問題と同じですね
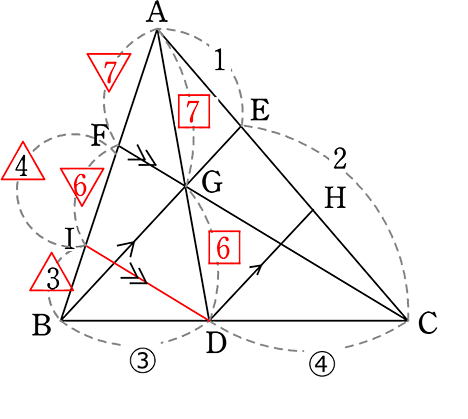
Iから補助線
△AIDの「山」より
AF:FI = 7:6
△BCFの「山」より
BI:IF = 3:4
比の統一
AF:FI:IB = 14:12:9
∴ AF:FB = 14:21 = 2:3
「補助線」でも解けますね! ですが、なかなか大変ですね
【 チェバの定理の証明 】
余談中の余談です…
「チェバ」の原理は「面積比」の利用です
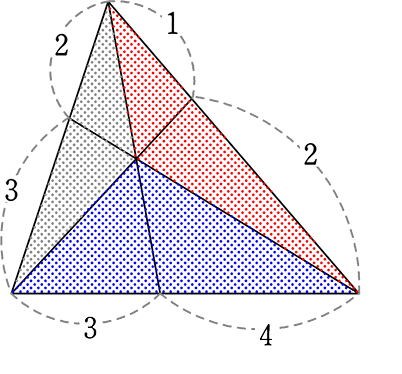
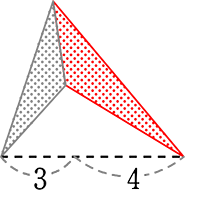
黒面積:赤面積
= 3:4
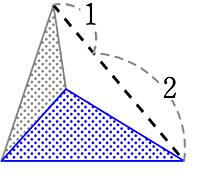
黒面積:青面積
= 1:2
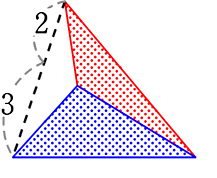
赤面積:青面積
= 2:3
確かに、底辺は共通なので「底辺にあたるもの」と言えますが、
点線の比は「共通」でもなく「平行」でもなく「底辺との角度が同じ」
でもないのに、「高さにあたるもの」となる?
(証明)
黒と赤でいきますね
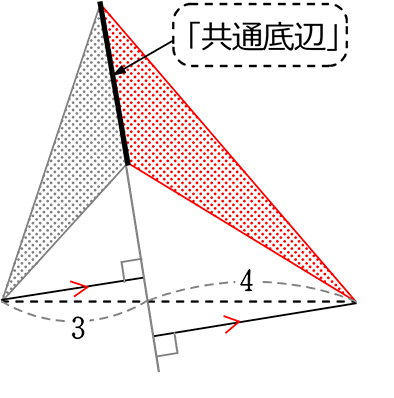
「高さにあたるもの」がないので
①正真正銘の「高さ」である
「底辺に対する垂線」を落とします
②同じ線に対する垂線どうしは「平行」
③ということは細い三角形どうしは
「ちょう型」ですね
④ということは、左垂線:右垂線も「3:4」
⑤すなわち、点線の比は「高さにあたるもの」
3:4ということができますね
⑥すなわち、3→黒面積、4→赤面積を
ということですね
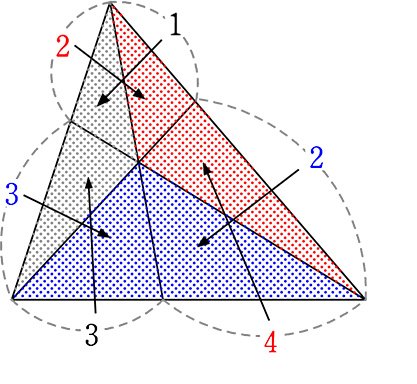
左図は各辺の数字が表す面積です
ex. 2は  を表す
を表す
4も  を表す
を表す
これを文字に置き換えると…
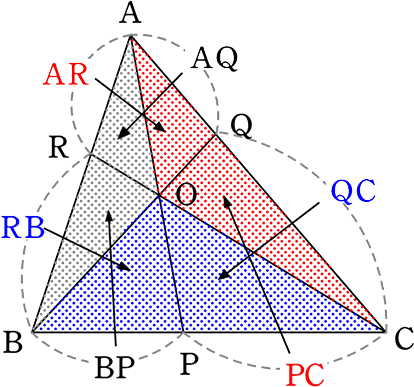
チェバの定理は \(\large{\frac{RB}{AR}}\)・\(\large{\frac{PC}{BP}}\)・\(\large{\frac{AQ}{QC}}\) = 1
各辺が表す面積に置きかえると
\(\large{\frac{RB}{AR}}\)・\(\large{\frac{PC}{BP}}\)・\(\large{\frac{AQ}{QC}}\) = \(\large{\frac{△OBC}{△OAC}}\)・\(\large{\frac{△OAC}{△OAB}}\)・\(\large{\frac{△OAB}{△OBC}}\)
これらを約分すると = 1 確かに「1」!
= 1 確かに「1」!
→ チェバの定理は成り立っている
【 外部でもOK 】
チェバは1点で交わる点が三角形の外部であっても成り立ちます
同じく、余談中の余談です
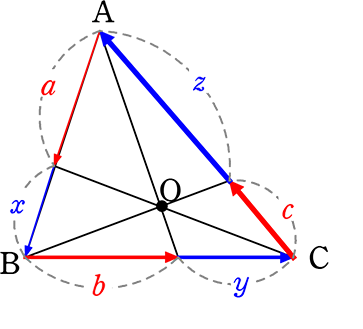
通常の「内部チェバ」ですね
a・b・c = x・y・z
考え方は同じですが、対応する辺がややこしいですね
(順に鉛筆で「左、右、左、右、左、右」と何度もなぞって、慣れてくださいね)
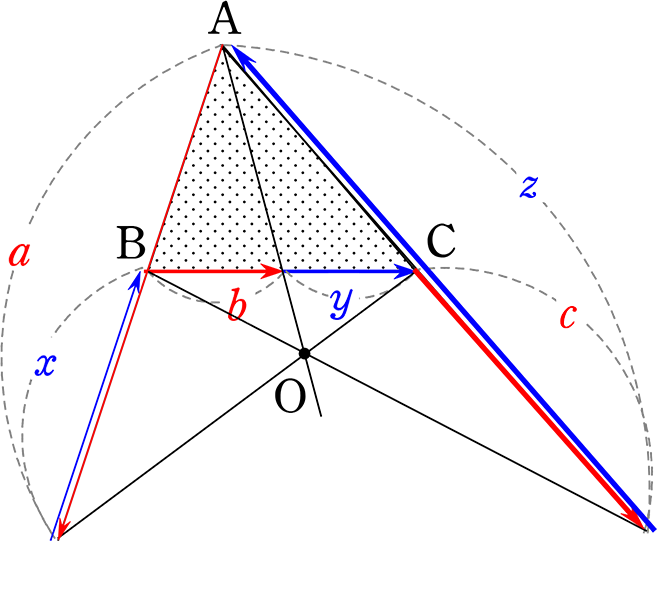
a・b・c = x・y・z
Aから交点 交点からB Bから交点 交点からC Cから交点 交点からA
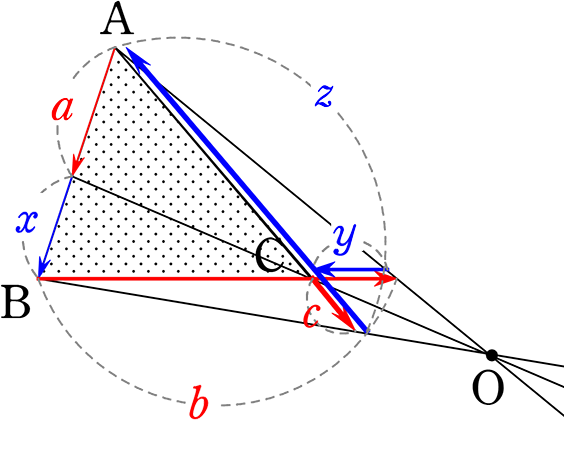
a・b・c = x・y・z
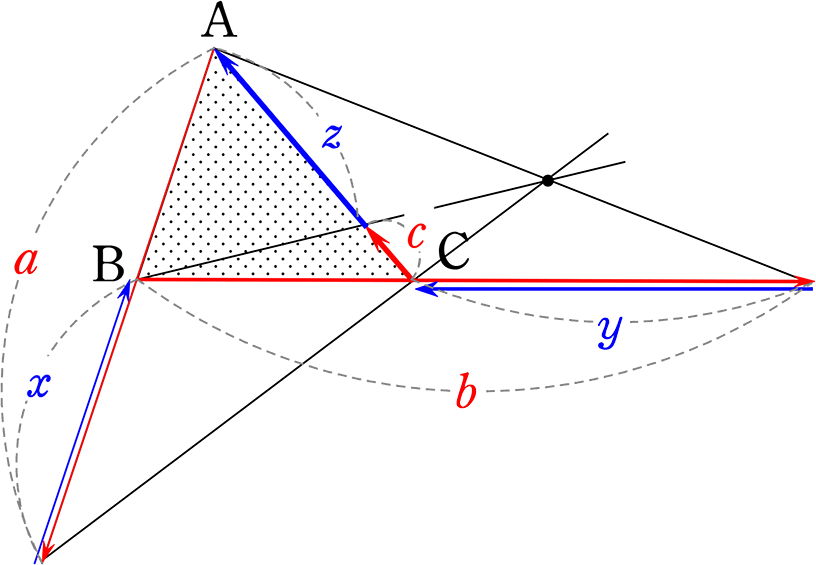
a・b・c = x・y・z
【 メネラウスのイメージ 】
再度
〔 メネラウスの定理 〕

3点 P, Q, R, が一直線上
チェバとの違いは
APという三角形の「辺」ではなく
ACという三角形内部の直線ですね
| ・ | CPのようなはみ出た部分を「はみ出た(はみ右, はみ左)」としますね |
| ・ | BPのような食い込まれた辺を「食い込まれた辺(全左, 全右)」としますね |
メネラウス
→ はみ出た(右)×右×右 = 全(左)×左×左
→ はみ出た(左)×左×左 = 全(右)×右×右
図により左右を変えればOKですね
「はみ出た:全部」 の部分だけは「外分」ということですね
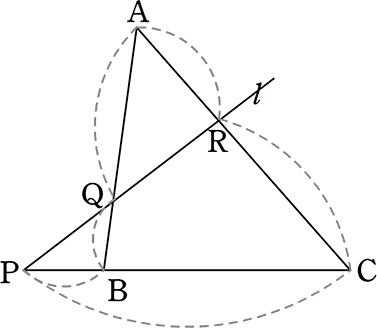
途中 右, 左が?になった場合は、B, R, Q に天秤の支点▲を外側から配置してくださいね (天秤のイメージ)
(天秤のイメージ)
《 例 》
図のようなとき、AF:FCを求めましょう
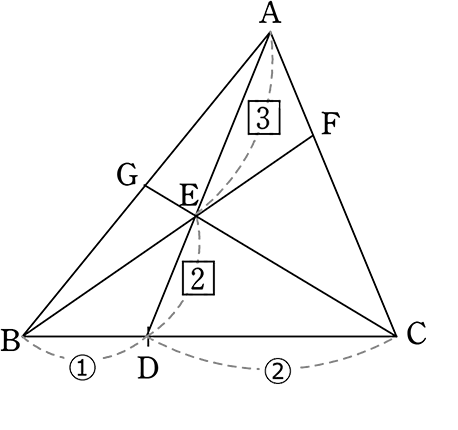
メネラウスより
1・CF・3 = (1+2)・AF・2
3CF = 6AF
∴ CF:AF = \(\large{\frac{1}{3}}\):\(\large{\frac{1}{6}}\) = 2:1 (=でつながるものを比にする)
A. AF:CF = 1:2
(別解:メネラウスを使わない)
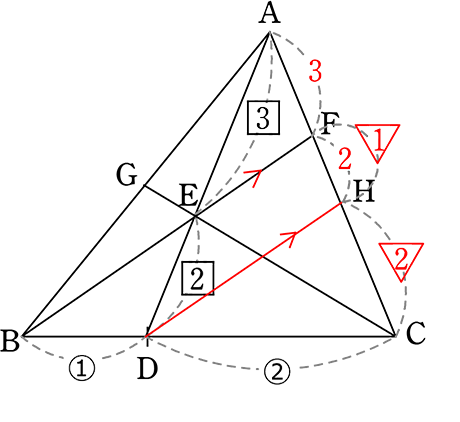
・DからBFと平行な補助線で「山」作り
・△ADHの「山」より
→ AF:FH = 3:2
・△CFBの「山」より
→ CH:HF = 2:1
・比の統一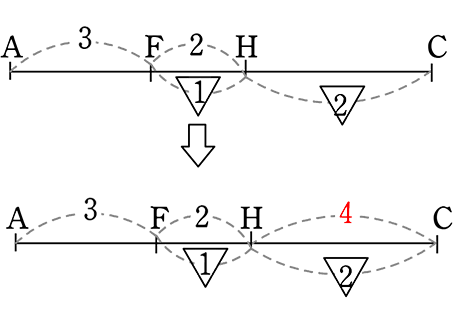
∴ AF:FC = 3:6 = 1:2 //
《 例 》
図のようなとき
(1) AF:FD を求めましょう
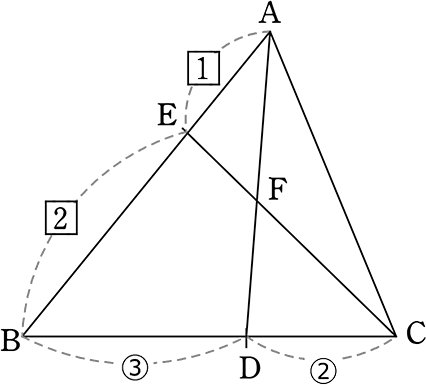
メネラウスで
2・2・AF = (3+2)・1・FD
4AF = 5FD
∴ AF:FD = \(\large{\frac{1}{4}}\):\(\large{\frac{1}{5}}\) = 5:4
補助線なら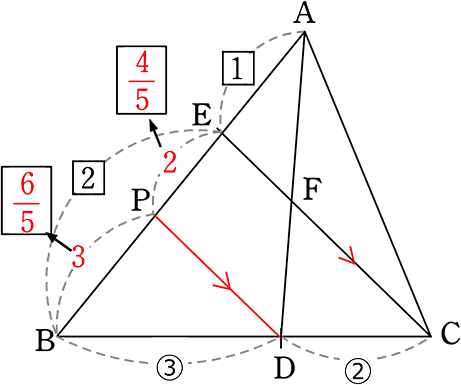
| → | 1本でOKですね (Bからそれぞれの比が始まってるな → DPを足してみるか) |
・△BCEの山から、 BP:PE = 3:2
・比を統一して、 BP:PE:EA =\(\large{\frac{6}{5}}\) ← \(\large{\frac{\boxed{\scriptsize{2}}}{5}}\)×3:\(\large{\frac{4}{5}}\):1
∴ △APDの山から、 AF:FD = 1:\(\large{\frac{4}{5}}\) = 5:4 ですね!
(2) △ABCと△FDC の面積比を求めましょう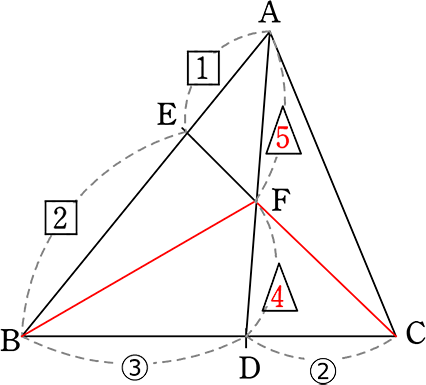
まず、△ABC:△FBC
| = | △ABCの(底辺にあたるもの)・(高さにあたるもの):△FBCの(底辺にあたるもの)・(高さにあたるもの) (「あたるもの」の考え方) |
| = | BC・AD:BC・FD |
| = | AD:FD 比は同じ数字, 文字で割っても掛けてもよい = 分数の約分, 逆約分 |
| = | (1)より、5+4:4 = 9:4 |
次に、△FBC:△FDC
| = | △FBCの(底辺にあたるもの)・(高さにあたるもの):△FDCの(底辺にあたるもの)・(高さにあたるもの) |
| = | BC・FD:DC・FD |
| = | BC:DC |
| = | 3+2:2 |
| = | 5:2 |
| ∴ △ABC | :△FBC | :△FDC |
| 9 | : 4 | |
| 5 | : 2 | |
| → 45 | : 20 | : 8 |
∴ △ABC:△FDC = 45:8
もちろん「あたるもの」に慣れている場合は、一気に
△ABC:△FDC
= (3+2)(5+4):(2)(4)
= 45:8 でもOK
お疲れ様でした!
その他の問題は、「問題集」で !!