| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 比例、反比例 |
| ア | 関数関係の意味 |
|---|---|
| ・ | 関数の分類表 |
| イ | |
| ・ | 比例の式 |
| ・ | 反比例の式 |
| ウ | 座標の意味 |
| ・ | 座標の各部名称 |
| ・ | 座標の意味 |
| エ | 比例、反比例の特徴 |
| ・ | 比例のグラフ (比例定数の求め方) |
| ・ | 反比例のグラフ (比例定数の求め方) |
| ・ | 反比例なのに比例定数? |
| オ | 比例、反比例を用いた具体的な事象の説明 |
| ・ | 比例の具体例 |
| ・ | 反比例の具体例 |
| ・ | 変域 |
| ・ | 比例の変域 |
| ・ | 反比例の変域 |
| a | 比の計算 |
| ・ | 比の値 |
| ・ | 比の計算 (方程式) |
| ・ | 連比 |
| ・ | =でつながるものを比に戻す |
比例・反比例
ア 関数関係の意味
関数とは、ともに関わりあう数字ですね。
もう少し具体的に言うと、
xが決まれば、yの値がただ一つ決まる関係ですね。
例えば、
| ・ | ハワイ島は1年間で、9cm日本に近づいている → 関数ですね(2年で18cm) |
| ・ | 人は1年間で、9cm身長が伸びる → 関数ではない(2年で3cmの人もいれば、10cmの人もいる) |
| ・ | 1時間 機械を動かせば、製品が50個できる → 関数(2時間で100個) |
| ・ | 1時間 勉強すれば、成績が2点上がる → 関数ではない(3点上がる人もいる) |
xに色々な数字を入れてみた時、
yが「複数」あるもの(=1つに決まらないもの)は、 「関数ではない」ということですね

関数の分類
関数
分数関数
反比例 (中1)
1次関数 (中2)
比例 (中1)
2次関数 (高校)
関数y=ax2 (中3)
3次関数 (高校)
・
・
・
「比例(y = ax)」は、
「1次関数(y = ax+b)(中学2年)」の「基礎」「簡単バージョン」ですね
| ・ | 「比例」のグラフは必ず「原点を通る」、だから「+b」がないですね |
y=\(\large{\frac{3}{2}}\)x
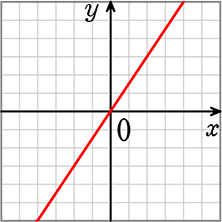
| ・ | 対して、「1次関数」のグラフは、「原点を通っても、通らなくてもよい」 → 通るときは 「+b」 が 「+0」 になるだけ(y=\(\large{\frac{3}{2}}\)x+0 → y=\(\large{\frac{3}{2}}\)x)ですね |
y=\(\large{\frac{3}{2}}\)x+2
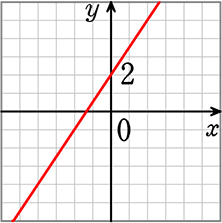
| ⇒ | 1次関数 y=ax+bでは「a」のことを「変化の割合」や「傾き」といいますが、
「比例」という、実は「特別な場合」には、aのことを「比例定数」と呼びますね |
ここでは、「比例式=関数」ではなく、
「比例は関数の中のごく小さな一場面」
ということだけを理解していてくださいね。
ちなみに、反比例(y = \(\large{\frac{a}{x}}\))は y = ax-1ともいえますね
-1次式(マイナス1次式)とは聞いたことがありませんが、
「1次関数ではない」ということは確かですね!
イ 比例、反比例の意味
比例の式
例えば、平均時速20kmで走っているときの、
「距離」と「時間」は
「比例」ですね
「式」で表すと、
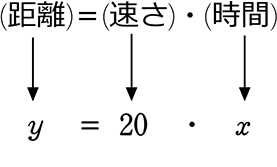
20・x の「・」は「
例えば、
x = 1のとき(1時間走った時)、 y = 20(距離は20km)
x = 2のとき(2時間走った時)、 y = 40(距離は40km)
よって、「比例」は式で表すと
比例定数: 直線の傾き具合を表す (ただしa≠ 0)
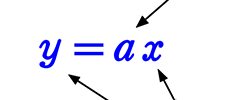 となります
となります
変数: 色々な数字を入れて試すことができる
cf
| 定数 … | その場面その問題において、『定まった数字」が入る |
| 変数 … | その場面その問題において、色々な数字を入れて試すことができる『箱のような文字』 |
よって、y = ax で表すことができるなら、「比例」ということになります
y = ax を、a = の式にすると、
↓ax = y
↓xa = y
→ a = \(\boldsymbol{\large{\frac{y}{x}}}\) となります
よって、逆に、
\(\large{\frac{y}{x}}\) (← y÷x)をしたとき、
aが常に「一定」のときも、「比例」ということですね

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)
まとめ
| 比例 ⇔ | y=ax で表せる a は一定 → \(\large{\frac{y}{x}}\) は一定 |
反比例の式
例えば、距離100kmを走るときの、
「速さ」と「時間」は「反比例」ですね
「式」で表すと、
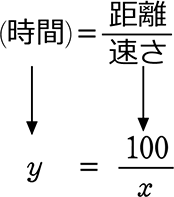
例えば
x = 20のとき(時速20kmの時)、y = 5(時間は5時間)
x = 40のとき(時速40kmの時)、y = 2.5(時間は2.5時間)
(「距離」は定まっているのだから、2倍の「速さ」で走れば、半分(\(\large{\frac{1}{2}}\))の「時間」で着くイメージ)
よって、「反比例」は式で表すと
比例定数: 双曲線の
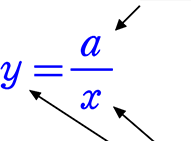 となります
となります
変数: 色々な数字を入れて試すことができる
よって、y = \(\boldsymbol{\large{\frac{a}{x}}}\) で表すことができるなら、「反比例」ということですね
この y=\(\large{\frac{a}{x}}\) を、a =の式にすると、
↓\(\large{\frac{a}{x}}\) = y
→ a = xy となります (xとyは逆数の関係ということですね!)
よって、逆に、
xy (← x×y)をしたとき、aが常に「一定」のときも、
「反比例」ということですね
反比例は、「xy=a」 、「y=\(\large{\frac{a}{x}}\)」の2つセットで「基本形」としてしまいましょうね
xy=a の方が反比例の意味を簡潔に表しているので


まとめ
| 反比例 ⇔ | y=\(\large{\frac{a}{x}}\) や xy=a で表せる a は一定 → xy は一定 |


ウ 座標の意味
座標の名称
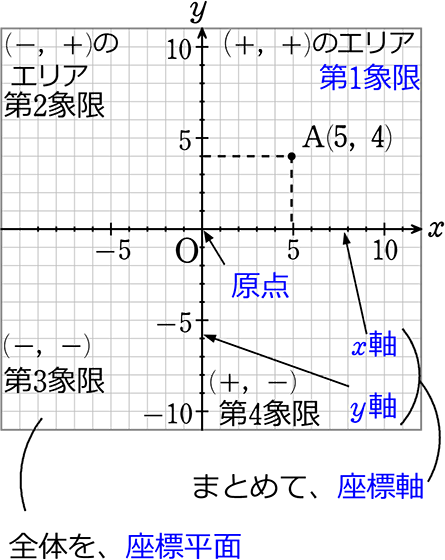
前、(点Aの) x座標

後ろ、(点Aの) y座標
座標の意味
イメージとして、
点が1つあれば、点の、
・「位置関係」 がイメージできますね
点が2つあれば、2点を結んだ線の、
・「位置関係」
・「長さ」
・「傾き加減」 がイメージできますね
点が3つあれば、3点をむすんだ平面の、
・「位置関係」
・「形」
・「大きさ(面積)」 がイメージできますね
その他、点達の関係性まで掴めますね
ですが、それはあくまで「イメージ」であって、
「正確かどうかもわからない」
「他人に伝えることもできない」
ですね。
しかし、「座標」を用いれば、
「正確に」それらのデータを「他者に」示すことができますね。


エ 比例、反比例の特徴
比例のグラフ (比例定数の求め方)
比例のグラフの特徴は
① 直線である
② 原点( 0, 0 )を通る
これだけですね!
そして、ポイントは、
| ① | y = ax の式で表すことができる(基本形) |
| ② | a = \(\boldsymbol{\large{\frac{y}{x}}}\) (y = ax をaの式にしただけですね) |
この比例定数(傾き具合) a = \(\large{\frac{y}{x}}\) は、もう少し正確にいうと、
a = \(\large{\frac{yの増加分}{xの増加分}}\) = \(\large{\frac{y_2-y_1}{x_2-x_1}}\) ですね
たとえば、
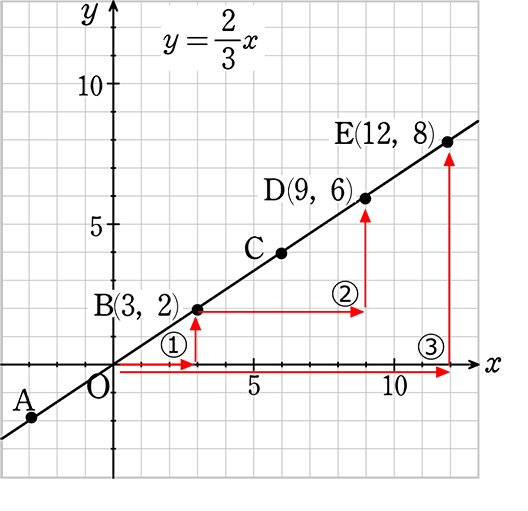
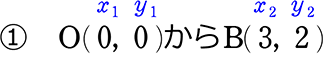
a = \(\large{\frac{yの増加分}{xの増加分}}\) = \(\large{\frac{y_2-y_1}{x_2-x_1}}\) = \(\large{\frac{2-0}{3-0}}\) = \(\large{\frac{2}{3}}\)

a = \(\large{\frac{yの増加分}{xの増加分}}\) = \(\large{\frac{6-2}{9-3}}\) = \(\large{\frac{4}{6}}\) = \(\large{\frac{2}{3}}\)

a = \(\large{\frac{yの増加分}{xの増加分}}\) = \(\large{\frac{8-0}{12-0}}\) = \(\large{\frac{8}{12}}\) = \(\large{\frac{2}{3}}\)
当然、同じ形の直角三角形なのですから「比例定数(傾き具合)」は、どこで図っても「\(\large{\frac{2}{3}}\)」ですね。
そして、1番簡単に計算できるのは、①か③ですね
そうです、「原点(0, 0)」を通る「直線」なら
(0, 0)を使わない手はないのです!
比例定数 a = \(\large{\frac{y}{x}}\) の本当の意味は、直角三角形の斜辺の「傾き具合」ですね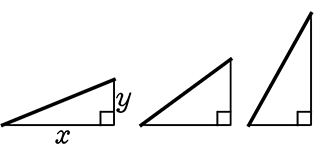
すなわち
→ \(\large{\frac{6高さ}{9底辺につき}}\) = \(\large{\frac{4高さ}{6につき}}\) = \(\large{\frac{2高さ}{3につき}}\) = \(\large{\frac{2}{3}}\)
背景に座標があれば
a = \(\large{\frac{yの増加分}{xの増加分}}\) = \(\large{\frac{y_2-y_1}{x_2-x_1}}\) = \(\large{\frac{y_2-0}{x_2-0}}\) = \(\large{\frac{y_2}{x_2}}\) = \(\large{\frac{y}{x}}\) だったのですね
(\(x_1,\ \ x_2\))、(\(y_1,\ \ y_2\)) はどちらの点を設定してもOKです
ex.
2点(0, 0)、(3, -2) を通る直線の比例定数は?
| → | \(\large{\frac{0-(-2)}{0-3}}\) = \(\large{\frac{+2}{-3}}\) = -\(\large{\frac{2}{3}}\) |
| → | \(\large{\frac{-2-0}{3-0}}\) = \(\large{\frac{-2}{3}}\) = -\(\large{\frac{2}{3}}\) |
| ⇒ | 同じですね、同じなら xの値が大きいほうを前にすれば、分母はいつもプラスにできますね(分母がマイナスは気持ち悪い) → 自分ルールを持てば間違いも減らせますね! |
2年生の話となりますが、
原点(0 , 0) を通らない 直線(y = ax+b)の場合は、
2つの点を利用する②の方法で「傾き」を求めることになりますね!

よって、原則は②で、
「(0, 0)を通る」ときは、①や③で楽ができる ということになります
もし、「xの増加量」と「yの増加量」…どっちが分母だったっけ? となったら…
・a は 高さの割合 → yが上(分子) ですね
または、
| ・ | 比例式「y = ax」を、aの式にしてくださいね!
y = ax → (ax=y) → a = \(\large{\frac{y}{x}}\) → xが下(分母) ですね! |


反比例のグラフ (比例定数の求め方)
反比例のグラフの特徴は
①
② 原点( 0, 0 )を通らない
③ 双曲線がx軸、y軸に接触しない
これだけですね!
そして、ポイントは、
| ① | y = \(\boldsymbol{\large{\frac{a}{x}}}\) または xy = aの式で表すことができる |
| ② | a = xy (aの式にしただけですね) |
「反比例」の問題は出題率的には低いので、3年生の後半には、
「反比例て…確か…xが増えたら…yが減る…?」
みたいになってしまいがちです。
そこで、絶対に忘れない「イメージ例」を、1つ2つ持っていると安心ですね
①
「36」は固定させます。あとは、「(x=)1のとき(y=)36、2のとき18、
3のとき12、4・9 = 36、6・6 = 36、9・4 = 36、…」
「ああ!積が36で一定のあれね!」
② 「距離」もよいですね
「距離」は決定させます。「速さ2倍で走れば、半分の時間で到着する、
速さ\(\large{\frac{1}{2}}\) で走れば(歩けば)、2倍の時間がかかる…」
というわけで、y = \(\large{\frac{a}{x}}\) よりも、(同じことを言っているのですが、)
xy = a の方が「反比例」を単純に表現しているといえますね
それでは、本題に戻りますね、
比例定数a は xyで求めることができる。 ←「比例」のときの「比例定数a」より簡単ですね!

反比例なのに比例定数?
反比例の式 y = \(\large{\frac{a}{x}}\) において、
aは「比例定数」ではなく「反比例定数」とは呼ばないの?
という小さな疑問がありますが、
比例式
となっていましたね
ということは、
反比例式
と考えることもできますね
というわけで、
反比例の式の「a」も「比例定数」と言ってかまわない、となります。
比例は
xの値が 1.5倍、2倍、3倍になると
yの値も 1.5倍、2倍、3倍になりましたが

反比例は
xの値が 1.5倍(\(\large{\frac{3}{2}}\)倍)、2倍、3倍になると
yの値は \(\large{\frac{2}{3}}\)倍、\(\large{\frac{1}{2}}\)倍、\(\large{\frac{1}{3}}\)倍、
逆数倍ですね
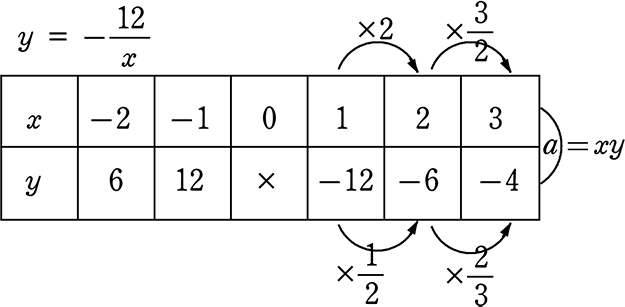
y = \(\large{\frac{12}{x}}\) (xy = 12) のグラフ
「第1象限 (+, +)のエリア」の拡大図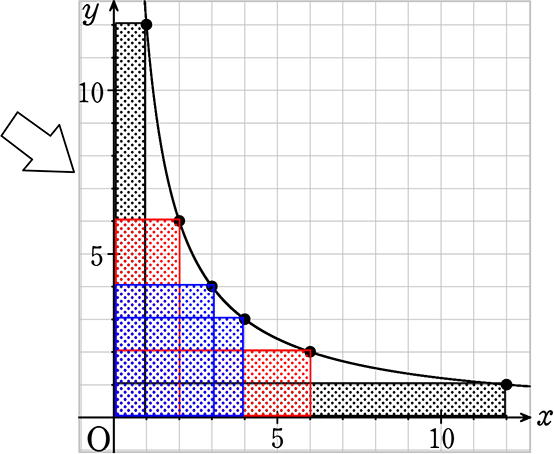
赤四角も青四角も黒四角も
面積が同じですね!
2×6 = 12
3×4 = 12
4×3 = 12
12×1 = 12
・
・
・
1200×0.01 = 12
「12」という「しばり」がある限り
x や y の値に「0」はありえないですね。
そういう意味で、
曲線は限りなくx軸やy軸に近づいていきますが、
軸には絶対に接触しないということです。
そして、第1象限の曲線は+(プラス)と+(プラス)ですので、
自然界のもので具体例をあげることができますね!
反比例の具体例…例えば…
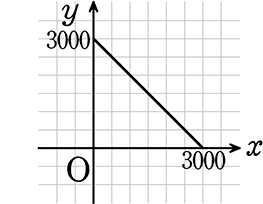
「予算3000円(y)で、x円使えば、手持ちが減る…」
これは、y = 3000-x で、
全然 y = \(\large{\frac{a}{x}}\) になっていませんね!
「自転車の5段目は少し踏めば、よく進む・・・『その代わり』重い
1段目はクルクル回しても、あまり進まない・・・『その代わり』軽い
「駅まで歩きの速さで行くと楽、・・・『その代わり』20分かかる」
「駅まで走る速さで行くと疲れる、・・・『その代わり』10分で着く」
「面積12の長方形の横を短い1にすると、『その代わり』縦は長い12が必要」
「面積12の長方形の横を長い12にすると、『その代わり』縦は短い1ですむ」
・・・わかりにくいですね・・・
反比例の具体例は『その代わり』というフレーズがお似合い ということは確かなのですが…
お父さん! お母さん! 腕の見せ所です!
子供たちが納得する「良い例」を聞かせてあげてくださいね!
第2象限(左上)、第3象限(左下)、第4象限(右下)は、
「マイナス」を扱いますので
「自然界」のもので具体例をあげることはできません
よって、「理論」で説明するしかないですね!
では、aがマイナスのグラフは・・・
ex) y = -\(\large{\frac{12}{x}}\) (xy = -12) のグラフ(赤双曲線)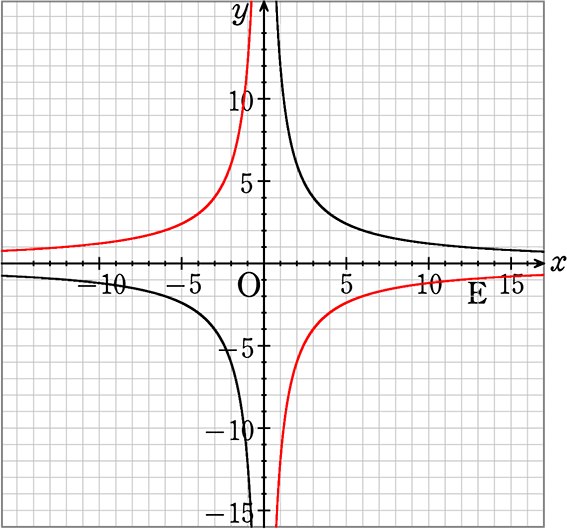
y = \(\large{\frac{12}{x}}\) (xy = 12)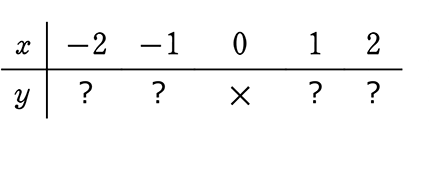

y = -\(\large{\frac{12}{x}}\) (xy = -12)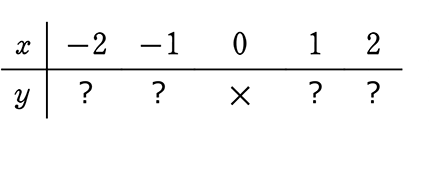

確かに原点(0, 0)の反対側にも同じ曲線がありますね! → 双曲線
| : 2つ |
ここで、上の「対応表」において、
xが0のとき、yは「×(バツ)」となっています。
これは、反比例の式 y = \(\large{\frac{a}{x}}\) の xに
「0」を代入(y=\(\large{\frac{a}{(\color{red}{0})}}\))しようとするものですが…
そうですね! 数学では「分母が0 (0で割る)」は定義しない、(扱わない)でしたね!
オ 比例、反比例を用いた具体的な事象の説明
比例の具体例
● 平行四辺形系 (長方形、正方形、ひし形)の面積yと、底辺、高さ
(高さが一定(定数)な場合)
面積y = 一定高さa×底辺x 
y = 2x という比例ですね
同様に、(底辺が一定(定数)な場合)
平行四辺形系 (長方形、正方形、ひし形)の面積y、底辺a、高さx
面積y = 一定底辺a×高さx 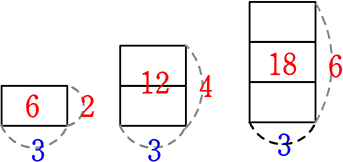
y = 3x という比例ですね
cf.
ちなみに、底辺も、高さも 2倍、3倍になると…
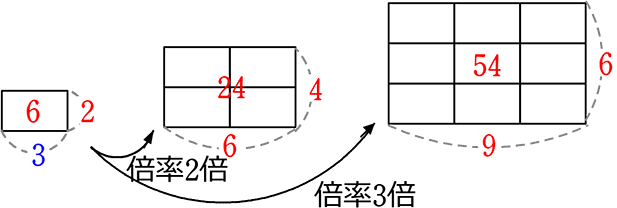
y = 6x2 という「関数y = ax2」の話の一部ですね
また、「倍率の2乗」が、「面積の比」になっている
これが「相似比の2乗は面積比になる」という
中学3年の「相似」の話の一部ともいえますね
「相似比の2乗は面積比になる」は三角形でも円でも同様に使えますね
● 三角形の面積y、底辺、高さ
(高さが一定(定数)な場合)
面積y = \(\large{\frac{1}{2}}\)×一定高さa×底辺x
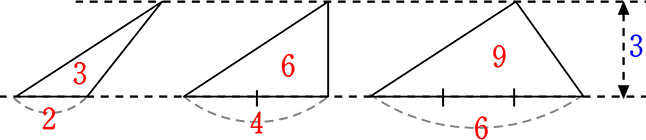
y = \(\large{\frac{1}{2}}\)・3・x = \(\large{\frac{3}{2}}\)x → y=\(\large{\frac{3}{2}}\)x という比例ですね ←数字部分は計算できるので y=ax の型に → 比例だ
同様に、(底辺が一定(定数)な場合)
面積y = \(\large{\frac{1}{2}}\)×一定底辺a×高さx
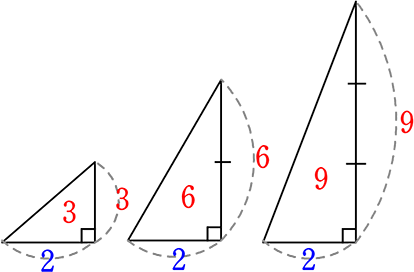
y = \(\large{\frac{1}{2}}\)・2・x = 1x = x → y=x という比例ですね
● 正方形の周囲の長さy、1辺x
周囲の長さy = 4×1辺x
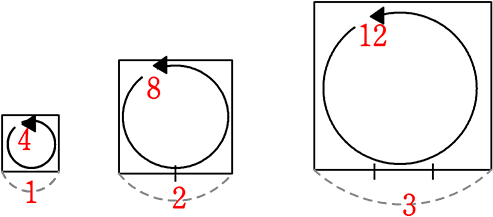
y = 4x という比例ですね
● 円周y、円周率π、半径x
円周y = 円周率π×2×半径x
y = 2πx という比例ですね
● 距離y、速さa、時間x → y = ax
距離y、速さx、時間a → y = ax
● バネの「延び」y、重りx、伸び率a
バネの「延び」y = 重りx×伸び率a
ex. 伸び、10gで2cmのバネ
→ 1g で0.2cmのびる → \(\large{\frac{0.2}{1につき}}\)
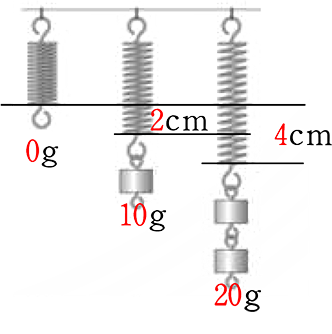

y = 0.2x という比例ですね
cf.
バネの「延び」ではなく、バネの「長さ」になると…
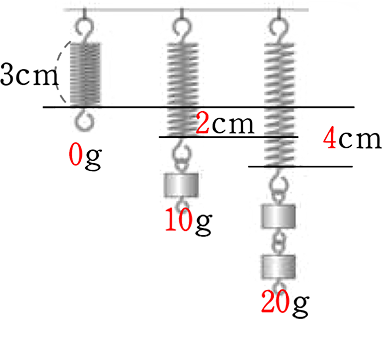

2年生の、y = 0.2x+3 ← 一次関数ですね
● 水槽の水位y、噴出率a、時間x → y = ax
などなど
上の他にも、たくさんありますが、
基本的には 公式などでよく見かける形
〇=□×△×◎×・・・ のように「×(掛ける)だけでつながっているものは、
右辺の1文字だけを「x」、右辺の残り全てを「定数(数字)」にできれば、
全て比例式ということですね!
例えば、
・三角形の面積 = \(\large{\frac{1}{2}}\)×底辺×高さ なら
「底辺」か「高さ」のどちらかを何か数字で固定すれば「比例」ですね!
・ひし形の面積 = \(\large{\frac{1}{2}}\)×底辺×(合計高さ) も同様ですね (ひし形の面積)
・文字= 数字 数字 数字 文字
↓数字は計算できるので
↓結局は…
y = ax → 比例式ということですね!
・台形の面積 = \(\large{\frac{1}{2}}\)×上底+下底 × 高さ
→ (上底+下底)セットで固定で、高さがxなら「比例」
→ 高さが固定で、(上底+下底)セットでxなら「比例」
→ 上底か下底のどちらかだけがxならアウト →「1次関数」ですね
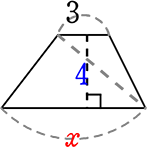
y = \(\large{\frac{1}{2}}\)×(3+x)×4 → y = 2x+6 アウト!! → 「一次関数」 ですね
反比例の具体例
| ● | 面積が固定されている、平行四辺形系、三角形 (24は例です↓) |
・平行四辺形の面積24 = 底辺x×高さy
・三角形の面積24 = \(\large{\frac{1}{2}}\)×底辺x×高さy → 48 = 底辺x×高さy
● 距離が固定されている、「速さ」と「時間」
24 = 速さx・時間y
● つり合っている天秤の「重り」と「距離」 (てこの原理)
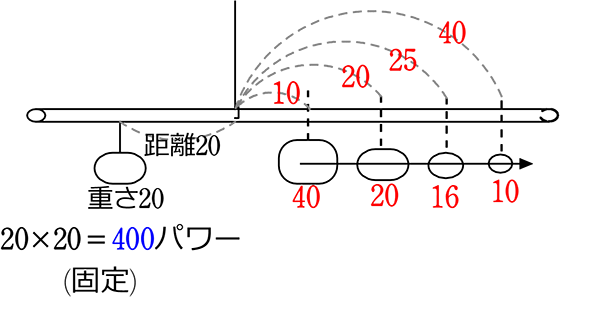
支点から離れるほど
軽い重りで
つり合うことができる
● 歯車の回転、
動力源歯車の「歯数」×「回転数/時間」=相手歯車の「
動力源歯車の「歯数」×「回転数/時間」とは → 結局は時間あたりにこなせる歯数
ex.
動力源歯車「30歯」×「2回転/秒」 = \(\underbrace{ 60歯車/秒}_{a }\) (固定)
(相手歯車)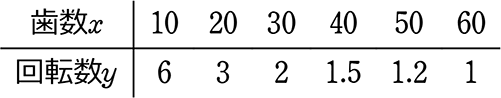
60 = xy という反比例ですね
《 例 》
歯数が15で毎分6回転する歯車Aとかみ合って回転する歯車Bの歯数をx、1分間の回転数をyとするとき、yをxの式で表しなましょう
→ A = 1分で、15歯×6回転 = 90歯/分
→ B = 1分で、x歯×y回転 = xy歯/分
⇒ A=B より 90歯/分 = xy歯/分 → 90=xy → y=\(\large{\frac{90}{x}}\)
cf.
Aの歯数/分 = Bの歯数/分 → 動いている「時間」は絶対同じ(歯車でどちらかだけが動いている状態はない) → 結局、両辺に同じ△分をかけて(等式の性質)、Aの歯数 = Bの歯数 でもよいですね
→ 90歯 = xy歯 → 90=xy → y=\(\large{\frac{90}{x}}\)
反比例の具体例は
〇 = □×△ のように「×(掛ける)でつながっているもの」で、
左辺が数字で固定されているものが「反比例」ですね!

数学には公式のようなものがたくさんありましたね

文字=定数・文字 などは、積である が大体1番大きいですね
∴ 大きいものを 「y」 とすれば → 比例

数字=文字・文字 などは、積である が大体1番大きいですね
∴ 大きいものが「定数」 として固定されていれば → 反比例
変域
「変域」とは「変数(xやy)の値の、「とりうる範囲」ですね!
ここまでは、
xの値を決めれば(定義すれば)、
yの値という『点』が決まりましたね
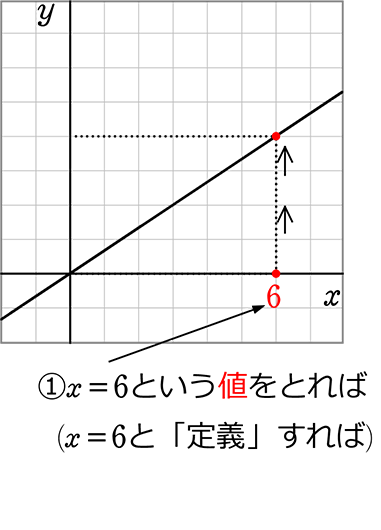
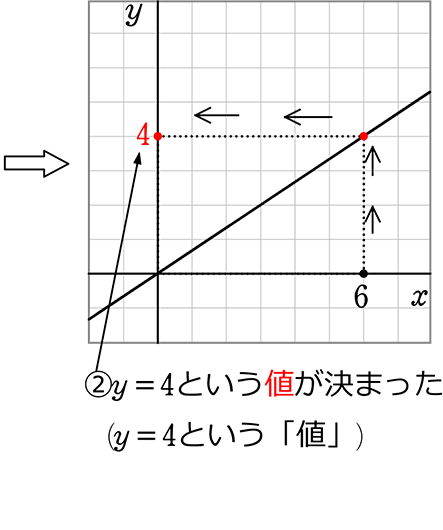
「変域」はただ「値」に幅がある、
『点』ではなく『範囲』というだけですね
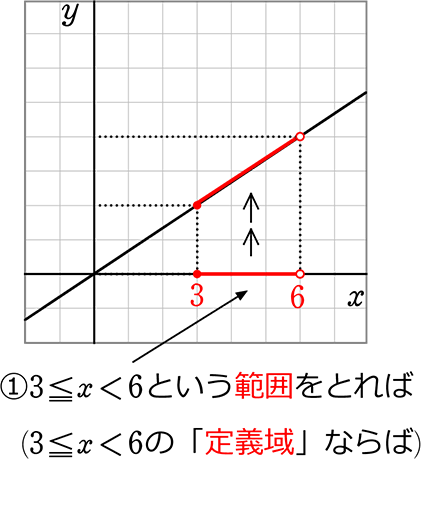
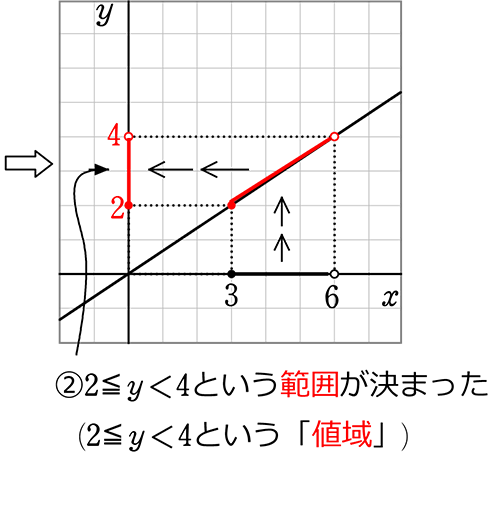
「xの値の範囲」を「
「yの値の範囲」を「
【 比例の変域 】
「変域」は、「物理的に決まってしまうもの」と「問題が指定しているもの」がありますね
たとえば、
1円の枚数をx、重さをyとします。1円の重さは1gですので、式で表すと、
y=1x → y=x ですね
ここで、A君が1円玉を数枚握りしめています、
(A君の手の大きさでは「0枚~24枚しか握ることができませんが、)
今は、どうやら「10枚~20枚」のようです。
重さは? と聞かれた時、
xは、
日本語で表現すれば、「10から20」や「10~20」や「10以上20以内」ですね
さらに数学的に表現すれば、「10≦x≦20」ですね。
そして、対応する重さyは、
「10枚のとき10g」「12枚のとき12g」「13枚のとき13g」…「19枚のとき19g」…、面倒ですね!
やはり、yも、「10から20」や「10~20」や「10以上20以内」と楽したいですね!
これを数学的に表現すれば、「10≦y≦20」ですね
これが、『変域』です、xやyの値に「幅」があるというだけです
いままでは、「xが5のとき、yの値は? という『点』でしたが、
「xが、●<x<〇のとき、yは、□<y<■ ?という『線』になっただけですね!
これをグラフで表すと、
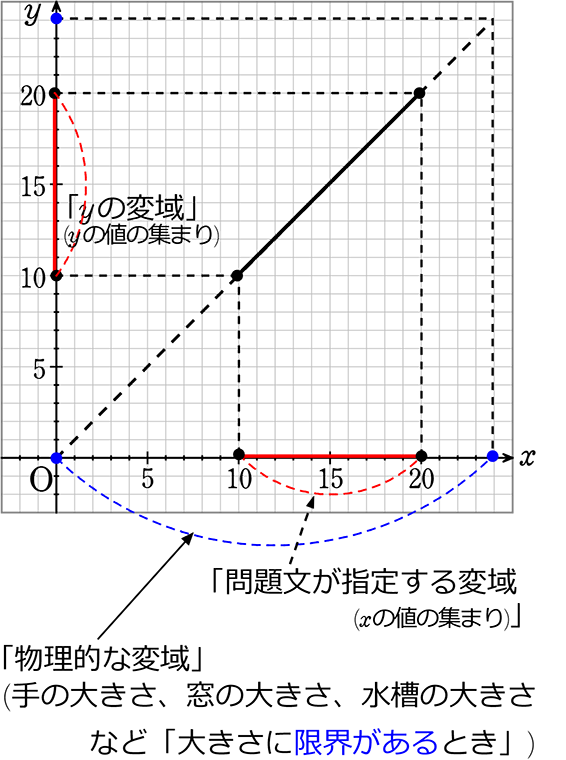
xが、10から20のとき、
すなわち、10≦x<20 のとき、
yは、10から20
すなわち、10≦y<20 ですね!
もちろん、「問題文が指定する変域」が最優先!ですね!
そして、具体例もなく、 y = -2x において、xの変域が -2<x ≦4 のとき、
yの変域は? という場合は、「物理的な変域」はないので、
グラフも、無限に使用できますね
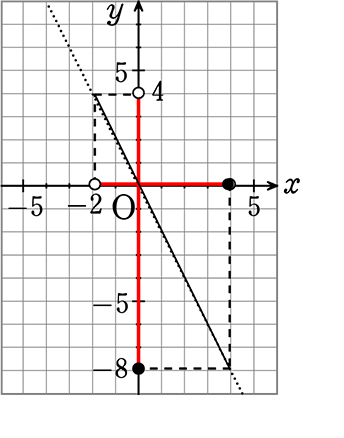
yの変域は、
「x = -2」、「x =4」を y = -2xに代入して、
(xが-2のとき yは4、 xが4のとき yは-8)
yは、4~ -8と表現できれば楽なのですが、
不等号で表わさなければ ですね
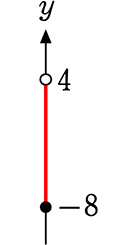
左図を不等号で表すと、
(xのことは切り離しておいてくださいね)
-8≦y<4 (4>y≧-8) ですね!
比例(などの直線)の変域を軽くまとめますと
① 正の比例式y = +axの場合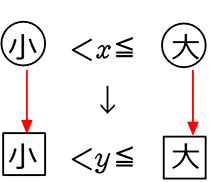
機械的に作業をしても可
② 負の比例式y =-axの場合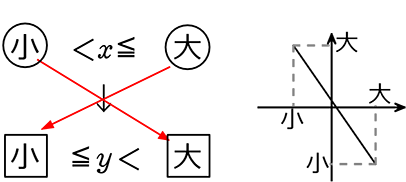
クロス!
となりますがっ!
① 公式風に憶えることは大変な割に
② 間違えやすい!
ので
対応する「範囲」を求める場合は、
(今後の、不等式、一次関数、二次関数においても)
簡単で構いませんので、
必ず、略図を書いて下さいね!!
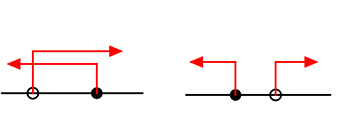

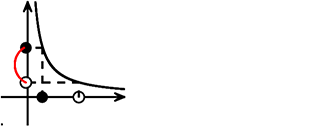

などなど、それが範囲を求める「コツ」ですね!!
【 反比例の変域 】
反比例の変域も同様ですね!
「簡単な図」を書けばいいだけです!


a 比の計算
せっかく「比例」を学びましたので
「比」について確認していきますね
【「比」の復習 】

4:x である。xを求めなさい ・・・困りますね
目測で 4:2.5 くらい?
または、定規を持ってきて測るしかないですね
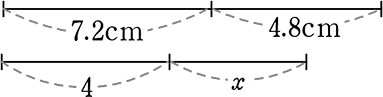
4.8cm:7.2cm = 4:x → x = 3
このように「比」は、「比べる何かが他に2つ以上」ないと「比」にする必要がないですね
すなわち一番上の図のようであれば「xを定規で測りなさい」が正しい問ですね
【 比の値 】
小学生の復習ですね
《 例 》
3:2の比の値は?
→ (小学なら) \(\large{\frac{3}{2}}\) = \(\large{\frac{1.5}{1}}\) = 1.5
→ (中学なら) \(\large{\frac{3}{2}}\) まででOKですね

●:〇の比の値 = \(\large{\frac{前}{後ろ}}\) = \(\large{\frac{●}{〇}}\)
(ウイリーのイメージですね)

《 例 》
塩5g:食塩水100g の比の値は?
すなわち「比の値は?」 = 「前の割合は?」 = 「塩の割合は?」または「食塩水の1化は?」 = 「食塩水の濃度は?」
前÷後ろ = 5g÷100g
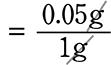
cf.
⇒ 食塩:食塩水の比の値は? → \(\large{\frac{食塩}{食塩水}}\) → (食塩水に対する食塩の割合) → \(\large{\frac{塩}{\color{red}{全体}}}\) = 『食塩水の濃度』
⇒ 食塩:水の比の値は? → \(\large{\frac{食塩}{水}}\) → 『水に対する食塩の割合』というだけの意味 ←濃度ではない
《 例 》
80円:1000円 の比の値は?

→ 80円の(1000円に対する)割合ということですね ← 8%と同じことですね
【 比の計算 (方程式) 】

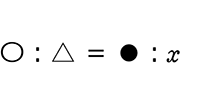

外側のどうしの積 = 内側どうしの積
→ 〇x = △● → x = \(\large{\frac{△●}{〇}}\)
(もちろん 内側どうしの積 = 外側のどうし積でもOKです)

クロスでイコール
→ 〇x = △● → x = \(\large{\frac{△●}{〇}}\)
〔どうして、外側の積 = 内側の積 が成り立つの?〕
→「比」 = 「割合」なので
3:2 = x:5 などは、比の値で表すと
\(\large{\frac{3}{2}}\) = \(\large{\frac{x}{5}}\) ですね
さらに、「対応するものが間違ってなければ何でもよい」ので
\(\large{\frac{2}{3}}\) = \(\large{\frac{5}{x}}\) でも \(\large{\frac{x}{3}}\) =\(\large{\frac{5}{2}}\) でも \(\large{\frac{3}{x}}\) = \(\large{\frac{2}{5}}\) でもよいとなります
割合や比は「ぶんの」と読まずに「につき」と読むとイメージしやすかったですね
\(\large{\frac{3}{2}}\) = \(\large{\frac{x}{5}}\) ← 「2につき3は、5につきx」
イメージが定着したら「ぶんの」でもOK!
3:2 = x:5 も「3たい2は、xたい5」ですが
「2につき3は、5につきx」と読んでもOKですね
⇒ 表現は違えど まったく同じ意味
\(\large{\frac{3}{2}}\) = \(\large{\frac{x}{5}}\) の計算過程では、まず
①分数をなくすために両辺に「2・5」を掛けますね (分かりにくければ「10」を掛けますね)
→ \(\large{\frac{3\ \cdot \ 2\ \cdot \ 5}{2}}\) = \(\large{\frac{x\ \cdot \ 2\ \cdot \ 5}{5}}\)
→ 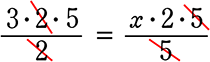
→ 3・5 = x・2 ← この形は
外側の積 = 内側の積 ですね。ただそれだけです、途中式を省いただけの公式ですね
《 例 》
・ x:4 = 8:7
→ 7x = 32 → x = \(\large{\frac{32}{7}}\)
・ \(\large{\frac{5}{x}}\) = \(\large{\frac{2}{3}}\)
→ 両辺に「x・3」を掛けて
→ \(\large{\frac{5\ \cdot \ x\ \cdot \ 3}{x}}\) = \(\large{\frac{2\ \cdot \ x\ \cdot \ 3}{3}}\) (←なれてくると省略できる途中式)
→ 15 = 2x (←いきなりこれにこれるようになります)
→ x = \(\large{\frac{15}{2}}\)
・\(\large{\frac{x}{4}}\) = \(\large{\frac{5}{3}}\)
→ 両辺に「4・3」を掛けて
→ \(\large{\frac{x\ \cdot \ 4\ \cdot \ 3}{4}}\) = \(\large{\frac{5\ \cdot \ 4\ \cdot \ 3}{3}}\)
→ 3x = 20
→ x = \(\large{\frac{20}{3}}\)
・\(\large{\frac{x}{4}}\) = \(\large{\frac{5}{3}}\)
→ \(\large{\frac{ }{4}}\) 、\(\large{\frac{ }{3}}\) は どうせ消えるし、クロスに掛けるだけ
→ 
→ 3x = 20
→ x = \(\large{\frac{20}{3}}\)
【 連比 】
《 例 》
2:3:5 = 7:x:y
→ 2に対応する7を見ると\(\large{\frac{7}{2}}\)倍とわかる
∴ x = 3×\(\large{\frac{7}{2}}\) = \(\large{\frac{21}{2}}\) y = 5×\(\large{\frac{7}{2}}\) = \(\large{\frac{35}{2}}\)
《 例 》
a:b = 1:3、 b:c = 16:1 のときa:b:cは?
→ 両方に使われている「b」で合わせばよいですね
(16を3に近づけるイメージ)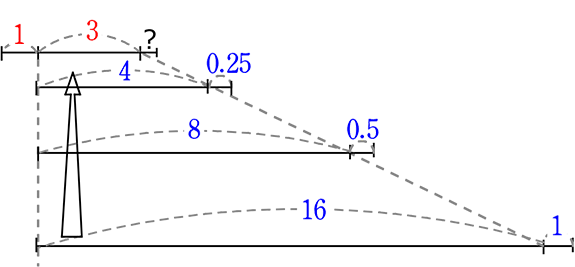
→ 3と16の最小公倍数は…「互いに素」なので 3×16 (=48)ですね
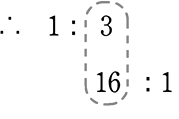
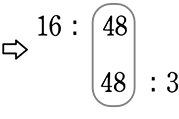
∴ 16:48:3 ですね
《 例 》
ある店のすき焼きの割り下は、醤油3:酒1、 醤油16:砂糖1でした
酒480gのとき、酒:醤油:砂糖は?
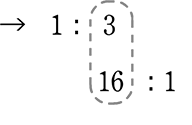
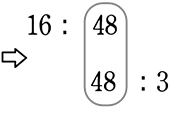
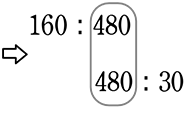
∴ 160g:480g:30g ですね
(きれいにかぶる部分がない場合)
《 例 》
図のようなとき、a:b:cは?
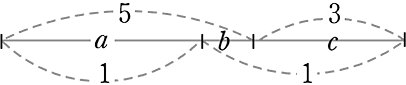
→全体を「1」とすると
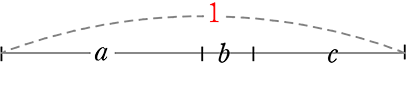
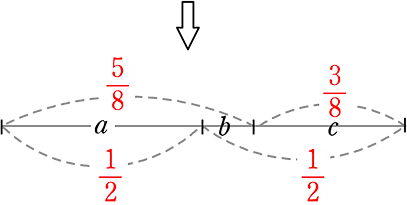
→ 「通分」すると
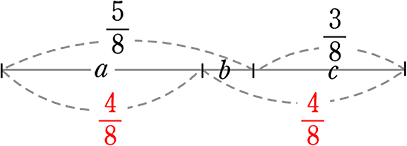
∴ b = \(\large{\frac{5}{8}}\)-\(\large{\frac{4}{8}}\) = \(\large{\frac{1}{8}}\)
∴ a:b:c = \(\large{\frac{4}{8}}\):\(\large{\frac{1}{8}}\):\(\large{\frac{3}{8}}\) = 4:1:3
《 例 》
a+b:c = 5:3、 a:b+c = 1:1のとき、a:b:cは?
→ 図を書いてみると
→ 先ほどと同じ問題ですね
∴ a:b:c = 4:1:3
cf.
中学2年生なら連立方程式でもよいですね
→ \(\small{\begin{cases}
\large{\frac{a+b}{c}}=\large{\frac{5}{3}} \scriptsize{…\large{①}}\\
\large{\frac{a}{b+c}}=\large{\frac{1}{1}} \scriptsize{…\large{②}}
\end{cases}}\)
→ \(\small{\begin{cases}
\large{\frac{a+b}{c}}=\large{\frac{5}{3}} \scriptsize{…①}\\
\large{\frac{a}{b+c}}=\large{\frac{1}{1}} \scriptsize{…②}
\end{cases}}\)
=\(\small{\begin{cases}
3a+3b=5c\\
a=b+c
\end{cases}}\)
(下を上に代入) 3(b+c)+3b=5c → 6b=2c ∴ b:c = \(\large{\frac{1}{6}}\):\(\large{\frac{1}{2}}\) = 1:3
(6b=2c より) c=3b → (これを下に代入) a=b+(3b)=4b ∴ a:b=\(\large{\frac{1}{1}}\):\(\large{\frac{1}{4}}\)=4:1 (「=でつながるものを比に戻す」は次で説明しますね)
∴ bがたまたまそろっているので、そのままつなげて、a:b:c = 4:1:3
【 =でつながるものを比に戻す 】
(=で結ばれたものを比に戻すの理由)
《 例 》
2a = 3b のとき a:bは?
「=でつながるものを比にする」には「係数を逆数にするだけ」となります
∴ a:b = \(\large{\frac{1}{2}}\):\(\large{\frac{1}{3}}\) = 3:2
ex)
a = 2b で考えるととイメージしやすいですね
→ 式は、aはbの2倍という意味、 ということは、 a:b = 2:1ですね
→ 「係数逆数方式」なら
a:b = \(\large{\frac{1}{1}}\) :\(\large{\frac{1}{2}}\) = 2:1 ですね
cf)
a:b = 2:1 のときaを求めよ
→ 外側の積 = 内側の積 → a = 2b ← 途中のこの形とも言えますね!
→ 逆の作業ということですね
ex)
2a = 3b → a = \(\large{\frac{3}{2}}\)b
→ aはbを\(\large{\frac{3}{2}}\)倍したものという意味
ということは、a:b = \(\large{\frac{3}{2}}\):1 = 3:2
…考える必要がないぶん やっぱり「係数逆数方式」の方が楽ですね
お疲れ様でした !!
その他の問題は、「問題集」で !!















