| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 正の数・負の数 | (2) 文字を用いた式 | (3) 一元一次方程式 |
| ア | 方程式などの意味 |
|---|---|
| ・ | 「方程式」という名前の由来 |
| ・ | 〇元〇次の意味 |
| イ | 等式の性質と方程式 |
| ・ | 等式とは |
| ・ | 『等式の性質』 |
| ウ | 簡単な一元一次方程式の解法と活用 |
| ・ | 方程式を解く道具 ①移項 |
| ・ | 方程式を解く道具 ②本体の改造 |
| ・ | 方程式を解く道具 ③全とっかえ |
| ・ | 方程式を解く道具 ④全符号かえ |
| ① | 不等式 |
| ② | 年齢 (文章問題) |
| ③ | 距離 (文章問題) |
| ・ | 「分」を「時間」に直す |
| ・ | 速さとは |
| ・ | 3つの速さ |
| ・ | 問題集の解答例と違っても… |
| ・ | 3つのうち2つが解れば残りも解る |
| ④ | 割合 (文章問題) |
| ・ | 百分率とは、歩合とは |
| ・ | 分子の方が大きい割合の意味 |
| 1 | 「食塩水」の問題 |
| 2 | 「値段」の問題 |
| ・ | 利益率とは |
| ・ | 利益率で何を知る? |
| ・ | 競争率とは |
| ・ | 勾配の%とは |
| ・ | 割合のイメージ画像 |
| ⑤ | その他文章問題 |
| ・ | 文章問題の出題傾向 |
一次方程式 (一元一次方程式)
ア 方程式などの意味
「方程式 (ほうていしき)」・・・何か言葉だけで威圧されてしまいますね。
ですが、構える必要は全くないです。
順を追って説明しますね
《 例 》
3x+2=8 という式があるとします。
等号(または不等号)の、左を「左辺」、右を「右辺」といいます。

3x+2=8 は x=2のときだけ、式として成り立ちますね (代入してみて下さいね)
これは方程式です
対して、
x+2x=3x という式は、
x=1(→1+2=3)でも、x=2(→2+4=6)でも、x=3(→3+6=9)でも、
何でも成り立ちますね!
これは方程式ではありません!
簡単に言えば、「xを求めることができる等式が方程式」
そして、方程式の目的は、
「xの値(解)を求めたい! できれば簡単に!」それだけです!

「方程式」という名前の由来
| 方・・・ | 昔、「方」とは「左右」という意味でした |
| 程・・・ | どれ程(ほど)か比べること |
| 「方程式」・・・ | 「左右を比べる式」 だったようですね。 |
もう少し言葉を補足すれば、
「左右を比べて、未明な値(解)を求めるための式」といった感じでしょうか。

〇元〇次の意味 (次数)
| 〇元 … | 使われている文字の種類数 一元 → 1種類 |
| 〇次 … | 文字どうしの掛け合わせ数 一次 → かけ合わせがなく、最高1乗 |
《 例 》
| x+y=0 | → 二元一次式 |
| 3(x+1)=9 | → 一元一次 |
| xy=6 | → 二元二次 |
| a2+2a2b+b2=0 | → 二元三次 |
| x2+2x+1=0 | → 一元二次 |
| abc=3 | → 三元三次 |
「~
1年生で今 学んでいる 一次方程式は
正確には、「一元一次方程式」ということですね
イ 等式の性質と方程式
等式とは

のように「左辺」と「右辺」が「等号」の関係である式を「等式」といいます。
簡単に言えば、「=(イコール)で結ばれている式が等式」
ということは、「 <, >(不等号)で結ばれているいる式は不等式」ですね。
アの《 例 》の x+2x = 3x は「方程式」ではないですが「等式」ではありますね。
〇 =
のように、「右辺」がないものは、「等式」ではなく、
今まで学習してきた「計算せよ!」ですね!
実際は、「計算せよ!」の問題では、「=(イコール)」は書かれていませんね!
自分で「=」を書き出します。
今後、難解な「計算せよ」を計算していると、
うっかりミスで、
つい自分の作り出した「=(イコール)以下」を
「等式の右辺」と勘違いしてしまい、
両辺を、つい「2」で割ってみたりしてしまいます。
これができるのは等式・不等式だけですね!
なぜダメなのか・・・
ex) 「計算せよ」6+4 は?・・・
6+4=10 両辺を「2」で割ってしまうと 3+2=5 答え.5
・・・違いますよね!
問題は、6+4 でしたよね。答えは10ですよね。
「計算せよ」は「等式」ではない!
ということを忘れないでくださいね!
「計算せよ」に「等式の性質」(後述)は、使ってはいけません~!
〇 = 0
左辺 右辺
右辺が「0 (ゼロ)」! これは「等式」ですね!
等式の性質
方程式を解く( xを求める) ためには、「等式の性質」を利用します。
例えば、赤のペットボトル(1本500g) を2本と、
青のペットボトル(同500g) を2本、
天秤にのせます。 つり合っていますね。
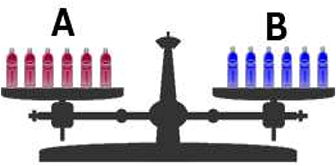
| ① | それぞれに、500gの重りを足し(+)ます。 つり合っていますね。 |
| ② | それぞれから、1本引き(-)ます。 つり合っていますね。 |
| ③ | それぞれを、2倍(×)します。 つり合っていますね。 |
| ④ | それぞれを、2で割り(÷)ます。 つり合っていますね。 |

等式の性質
A=B ならば、
| ① | A+c = B+c (同じものなら、両辺に足しても成り立つ) |
| ② | A-c = B-c (同じものなら、両辺から引いても成り立つ) |
| ③ | A・c = B・c (同じものなら、両辺に掛けても成り立つ) |
| ④ | A÷c= B÷c (同じものでなら、両辺を割っても成り立つ) |
となりますが、
実際、方程式を解くときは、①(両辺に+)と②(両辺に-)は「移項」(後述)でカバーしますので、
結局、使うものは、 「移項」・③・④だけとなっていきます!
ウ 簡単な一元一次方程式の解法と活用
移項
例えば、次の等式の左辺を5だけにしたい場合

(ここを0にできればよい)
5+3-3 = 8-3 (「等式の性質」を利用して、両辺に-3を足した)
5 = 5
ですが、これは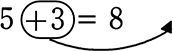 +3の項を、-3にして右辺に移動させたことと同じですね!
+3の項を、-3にして右辺に移動させたことと同じですね!
5 = 8-3 項を移動 →
マイナスも同様です
左辺を5だけにしたい場合
5-2 = 3
5-2+2 = 3+2 「等式の性質を」を利用して、両辺に2を足した
5 = 5
ですが、これは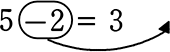 -2の項を、+2にして右辺に移動させたことと同じですね!
-2の項を、+2にして右辺に移動させたことと同じですね!
5 = 3+2
それでは、上の例の「5」を「x」に置き換えて、
同様にできることを確認してみましょう

5 = 8-3
5 = 5
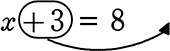
x = 8-3
x = 5
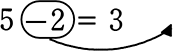
5 = 3+2
5 = 5
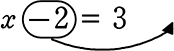
x = 3+2
x = 5
当然、右辺から左辺 に移項しても符号が変わります
まとめますと、
項(元)は、 = (イコール)をまたぐと符号が変わる
それだけです!
本体の改造
移項が終わったら、次は残った本体の「項自体の改造」ですね
「等式の性質」の 3, 4 を使います。
たとえば、
3・6=18 で左辺を「6」だけにしたいとします
「等式の性質」を使って、両辺を3で割る(=\(\large{\frac{1}{3}}\)を掛ける)だけですね!
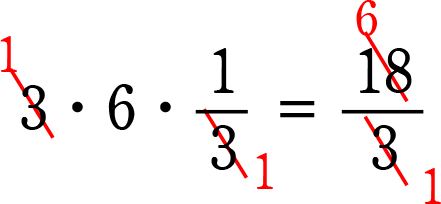
6 = 6 ですね!
では、次に
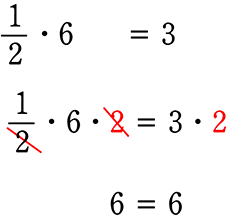
\(\large{\frac{1}{2}}\)・6=3 の左辺を「6」だけにするには、
もう言うまでもないですか・・・・両辺に「2」を掛けるだけですね!
![]()
6=6ですね!
それでは、「6」を「x」に置き換えて
同様にできることを確認してみましょう
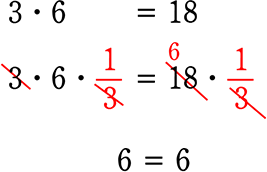
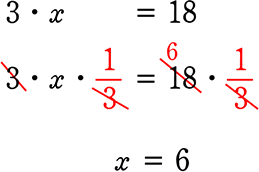
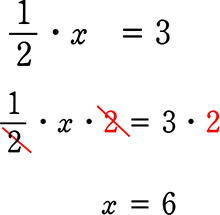
結局は、「どうすれば xの係数が『1』になるか」ということですね!
全とっかえ
言うまでもないとは思いますが、
3・2 = 6 は
6 = 3・2のように左辺と右辺を、まるまる入れ替えられますね。
全符号かえ
両辺に「-1」を掛けると、全ての項の符号が変わりますね
7×3 = 21
-1(7×3) = -1(21)
-(7×3) = -21
5+3 = 3×2+3-1
-1(5+3) = -1(3×2+3-1)
-(5+3) = -(3×2+3-1)

項のイメージ
正の数・負の数の余談の「(カッコ)の意味」でお話しましたが、
もう一度!
●「×÷」でつながっている

「元」は1つ
(「元」がどのように「変形」したのか
イメージ:横に大きくなって、次に縦に大きくなって、次は全体的に小さくなって・・・ )
例) 3 → 1×3
xy → 1×x×y
\(\large{\frac{1}{2}}\)xyz → 1÷2×x×y×z
●「+-」でつながっている
![]()
「元」は 複数 ある
(「元」に「何がくっついてきたのか」
「何が引かれてしまったのか」 )
例) 1+2
x+y
\(\large{\frac{1}{2}}\)+x+y+z
( )で囲まれているということは、それで「一文字」です!
それで「元」です!
それで「項」と思ってよいです!
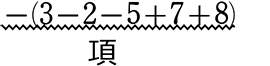
↑本来は計算した -(+11) = +(-11)→「-11」が項
cf.
-6・2・3・2 のように「×÷」でつながっているものは、元々、「元」が一つ(=一つの項)、
(カッコ)で囲む必要がないということですね!
長くなってしまいましたが
一次方程式を解く「ツール」は結局、
| 1. | 移項 |
| 2. | 等式の性質3、4、 (項自体の改造) |
| 3. | 全とっかえ 5=x+2 → x+2=5 |
| 4. | 全符号かえ -x-3=7 → -(-x-3)=-(7) |
だけですね!
では、「方程式を解いていきましょう」
左辺を「x」だけにする作業です

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)
① 不等式
不等式の解を求めることも、ほぼ、一次方程式を解く方法と同じですね。
違う点は、
| 3. | 全とっかえ をすると当然、不等号の向きもそれに伴う向きになりますね |
5>x+1 → x+1<5
| 4. | 全符号かえ(両辺にそれぞれ -1を掛ける) をすると、 「不等号」の向きが変わる |
-x>6
↓
x<-6
それだけです!
1.の移項 2.の本体自体の改造
は一次方程式と全く同様に使えますね!


② 年齢
《 例 》
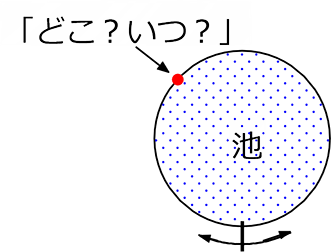
現在母の年齢は39歳、子は15歳、母の年齢が子の年齢の3倍であったのは何年前でしょうか。
| ① | イメージするために簡単な図を描きましょう |
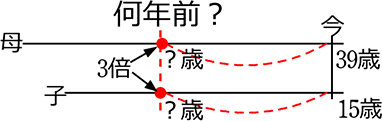
| ② | 何を xと置くと楽か 図を見ながら考えましょう。 (これをxとしなければならない、ということはありません。 答えと理論が正しければ 〇です。) |
おおよそ、「求めよ」といわれているものが「x」になりますね
「何年前の「何」がxかな」
「2人の「x年前の「年齢」」が3倍の関係か・・・」
| ③ | 母のx年前の年齢 …(39-x)歳
子のx年前の年齢 …(15-x)歳 |
| ④ | 「2つの年齢が3倍の関係か・・・」ということは
子の方を3倍にすれば「=」の関係になるということか |
もちろん、母の年齢を\(\large{\frac{1}{3}}\)倍すれば「=」の関係か・・・でもOKです
\(\large{\frac{1}{3}}\)(39-x)=15-x でもよいですね
とりあえず解いてみると・・・x=3
⑤ 確認作業、xに3を代入してみると
・母 39-3=36歳
・子 15-3=12歳
ちゃんと3倍の関係になってる!
A. 3年前
③ 距離
《 例 》
Aさんは2300mはなれた公園にいくのに、はじめは毎時4.2kmの速さで歩き、
途中から毎時9kmの速さで走ったら、26分かかりました。
このときAさんが歩いたのは何分間でしょうか。
① 前提として、
距離、時間、速さ の関係が頭に浮くようにしましょう
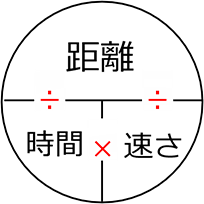
ですね。数学の基本は
「3つのうち、2つが解れば、残りの1つは求まる」ですね。
距離=速さ×時間、 時間=距離÷速さ、 速さ = 距離÷時間
と個別に憶える必要はありませんね。
「距離」「時間」「速さ」の3単語を憶えて、
1番大きいもの(マル図でいえば上)は距離」と憶えると楽ですね。
| ・ | (だいたい掛けると大きいものが出るから、) 小2つを掛けると大(距離) |
| ・ | 大(距離)を小(時間)で割ると、もう一方の小(速さ) |
| ・ | 大(距離)を小(速さ)で割ると、もう一方の小(時間) |
が求まるという図です
イメージできるまでは、毎回、〇図(マル図)を書きましょう
(もちろん、問題をたくさん解いているうちに、
距離=速さ×時間、 時間=距離÷速さ、 速さ = 距離÷時間
対象 = 割合×全体、 全体 = 対象÷割合、 割合 = 対象÷全体
と個別にも憶えてしまいますね)
② 簡単な図 を描きましょう
「分」と「時(毎時)」、「km」と「m」が混ざっているので、
楽な方に統一しながら・・・
(大体、中学では 「mと分」「kmと時間」がセットですね)
再度、問題文です
Aさんは2300mはなれた公園にいくのに、はじめは毎時4.2kmの速さで歩き、途中から毎時9kmの速さで走ったら、26分かかりました。
このときAさんが歩いたのは何分間でしょうか。
・4.2km/1時 = 4200m/60分 = 70m/分
・9km/1時 = 9000m/60分 = 150m/分
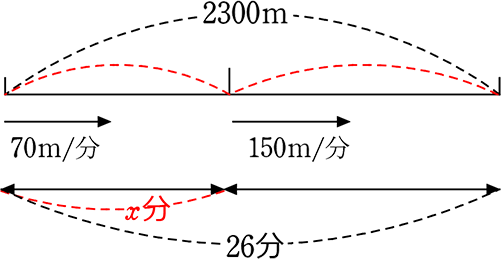
| ③ | 何を x と置くと楽か図を見ながら考えましょう。
70m/分で歩いた時間かな・・・x分間 ( 図にどんどん書き足しましょう) |
「150m/分で歩いた時間」もわからないな・・・y分間とするか・・・
でもいいのですが、これは2年生の「連立方程式」ですね!
ちなみに
\(\small{\begin{cases}
x+y=26 (時間) \\
70x+150y=2300 (距離)
\end{cases}}\)
ですね、
少し整理して
→ \(\small{\begin{cases}
y=26-x \\
7x+15y=230
\end{cases}}\)
→ 7x+15y = 230 の式に y=26-x を代入して
xだけの式にします → 7x+15(26-x) = 230 → x=20 A. 20分
戻って、ここに、「150m/分で歩いた時間」のヒントがありますね!
そうです y=26-x の右辺です。yの正体は26-x 「全体-x」だったのですね。
yを使わなくても、xだけで表すことができるということですね。
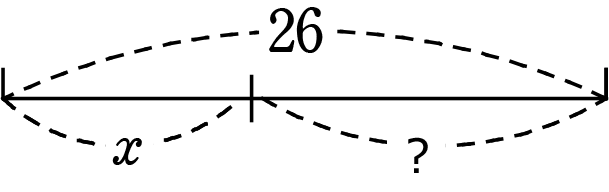
・?を「y」とおく → 連立方程式 (2年)
・?を「26-x」とおく → 一次方程式
| ④ | 式を立ててみる (習っていない技は定期テストでは使ってはいけないので)
連立方程式ではなく、一次方程式の式をたてる |
● 時間+時間 = 全時間
x+(26-x)=26 → 26=26 → xを求められない → 方程式ではない
では、
● 距離+距離=全距離
→ 速さ・時間+速さ・時間=全距離
→ 70・x+150・(26-x)=2300 → 70x+150(26-x)=2300
∴ x=20 A. 20分間
問題集の解答だとおそらく、
\(\large{\frac{4200}{60}}\)x+\(\large{\frac{9000}{60}}\)(26-x)=2300
だと思いますが
これは、
① km/時 を m/分 になおす
② 式を立てる
を同時に処理していますね
ですが 段階的に処理しても大丈夫です。
入試では答えが合っていればいいのですから。
定期テストでは「考え方」と「答え」が合っていればいいのですから!

「分」を「時間」になおす
例えば「5分」は「\(\large{\frac{5}{60}}\) 時間」ですね
どうして 「分」を「時間」にするには「60」で割るの?
という、素朴な疑問の回答として・・・
まずは 「60で割る」というフレーズを忘れていただいて、
⇒ 「1分」=「\(\large{\frac{1}{60}}\)時間」ということは、なにかイメージできますね
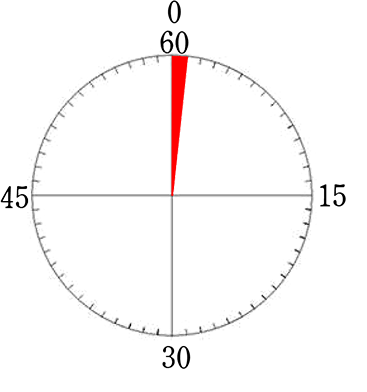
→ 1時間には60の目盛りがある
→ 1目盛り
\(\large{\frac{1}{60}}\)は、1分である
→ 15分なら \(\large{\frac{1}{60}}\)×15 = \(\large{\frac{15}{60}}\)時間
これだけですね
結果、「\(\Large{\frac{}{60}}\) 」が「60で割っている」形と見えるだけ
∴ 「60で割る」 というより「\(\large{\frac{1}{60}}\)時間を何個使うか」というイメージが楽ですね
「分」はその数字に \(\Large{\frac{}{60}}\) を付ければ 「時間」になる
数学では「分数のまま」が計算しやすいですね(小数にする必要はないですね)
「実社会」は小数表記が多いですが、代表的な小数だけ憶えていれば十分ですね

0.25時間 = \(\large{\frac{1}{4}}\)時間 = \(\large{\frac{15}{60}}\)時間 = 15分
0.5時間 = \(\large{\frac{1}{2}}\)時間 = \(\large{\frac{30}{60}}\)時間 = 30分
0.75時間 = \(\large{\frac{3}{4}}\)時間 = \(\large{\frac{45}{60}}\)時間 = 45分



速さとは
200kmを4時間で行った時の速さは?
200kmを4時間で行くような速さ !! でも〇なのですが、
4時間速200km! 3時間速120km!
0.5時間速50km!
「早いのか、遅いのか」イメージできませんね!
「距離」には「定規」、「時間」には「時計」があって、イメージできますが、
「速さ」自体には基準がないから、イメージできないですね。
そこで、
「1時間あたりに進む距離 を速さ」(1時間速→時速)
「1分間あたりに進む距離 を速さ」(1分間速→分速)
など
「時間」あたりの「距離」を「速さ」
と基準づけたのです。

そして、「速さ」と言ってもただの「割合」であることには間違いないので、
それが、「早いのか」「遅いのか」を
「イメージしたもの」が本当の意味の「速さ(スピード感)」ですね。
「イメージ」ということは、「経験」を重ねていくしかないのでしょうね。
動く点を紙に書いて表現することはできないですものね。
小さなお子様に、
はるか上空のジェット機を指して、
「早いね~」と言っても
経験がない分、「遅い!」と言うかもしれませんね。
ちなみに、電車の運転士さんは、
スピードメーターを見なくても、流れる景色から
「現在、時速67km!」とか、わかるらしいです。
「絶対音感」ならぬ、「絶対スピード感」ですね!
長くなりましたが、
もしかしたら、昔の人が
「速さ」=「時間」÷「距離」と基準づけしていたら
「1kmあたり〇時間かかるような速さ」(1km間速)
となっていたかもしれませんね!
「慣れ」ってすごいですね!
「大谷選手出たー! 160km(/時)!」
「大谷選手出たー! 22.5秒(/km)!」
なんてね。

3つの速さ
中学数学の方程式では、3種類の「速さ」がありますね
①「(絶対)速さ」
例えば、60km離れた地点に、1時間で行けたら・・・
誰が見ても「絶対的に」
「速さ」= 60÷1 = 60km/時ですね

最もポピュラーな「速さ」ですね
-絶対速さ-
| ・ | 両地点が 動かない (基準がある) |
| ・ | 他の力が 影響しない (自分の実力のみ) |
②「乗っかる速さ」 (親中用語)
例えば、流速30km/時の川で
60km離れた下流地点に、1時間で行けたら
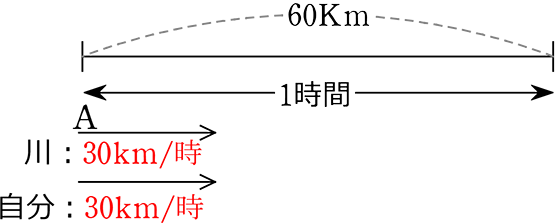
「速さ」= 60÷1 = 60km/時ですが
内訳は
・川の速さ 30km/時
・ボートの速さ 30km/時 ( 実力 )
ボートの「乗っかる速さ」 = 川の「速さ」+ボートの「速さ」= 60km/時ということですね
乗っかる速さ=本体の速さ±足元の速さ =実力±x
-乗っかる速さ-
| ・ | 両地点が動かない (基準がある) |
| ・ | 他の力が影響する (自分の実力±足元の速さ) |
逆に、上流に向かう場合は 30km/時-30km/時 = 0km/時で
ルームランナーのようにその場にとどまっていますね
ex) エスカレーター、動く歩道を歩く人
電車の中を歩く人
気流の中の飛行機
③ 「相対速さ」 (親中用語)
例えば、「宇宙空間で」「周りに星がない(基準がない)」空間で
星Aと60km離れた星Bが 1時間後に衝突しました
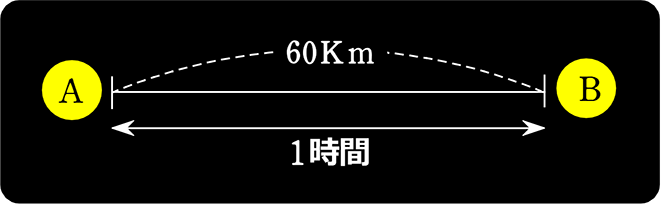
Aの速さは? と言われても…
Bが止まっているなら Aは右に60km/時
Aが止まっているなら、Bが左に60km/時
Bが左に30km/時なら、Aは右に30km/時
Bが右に30km/時なら、Aは右に90km/時 ・・・
∴ Aの速さは、Bを「止めて」考えるのがよいですね
| → | Aの「相対速さ」 = Aの速さ±Bの速さ |
| → | Aが進んだ距離+Bが進んだ距離=60km
(同方向なら、Aが進んだ距離-Bが進んだ距離=60 |
| → | Aの動いた時間 = 1時間 (Bの速さがなんであれ) |
-相対速さ-
| ・ | 両地点が動く (基準がない) |
| ・ | 他の力が影響する (自分の速さ±相手の速さ) |
ex) 電車に抜かれる人、すれ違う人
方程式の問題では、
「衝突する」「出会う」「追いつく」『地点』までの
「距離」「時間」がわからないことが多いですね
(それぞれの「速さ」「2つの間の距離」はわかっている問題が多い)ので
立てる式は・・・
| ・ | 「全距離 = A距離+B距離」→「全距離=A速さ・x時間+B速さ・x時間」 |
| ・ | 「A距離 = B距離」→「A速さ・x時間 = B速さ・x時間」など |
「距離」を基本に式を立てることが多いですね
(「出会う地点までの距離か時間がわかっていれば、方程式など立てなくても普通の計算問題ですものね)

問題集の解答例
どのような数学の問題集の解答も「解答例」です。
あくまで「例」です。
最後の答えだけは「唯一無二」ですが・・・
途中の計算式は、違っていて当然ですね。
答えにたどり着くまでのアプローチはたくさんありますので、
自分のアプローチと解答例が違っていても
「自分の解き方はダメだ」と、思わないで下さいね!
「良い解き方」を探している段階なのですから!
逆に、「この問題集はダメだ」とも思わずにいてくださいね。
「この解答例は、どういう考え方なのか」を追求することも、
とても勉強になります。
人と人との付き合いも全く同様ですね!

数学の大原則
数学では、「3つのうち2つが解れば、残りの1つは必ずわかる」ですね!
x+y=z 、xy=z 、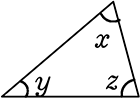 、
、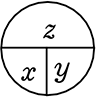 、などなど
、などなど
・x、y が解れば → 残りの zが解る
・x、z が解れば → 残りの yが解る
・y、z が解れば → 残りの xが解る

に派生していきますね!
④ 割合
割合とは
割合とは・・・一言で言うと・・・
『分母の数に対する 分子の数』です ただそれだけです!
例えば、
● 40人クラスに 鈴木さんが2人 『(クラスに対する) 鈴木さんの割合は?』
答.
鈴木さんの(クラスに対する)割合は… \(\Large{\frac{2人}{40人}}\) 
これだけです!
日本語で言うと、全40人につき(分母)、2人が鈴木さん(分子)

● 200gの食塩水に 食塩が20g『(食塩水に対する) 食塩の割合は?』=『食塩水の濃度は?』
答.
食塩の(食塩水に対する)割合(=濃度)は…\(\Large{\frac{20g}{200g}}\) 
これだけです!
日本語で言うと、全200gにつき(分母)、20gが食塩(分子)
● 定価1000円に 値引き額が200円 『(定価に対する) 値引き額の割合は?』
答え.
値引き額の(定価に対する)割合は… \(\Large{\frac{200円}{1000円}}\) ![]()
これだけです
日本語で言うと、全1000円につき(分母)、200円が値引き額(分子)
● 昨日の来場者2000人に 今日は20人減少 『(昨日に対する) 減少者の割合は?』
答え.
減少者の(昨日に対する)割合(=減少率)は… \(\Large{\frac{20人}{2000人}}\) 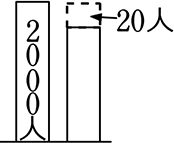
これだけです
日本語で言うと、全2000人につき(分母)、20人が減少数(分子)
● 100mの横に対し、50mの高さ 『(横に対する) 高さの割合は?』
答え.
高さの(横に対する)割合(=傾き)は… \(\Large{\frac{50 m}{100 m}}\) 
これだけです
日本語で言うと、100mにつき(分母)、50mの高さ(分子)
→ 「比例定数」「変化の割合」「傾き」「勾配」のことですね
それぞれ名前は違いますが、全て『高さの割合』ということですね
● 2時間で100km 『(時間に対する) 距離の割合は?』
距離の(時間に対する)割合(=速さ)は… \(\Large{\frac{100km}{2時間}}\) 
これだけです!
日本語で言うと、2時間につき(分母)、100kmの距離(分子)
(「単位」どうしが約分できないものは「km/時間」などが残りますね
「km/分」「m/分」「人/日」「点/人」などなど たくさんありますね!
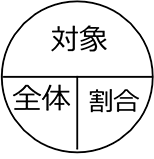
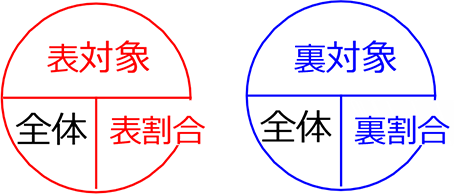
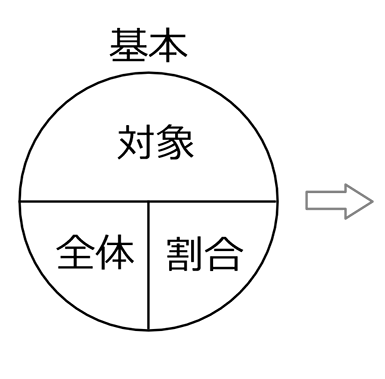
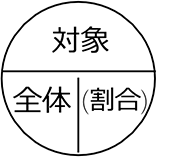
● 全体の数に対し これだけの対象の数 『(全体に対する) 対象の割合は?』
答え.
対象の(全体に対する)割合は… \(\Large{\frac{対象}{全体}}\) 
これだけです!
日本語で言うと、全体の数につき(分母)、これだけの対象の数(分子)
◎ 主役を分子にもって来るだけですね!
「割合」はただこれだけです!
「分数」にするだけで「につき」「ごとに」などの割合になります!
・・・ですが、 『約分』できるものがありますね
鈴木さんの割合 \(\large{\frac{2人}{40人}}\)などは、\(\large{\frac{1人}{20人}}\)
日本語で言うと、20人につき(分母)、1人が鈴木さん(分子)
「逆約分 (造語です)」すれば、80人につき4人が鈴木さん、160人につき8人が鈴木さん…ですね
「割合といえば…『0.03.』とか『3割3分』とか『30%』とかではないの?」
→ 上の例もちゃんと 全く同じことを言っているのです
ex)
200gの食塩水中に 食塩が20g 濃度(塩の割合)は?

確かにどれも「 = 」ですね、(少数まで計算すればどれも「0.1=10%」)
| ・ | 「数学」ではどれも「割合」ですが |
| ・ | 「世間一般の割合」は『分母が1化』されたものを「割合」と言いますね |
→「1化」されて「単位も約分」できたものは「百分率 (%)」や「歩合 (割、分、厘)」で表現することがゆるされますね
「濃度0.1」 = 「濃度10%」 = 「濃度1割」
ここまでくると 従来の
割合 = 「対象」を「全体」で「割る」という意味もわかりましたね
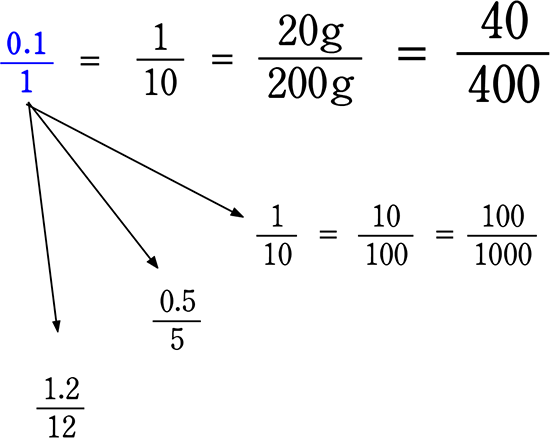
例えば\(\large{\frac{20}{200}}\) で分母を1化するためには分母を200で割りますね、 当然分子も200で割らなければいけませんね \(\large{\frac{20÷200}{200÷200}}\) = \(\large{\frac{0.1}{1}}\)
(結果「分子」も「分母と同じ数」で割る → 「分子」を「分母」で割る → 「対象」を「全体」で「割る」
ということにつながりますね 「本来は分母を「1」にするのが目的」だった)
● 割合 = 全体(分母)の1化 → 結果、「対象÷全体」
では、どうして分数のままでも「割合」なのに、
「約分」を通り越して わざわざ「分母の1化 (以後1化)」までするのでしょうか?
答えは2つですね
理由1.「イメージしやすいから」 → 「%」「何割何分何厘」が使える
ex)
果汁30%の350ccの缶ジュースを持って「これの30%が天然果汁か」

「30%かぁ これくらいかな(イメージしやすい)」
「\(\large{\frac{105cc}{350cc}}\) よりイメージしやすいですね」
・100円硬貨(4.8g)の金属含有率「ニッケルは1.2g」も1化すると・・・
「 ニッケル0.25(25%)、銅0.75(75%)」

「100円硬貨のイチカ」 (右の赤部分がニッケル、左が銅)
リアル:「100円硬貨(4.8g)は、1.2gがニッケル」
1化後:「100円硬貨の25%はニッケル」
・閉店間際の処分価格弁当(500円)の 「半額(= 50%引き)シール」

「500円弁当のイチカ」
リアル:「500円弁当が、250円値引」
1化後:「500円弁当が、50%引き(半額)」なぜかお得なイメージ
これは、心理学的なことで数学の話ではなかったですね。
ちなみに「車」のような高価なものは、「1化」表示しない方がお得感がありますね
「この200万円の車、1割引きしますよ!」
「この200万円の車、20万円値引きしますよ!」「20万も!」
理由2. 「暗算しやすいから」
→ 1化していると暗算しやすいですね
「10% = 0.1 = \(\large{\frac{1}{10}}\) =\(\large{\frac{0.1}{1}}\)=\(\large{\frac{②塩は 0.1g}{①食塩水 1gにつき}}\) という「基準(お墨付き)」を得た!」ので
| ・ | 食塩水1000gなら…分母が1000倍、 分子も1000倍 → 結果0.1×1000= 100g!」 |
| ・ | 食塩水5gなら…結果0.1×5 =0.5gが塩!」 |
| ・ | 食塩水12gなら…結果0.1×12 =4.2gが塩!」 |
「暗算」しやすいですね、
ですが「計算」は「分数のまま」の方が全然楽ですね
ex)
306gの水に塩を54g混ぜた食塩水を120gと190gに分けたとき、
120gの方には塩が何g含まれているか?
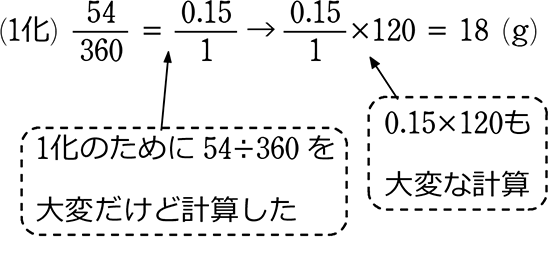
(分数のまま)  = \(\large{\frac{54}{3}}\) = 18 (g)
= \(\large{\frac{54}{3}}\) = 18 (g)
1化より楽ですね! 約分はどれとしてもよい!のですから
よって
数学の割合の計算では分数表記で慣れていきましょうね
文字式をつくるときも分数表記になってしまいますので!
ex)
水agに 塩bg を混ぜた時の濃度は何%?
→ 濃度=塩の割合 =\(\large{\frac{対象}{全体}}\) =\(\large{\frac{塩}{食塩水}}\) =\(\large{\frac{b}{a+b}}\) → (%表示指定より) → \(\large{\frac{100b}{a+b}}\) (%)
(\(\large{\frac{b}{a+b}}\)は、少数にしようがないですものね)
他方、「マル図」の
「対象」「全体」「割合」の3つの関係は当然といえば当然ですね
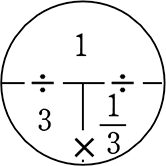
1 = 3×\(\large{\frac{1}{3}}\)
3 = 1÷\(\large{\frac{1}{3}}\)
\(\large{\frac{1}{3}}\) = 1÷3
当たり前の関係ですね
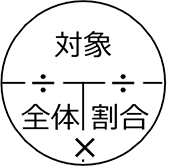
対象 = 全体×割合
全体 = 対象÷割合 = \(\large{\frac{対象}{割合}}\)
割合 = 対象÷全体 = \(\large{\frac{対象}{全体}}\)
当たり前の関係と思うようになっていきますね
まとめ
| ◎ | 「割合」とは 『分母の数に対する 分子の数』
(分数にしただけで 『分母につき分子』 の意味になる) |
| ◎ | 世間一般の割合は 『分母を1化までしたもの』 |
| ◎ | 1化の方法は 「分母」「分子」ともに「分母と同じ数(文字)で割る」
(結果「分子」÷「分母」) |
| ◎ | 「イメージ」と「暗算」は『1化』が有利
「計算」は『分数のまま』が有利 |
◎
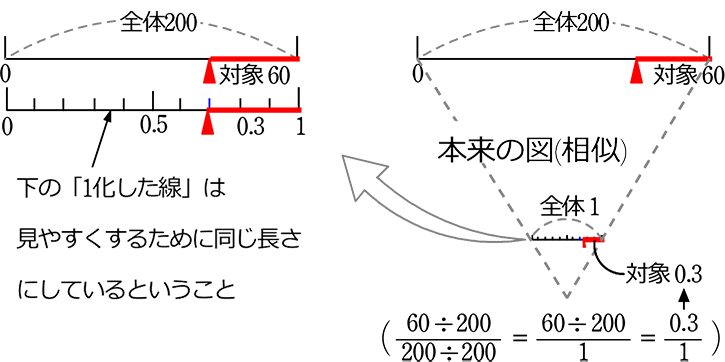
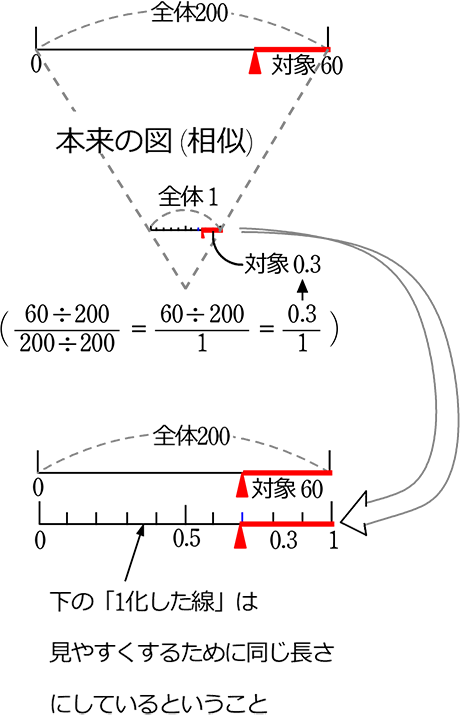
それでは、問題を解く上での簡単な「割合」の略図の書き方です
ex)
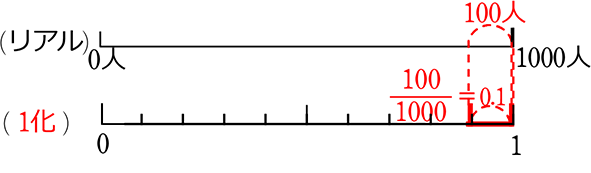
1000人中、左利き100人の割合は?

2本書きます、(「相似」の関係ではありますが、見やすさを優先して同じ長さでOKです)
| ・ | 100人(対象)÷1000人(全体)で、\(\large{\frac{1}{10}}\)(割合)が出ますね |
| ・ | 100人(対象)÷\(\large{\frac{1}{10}}\)(割合)で、1000人(全体)が出ますね |
| ・ | 1000人(全体)×\(\large{\frac{1}{10}}\)(割合)で、100人(対象)が対象が出ますね |
(もちろん \(\large{\frac{1}{10}}\) は 0.1 でもOKです)
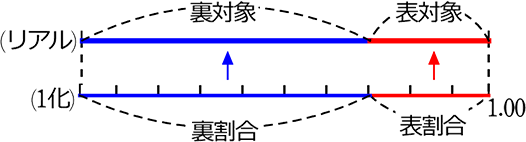
そして、大事なことが隠されていますね、 「裏対象 (造語)」「裏割合 (造語)」です!
スポットの当たっていない側の「対象」「割合」ですね
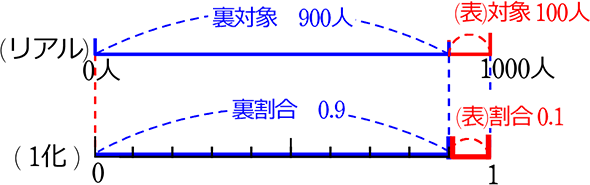
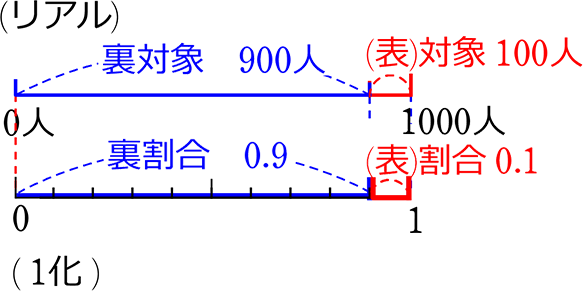
表対象同様に
| ・ | 900人(裏対象)÷1000人(全体)で、0.9(裏割合)が出ますね。または(1-0.1(表割合)) |
| ・ | 900人(裏対象)÷0.9(裏割合)で、1000人(全体)が出ますね |
| ・ | 1000人(全体)×0.9(裏小数)で、900人(裏対象)が出ますね。または(1000-100(表対象) ) |
そうです、「右利き」です。食塩水でいえば「水」です
そして、ひっかけは・・・

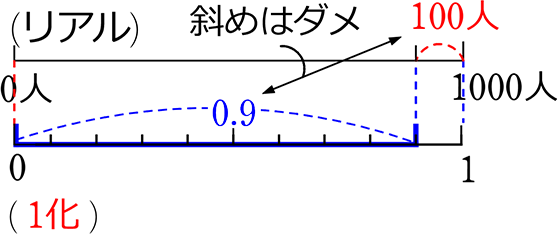
のように、「対象」と「割合」が対応していない場合です。
「表対象」からは「表割合」、「裏対象」からは「裏割合」しか出ないですね!
あと、従来の勘違いしやすいところをはっきりさせておきましょうね
例えば、『濃度1%の食塩水』とは、どのようなイメージなのでしょうか?
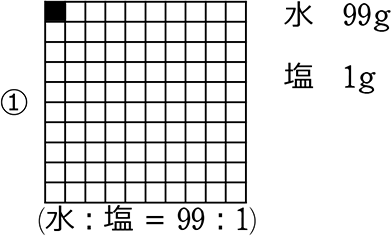
 = \(\large{\frac{1}{99+1}}\) = \(\large{\frac{1}{100}}\) = 0.01
= \(\large{\frac{1}{99+1}}\) = \(\large{\frac{1}{100}}\) = 0.01
1% ですね
そして、勘違いしやすいイメージがこれですね!
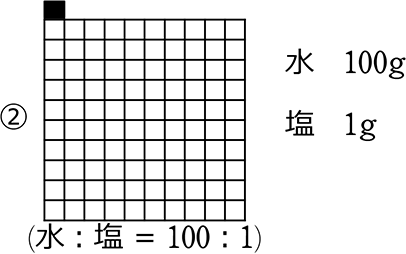
 = \(\large{\frac{1}{100+1}}\) = \(\large{\frac{1}{101}}\) = 0.0099…
= \(\large{\frac{1}{100+1}}\) = \(\large{\frac{1}{101}}\) = 0.0099…
0.99…%ですね!
「全体」というからには「対象」も含んで「全体」です!
「対象」は「全体」の中にいます!
ちなみに、
②の食塩水を1化したイメージ図は

百分率(%)、歩合(割、分、厘)
割合は「対象」の方が「全体」より少なければ
必ず、0~1 の中にありますから必ず「小数や分数」になりますね
では、どうして、「0.△△」や「\(\large{\frac{△△}{100}}\)を、100分率(%)や 歩合( _割り_分(ぶ)_厘(りん))
になおすのでしょうか。
⇒ 言葉にしたときに、「割合~と言わなくても、『割合』の話だなと分かる」
「イメージもしやすい」からですね
| ・ | 「割合 0.05の食塩水を作ってください」 ↓ 「5%の食塩水を作ってください」 |
| ・ | 「割合0.32のバッター」 ↓ 「3割2分のバッター」 |
(確認)
(計算時に使う)
「割合」→ \(\large{\frac{3642}{10000}}\) または 0.3642 ⇒ 「数値」だ!
(表現時に使う)
| ・ | %は、「1化」ならぬ「100化」ですね → 36.42% ⇒「言葉」だ! |
| ・ | 割分厘毛は、「イチカの位別の読み方」みたいなものでしょうか → 3割6分4厘2毛 ⇒ 「言葉」だ! |
割合が、なんとなくややこしくなる理由の一つは、
これらの「表現方法」(%や、~割)を、
計算途中では「分数、小数」になおすからだと思います。
ですから、完全分離させてくださいね
| ① | 計算のときは、分数または小数しか使ってはいけない |
・ 20%は → \(\large{\frac{20}{100}}\) や \(\large{\frac{2}{10}}\) や 0.2になおす
| ② | 最後の答えだけ、問題にあった表現方法「%」や「割分厘毛」で表現する |
・ 0.2は → 0.2×100 = 20% と表現できる
・ \(\large{\frac{a}{a+b}}\) → \(\large{\frac{a}{a+b}}\)×100 で \(\large{\frac{100a}{a+b}}\)%
というわけで、割合の問題で使う道具(公式)は、やはり

だけになりますね!
あとは、どのように使うかという「考え方」ということで、
これ以上「公式化」する必要はないと思います。
「公式化」すればするほどややこしくなる分野と思います。

分子の方が大きい割合の意味
《 例 》
クラスの全体は40人、鈴木さんという苗字が2名の場合
● 鈴木さん(=対象)の、(クラス40人に対する)「割合」は?
割合 = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{2}{40}}\) = \(\large{\frac{0.05}{1}}\) A. 5%
● では、逆にしてみた場合の、\(\large{\frac{40}{2}}\) とは、
どんな意味になるのでしょうか
割合 = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{40}{2}}\) = \(\large{\frac{20}{1}}\)
クラス(=対象)は鈴木さんの「20倍」という
小学算数のイメージ通りですが、
「20倍」=「2000%」とすれば、
ちゃんと「割合」の話ということがわかりますね
⇒ クラス40人(=対象)の、(鈴木さん2人に対する)「割合」
割合 = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{40}{2}}\) = \(\large{\frac{20}{1}}\) A. 2000%
1. 食塩水
まずは、小学生の復習です。
「濃度」とは、「塩」の(食塩水に対する)割合ですね
(食塩水 = 水+塩 = 全体)

・ 濃度 = \(\large{\frac{塩}{全体}}\)
・ 塩 = 全体×濃度(割合)
・ 全体 = \(\large{\frac{塩}{割合}}\)
3つのうち、2つがわかれば、残りの1つは求まるという基本ですね





《 例 》
6%の食塩水150gに、水を加えて2%にしたい、水を何g足せばよいでしょう。
① 簡単な図を描いて、正体を明らかにしましょう
A図
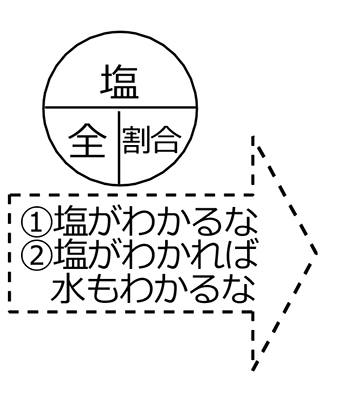
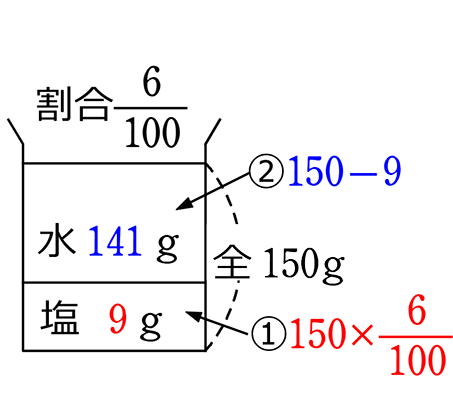
B図
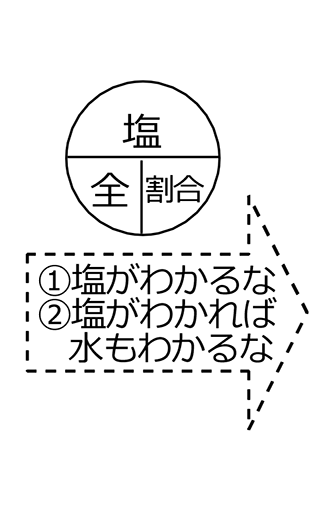
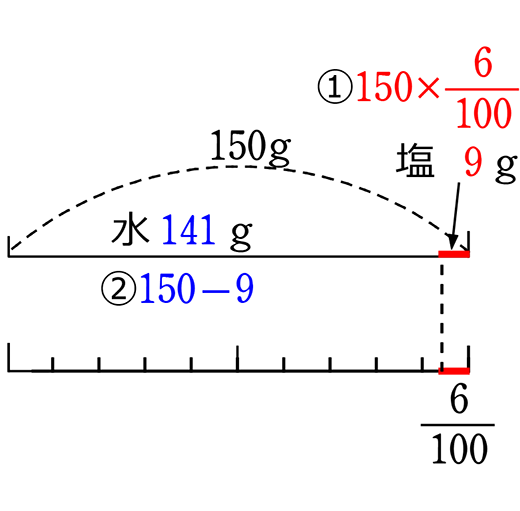
図は自分の解りやすいもの選んでくださいね(親子中学では今後、食塩水ではA図でいきます)
③ 水を加えて2%にしたい → 式を考えましょう
「塩の量は変わらず9gかぁ」「割合を\(\large{\frac{2}{100}}\)かぁ」「加える水をxとして」
→ 9÷全=\(\large{\frac{2}{100}}\) → 9÷(150+x) = \(\large{\frac{2}{100}}\) 「水の量141gはいらなかったのかぁ」
(水単体の量を求めることは、ほぼありません)
cf. 式を「1本で立て」たいなら・・・
③の式で、自分で先に求めた値を式に戻しましょう
塩9gは150×\(\large{\frac{6}{100}}\)で求めましたね。9を 「150×\(\large{\frac{6}{100}}\)」に戻すだけですね
\(\large{\frac{\color{red}{9}}{150+x}}\) = \(\large{\frac{2}{100}}\) → \(\large{\frac{\color{red}{150×0.06}}{150+x}}\) = \(\large{\frac{2}{100}}\)
●模擬試験や入試 → 答えだけでいいので、 9÷(150+x)=\(\large{\frac{2}{100}}\)を解きましょう
\(\large{\frac{9}{150+x}}\)=\(\large{\frac{2}{100}}\) → 両辺に (150+x)(100)を掛けて (分数方程式求め方)、![]() → 900=2(150+x) → 両辺を2で割って 450=150+x A. 300g
→ 900=2(150+x) → 両辺を2で割って 450=150+x A. 300g
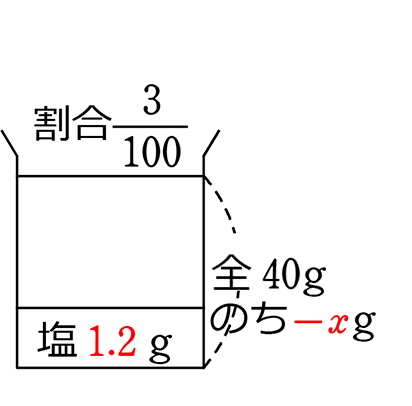
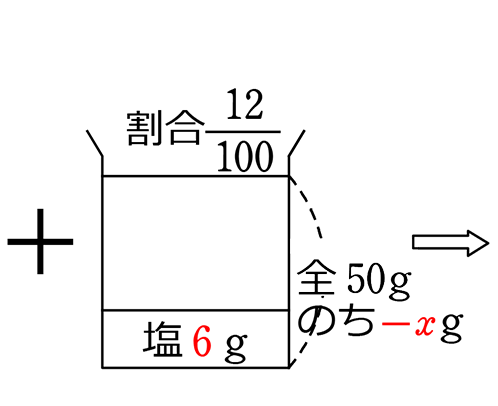
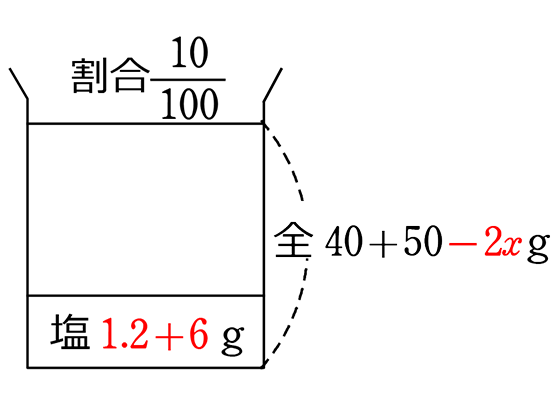
《 例 》
3%の食塩水40gと12%の食塩水50gがあります。それぞれの食塩水からxgの水を蒸発させて、両方の食塩水を1つに混ぜ合わせると10%の食塩水ができました。xを求めましょう。
(注:塩は蒸発しません、「蒸発」は水だけを減らしたい時によく使われます)
① 簡単な図をかいて ②マル図の計算で出るところを書き込んで
② 方程式式を考えましょう
出来上がった食塩水の濃度 0.1 = \(\large{\frac{塩}{全}}\) → \(\large{\frac{1.2+6}{40+50-2x}}\)=\(\large{\frac{10}{100}}\)
●「1本式」なら → 
●模擬テストや入試 → xの値を求めるだけ → 1本式不要
\(\large{\frac{1.2+6}{40+50-2x}}\)=\(\large{\frac{10}{100}}\) → \(\large{\frac{7.2}{90-2x}}\)=\(\large{\frac{1}{10}}\) → 両辺に(90-2x)(10)を掛けて、![]()
→ 72=90-2x → 2x=18 A. x=9
食塩水の問題のコツ
| 1. | 移り変わりのイメージ図を書く |
| 2. | 塩、全体、濃度の3つで ある作用を加えたとき、変化するもの、しないものを判別できるように |
| 3. | 変化するものは、書き換え、または再計算 |
| 4. | 式が複雑になってきても焦らない! |
ですね!!
2. 値段、原価、売値、利益(率)
値段問題も「割合」の問題ですから、
使える道具はただ一つ

だけですね
では、
「仕入れ値」「定価」「原価」、
「売値」「損害額」「値引き額」「値上げ額」「定価」「利益」
「値引き前の価格」「利益を見込んだ価格」
「値上げ率」「値下げ率」「利益率」「損害率」
などなど、何かたくさんの言葉が出てくる分野ですが、
これらは、マル図のどこに当てはまるのでしょうか・・・
…実は、かたくなに当てはめようとしてはいけないのです!
マル図のマスは3つ、ということは、3つしか何かが求まらないのです!
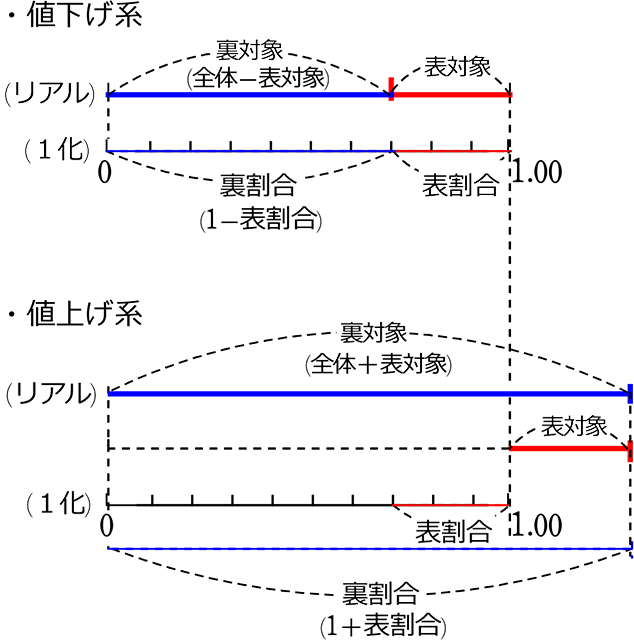
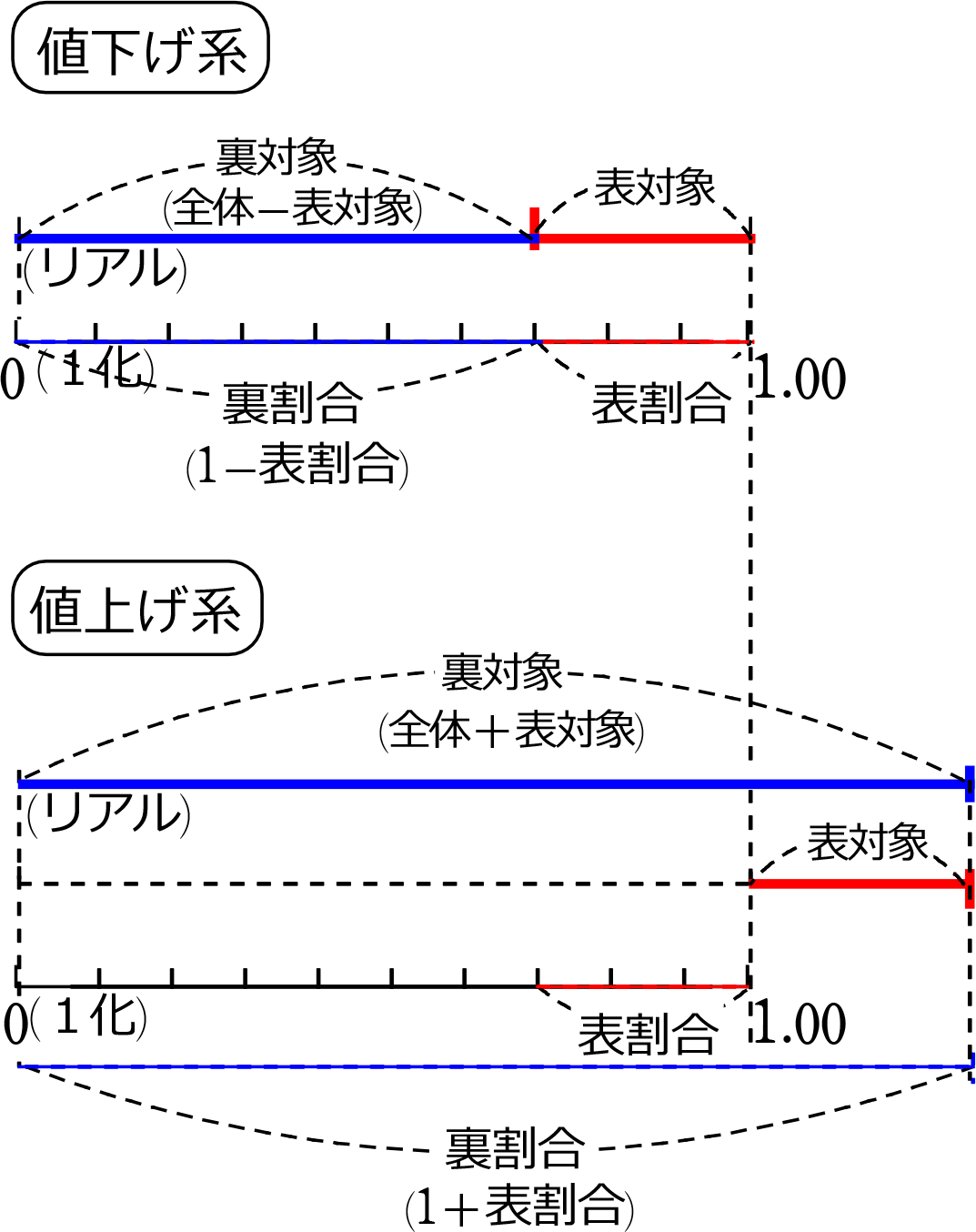
(付随的に、裏対象、裏割合が求まりますが)
価格問題では、この「裏対象」「裏割合」がけっこう重要になります。
『食塩水』では、表対象が「塩」、裏対象は「水」と決まってましたね、
『価格』では、表対象が 「値引き額・値上げ額」、裏対象が 「値上げ後額・値引き後額」になります。
例えば、
「1000円の商品を3割引きした『商品価格』は?」
表対象の「値引き額(3割の金額) は?」ではなく、
聞かれているものは「裏対象の売値(3割引きしたあとの値段)」ですね
(1000gの食塩水で濃度30%のとき、『水の量』は?みたいな感じですね)

マル図の公式は、
「表割合」からは「表対象」しか
求められなかったですね
ずれていてはいけないのです。
ということは、2ステップ必要ということになりますね。
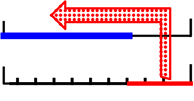
① 表対象を求めてから、 全体-「表対象」 =「裏対象」
または
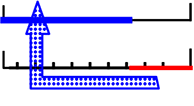
② 裏割合を求めてから、 全体×「裏割合」 =「裏対象」
日本語なら
| ①は、 | 「1000円」から「1000円の3割 300円」を引いた値段 → 700円 |
| ②は、 | 「1000円の7割」の値段 → 700円 |
cf. くくれば裏割合
1000円の30%引きの値段は?
・ 全体-「表対象」=裏対象
→
=
ここで、左辺を「全体」である1000でくくると …
→
=
ということは、(1-\(\large{\frac{30}{100}}\))も裏割合だったということですね
⇒ くくると
全体-「表対象」=裏対象が、
勝手に 全体×「裏割合」=裏対象になる!(くくる とは)
1000円の x % 増しの値段は?
・全体+「表対象」=裏対象
→
=
「全体」である1000でくくると …
→
x %引きの値段なら
→
⇒ くくると
全体+「表対象」=裏対象 が、
値引き、値上げに関わらず
勝手に 全体×「裏割合」=裏対象 になる!
| ⇒ | 裏割合を表す、(1+\(\large{\frac{x}{100}}\)), (1-\(\large{\frac{x}{100}}\)) の表現方法には是非是非 慣れてしまってくださいね !! |
そして、値段問題で もう一つの注意点が、
何をもって、「全体(1化)」としているのかが一定ではない ということです。
例えば、
| 1. | 「『仕入れ値』の2割の利益を見込んで『定価』をつけた」 |
| 2. | 「品薄なので『定価』の2割増しの『売値』にした」 |
上の2つは『定価』の使い方が全然違いますね!!
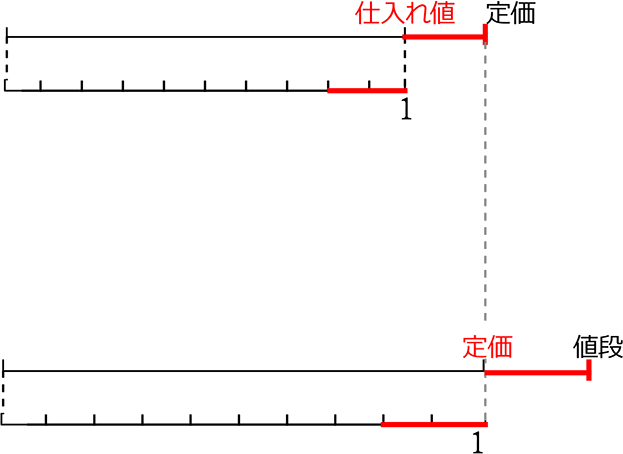
「仕入れ値」が「全体(1化)」!
「定価」は「裏対象」
2. は
「定価」が「全体(1化)」!
「値段」が「裏対象」
⇒ 基準が変わると、1目盛の価値も違いますね
このように、問題文によって「定価」が、 マル図の「全体」であったりなかったり(裏対象)します。
かたくなに当てはめてはいけない理由が少し見えてきましたね!
そうです、問題文によって、何を基準に「1」としているのかが違うのです!
何が基準(全体)になっているかの判別方法は簡単です。
| ・ | 〇〇 |
| ・ | 〇〇 |
| ・ | 〇〇 |
価格問題は、問題の文脈に応じて、柔軟に対応しましょうね!

【まとめ】
まずは、小学生の復習です。

《 例 》
商品に原価の4割の利益を見込んで、定価をつけた。
この商品を定価の2割引きで売っても2640円の利益があります。
この商品の原価を求めましょう。
① 簡単な図を描きましょう
原価
.png)
sp.png)
② 方程式を考えましょう
最終価格-原価=2640
→ 原価をxとすると
・ 定価 =原価の4割増 =
・ 最終価格 =定価の2割減 =
cf.
x(1+\(\large{\frac{4}{10}}\))(1-\(\large{\frac{2}{10}}\))は、(原価)(数字)(数字) → (原価)×( )×( )
→ 積でつながっていいる形 → 「元」が1つでそれがどのように変化するかというイメージを思い出すと理解が深くなりますね
∴ 最終価格-原価=+2640円 より
\(\large{\frac{x\ \cdot \ 14\ \cdot \ 8}{100}}\)-x=2640 (あとは解くだけ)
14・8・x-100x=264000 楽ができるかもしれないので、すぐにはかけ算の計算をしなかった
12x=264000 楽はできなかった…
x=\(\large{\frac{264000}{12}}\)=\(\large{\frac{44000}{2}}\)=22000 A. 原価xは 22000円

利益率とは
一次方程式の文章問題で出てくる値上げ方向を、
ここでは「値上げ率」と言わせていただきますね。
この「値上げ率」と
実社会経済で使われる「利益率」は別物です!
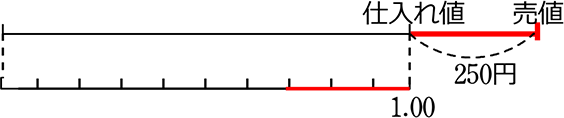
例えば、
仕入れ値1000円、売値1250円の商品の利益は250円ですね。
では、「値上げ率」はいくらでしょうか、計算式は、
対象(利益)÷仕入れ値 = (1250-1000)÷1000= 250÷1000=0.25
「0.25」=25%、 値上げ率は 25% ということになりますね。(仕入れ値に対する利益)
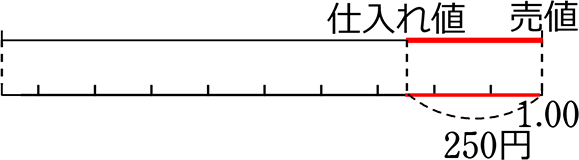
対して、「利益率」の計算式は、
対象(利益)÷「売上(売値)」=(1250-1000)÷1250 = 250÷1250 = 0.2
「0.2」=20%、 利益率は 20% ということになります。(売値に対する利益)
そうです、なにをもって「全体」とするかが違うのです!
・値上げ率

・利益率

「値上げ率」の基準(全体)は、「仕入れ値」
「利益率」の基準(全体)は、「売値(売上)」 !!
利益率は1次方程式の、「~を値下げしました」というイメージ図と同じですね。
中学数学で「利益率は?」 という問題はないとは思いますが、
雑学として、「利益率」は、基準が「売値(売上)」 であるということを
知っていて損はないのかなと思います。

利益率はやりたい仕事の指標
全くの余談になりますが、・・・
「Aの商品は、一つ売ると250円の利益がある」
「Bの商品は、一つ売ると5万円の利益がある」
皆様はどちらの商品を扱いたいですか?
Bですよね~
ですが、仕入れ値が、
Aは1000円、Bが100万円だとしたら・・・
「Aは売値1250円・・・広く売れるかな」
「Bは売値105万円・・・そうそうは売れないかな」
と感じますね。
そして、「利益率」で表すと、
Aは、 250÷1250=0.20 (利益率20%)
Bは、 50000÷1050000=0.048 (利益率4.8%)
なんだかAを扱った方がいいのかなという気がしてきましたね。
実社会ではどうなんでしょうね?

競争率とは
志望校の入試情報を調べると、「競争率(倍率)」という項目がありますね
倍率2.3など、一体どういう意味なのでしょうか
「入試倍率」も割合の話ですので、使えるものは
 だけですね
だけですね
そして、比べるものは、「受験者数 (志願者数)」と「合格者数 (定員)」だけですね
たとえば、定員280人の高校に、476人の志願があれば、
・競争率(倍率) = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{受験者}{合格者数}}\) = \(\large{\frac{476}{280}}\) = 1.7 (倍)
競争率での「対象」は、私たち「受験者」ですね
「受験者の割合(合格者に対する) 」ですね!
・合格者率 = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{合格者数}{受験者数}}\) = \(\large{\frac{280}{476}}\) = 0.59
合格者率での「対象」は、当然「合格者」ですね
「(受験者に対する) 合格者の割合」ですね!


道路標識の「勾配」「%」の意味

10%とは「何の割合?」「坂の角度が10°ということ?」と、
なんとなくイメージが定かではないですね。
この「10%」とは、
こんな感じです。


「高さ (標高)」÷「 底辺 (地図上の距離)」
「角度」も「斜辺 (実走行距離)」も使わないのです!
実際、運転する者の身からすれば、
前もって、「地図上」で坂道部分だけ距離を測ることはないですし、
どちらかというと、
運転席のスピードメーター内の「トリップメーター」 を見て
を見て
「〇〇m走ったのか…」
ということは「坂の始めから、300m高くなったのか」と思いたいですよね
どうせだったら、「高さ」÷「地図上の距離」ではなく、
「高さ」÷「実走行距離(斜辺)」の方が、実用性があるの
かなと、個人的には思いました。
(10% → 100m走ったら10m上がっている!)みたいに。
中学3年生は、上の三角形の斜辺の長さを求めることができますね。
三平方の定理(ピタゴラスの定理)ですね
「斜辺」=\(\small{\sqrt{(底辺)^2+(高さ)^2}}\) ですね、
=\(\small{\sqrt{10000+100}}\)=\(\small{\sqrt{10100}}\) =10\(\small{\sqrt{101}}\) =10×約10.045 =約100.45m
10%の坂道では「地図上の距離(底辺)」と「実走行距離(斜辺)」は大差・・・ないですね…
ということは、
「10%は、大体100m強走れば、10m上がっている」 で十分ですね!
これは、実社会の話ですので、
中学生の数学では、 きちんと「計算」してくださいね!
また、実社会が「適当」であると言っている訳でもないのであしからずです。
また、上の図で角度を求めるとなると至難の業(わざ)ですね!
Excel関数を使えば一発ですので、興味のある方は試してくださいね。
関数を記しておきます。
| A | B | |
| 1 | B1に高さを入力 | |
| 2 | B2に底辺の長さを入力 | |
| 3 | 角度をB3に返す | =ATAN(B1/B2)*180/PI() |
ということで、上図の角度は、およそ 5.71° でした
ちなみに、「100%の坂道」の角度は「45°」です。
「90°」ではないですよ~! ( 1÷1=1.00)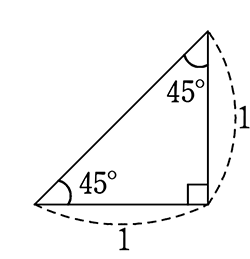
ということで、勾配の「%」とは、
分数表示にしたとき、
直角三角形の「底辺」に対する「高さ」の割合でした!!
勾配15%であれば → 0.15 → \(\large{\frac{15}{100}}\)
「100の距離があれば、15の高さがあるような直角三角形の角度」ですね
![]()
高校生なら、tanθ= \(\large{\frac{15}{100}}\) ですね、θ(シータ)=整数となるのは数種類しかないですね。
整数にならないなら、tanθ のまま計算を続けますね。
πも整数にならないから、πのまま計算していきますね。
√も整数にならない部分は、√ のまま計算していきますね!

ちなみに、日本で一番きつい坂道は、
大阪府と奈良県の境にある「暗峠(くらがりとうげ)」の
最大斜度37%、 平均斜度20%です!
しかも歴(れっき)とした国道ですね(国道308号)! すごい!!

割合のイメージ
例えば「30%」
30% = 3割 = \(\large{\frac{30}{100}}\) = \(\large{\frac{3}{10}}\) = 0.3
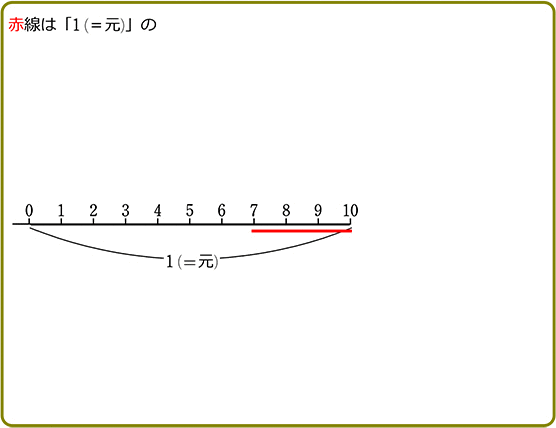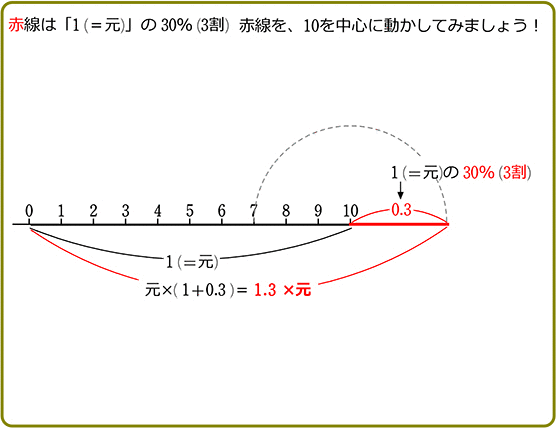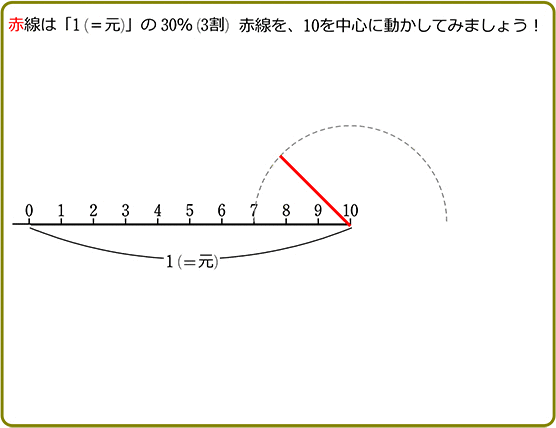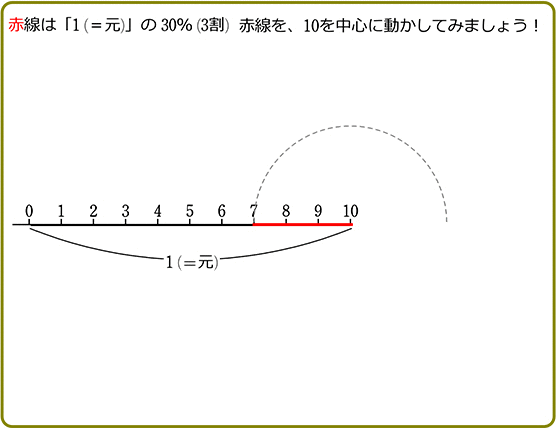
「何を、どちらに、折り返すのか?」 ということですね
⑤ その他の文章問題



文章問題の出題傾向
公立高校入試において、1次方程式の文章問題は、
東日本では、あまり出ない、または出ても難易度が低い、
西日本では、よく出る、難易度もそこそこな感じがあります。
あくまで傾向でありますので、お住いの都道府県の入試過去問で
確認をお願いしますね。
難関私学では当然難関な文章問題が出題されています。
傾向があるとは言いましたが、
この1次方程式の文章問題は、「数学的思考法」を磨くには
もってこいの分野ですので、
できる限り多くの問題にあたることが望ましいかな、と思います。
お疲れ様でした !!
その他の問題は、「問題集」で !!















