| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平方根 | (2) 式の展開・因数分解 | (3) 二次方程式 |
| ア | 単項式と多項式の乗法、多項式を単項式で割る除法 |
|---|---|
| ・ | 単項式と多項式の乗法 |
| ・ | 単項式と多項式の除法 |
| イ | 簡単な一次式の乗法、簡単な式の展開や因数分解 |
| ・ | 多項式と多項式の乗法 |
| ① | 展開公式まとめ |
| ② | 因数分解の方法 |
| L1 | 共通因数でくくる |
| L2 | 展開公式の逆 |
| L3 | 置き換え |
| L4 | 1度展開 |
| L5 | 部分因数分解 |
| L6 | 〇2-△2の意識 |
| ・ | 因数分解ポイントまとめ |
| ・ | 難しい因数分解の例題 |
| ・ | たすき掛けの方法 |
| ウ | 文字を用いた式による数量関係の説明 |
| ① | 工夫して計算を楽にする |
| ② | 式の値 |
| ③ | 式の計算を利用した証明 |
| ④ | 式の計算の利用(図形) |
| ・ | =で結ばれたものを「比」にする (連比) |
式の展開・因数分解
ア 単項式と多項式の乗法、多項式を単項式で割る除法
単項式と多項式の乗法
これは、2年生で学んだ「文字を含んだ乗法・除法」に毛が生えただけですね!
| 単項式 … | 項(元)が1つ
ex) 6, a, x2, 2x, xy, xy2 などなど |
| 多項式 … | 項(元)が2つ以上
ex) 2+3, 2-b, x+y, x2-2xy+y2 など |
でしたね!
そして、単項式×多項式ということは、
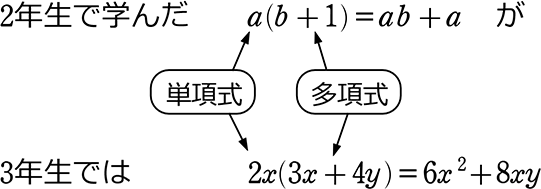
というふうに1つの「項」自体が少し複雑になっただけで
『分配法則』さえ知っていれば、全く同じ手順ですね!

クリック・タップで答え (反応が遅い場合があります)
単項式と多項式の除法
これも、2年生と全く同様ですね!
「÷〇」 の〇を逆数にして
「×\(\large{\frac{1}{〇}}\)」」とするだけですね!


イ 簡単な一次式の乗法,簡単な式の展開や因数分解
多項式と多項式の乗法
多項式どうしの乗法(掛け算)も、「分配法則」さえ知っていれば計算(展開)できますね、
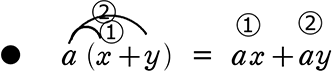

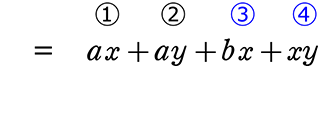


● (a+b)(c+d)(x+y) = acx+acy+adx +ady+bcx+bcy+bdx+bdy
このような「ルール(展開方法)」でしたね!
ですが、今後は特に
(●+△)(●+□) のような形が、多く出てきます!
すなわち、 2つの(カッコ) の中の先頭の項が「同じ」ものですね!
《 例 》
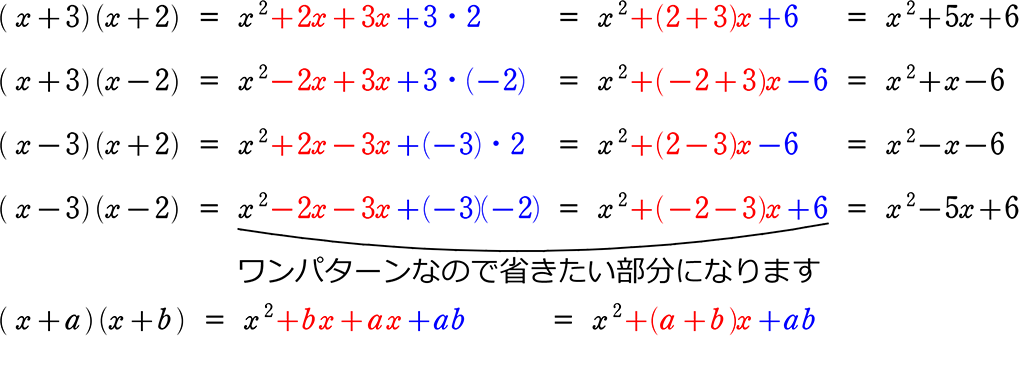
問題と答えを見比べると、「規則性」がありますね
というわけで、1つ目の公式の完成です

これで、今後は途中式を省けますね!
ex.
(x-4)(x+5) = x2+x-20 !!
《 例 》

2+2 = 2×2 = 4
3+3 = 3×2 = 6
4+4 = 4×2 = 8
8+8 = 8×2 = 16
a+a = a×2 = 2a
当たり前ですが、
ど忘れしてしまう
「同じものの足し算」= 2倍

というわけで、(x+a)(x+b) の公式をマスターしていれば、十分足りるのですが、
憶える労力の割には「大変使える!」ので、2つ目の公式として、

ex)
(x+4)2 = x2+8x+16 !!
「x2プラスニシが8x+しし16」
《 例 》
(x-3)2
= (x-3)(x-3)
= x2+(-3-3)x+(-3)2
= x2+2(-3)x+9
= x2-2(3)x+9
= x2-6x+9
(x-8)2
= (x-8)(x-8)
= x2+(-8-8)x+(-8)2
= x2+2(-8)x+64
= x2-2(8)x+64
= x2-16x+64
(x-a)2
= (x-a)(x-a)
= x2+(-a-a)x+(-a)2
= x2+2(-a)x+a2
= x2-2(a)x+a2
= x2-2ax+a2
というわけで、3つ目の公式

ex)
(x-6)2 = x2-12x+36 !!
「x2マイナス ニロク12x プラスロクロク36」
最後に、1番スッキリ気分なものを!
《 例 》
(x-1)(x+1)
= x2+(-1+1)x+(-1)(+1)
= x2+0x-1
= x2-1
(x+7)(x-7)
= x2+(7-7)x+(+7)(-7)
= x2+0x-49
= x2-49
(x+a)(x-a)
= x2+(a-a)x+(a)(-a)
= x2+0x-a2
= x2-a2
というわけで、4つ目の公式

真ん中にあるはずの (後どうしの和)×先頭 が打ち消しあって「消滅」 !!
ex)
(x-4)(x+4) = x2-16 !!
(x+4)(x-4) = x2-16 !!

展開公式
(x+a)(x+b) = x2+(a+b)x+ab
(x+a)2 = x2+2ax+a2
(x-a)2 = x2-2ax+a2
(x+a)(x-a) = x2-a2
→ 忘れたら、地道に展開していけばよいだけですね!
《 例 》
計算しましょう (=展開しましょう)
・(2x+3)(2x+4) = 4x2+14x+12
・(3x-1)(3x+2) = 9x2+3x-2
・(x+2y)(x+3y) = x2+5xy+6y2
| ・ | (x+3)(2x+2) →先頭が異なるので「地道展開」ですね
= 2x2+2x+6x+6 = 2x2+8x+6 |
・(x+1)(3+x) = (x+1)(x+3) = x2+4x+3
| ・ | (-x-2)(x+5) = -(x+2)(x+5)= -(x2+7x+10)= -x2-7x-10 |
| ・ | (x+y+2)(x+y-5) → x+yをX(ラージエックス)とおくと
= (X+2)(X-5) = X2-3X-10 → Xをx+yに戻すと |
ですが、(カッコ)を「1文字」と見れるなら… x+yに(カッコ)をつけて、
| = | (x+y+2)(x+y-5) |
| = | {(x+y)+2}{(x+y)-5} ←(x+y)を「1文字」と見れる人 |
| = | (x+y)2-3(x+y)-10 |
| = | x2+2xy+y2-3x-3y-10 |
・(x-y+3)2
= {(x-y)+3}2
= (x-y)2+6(x-y)+9
= x2-2xy+y2+6x-6y+9
・(x+2y-3)(x+2y+3)
= {(x+2y)-3}{(x+2y)+3}
= (x+2y)2-9
= x2+4xy+4y2-9
《 例 》
(x+a)(x-a) = x2-a2を利用して、有理化しましょう (有理化とは)
・\(\large{\frac{2}{\sqrt{5}+\sqrt{3}}}\)
どのような「1」を掛けましょうか?
→ \(\large{\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}-\sqrt{3}}}\) という「1」ですね!
= \(\large{\frac{2\color{red}{(\sqrt{5}-\sqrt{3})}}{(\sqrt{5}+\sqrt{3})\color{red}{(\sqrt{5}-\sqrt{3})}}}\)
= \(\large{\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^2-(\sqrt{3})^2}}\)
= \(\large{\frac{2(\sqrt{5}-\sqrt{3})}{5-3}}\)
= \(\small{\sqrt{5}}\)-\(\small{\sqrt{3}}\)
| ・ | \(\large{\frac{2}{3-\sqrt{7}}}\) = \(\large{\frac{2\color{red}{(3+\sqrt{7})}}{(3-\sqrt{7})\color{red}{(3+\sqrt{7})}}}\) = \(\large{\frac{6+2\sqrt{7}}{9-7}}\)= \(\large{\frac{6+2\sqrt{7}}{2}}\) = 3+\(\small{\sqrt{7}}\) |
・\(\large{\frac{3}{\sqrt{5}-\sqrt{2}}}\) = \(\large{\frac{3(\sqrt{5}+\sqrt{2})}{5-2}}\) = \(\small{\sqrt{5}}\)+\(\small{\sqrt{2}}\)
慣れてくると途中式を省けるようになりますね!


因数分解
素因数分解や因数分解の意味や必要性やイメージは
もう2年生課程で見てきましたので、ここでは省略しますね(素因数・因数の意味とその必要性)
3年生過程では、具体的な因数分解の方法を見ていきましょうね!
〈レベル1〉共通因数でくくる
a(a+1)を展開すると → a2+a でしたね
因数分解は、その逆の作業でしたから
a2+a を因数分解すると、 = a(a+1) ですね
↑(a)・(a+1)
(カッコ)を「1文字」と見れれば、〇×〇の形であるとわかりますね
⇒ すべての「単項式」「多項式」が「
このとき、
a2 は a×a なので 因数「a」を2つ持つ
a は a なので 因数「a」を1つ持つ
共通因数は 『a(1つ)』、それぞれその「aを1つ」を出すことを
「共通因数でくくる」と表現しますね!
→ a2+a = a(a+1)


《 例 》 因数分解しましょう
・4ax+8ay = 4a(x+2y)
| → | 4(ax+2ay) や a(4x+8ay) や 2a(2x+4ay) では
因数分解しきれていないということですね! → 共通因数が残っている |
| → | 素因数分解でいう、30=(5)(6)ですね → (5)(2)(3) までして正解!
自転車のイメージなら、前タイヤは外したけど、後ろタイヤを外し忘れですね |
→ | 22a(x+2y) まではしなくてもよいですね → 数字だけの部分は素因数分解表示しなくてもよい |
・8xy2-6xy = 2xy(4y-3)
〈レベル2〉 展開公式の逆
展開公式は
| 1. (x+a)(x+b) | = x2+(a+b)x+ab |
| 2. (x+a)2 | = x2+2ax+a2 |
| 3. (x-a)2 | = x2-2ax+a2 |
| 4. (x+a)(x-a) | = x2-a2 |
でしたね
逆を言えば、
| 1. | x2+(a+b)x+abのような形に見えれば、 (x+a)(x+b)になるかもと疑う |
| 2. | x2+2ax+a2のような形に見えれば、 (x+a)2になるかもと疑う |
| 3. | x2-2ax+a2のような形に見えれば、 (x-a)2になるかもと疑う |
| 4. | x2-a2のような形に見えれば、 (x+a)(x-a) になるかもと疑う
ですね! |
ですが最初は、真ん中の2つは「x2+(a+b)x+ab」と同じと考えましょうね
よって
| 1. | x2+(a+b)x+abのような形に見えれば、 (x+a)(x+b)になるかもと疑う |
| 4. | x2-a2のような形に見えれば、 (x+a)(x-a) になるかもと疑う |
の2つで十分です!


《 例 》 因数分解しましょう
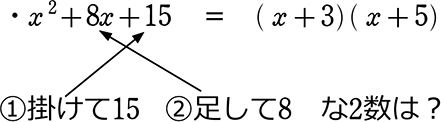
←(x+5)(x+3) でももちろんOKです
・ x2+3x-28 = (x+7)(x-4)
・ x2-9x+18 = (x-3)(x-6)
・ x2+10x+25 = (x+5)(x+5)
= (x+5)2
←ここまでして正解です
ex) 4を素因数分解しましょう
→ 4 = 2×2 = 22 でしたね
そして、
x2+2ax+a2 = (x+a)2
x2-2ax+a2 = (x-a)2
の2つが、不要という理由ですね
→ まずは x2+(a+b)x+ab で十分!
→ 結果同じものだったら、
2乗の型にすればよいだけ
・ x2-16x+64 = (x-8)(x-8) = (x-8)2
・ x2+5xy+6y2 = (x+2y)(x+3y)
・ x2+xy-20y2 = (x+5y)(x-4y)
・ x2-4xy+4y2
= (x-2y)(x-2y)
= (x-2y)2
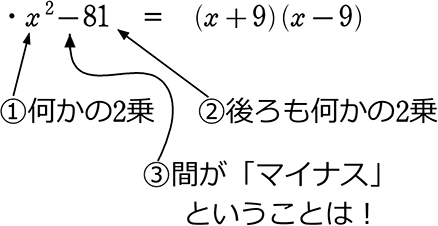
・ x2-9y2 = (x+3y)(x-3y)
・ 4x2-36y2
= (2x+6y)(2x-6y)
= 2(x+3y)・2(x-3y)
= 4(x+3)(x-3y)
または
=4(x2-9y2)
=4(x+3y)(x-3y)
〈レベル3〉 置き換え ←(カッコ)を付けて「1文字」と見る
(x+1)2-7(x+1)+12
→ なんとなく 〇2-7〇+12が見えますね!
→ ・(カッコ)をX(ラージエックス)などに
置き換えてもよいし
・「1文字」と見れるなら
そのまま進めてOKですね
→ (x+1) = X とおくと
与式 = X2-7X+12= (X-3)(X-4)
Xを (x+1) に戻すと
{(x+1)-3} {(x+1)-4} = (x-2)(x-3)
・(カッコ)を「1文字」と見れる人は
((x+1)-3)((x+1)-4) = (x-2)(x-3)
《 例 》 因数分解しましょう
・(x+y)2-2(x+y)-3 = ((x+y)-3)((x+y)+1) = (x+y-3)(x+y+1)
・(x2+6x)2-2(x2+6x)-35
→ X2-2X-35 = (X-7)(X+5)
→ ((x2+6x)-7)((x2+6x)+5)
= (x2+6x-7)(x2+6x+5) ←まだいけそう
= (x+7)(x-1)(x+5)(x+1)
・
→ X2-2XY+Y2 = (X-Y)2
→ {(2x+y)-(x+2y)}2
= (2x+y-x-2y)2
= (x-y)2
〈レベル4〉 1度展開
(カッコ)が 2, 3個あるのに「共通因数」が見当たらない場合、1度展開してみる
《 例 》
・ (x-1)(x-2)-6 = x2-3x+2-6 = x2-3x-4 = (x-4)(x+1)
・ (x+1)2-5(x-1)-16 = x2+2x+1-5x+5-16 = x2-3x-10 = (x-5)(x+2)
〈レベル5〉 部分因数分解
| ・ | 部分部分で「共通因数でくくる」と、残りが「全体の共通因数」になっていたり |
| ・ | 部分部分で「因数分解する」と、残りが「さらに因数分解できる形」になっていたり |
することがありますが、それを先に意識して「共通因数」を作り出す ですね
《 例 》
・ ax-by-ay+bx = a(x-y)+b(x-y) = (x-y)(a+b)
最初に x, y でくくると → x(a+b)-y(a+b) = (a+b)(x-y) ←同じですね
・a(x-y)+b(x-y) → (x-y)(a+b) のくくり作業がいまいち不安な人は、面倒でも毎回共通因数(x-y)をXなどに置きかえて考えてみてくださいね。
あまりよくはないですが、Xではなく具体的な数字に置きかえると,、もっとイメージしやすくなりますね
a(x-y)+b(x-y) → 3a+3b → 3(a+b) → (x-y)(a+b)
・ ax2+3x-2ax-6
| → | xでくくると① → x(ax-2a+3)-6 手詰まり |
| → | xでくくると② → x(ax+3)-2(ax+3)
= (ax+3)(x-2) 正解! |
| → | aでくくると → a(x2-2x)+3(x-2)
xも出してみると → ax(x-2)+3(x-2) |
・ x2+2xy-4+y2
= x2+2xy+y2-4
= (x+y)2-4 ← X2-Y2の型
= (x+y-2)(x+y+2)
「何を」「何で」くくれば「共通因数」が浮かび上がってくるか、
「どこを因数分解」すれば「さらに進める」かを
先に暗算で計算することは何気に難しいので、
色々「当たり」を加減をしながら見つけてくださいね!
(多くくくればよい というものではないということですね)
「くくり方しだいで、共通因数が浮いてくるはずだ」
「部分因数分解しだいで、共通因数が浮いてくるかも」
みたいな感じでしょうか
《 例 》 (カッコ)の中が似ている → 符号を変えたい
・ (2a-b)x-2(b-2a)y = (2a-b)x+2(2a-b)y = (2a-b)(x+2y)
〈レベル6〉 〇2-△2 = (〇+△)(〇-△) を常に意識
→ (複雑な式)2 -1
(複雑な式)2 -4
(複雑な式)2 -9
(複雑な式)2-16
↙12
↙22
↙32
↙42
(複雑な式)2-(複雑な式)2
などは、ふと (〇+△)(〇-△) になることを見落としがちですね
《 例 》
・ (2x+y)2-1 = (2x+y+1)(2x+y-1)
これを展開してしまうと、
4x2+4xy+y2-1 → アリ地獄?
ですが、それも勉強ですね!
・ x2-(y-2)2
= (x-(y-2))(x+(y-2))
= (x-y+2)(x+y-2)
・ x4-1
= (x2-1)(x2+1)
= (x+1)(x-1)(x2+1)
・ x2-9(x-y)2
| = | x2-32(x-y)2 |
| = | x2-{3(x-y)}2 ←m2・n2 = (mn)2 |
| = | {x-3(x-y)}{x+3(x-y)} ←いきなりここからでもOKですね |
| = | (x-3x+3y)(x+3x-3y) |
| = | (-2x+3y)(4x-3y) |
「因数分解」は「知恵の輪」みたいなものですね!
難しい因数分解は、色々試しながら分解するしかないですね
1回で分解できたら「ラッキー!」くらいの気持ちで!
因数分解ポイント
| ・ | 共通因数でくくる |
| ・ | 展開公式の逆 |
| ・ | 置き換え =(カッコ)を付けて「1文字」と見る |
| ・ | 1度展開 |
| ・ | 部分因数分解 |
| ・ | 〇2-△2 = (〇+△)(〇-△) を常に意識 |
《 例 》 難しい因数分解
・ (x+1)2(x-2)2-14(x+1)(x-2)+40
| = | {(x+1)(x-2)}2-14(x+1)(x-2)+40 ←m2・n2 = (mn)2 |
| = | X2-14X+40 ←(x+1)(x-2)をXに置き換え |
| = | (X-10)(X-4) ←展 開 公 式 の 逆 |
| = | {(x+1)(x-2)-10}{(x+1)(x-2)-4} ←Xを(x+1)(x-2)に戻した |
| = | (x2-x-2-10)(x2-x-2-4) ←中を展開した |
| = | (x2-x-12)(x2-x-6) |
| = | (x-4)(x+3)(x-3)(x+2) ←展開公式の逆 |
・ a2-ad-ab+bd-ac+cd
→ 「項」が6個(偶数)なので、想像できる「因数が浮き出る途中形」は
| ① | ●(〇+△)+■(〇+△)+▼(〇+△) = (〇+△)(●+■+▼) |
| ② | ●(〇+△+□)+▼(〇+△+□) = (〇+△+□)(●+▼) |
→ ②で調べる方が楽
aは4つの項で使われている
bは2つの項
cは2つの項
dは3つの項
| → | a(4個の内3個使いたい)とd(3個の内3個使いたい)かな → dがあやしい |
| = | a2-ab-ac-d(a-b-c) ←dを含む項をdでくくった |
| = | a(a-b-c)-d(a-b-c) ←因数が浮き出た |
| = | (a-b-c)(a-d) // |
・ x2+xy+3x+y+2
| → | 項が5個(奇数)なので、「展開公式の逆」で、3つの項を2つにするのだろうな |
展開公式の真ん中は「数字×文字」、最後は「掛け合わせ」

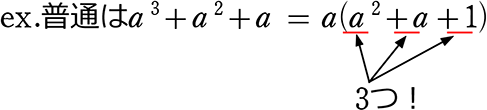
というわけで、x2 は使うだろうな…
真ん中が xy なら y2 があるはず → ないのでxyではない → 3xだろうな
∴ x2+3x+2 +xy+y
= (x+1)(x+2)+xy+y
= (x+1)(x+2)+y(x+1)
= (x+1){(x+2)+y}
= (x+1)(x+y+2) //
・ a2c2+b2d2-a2b2-c2d2+4abcd
| → ① | 〇2-△2 = (〇+△)(〇-△)がいっぱいあるな!に第一感 |
a2c2-a2b2 +b2d2-c2d2 +4abcd
→ 4abcd がさばけないかも…
| → ② | 4abcd は、真ん中の「2ab」の部類かな!に第一感 |
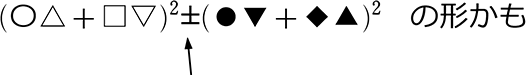
さらにここが「-」なら、完璧!
→ それなら、4abcd 1つでは足りない
4abcd → 2abcd+2abcd
②で行きますね
a2c2+b2d2-a2b2-c2d2+4abcd
| = | a2c2+b2d2-a2b2-c2d2+2abcd+2abcd |
| = | a2c2+2abcd+b2d2- (a2b2-2abcd+c2d2) ←並び替え |
| = | (ac+bd)2-(ab-cd)2 ←さらに「〇2-△2」の形! |
| → | X2-Y2 = (X+Y)(X-Y) |
| = | {(ac+bd)+(ab-cd)}{(ac+bd)-(ab-cd)} |
| = | (ac+bd+ab-cd)(ac+bd-ab+cd) // |

たすき掛け
中学の因数分解では扱わないはずですが、
高校では
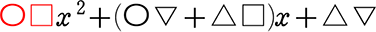

ex)
・ (ax+b)(cx+d)
= acx2+adx+bcx+bd
= acx2+(ad+bc)x+bd
・ (x+2)(3x+5)
= 3x2+(5+6)x+10
= 3x2+11x+10
では、 3x2+11x+10 を因数分解しましょう とこられたら
どうすればよいのでしょうか?
(ax+b)(cx+d) をひっ算で行うと…


これの逆の作業を、「当たりをさぐりながら」見つけるしかありませんね
| 1. | 「先頭」と「最後」はただの掛け合わせ → 候補が見つけやすい |
| 2. | 「真ん中」はその候補をクロスで掛けて、 足したもの (bc+ad)x |
ex)
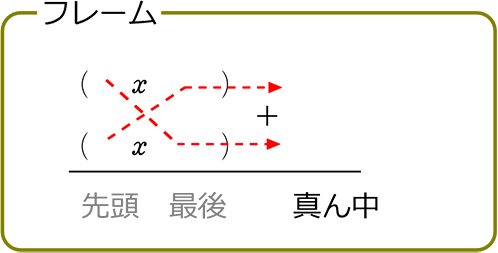
3x2+11x+10 = (x )(x ) を横ではなく、縦に書くと考えやすくなりますね
(もちろん、仕組みがわかれば 横 (x )(x )のままでもOKです)

↑
① フレームを書く
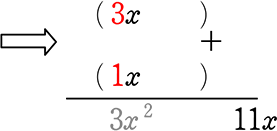
②「先頭」の候補探し
→ 3×1 だけでOK
→ -3×(-1) は不要
(同じことなので)
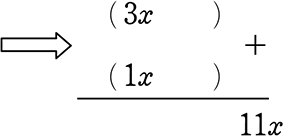
③「最後」の候補探し
→ 2×5、-2×(-5)
1×10、-1×(-10)
(「同じこと」でないので
マイナスの方も候補)

④「最後」の候補選び
→ クロスで「真ん中」
になるような
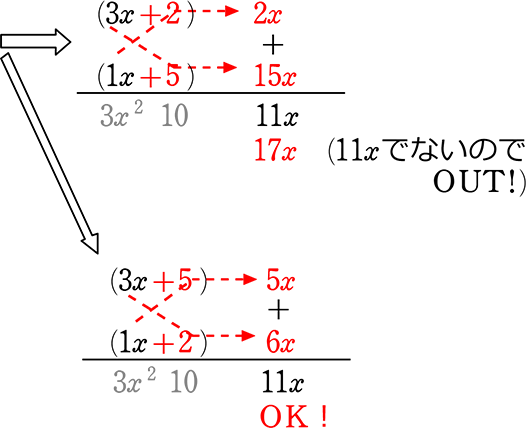
| A. | (3x+5)(x+2) |
ちなみに、「先頭」を -3×(-1)で行うと
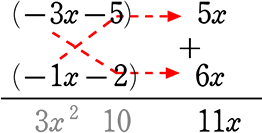
= (-3x-5)(-x-2)
= -1(3x+5)(-1)(x+2)
= (-1)(-1)(3x+5)(x+2)
= (3x+5)(x+2) → よって、「同じこと」
このような感じで、違っていたらフレームを残して、数字だけを消しゴム
で消して、試し試し見つけていくことになりますね
・ 3x2+15x+18 を因数分解しましょう
| → | 「先頭」の「3x2 」が「何かの2乗」ではないからと言って
いきなり「クロス作業」ではないですね! |
| → | 3(x2+5x+6) = 3(x+3)(x+2) |
・ 6x2+35x-6 を因数分解しましょう
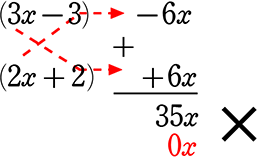
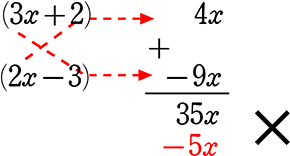
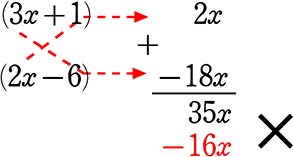
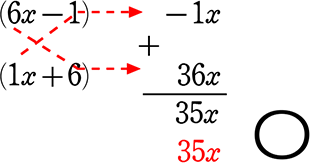
| A. | (6x-1)(x+6) |
「仕組み」に慣れてきましたら、「フレーム」を書かずに

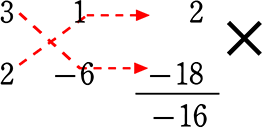

というふうに数字だけでできますが、(いわゆる「たすき掛け因数分解」)。
慣れるまでは「フレーム」を書くことをお勧めしたいと思います
なぜなら、「たすき掛け」は思ったよりは、たまにしか出てこないので
たまに「たすき掛け」をすると・・・
「クロス」に意識が行き過ぎて、「縦がセット? 横がセット?」
「何が、縦? 横? 斜め? 」と根本をど忘れしてしまいがちですね!
「たすき掛け」は「やり方(方法)」を憶えるのではなく、
「フレーム」を憶える!だと思います
ウ 文字を用いた式による数量関係の説明
「展開公式」や「因数分解」を有効利用しよう という意味ですね
① 工夫計算
《 例 》 計算しましょう
(1) 9982 は?
| → | 「ミチミチひっ算」で求めてもかまいませんが…
できれば、「いい方法(良く言えば)」(悪く言えば「楽な方法」)で解きたいですね |
| → | 0.012 = 0.0001 0.12 = 0.01 102= 100 1002 = 10000
のように歯切れがよければ、暗算でできるのに! |
| → | 「歯切れのよい数字」に改造してみる |
∴ 9982 = (1000-2)2
= 10002-2・2・1000+4 ←「展開公式(x-a)2 = x2-2ax+a2」
= 1000000-4000+4
= 996004 //
(2) 10022 = (1000+2)2
= 10002+2・2・1000+4
= 1000000+4000+4
= 1004004 //
(3) 1016×984 = (1000+16)(1000-16) ←「展開公式 (x+a)(x-a) = x2-a2」
= 1000000-162
= 1000000-256
= 999744 //
(4) 1422-422 = (142+42)(142-42) ←「展開公式の逆 x2-a2 = (x+a)(x-a)」
= 184・100
= 18400 //
(5) 3916×3912-3910×3918
= (3914+2)(3914-2)-(3914-4)(3914+4)
= (39142-22)-(39142-42)
= 39142-22-39142+42
= -22+42
= -4+16
= 12 //
(6) 1022+1012+1002-992-982
= 1022-992+1012-982+1002
= (102+99)(102-99)+(101+98)(101-98)+1002
= 201・3+199・3+1002
= 3(201+199)+10000
= 3・400+10000
= 11200 //
● 問題により、色々な工夫がありますが、
根本的には答が出ればよいのであって、「最良の方法」でなくても
「ミチミチ計算」よりは「楽」だったら、それで十分ですね!
② 式の値
《 例 》
x = 20.4、y = 10.4 のとき、以下の式の値を求めましょう。
(1) x2-2xy+y2
→「いきなり直接代入ミチミチ計算」は、大変そうですね
= x2-2xy+y2
= (x-y)2 ←因数分解
= (20.4-10.4)2 ←ここで代入すると楽!
= (10)2
= 100 //
(2) x2-y2
= (x+y)(x-y)
= (20.4+10.4)(20.4-10.4)
= (30.8)(10)
= 308 //
《 例 》
x = \(\small{\sqrt{3}}\)+2、y= \(\small{\sqrt{3}}\)-2 のとき、以下の式の値を求めましょう。
(1) x2-y2
= (x+y)(x-y)
→ {(\(\small{\sqrt{3}}\)+2)+(\(\small{\sqrt{3}}\)-2)} {(\(\small{\sqrt{3}}\)+2)-(\(\small{\sqrt{3}}\)-2)}
= (\(\small{\sqrt{3}}\)+2+\(\small{\sqrt{3}}\)-2) (\(\small{\sqrt{3}}\)+2-\(\small{\sqrt{3}}\)+2)
= (2\(\small{\sqrt{3}}\))(4)
= 8\(\small{\sqrt{3}}\) //
(2) x3y+2x2y2+xy3
= xy(x2+2xy+y2)
= xy(x+y)2
→ (\(\small{\sqrt{3}}\)+2)(\(\small{\sqrt{3}}\)-2) (\(\small{\sqrt{3}}\)+2+\(\small{\sqrt{3}}\)-2)2
= (\(\small{\sqrt{3^2}}\)-22)(2\(\small{\sqrt{3}}\))2 ←前:展開公式
= (3-4)(4・3)
= -1・12
= -12 //
《 例 》
x = \(\large{\frac{3+\sqrt{5}}{2}}\)のとき、以下の式の値を求めましょう。
(1) x+\(\large{\frac{1}{x}}\)
→ 「いい方法」がないので、「ミチミチ直接代入」ですね…
→ \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{1}{\large{\frac{3+\sqrt{5}}{2}}}}\)
= \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{2}{3+\sqrt{5}}}\)
↑後半の分数に
\(\large{\frac{2}{2}}\)という「1」を掛けた
= \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{2(3-\sqrt{5})}{(3+\sqrt{5})(3-\sqrt{5})}}\) ←有理化
= \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{6-2\sqrt{5}}{9-5}}\)
= \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{6-2\sqrt{5}}{4}}\)
= \(\large{\frac{3+\sqrt{5}}{2}}\)+\(\large{\frac{3-\sqrt{5}}{2}}\)
= \(\large{\frac{6}{2}}\)
= 3 // x+\(\large{\frac{1}{x}}\) = 3 という武器を得た !
(2) x2+\(\large{\frac{1}{x^2}}\)
→ x2+\(\large{\frac{1}{x^2}}\) に似た \(\left( x+\frac{ 1 }{ x } \right )^2\) を計算してみると
↑テクニックな部分
\(\left( x+\frac{ 1 }{ x } \right )^2\) = x2+2・x・\(\large{\frac{1}{x}}\)+\(\large{\frac{1}{x^2}}\)
= x2+\(\large{\frac{1}{x^2}}\)+2 ←「2」増えてしまうと判明
∴ x2+\(\large{\frac{1}{x^2}}\) = \(\left( x+\frac{ 1 }{ x } \right )^2\)-2
↑頻出かつ重要な「形」ですね
多いものを引いたり足したりして同じにする
∴ (1)の x+\(\large{\frac{1}{x}}\) = 3 より
→ x2+\(\large{\frac{1}{x^2}}\) = \(\left( x+\frac{ 1 }{ x } \right )^2\)-2
= (3)2-2
= 9-2
= 7 // x2+\(\large{\frac{1}{x^2}}\) = 7 という武器を得た !
(3) x3+\(\large{\frac{1}{x^3}}\)
→ x3+\(\large{\frac{1}{x^3}}\) に似た形になるかもしれない \(\left( x+\frac{ 1 }{ x } \right )\)\(\left( x^2+\frac{ 1 }{ x^2 } \right )\) を計算すると
\(\left( x+\frac{ 1 }{ x } \right )\)\(\left( x^2+\frac{ 1 }{ x^2 } \right )\) = x3+\(\large{\frac{1}{x}}\)+x+\(\large{\frac{1}{x^3}}\)
∴ x3+\(\large{\frac{1}{x^3}}\) = \(\left( x+\frac{ 1 }{ x } \right )\)\(\left( x^2+\frac{ 1 }{ x^2 } \right )\)-\(\left( x+\frac{ 1 }{ x } \right )\)
∴ (1)の x+\(\large{\frac{1}{x}}\) = 3 (2)の x2+\(\large{\frac{1}{x^2}}\) = 7 より
→ x3+\(\large{\frac{1}{x^3}}\) = \(\left( x+\frac{ 1 }{ x } \right )\)\(\left( x^2+\frac{ 1 }{ x^2 } \right )\)-\(\left( x+\frac{ 1 }{ x } \right )\)
= (3)(7)-(3)
= 21-3
= 18 //
《 例 》
(1) x+y = 3、xy = 1 のとき、x2+y2 の値を求めましょう
x2+y2 = (x+y)2-2xy ←多いものを引いて同じにする
∴ (3)2-2(1) = 9-2 = 7
(2) x+y = \(\small{\sqrt{2}}\)、x-y = \(\small{\sqrt{3}}\) のとき、x2+y2 の値を求めましょう
それぞれ両辺2乗すると
・ (x+y)2 = 2
・ (x-y)2 = 3
それぞれ展開すると
・ x2+2xy+y2 = 2 …①とします
・ x2-2xy+y2 = 3 …②とします
①+② をしてみると
x2+2xy+y2 = 2
+) x2-2xy+y2 = 3
2x2 +2y2 = 5
→ 2(x2+y2) =5
∴ x2+y2 = \(\large{\frac{5}{2}}\) //
→もちろん①-②で xy の値を求めて、xyの値を①か②に代入でも同じですね
(3) x+y = \(\small{\sqrt{5}}\)、x-y = \(\small{\sqrt{3}}\) のとき、xy の値を求めましょう
それぞれ両辺2乗すると
・ (x+y)2 = 5
・ (x-y)2 = 3
それぞれ展開すると
・ x2+2xy+y2 = 5 …①としますね
・ x2-2xy+y2 = 3 …②としますね
①-②
x2+2xy+y2 = 5
-) x2-2xy+y2 = 3
4xy = 2
∴ xy = \(\large{\frac{1}{2}}\) //
準公式
| ● | (x+y)2+(x-y)2 = 2(x2+y2) (両端が生き残る) |
| ● | (x+y)2-(x-y)2 = 4xy (真ん中が生き残る) |
| → | 知っていて損はないですね! |
| → | 何が消滅して、何が生き残るのか、暗算で検討がつきますが
最初の「気づき」程度にでも知っていれば、役立ちますね |
《 例 》
\(\large{\frac{1}{x}}\)+\(\large{\frac{1}{y}}\) = 5 のとき、\(\large{\frac{5xy}{x+y}}\) の値を求めましょう
| → | 通分するためには「\(\large{\frac{y}{y}}\)」と「\(\large{\frac{x}{x}}\)」を掛けますね |
| → | \(\large{\frac{y}{xy}}\)+\(\large{\frac{x}{xy}}\) = 5 → \(\large{\frac{x+y}{xy}}\) = 5 → x+y = 5xy |
| → | 与式\(\large{\frac{5xy}{x+y}}\) にx+y = 5xyを代入
\(\large{\frac{5xy}{(5xy)}}\) = 1 |
∴ \(\large{\frac{5xy}{x+y}}\) = 1 //
| ● | 値を直接代入することは、ほぼ「ない」ですね!
「何らかの変形」(因数分解など)ですね |
| ● | √ があれば、ほぼ「問題の式を2乗」や逆に「与えられた条件を2乗」で糸口が見えますね |
③ 「式の計算」を利用 「整数の特徴の証明」
前提として、「整数」はよく「m」や「n」で表しますね (natural number)
・「偶数」を表す式は「2n 」
・「奇数」を表す式は「2n+1」でしたね!
《 例 》
連続する3つの整数で、最も大きい整数の2乗から最も小さい整数の2乗を引いた差は、真ん中の整数の4倍になることを証明しましょう
(証明)
連続する3つの整数を、n、n+1、n+2、とする
(もちろん、n-2、n-1、n、でも n-1、n、n+1としてもOKです)
最も大きい整数の2乗から最も小さい整数の2乗を引いた差は
(n+2)2-n2 …①
真ん中の整数の4倍は
4(n+1) …②
①を整理すると、
n2+4n+4-n2 = 4n+4 = 4(n+1)
∴ ① = ②より、最も大きい整数の2乗から最も小さい整数の2乗を引いた差は、真ん中の整数の4倍である
《 例 》
連続する 2つの奇数(ex. 1、3や5、7など)において、2つの奇数の積から 小さい方の奇数の2倍を引いた数は、小さい方の奇数の 2乗に等しくなることを証明しましょう
(証明)
連続する2つの奇数を、2n+1、2n+3、とする
2つの奇数の積から小さい方の奇数の2倍を引いた数は
(2n+1)(2n+3)-2(2n+1) …①
小さい方の奇数の 2乗は
(2n+1)2 …②
①を整理すると、 4n2+8n+3-4n-2 = 4n2+4n+1
②を整理すると、 4n2+4n+1
∴ ① = ②より、連続する 2つの奇数において、2つの奇数の積から小さい方の奇数の2倍を引いた数は、小さい方の奇数の2乗である
| ● | 「証明」に決まった書式はありません、自由です!
言っている |
| ● | 読む相手が、その内容を「理解しやすければ」なお良しですね! |
④ 「式の計算」の利用 「図形の証明」
《 例 》
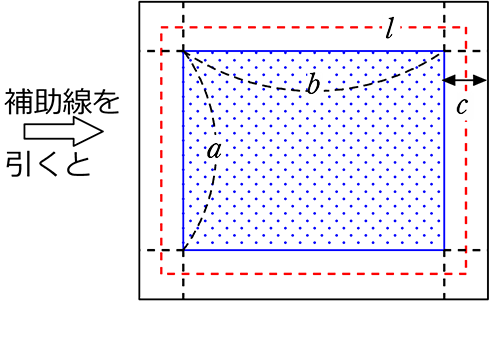
縦がam、横がbmの長方形の池のまわりに,幅がc mの道があります。
道の中央を通る⾧方形の周りの⾧さをlm、道の面積をSm2とするとき、
S = cl となることを証明しましょう
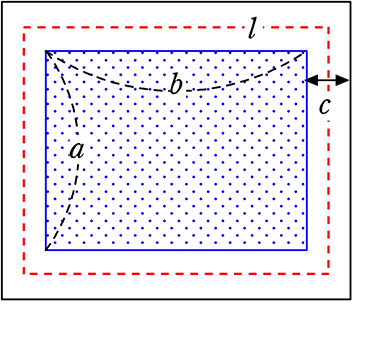
(証明)
道の面積S
= (黒四角形)-(青四角形)
= (a+2c)(b+2c)-ab
= ab+2ac+2bc+4c2-ab
= 2ac+2bc+4c2 …①
l の長さ
= a+b+a+b+8\(\left( \large{\frac{ c }{ 2 }} \right )\)
= 2a+2b+4c …②
②に道幅cを掛けてみると
cl = c(2a+2b+4c)
= 2ac+2bc+4c2 …③
∴ ① = ③ より 道面積S = cl である
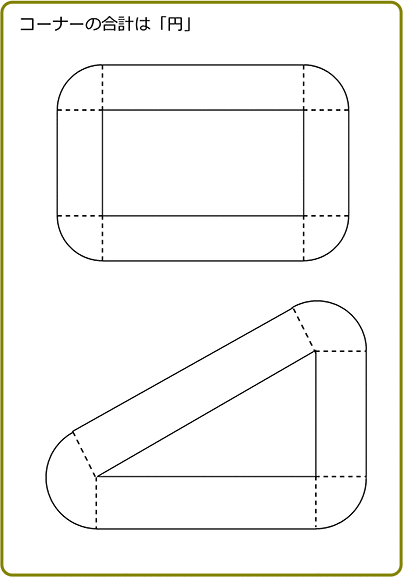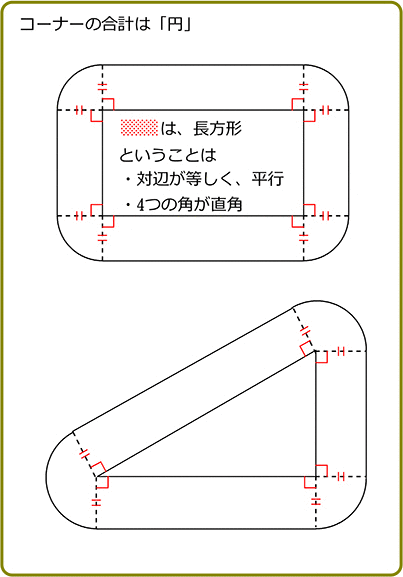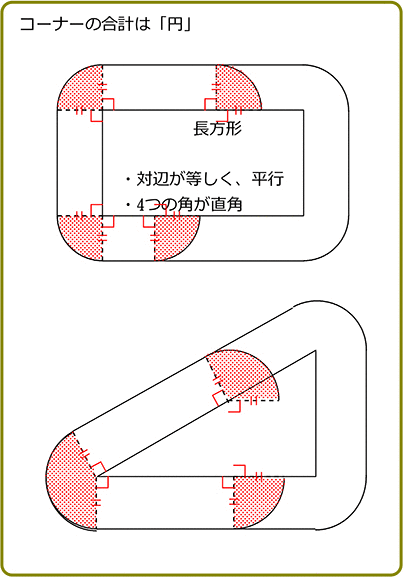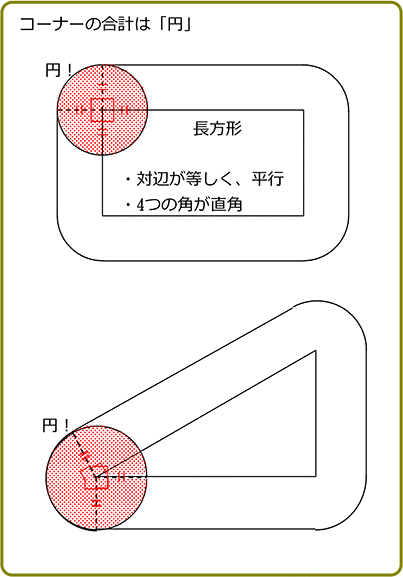
《 例 》
三角形の土地のまわりに、幅が a m、中央を通る線の⾧さが l mの道があります。この道の面積を S m2とするとき、
S = al となることを証明しましょう
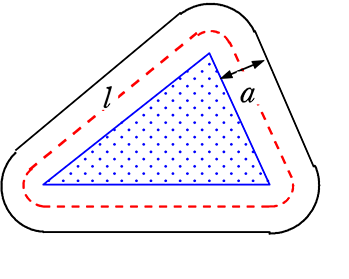
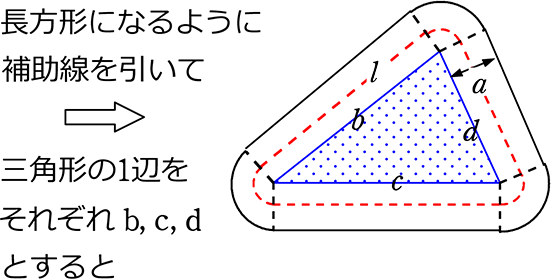
(証明)
三角形の1辺をそれぞれ b、c、d とすると
3つのコーナー部分の合計面積は、πa2

コーナーを集めると円になる
円の面積 πr2、 円周 2πr
道の面積S = ab+ac+ad+πa2 …①
l の長さ = b+c+d+2π\(\left( \frac{ a }{ 2 } \right )\)
= b+c+d+πa …②

②にaを掛けてみると al = ab+ac+ad+πa2 …③
∴ ① = ③ より S = al である
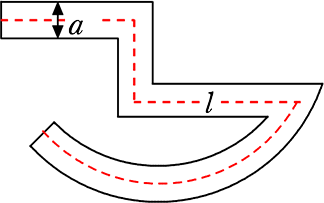
上の「証明」より
「道の面積 = 中央線 lの長さ × 道幅 a」
ということの方が、
実社会では役に立ちそうですね
《 例 》
下の図のように点Oを中心とする半円がある。斜線部分の面積をS、
点O1を中心とする半円の面積をS1、半円O1、O2の半径をそれぞれ a、b とするとき、以下の問いに答えましょう

(1) S1をaを用いて表しましょう
S1 = \(\large{\frac{1}{2}}\)πa2
(2) Sをa、b を用いて表しましょう
S = \(\large{\frac{1}{2}}\)大円面積-\(\large{\frac{1}{2}}\)中円面積-\(\large{\frac{1}{2}}\)小円面積
= \(\large{\frac{1}{2}}\)π(a+b)2-\(\large{\frac{1}{2}}\)πa2-\(\large{\frac{1}{2}}\)πb2
= \(\large{\frac{1}{2}}\)π{(a+b)2-a2-b2}
= \(\large{\frac{1}{2}}\)π(a2+2ab+b2 -a2-b2
= \(\large{\frac{1}{2}}\)π(2ab)
∴ S = πab
(3) S = S1のとき、a:b をもっとも簡単な整数の比で表しましょう
S = S1 より πab = \(\large{\frac{1}{2}}\)πa2
これを整理(両辺をπaで割る)すると、
b = \(\large{\frac{1}{2}}\)a
∴ b:a = \(\large{\frac{1}{1}}\):\(\large{\frac{2}{1}}\) = 1:2
∴ a:b = 2:1

=で結ばれたものを「比」にする (連比)
〇a = 〇b = 〇c = 〇d を 「比」で表す「方法」は、
それぞれの「係数の逆数」がそのまま「比」となりますね
ex)
・\(\large{\frac{1}{2}}\)a = b → a:b = \(\large{\frac{2}{1}}\):\(\large{\frac{1}{1}}\) = 2:1
・3a = 6b = c = \(\large{\frac{3}{2}}\)d → a:b:c:d = \(\large{\frac{1}{3}}\):\(\large{\frac{1}{6}}\):\(\large{\frac{1}{1}}\):\(\large{\frac{2}{3}}\) = 2:1:6:4 ←全てに「6」を掛けて「整数比」にした
これの「仕組み」は
①




②
長さがそろった
= 目盛りがそろった
= 共通の定規(共通の価値)
③ 3、6、1、\(\large{\frac{3}{2}}\) の価値をそろえると、
比較できる = 「比」
よって、目盛りが共通であるので、単純に
\(\large{\frac{1}{3}}\):\(\large{\frac{1}{6}}\):\(\large{\frac{1}{1}}\):\(\large{\frac{2}{3}}\) とできる
そして、これは「形的に見ると、係数の逆数」になっている ですね!
《 例 》
図のような長方形ABCDがあります(AB = a、BC = bとします)
aを1辺とする正方形の頂点をE、F
FCを1辺とする正方形の頂点をG、H
DHを1辺とする正方形の頂点をI、Jを順次作成すると
長方形EGJIができました
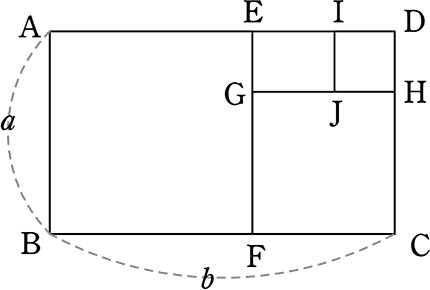
(1) 正方形GFCHの面積を a, b で表しましょう
FC = b-a ∴ (b-a)2
(2) 正方形IJHDの面積を a,b で表しましょう
DH = a-(b-a)
∴ {a-(b-a)}2 = (a-b+a)2 = (2a-b)2
(3) 長方形EGJIの面積を a, b で表しましょう
・IJ = DH = a-(b-a) = ID
・EI = FC-ID = (b-a)-{a-(b-a)}= b-a-a+b-a = -3a+2b
∴ 長方形EGJI = (2a-b)(-3a+2b)
→ (1)、(2)、(3) ともに「展開」した形でも、解としてOK正解ですね
図形の場合は、ただ「文字」で「面積」や「距離」を表せばよいだけですね
お疲れ様でした !!
その他の問題は、「問題集」で !!















