| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 図形の相似 | (2) 円周角・中心角 | (3) 三平方の定理 |
図形の相似
ア 図形の相似の意味,三角形の相似条件
相似とは
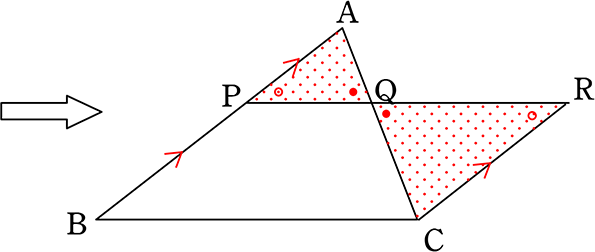
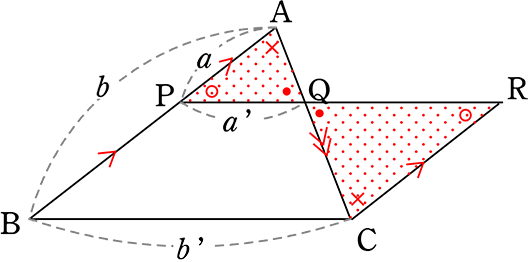
| ・ | 「合同」は一言でいうと、「同じ形」+「同じ大きさ」でしたね |
| ・ | 「相似」は一言でいうと、「同じ形」なだけです!「大きさ」は自由!ですね |
「合同」は、「裏返し」「回転」「平行移動」すれば2つの図形がピッタリ一致!
「相似」は、それらプラス「拡大・縮小」してもよいですね
ということは、「合同」より「条件」がゆるいということになります
そして、
「辺」は図形の「大きさ」を決定づけるもの
「角度」は図形の「形」を決定づけるものでしたね!
ということで、「大きさ」も同じでなければならない「合同」は
「辺の長さ」も「同じ」でなければならならかったですが、
「大きさ」は同じでなくてもよい「相似」は
「辺の比」が「同じ」であればよい ということになります!
当然、「角度」は「形」を決定づけるものですから、「合同」でも「相似」でも同じでなければなりませんね!

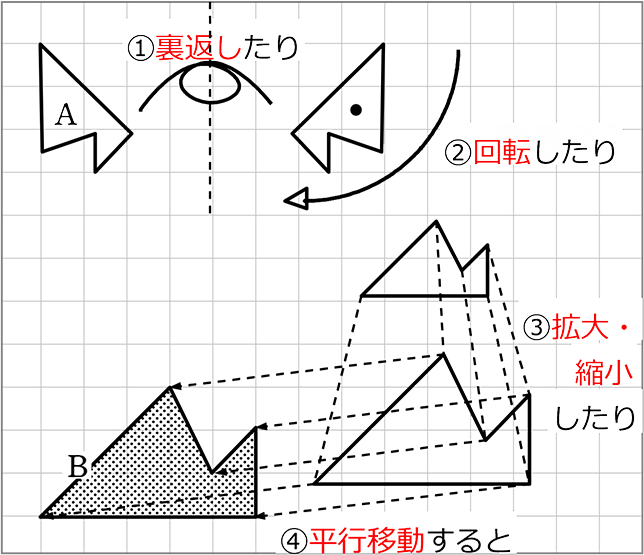
ピッタリ一致しましたね
このとき、図形Aと図形Bは「相似(そうじ)」であるといいます
記号は「∽」を用いて、図形A ∽ 図形B(「図形Aそうじ図形B」)と表現します
相似な図形は、三角形であろうと四角形であろうとn角形であろうと
対応する「辺」の「比」は、どの辺であろうと全て等しい
(対角線の長さ、半径の長さ、弧の長さなどの比も もちろん等しい)
当然、対応する「角」の「大きさ」は、それぞれ等しい ですね
そして、そのときの「対応する線分」の「比」を、「相似比」と言います
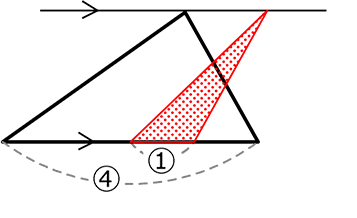
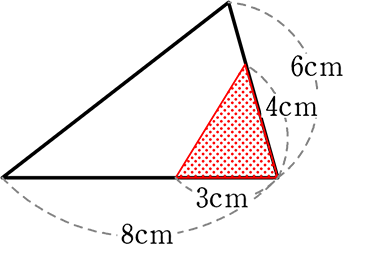
《 例 》
△ABC ∽ △DEFであるとき、以下の問いに答えましょう
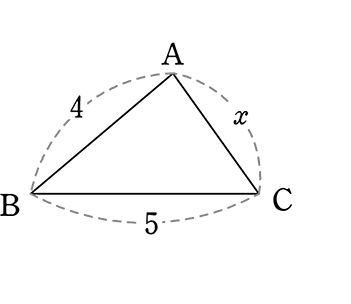
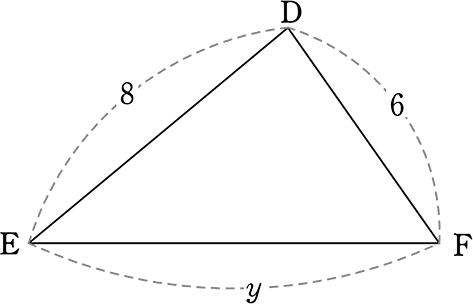
(1) △ABCと △DEF の 相似比 を求めましょう
→ 対応する辺の比が、どちらも「数字」なのは、ABとDE
∴ 4:8 A. 1:2
(2) △DEF と △ABC の 相似比 を求めましょう
→ 8:4 A. 2:1
(3) xを求めましょう
| x:6 | = | 1:2 (相似比) |
| 2x | = | 6 |
| x | = | 3 |
a:b = s:t
→ 内側どうしの積 = 外側どうしの積
∴ at = bs でしたね
(4) yを求めましょう
| 5:y | = | 1:2 (相似比) |
| y | = | 10 |

『相似』!なら…「対応する辺」と「順番」さえ合っていればよい
① 2つの三角形が『相似』だった場合、ある辺の長さを求めるための表現は 実は自由です
このあと「平行線と線分の比」や「方べき」などで
「この辺」:「この辺」は「この辺」:「この辺」という公式のようなものがたくさん出てきますが
② 「対応する辺」と「順番」さえ合っていれば なんでもよい ということですね
例えば、次の三角形が『相似』だった場合
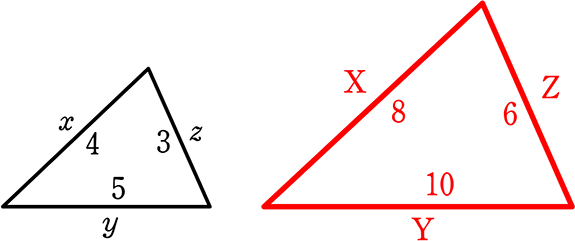
(標準)
x:X = y:Y
x:X = z:Z
y:Y = x:X
y:Y = z:Z
z:Z = x:X
z:Z = y:Y
(確かめ)
| → x:8 | = | 3:6 |
| 6x | = | 24 |
| x | = | 4 |
| → x:8 | = | 5:10 |
| 10x | = | 40 |
| x | = | 4 |
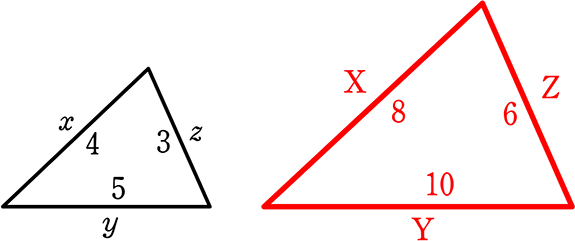
(図形内の比でもよい)
x:y = X:Y
x:z = X:Z
y:x = Y:X
y:z = Y:Z
z:x = Z:X
z:y = Z:Y
(確かめ)
| → x:5 | = | 8:10 |
| 10x | = | 40 |
| x | = | 4 |
| x:3 | = | 8:6 |
| 6x | = | 24 |
| x | = | 4 |
『分数表記』にも慣れてくださいね
「これ」ぶんの「これ」は「これ」ぶんの「これ」と読むと難しいことをしているみたいなので
「図形」の場面では
「これ(分母)」につき「これ」は「これ」につき「これ」と読むとイメージがしやすくなりますね (割合とは)
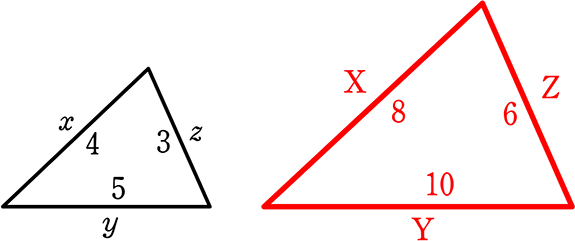
(標準)
\(\large{\frac{\color{red}{X}}{x}}\) =\(\large{\frac{\color{red}{Y}}{y}}\) 「xにつきXは yにつきY」
\(\large{\frac{\color{red}{X}}{x}}\) =\(\large{\frac{\color{red}{Z}}{z}}\)
\(\large{\frac{x}{\color{red}{X}}}\) =\(\large{\frac{y}{\color{red}{Y}}}\)
\(\large{\frac{x}{\color{red}{X}}}\) =\(\large{\frac{z}{\color{red}{Z}}}\)
\(\large{\frac{\color{red}{X}}{x}}\) =\(\large{\frac{\color{red}{Z}}{z}}\)
(確かめ)
\(\large{\frac{\color{red}{8}}{x}}\) =\(\large{\frac{\color{red}{10}}{5}}\) → 40=10x → x=4
\(\large{\frac{x}{\color{red}{8}}}\) =\(\large{\frac{5}{\color{red}{10}}}\) → 10x=40 → x=4
\(\large{\frac{\color{red}{8}}{x}}\) =\(\large{\frac{\color{red}{6}}{3}}\) → 24=6x → x=4
\(\large{\frac{\color{red}{x}}{8}}\) =\(\large{\frac{3}{\color{red}{6}}}\) → 6x=24 → x=4
(確かめ)
\(\large{\frac{\color{red}{8}}{x}}\)=\(\large{\frac{\color{red}{10}}{5}}\) → 40=10x → x=4
\(\large{\frac{x}{\color{red}{8}}}\)=\(\large{\frac{5}{\color{red}{10}}}\) → 10x=40 → x=4
\(\large{\frac{\color{red}{8}}{x}}\)=\(\large{\frac{\color{red}{6}}{3}}\) → 24=6x → x=4
\(\large{\frac{\color{red}{x}}{8}}\)=\(\large{\frac{3}{\color{red}{6}}}\) → 6x=24 → x=4
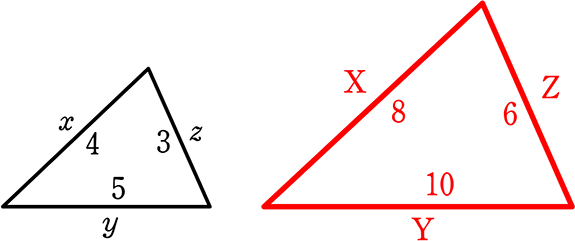
(図形内の比でもよい)
\(\large{\frac{y}{x}}\) =\(\large{\frac{\color{red}{Y}}{\color{red}{X}}}\) 「xにつきyは XにつきY」
\(\large{\frac{z}{x}}\) =\(\large{\frac{\color{red}{Z}}{\color{red}{X}}}\)
\(\large{\frac{z}{y}}\) =\(\large{\frac{\color{red}{Z}}{\color{red}{Y}}}\)
(確かめ)
\(\large{\frac{5}{x}}\) =\(\large{\frac{\color{red}{10}}{\color{red}{8}}}\) → 40=10x → x=4
\(\large{\frac{x}{5}}\) =\(\large{\frac{\color{red}{8}}{\color{red}{10}}}\) → 10x=40 → x=4
\(\large{\frac{3}{x}}\) =\(\large{\frac{\color{red}{6}}{\color{red}{8}}}\) → 24=6x → x=4
\(\large{\frac{x}{3}}\) =\(\large{\frac{\color{red}{8}}{\color{red}{6}}}\) → 6x=24 → x=4
(確かめ)
\(\large{\frac{5}{x}}\)=\(\large{\frac{\color{red}{10}}{\color{red}{8}}}\) → 40=10x → x=4
\(\large{\frac{x}{5}}\)=\(\large{\frac{\color{red}{8}}{\color{red}{10}}}\) → 10x=40 → x=4
\(\large{\frac{3}{x}}\)=\(\large{\frac{\color{red}{6}}{\color{red}{8}}}\) → 24=6x → x=4
\(\large{\frac{x}{3}}\)=\(\large{\frac{\color{red}{8}}{\color{red}{6}}}\) → 6x=24 → x=4
よって、
①『相似』であれば
②「対応する辺」と「順番」さえ合っていれば なんでもよい
cf.
相似である2つの三角形は
必ず重ねると「山型」になる
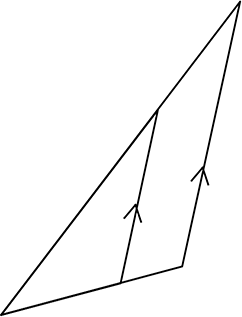
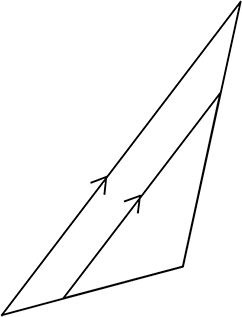
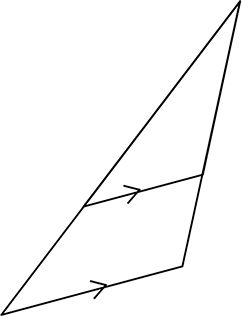
(後述)
| ・ | 「平行線と線分の比」の  型、 型、 型、 型、 型の比も実は「対応する辺」と「順番」さえ合っていればなんでもよいということですね 型の比も実は「対応する辺」と「順番」さえ合っていればなんでもよいということですね |
| ・ | 「方べき」も「裏返し」て「重ねたら」、当然「山型」になりますね |
このように、
「相似」であるという「前提」があれば、図形の「角度」が求められるし、
「相似比」が解れば、図形の「線分(辺や対角線)の長さ」が求められるし、
「相似」は、何やら図形のあらゆるデータを求めるのに役立ちそうですね!
よって、相似かどうか分からない場合、「相似である!」と
証明できれば、色々なデータが求められる!ということですね!
三角形の相似条件
「三角形の合同条件」は、「形」も「大きさ」も同じというための条件。
「三角形の相似条件」は、「形」さえ同じであればよいという条件ですので、
「合同」より条件がゆるいですね!
もう少し正確に言うならば、
「大きさ」を決める「辺の長さ」に対する条件がゆるいですね!

三角形の相似条件 (フィルター集⑦)
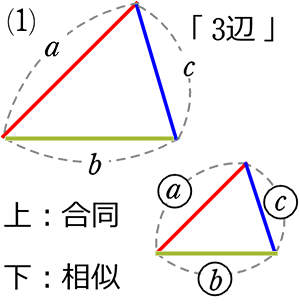
| 合同 | 「3組の辺 がそれぞれ等しい」 |
| 相似 | 「3組の辺の比 がすべて等しい」 a:a’= b:b’= c:c’ |
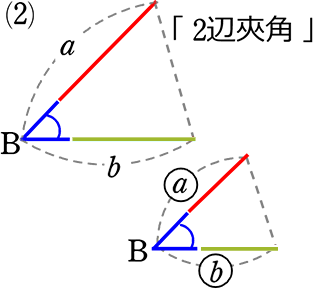
| 合同 | 「2組の辺 と その間の角がそれぞれ等しい」 |
| 相似 | 「2組の辺の比とその間の角がそれぞれ等しい」
a:a’ = b:b’ |
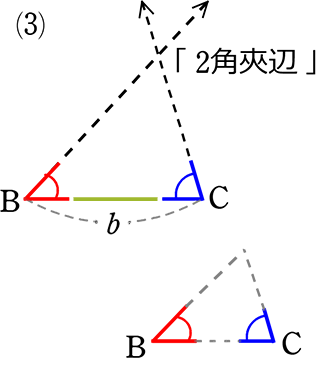
| 合同 | 「1組の辺とその両端の角がそれぞれ等しい」
↑「大きさ」を一致させるために辺が1つは必要 |
| 相似 | 「2組の角 がそれぞれ等しい」
∠B = ∠B’ ↑三角形は、2つの角で「形」が決まるので 「形」さえ同じであればよいという 「相似」に「辺」は不要ですね! |
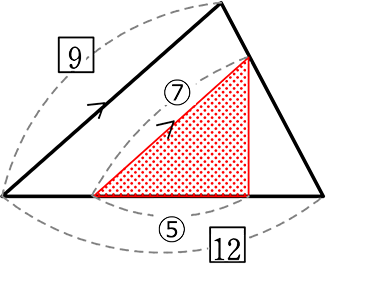
《 例 》
△ABC∽△DCAであることを証明しましょう
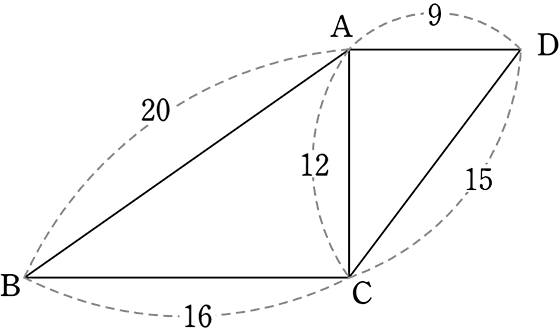
→ 角の情報がない、「3辺の比が…」だろうな
(証明)
△ABCと△DCAにおいて …合同の証明同様の決まり文句
仮定より、
AB:DC = 20:15 = 4:3 …① …既成事実 (証拠)
BC:CA = 16:12 = 4:3 …② …既成事実 (証拠)
CA:AD = 12:9 = 4:3 …③ …既成事実 (証拠)
①②③より 3辺の比がすべて等しいので …相似条件
△ABC∽△DCA
《 例 》
△ABC∽△ADBであることを証明しましょう

→ かぶった図形には「共通使用の角」があるはず
(証明)
△ABCと△ADBにおいて
∠A = ∠A (共通) …①
AB:AD = 6:4 = 3:2 (仮定より) …②
AC:AB = 9:6 = 3:2 (仮定より) …③
①②③より 2組の辺の比とその間の角が等しいので
△ABC∽△ADB
《 例 》
△ABC∽△ADEであることを証明しましょう
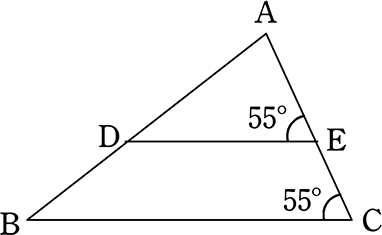
(証明)
△ABCと△ADEにおいて
∠A = ∠A (共通)
∠C = ∠E = 55° (仮定)
よって、2組の角がそれぞれ等しいので
△ABC∽△ADE
証拠が並んでいたら、わざわざ①②としなくてもよいですね
①②③などは、証拠が離れているときに有効ですね
| → | 相似条件は、合同の「条件」より 「ゆるい」「少ない」ぶん、早い段階で証明が終了しますね! |
| → | 早い段階で「相似!」と言える → 合同より証明が簡単 |

直角三角形の相似条件
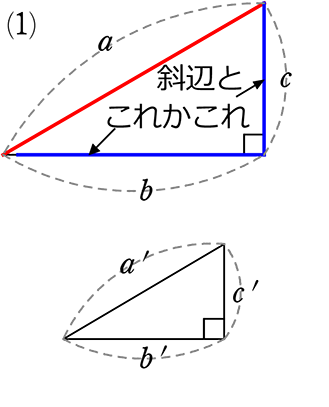
| 合同 | 「斜辺」と「他の1辺」 がそれぞれ等しい |
| 相似 | 「対応する2組の辺の比 がそれぞれ等しい」
↑どの組合せでもよい どの組合せでもよい
・a:a’ = b:b’ \(\large{\frac{b}{a}}\) = \(\large{\frac{b’}{a’}}\) |
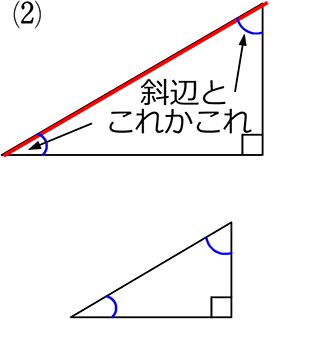
| 合同 | 「斜辺」と「1つの鋭角」がそれぞれ等しい |
| 相似 | 「1つの鋭角」が等しい
↑どちらの鋭角でもよい |
普通相似条件の「2組の角 がそれぞれ等しい」の1つは90°と決まってるし!でもよいですね
(直角三角形は「斜辺中心主義」でしたね)
もちろん、普通の相似条件で証明してもOKです!
相似の位置・相似の中心
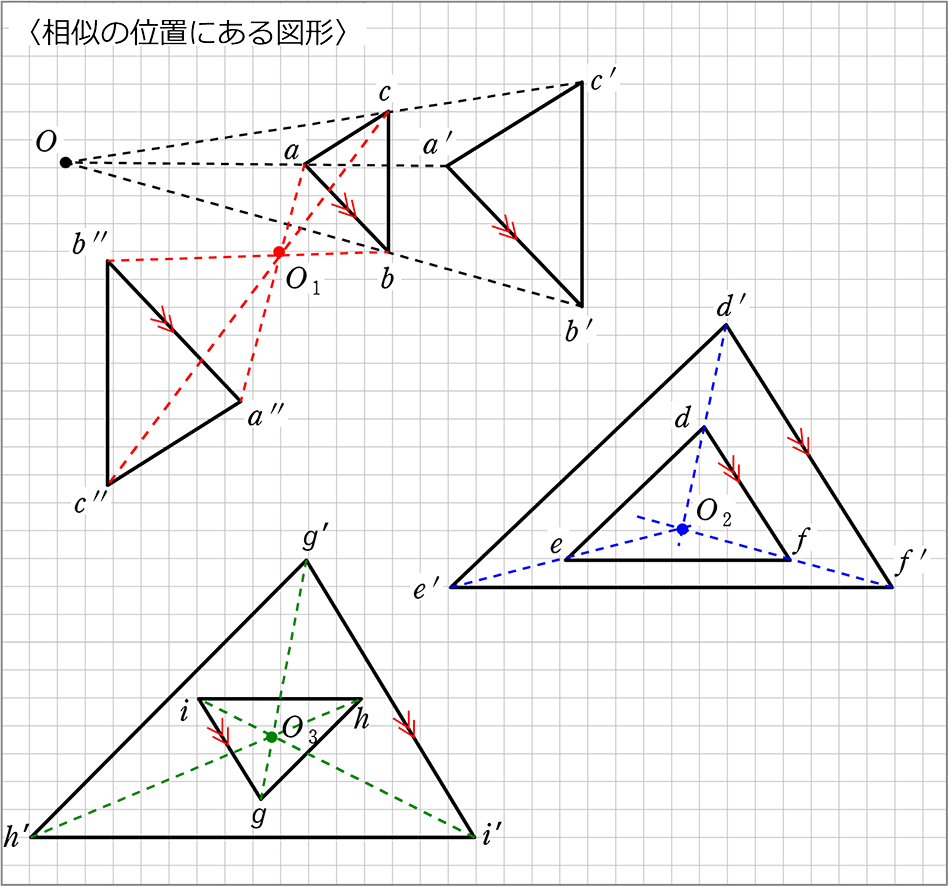
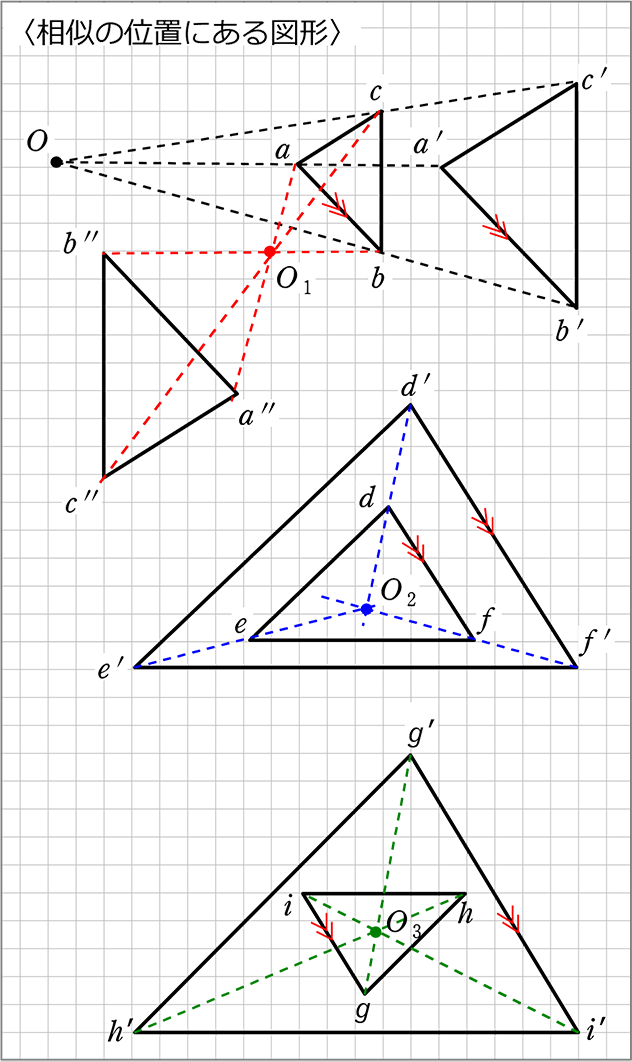
「相似の中心」とは
| ① | 対応する点を通る直線が1点で交わるところ
→ O , O1, O2 のことですね |
かつ
| ② | Oから対応する点までの⾧さの比がすべて等しい ような点
→ Oa:Oa’ = Ob:Ob’ = Oc:Oc’ |
相似の位置にある図形は、対応する辺が平行なので…
それぞれの三角形が、必ず『山型』か『ちょう型』になっていますね
ex)
Oc:Oc’ = 3:5 なら
Oa:Oa も3:5
Ob:Ob も3:5
→ ac:a’c’ = ab:a’b’ = bc:b’c’ も 3:5 = 相似比
逆に、abc の2倍の図を書きたい場合は、
Oa:Oa’ = Ob:Ob’ =Oc:Oc’ = 1:2 の場所にa’b’c’ をとればよいということですね!
| ・ | 左上の図の関係は、ドラえもんの「スモールライト」「ビックライト」みたいですね! |
| ・ | 左下の図は、理科の網膜に映った画像のようですね! |
| ・ | 右下の図は、スモールライトの光を正面から浴びてしまった感じですね! |
| 「相似の位置」… | 上のような関係にある図形を「相似の位置にある」といいます |
| → 相似の位置にある図形 | 対応する辺が全て平行 |
ex) ac\(/\!/ \)a’c’ ab//a’b’ bc//b’c’
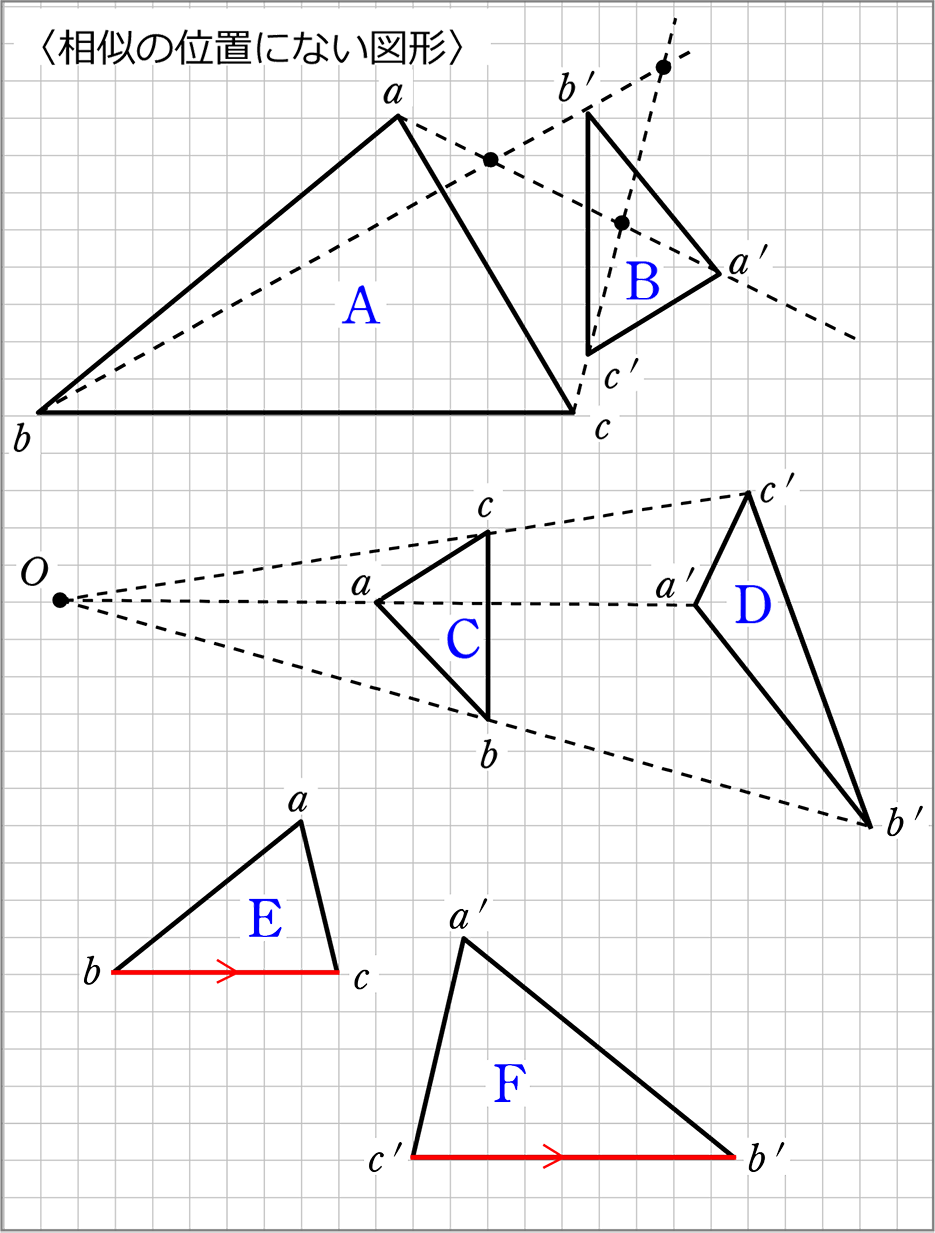
・AとBは、「相似」ではありますが、「相似の位置」にはないですね
当然「相似の中心O」もありませんね
→ 「相似の位置」にあるかないかは、点線を引かなくても、
対応する辺がそれぞれ平行か平行でないか、パット見でわかりますね!
ex) 辺abと辺a’b’を見比べて…平行でない!→相似の位置にない!
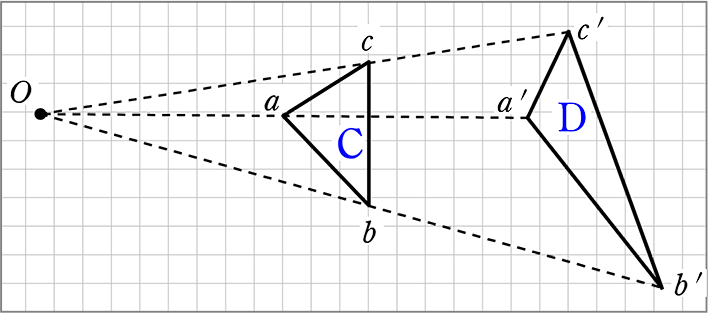
・CとDは、パット見すでに「相似」でもありませんが、正確には
→ Oa:Oa’ ≠ Ob:Ob’ ≠Oc:Oc’ → 比が違う!いうことですね
よって、CとDは「相似の位置にない」
よって、Oも「相似の中心」ではなく「たまたま延⾧線が一致した点」
とでも言うべきでしょうか
ここでも、対応する辺が平行か平行でないか、パット見でわかりますね!
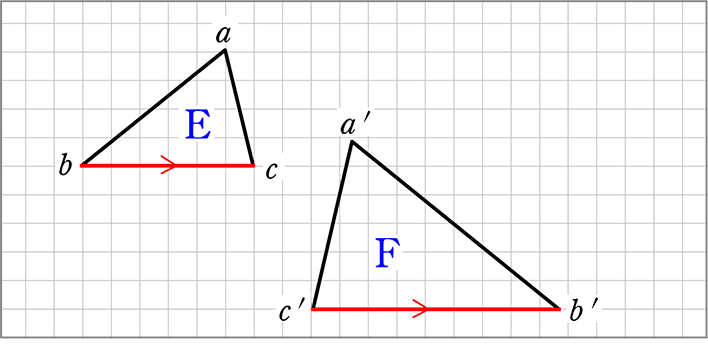
・EとFは、裏返しの相似ですが、1組の対応する辺を平行にすると、 他の対応する辺は平行にならない
| ⇒ | 裏返しの図形に相似の位置はない |
| ⇒ | ただし、裏返したのか返してないのか わからないような図形には、相似の位置があり得る (正三角形、正方形、長方形、ひし形、円など) |
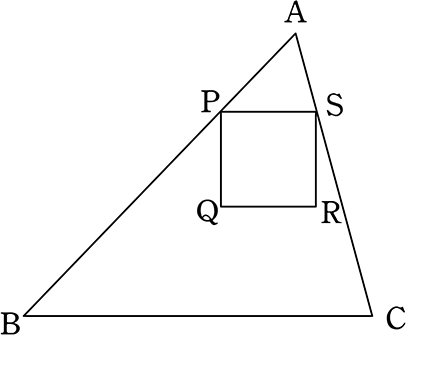
《 例 》
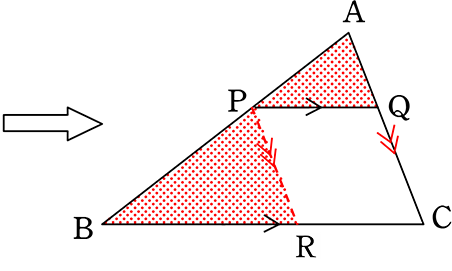
QR//BC な正方形PQRSを拡大して、△ABCに納まる最大の正方形を作図しましょう
ただし、最大の正方形と元の正方形は相似の位置にあるものとします
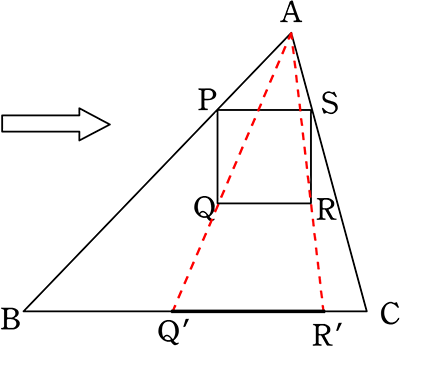
→Aを「相似の中心」とみなし、
BC上にQ’とR’をとると、
△AQR∽△AQ’R’
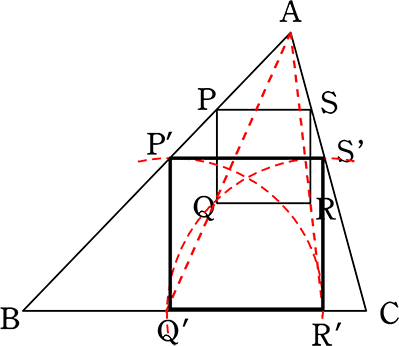
∴ 新P’Q’R’S’は正方形ですので Q’R’を半径とする 円とAB、ACの交点がP’、S’
→ いきなり内接正方形を書くのは難しいので、まずはPQRSのような正方形を用意すれば、簡単に書けますよ~という問題ですね!
まとめ
| ・ | 「相似の位置」にあるかないか
→ 対応する辺が平行か平行でないか、パット見でわかる |
| ・ | 相似の位置にあるならば
→「相似の中心」がどこかにある |
| ・ | 「相似の中心」の場所は
→ 対応する点を結ぶ線を、大げさに⾧く書いたときの交点 |
「相似の位置」「相似の中心」は、問題的にはふくらましにくいので
定期テスト的、単発的な問題になると思われます
イ 三角形の相似条件を用いた図形の性質の論証
《 例 》
地面に垂直に立つ木の高さを求めましょう
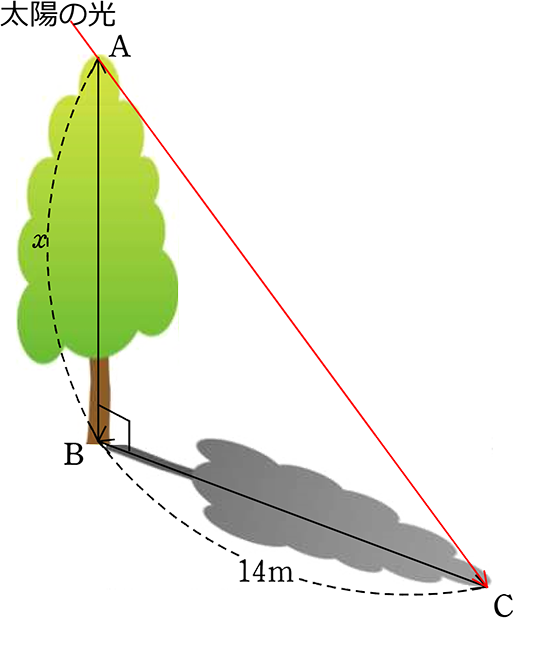
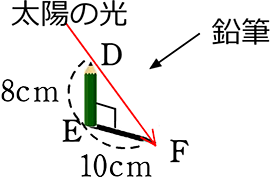
| → | ∠C = ∠F (太陽光の角度は同じ) …①
∠B = ∠E= ∠R (仮定より) …② ∠Rとは 90°を意味します |
①②より 2組の角がそれぞれ等しい ので
△ABC ∽ △DEF
| ∴ x:8 | = | 14:10 |
| 10x | = | 112 |
| x | = | 11.2 A. 11.2 m |
↑その他 \(\large{\frac{x}{14}}\) = \(\large{\frac{8}{10}}\)、 \(\large{\frac{x}{8}}\) = \(\large{\frac{14}{10}}\)
…何でもかまいませんね!

対応する辺の混乱防止
相似の問題を解いていると、単純な図形なのに
「この辺に対応する辺は・・・え~と・・・さっき1度わかったのに・・・」と
こんがらがってしまうことがありますね
混乱防止の1つの方法として、

△〇〇〇の書き出す順番として
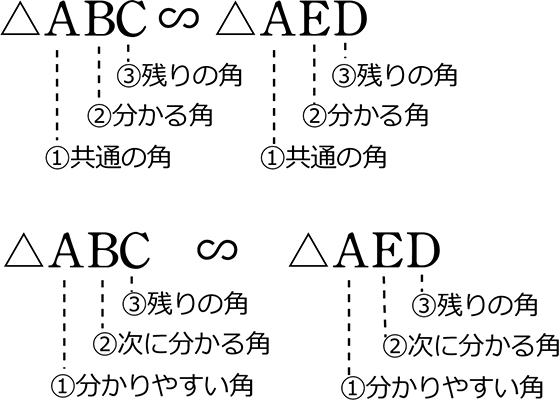
など、自分ルールでABCの書く順を決めるのもよいですね
そして、この『△ABC∽△AED』の前提さえしっかりしていれば、
「辺」も対応しているのですから、混乱防止になりますね!
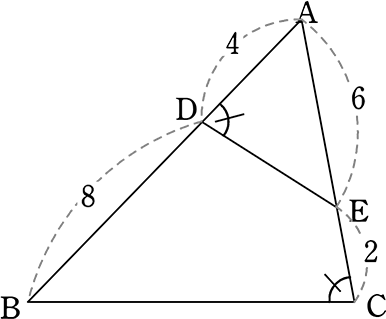
ex)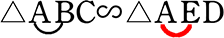 「辺ABに対応するのは(図形も見つつ)…AE!」
「辺ABに対応するのは(図形も見つつ)…AE!」
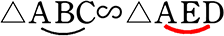 「辺ACに対応するのは(図形も見つつ)…AD!」
「辺ACに対応するのは(図形も見つつ)…AD!」
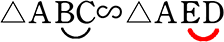 「辺BCに対応するのは(図形も見つつ)…ED!」
「辺BCに対応するのは(図形も見つつ)…ED!」
cf. 合同でも使えるルールですね
ウ 平行線と線分の比
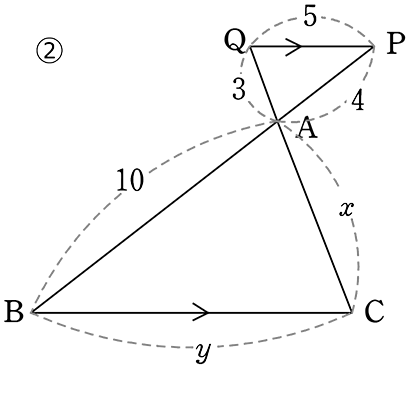
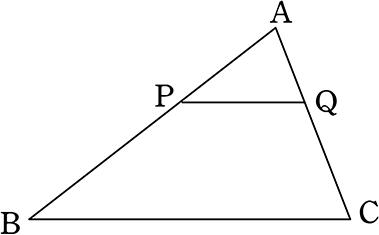
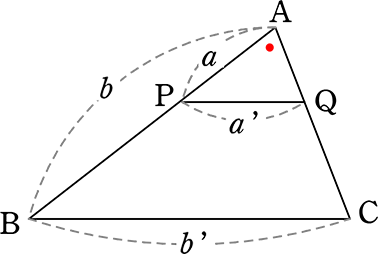
《 例 》
x, y, a, b を求めましょう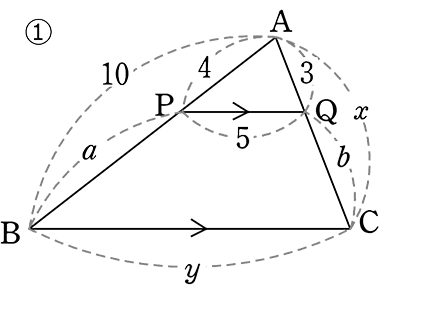
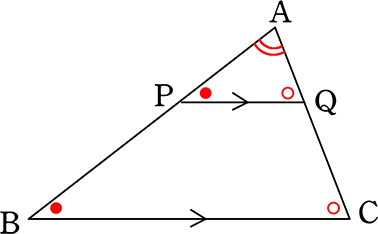
まずは「相似の証明」ですね
(①の証明)
△APQと△ABCのおいて
・∠A = ∠A (共通)
PQ//BC より
・∠APQ = ∠ABC (同位角)
(または)
・∠AQP = ∠ACB (同位角)
2角が等しい
∴ △APQ∽△ABC
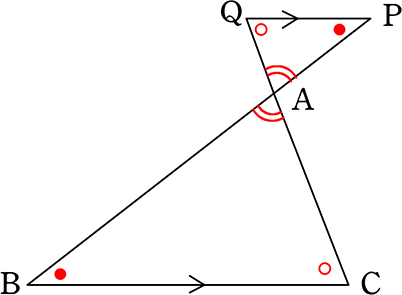
(②の証明)
△APQと△ABCのおいて
PQ//BC より
・∠A = ∠A (対頂角)
・∠APQ = ∠ABC (錯角)
(または)
・∠AQP = ∠ACB (錯角)
2角が等しい
∴ △APQ∽△ABC
再度図です。x, y, a, b の値は?
∴ 相似な三角形は「3組の辺の比が全て等しい」ので
4:3 = 10:x
4x = 30
x=\(\large{\frac{15}{2}}\)
4:5 = 10:y
4y = 50
y = \(\large{\frac{25}{2}}\)
a = 10-4
=6
b = x-3
= \(\large{\frac{15}{2}}\)-3
= \(\large{\frac{9}{2}}\)

∴ 相似な三角形は「3組の辺の比が全て等しい」ので
| \(\large{\frac{10}{4}}\) | = | \(\large{\frac{x}{3}}\) |
| 4x | = | 30 |
| x | = | \(\large{\frac{15}{2}}\) |
| \(\large{\frac{10}{4}}\) | = | \(\large{\frac{y}{5}}\) |
| 4y | = | 50 |
| y | = | \(\large{\frac{25}{2}}\) |
この手の問題を解くときに、毎回ワンパターンな「三角形の相似の証明」をするのは面倒ですね!
そして今、「数値」ではなく「文字」で証明しましたので
→ 証明したものでよく使うものは
→ 「定理」に昇格ということで・・・
平行線と線分の比 (仮定理)
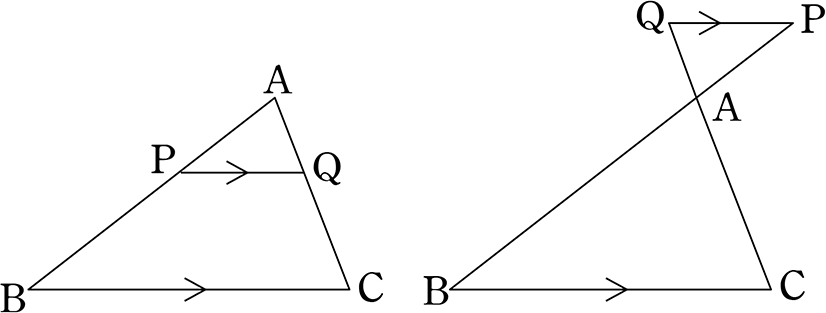
| ① PQ//BC | AP:AB = AQ:AC など (  型) ←造語です 型) ←造語です |
|
| ② PQ//BC | AP:AB = PQ:BC
AQ:AC = QP:CB |
| ③ PQ//BC | AP:PB = AQ:QC など (  型) 型) |
「対応している辺」の順番を間違わなければ
AP:PQ = AB:BC
\(\large{\frac{AP}{AQ}}\) = \(\large{\frac{AB}{AC}}\)
等々何でもOKでしたね!(「相似」なら何でもOK」)
〇:〇 = △:△「これ対これは、これ対これ」
〇:△ = 〇:△「これ対これは、これ対これ」
\(\large{\frac{\color{red}{〇}}{〇}}\) = \(\large{\frac{\color{red}{△}}{△}}\)「これにつきこれは、これにつきこれ」
\(\large{\frac{△}{〇}}\) = \(\large{\frac{\color{red}{△}}{\color{red}{〇}}}\)「これにつきこれは、これにつきこれ」
と鉛筆で何度もなぞってみてくださいね!
そして、この形( )と この形(
)と この形( )は今後相似の応用問題を解くための「 カギ」となりますので
)は今後相似の応用問題を解くための「 カギ」となりますので
親子中学では
この形 を「山型」や「山」
を「山型」や「山」
この形 を「
を「
・「
③の  型はまだ証明していませんね
型はまだ証明していませんね
| PQ//BC | AP:PB = AQ:QC (  型) 型) |

(証明)
ACに平行な(補助線)PRをひく
△APQと△PBRにおいて
∠PAQ = ∠BPR (平行線の同位角)
∠APQ = ∠PBR (平行線の同位角)
∴ 2組の角 がそれぞれ等しいので △APQ∽△PBR
→ AP:PB = AQ:PR だ …①
また、四角形PRCQは平行四辺形(2組の対辺がそれぞれ平行)より
→ PR = QC …②
①②より、(①のPRをQCに置き換えて)
| PQ//BC | AP:PB = AQ:QC (  型) ですね! 型) ですね! |

「山」「蝶」は兄弟!
《 例 》
x, y の値を求めましょう
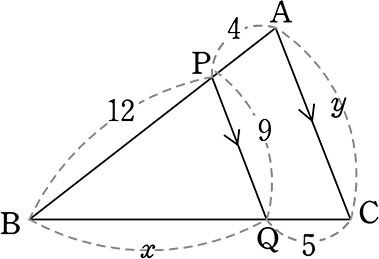
→ PQ//AC より
↑一言ですむ、(相似の証明が不要) 楽ですね!
12:4 = x:5
4x = 60
∴ x =15
12:9 = (12+4):y
12y = 144
∴ y = 12
( yを求めるときによくある間違いが)
12:9 = 4:y
ですね →  型と
型と  型を混同してしまっていますね
型を混同してしまっていますね
あくまで根本は 「2つの三角形の相似」ということを忘れないように!ですね
平行線で区切られた線分の比
《 例 》
AD//BCな台形ABCDに、BCに平行なPQを引いたとき
AP:PB = DQ:QC であることを証明しましょう
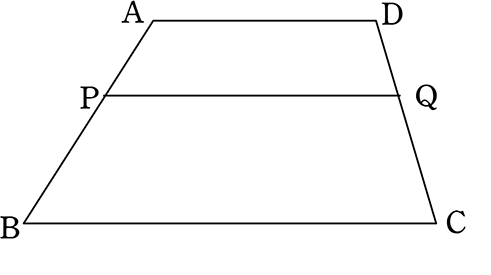
(証明)
AからDCと平行な直線をひき、PQ、BCとの交点をR、Sとすると
PR//BSより AP:PB = AR:RS …①
四角形ARQDと四角形RSCQは
「2組の対辺がそれぞれ平行」なので平行四辺形
よって
AR = DQ、 RS = QC …②
①②より
AP:PB = DQ:QC //
平行線で区切られた線分の比の定理
「平行線と比の定理」の 型と
型と 型は、台形のようなものにも応用できますね!
型は、台形のようなものにも応用できますね!
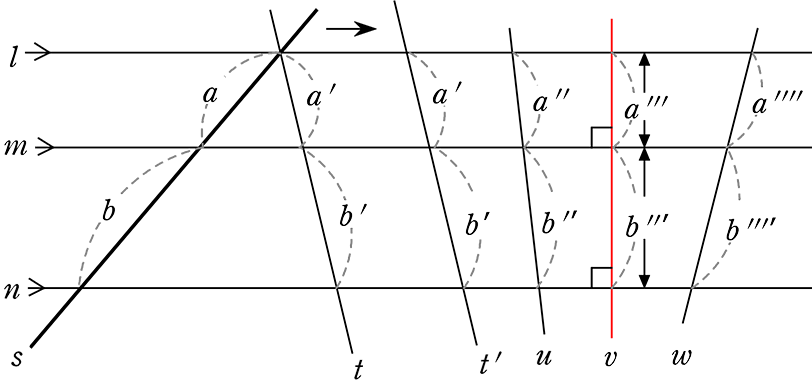
直線 t を平行移動させた t’ も、
当然 a’:b’ ですね! (t と t’ の間の空間は平行四辺形)
実は、3本の平行線(に交わる直線の「比」は、全てa:b!
a:b = a’:b’ = a’’:b’’ = a’’’:b’’’ = a’’’’:b’’’’
| ⇒ | 複数平行線に交わる直線の間の比は 傾きに関わらず「すべて同じ」 |

平行線で区切られた線分の比
3本の平行線に交わる直線では 型 a:(a+b) = a’:(a’+b’)
型 a:(a+b) = a’:(a’+b’)  型 a:b =a’:b’
型 a:b =a’:b’
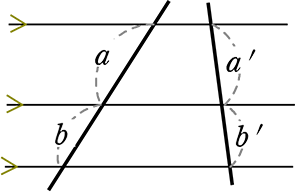
もちろん
\(\large{\frac{a}{b}}\) = \(\large{\frac{a’}{b’}}\) でも\(\large{\frac{b}{a}}\) = \(\large{\frac{b’}{a’}}\) でも \(\large{\frac{a}{a+b}}\)= \(\large{\frac{a’}{(a’+b’)}}\) でも \(\large{\frac{a}{a’}}\) =\(\large{\frac{b}{b’}}\)
など 何でもOKですね
《 例 》
xの値を求めましょう
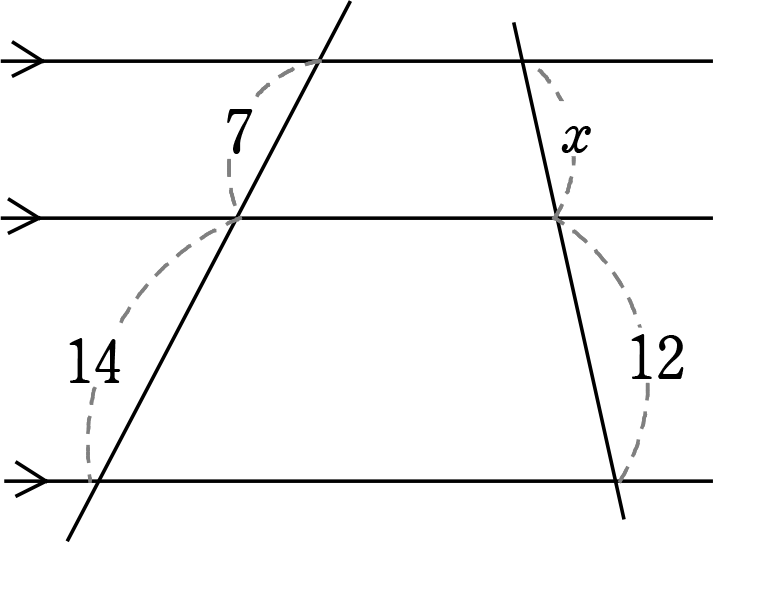
7:14 = x:12
14x = 84
x =6
\(\large{\frac{7}{14}}\) = \(\large{\frac{x}{12}}\)
\(\large{\frac{1}{2}}\) = \(\large{\frac{x}{12}}\)
2x = 12
x = 6
《 例 》
x の値を求めましょう
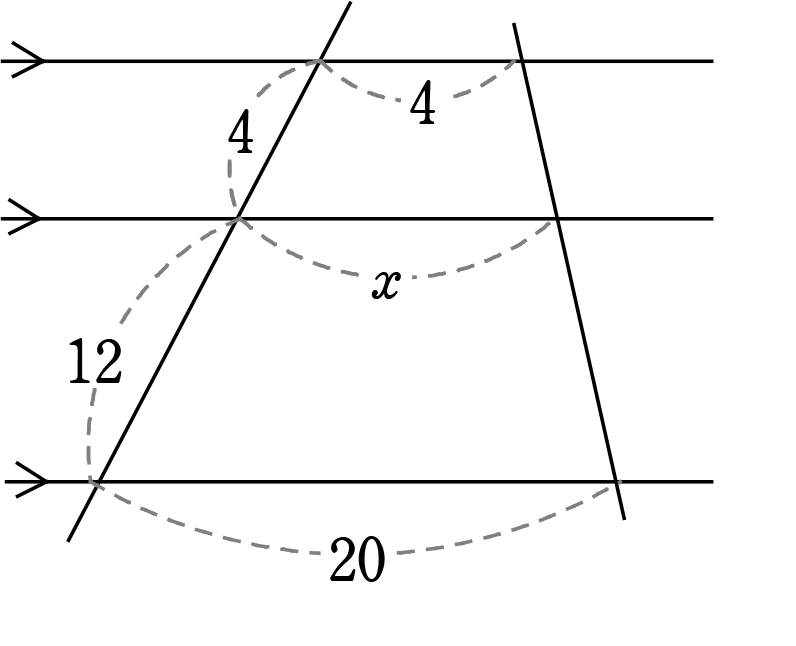
4:x = 16:20 → 16x = 80 → x = 5ダメですね!
→ 「平行線で区切られた線分の比の定理」に  型はなかったですね!
型はなかったですね! 型と
型と 型だけでしたね!
型だけでしたね!
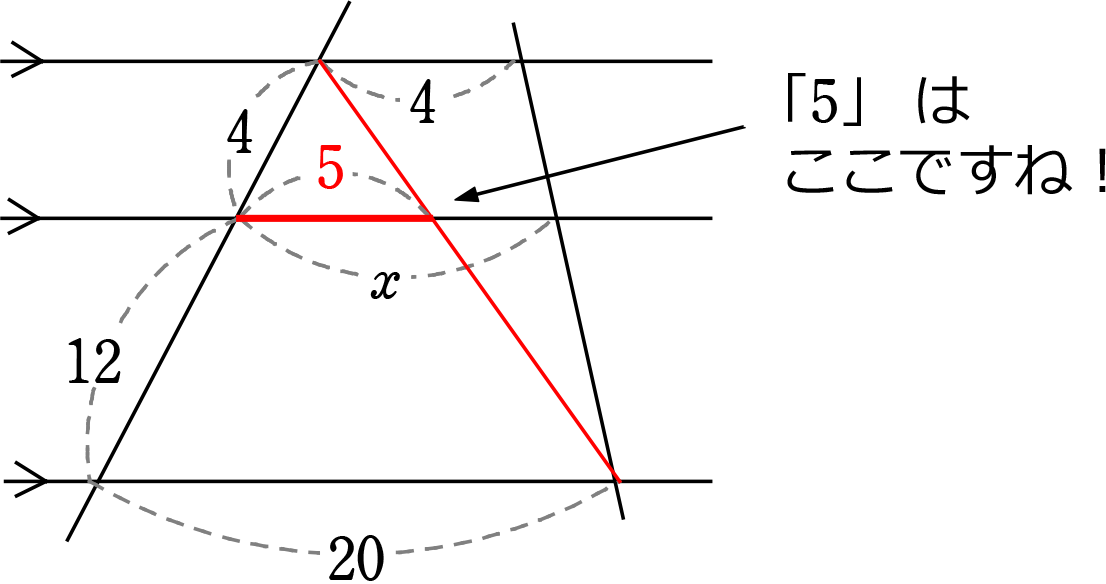
 型OKなのは「三角形」
型OKなのは「三角形」
のときだけですね!
ということは
〇や□や△で囲んだ数字は
実数値ではなく「比」
を表します
(→実数値との混同防止)
もちろん
④:⑫ → ①:③にしてもOKです
yを求めればよいということですね
| ⑫:y | = | (⑫+④):4 |
| 16y | = | 48 |
| y | = | 3 |
∴ x = 5+y = 5+3 =8
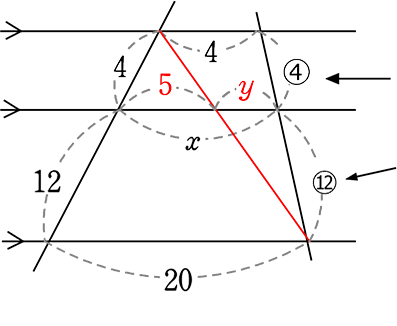
どうして、 型と
型と  型は三角形でなくても使えるの?
型は三角形でなくても使えるの?
| → |  型、 型、 型は「横線」を使いませんので 型は「横線」を使いませんので
|
| ⇒ |  型、 型、 型は 「三角形」にも「平行線」にも使える 型は 「三角形」にも「平行線」にも使える |
《 例 》
x の値を求めましょう
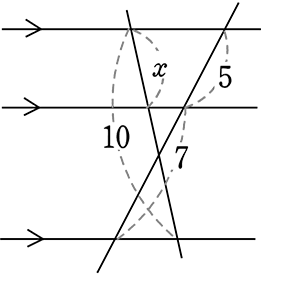
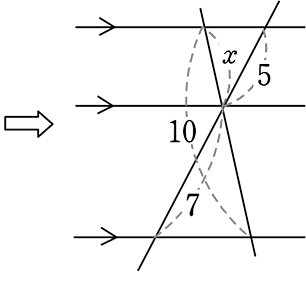
| x:10 | = | 5:(5+7) |
| 12x | = | 50 |
| x | = | \(\large{\frac{25}{6}}\) |
① 線分の比と平行線 (平行線と線分の比の逆)
上の「平行線と線分の比の定理」の逆も成り立てば、もっと鋭い武器になりますね!
すなわち、「ここと、ここの比が同じならば、2直線は平行である!」と言いたいですね!
「~ならば、~である」の逆、「~であるならば、~である」は当然には成立しませんでしたね(仮定と結論)
証明ができて初めて、矢印(⇒)が双方向矢印(⇔)になるのでしたね!
平行線と線分の比の逆の証明
| ① PQ//BC | AP:AB = AQ:AC (  型 ) 型 ) |
の逆
AP:AB = AQ:AC (  型) 型) | PQ//BC |
は成り立つのでしょうか?
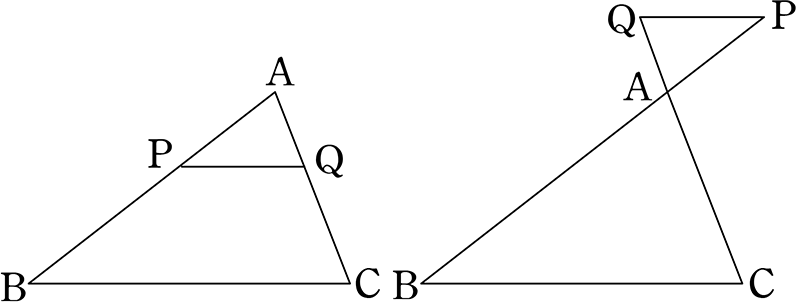
(証明)
△APQと△ABCにおいて
・∠A = ∠A (共通) (右図は対頂角)
・AP:AB = AQ:AC (仮定より)
∴ 2組の辺の比 と その間の角がそれぞれ等しいので
△APQ∽△ABC
ここまで相似の証明
∴ ∠APQ = ∠ABC
∴ 同位角 (右図は錯角)が等しいので PQ//BC
平行であるという証明
∴ AP:AB = AQ:AC (  型) 型) | PQ//BC |
証明ができましたので
| ① PQ//BC | AP:AB = AQ:AC (  型) 型) |
↑両矢印になりましたね!
次は先に③  型に行きますね
型に行きますね
| ③ PQ//BC | AP:PB = AQ:QC (  型 ) 型 ) |
の逆
AP:PB = AQ:QC (  型) 型) | PQ//BC |
は成り立つのでしょうか?
(証明)
点Cを通りBAに平行な直線とPQの延⾧との交点をRとする
△APQと△CRQにおいて
・∠AQP = ∠CQR (対頂角)
・∠APQ = ∠CRQ (平行線の錯角)
∴ 2組の角がそれぞれ等しいので
△APQ∽△CRQ
よって、 AP:CR = AQ:CQ といえる
また、仮定より AP:PB = AQ:QC であるので
AP:PB = AP:CR
よって PB = CR
∴ 四角形PBCR「1組の辺が平行で等しい」ので平行四辺形
∴ PQ//BC
∴ AP:PB = AQ:QC (  型) 型) | PQ//BC |
証明ができましたので
| ③ PQ//BC | AP:PB =AQ:QC (  型 ) 型 ) |
↑両矢印になりましたね!
L型の逆は成立しない
最後に
| ② PQ//BC | AP:AB = PQ:BCや
AQ:AC = PQ:BC ( |
の逆
AP:AB = PQ:BC (  型) 型)
(AQ:AC = PQ:BC ( | PQ//BC |
は成り立つのでしょうか?
研究
(証明) △APQと△ABC
・∠A = ∠A (共通)
| ・ | AQ側の比がない → 「2組の辺の比 と その間の角が」使えない |
→ 相似の証明できない
2組の比が解っている「間の角」∠APQで同様に行うと…
∠APQ = ∠ABC が言えない
(↑PQ//BCという前提がないので同位角が等しいと言えない)
→ 相似と証明できない
(証明2)
△APQ∽△CRQは  型同様、OK
型同様、OK
あとは、四角形PBCRが「平行四辺形」である につなげたい
| → | PB//CR は〇マル しかし PB= CR がどうしても証明できない |
→ 平行四辺形と証明できない
逆を言えば、  型の比が同じなのに「平行ではない場合」があるということですね!
型の比が同じなのに「平行ではない場合」があるということですね!
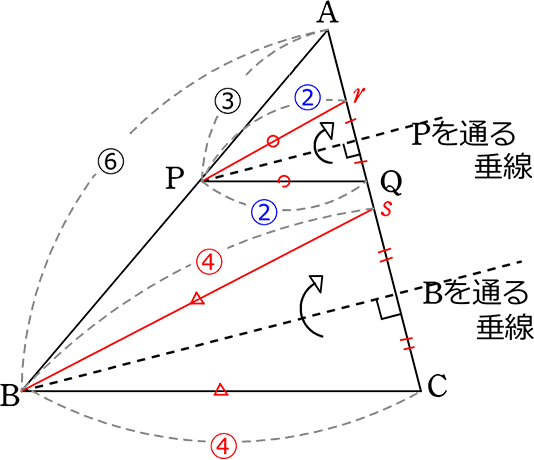
PQとBCをそれぞれ垂線で線対称に折り返すと
△PQr も △BCsも二等辺三角形 (頂角の二等分線が底辺の垂直二等分線)
→ PQ = Pr
BC = Bs
∴ AP:PQ も AP:Pr も → 3:2
AB:BC も AB:Bs も → 6:4
ということは
Pr、Bsの組合せ → 平行
Pr、BCの組合せ → 平行ではない
PQ、Bsの組合せ → 平行ではない
PQ、BCの組合せ → 平行
| ⇒ |  型のときは、必ずしも平行ではない ということですね 型のときは、必ずしも平行ではない ということですね |
② AP:AB = PQ:BC ( 型) 型) | PQ//BC |
は成立しない「
但し、△ABCが「直角三角形の場合」は  型もOKです!
型もOKです!
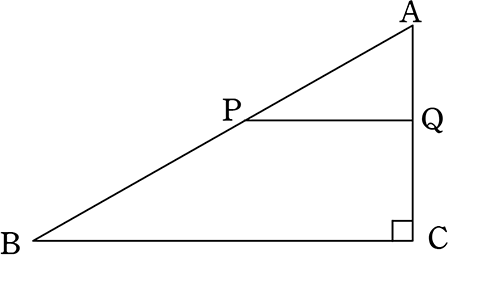
AP:AB = PQ:BC より
「2組の辺の比 がそれぞれ等しい」ので
(↑直角三角形の相似条件)
△APQ∽△ABC → ∠Qも90°
同位角が等しいので PQ//BC
(1つ前の図の Pr や Bsのような直線がない! 折り返せる部分がない)
 (まとめ)
(まとめ)
平行線と線分の比 の定理

| ① PQ//BC ⇔ | AP:AB =AQ:AC
(AP:AQ=AB:AC) ( |
| ② PQ//BC ⇒ | AP:AB = PQ:BC (AQ:AC = PQ:BC)
AP:PQ = AB:BC (AQ:QP = AC:CB) ( |
| ③ PQ//BC ⇔ | AP:PB = AQ:QC
(AP:AQ = PB:QC) ( |
指で辺を何回もなぞってくださいね! (文字より場所で理解)
まとめのまとめ
| // | ⇒  、 、  、 、  |
 、 、  | ⇒ // |
平行線で区切られた線分の比 の定理
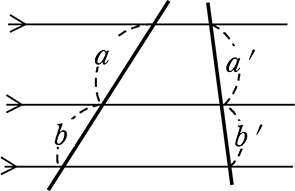
| ① 3本が平行 ⇔ | a:(a+b) = a’:(a’+b’) ( 型 ) 型 ) |
| ③ 3本が平行 ⇔ | a:b = a’:b’
a:a’ = b:b ’ ( |
| ● | 三角形になっていない場合(平行線の場合)、  型は双方向成立しない 型は双方向成立しない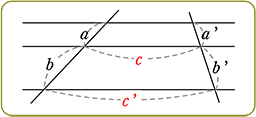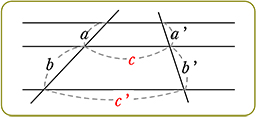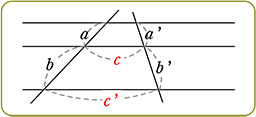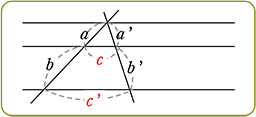 a:b 系の比は一定ですが、〇:c 系の比は一定ではないですね |
まとめのまとめ
三角形でない場合は
 、
、
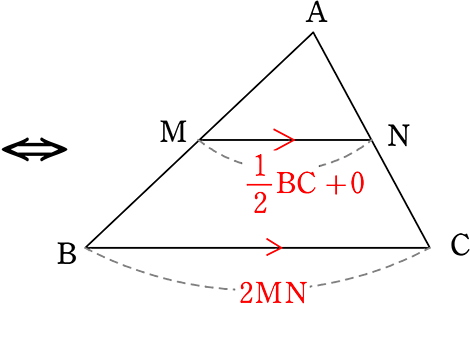
② 中点連結定理
「中点連結定理」 カッコイイ名前の定理ですね!
結論から言いますと…

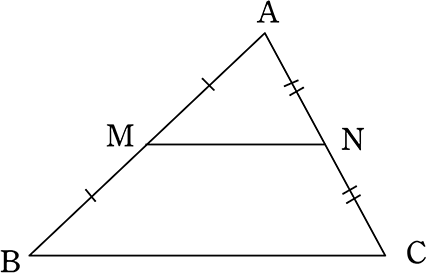
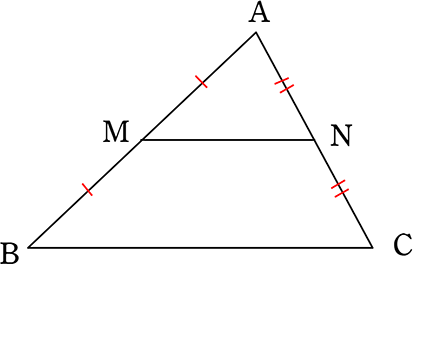
中点連結定理
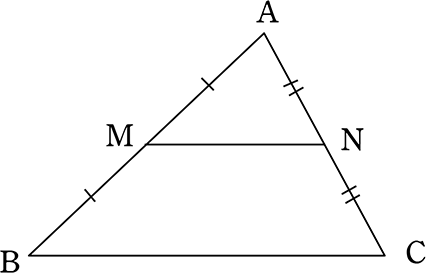
| M, Nがそれぞれ中点 | MN//BC かつ MN = \(\boldsymbol{\large{\frac{1}{2}}}\)BC |
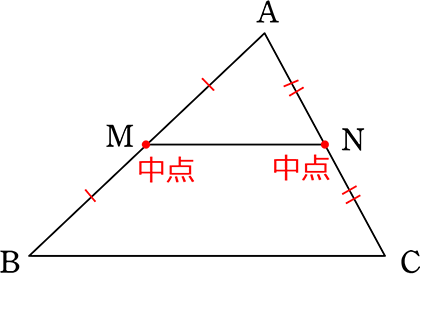
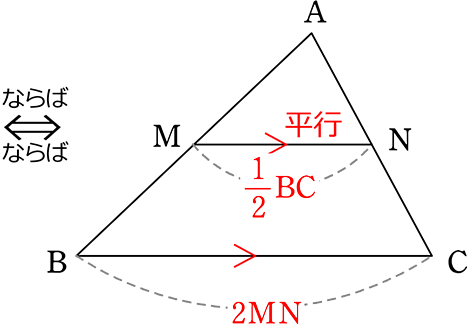
ですね
「中点連結定理」を証明せよ という問題は、定期テスト以外では出ないと思いますが、
念のため (「道具・武器」の「原理(証明)」は知っていて損はないですね!) 証明しますね
【 中点連結定理の証明 】
| M, Nがそれぞれ中点 | MN//BC かつ MN = \(\large{\frac{1}{2}}\)BC |

(証明)
△AMNと△ABCおいて
・∠A = ∠A (共通)
・AM:AB = AN:AC = 1:2 (仮定より)
∴ 2組の辺の比 と その間の角がそれぞれ等しいので
△AMN∽△ABC
∴ ∠AMN = ∠ABCより、2直線の同位角が等しいので MN//BC
相似比が 1:2 より、
MN = \(\large{\frac{1}{2}}\)BC、
【 中点連結定理の逆の証明 】
| MN//BC かつ MN=\(\large{\frac{1}{2}}\)BC | M, Nはそれぞれ中点 |
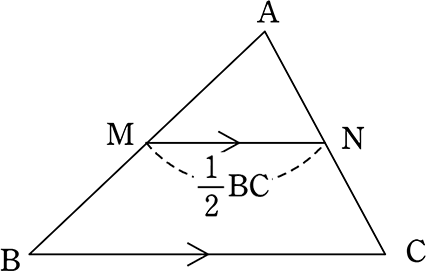
(証明)
△AMNと△ABCにおいて
・∠A = ∠A (共通)
・∠AMN = ∠ABC (平行線の同位角)
∴ 2組の角がそれぞれ等しいので
△AMN∽△ABC
MN = \(\large{\frac{1}{2}}\)BCより、
△AMNと△ABCの相似比は1:2
∴ AM:AB = AN:AC = 1:2
∴ (AM:MB = AN:AC = 1:1より) M、Nはそれぞれ中点である //
《 例 》
四角形ABCDのそれぞれの辺の中点を結んだ四角形PQRSはどのような四角形でしょう
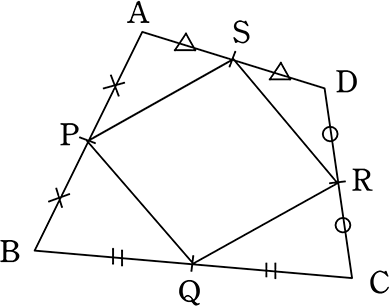
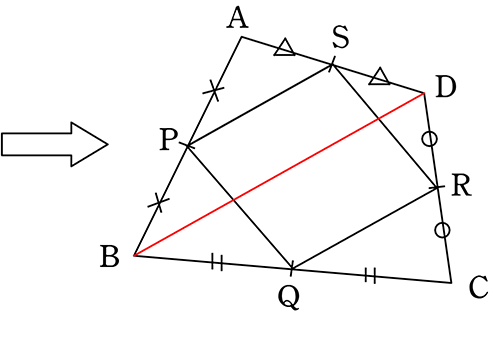
(証明)
対角線BDを引く (ACでも同様にできますね)
△APSと△ABDにおいて
点P、Sは辺AB、辺ADの中点より
↑一言で済む(相似の証明不要)、「中点連結定理より」でも可
PS//BD PS = \(\large{\frac{1}{2}}\)BD …①
同様に △CQRと△CBDにおいて
↑同じ作業の場合は 「同様に」+「結論」でOK
QR//BD QR = \(\large{\frac{1}{2}}\)BD …②
①②より PS//QR PS = QR
∴ 四角形PQRSは「1組の辺が平行で等しい」ので平行四辺形 //
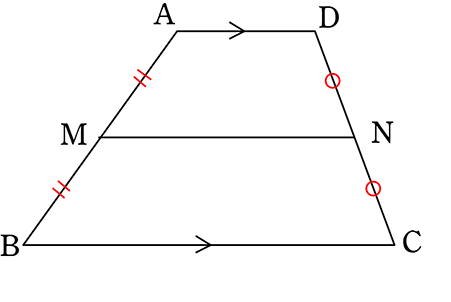
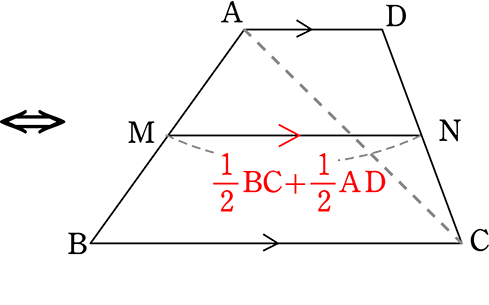
中点連結定理の台形への応用
「中点連結定理」は台形(2辺が平行)のような図形にも応用がききますね!
《 例 》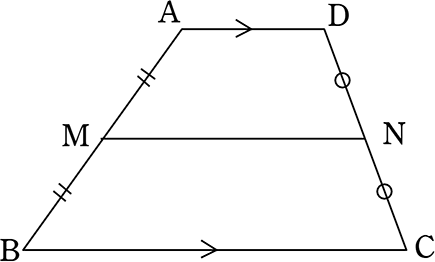
台形ABCDにおいて、中点を結んだMNはどのような性質があるでしょうか
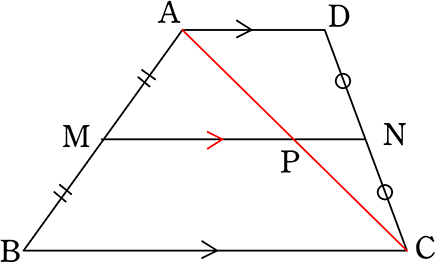
AD//BC、 AM:MB = DN:NC = 1:1より AD//BC//MN
対角線ACを引くと AM:MB = DN:NC = AP:PC = 1:1
中点連結定理より
MP = \(\large{\frac{1}{2}}\)BC
NP = \(\large{\frac{1}{2}}\)AD
∴ MN = MP+NP = \(\large{\frac{1}{2}}\)BC+\(\large{\frac{1}{2}}\)AD = \(\large{\frac{1}{2}}\)(AD+BC)
よって
| M, Nがそれぞれ中点 | MN//BC かつ MN=\(\large{\frac{1}{2}}\)(AD+BC) |
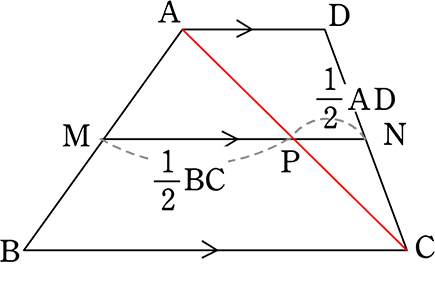 → = \(\large{\frac{1}{2}}\)BC+\(\large{\frac{1}{2}}\)AD =\(\large{\frac{1}{2}}\)(AD+BC)
→ = \(\large{\frac{1}{2}}\)BC+\(\large{\frac{1}{2}}\)AD =\(\large{\frac{1}{2}}\)(AD+BC)
同様に逆も真ですが、逆は利用場面が少く、同様の証明ですので省きますね
MN//BC かつ MN=\(\large{\frac{1}{2}}\)(AD+BC)
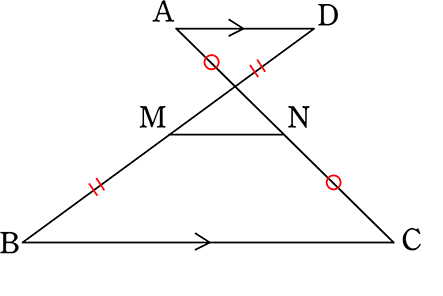
《 例 》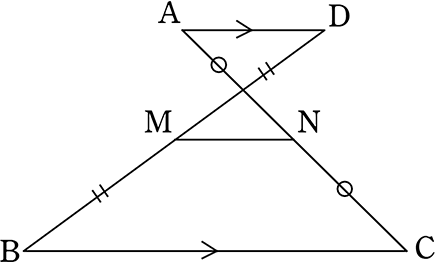
M、Nがそれぞれ中点
であることを証明しましょう
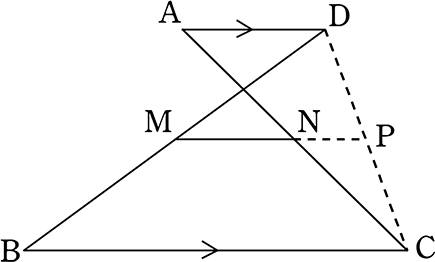
(証明)
図のような補助線や点をとる
中点連結定理より
・MP=\(\large{\frac{1}{2}}\)BC かつ BC//MP
・NP=\(\large{\frac{1}{2}}\)AD かつ AD//NP
| ∴ MN | = | MP-NP |
| = | \(\large{\frac{1}{2}}\)BC-\(\large{\frac{1}{2}}\)AD | |
| = | \(\large{\frac{1}{2}}\)(BC-AD) |
よって
M, Nがそれぞれ中点
→ 逆も同様に成り立ちます
cf
このように考えると、本来の「中点連結定理」でのMNは
MN = \(\large{\frac{1}{2}}\)(BC±0) = \(\large{\frac{1}{2}}\)BC
↑台形の「上底」がない
とも考えることができますね!
 (まとめ)
(まとめ)
中点連結定理の台形への応用
| M, Nが各々中点 | MN//BC かつ MN = \(\large{\frac{1}{2}}\)BC |
| M, Nが各々中点 | MN//BC//AD かつ MN = \(\large{\frac{1}{2}}\)(BC+AD) |
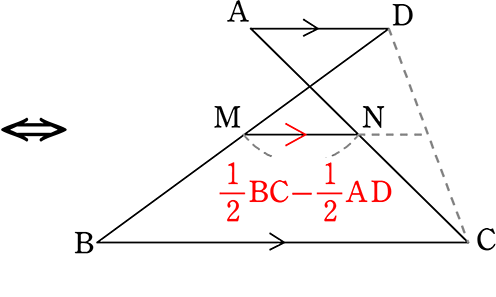
| M, Nが各々中点 | MN//BC//AD かつ MN = \(\large{\frac{1}{2}}\)(BC-AD) |
補助線をひけば当たり前と感じますね!!
③ 角の二等分線と辺の比の定理
こちらも結論から

角の二等分線と辺の比の定理
① 内角の二等分線と辺の比

a:b = a:b
(AB:AC = BD:CD)
(∠Aの「内角」の二等分線は、対辺をAB:ACに内分する)
② 外角の二等分線と辺の比
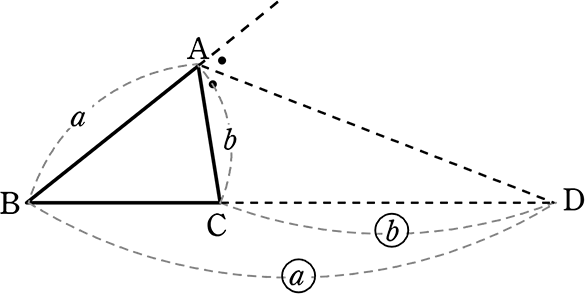
a:b = a:b
(AB:AC = BD:CD)
(∠Aの「外角」の二等分線は、対辺をAB:ACに外分する)
cf. 内分・外分のイメージ
「内分する」は、イメージが普通にできますね
ex)
● ABを 5:1 に内分する点p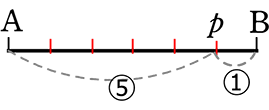
| → | ABを6等分←5+1して、A ←始点から5でp、pから1でB |
● 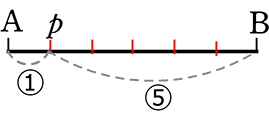
| → | ABを6等分←5+1して、B ←始点から5でp、pから1でA |
「外分する」は、少しイメージしにくいですね
ex)
● ABを 5:1 に外分する点p
| → | ABを4等分←5-1して、A ←始点から5でp、pから1でB |
● ABを 1:5 に外分するp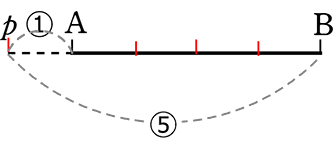
| → | ABを4等分←5-1して、A ←始点から1でp、pから5でB
(Aから右に①、左に⑤ではBにたどり着けない |
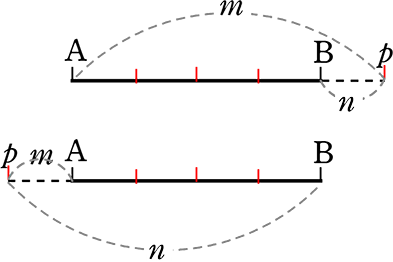
m:n → m>n なら Bの外
m:n → m<n なら Aの外
《 例 》
図のようにOが△ABCの内心であるとき、AO:ODを求めましょう
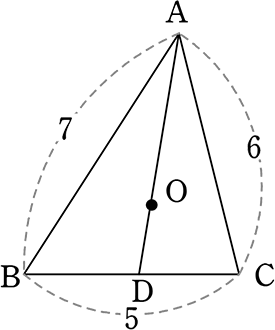
内心ということは → ADは∠Aの二等分線
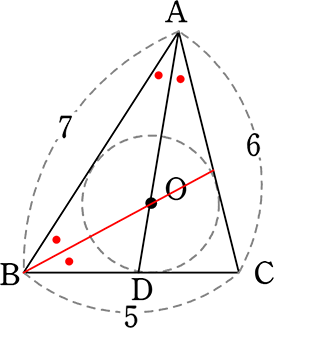
BOを引くと、BOも(∠Bの)二等分線
→「角の二等分線と辺の比」より、
AO:OD = BA:BD
(→ BAは7、あとBDを求めればよいのだな)
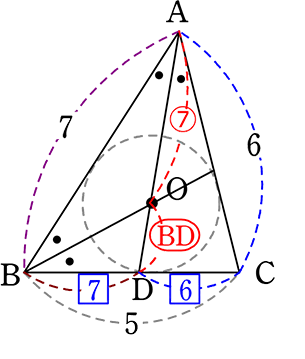
「角の二等分線と辺の比」より
BD:DC = 7:6
∴ BD = 5×\(\large{\frac{7}{13}}\)
↑「5」を13コに分けたうちの7コ
= \(\large{\frac{35}{13}}\) ←実数値
∴ AO:OD = BA:BD = 7:\(\large{\frac{35}{13}}\) = 91:35 = 13:5 //
《 例 》
図のようなとき、PQを求めましょう

→ PQ = PC+CQ
→ PCは「角の二等分線と辺の比」の「内分」の方だな
→ CQは「角の二等分線と辺の比」の「外分」の方だな
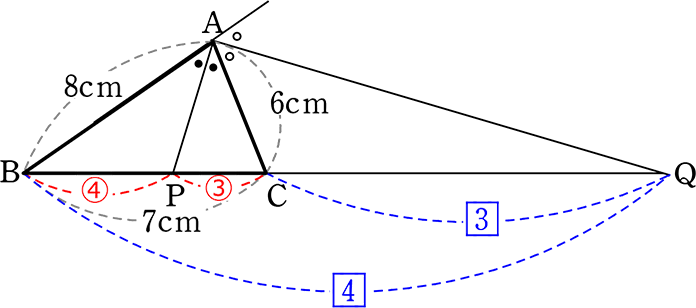
PC = 7cm×\(\large{\frac{③}{④+③}}\) = 3 cm
CQは?
→ BC:CQは 4-3:3 = 1:3
→ 7cm:CQ = 1:3
CQ = 21 cm
∴ PQ = PC+CQ = 3+21 = 24 cm //
角の二等分線と辺の比の証明(内角の場合)
余談ですが、念のため、「角の二等分線と辺の比」の証明をしておきますね!
〔 内角の場合 〕
(内角の) 二等分線
(証明)
① CからADと平行な線と
BAの延長との交点をEとする
② △BADと△BECにおいて
∠B = ∠B (共通)
∠BAD = ∠BEC (同位角)
「2組の角 がそれぞれ等しい」ので
△BAD∽△BEC
∴ a:AE = a:b…(1)
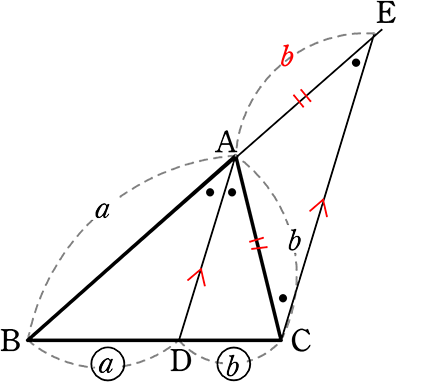
③ ∠DAC = ∠ACE (錯角)
∴ ∠BAD = ∠DAC = ∠AEC = ∠ACE
∴ △ACEは2角が等しいので二等辺三角形
∴ AC = AE = b …(2)
(1)(2)より
a:b = a:b //
角の二等分線と辺の比の証明(外角の場合)
〔外角の場合〕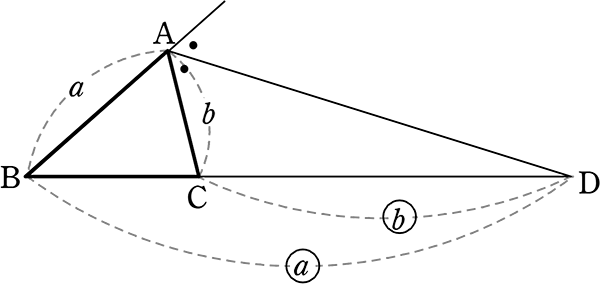
(外角の) 二等分線
(証明)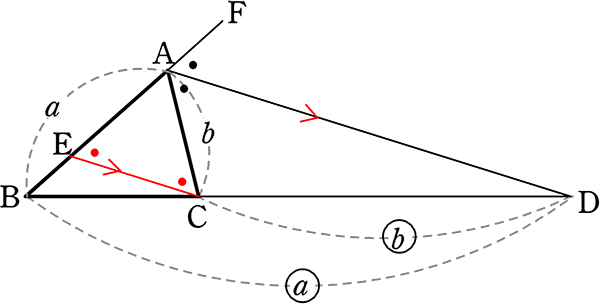
CからDAに平行な線と、ABとの交点をEとする
(後は内角の場合と同じですね)
∠B (共通)
∠BCE = ∠BDA (同位角)
∴ 2角が等しいので △BCE∽△BDA
∴ a:EA = a:b
∠DAC = ∠ACE (錯角)
∠FAD = ∠AEC (同位角)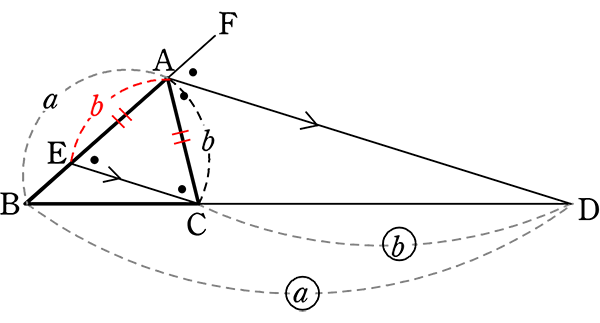
∴ △AECは二等辺三角形
∴ AE = AC = b
∴ a:b = a:b //
逆の証明は、ただ逆にするだけですので省略しますね!
(比が同じ → 相似 → 角度が等しい → 二等辺三角形 → 二等分線である )
エ 相似な図形の面積比と体積比
相似比と周長の関係
相似比が分かると、当然周長の比(図形の1周の長さの比)がわかりますね!
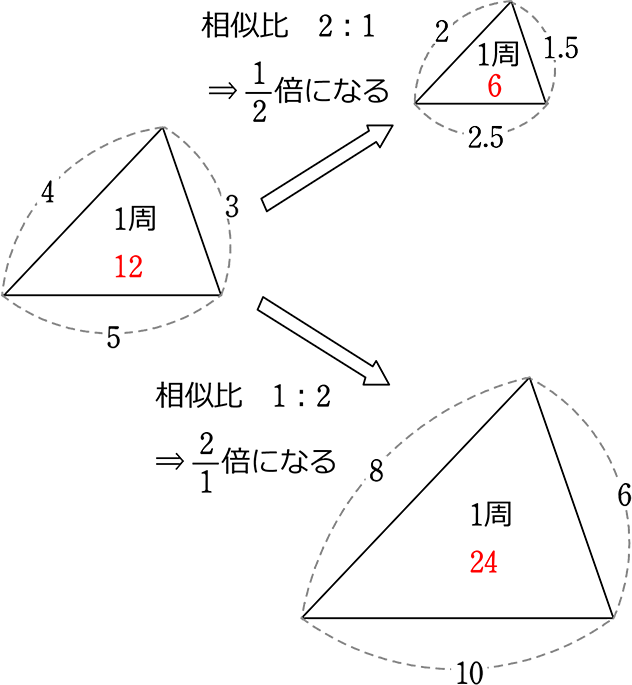
(当然であるという確認)
→ 2+1.5+2.5 = \(\large{\frac{4}{2}}\)+\(\large{\frac{3}{2}}\)+\(\large{\frac{5}{2}}\) = \(\large{\frac{1}{2}}\)(4+3+5) = \(\large{\frac{1}{2}}\)・12 = 6
→ 8+6+10 = 2・4+2・3+2・5 = 2(4+3+5) = 2(12) = 24
「相似比」とは「対応する
1周の⾧さは、そのまま「相似比」になりますね!
相似な図形の「周長比」は、相似比「そのもの」に等しい
相似比 = 周長比
・中:小 = \(\underbrace{ 2:1 }_{相似比} = \underbrace{ 12:x }_{1周比}\) → x = 6
または 12×\(\large{\frac{1}{2}}\) = 6
・中:大 = 1:2 = 12:x → x = 24
または 12×\(\large{\frac{2}{1}}\) = 24
これは、四角形であれ n角形であれ 円であれ当然同様ですね!
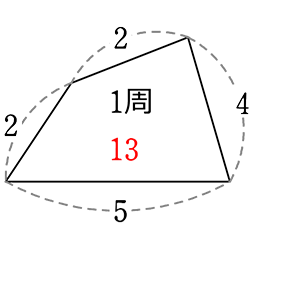
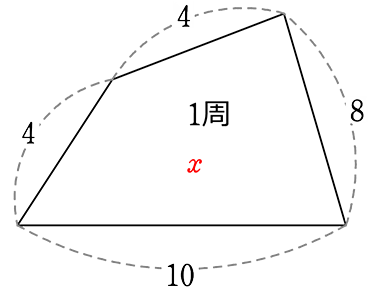
相似比 = (適当な1辺から) 1:2
大の1周 → \(\underbrace{ 1:2 }_{相似比} = \underbrace{ 13:x }_{1周比}\) → x = 26


相似比 = (半径から) 2:3
大の1周 → \(\underbrace{ 2:3 }_{相似比} = \underbrace{ 4π:x }_{1周比}\) → x = 6π
相似比と面積比の関係
「相似比」が判明すると、 「面積比」も判明しますね!
相似な図形の「面積比」は、相似比の「2乗」に等しい
原理は簡単ですね
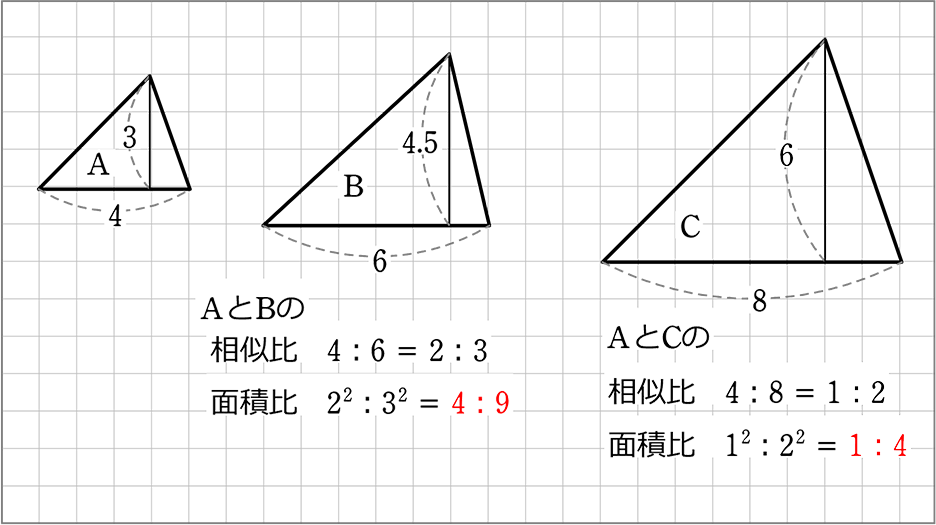
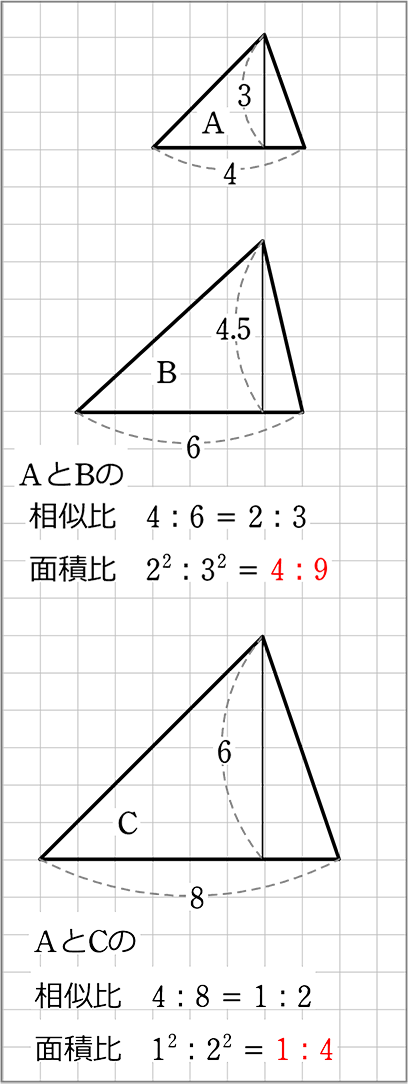
| → | 面積は、基本「底辺×高さ」、座標でいえば「縦×横」
同じ相似比を「2回使う(縦×横)」→「辺×辺」→「2乗」ですね! |
(確認)
Aの底辺:Bの底辺:Cの底辺
= 4:6:8
= 2:3:4
Aの面積:Bの面積:Cの面積
= (\(\large{\frac{1}{2}}\)・4・3):(\(\large{\frac{1}{2}}\)・6・4.5):(\(\large{\frac{1}{2}}\)・8・6)
= (4・3):(6・4.5):(8・6)
= 12:27:48
= 4:9:16 ← 22:32:42
(1辺の比の2乗 = 相似比の2乗ですね!)
問)
AとBの面積比は?
→ 相似比は 2:3
∴ 面積比は 22:32 = 4:9
問)
A,B,Cが「相似」であるが「もしBの高さがわからない」場合 Bの面積は?
→ 22:32 = (\(\large{\frac{1}{2}}\)・4・3):x
4:9 = 6:x
4x = 54
x = 13.5 ∴ Bの面積は 13.5
円でも何でも同様ですね (三角形に限らず四角形であろうが台形であろうが)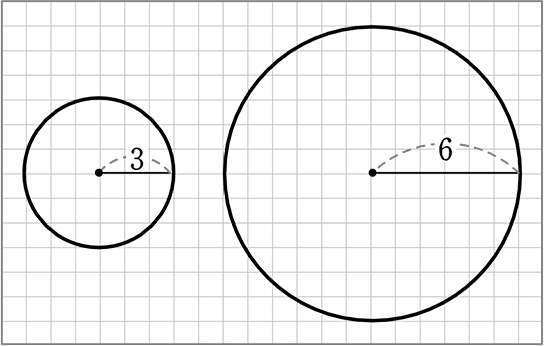
相似比は 3:6 → 1:2
ということは、面積比は 12:22 = 1:4
小の面積は 9π
大の面積は 1:4 = 9π:x → x = 36π
(Bの面積 = πr2 = 36π 確かに同じ!)
《 例 》
図形Aと図形Bの相似比が 2:5で、図形Aの面積が4のとき
図形Bの面積を求めましょう
| → | 何角形か円か図形の形が全く分かりませんが、相似比がありますね! |
→ 面積比は 22:52 = 4:25
| ∴ 4:25 | = | 4:x |
| 4x | = | 100 |
| x | = | 25 |
∴ Bの面積は 25 //
もちろん 分数で計算もOKですね
相似比 2:5 ⇒ \(\large{\frac{5}{2}}\)倍になる
↑
| ・ | 「左が分母、右が分子」でもよいですが、
忘れますので、 |
| → | 元より大きくなるなら大が分子 (分数>1) |
| → | 元より小さくなるなら大が分母 (分数<1) |
で十分ですね
面積比 \(\large{\frac{5^2}{2^2}}\) = \(\large{\frac{25}{4}}\)
x = 4×\(\large{\frac{25}{4}}\) = 25 //
《 例 》
図形Aの面積が4、図形Bの面積が144のとき、相似比は?
→ 面積比 A:B = 4:144
→ 相似比 A:B = \(\small{\sqrt{4}}\):\(\small{\sqrt{144}}\) = 2:12 = 1:6
《 例 》
一辺が8cmの正三角形ABCの面積を2等分するBCに平行なPQがあるときAPの長さを求めましょう
→ まずは図ですね

考え方は

のどちらかですね
| → | 考え方は、イ)の方が楽ですね |
| → | まず、△APQ∽△ABC (2組の角がそれぞれ等しいので) |
| → | 相似比がわかれば面積比が分かるので、△APQと△ABCの相似比は? |
APをxとすると、相似比は 『x:8』
∴ x2:82 = 1:2 ←相似比の2乗は面積比。それが 1:2
| 2x2 | = | 64 |
| x2 | = | 32 |
| x | = | ±\(\small{\sqrt{32}}\) = ±4\(\small{\sqrt{2}}\) |
x>0より A. AP = 4\(\small{\sqrt{2}}\) cm
相似比と表面積比の関係
「表面積比」も「面積比」同様「相似比」を2回使い、それらの足し合わせですので
結局、ただの面積比同様に考えてOKですね
相似な図形の「表面積比」は、相似比の「2乗」に等しい
ですね!
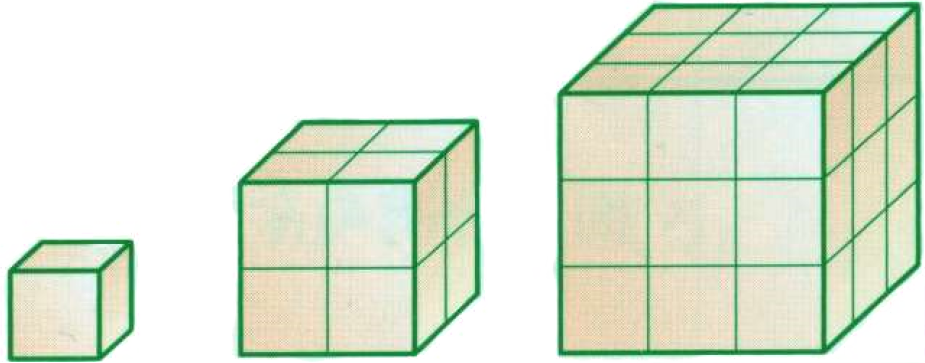
上図の1つの面に注目すれば
相似比は 1:2:3
面積比は 12:22:32 = 1:4:9
ただ、それが6面あるだけですね
1×6面:4×6面:9×6面 = 1:4:9
(↑比ですので「6面」は打ち消してよい ≒ 約分)
結局「表面積比」も「面積比」同様「2乗」ですね
《 例 》
次の2つの球の表面積比は?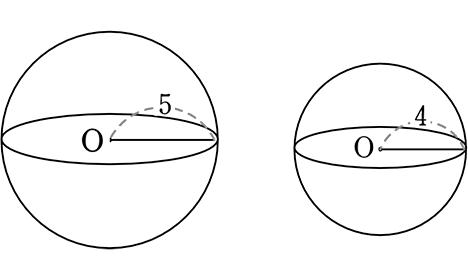
→ 相似比は、5:4
∴ 表面積比は、52:42 = 25:16
(確認)
球の表面積は、4πr2
→ 大球 = 4・π・(5)2
→ 小球 = 4・π・(4)2
∴ 4・π・(5)2:4・π・(4)2
相似比と体積比の関係
「体積比」は「相似比」を 3回 使いますね!
→ 面積は、基本「縦×横×高さ」ですね
同じ相似比を「
相似な図形の「体積比」は、相似比の「3乗」に等しい
《 例 》
2つの三角錐が相似であるとき、相似比、表面積比、体積比を求めましょう

相似比 → 2:3
表面積比 → 22:32 → 4:9
体積比 → 23:33 → 8:27
 まとめ
まとめ
相似比 と 面積比 や 体積比 の関係
| ・ | 相似な図形の「周長比」は、相似比の「そのもの」に等しい |
| ・ | 相似な図形の「面積比」は、相似比の「2乗」に等しい |
| ・ | 相似な図形の「表面積比」は、相似比の「2乗」に等しい |
| ・ | 相似な図形の「体積比」は、相似比の「3乗」に等しい |
まとめのまとめ
図形が相似なら
「線関係」 → 「そのまま相似比」
「面積関係」 → 「2乗 (平方)」
「体積関係」 → 「3乗 (立方)」
ですね
相似ではない場合の面積比・体積比、『あたるもの』の考え方
相似のメインどころといえますね!
前提となるポイントを2つほどお話させていただきますね

ポイント① 底辺、高さと面積の関係
「比」というからには、三角形が2つ以上あるはずですね
1つでは「比」較しようがないからですね!
2つの三角形の面積比は
\(\large{\frac{1}{2}}\)(正確な底辺の長さ)×(正確な高さの長さ):\(\large{\frac{1}{2}}\)(正確な底辺の長さ)×(正確な高さの長さ)
のはずですね
そして、それぞれ「2倍」して
(正確な底辺の長さ)(正確な高さの長さ):(正確な底辺の長さ)(正確な高さの長さ)
のはずですね
cf.
比はそれぞれ○倍して 0.5:1.5 → 1:3 とできましたね
| → | 比は分数と同じことなので、分母分子に同じ数をかけてもよいように、それぞれに同じ数字をかけても成り立つ でしたね |
では、「正確な面積」と「面積比」の関係について
よって、「正確な面積の数値」が無くても「高さの比」や「底辺の比」だけで
2つの三角形の「面積比」がわかるということにつながりますね!
元の面積を「S」とすれば、
| ・ | 高さが2倍( = 1:2)なら → (右図形は)2S
高さが\(\large{\frac{1}{2}}\)倍( = 2:1)なら → \(\large{\frac{1}{2}}\)S |
| ・ | 底辺が2倍( = 1:2)なら → (右図形は)2S 底辺が\(\large{\frac{1}{2}}\)倍( = 2:1)なら → \(\large{\frac{1}{2}}\)S |
ex)
| ・高さが 2:3 → | 右三角形の面積は\(\large{\frac{3}{2}}\)倍(1.5倍) → \(\large{\frac{3}{2}}\)S |
| ・底辺が 4:1 → | 右三角形の面積は\(\large{\frac{1}{4}}\)倍(0.25倍) → \(\large{\frac{1}{4}}\)S |
そして、これは「高さ」と「底辺」同時に変化しても成立します
注:正確な面積(2や6)は確認がてら見てくださいね!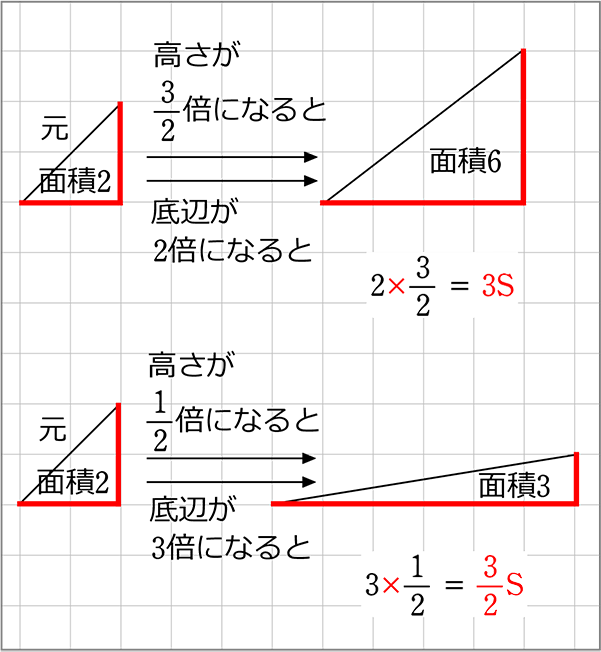
そして、実は、底辺と高さの倍率が同じとき(相似のとき)…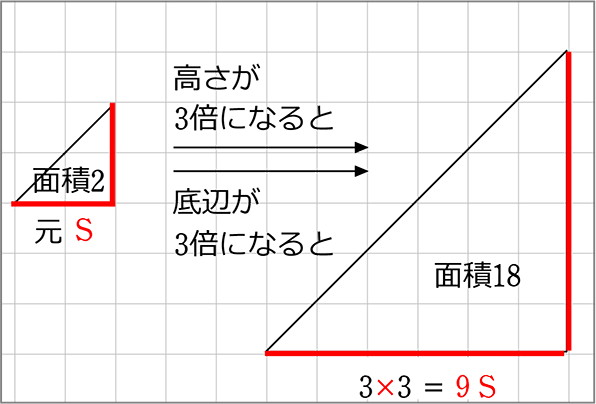
そうです、相似は
「底辺が3倍になると」「高さが3倍になると」は
「底辺が3倍になると」「高さも3倍になる」だったのですね
そして、底辺倍率×同倍率高さ = (相似比)2 = 面積比 ということになりますね!
以上を要約すると、三角形では(実は平行四辺形系(正方形・長方形・ひし形)もですね)、
| ・ | 高さが半分になれば、面積も半分になる |
| ・ | 底辺が半分になれば、面積も半分になる |
| ・ | 高さも底辺も半分になれば、\(\large{\frac{1}{2}}\)倍×\(\large{\frac{1}{2}}\)倍=\(\boldsymbol{\large{\frac{1}{4}}}\)倍になる |
言葉より、図の方が直感的に分かりやすいと思いますので、
下の問題を解いてみましょう

クリック・タップで答え (反応が遅い場合があります)

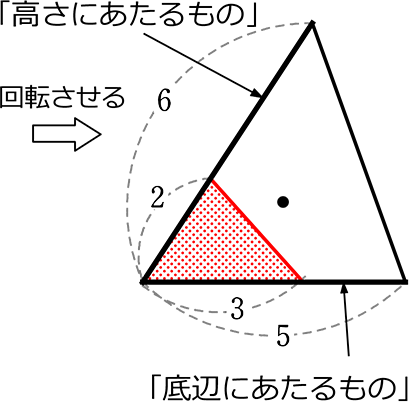
ポイント② 底辺にあたるもの、高さにあたるもので面積比
ポイント①で、「2つの三角形だけの関係においては『正確な面積の値』は不要」ということと、
「底辺と面積の関係」「高さと面積の関係」がわかりましたね
そして、ポイント②として、「高さ」「底辺」について思い出してみると…
…まずは、イメージしやすい「高さ」からいきますね
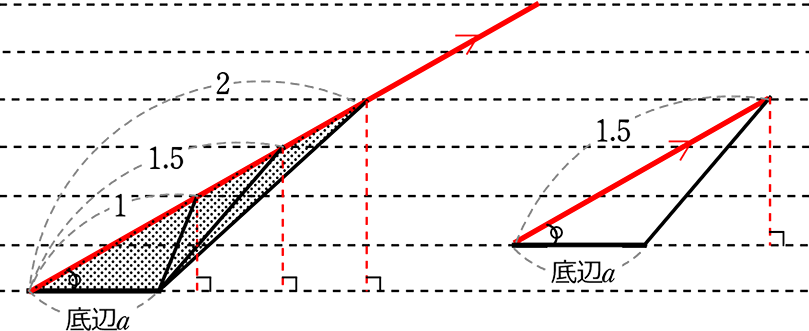
図の場合、「斜辺に見えるもの(赤線)」の長さが、
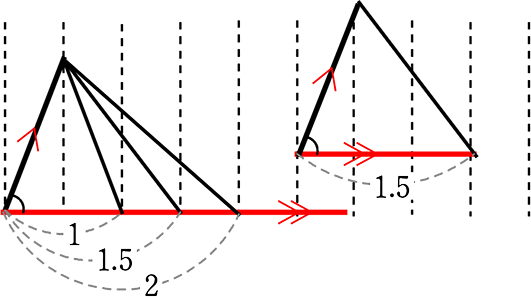
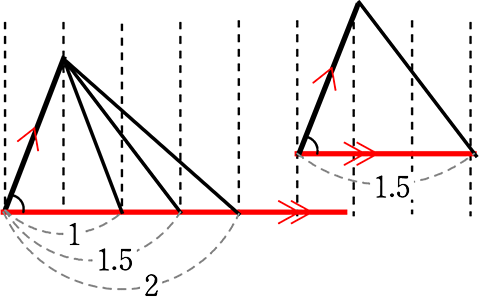
| 1.5倍になれば → | 「本高さ(赤点線)」も1.5倍になっていますね! |
| 2倍になれば → | 「本高さ」も2倍になっていますね! |
ということは、
| ① | 斜辺が一直線状(上)にある場合 (共有状態)や |
| ② | 斜辺が平行である場合 (右の図形)や |
| ③ | 斜辺と底辺の間の角度が同じ場合 |
①②③は実は同じような意味(=基準が同じ=底辺に対する斜辺の角度が同じ)
の三角形や平行四辺形系の「斜辺のような線」は
「高さ」とみなすことができますね!
親子中学ではこのような辺を…「高さにあたるもの」と言いますね!
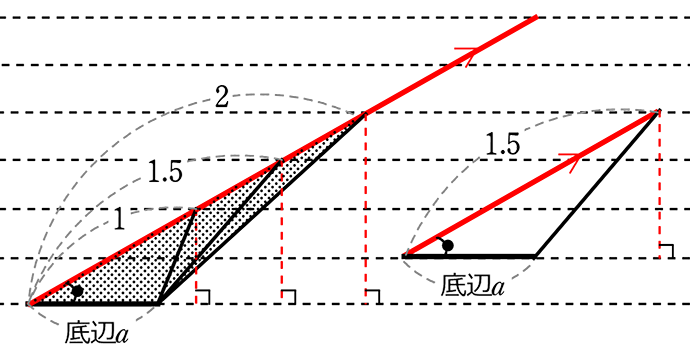
というわけで、上図の
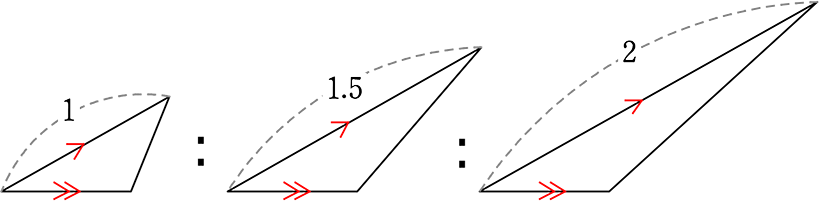
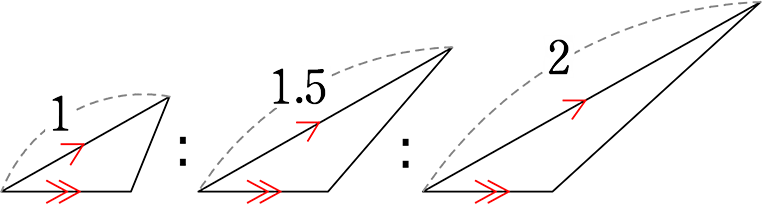
の面積比は
\(\large{\frac{1 }{2}}\)・(底辺)・(高さにあたるもの):\(\large{\frac{1}{2}}\)・(底辺)・(高さにあたるもの):\(\large{\frac{1}{2}}\)・(底辺)・(高さにあたるもの)
= (底辺)・(高さにあたるもの):(底辺)・(高さにあたるもの):(底辺)・(高さにあたるもの)
= (高さにあたるもの):(高さにあたるもの):(高さにあたるもの)
= 1:1.5:2 ですね!
(最小三角形をSとするならば → S:\(\large{\frac{3}{2}}\)S:2 S )
(最大三角形をSとするならば → \(\large{\frac{1}{2}}\)S:\(\large{\frac{3}{4}}\)S:S )
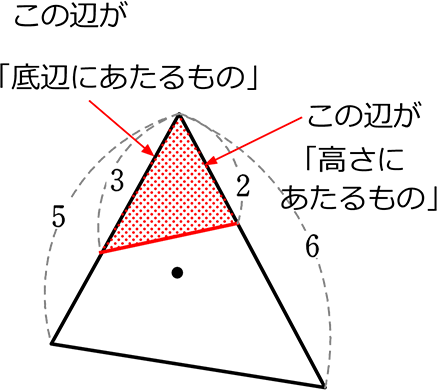
では次に、「底辺」について
「高さにあたるもの」と全く同じ考え方ができますね!
| ① | 底辺が一直線状(上)にある場合 (共有状態) |
| ② | 底辺が平行である場合 (右の図形) |
| ③ | 「高さにあたるもの」と底辺の角度が同じ場合 |
①②③は実は同じような意味(=基準が同じ)
の三角形や平行四辺形系の「底辺のような線」は
「底辺」とみなすことができますね!
親子中学ではこのような辺を…「底辺にあたるもの」と言いますね!
というわけで、上図の
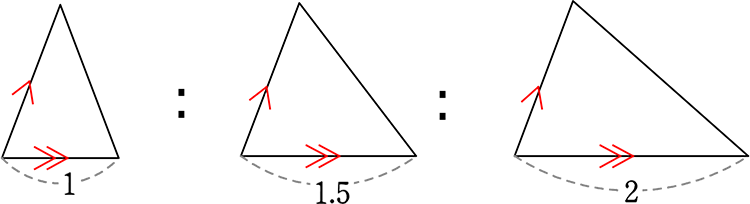
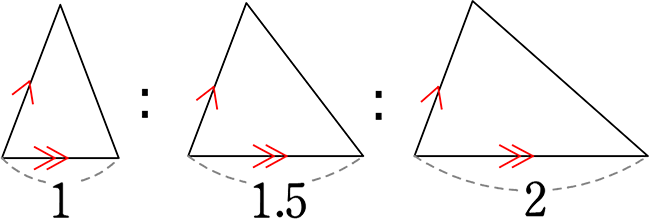
の面積比は
\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さ):\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さ):\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さ)
= (底辺にあたるもの)・(高さ):(底辺にあたるもの)・(高さ):(底辺にあたるもの)・(高さ)
= (底辺にあたるもの):(底辺にあたるもの):(底辺にあたるもの)
= 1:1.5:2 ですね!
(最小三角形をSとするならば → S:\(\large{\frac{3}{2}}\)S:2 S )
(最大三角形をSとするならば → \(\large{\frac{1}{2}}\)S:\(\large{\frac{3}{4}}\)S:S )
そして、最後に「高さにあたるもの」「底辺にあたるもの」が同時に変化しても
同様に考えることができるというこということですね!
すなわち、基準が同じ(それぞれ平行や一直線上や間の角が同じ) 場合
すなわち、相似条件②「2組の辺の比とその間の角が等しい」の「2組の辺の比だけが一定でない」ような図形の場合、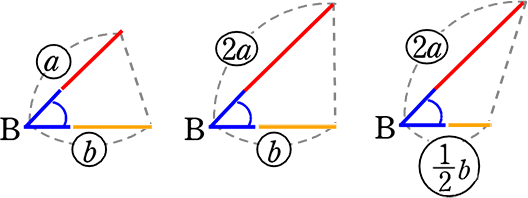
⇒ 三角形や平行四辺形系の「面積比」は
\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さにあたるもの):\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さにあたるも):\(\large{\frac{1}{2}}\)・(底辺にあたるもの)・(高さにあたるもの)
= (底辺にあたるもの)(高さにあたるもの):(底辺にあたるもの)(高さにあたるもの):(底辺にあたるもの)(高さにあたるもの)
ですね!
→ 上の3つの図の面積比は、ab:2ab:ab ですね
正確な面積の値は解りませんが、2つや3つの図形の関係においては
「正確な高さの値」や「正確な底辺の値」は不要!ということですね!
ex.
兄のお小遣い:お弟の小遣い = 2:1
| → | 一方の金額が解れば直ちに他方も解る → ですが金額はどうでもよい |
| → | よって、この金額の手前の「比2:1」まででよいのです (=関係性の問題) |
以上を要約すると、三角形 (平行四辺形系もですね!)の『面積比』は
結論
基準が同じ(平行や一直線上や間の角が同じ)場合、面積比は
(底辺にあたるもの)(高さにあたるもの):(底辺にあたるもの)(高さにあたるもの)
ということですね
《 例 》
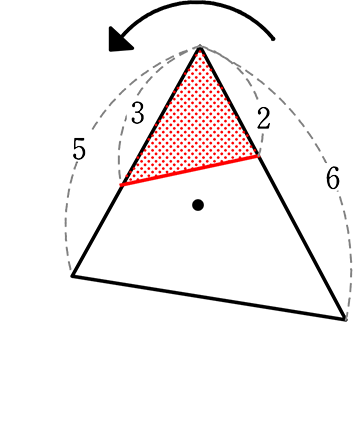
 対
対 は
は
5×6:3×2 = 30:6
= 5:1
 がSなら
がSなら は\(\large{\frac{1}{5}}\)S
は\(\large{\frac{1}{5}}\)S
回転させなくても…
と見れたら鬼金棒ですね!
もちろん「底辺にあたるもの」と「高さにあたるもの」を逆にとらえてもOKです!
《 例 》



(1)
| → | 平行なので、「高さ」は同じということですね |
(ポイント①の問題ですね)
∴ 面積比 = 底辺の比 = 4:1
赤△ = \(\large{\frac{1}{4}}\)S
(2)
| → | 「底辺にあたるもの」、「高さにあたるもの」の共有タイプですね |
→ 単位があっても同様ですね
→ 8×6:3×4 = 48:12 = 4:1
赤△ = \(\large{\frac{1}{4}}\)S
(3)
→ 1つは共有、1つは平行タイプですね
→ 12×9:5×7 = 108:35
赤△ = \(\large{\frac{35}{108}}\)
(4)
→ 両方とも平行タイプですね
→ 30:3 = 10:1
赤△ = \(\large{\frac{1}{10}}\)S
(5)
→ 間の角が同じと言うことは、
⑧と④を平行にすれば
7と6も平行ですね


→ 7×8:6×4 = 56:24 = 7:3
赤△ = \(\large{\frac{3}{7}}\)S
(6)
→ 6×4.5:4×3 = 27:12 = 9:4
赤△ = \(\large{\frac{4}{9}}\)S
→ 実は3辺が平行なので「相似」ですね!( ついでに「相似の位置」ですね)
ということは、「1辺の比(相似比)」さえ解れば「面積比」が出ましたね!
(底辺が\(\large{\frac{2}{3}}\)倍なら、自動的に高さにあたるものも\(\large{\frac{2}{3}}\)倍になる)
∴ 相似比 = 6:4 = 3:2
面積比 = 32:22 = 9:4 (上と同じですね!)
(7)
→ 直角マークは引っ掛けですね (関係ない)
→ 10×4:6×7 = 40:42 = 20:21
赤△ = \(\large{\frac{21}{20}}\)S
(8)
→ (2+4)×1:2×(1+1) = 6×1:2×2 = 6:4 = 3:2
赤△ = \(\large{\frac{2}{3}}\)S
→ 回転させなくても、「底辺にあたるもの」「高さにあたるもの」が見えましたか?
(9)
→ BC×3:BC×1 = 3:1
(↑分数の通分のように両方をBCで割った)
赤△ = \(\large{\frac{1}{3}}\)S
(10)
もう「底辺にあたるもの」「高さにあたるもの」が浮いて見えるようになってきましたね
| → | 「底辺にあたるもの」×「高さにあたるもの」:「底辺にあたるもの」「高さにあたるもの」 |
= 7×12:6×8 = 84:48 = 21:12 = 7:4
赤△ = \(\large{\frac{4}{7}}\)S
イメージしにくければ…
ひっくり返して…
高さの方をずらせばよいですね
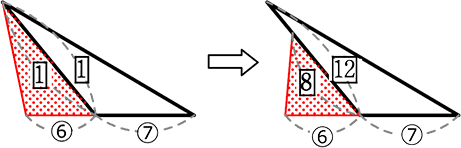
間の角度こそ違いますが、底辺あたるものに対する高さにあたるものが同じ直線上
→ 高さにあたるものの比にくるいは出ない
⑦を⑥側に持っていくと よりはっきりしますね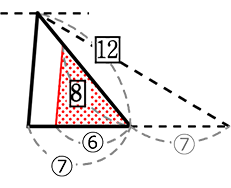
(10) 黒も平行四辺形、赤も平行四辺形です
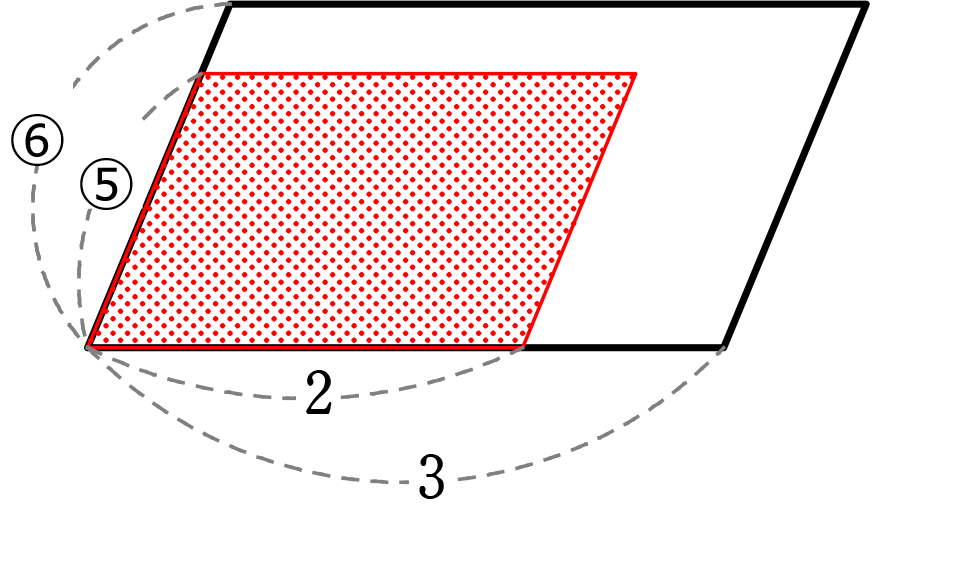
→ 平行四辺形系も同様に考えられますね
→ 3×6:2×5= 18:10 = 9:5
赤 =\(\large{\frac{5}{9}}\)S
=\(\large{\frac{5}{9}}\)S


「あたるもの」の確認
面積比を考える時、「底辺にあたるもの」「高さにあたるもの」の考え方は大切ですね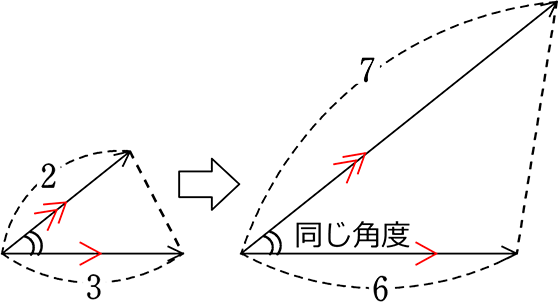
「高さにあたるもの」「底辺にあたるもの」で考えると
面積比 3×2:6×7 = 6:42 = 1:7

面積比 3×2:6×4 = 6:24 = 1:4
または、 実は相似なので
「面積比は相似比の2乗」より
面積比 32:62 = 9:36 = 1:4
(問)
下図は相似である。面積比を求めましょう


相似比 2:3 → 面積比 22:32 = 4:9 ですが
適当に「高さにあたるもの」を設定して


2×②:3×③ = 4:9 や


2×3:3×4.5 = 6:13.5 = 12:27 = 4:9 でも求めることができますね
以上より、
「高さにあたるもの」「底辺にあたるもの」の考え方は
相似でなくても、相似でも使える
「あたるもの」は「相似比の2乗は面積比」の考え方をカバーする
「高さにあたるもの」
×「底辺にあたるもの」
「相似比の2乗は面積比」
● 体積比でも同様に考えることができますね
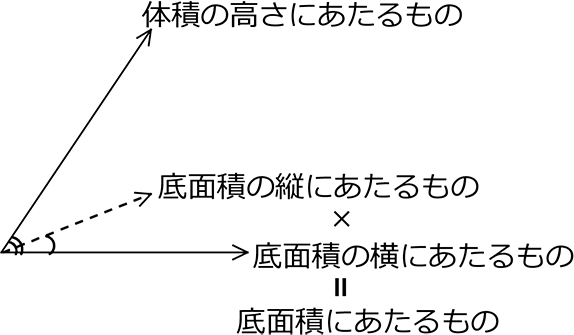
体積比は
⇒ (底面積にあたるもの)(高さにあたるもの):(底面積にあたるもの)(高さにあたるもの)
ということですね
ex.
対応する矢印はそれぞれ平行である。体積比は?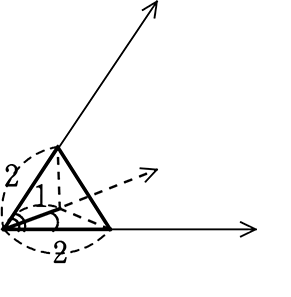
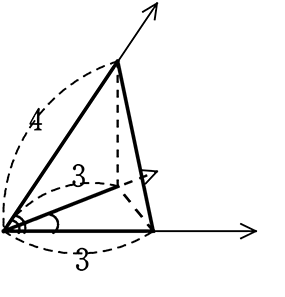
体積比 = 2×1×2:3×3×4 = 4:36 = 1:9
同様に、相似の場合のみ
「体積比 = 相似比3」が使えるということですね
オ 相似な図形の性質の活用
それでは具体的に、「辺の長さ」や「辺の比」「面積」や「面積比」を求めていきましょう!
| 1. | 「実数値」と「比」の区別 (比は○ △ □で囲む など) |
| 2. | 「 山型 」「蝶型 」「蝶型  」を浮き彫りに見れる 」を浮き彫りに見れる |
| 3. | 有効な「補助線」を引ける |
| 4. | 「比の統一 (比の合成)」 |
ですね!
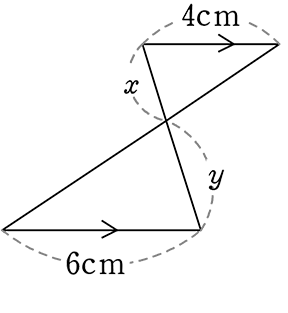
1.「実数値」と「比」をきちんと区別する
x:y は? → 実数値と区別するため「比」は〇や△や□で囲む
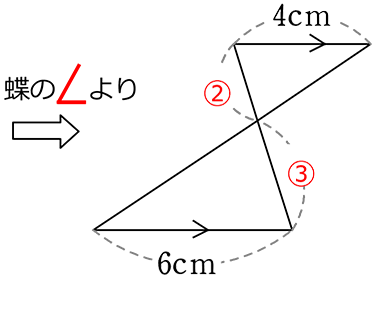
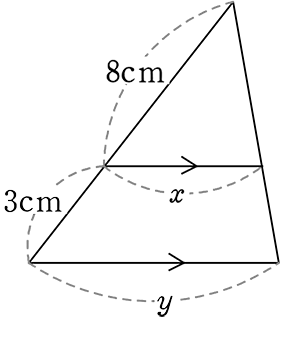
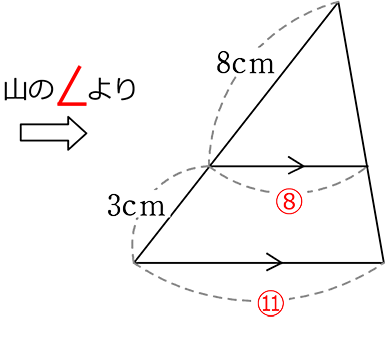
2. 山型・蝶型を発見する、浮き彫りに見れる
「山型」「蝶型」をなぞりましょう
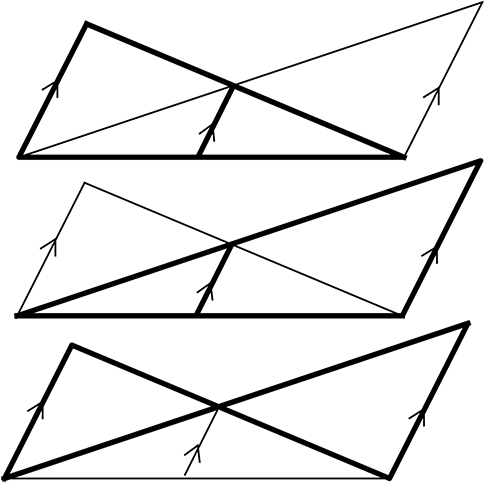
蝶型ではありません!(∵ 平行でない)
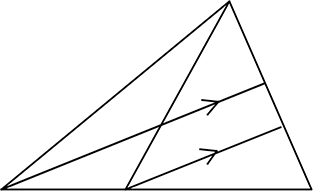
3.「補助線」を引いて、「山型」「蝶型」をつくる
補助線を引いて「山型」「蝶型」を作りましょう (以下:山ちょう)

山1
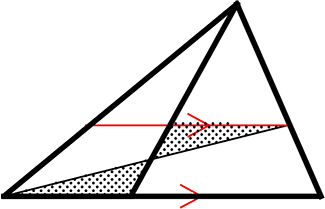
山3 ちょう1
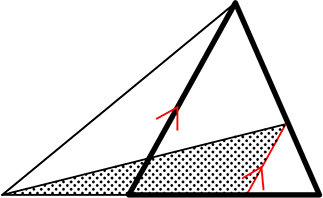
山2
など
平行四辺形
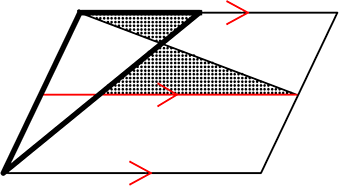
山1ちょう1
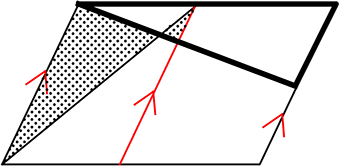
山1ちょう1
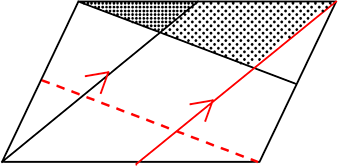
山1 など
(2本引くことも
あると思います)
⇒ 基本的に、
補助線は「何かに平行」で「何かの点を通る」で「山ちょう」を作る ですね!
4. 比を統一する (比の合成)
比を統一しましょう
平行四辺形
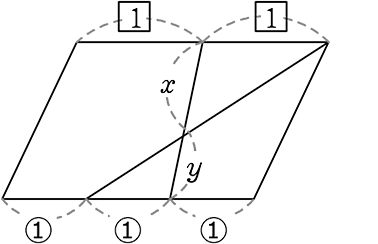
x:y = 1:1 ではないですね!
→ 同じ1でも1と①では価値が違う
→ 「比の統一(合成)」が必要ですね
方法①【 1辺を「1」と見る 】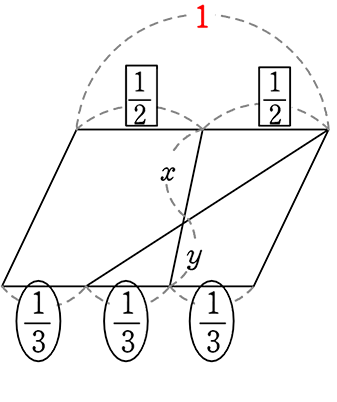
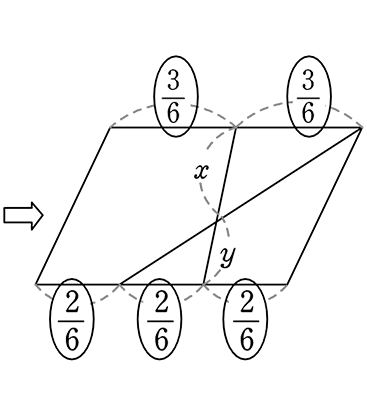
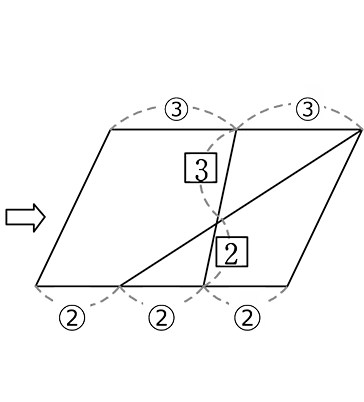
| 方法② | 【 1辺を「6」と見る (2目盛り(上辺)と3目盛り(下辺)をカバーできるのは 6目盛り(2と3の公倍数)】 |
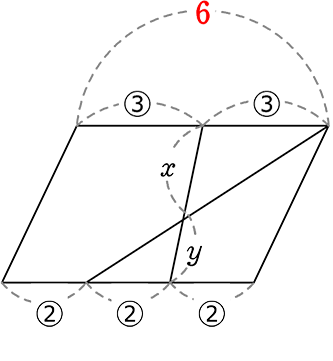
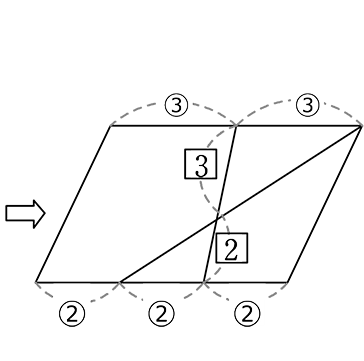
→ 後で通分するか、先に通分するかの違い といえますね
どちらでもOKです
【 かぶる部分がある 】
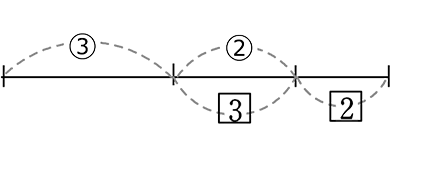
かぶる部分で一致させる
(最小公倍数などで)
【 かぶる部分がない 】
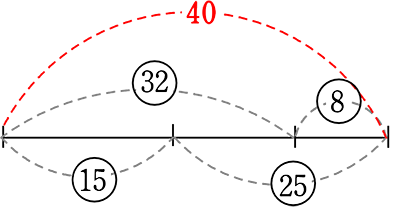
● 平行四辺形同様、全体を「1」とする方法
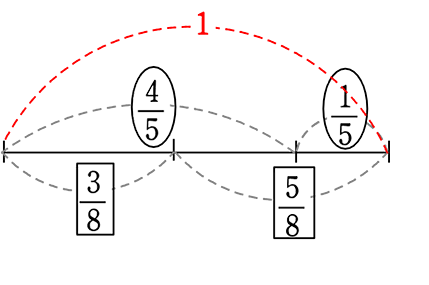
 = \(\large{\frac{32}{40}}\)-\(\large{\frac{15}{40}}\) = \(\large{\frac{17}{40}}\)
= \(\large{\frac{32}{40}}\)-\(\large{\frac{15}{40}}\) = \(\large{\frac{17}{40}}\)
または \(\large{\frac{25}{40}}\)-\(\large{\frac{8}{40}}\) = \(\large{\frac{17}{40}}\)

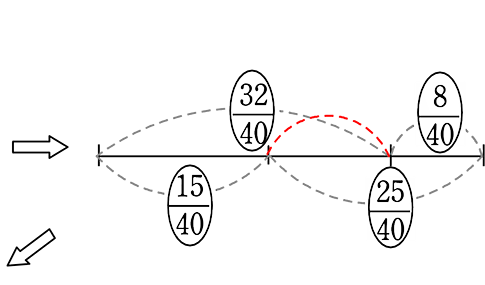
●平行四辺形同様、全体を「40」とする方法

上の目盛りは40÷(4+1) = 8
下の目盛りは40÷(3+5) = 5
以上 ポイントを意識しながら解いていきましょうね!
① 台形
《 例 》
図のようなとき、x, y を求めましょう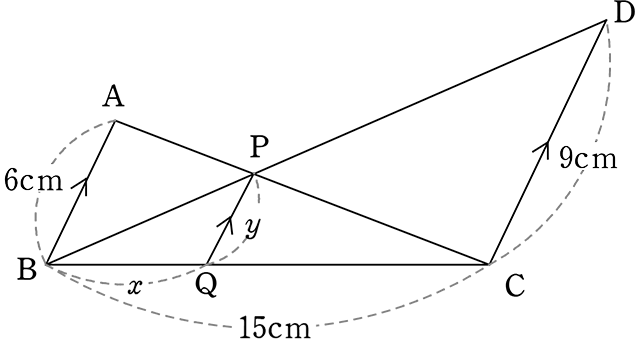
→ 山ちょうがたくさんありますね → ヒントがたくさんあるということですね
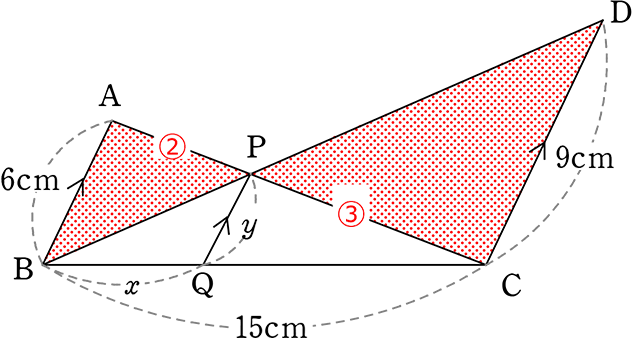
「ちょうの 」より CP:PA (= DC:AB) = 9:6 = 3:2
」より CP:PA (= DC:AB) = 9:6 = 3:2
・「山の  」より CQ:QB (=CP:PA) = 3:2
」より CQ:QB (=CP:PA) = 3:2
∴ x = 15cm×\(\large{\frac{2}{5}}\) ←15cmを5等分したうちの2つ
=6 cm
(3:2 = (15-x):x でももちろん可)
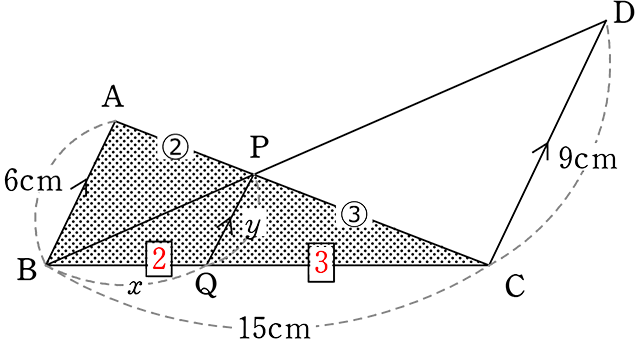
・「山の 」より
」より
| CP: y | = | CA:AB |
| 3:y | = | 5:6 |
| y | = | \(\large{\frac{18}{5}}\) cm |
平行四辺形
《 例 》
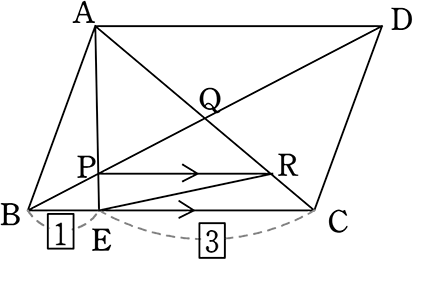
図のような▱ABCD (= 平行四辺形ABCD)のとき、BR:RQ を求めましょう
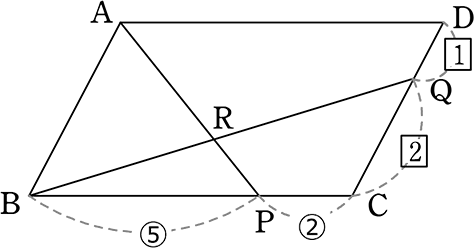
→ 「山ちょう」がありませんね → 「山ちょう」をつくる「補助線」ですね
補助線は色々引いてみてくださいね
そうすれば「これかな!」というものが段々見えるようになってきます
どちらも 1本で「山・ちょう」ができますね
(イ)で行ってみますね
BR:RQということは(ちょう)BP:SQを求めることと同じですね
△ABPの「山の  」より
」より
1:3= TS:5
3TS = 5
TS = \(\large{\frac{5}{3}}\)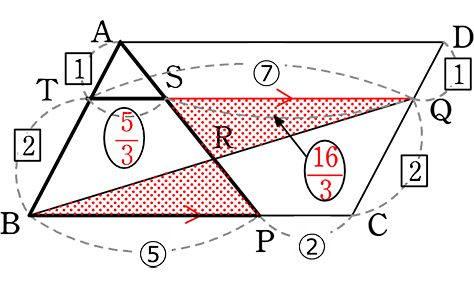
∴ SQ = 7-\(\large{\frac{5}{3}}\)
= \(\large{\frac{16}{3}}\)
∴ BR:RQ (= ちょうの  BP:SQ) = 5:\(\large{\frac{16}{3}}\) = 15:16
BP:SQ) = 5:\(\large{\frac{16}{3}}\) = 15:16
三角形
《 例 》
図のようなとき、BF:FE を求めましょう
→ 「山ちょう」がありませんね → 「補助線」
「山3ちょう1」同時発生ですね
↑△CAD山、△CBD山、△CAB山、蝶
BF:FE = BD:EQ (ちょう)
でOKそうですね
△CADの「山の 」より
」より
| 1:EQ | = | 3:1 |
| 3EQ | = | 1 |
| EQ | = | \(\large{\frac{1}{3}}\) |
∴ BF:FE (= BD:EQ(ちょう)) = 1:\(\large{\frac{1}{3}}\) = 3:1
(別解)
「メネラウスの定理」を知っている場合
→
→ 1・①・BF = (1+2)・① ・ FE
→ 1BF = 3FE
∴ BF:FE = \(\large{\frac{1}{1}}\):\(\large{\frac{1}{3}}\) = 3:1
《 例 》
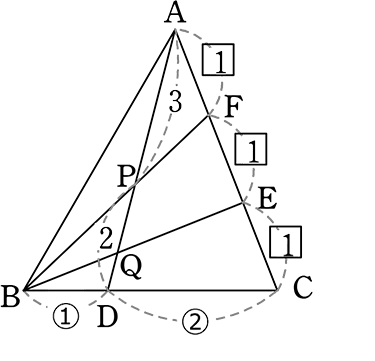
図のようなとき、問いに答えましょう
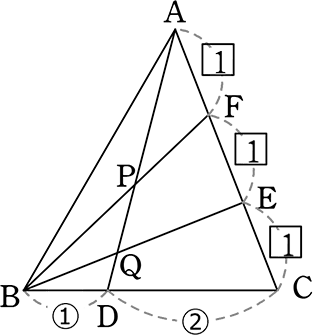
(1) AP:PD を求めましょう
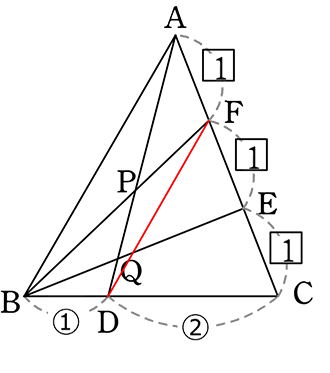
FDを結ぶと
CD:CB も CF:CA も
2:1 →  型の逆より
型の逆より
FD//AB
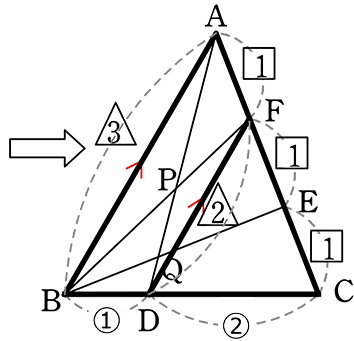
「山の 」より
」より
FD:AB (= CD:CB) = 2:3
「ちょう」より
AP:PD = 3:2
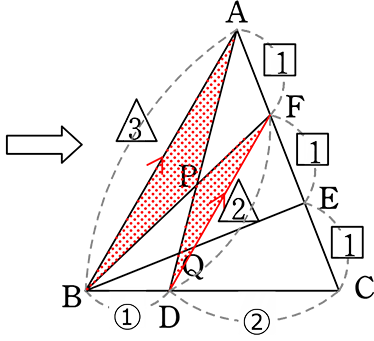
(2) AP:PQ:QD を求めましょう
→ PQ:QDを求めたい
→ DからBEに平行な直線
を引くと
役立ちそうな (△ADGの  )
)
AE:EG = AQ:QD
がうっすらと見える
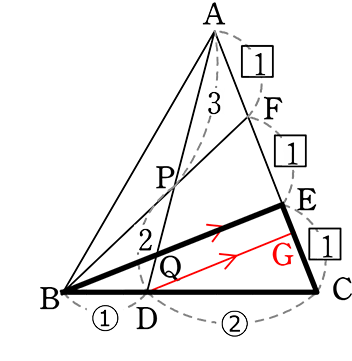
「△CBEの山の  」より
」より
CD:DB = CG:GE
∴ CG:GE = 2:1
→ CEは1より
CG:GE = \(\large{\frac{2}{3}}\):\(\large{\frac{1}{3}}\)
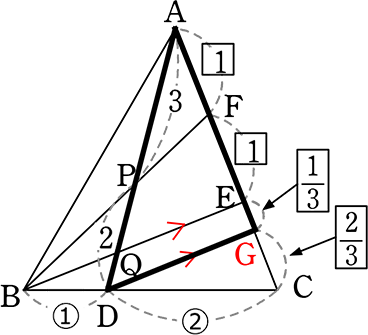
「△ADGの山」を浮き上がらせると
| AE:EG | = | 2:\(\large{\frac{1}{3}}\) |
| = | AQ:QD (  型) 型) |
|
| = | 6:1 (整数比にした) |
最後に「比の統一」 → 見やすいように AD を取り出しますね
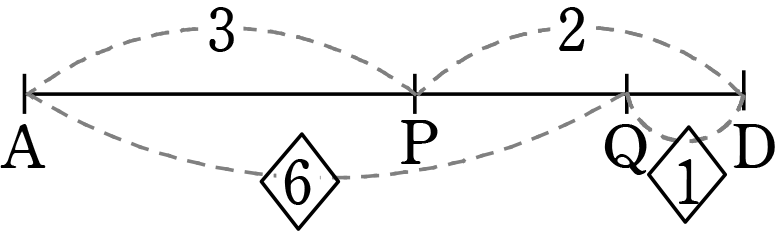
ADを「1」とする方でいきますね
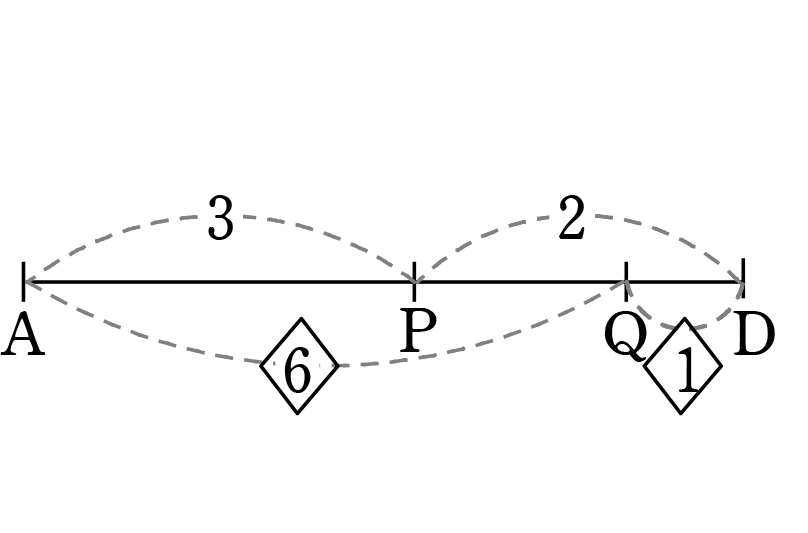
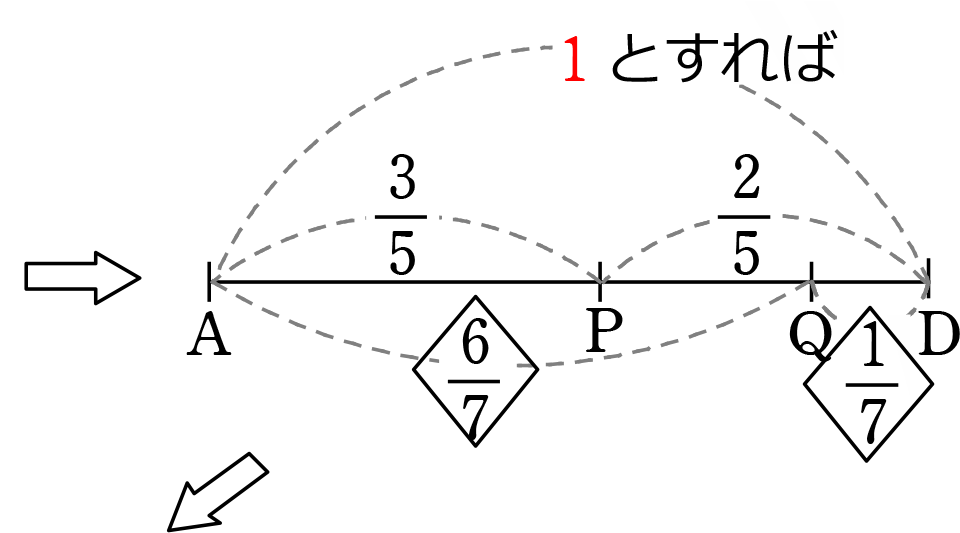
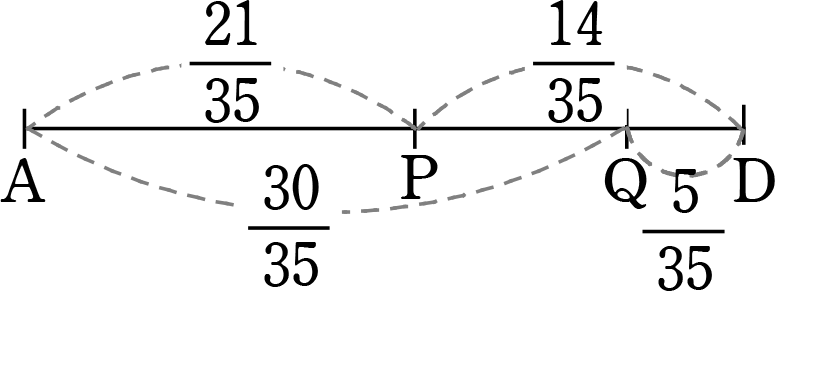

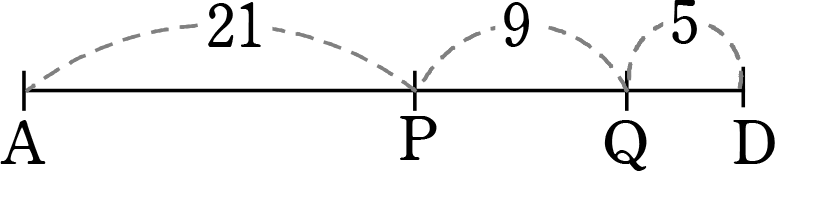
∴ AP:PQ:QD = 21:9:5
(難しい部類の問題です!)
(別解)
もちろん「メネラ」でもOKです

→ BD・CF・AP = BC・FA・PD
1・2・AP = 3・1・PD
2AP = 3PD
∴ AP:PD = 3:2
→ BD・CE・AQ = BC・EA・QD
1・1・AQ = 3・2・QD
1AQ = 6QD
∴ AQ:QD = 6:1
→ 比の統一は上と同様なので省略しますね
AP:PQ:QD = 21:9:5
それでは、面積系の問題を解いていきましょう
《 例 》
図のようなとき、 △FECと台形ABCDの面積比を求めましょう
(流れ)
(考え方1-比で行く)
まず① 台形ABCD:△ABCは?
→ △CAD:△ABC で「高さにあたるもの(AC)」が共通なので
△CAD:△ABCの面積比は、
「底辺にあたるもの(AD)」:「底辺にあたるもの(BC)」→ADが不明
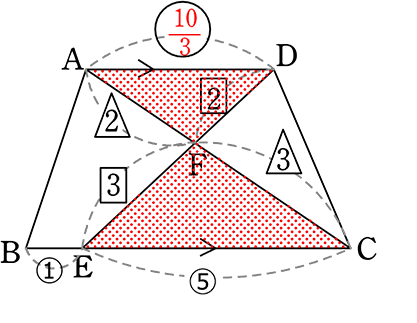
「ちょう」より
AD:EC = 2:3
AD:⑤ = 2:3
AD = \(\large{\frac{10}{3}}\)
∴ △CAD:△ABC (= AD・AC:BC・AC) = AD:BC = \(\large{\frac{10}{3}}\):5+1 = \(\large{\frac{10}{3}}\):6 ←あたるもので面積比
∴ 台形:△ABC = △CAD+△ABC:△ABC = \(\large{\frac{10}{3}}\)+6:6 = \(\large{\frac{28}{3}}\):6 = 28:18 = 14:9
次に② △ABC:△FECは?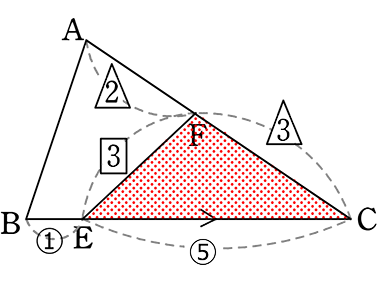
| → | △ABCの(高さにあたるもの)(底辺にあたるもの):△FECの(高さにあたるもの)(底辺にあたるもの) |
= (3+2)(5+1):(3)(5) = 30:15 = 2:1
| ∴ 台形: | △ABC | :△FEC |
| → 14 : | 9 | |
| 2 | : 1 |
∴ 28:18:9
A. △FEC:台形ABCD = 9:28
(考え方2-〇Sで行く) △FECを「削りだすイメージ」

台形ABCDをS(=1S)とすると、△FECは何S?
まず① △ABCは何S (△CADの切り落とし)
「ちょう」より、AD:EC = 2:3
AD:⑤ = 2:3 → AD = \(\large{\frac{10}{3}}\)
∴ △CAD:△ABC = \(\large{\frac{10}{3}}\):6 = 5:9
∴ △ABC = \(\large{\frac{9}{14}}\)S
次に② △ABCが\(\large{\frac{9}{14}}\)Sのとき、△FECは何S(四角形ABEFの切り落とし)
→ △CFE:△CAB = (3)(5):(3+2)(5+1) = 15:30 = 1:2
∴ △FEC = \(\large{\frac{1}{2}}\)△ABC = \(\large{\frac{1}{2}}\)\(\left(\large{\frac{9}{14}}\small{S} \right )\) = \(\large{\frac{9}{28}}\)S
∴ (問題に合わせて) △FEC:台形 = \(\large{\frac{9}{28}}\):1 = 9:28 //
※ やっていることは(考え方①)と同じですが「イメージ」がしやすいかと思います
→「これを一直線で切り落として、次にこれを一直線で切り落とせば、目的物が出てくるな!」みたいな
「一直線で切り落とし」→ 1度入れた包丁は途中で方向を変えられない → スパッと切り落とすイメージ
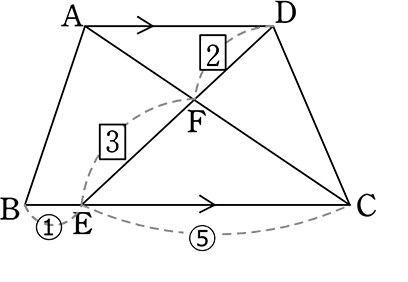
《 例 》
平行四辺形が図のようなとき、 △AERと  ABCDの面積比を求めましょう
ABCDの面積比を求めましょう
(見通し) ABCDから△ACDを切り落として
ABCDから△ACDを切り落として
次に△ABCから△ABEを切り落として
次に△AECから△ERCを切り落とせば
△AERが出てくるな
 ABCDをSとすると、ACは対角線より
ABCDをSとすると、ACは対角線より
△ABCは\(\large{\frac{1}{2}}\)S (平行四辺形を2分する線)
△ABCと△AECにおいて
BE:EC = 1:3より
(高さが共通なので) △ABE:△AEC
∴ △ABC:△AEC = 4:3
∴ △AEC = \(\large{\frac{3}{4}}\)△ABC = \(\large{\frac{3}{4}}\)\(\left(\large{\frac{1}{2}}\small{S} \right )\) = \(\large{\frac{3}{8}}\)S
あとは△EARと△ECRの比→AR:RCだな
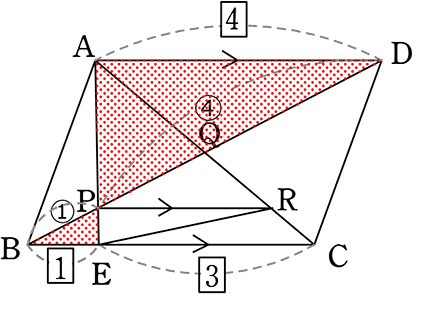
平行四辺形より AD = 4
「ちょう」より BP:PD = 1:4
Qは中点より BQ:QD = 1:1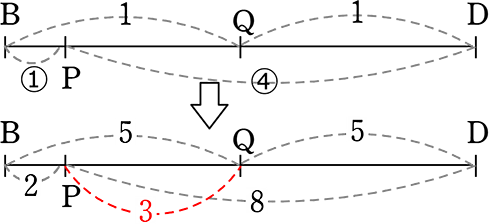
∴BP:PQ:QD = 2:3:5
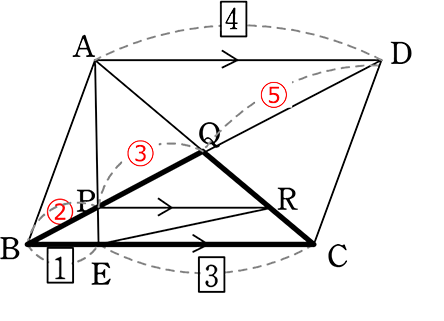
△QBCの「山の  」より
」より
QR:RC = 3:2
Qは中点より AQ:QR:RC = 5:3:2
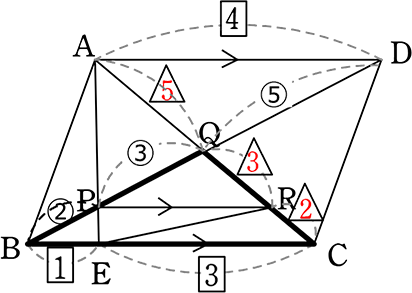
∴ △EAR = \(\large{\frac{8}{10}}\)△EAC = \(\large{\frac{8}{10}}\)\(\left(\large{\frac{3}{8}}\small{S} \right )\) = \(\large{\frac{3}{10}}\)S
∴ (問題の問に合わせて)
△AER: ABCD = \(\large{\frac{3}{10}}\)S:1S = 3:10 //
ABCD = \(\large{\frac{3}{10}}\)S:1S = 3:10 //
(2) つけ足し問題として、△AERをSとすれば ABCDは何Sでしょうか
ABCDは何Sでしょうか
→ \(\large{\frac{10}{3}}\)S ですね!
すなわち 最後の「調整」は簡単ですので、
| ● | 1番大きな元図形をS、そこから「切り落とし」て目的の図形を削り出す |
| ● | 1番小さな図形をS、そこから「付け足して」て1番大きな元図形を導く |
どちらでもOKです!やりやすい方で解いて下さいね
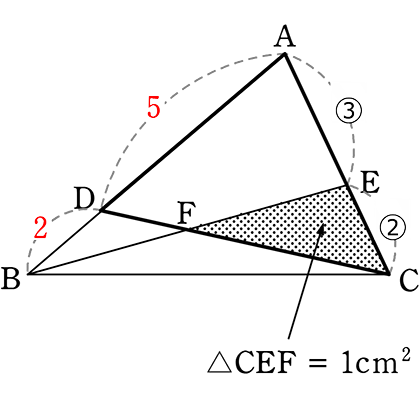
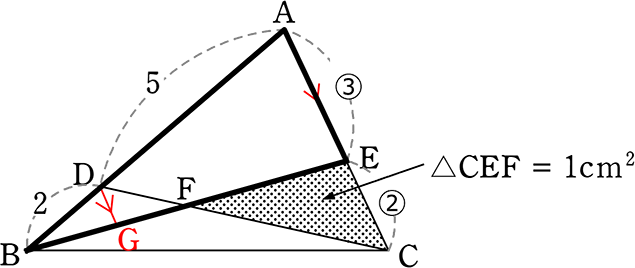
《 例 》
図のようなとき、△ABCの面積は何cm2でしょうか
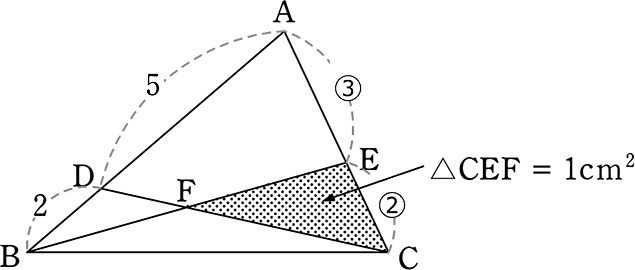
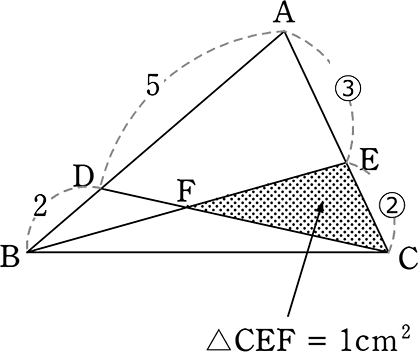
(見通し)
| ア | △BAEの切り落とし→△BECと△FECの関係でいくか |
| イ | △CDBの切り落とし→△CADと△CEFの関係でいくか |
| → | アは△BAEを切り落とした後のデータが「ECの②」のみ |
| → | イは△CDEを切り落とした後のデータが「②③5」の3つ |
イでいきますね
△ABCをSとすると
△CAD = \(\large{\frac{5}{7}}\)S …①
あとは CF:FD がわかれば
△CFEと△CDAの「底辺にあたるもの」「高さにあたるもの」がそれぞれわかるな
DからACと平行な補助線をひくと
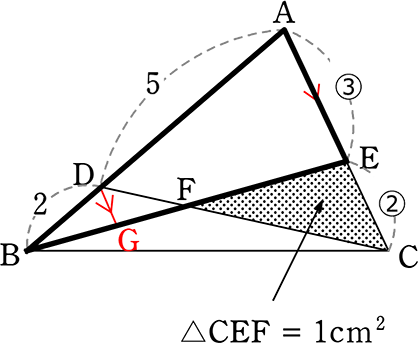
△BAEの「山の  」より
」より
| → 2:DG | = | (2+5):③ |
| 7DG | = | 6 |
| DG | = | \(\large{\frac{6}{7}}\) |
「ちょう」を浮かび上がらして
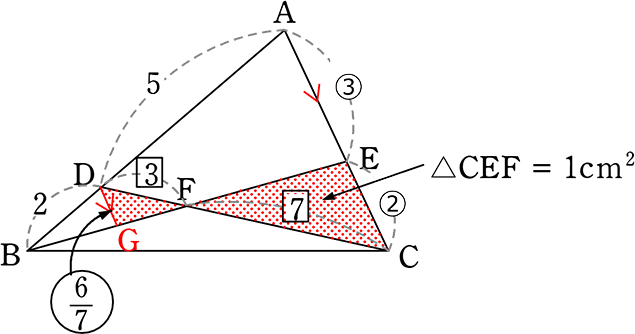
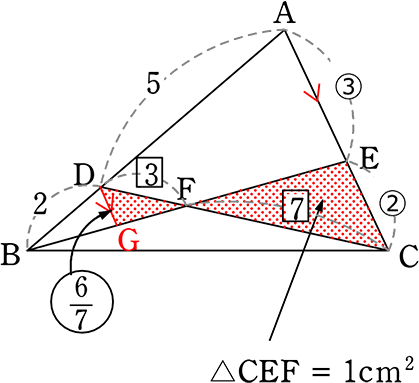
「ちょう」より DF:FC = \(\large{\frac{6}{7}}\):2 = 6:14 = 3:7
∴ △CEF:△CAD = 2×7:(2+3)×(7+3) = 14:50 = 7:25
∴ △CEF = \(\large{\frac{7}{25}}\)△CAD = \(\large{\frac{7}{25}}\)\(\left(\large{\frac{5}{7}}\small{S} \right )\) = \(\large{\frac{1}{5}}\)S
∴ △CAB = 5△CEF = 5(1cm2) = 5cm2 //
もちろん、「メネラ」でBF:FE、
「あたるもの」で△BCA:△ECEで
もっと簡単に求めることができますが
『補助線』で「山型」「ちょう型」を駆使して解く「工夫力」が相似の応用図形問題を解くためには大切であると思いますので、まずは「補助線」で!
求め方は1つではありませんので
解答例と手順が違っていても
答が合っていれば、マル! です!
中学数学のメインどころであり
しかも練習あるのみの部分ですね!
お疲れ様でした!
その他の問題は、「問題集」で!!















