| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 標本調査 |
| ア | 標本調査の必要性と意味 |
|---|---|
| ① | 全数調査と標本調査 |
| ・ | 2つの調査を分ける基準 |
| ・ | 専門用語 |
| ② | 無作為に抽出 |
| イ | 標本調査による母集団の傾向の説明 |
| ① | 標本平均と母集団の平均値 |
| ② | 標本調査の利用 |
標本調査
ア 標本調査の必要性と意味
とうとう中学数学最後の章ですね！
3年生の「資料の活用」の「標本調査」の章は
「関数」「図形」の章が分厚かった分、
配分的な問題なのか、かなり奥行きのない章となっていますね！
2年生の「資料の活用」の「確率」の章の方がよっぽど難しかったと思います
それではあと少しです 頑張っていきましょう！
① 全数調査と標本調査
「標本(ひょうほん)調査」の簡単なイメージは・・・
ある程度のデータを集めて、全体のデータもこんなものだろうと推測する調査ですね
(「標本」 ＝ サンプル )
良く言えば、全部を調べる労力を省く
悪く言えば、楽して調べたい ですね！
| ・標本調査 | … | 集団の中から一部を取り出して調査し、集団全体の傾向を推測する調査方法 |
| ex ) | 選挙出口調査、選挙当落速報(全部開票しても逆転はないだろう という頃)、テレビ視聴率、世論調査(せろんちょうさ)(内閣支持率などを調べる) など |
対して
| ・全数調査 | … | 集団の全てについて行う調査方法 |
| ex ) | 選挙結果、国勢調査(世帯構成などを調べる、世帯の身体測定のような感じ)、健康診断、入試テスト など | |
2つの調査を分ける基準
上のex )を見ると
「標本調査」に向いている調査、「全数調査」でないといけない調査、
2つを分ける「基準」が少し予想できますね
絶対的基準
| 全数調査 | 標本調査 |
|
絶対的に正確でないといけない
(間違っていると 社会的に大問題になる) |
ある程度正確ならよい
(間違っていても 社会的に許される) |
現実的基準
| 全数調査 | 標本調査 |
| 母集団が少ないことだし…全数でいくか | 母集団が多すぎるから…標本でいくか |
| 全数調べてもコストが低そうだし…全数でいくか | 全数調べるとコストが高いから…標本でいくか |
| 全数調べることができそうだし…全数でいくか | 全数調べることが現実的に不可能だから…標本でいくか |
絶対的基準は、すなわち「譲れない基準」ですね
コストがかかろうが、母集団が多かろうが、
「正確でないと、問題になる、意味がない」ものは、全数調査ですね！
それ以外なら、標本調査でもOKな可能性がありますね
2次的基準は、現実的な価値観ですね
総合考慮してどちらの調査がよいか判断しますので
人により「全数！」「標本！」と別れることがあるはずですね
ですが、統計の問題では、「一般的に考えて」を念頭に
どちらがよいか選んでくださいね！
自分の価値観を大事にしつつ、一般の価値観も知る…
「彼を知り己を知れば百戦殆うからず」ですね！
クリック・タップで答え (反応が遅い場合があります)
クリック・タップで答え (反応が遅い場合があります)
というわけで、「標本調査」の必要性を一言で言ってみると、
「(前提：母集団のデータ収集は社会の発展に必要であるので、)
全数調査が総合考慮の上できない場合、次に標本調査が有効であるため」
という感じでしょうか
専門用語
全体から一部を取り出すというイメージ図は
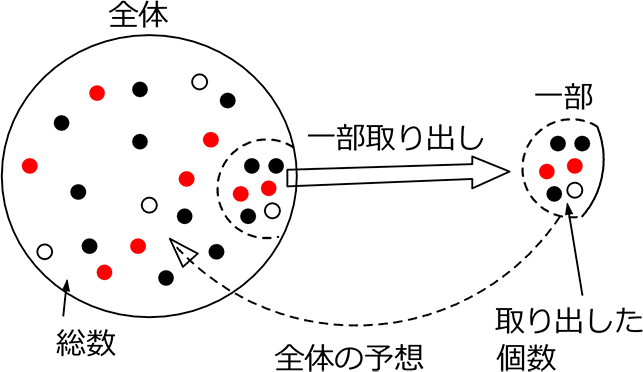
このような感じでしょうか
この手順を、この章(標本調査)で専門的に言い換えると
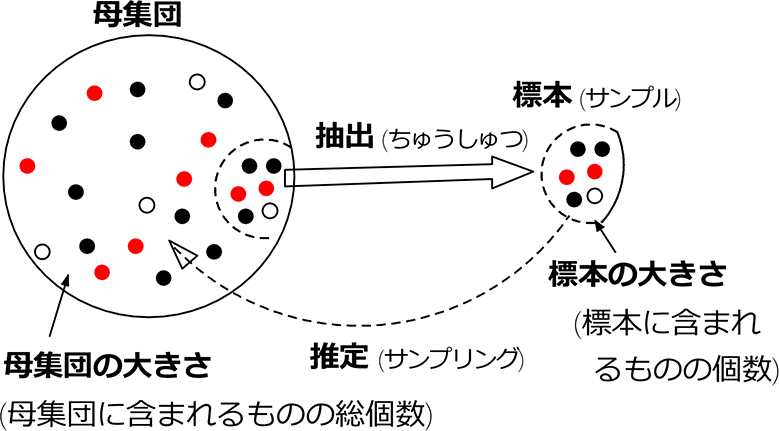
となりますね！ それだけです
《 例 》
ある中学校の
1年生は男子60人・女子は74人、
2年生は男子65人・女子70人、
3年生は男子68人・女子は75人でした。
次の各調査における「母集団の大きさ」と「標本の大きさ」を求めましょう
(1) 1年生の女子全員から20人を選んで好きな雑誌について調査する。
A. 母集団の大きさ 74 ( ←1年生女子)、 標本の大きさ 20
(2) 2年生全員から30人を選んで1年間に図書室を利用した回数を調査する。
A. 母集団の大きさ 135 ( ←2年生男子65＋女子70)、 標本の大きさ 30
(3) 全校生徒から50人を選んで、通学時間を調査する。
A. 母集団の大きさ 412 (←全生徒60＋74＋65＋70＋68＋75)、標本の大きさ 50
② 無作為に抽出する
「抽出」のしかたのお話ですね
抽出のしかたによって「推定」結果が違ってくるのですから、大切な場面ですね
いくら「理論(法)」が正しくても「方法(手続き)」が間違っていたら「間違った答え」が出る
ということですね！
一般的な意味
| ・ | … | わざと、意図的に、 |
| ・無作為 | … | 作為がないこと ＝ わざとでない、意図的でない、人為的でない |
例えば、記者A、記者B、記者C、記者Dは それぞれ もくろみを持って
そして、記者Eは何も考えずに、
下図のように「抽出」したとします
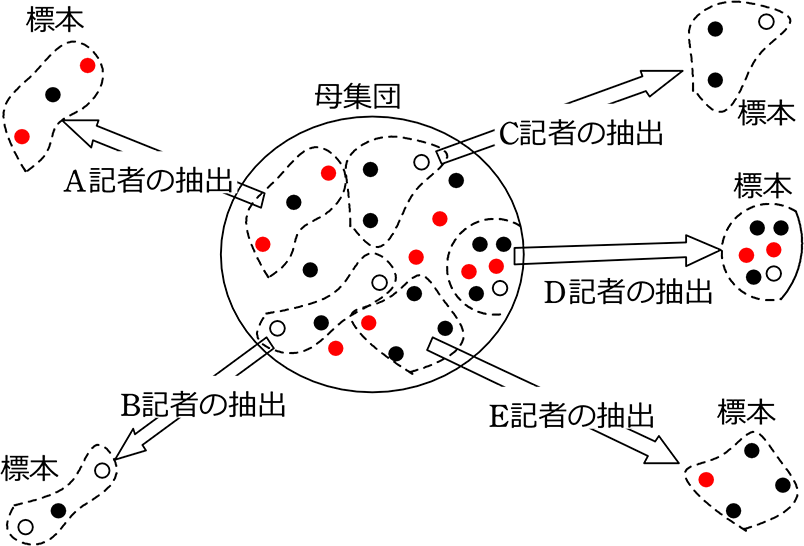
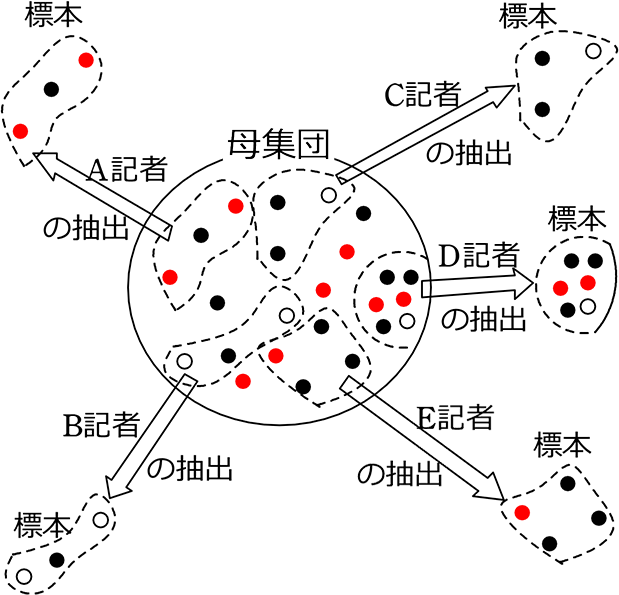
それぞれの目論見(意図)は…
| A記者 | → | 母集団も「赤」が多いと世間に発表したい ・・・作為あり |
| B記者 | → | 母集団も「白」が多いと世間に発表したい ・・・作為あり |
| C記者 | → | 母集団も「黒」が多いと世間に発表したい ・・・作為あり |
| D記者 | → | 母集団もできる限り「このようである」と世間に発表したい |
| E記者 | → | 母集団も「こんな感じ？」と世間に発表したい |
A、B、C はさておき ←(A、B、C、はマスコミ操作というものですね)
「作為がある」を通り越して「悪意すらあり」ますね
Dは「母集団を正確に表現したい」という「作為」がありますね
Eは「何も考えていない」のですから、まさしく「無作為」ですね
ですが、「標本調査」の世界では、EではなくDの「母集団を正確に表現したい」
と考えながら「抽出」することを… 「無作為に抽出する」といいます
標本を 「無作為に抽出する」 とは
かたよりがないように(考えながら)、
標本を取り出すこと
よって、今後は「無作為に抽出した」というフレーズがあれば
母集団と標本は「相似である」と『保証』されたということになります
まとめ
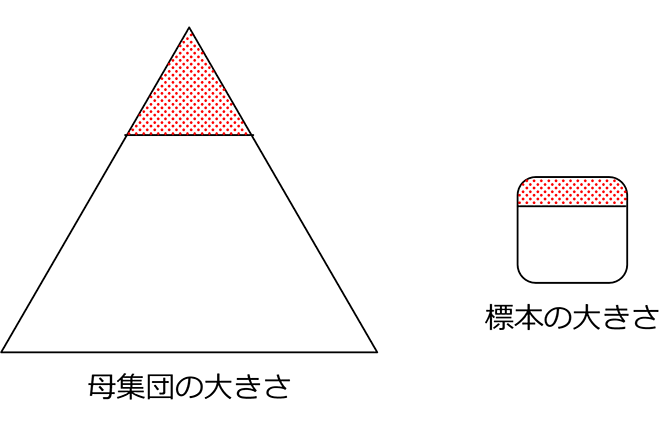
 | 「無作為に抽出」というフレーズがあれば |
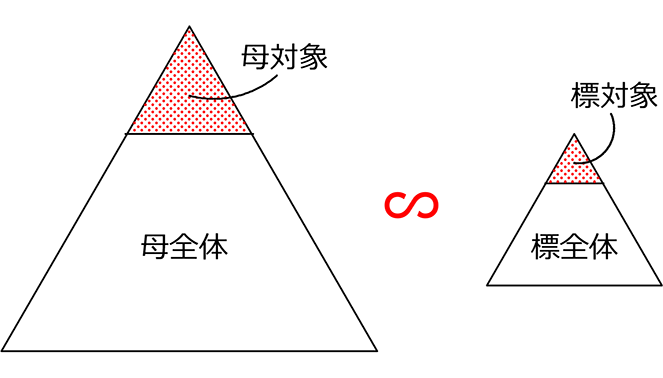
『相似というお墨付き』を与えられた ということ！
そして相似ということは、図形内の割合が同じなので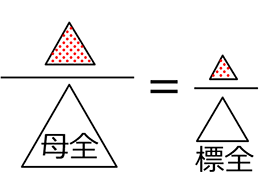
→\(\large{\frac{母集団の対象物数}{母集団の大きさ}}\)＝\(\large{\frac{標本の対象物数}{標本の全体}}\)
略して、\(\large{\frac{母対}{母全}}\) ＝ \(\large{\frac{標対}{標全}}\)
(分数の横棒は、「ぶんの」と読まずに「につき」と読めばイメージがしやすい)
標本調査の問題を解くときは、
常に をマル図のように用意して、どこが x になるかを考えればよいですね
もちろん相似なので、
型で 
でもOKですが、
を求めるのも手間ですし、問われることもないと思いますので。 (H型)
で十分ですね
付随するフレーズ
「無作為に抽出」と明言されていなくても
お墨付きを与えられるフレーズがたくさんありますね
| ・「よく混ぜて」 | → | どこを抽出しても割合が同じだ |
| ・「しばらくして」 | → | まんべんなく混ざった頃 → どこを抽出しても割合が同じだ |
| ・「乱数」 | → | 人為が及ばない → 同様に確かだ |
| ・「ランダム」 | → | 人為が及ばない → 同様に確かだ |
などなど、色々ありますが
結局は「抽出したものも、相似だろうな～」と感じられれば
＝ 「無作為に抽出」でOKですね
そもそも相似でないと解けませんので
確率同様「同様に確か」、「無作為に」が省略されている問題もありますね
| ・ | 2年生の確率の 「同様に確からしい」というのも「お墨付き」ですね |
| ex. | サイコロの各目が出る確率(割合)は、\(\large{\frac{1}{6}}\)というお墨付き |
| ∴ | 1か2の目が出る確率(割合)は、(\(\large{\frac{1}{6}}\)と信じて) ×(それが2パターン) ＝ \(\large{\frac{2}{6}}\) |
| ・ | 1年生の1次方程式の 「割合」というのも「お墨付き」ですね |
| ex. | この食塩水の濃度は20％、20％というお墨付き (まんべんなく混ざっているので、どこを取っても20％と保証しますよ～) |
| ∴ | 100gの食塩水中の塩の重さは、100×(\(\large{\frac{20}{100}}\)と信じて) ＝ 20g |
イ 標本調査による母集団の傾向の説明
①「標本平均」と「母集団の平均値」
「母集団の平均値」は今まで学んできたもののことですね
→「全数平均」とでもいう感じでしょうか
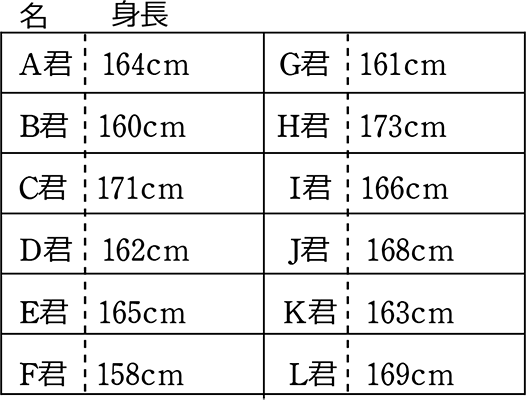
イメージ図にしろ、表にまとめたにしても
3年2組の男子という母集団の平均身長(母集団の平均値)は・・・
平均
= \(\large{\frac{個体のデータの合計}{個体数}}\)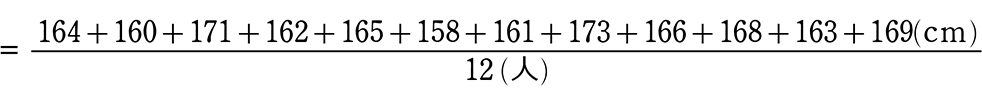
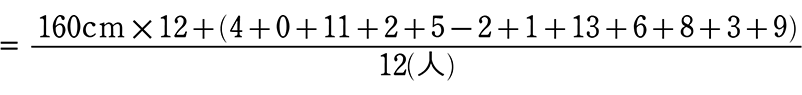
もちろん、
0を基準に地道に164+160+ … ÷12でもOKです
上の計算は160を基準にしていますね → 「みんな160はあるとして」
では「標本平均」とは・・・
抽出した標本の方の平均値です
ただそれだけです！
例えば上の例で、
標本を無作為に5人抽出したら、B君、D君、H君、J君、K君だったとします
標本平均
上で「母集団の平均値」を求めてしまっていますが、もし不明であった場合は
『母集団の平均値は(も)、165.2と「推定」される』となりますね
《 例 》
あるリンゴ園で収穫した12個のリンゴの重さを量ったところ、次の表でした
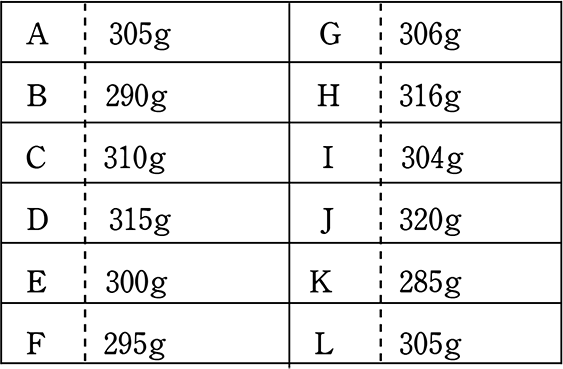
(1) 大きさが 5 である標本( ＝ 標本の大きさが 5 ＝ 標本の個数が5個 → 大きさと言いますが個数ですね ) を無作為に抽出したところ
標本は次の5つでした。このとき「標本平均」を求めましょう
B D E H K
標本平均
＝ \(\large{\frac{290+315+300+316+285}{5}}\)
＝ \(\large{\frac{300×5+(-10+15+0+16-15)}{5}}\)
＝ \(\large{\frac{300×5+(6)}{5}}\)
＝ 300+1.2
＝ 301.2
A. 301.2 g
(2) 収穫した12個のリンゴの1個あたりの重さを「推定」しましょう
→ (1)より (母集団の平均値も)
A. 301.2ｇ(と推定される)
(3) 実は「母集団の平均値」は 304.25ｇであった
「母集団の平均値」と「標本平均」の「差」を求めましょう
→ 「母集団の平均値」－「標本平均」 ＝ 304.25－301.2 ＝ 3.05
A. 3.05ｇ
↑もし「誤差を求めよ」 だったら
誤差 ＝ 近藤さん-真彦さん ＝ 近似値-真の値 ＝ 301.2-304.25 ＝ -3.05g
(真の値よりどれだけ大きいか小さいか) (誤差)
まとめ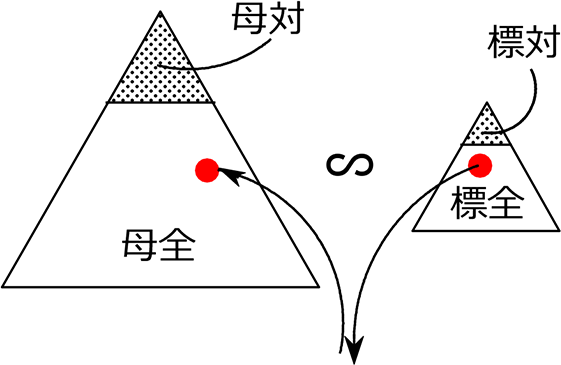 
個々の「平均値」の大きさは
『同じ』とみなしてよい
↓
標本平均 ≒ 母集団の平均
(対象の割合の話ではなく、平均の話)
「図形」「関数」を乗り越えてきた私たちにとっては、「この程度？」
という「拍子抜け」感がありますね！
② 標本調査の利用
《 例 》
袋の中に赤玉と白玉が合計400個入っています。これをよくかき混ぜて
20個の玉を取り出したところ、赤玉が15個、白玉が5個でした。
(1) 袋の中にある白玉の個数を推定しましょう
⇒ 確率風、割合風に考えると
「標本」の白玉の確率 = \(\large{\frac{標対}{標全}}\) = \(\large{\frac{5}{20}}\) = \(\large{\frac{1}{4}}\)
| ∴ | 「母集団」の白玉の確率(割合)も\(\large{\frac{1}{4}}\) と考えられるので |
400×\(\large{\frac{1}{4}}\) = 100 A, 100個
⇒ 相似風に考えると → \(\large{\frac{母白玉}{母全}}\) = \(\large{\frac{標白玉}{標全}}\)
| → \(\large{\frac{x}{400}}\) | = | \(\large{\frac{5}{20}}\) |
| x | = | \(\large{\frac{400\ \cdot \ 5}{20}}\) 両辺に400をかけた |
| x | = | 100 A. 100個 |
| ⇒ | 型でも本当に大丈夫？ → ここで試してみると |
→ \(\large{\frac{母白玉}{母赤玉}}\) = \(\large{\frac{標白玉}{標赤玉}}\)
| → \(\large{\frac{x}{400-x}}\) | = | \(\large{\frac{5}{15}}\) |
| 15x | = | 5(400-x) (分数比の計算) |
| 3x | = | 400-x |
| 4x | = | 400 |
| x | = | 100 A. 100個 OKですね |
⇒ 比で考えると
白玉x：母集団400 = 白玉5：標本20 (比の計算は内側の積 ＝ 外側の積)
| → 20x | = | 2000 |
| x | = | 100 A. 100個 |
どれでも同じことですので 理解しやすい方法で！
(2) (このような問題は出ませんが) 20個を取り出した後(戻さずに)残った袋にある白玉の個数を推定しましょう
⇒ 確率は同様に\(\large{\frac{1}{4}}\)
残りの玉(400-20)×\(\large{\frac{1}{4}}\) = 95 A. 95個
⇒ (相似で) \(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\)
| → \(\large{\frac{x }{400-20}}\) | = | \(\large{\frac{5}{20}}\) |
| \(\large{\frac{x}{380}}\) | = | \(\large{\frac{1}{4}}\) |
| x | = | \(\large{\frac{380}{4}}\) |
| x | = | 95 A. 95個 |
⇒ (1)で求めた白玉＝100個を利用して、
→ 白玉5個取り出されているので → 100-5 ＝ 95 A. 95個
※ (1)の「袋の中にある」とは
「標本を母集団に戻した」「標本を取り出す前は」の意味になりますね
もっと親切に「袋の中にあった白玉の個数を推定しましょう」などに
してほしいかなとも思いますね
→ よって、「残りの～」などのワードがない限り「完全体の母集団」を問われていると考えてよいですね
「調査」に重きを置いているので、
「確率」のように戻す戻さないにこだわらず、
当然、「調査対象 ＝ 母集団 ＝ 完全体の母集団」ということですね
《 例 》
養殖池にいる魚の数を調査するため、40匹の魚を捕まえて、
それらに印をつけて池に戻しました
しばらくして、再び40匹を捕まえたところ
印のついた魚が2匹混ざっていました
このとき、この池には およそ何匹の魚がいると推定されるでしょうか
→ 数値が、\(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) のどこにあてはまるかを考えればよいだけですね
(再度)
養殖池にいる魚の数を調査するため、40匹の魚を捕まえて、
それらに印をつけて池に戻しました
「捕まえた」が「戻した」のでこの部分は「標本」ではないですね → (印をつけたまま)池に散っていった
\(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) の \(\large{\frac{\color{red}{40}}{母全}}\) = \(\large{\frac{標対}{標全}}\) の部分になりましたね
しばらくして、
魚が「まんべんなく散った」 → 1部取り出しても「無作為に抽出」のお墨付き
\(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) の \(\large{\frac{40}{母全}}\) ＝ \(\large{\frac{標対}{標全}}\) が保証されたということですね
再び40匹を捕まえたところ
40匹の抽出 \(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) の \(\large{\frac{40}{母全}}\) = \(\large{\frac{標対}{\color{red}{40}}}\) の部分ですね
印のついた魚が2匹混ざっていました
言うまでもなく \(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) の \(\large{\frac{40}{母全}}\) = \(\large{\frac{\color{red}{2}}{40}}\) の部分ですね
このとき、この池には およそ何匹の魚がいると推定されるでしょうか
母集団の全体数を聞いていますね \(\large{\frac{母対}{母全}}\) = \(\large{\frac{標対}{標全}}\) の \(\large{\frac{40}{\color{red}{x}}}\) = \(\large{\frac{2}{40}}\) の部分ですね
あとは解くだけ
| \(\large{\frac{40}{x}}\) | = | \(\large{\frac{2}{40}}\) |
| 2x | = | 1600 |
| x | = | 800 A. 800匹 |
簡易計算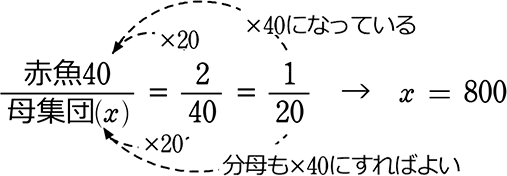 
もちろん
・逆数になっていてもOK \(\large{\frac{x}{40}}\) = \(\large{\frac{40}{2}}\)
( 相似なら何でもOK)
《 例 》
瓶に豆がたくさん入っています。標本調査を利用して瓶の中の豆の総個数を
知るための方法を考えましょう
→ 「標本調査」を利用ですので、重さを量る「量り」は使えないですね
量りがあれば、10粒の重さから1粒の重さを求め(←1粒自体を量るより誤差が少ない)
次に、全体の重さ－瓶の重さ ＝ 全豆の重さ
そして、 \(\large{\frac{全豆の重さ}{1粒の重さ}}\) = 総個数 ですね
→ 上の《 例 》と全く同じ問題ですね
∴ ① 何粒か取り出し
( 20粒取り出し)
② 印をつけて
(その20粒を赤色に塗る)
③ 瓶に戻してよく振る
(無作為抽出の準備)
イメージ 
④ 再び何粒か取り出し
(標本20粒)
⑤ 印のついた豆を数える
(赤豆は2個だったとする)
| ⑥ | (標本全体に対する)標本の印のついた豆の割合と、(母集団全体に対する)母集団の印のついた豆の割合は同じと 考えられることを利用して総個数を求める(推測する)ことができる// |
| \(\large{\frac{母対}{母全}}\) | = | \(\large{\frac{標対}{標全}}\) |
| \(\large{\frac{20}{x}}\) | = | \(\large{\frac{2}{20}}\) |
| 2x | = | 400 |
| x | = | 200 ∴ 200粒 |
《 例 》
赤、青、白の玉が、合わせて400個入った箱がある。
この箱の中から無作為に10個抽出し 赤玉、青玉、白玉の個数を調べる。
次に抽出した玉を箱に戻す。この作業を5回繰り返して下の表を得た。
このとき箱の中にある白玉の個数を推定しましょう
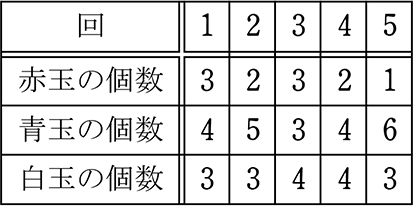
→ 5回で取り出した玉の合計は
10個×5回 = 50個
→ 5回で取出せた白玉の合計は
3+3+4+4+3 = 17個
| ・ | 標本全体に対する標本内の白玉の割合は …\(\large{\frac{17}{50}}\) |
| ∴ \(\large{\frac{x}{400}}\) | = | \(\large{\frac{17}{50}}\) |
| x | = | \(\large{\frac{17\ \cdot \ 400}{50}}\) |
| = | 17・8 | |
| = | 136 Ａ. およそ 136個 |
もし、1回目の抽出だけで推測すると、
\(\large{\frac{白3個}{10個中}}\) ∴ 母の白x ＝ 400×\(\large{\frac{3}{10}}\) ＝ 120個
もし、3回目の抽出だけで推測すると、
\(\large{\frac{白4個}{10個中}}\) ∴ 母の白x ＝ 400×\(\large{\frac{4}{10}}\) ＝ 160個
| → | 5回行ったことで母の白は136個と推測 |
⇒ 正確性が上がったということですね
| ● | 母集団のデータをできる限り正確に推測する方法 |
| ① | 「標本の大きさ」をできる限り大きくする |
| → | 大きければ大きいほど「全数調査」に近づく |
| ② | 「標本」を抽出する回数をできる限り多くする |
| → | 標本を大きくすることと同じ効果が期待できる |
この問題は②で正確性を上げようとしていますね！
お疲れ様でした！
その他の問題は、「問題集」で !!
