| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 場合の数 | (2) 確 率 |
| ア | 確率の意味と求め方 |
|---|---|
| イ | 確率を用いた不確定な事象 |
| ・ | 確率総論 |
| ・ | 区別があるもの ないもの |
| ・ | 同様に確からしいとは |
| ・ | 数え方の種類 |
| ・ | 全通り(分母にくるもの)は「計算」で求まる |
| ・ | ぞろ目ラインがあるとどうして順列数え? |
| ・ | 余事象 |
| ・ | 確率総論まとめ |
| ウ | 確率の個別的な問題の研究 |
| a | 複数特徴系 (サイコロ・コイン・じゃんけん) |
| ① | サイコロ |
| ・ | サイコロ1個 |
| ・ | サイコロ2個 |
| ・ | ぞろ目は出にくい |
| ・ | 親中数え |
| ・ | 親中数えの適用判断 |
| ・ | 複数特徴系の列挙のイメージ |
| ・ | サイコロ3個 |
| ・ | サイコロの複合問題 |
| ・ | 右回り=時計回り=外回り |
| ② | コイン |
| ・ | コイン2枚 |
| ・ | コイン3枚 |
| ・ | 表裏の値がそれぞれ違う |
| ③ | じゃんけん |
| ・ | あいこは余事象 |
| b | 1特徴系 (カード・玉・くじ・人) |
| ① | 玉・カード・くじ・人 |
| ・ | 2個とる |
| 1 | 「戻して」系 |
| 2 | 「袋2つ」系 |
| 3 | 「続けて」系 |
| ・ | 「続けて」系の列挙のイメージ |
| 4 | 「同時に」系 |
| ・ | 「同時に」の列挙のイメージ |
| ・ | C/C?P/P? |
| 5 | 区別がない (同じものを含む) |
| ・ | 確率の乗法定理 (確率どうしのかけ算) |
| ・ | 日本語の意味をはっきりさせる |
| ・ | 独立とは |
| 6 | 「とにかく○番目に当たる」系 |
| ・ | 排反とは (どういうときに足す?) |
| ・ | 3個とる |
| 7 | 人 |
| c | いろいろな問題 |
| ・ | 最短経路の確率 (同じものを含む全順列か反復試行か) |
| ・ | 宝くじの確率 |
| d | (確率の問題文の読み方まとめ) |
確率
ア 確率の意味と求め方
『確率』とは、ある事柄の起こりやすさ、の程度ですね
例えば、
サイコロ1個を投げて6の目が出れば当たりです
他の1~5の目ははずれです
1回投げて、当たりの確率は?
→ このようなとき、直感的に当たりの確率は\(\large{\frac{1}{6}}\)ですね
これは正確には 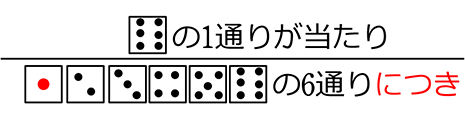 ということですね
ということですね
分母は「全事象(起こり得るすべての場面)」、分子は「問題文の指定する当該事象」ですね
当然、実際一発で6が出た!
→ 6の目が出る確率は1(100%)!ではないですね!
⇒ 確率は投げる前の「予想」です (一発で6が出たのはただの結果論!)
また、はずれ1~5も区別して数えていますね
「はずれ」か「当たり」の2通りではないですね
今回は1の目~5の目は明らかに違うと自然に区別できましたが
赤玉1個と白玉5個であっても、赤球1、白玉2、白玉3、白玉4、白玉5、白玉6、(または 赤球1、白玉1、白玉2、白玉3、白玉4、白玉5、) と区別をつけます
⇒ 確率は区別がないものはこちらで区別をつける
⇒ そして、確率も結局は「割合」なので、

(全てに区別をつけて)
確率 = \(\large{\frac{対象}{全体}}\) = 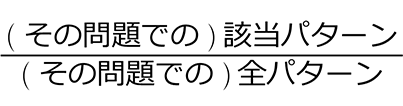 =
= 
ですね
《 例 》 1つのサイコロを1回振って、「2」か「4」が出る確率は?
確率 = 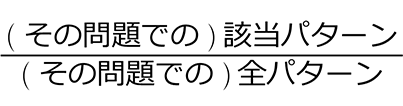
「2」が出るパターン+「4」が出るパターン → 2パターン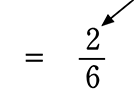 = \(\large{\frac{1}{3}}\) ですね
= \(\large{\frac{1}{3}}\) ですね
⇒ 確率はの答は「既約分数(最も約分された形)」で表現します
(約分しないほうがイメージしやすいのですが・・・約分です!)
イ 確率を用いた不確定な事象の説明
〔 確率総論 〕
「確率」とは、その事柄の起こりやすさを数値化したものでしたね!
全てに区別をつけて
確率(p) =  =
=  でしたね
でしたね
● 区別があるかないかの判断
《 区別があるもの 》
⇒ 特徴が違うもの
| ・ | 数字やアルファベットがふられたもの (サイコロ、コイン、じゃんけん、数字のふられたカード・玉など) |
| ・ | 人 (男子3人といっても男子1、男子2、男子3です) |
| ・ | りんごとみかん (名詞が違う) |
→ 「(サイコロの)目(1~6)」、「(コインの)表, 裏(0~1)」 、「(じゃんけんの)グー~パー(1~3)」がもう数字と見れますものね。
問題文では「大小2つのサイコロ」「コインAコインB」「AさんBさんの2人がじゃんけんをして」と親切に区別をつけてくれていますが、なくても実はサイコロA、コインB、手C ですね
⇒ 「サイコロ」、「コイン」、「じゃんけん」 というフレーズがあれば無条件で「区別がある」
その中でも、1つなのに特徴を複数もつもの (複数特徴系)
| ・ | サイコロ (1つで1~6の6つの特徴) |
| ・ | コイン (1つで表~裏の2つの特徴 (≒0, 1だけの目のサイコロ)) |
| ・ | じゃんけん (1つでグー・チョキ・パーの3つの特徴(1, 2, 3だけの目のサイコロ)) |
ということは、1つにつき 1特徴なもの (1特徴系)
| ・ | 数字やアルファベットがふられたもの (1と書かれたカード、2と書かれた玉、3と書かれたはずれくじ など) |
| ・ | 人 (女子1、女子2) |
《 区別がないもの 》
⇒ 特徴がないもの
| ・ | 白玉3個、白いカード4枚、はずれくじ5本、フルーツ3個、みかん4個、お菓子5個、など |
| → | これらは確率の場面では「同様に確からしい」を確保するためにこちらで必ず区別をつける |
4枚の白カード → 白カード1、白カード2、白カード3、白カード4 ← 上の「1つにつき 1特徴なもの(1特徴系)」に昇格!
⇒ 結局、確率の場面では「すべて異なる」ものしか扱わないということにつながりましたね、難しかった同じものを含む順列や同じものを含む組合せは扱わないということですね (ただし、数えるためのテクニックとして「同じものを含む全順列」の知識があれば、少し楽に当該事象を数えられますね(親中数え) (後述)
ex. 白玉4つから1つを選ぶ、何通り?
「確率」の場面ではない場合(「場合の数」の問題の場合)・・・
(区別がないので) 〇〇〇〇 → 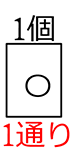 → 1通り
→ 1通り
「確率」の問題のときは、何通り?
(区別をつけて) ①②③④ → 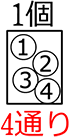 → 4通り
→ 4通り
※ 存在している以上 神の目では別物ではありますが「人間の目では区別できない」というだけ → 確率のときはこちらで数字などを書いて区別をつける!
cf..
確率も結局は、\(\large{\frac{対象}{全体}}\) という「割合」ですね
ex.
食塩水100g中、塩が20g、濃度(塩の割合)は?
→ \(\large{\frac{対象}{全体}}\) = \(\large{\frac{20}{100}}\) = \(\large{\frac{1}{5}}\) ( = 20%)
(イメージ)
水1つぶ1つぶを区別のある「1g」、塩1つぶ1つぶを区別のある「1g」とイメージすると、
1つぶ1つぶを区別しなければ、\(\large{\frac{塩}{食塩水}}\) = \(\large{\frac{塩}{水+塩}}\) = \(\large{\frac{1通り}{1通り+1通り}}\) = \(\large{\frac{1}{2}}\) (50%) となってしまいますね
1つぶ1つぶを区別しているので、\(\large{\frac{塩}{食塩水}}\) = \(\large{\frac{塩}{水+塩}}\) = \(\large{\frac{20通り}{20通り+80通り}}\) = \(\large{\frac{20}{100}}\) = \(\large{\frac{1}{5}}\) ( = 20%) となるのですね
| ⇒ | 割合のときは 無意識に区別をつけて数えていた |
| ⇒ | 確率も割合ですね、「確率のときはすべてに区別を付けて数える」は → 当たり前のことを言われているだけだった! |
● 同様に確からしい
「同様に確からしい」とは
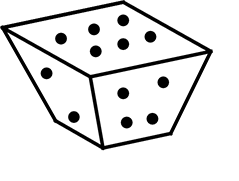
このようなサイコロは
「同様に確からしくない」ですね!
本能的に「6」が出にくい感じですね
すなわち、「同様に確からしい」とは、「物理的」にも「データ(統計)的」にも、
それぞれが「平等(まんべんない)」ということですね!
| → | 全36通りなら、36回の試行ですべて1回ずつ起こる! |
| → | 1つ1つの事象を見たとき分母、分子がすべて同じということ |
1の目\(\large{\frac{1}{6}}\)、2の目も\(\large{\frac{1}{6}}\)、3の目も4も5も6も\(\large{\frac{1}{6}}\)、\(\large{\frac{1}{6}}\)、\(\large{\frac{1}{6}}\)、\(\large{\frac{1}{6}}\)、合計 1
⇒ この「同様に確か」という前提がなければ、正しい確率が求められませんので、確率の問題の大前提になります

「同様に確からしい」を確保するために…
| ① | サイコロ、コイン、じゃんけんなど複数特徴系はマスに基準名をつける(順列な数え方) |
| ② | 区別のない玉、カード、は区別をつけて1特徴系に昇格させる (マスの基準名は問題次第) |
① 2個のサイコロの出目全36通り中、1と 2の目が出るのは何通り?
→ ( ) と (
) と ( ) の2通り
) の2通り
→ 基準名( ) をなくして〈1, 2〉の1通り(組合せ数え)としては「同様に確からしい」という前提がくずれてしまいます。〈1, 2〉{(
) をなくして〈1, 2〉の1通り(組合せ数え)としては「同様に確からしい」という前提がくずれてしまいます。〈1, 2〉{(
・ 同様に(
・ 同様に(
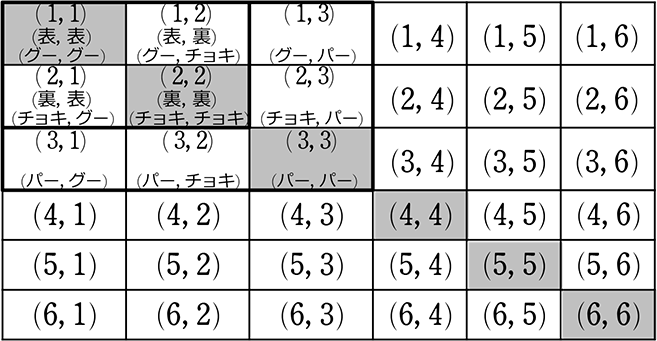
⇒ 複数特徴系は →ぞろ目ラインがある → 必ず順列数え‼
ex. (
②番(区別のないもは区別をつける)
これは先に説明済みですね。区別のないまま数えると、①とは別の意味で「同様に確からしい」という前提がくずれてしまうということですね
| ↓ | 「同様に確か」のために、区別をつける |
123456
宝くじのはずれは全1000万本中何通り? → 確率の場面では 1通りではないですね、はずれ達に区別をつけて…999万9999通り!
1等の当たる確率は? → 当たりかはずれの\(\large{\frac{1}{2}}\) …ではないですね!\(\large{\frac{1}{1000万}}\)
⇒ 区別のないものは 区別をつけて1特徴系に昇格させる
● 数え方の種類
2種類の数え方があります
① (並びにこだわる)順列数え
② (並びにこだわらない)組合せ数え
(場合の数の数え方)
ex.
12345の玉から、続けて2回とるとき、2つの玉が2と4となるのは何通り?
→ 「続けて」より → 1回目2回目という順番がある → 並びにこだわる → 順列数え
∴ (
ex.
12345の玉から、続けて2回とるとき、1回目の玉が2、2回目の玉が4となるのは何通り?
→ 「続けて」より → 1回目2回目という順番がある → 並びにこだわる → 順列数え
∴ (
ex.
12345の玉から、同時に2つとるとき、2つの玉が2と4となるのは何通り?
→ 「同時に」より → (2, 4)も(4, 2)も組合せ的に同じだ! → 並びにこだわらない → 組合せ数え
∴ 〈2, 4〉の1通り
親中ではどちらで数えたのかわかりやすいように
| ① | 順列数えで数えたものは (丸カッコ)にしますね |
| → | 順列数えは必ず( |
| ② | 組合せ数えで数えたものは 〈クカッコ〉にしますね |
→ 組合せ数えには基準名はありません、自動で昇順に並び変わるイメージ 〈4, 2〉 → 〈
問題文から、どちらの数え方なのかという判別方法は 後々しっかり説明しますね
確率をマスターしようとするとき、親中では、この「どちらの数え方なのか」を判別できることが、第1の目標になると考えています
→ 判別できなければ、正しい樹形図や表や列挙が そもそも書けないですものね!
● 全通り(=全事象 → 分母にくるもの)は「計算」で求まる
⇒ 1つにつき複数特徴(サイコロ、コイン、じゃんけん)の全事象は
( ・・・)
・・・)
( ・・・)
・・・)
(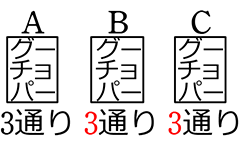 ・・・)
・・・)
次のマスも前のマスと同じ通り数分選べる → 重複順列的ですね
・ サイコロ2個の全事象は? → 62通り=36通り
・ サイコロ3個の全事象は? → 63通り=216通り
・ コイン3枚の全事象は? → 23通り=8通り
・ コイン4枚の全事象は? → 24通り=16通り
・ 3人のじゃんけんの全事象は? → 33通り=27通り
・ 4人のじゃんけんの全事象は? → 34通り=81通り
⇒ 1つにつき1特徴(人、カード、玉、くじ、みかんなど)の全事象は
(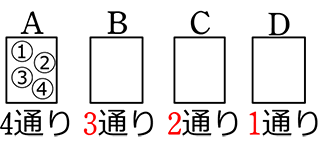 )
)
1つ目のマスに1つしかない自分が入ったら、次のマスに自分は入れない!
ということは
次のマスは前のマスより1通りずつ減少した通り数になる → 普通順列的ですね
・ 1~6の玉6個から3つを選び並べる(=並びにこだわる)全事象は?
→ ( )=\({}_6 \mathrm{ P }_3\) =6!の前3つ =6×5×4=120通り (Pの意味)
)=\({}_6 \mathrm{ P }_3\) =6!の前3つ =6×5×4=120通り (Pの意味)
・ 1~6の玉6個から3つを選ぶ(=並びにこだわらない)全事象は?
→ ( )÷3!= \({}_6 \mathrm{ C }_3\) = 6!の前3つ÷かぶりをなくすための3! = \(\large{\frac{6×5×4}{3×2×1}}\) = 20通り (Cの意味)
)÷3!= \({}_6 \mathrm{ C }_3\) = 6!の前3つ÷かぶりをなくすための3! = \(\large{\frac{6×5×4}{3×2×1}}\) = 20通り (Cの意味)
・ 1~4のカード4枚から2枚を「選び並べる」全事象は?
→ ( )=\({}_4 \mathrm{ P }_2\) =4!の前2つ =4×3=12通り
)=\({}_4 \mathrm{ P }_2\) =4!の前2つ =4×3=12通り
・ 1~4のカード4枚から2枚を「選ぶ」全事象は?
→ ( )÷2!=\({}_4 \mathrm{ C }_2\) =4!の前2つ÷2! =4×3÷2=6通り
)÷2!=\({}_4 \mathrm{ C }_2\) =4!の前2つ÷2! =4×3÷2=6通り
・ 5人から2人を「選び並べる」全事象は?
→ ( )=\({}_5 \mathrm{ P }_2\) =5!の前2つ =5×4=20通り
)=\({}_5 \mathrm{ P }_2\) =5!の前2つ =5×4=20通り
・ 人5人から2人を「選ぶ」全事象は?
→ ( )÷2!=\({}_5 \mathrm{ C }_2\) =5!の前2つ÷2! =5×4÷2=10通り
)÷2!=\({}_5 \mathrm{ C }_2\) =5!の前2つ÷2! =5×4÷2=10通り
| ・ | 複数特徴系 → 絶対重複順列 |
| ・ | 1特徴系 → 問題により普通順列や普通組合せ |
| ⇒ | 分子の当該事象数は、必要ならば「樹形図」「表」を作成、できれば「列挙」で求めたいですね |
● ぞろ目ラインがあるとどうして順列数え?
→ 複数特徴のサイコロ、コイン、じゃんけんは「同様に確からしい」という前提をくずさないために(ぞろ目は少ない)、必ず順列数えでとなります。(1, 2)と(2, 1)で2通り、(表, 裏)と(裏, 表)で2通り、(グー, チョキ)と(チョキ, グー)で2通りですね
(〈1, 2〉で1通り、〈表, 裏〉で1通り、〈グー, チョキ〉で1通りという「組合せ数え」をしてはいけない!)

→ 大が1の目、小が2の目になるのは何通り? ( → \(\large{\frac{順列数え}{重複順列}}\)
→ \(\large{\frac{順列数え}{重複順列}}\)
→
対自動成立 → \(\large{\frac{対象}{全体}}\) =  → \(\large{\frac{親中数え}{重複順列}}\)
→ \(\large{\frac{親中数え}{重複順列}}\)
組合せ数えのようなことをすると →  や
や  で割合がおかしくなってしまう ← ぞろ目ラインを入れて計算しても、入れずに計算しても、正確ではないということですね
で割合がおかしくなってしまう ← ぞろ目ラインを入れて計算しても、入れずに計算しても、正確ではないということですね
∴ ぞろ目ラインがある → 必ず順列数え
→ この点、1特徴の人、数字を書いたカード・玉・物は、問題により並びにこだわらない「組合せ数え」でもよいときがありますね
・ 6個の(①②③④⑤⑥)から2個「選び」「並べる」全通りは? →30通り!(\({}_6 \mathrm{P }_2\))
↑ぞろ目ラインがないですね
→ 1回目が1番、2回目が2番は何通り?
(
対不成立 → \(\large{\frac{対象}{全体}}\) =  → \(\large{\frac{順列数え}{順列}}\)
→ \(\large{\frac{順列数え}{順列}}\)
そのとき、確率は? \(\large{\frac{1}{30}}\)
→
(1, 2)+(2, 1) で2通り!
対自動成立 → \(\large{\frac{対象}{全体}}\) =  → \(\large{\frac{順列数え}{順列}}\)
→ \(\large{\frac{順列数え}{順列}}\)
そのとき確率は? \(\large{\frac{2}{30}}\)=\(\large{\frac{1}{15}}\)
もう少し踏み込んで…ぞろ目ラインがない → 対が自動成立するものは斜め線で折りたたんでも「同様に確か」が崩れない
・ 6個から2個「選ぶ」全通りは? → 15通り!(\({}_6 \mathrm{C }_2\))
→ 「続けて」2回とって、
「並びにこだわる」→「順列数え」
→ ですが「並びにこだわらなくても結果同じ」
対自動成立 →  (\(\large{\frac{順列数え}{順列}}\))
(\(\large{\frac{順列数え}{順列}}\))
=  (\(\large{\frac{組合せ数え}{組合せ}}\)) ←割合がくずれない(約分のイメージ)
(\(\large{\frac{組合せ数え}{組合せ}}\)) ←割合がくずれない(約分のイメージ)
→ 組合せ数え(で楽をしてもよい) → 〈1, 2〉で1通り!
そのとき確率は? \(\large{\frac{1}{15}}\) (上と同じですね!)
→ 「同時に」2個とって、1番
「並びにこだわらない」 → 組合せ数え(でなければいけない) → 〈1, 2〉の1通り! (ルール)
(ルール)
1特徴系は
後に詳しくお話しますが、さわりだけ
● 「続けて」 → 「順列数え」
| ・ | 結果、並びにこだわっても同じこと なら → 組合せ数え(でもよい) |
| ex. | 「続けて」2個で、2つの和が3となる確率 → (1, +2)=3 も (2, +1)=3も並びにこだわる意味がない(対も自動成立) →組合せ数えで楽してもよい |
| → | 答だけなら、組合せ数えで楽ができる |
| → | 求める過程も書け なら、さすがに順列数え |
| ● | 「同時に」 → 「組合せ数え」(数学ルール) |
・ ただし、分母と分子の数え方は同じ数え方ということを忘れないでくださいね!
\(\large{\frac{順列数え}{n^r}}\)〇、\(\large{\frac{順列数え}{P}}\)〇、\(\large{\frac{組合せ数え}{C}}\)〇、\(\large{\frac{順列数え}{C}}\)×、\(\large{\frac{組合せ数え}{P}}\)×
⇒ 複数特徴系のように、ぞろ目ラインがあるものは、表を折り返すと
ぞろ目ラインは残る側?消える側?
| → | どちらにしても「同様に確か」が崩れる |
| ∴ | 複数特徴系 → ぞろ目ラインがある → 組合せ数えダメ → 絶対順列数え ということですね |
⇒ 複数特徴系と1特徴系での「とにかく〈1, と2〉」の意味は全然違いますね
・ 複数特徴系の「とにかく」 → 「対」になるものも「自動成立」
(1通りが、2通りになるイメージ)
・ 1特徴系の「とにかく」 → 「数え方」を「組合せ数え」にしてもいいよ
(2通りが、1通りになるイメージ)
少し難しいところだと思います、後半で個別問題を解いているときに「なんとなく混乱してきた時」、ここに戻ってきてくださいね
● 余事象
事象Aに対して、「事象Aが起こらない」という事象を、事象Aの余事象と言いますね

| ・ | 問題文がスポットを当てている方 → 当該事象 |
| ・ | 反対側の方 → 余事象 |

当該事象の確率+その余事象の確率 = 1 (全部:100%) ですので、
当該事象の確率 = 1 - その余事の確率 と移項できますね
または
当該事象+その余事象 = 全通り
当該事象 = 全通り - その余事象
そして、当該事象を求めるより、余事象を求める方が楽な場合は
「1 - 余事象の確率」または「全通り-余事象」を利用しない手はないですね!
《 例 》
3枚のコインを投げて、
この「少なくとも」というフレーズが出てきたら、「余事象」を求める方が楽なことが多いですね
なぜなら、「少なくとも1枚が表」とは、 (表を0、裏を1としますね)
全部表の(0, 0, 0) 2枚表の(1, 0, 0) (0, 1, 0) (0, 0, 1) 1枚表の(1, 1, 0) (1, 0, 1) (0, 1, 1) の 7通りもありますね (全事象は23=8通りなのに)
「少なくとも~」 ⇒ 結構多いというイメージ
→ 全8通り中、7通りも挙げるならそうでないパターンを挙げて、「全部-そうでない」をするほうが楽ということですね
(もちろん、パット見 当該事象とそうでない方のどっちが多いかわからないときは当該事象を挙げていけばよいだけですね)
では、「少なくとも1枚が表」の余事象は?
「少なくとも1枚が表」 =「1枚
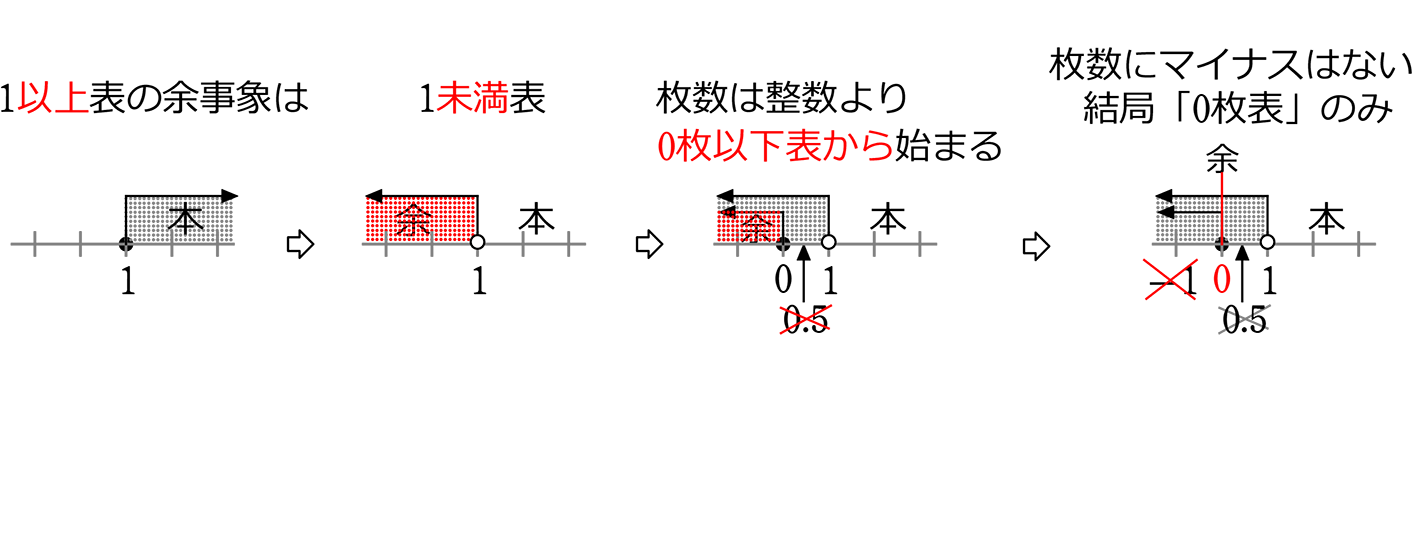
では「全部裏」の確率は?
サイコロのぞろ目と同じですね! 「6面体」→「2面体」になっただけですので、
→ (1, 1, 1)の1通り → 全部裏の確率は \(\large{\frac{1}{2^3}}\)= \(\large{\frac{1}{8}}\)
∴ 本事象「少なくとも1枚が表」の確率は、 1-\(\large{\frac{1}{8}}\) = \(\large{\frac{7}{8}}\) ですね!

「少なくとも」や「(じゃんけんの)あいこ」というフレーズが出てきたら 余事象 を考える
ですが、「簡単になる」とよく言いますが
「余事象」がなんなのかは何気に難しいですね!
練習あるのみです

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)

↑3本中、2つのうち、などは前提条件です → 変化しません
ここまでのまとめ
| ・ | 確率を考えるときは、区別のないものは区別をつける |
・確率 = \(\large{\frac{対象}{全体}}\) = 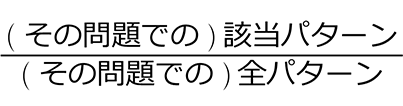 =
= 
| ・ | 数え方には2種類ある ① 並びにこだわる 順列数え ② 並びにこだわらない 組合せ数え |
| ・ | 複数特徴のサイコロ、コイン、じゃんけんは |
| → | 無条件で区別がある (数字が書いてあるので) |
| → | 必ず「順列数え」 (同様に確かのため:ぞろ目ラインがある) |
| → | 全事象(分母)は重複順列(樹形図の枝分かれは永遠に同数) |
| ・ | 1特徴の、人、数字を書いた物(カード、玉、くじ等)は |
| → | 数字があるので区別がある(人は無条件で区別がある) |
| → | 問題により「順列数え」「組合せ数え」 |
| → | 全事象(分母)は普通順列か組合せ(樹形図の枝は減っていく) |
| ・ | 区別のないものは、こちらで区別をつけて(「同様に確か」のため)、1特徴系に昇格させる |
| ・ | 分母は計算で求まる、分子はその都度考える |
| ・ | 「少なくとも」「あいこ」というフレーズがあれば、余事象を考える |
| ・ | 順列数え → 並びに「こだわる」数え方 |
→ 〈1, 2〉は、(
→ (
| ・ | 組合せ数え → 並びに「こだわらない」数え方 |
| → | ( |
| → | 1と2が〈クカッコ〉の中で勝手に小さいもの順に整列してしまう!イメージ |
〈2, 1〉 → 〈1
確率の個別的な問題の研究
それでは個別的に問題を見ていきますね
まず、確率の問題を解くうえで、知っていると「理解が速くなる」「解く時間が早くなる」『場合の数』の知識
| ・ | 普通順列 |
| ・ | 全順列 |
| ・ | 同じものを含む全順列 |
| ・ | 組合せ |
| ・ | 組合せ3つのイメージの1つ「型のイメージ」 |
これらを理解できていると、勉強途中で起こると思われる「混乱」が防げるのかなと思います
a 複数特徴系 (サイコロ、コイン、じゃんけん)
① サイコロ
● サイコロ1個
《 例 》
1つのサイコロを投げるとき、
◎全事象は何通り?
→ 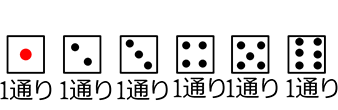 で6通り
で6通り
→ または、マスで ( 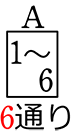 ) で6通り
) で6通り
→ または、計算で 61で6通り
◎ 3の目が出る確率は?
→ 3の目を列挙すると、(3, )の1通り
∴ 確率=\(\large{\frac{当該事象}{全事象}}\)=\(\large{\frac{1通り}{6通り}}\)=\(\large{\frac{1}{6}}\)
◎ 4か6の目が出る確率は?
→ 4か6の目を列挙すると、(4, )(6, )の2通り
∴ \(\large{\frac{1通り+1通り}{6通り}}\)=\(\large{\frac{2}{6}}\)=\(\large{\frac{1}{3}}\)
cf. 今、分子は1通り+1通りと自然に「+」にできたと思います。
ですが、複雑な問題を解いているときに、「どうしてここがプラス?」と疑問に思う時が来るかもしれません
そんな時は、この1番シンプルな形なここに戻ってきてくださいね!原理はこの問題と同じということですね
◎ 偶数の目が出る確率は?
→ 偶数を列挙すると、(2, )(4, )(6, )の3通り
∴ \(\large{\frac{1+1+1}{6}}\)=\(\large{\frac{3}{6}}\)=\(\large{\frac{1}{2}}\)
◎ 1以上3未満の目が出る確率は?
→ 1以上3未満を列挙すると、(1, )(2, )の2通り (未満なので「3」は入らない)
∴ \(\large{\frac{1+1}{6}}\)=\(\large{\frac{2}{6}}\)=\(\large{\frac{1}{3}}\)
◎ 2以上の目が出る確率は?
→ 2以上を列挙すると、(2, )(3, )(4, )(5, )(6, )の5通り
∴ \(\large{\frac{5}{6}}\) でもよいですし
→ 余事象=2未満=(整数なので)  1以下=(1, )の1通り
1以下=(1, )の1通り
本事象=全通り-余事象=6-1=5通り ∴ \(\large{\frac{5}{6}}\)でもよいですし
本確率=1-余事象の確率=1-\(\large{\frac{1}{6}}\)=\(\large{\frac{5}{6}}\)でもよいですね
● サイコロ2個 (中学確率のメイン)
《 例 》
2つのサイコロを同時に投げるとき、
◎ 全事象は何通り?
→ ( ) で
) で
6通り+6通り=12通り?
6通り×6通り=36通り?どっちでしょう?
もうわかりますね!「
念のため確認してみると、
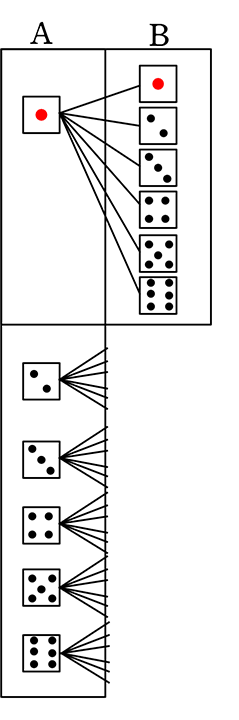
Aの1通りにつき6通りある (積の法則の「
そのAは全部で、6通りある (九九の「
(↑本来は、6通り+6通り+6通り+6通り+6通り+6通り
= 36通り (和の法則の場面))
すなわち、
6通り
縦から先に考えても同じことですね
6通り
◎ 全事象の表を作りましょう
→ (大, 小)の順で。(赤, 白)でも(1回目, 2回目)でも何でもよいですね

1つから6枝も出るサイコロの「樹形図」は大変すぎですね
サイコロは「列挙」か「表」でいきますね
表も早く書きたいなら
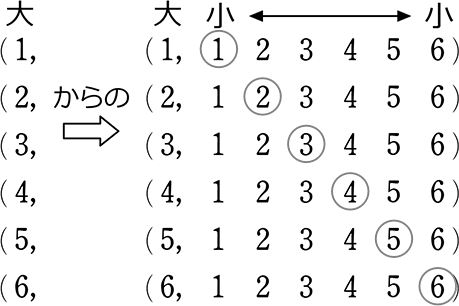
で十分ですね
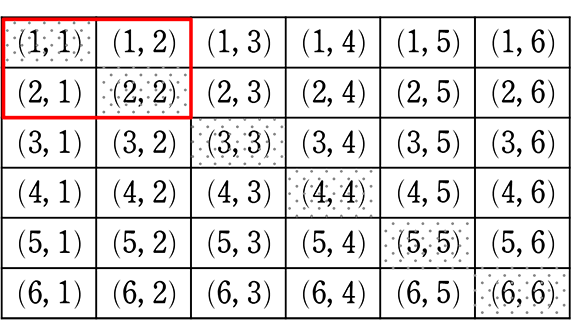
◎ 上の表で〈2, 5〉の目になるものを黒枠、〈3, 3〉の目になるものを赤枠で囲みましょう
→ 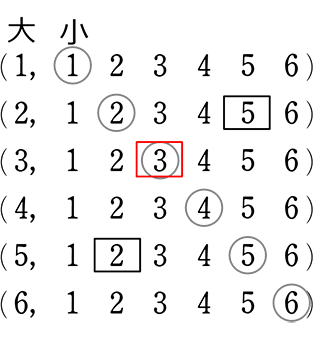
→ 〈2, 5〉は(
〈3, 3〉は(
ぞろ目は出にくい(若干)
サイコロの問題を解いていると、
ぞろ目(

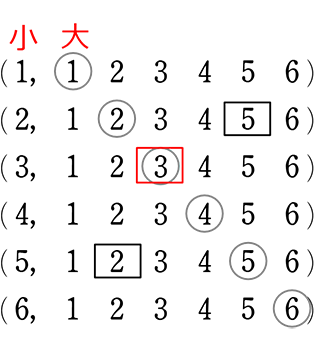
全事象は(大→小で数えた)36 + (小→大で数えた)36=72通り、
〈2, 5〉は全部で4通り
∴ \(\large{\frac{4}{72}}\)=\(\large{\frac{2}{36}}\)
〈3, 3〉は全部で2通り
∴ \(\large{\frac{2}{72}}\)=\(\large{\frac{1}{36}}\)
⇒ 同じことですね!
ex. 1~10に3は何個?1個! 10~1に3は何個?1個 → 3は20個中2個=10個中1個 → 10~1を数える意味は…ないですね
⇒ というわけで、ぞろ目は出にくい(若干)!表の面積割合からも分かりますね、ぞろ目の斜め面積とそれを挟む2つの三角形の合計面積は全然違いますものね!
◎ 2つ同時に投げて、和が9になる確率は?
・ 「サイコロ」より → 絶対順列数え
→ 和が9を列挙すると、(3, 6)(4, 5)(5, 4)(6, 3)の4通り
・ 全事象 = 62 = 36通り
∴ \(\large{\frac{4}{36}}\) =\(\large{\frac{1}{9}}\)
親中数え
複数特徴系は「必ず順列数え」ですが、
順列数えで列挙していくことは何気に大変ですね
そこで
ぞろ目(〇, 〇)は1通り、(〇, △)のように2数が異なるものは2通りある(対になるもの)ということで、
(3, 6)や(4, 4)のように 上がるか水平のものだけ列挙して、
上がるか水平のものだけ列挙して、
(6, 3)のように 下がるものは列挙せずに行きますね
下がるものは列挙せずに行きますね
→ 下がる方は列挙漏れしやすい
→ 考える時間の省略
ex. 〈3, 6〉 〈4, 4〉 〈5, 6〉 なら、2通り+1通り+2通り=5通り
・ 対になるものも成り立つ → 親中数えOK
ex. 和が3 → (1, +2)も対の(2, +1)も和が3
・ 対になるものは成り立たない → 親中数えダメ → 真面目に順列数え
ex. (1回目)-(2回目)が5 → (6, -1)=5、対の(1, -6)=-5

本当の原理は
「同じものを含む全順列」ですね
〈1, 1〉 → \(\large{\frac{2!}{2!}}\) = 1通り (1, 1を並び替えてできる数字)
〈1, 2〉 → 2! = 2通りを持つ (1, 2を並び替えてできる数字)
〈1, 1, 1〉→ \(\large{\frac{3!}{3!}}\) = 1通り
〈1, 1, 2〉 → \(\large{\frac{3!}{2!}}\) = 3通りを持つ
〈1, 2, 3〉 → 3! = 6通りを持つ
ex.
〈1, 2〉 → (
〈1, 2, 3〉 → (
〈1, 1, 2〉 → (
⇒ 「組合せ数え」からの「順列数え」訂正 = 「親中数え」としますね
→ 「組合せ数え」の列挙スピードは、「順列数え」列挙スピードより3倍くらい早いと思います(列挙漏れの可能性も少なくなります)
⇒ 念のため、( , )は実は(
⇒ 親中数えは、組合せ数えを利用した「順列数え」です
もちろん、問題が「すべて挙げよ」なら、(3, 6) (6, 3) (4, 4) (5, 6) (6, 5)とすべて書くしかないですが…

◎ 同じ問題です、2つ同時に投げて、和が9になる確率は?
・ 「サイコロ」より → 絶対順列数え
→ (3, +6)も(6, +3)も意味が変わらない → 親中数えOK
→ 和が9を列挙すると、〈3, 6〉〈4, 5〉=2通り+2通り=4通り
・ 全事象 = 62=36通り
∴ \(\large{\frac{4}{36}}\)=\(\large{\frac{1}{9}}\)
◎ 和が「5以上」になる確率は?
・ 「サイコロ」より → 絶対順列数え
・ (1, 4)(1, 5)… 結構ありそうだな
→ 余事象はどうかな?
・ 「5
・ (1,+3)も(3,+1) も意味が変わらない → 親中数えOK和、積は親中数えOK
・ 和の範囲2~12で、「4以下」の(見本)… 2, 3, 4
→ 〈1, 1〉〈1, 2〉〈1, 3〉〈2, 2〉= 1+2+2+1 ←親中数えですね
= 6通り
∴ 本事象の「5以上」=36-6 = 30通り
∴ 確率は \(\large{\frac{30}{36}}\) = \(\large{\frac{5}{6}}\)
列挙になれてくると普通列挙でも早いですね
(1, 4 5 6)(2, 3 4 5 6)(3, 2 3 4 5 6)(4, 全)(5, 全)(6, 全) =3+4+5+6+6+6 =30通り
◎ 少なくとも1つは「3
・ 「サイコロ」より → 絶対順列数え
・ 「少なくとも」 → 余事象は?→「全部3
・ (1, 2)も(2, 1) も意味が変わらない → 親中数えOK
→ どちらも3以下を列挙すると、〈1, 1〉〈1, 2〉〈1, 3〉〈2, 2〉〈2, 3〉〈3, 3〉 → 1+2+2+1+2+1= 9通り
∴ 本事象= 36-9 = 27通り
∴ 確率は \(\large{\frac{27}{36}}\) = \(\large{\frac{3}{4}}\)
◎ 一方の目が「他方の約数」になる確率は?
・ 「サイコロ」より → 絶対順列数え
・ (2, 4)も(4, 2) も意味が変わらない → 親中数えOK
→ よい考えが浮かばないので「列挙」
〈1, 1〉〈1, 2〉〈1, 3〉〈1, 4〉〈1, 5〉〈1, 6〉〈2, 2〉〈2, 4〉〈2, 6〉〈3, 3〉〈3, 6〉〈4, 4〉〈5, 5〉〈6, 6〉 = 1通り×6コ+2通り×8個= 22通り
∴ \(\large{\frac{22}{36}}\) = \(\large{\frac{11}{18}}\)
◎ 2つ同時に投げて、和が「偶数」になる確率は?
①偶数+偶数 = 偶数
②偶数+奇数 = 奇数、奇数+偶数=奇数
③奇数+奇数 = 偶数
↑憶える必要はありません
簡単な数字でその都度試しましょうね
2+2=4偶数、 2+3=5奇数、 3+3=6偶数
②(余事象)を羅列する方が楽そうですね
・ 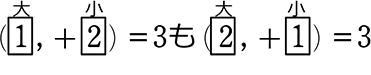 → も意味が同じ(対になるものも当然に成り立つ) → 親中数えOK
→ も意味が同じ(対になるものも当然に成り立つ) → 親中数えOK
・ 2つのサイコロの和の範囲 最小2~最大12
・ その中で奇数になるものは?(見本) 3, 5, 7, 9, 11
→ (見本)を見ながら列挙すると、
〈1, 2〉〈1, 4〉〈2, 3〉 〈1, 6〉〈2, 5〉〈3, 4〉〈3, 6〉〈4, 5〉〈5, 6〉 = 2+2+2+2+2+2+2+2+2 = 18通り ←親中数えですね
∴ 本事象 = 36-18 = 18通り
∴ \(\large{\frac{18}{36}}\)=\(\large{\frac{18}{36}}\)=\(\large{\frac{1}{2}}\)
結果、半分なので偶数を数えてもよかったですね
◎ 2つの目の積が「偶数」になる確率は?
①偶数×偶数=(2×2=)偶数
②偶数×奇数=(2×3=)偶数
③奇数×奇数=(3×3=)奇数
③で数える方が数えやすいかな?
→ (奇, 奇)を列挙すると、(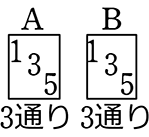 ) = 9通り(奇数になる目の出方)
) = 9通り(奇数になる目の出方)
∴ 本事象の偶数= 36-9 = 27通り
∴ 確率は \(\large{\frac{27}{36}}\) = \(\large{\frac{3}{4}}\)
(列挙方法はどんどん楽な方法になっていくはずですね)
・ 積が奇数を列挙
| → | (1, 1)(1, 3)(1, 5)(3, 1)(3, 3)(3, 5)(5, 1)(5, 3)(5, 5) =9通り |
| → | 〈1, 1〉〈1, 3〉〈1, 5〉〈3, 3〉〈3, 5〉〈5, 5〉=1+2+2+1+2+1 =9通り |
| → | (1, 1 3 5)(3, 1 3 5)(5, 1 3 5) =1×3+1×3+1×3 =9通り |
| → | 〈1, 1 3 5〉〈3, 3 5〉〈5, 5〉 = 1+2+2+1+2+1 = 9通り |
| → | (1 3 5, 1 3 5) = 3×3 = 9通り |
\(\parallel \)
( )=9通り
)=9通り
※ 「列挙」がパターン化できる → 「マス」になる
ということは、
全事象=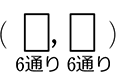 =36通り などは、「1パターン化できた」『列挙』ということですね
=36通り などは、「1パターン化できた」『列挙』ということですね
→ 「全事象は計算で求まる」は ⇒ 正しくは「全事象の列挙は1パターンで表現できる」 ということですね
◎ 大小2つのサイコロを同時に投げて、大きいサイコロの出た目の数をa、小さいサイコロの出た目の数をbとするとき、方程式 x2=ab の2つの解がともに整数となる確率は? (整数とは)
・ x2=ab → x=±\(\small{\sqrt{ab}}\) → √が残らないa,bは? → abの積が平方数になるのは? (3年:平方根の求め方)
・ (1,×4)も(4,×1) も意味が変わらない → 親中数えOK
・ a×bの範囲は1~36 (見本)は、12=1、22=4、32=9、42=16、52=25、62=36
→ 〈1, 1〉〈1, 4〉〈2, 2〉〈3, 3〉〈4, 4〉〈5, 5〉〈6, 6〉 =1+2+1+1+1+1+1 =8通り
∴ \(\large{\frac{8}{36}}\)=\(\large{\frac{2}{9}}\)
《 例 》
1個のサイコロを続けて2回投げるとき、
◎ 下の全事象の表から1回目の目が2、2回目の目が5になるものを囲みましょう
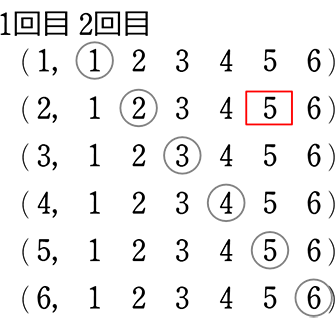
→ 「同時に投げる」とにかく系と違い いつもセットの(
◎ 1回目に出る目から2回目に出る目をひいた値が負の数になる確率は?
・ 1回目<2回目ということですね
・ (1,<2)も(2,<1) で意味が違う(対になるものは当然には成り立たない) → 親中数えダメ
→ 上の表を利用すれば、ぞろ目斜め線より右側にあるもの達ですね=15通り
→ 列挙するなら、(1のとき, 2 3 4 5 6)の5通り +(2のとき, 3 4 5 6)の4通り +(3, 4 5 6)の3通り +(4, 5 6)の2通り +(5, 6)の1通り =15通り
∴ \(\large{\frac{15}{36}}\)=\(\large{\frac{5}{12}}\)
◎ 出る目の積が3の倍数になる確率は?
・  も意味が変わらない → 親中数えOK
も意味が変わらない → 親中数えOK
→ もう同時に投げるとにかく系となんら変わりませんね
・ 2つのサイコロの積の範囲 1~36
(見本は) 3の倍数 → 因数に「3」を含むもの → 「3」と「6」が絡んでいるもの
→ 〈1, 3〉〈1, 6〉〈2, 3〉〈2, 6〉〈3, 3〉〈3, 4〉〈3, 5〉〈3, 6〉〈4, 6〉〈5, 6〉〈6, 6〉 =2+2+2+2+1+2+2+2+2+2+1 =20通り
∴ \(\large{\frac{20}{36}}\)=\(\large{\frac{5}{9}}\)
(別解)
余事象は「3の倍数でない」 = 「因数に3を含まない」 = 「3, 6 を使わない」
→ (3の目6の目を除いた×4×3の目6の目を除いた×4)= 16通り
→ 本事象 = 36-16 = 20通り
∴ \(\large{\frac{20}{36}}\) = \(\large{\frac{5}{9}}\)
「同時に2個投げる」「1個を続けて2回投げる」
⇒ 全く同じように考えてOKですね
基準名が (
ex.
1, 2の目になるのは?
→ (
→ (
大が1、小が2になるのは? = 1回目が1、2回目が2になるのは?
→ (
→ (
→ よく出てくるのは「同時に2個投げる」( ←9割の問題がこちら)

→ ですが複数特徴系はどのみち「順列数え」
⇒ 対になるものも成立なら親中数えOK
対になるものは成立しないなら親中数えダメというだけですね
ex. 1回目の目をa、2回目の目をbとする
・ (4,+2)も(2,+4)も同じこと → 「単純な和」は親中数えOK
・ (4,×2)も(2,×4)も同じこと → 「単純な積」は親中数えOK
・ (4,-2)と(2,-4)は意味が異なる → 「差」は親中数えダメ
・ (4,÷2)と(2,÷4)は意味が異なる → 「商」は親中数えダメ
・ (4,>2)と(2,>4)は意味が異なる → 「不等号」は親中数えダメ
・ (24,+2)と(22,+4)は意味が異なる → 「一方だけ変化」は親中数えダメ
◎ 1つのサイコロを2回投げるとき、1回目に出た目の数が、2回目に出た目の数の倍数となる確率は?
| ・ | 1回目≧2回目であること、(4,≧2)と(2,≧4) で意味が違う → 親中数えダメ |
・ 1倍も倍数
→ (1, 1) (2, 1) (2, 2) (3, 1) (3, 3) (4, 1) (4, 2) (4, 4) (5, 1) (5, 5) (6, 1) (6, 2) (6, 3) (6, 6) → 14通り
∴ \(\large{\frac{14}{36}}\)=\(\large{\frac{7}{18}}\)
◎ 大小2つのサイコロを同時に1回投げる。大きいサイコロの出た目の数をa、小さいサイコロの出た目の数をbとする。
このとき、\(\large{\frac{2a+b}{3}}\)の値が整数である確率を求めなさい
・ \(\large{\frac{2a+b}{3}}\)=整数 → 2a+b=3・整数 → 2a+bが3の倍数
・ (2×1,+4)=6と(2×4,+1)=9 → 意味が異なる → 親中数えダメ
2a+b が3の倍数ならよいということ、 3, 6, 9, 12, 15 18, 21…当てはめて順次確認するしかないですね
(aに1入れて…2、2+bが3になるのは1、6になるのは4、9になるのは7(7は6以上でout、次はaに2入れて・・・)
(1, 1) (1, 4) (2, 2) (2, 5) (3, 3) (3, 6) (4, 1) (4, 4) (5, 2) (5, 5) (6, 3) (6, 6) =12通り
∴ \(\large{\frac{12}{36}}\)=\(\large{\frac{1}{3}}\)
● 複数特徴系の「樹形図」「表」「列挙」について
中学の確率の問題の解き方は、
・ 「樹形図」の完成 → あてはまるものをpick outという手順が原則となりますが、
実際1日3個も樹形図を書くと嫌になってきますね → 練習量の不足 → 確率の苦手意識につながる可能性大
親子中学では
・ 「数え方の判別(順列数えか組合せ数えか)」 → 「列挙」 → 「全事象は計算」という手順で解いていきますね
| → | 列挙はわかってくると(慣れてくると)、楽しくなってくる |
| → | 楽しければ多くの問題をこなせる |
| → | 列挙ができるということは、樹形図をなぞっていることと同じ プラス同時にpick out作業もしているということ |
| → | 列挙ができる = 樹形図は書こうと思えばいつでも書ける ということになります |
| → | 「答えを求めるまでの過程も書け」という問題のときだけ樹形図を書けばよいですね |
その列挙がよく分からないないのですけど・・・
〔複数特徴系の列挙〕
《 例 》
サイコロA, Bを投げるときの全事象は何通り?
まずは、サイコロの数字
「1 2 3 4 5 6」を書いて
分かりにくければ
「1 2 3 4 5 6-1 2 3 4 5 6」 と2つ書いて・・・

⇒ 複数特徴系の列挙は
・ 見本の数字と
・  なフサフサが右に動いていくイメージでOKですね
なフサフサが右に動いていくイメージでOKですね
→ 複数特徴系でもコインは「表(0)」と「裏(1)」しかないので、もっと楽なイメージがありますので、後ほど説明しますね
じゃんけんは、数字の「値」より「勝ち負け」に注目しますので、独特な数え方が主流になります、こちらも後ほど。
● サイコロ3個
公立高校入試では2個までと思われますが念のため
3個までくると樹形図はおろか表も書いていられないですね
《 例 》
3つのサイコロを同時に投げるとき、
◎ 全事象は何通り?
→ (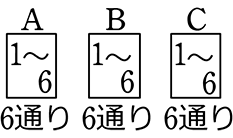 )=6×6×6=216通り
)=6×6×6=216通り
63=216 憶えてしまいたいですね!
◎ 和が「5」になる確率は?
・ 「和」 → 親中数えOK
・ 〈1, 1, 3〉 〈1, 2, 2〉 → \(\large{\frac{3!}{2!}}\)通り+\(\large{\frac{3!}{2!}}\)通り = 3+3 ←親中数えですね = 6通り
∴ \(\large{\frac{6}{216}}\)=\(\large{\frac{1}{36}}\)
◎ 積が「6」になる確率は?
・ 「積」 → 親中数えOK
・ 〈1, 1, 6〉 〈1, 2, 3〉 = 3+6 = 9通り
∴ \(\large{\frac{9}{216}}\) = \(\large{\frac{1}{24}}\)
◎ 少なくとも「2個同じ」になる確率は?
→ 「少なくとも」とくれば「余事象を考える」でしたね
「少なくとも2個同じ」 =「少なくとも2個以上同じ」 ⇒ 余事象は…「2個未満同じ」 = 目は整数より「1個以下同じ」 =「全て異なる」
→ なつかしい「普通の順列」を流用して → (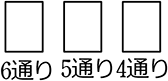 )←1マス目には6~1、2マス目には1マス目で使ったもの以外、3マス目には、それまでに使ったもの以外=結果出来上がった3つの数字はすべて異なっていますね → \({}_6 \mathrm{P }_3\) = 6×5×4 = 120通り
)←1マス目には6~1、2マス目には1マス目で使ったもの以外、3マス目には、それまでに使ったもの以外=結果出来上がった3つの数字はすべて異なっていますね → \({}_6 \mathrm{P }_3\) = 6×5×4 = 120通り
∴ 当該事象は 216-120 = 96通り (96通りは完全ぞろ目や2個ぞろ目)
∴ 確率は \(\large{\frac{96}{216}}\) = \(\large{\frac{4}{9}}\)
◎ 積が「5の倍数」になる確率は?
→ 因数に「5」が1つでもあると5の倍数になってしまいますので
余事象「5が1つも出ない」を考える方が楽ですね
→ 1~6の目から「5」を除くと
1, 2, 3, 4, 6 の5通り → (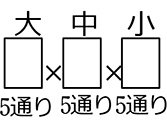 )= 125通り
)= 125通り
∴ 当該事象は 216-125 = 91通り
∴ 確率は \(\large{\frac{91}{216}}\)
◎ 積が「4の倍数」になる確率は?
→ 倍数系は余事象が楽ですね → 余事象は「4の倍数でない」
4(=22)の倍数でないは、因数に4すなわち「2を2個」含んではダメということですね
よって
① 1, 3, 5…A ←使用に制限なし組 (何回使っても22が発生しない)
② 2, 6(←2×3)…B ←制限あり組 (2か6の1つまでは使用OK)(Bを2回使うと22が発生!)
③ 4…C ←使ってはいけない
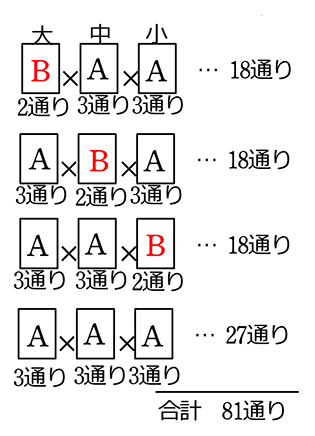
∴ 当該事象は 216-81 = 135通り
∴ 確率は \(\large{\frac{135}{216}}\)=\(\large{\frac{5}{8}}\)
◎ 積が「奇数」になる確率は?
→ 「奇数」×「奇数」×「奇数」のように全て奇数の場合のみ「奇数」ですね
よって、 3通り×3通り×3通り = 27通り
∴ 確率は \(\large{\frac{27}{216}}\) = \(\large{\frac{1}{8}}\)
◎ 順に3回投げる、1回目の目>2回目の目>3回目の目となるのは?
→ 実は654321の異なる6つから異なる3つをその場で選ぶことと同じ意味ですね
ex.  と選んでも
と選んでも と選んでも、同じものが含まれていないので自然に大中小になっていますね (普通組合せ:型のイメージ)
と選んでも、同じものが含まれていないので自然に大中小になっていますね (普通組合せ:型のイメージ)
なるほど~ですね!
よって、\({}_6 \mathrm{C }_3\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\) = 20通り
∴ 確率は \(\large{\frac{20}{216}}\) = \(\large{\frac{5}{54}}\)
1回目の目<2回目の目<3回目の目 なら や
や  で全く同じことですね
で全く同じことですね
● サイコロとの複合問題
〈 1回目の状態を図に書き込める問題 〉
《 例 》
図1のような正五角形ABCDEがあり、点Pは、頂点Aの位置にある。1個のサイコロを2回投げて、次の規則に従ってPを移動させる
規則
1回目は、出た目の数だけ正五角形の頂点上を反時計回りに移動させる
2回目は、1回目に止まった頂点から、出た目の数だけ時計回りに移動させる
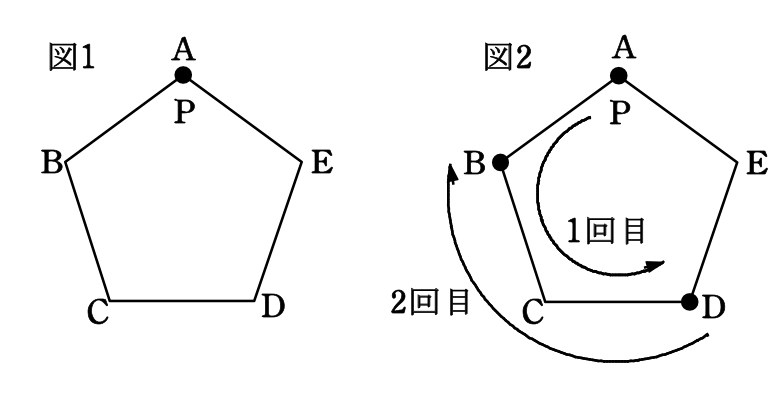
例えば、1回目に3の目が出て、2回目に2の目が出たとすると、Pは図2のように動き、頂点Bに移動する。
この規則に従ってPを移動させるとき、Pの最後の位置がAである確率を求めましょう。
→ 「1回目左、2回目右」より → (2, 3)→E と(3, 2)→B で意味が変る → 親中数えダメ
1回目の位置を書き込むと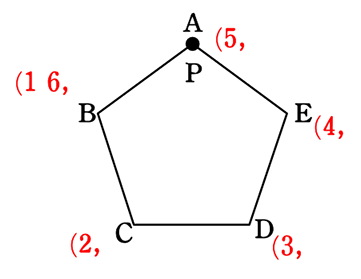
1回目の状態のみ記入
するのがコツですね
Aで止まる2回目の目は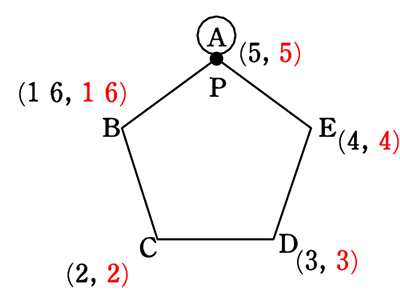
2回目は1回目の記入を
もとにシミレーション
(図のように書き込む必要
はありません
→ どこかに列挙
∴ Bの(2
・ 全事象=サイコロ2個 =62 =36通り
∴ \(\large{\frac{8}{36}}\) = \(\large{\frac{2}{9}}\)
《 例 》
下の段から順に1から8の番号をつけた階段があります。1から6までの目が出るサイコロを投げ、
奇数の目が出たときは、その目の数だけ階段を上がり、
偶数の目が出たときは、その目の数に関係なく1段だけ階段を下ります。
ただし、8番の段に達したときに、階段を上がる数が残っていれば、8番の段から残っている数だけ1ずつ階段を下ります。例えば、6段の段にいるときに5の目が出た場合、2段上がると8番の段に達します。階段を上がる数が3残るので、3段下りて5番の段につきます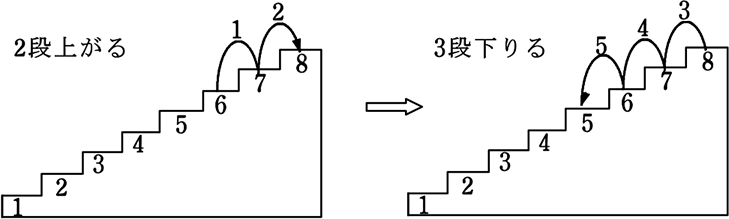
いま、4番の段にいるAさんが
サイコロを2回投げて、
ちょうど8番の段につく確率を求めましょう
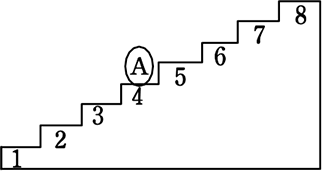
→ 1回目の目の場所を書き込むと…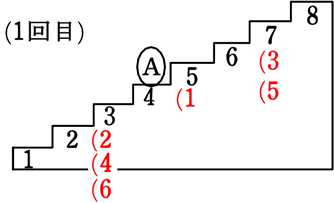
あとは2回目 → 例えば7段目から
最大の6が出ても5段目どまり
∴ 2回目で「降りることなく」8の段で
止まるものを探せばよいですね
奇数は出た目の分上、偶数は1段下ということを再確認してシミレーション

∴ 6通り
・ 全事象 = サイコロ2つ = 36通り
∴ \(\large{\frac{6}{36}}\) = \(\large{\frac{1}{6}}\)
《 例 》
点PがAを出発点として、サイコロの出た目により右回りに進みます
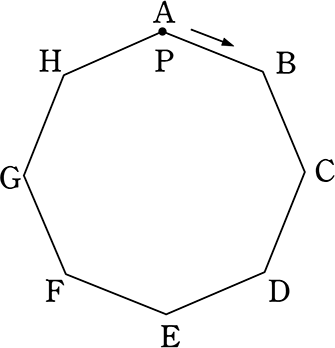
(1) 1回ふって、元のAで止まる確率は?
(「1回ふる」も「1個のサイコロ」も同じことですね)
八角形 → サイコロの最大の目、6 → 最大でも点Gまでしか行けない
∴ 確率は 0
(2) 2回ふって、その和だけ進むとき、元のAで止まる確率は?
<ということは>
→ これくらいなら1回目を書き込まなくてもできそうですね
2個の出目の「和」が、8の倍数 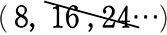 ← 最大6+6 = 12なので
← 最大6+6 = 12なので
→ 和が8の倍数を列挙すると、 〈2, 6〉〈3, 5〉〈4, 4〉
→ 2+2+1 = 5 通り ←親中数えですね
・2個のサイコロの全事象は → 6×6 = 36通り
∴ 確率は \(\large{\frac{5}{36}}\)
(3) 2回ふって、その積だけ進むとき、元のAで止まる確率は?
<ということは>
2個の出目の「積」が、8の倍数 
→ 積が8の倍数を列挙すると、 〈2, 4〉〈4, 4〉〈4, 6〉 = 2+1+2 = 5 通り
・2個のサイコロの全事象は36通り
∴ \(\large{\frac{5}{36}}\)
(4) 3回ふって、その和だけ進むとき、元のAで止まる確率は?
<ということは>
3個の出目の「和」が、8の倍数 ←最 大6+6+6=18なので
←最 大6+6+6=18なので
→ 3個の和が8の倍数を列挙すると、
〈1, 1, 6〉〈1, 2, 5〉〈1, 3, 4〉〈2, 2, 4〉〈2, 3, 3〉和が8はここまで
和が16は 〈4, 6, 6〉〈5, 5, 6〉
よって、3+6+6+3+3+3+3 = 27通り ←親中数えですね
・3個のサイコロの全事象は 216通り
∴ \(\large{\frac{27}{216}}\) = \(\large{\frac{1}{8}}\)
(5) 3回ふって、その積だけ進むとき、元のAで止まる確率は?
8の倍数は、8, 16, 24…216まで挙げていられないですね!
<ということで>
8 = 23 = 2×2×2 → 因数に「2」を3つ以上持てばよいですね(3つ以上あるものは8の倍数)
前提として
2 = 2 …1個
4 = 2×2 …2個
6 = 2×3 …1個
〈1, 2, 4〉〈1, 4, 4〉〈1, 4, 6〉〈2, 2, 2〉〈2, 2, 4〉〈2, 2, 6〉〈2, 3, 4〉〈2, 4, 4〉〈2, 4, 6〉〈3, 4, 4〉〈3, 4, 6〉〈4, 4, 4〉〈4, 4, 5〉〈4, 4, 6〉〈6, 6, 6〉=6+3+6+1+3+3+6+3+6+6+3+6+1+3+3+1=60通り
・ 全事象 = サイコロ3つ=216通り
∴ \(\large{\frac{60}{216}}\)= \(\large{\frac{5}{18}}\)
(樹形図なら)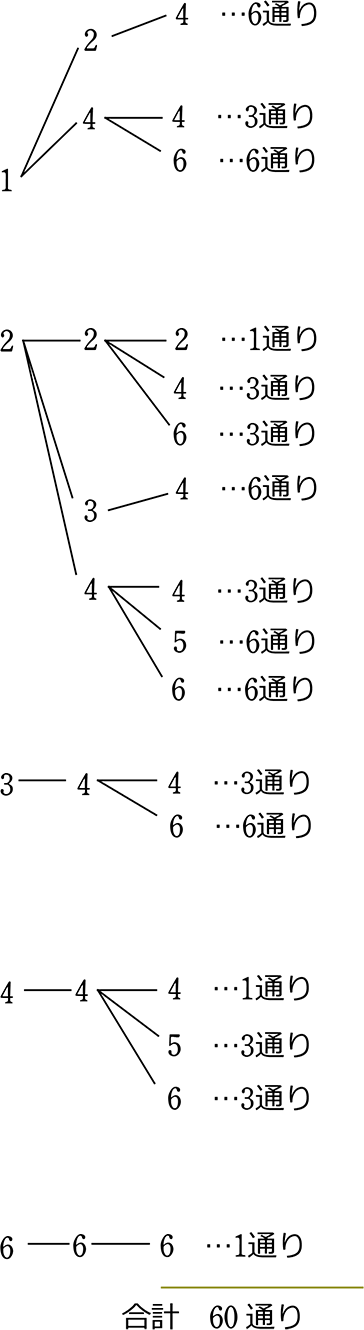
∴ 確率は \(\large{\frac{60}{216}}\) = \(\large{\frac{5}{18}}\)
〈 1回目の状態を図に書き込めないような問題 〉
《 例 》
黒い碁石と白い碁石がそれぞれ5個ずつある。
図のように、1から6までの数が1つずつ書かれた6マスのマス目に
黒い碁石を1個ずつ置く。この状態から、1から6までの目がある
大小2つのサイコロを同時に1回投げて、
次の(ア)、(イ)の操作を順に1回ずつ行う
〈操作〉
| (ア) | 大きいサイコロの出た目の約数が書かれたマス目においてある黒い碁石を、すべて白い碁石に置き換える |
| (イ) | (ア)の操作後の状態から、小さいサイコロの出た目の数が書かれたマス目に置いてある碁石を、その碁石が黒い碁石ならば白い碁石に、白い碁石ならば黒い碁石に置き換える |
| ① | 大きいサイコロの出た目の数が4、小さいサイコロの出た目が3であるとき、6マスのマス目に置いてある白い碁石は何個でしょう |
→ (4, 3)のとき → アで(〇〇●〇●●) → イで(〇〇〇〇●●) ∴ 白は4個
| ② | 6マスのマス目に置いてある白い碁石が3個となる確率を求めましょう |
1回目だけの状態(大サイコロだけの状態)を図に書き込めない場合
「面倒でも」1回目だけの状態(大サイコロだけの状態)を、自分で書き出すのがコツですね
→ アだけの状態を面倒でも書き出すと
| 大 | 約数 | 1 2 3 4 5 6 | |
| (1 | {1}, | → | (○●●●●●) |
| (2 | {1, 2}, | → | (○○●●●●) |
| (3 | {1, 3}, | → | (○●○●●●) |
| (4 | {1, 2, 4}, | → | (○○●○●●) |
| (5 | {1, 5}, | → | (○●●●○●) |
| (6 | {1, 2, 3, 6}, | → | (○○○●●○) |
| → | イの操作(出た目の石の色を取り替える)で 「白が3個」になるのは → 書き出しを利用してシミレーション
(大1のとき, 小が…なし)、(大2のとき, 小が…3 4 5 6の時白3個)、(3, 2 4 5 6)、(4, なし)、(5, 2 3 4 6)、(6, 1 2 3 6) |
| ∴ | 4通り+4通り+4通り+4通り=16通り |
| ・ | 全事象 = サイコロ2個=62=36通り |
∴ \(\large{\frac{16}{36}}\)=\(\large{\frac{4}{9}}\)

右回り=時計回り=外回り

は、輪の中心に立って見れば右手の方に移動していくので、「右回り」。
時計を正面から見るのと同じなので、「時計回り」。
日本では、電車、自動車は左側通行なので、

右回り、時計回りが、「外側」を走っているので、「外回り」 ですね!
山手線、大阪環状線など
その逆は、「左回り」「時計回りと逆(反時計回り)」「内回り」ですね!
右回り=時計回り=外回り
cf.
「正ネジ(右ネジ)」は、
「右回り」にすれば「締まる」
「左回り」にすれば「緩む」ですね
ほとんど95%以上は「右ネジ」ですね
固いネジで、「どっちに回したら緩むんだっけ?」となった場合は、
「時計はどんどん締まっていっている。針が止まったのは、電池が切れたからではなく、ネジが締まり切ったからなのです(あくまでイメージです!)、逆に回すと部品が取れて(緩んで)壊れる」
みたいなイメージを持てば、「反時計回しで緩む」となるのかなと思います。
男性の大人は身体が憶えているので、当たり前のようにネジを締めたり緩めたりしますが、利き手でない方で工具を持つと一瞬「ん?」となりますね!
そう、それがなつかしい「自分が子供の頃の実力」ですね!
「繰り返し、何度も」ネジを回してきたことで身体が憶えているのですね
数学も、その他何でも、同じことなのでしょうね!
くり返し使う = 自分のものになる
反時計回りに力が加わる場所で使われるようなネジは「逆ネジ」ですね
反時計回りで「締まる」ネジですね
いつも反時計回りに力がかかっているので、普通のネジでは、
何かの拍子で緩んで、部品が「落っこちた」では危ないですから、逆ネジですね
扇風機の羽本体をとめるネジ、自転車の左ペダル、トラックなどの左ホイールなどは逆ネジですね
乗用車の左ホイールは、なぜか正ネジがほとんどですね
「加速力」>「減速力」だから?
② コイン
まずは再確認
コインは
| ・ | 「表」「裏」を数字と見れるので無条件で「区別がある」 |
| ・ | 1つで複数特徴を持つ(0、1の目だけの目のサイコロ) → 全事象は重複順列  下がらない 下がらない |
| ・ | ぞろ目ラインがある → 同様に確からしいを確保するために必ず順列数え 〈表, 裏〉は( |
● コイン2枚
《 例 》
2枚の硬貨を同時に投げるとき、
◎ 全事象を樹形図と表で求めましょう
→ 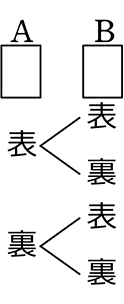
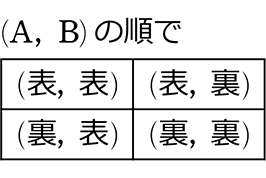
1つにつき枝が2本と少ないので樹形図もありですね
⇒ マスより2通り×2通り=4通り
樹形図より末端を数えて4通り
表より4セルで4通り
計算なら 22=4通り
今後、漢字が大変ですので「表」は0、「裏」は1で行きますね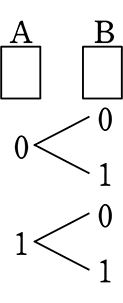
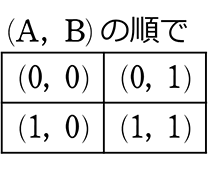
サイコロの表の左上の部分と見れますね
◎ 1枚が表、1枚が裏になる確率は?
・ 「硬貨」より → 絶対順列数え
→ サイコロでいう〈1, 2〉の目の出方ですね
(
∴ \(\large{\frac{2}{4}}\)=\(\large{\frac{1}{2}}\)
◎ どちらも表になる確率は?
→ サイコロでいう〈1, 1〉のぞろ目の出方ですね
〈0, 0〉 の1通り
∴ \(\large{\frac{1}{4}}\)
《 例 》
1枚の硬貨を2回投げる
◎ 1回
・ 「硬貨」より → 絶対順列数え
→ 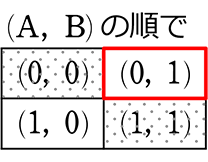
指定に「意味がある」ので → 親中数えダメ(
∴ \(\large{\frac{1}{4}}\)
◎ 1回は表、もう1回は裏の確率は?
→ 1回
∴ サイコロのとにかく系と同じなので、〈0, 1〉の2通り
∴ \(\large{\frac{2}{4}}\)=\(\large{\frac{1}{2}}\)
● コイン3枚以上
《 例 》
3枚の硬貨を同時に投げるとき、
◎ 全事象は何通り?
→ 計算で、23=8通り
→ 全列挙で、
・ 全部表(
・ 1枚裏(0, 0, 1)(0, 1, 0)(1, 0, 0) ←1が左に移動していくイメージ
・ 2枚裏(0, 1, 1)(1, 0, 1)(1, 1, 0) ←1が順次左に移動していくイメージ (または0が右に移動していくイメージ)
・ 全部裏(1, 1, 1) の合計8通り
↑3枚の全列挙は10秒くらいで書けるようになりたいですね!
◎ 2枚が表、1枚が裏の確率
→ 〈0, 0, 1〉=\(\large{\frac{3!}{2!}}\)=3通り (親中数え)
↑サイコロの目と思って列挙する
(ちゃんと列挙すると (
→ 樹形図なら 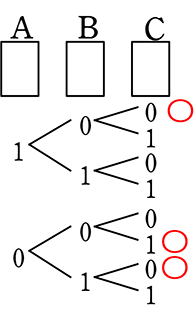 → 3通り
→ 3通り
∴ \(\large{\frac{3}{8}}\)
◎ 2枚以上表が出る確率は?
→ 〈0, 0, 0〉 〈0, 0, 1〉=1+3=4通り
∴ \(\large{\frac{4}{8}}\)=\(\large{\frac{1}{2}}\)
◎ 少なくとも1枚は表が出る確率は?
→ 「少なくとも」といえば余事象を考えるでしたね
余事象は「全部裏」ですね
余事象=〈1, 1, 1〉=1通り
∴ 当該事象=全8通り-余事象1通り=7通り
∴ \(\large{\frac{7}{8}}\)
《 例 》
1枚の硬貨を5回投げるとき、少なくとも1回は裏が出る確率は?
→ 余事象は「全回表」 → (0, 0, 0, 0, 0) の1通り
・ 全事象は25=4×4×2=32通り
∴ 当該事象=32-1=31通り
∴ \(\large{\frac{31}{32}}\)
《 例 》
1枚の硬貨を4回投げるとき、表が2回、裏が2回出る確率は?
→ とにかく 表2 裏2
→ 〈0, 0, 1, 1〉=\(\large{\frac{4!}{2!\ \cdot \ 2!}}\) (または\(\small{{}_4 \mathrm{ C }_2}\)) =6通り ←親中数え
↑コインは表裏の「2種類しかない」ので、〈0, 0, 1, 1〉を『1例』と見て、これの並び替え分とするのが楽ですね \({}_4 \mathrm{C }_2\)=6通り
・ 全事象 = 硬貨4回 = 24 = 16通り
∴ \(\large{\frac{6}{16}}\) = \(\large{\frac{3}{8}}\)
表裏の値がそれぞれ違う
ここまでは、表(0)、裏(1)だけでしたが
表A(0)に値、表B(0)にそれぞれ値があるというだけですね
《 例 》
100円玉,50円玉,5円玉がそれぞれ1枚ずつあります。この3枚の硬貨を同時に投げるとき、表の出る硬貨の合計金額について、
◎ 20円以上150円以下になる確率
→ 表のときは額面、裏のときは0円という数え方ですね
簡易表を作っておくと
\(\large{\frac{表}{裏}}\)の順で、\(\large{\frac{100}{0}}\)、\(\large{\frac{50}{0}}\)、\(\large{\frac{5}{0}}\)
(100円, 50円, 5円)の順に、全事象とついでに合計金額をシミレーションすると
(0, 0, 0) → 155円 (全部表群) ← 簡易表の をなぞった
をなぞった
(0, 0, 1) → 150円 (1枚裏群)
(0, 1, 0) → 105円 ←
(1, 0, 0) → 55円
(0, 1, 1) → 100円 (2枚裏群)
(1, 0, 1) → 50円
(1, 1, 0) → 5円
(1, 1, 1) → 0円 (全部裏群)
左が「列挙」 → 右が「当てはめ」⇒ 分離するのがコツですね
列挙がまだ厳しいという場合は…「樹形図」になります
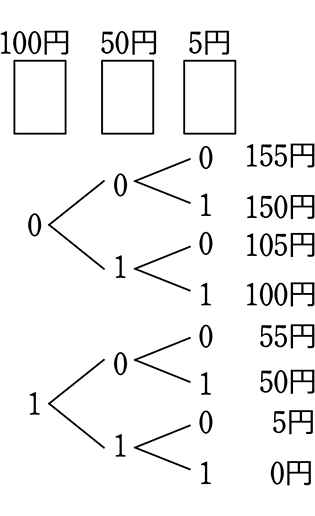
∴ 20円以上150円以下は、数えて5通り
・ 3枚の全事象は23=8通り
∴ \(\large{\frac{5}{8}}\)
◎ 金額の合計が10でわり切れない確率
→ 上の列挙を利用して、155, 105, 55, 5 の4通り
∴ \(\large{\frac{4}{8}}\)=\(\large{\frac{1}{2}}\)
《 例 》
50円,10円,5円の硬貨が1枚ずつある。この3枚の硬貨を同時に投げるとき、表の出る硬貨の金額の合計について、
◎ 60円 になる確率は?
簡易表を作っておくと、\(\large{\frac{50}{0}}\)、\(\large{\frac{10}{0}}\)、\(\large{\frac{5}{0}}\)
→ 60円になるのは(0, 0, 1)の1通り
∴ \(\large{\frac{1}{8}}\)
◎ 55円以上になる確率は?
→ 余事象「55円未満(50円以下)」でいくか…予想がつかないので本事象でいきますね
55円以上になるのは(50, 10, 5) の順で
(0, 0, 0) (0, 0, 1) (0, 1, 0) (0, 1, 1はOUT) (1, …OUT) そして、それぞれに金額設定があるので親中数えはしてはいけない
∴ 3通り
∴ \(\large{\frac{3}{8}}\) ↑コイン3枚くらいなら全事象を列挙してしまう方が間違いがないかもしれませんね
《 例 》
いろいろな種類の硬貨を同時に投げて、表が出た硬貨の合計金額を計算する。
次のような場合において、合計金額が100円より少なくなる確率は?
◎ 100円硬貨1枚,50円硬貨1枚,10円硬貨1枚
→ 余事象「100円以上」でいきますね。(100, 50, 10) の順で
(0, 0, 0) (0, 0, 1) (0, 1, 0) (0, 1, 1) (1…OUT
∴ 4通り、本事象は8-4=4通り
∴ \(\large{\frac{1}{2}}\)
◎ 100円硬貨1枚,50円硬貨2枚
→ 本事象100円未満は (100, 50, 50) の順で
(1, 1, 1) (1, 1, 0) (1, 0, 1) (0, OUT (1, 0, 0 OUT
∴ 3通り
∴ \(\large{\frac{3}{8}}\)
〔コインの列挙イメージ〕
《 例 》
コイン5枚を投げるときの全事象は?
→ サイコロをよりシンプルにした「0(表)」と「1(裏)」の2種類しかないので
「フサフサ(  )」が動くイメージよりも、「0」と「1」で、適当に1例を挙げて 並び方は何通りかをCで調べる のが楽ですね (Cの3つのイメージの1つ「型」)
)」が動くイメージよりも、「0」と「1」で、適当に1例を挙げて 並び方は何通りかをCで調べる のが楽ですね (Cの3つのイメージの1つ「型」)
再度、5枚の全事象は?
動き方を無理に覚えなくても、自分でかぶりがないように数えようとすると、このような動きになるかと思います
コインのまとめ
| ・ | 「表何枚、裏何枚」という問題 → 親中数えよりも、1例を挙げてその並び替え分 ex. 4枚投げて2枚表 → 1例〈0, 0, 1, 1〉 =\({}_4 \mathrm{C }_2\) =6通り ex. 6枚投げて3枚表 → 1例〈0, 0, 0 ,1, 1, 1〉 =\({}_6 \mathrm{C }_3\) =20通り |
| ・ | 「100円50円」など値がある問題 → 「簡易表」と「全列挙」 |
よく、問題集の解説で
「(●〇〇)の並び替え分あるので、\({}_3 \mathrm{C }_1\)で3通り」 とありますね
どうして、3つから1つを選ぶと、並び替え数?
| → | 実は3つは区別があります。そして |
| → | (1, 2, 3)からその場で1つを選ぶと、 (①, ②, ③) (①, ②, ③) (①, ②, ③) (Cの「型」のイメージ) |
| → | 数字を省略すると(●〇〇)(〇●〇)(〇〇●)の3通りですね |
| → | このとき、●を選んだと見れば、\({}_3 \mathrm{C }_1\) 〇を選んだと見れば、\({}_3 \mathrm{C }_2\)で、\({}_3 \mathrm{C }_1\) = \({}_3 \mathrm{C }_2\)ということも分かりますね \({}_n \mathrm{C }_r\) = \({}_n \mathrm{C }_{(n-r)}\) |
③ じゃんけん
まずは再確認
じゃんけんは
| ・ | 「グー」「チョキ」「パー」を数字と見れるので無条件で「区別がある」 または、元々は人なので区別がある |
| ・ | 1つで複数特徴を持つ (1、2、3の目だけの目のサイコロ) |
→ 全事象は重複順列 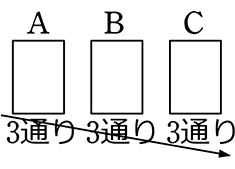 下がらない
下がらない
・ぞろ目ラインがある
| → | 同様に確からしいを確保するために必ず順列数え 〈グー, チョキ〉は( |
| ⇒ | ですが! じゃんけんは「誰が何人勝ち」を基準に考えるので、上記はあまり考慮しませんね(独特性) |
イメージ
まずは樹形図を見ていただいて
〈2人のじゃんけん〉

以下は公式を納得するための説明になります
不要な場合は → (じゃんけんの公式)へ
(分かったこと) Aがグーの山で
| ・ | 「A」だけが勝つのは、1通りしかない |
| → | 「特定の人」が勝つ手は、1山につき1通りしかない |
| ・ | 「誰か1人」が勝つのは、\({}_2 \mathrm{C }_1\)通りしかない |
| → | 「誰か1人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{1}\))通りしかない |
| ・ | Aのチョキやパーの山はグーのパターンとまったく同じ |
| → | Aのグーだけの山を考えて、3倍すればよい |
・
(
(グー, チョキ) → (〇, ●)
(グー, パー) → (●, 〇)
| ⇒ | (〇, ●)(●, 〇)は、1例〈〇, ●〉の並び替え数(\({}_2 \mathrm{C }_1\))といえる ∴ 「誰か1人勝ち」= \({}_{人数} \mathrm{C }_\color{red}{1}\) 通り |
⇒ 全通り-誰か1人勝ち=あいこ
〈3人のじゃんけん〉
グーチョキパーと書くのが大変なので
今後は、グー → ●、チョキ → V、パー → 〇としますね

(分かったこと) Aがグーの山で
・Aだけが勝つのは、1通りしかない
| → | 「特定の人」が勝つ手は、1山につき1通りしかない |
| ・ | 誰か1人が勝つのは、\({}_3 \mathrm{C }_1\)通りしかない |
| → | 「誰か1人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{1}\))通りしかない |
| ・ | ABだけが勝つのは、1通りしかない |
| → | 「特定の2人」が勝つ手は、1山につき1通りしかない |
| ・ | 誰か2人が勝つのは、\({}_3 \mathrm{C }_2\)通りしかない |
| → | 「誰か2人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{2}\))通りしかない |
| ・ | Aのチョキやパーの山は、グーのパターンとまったく同じ |
| → | Aのグーだけの山を考えて、3倍すればよい |
・ Aのグーの山を白星
| ( |
→ | ( |
|
| (●, ●, V) | → | (〇, 〇, ●) | \({}_3 \mathrm{C }_2\) の仲間 |
| (●, ●, 〇) | → | (●, ●, 〇) | \({}_3 \mathrm{C }_1\) の仲間 |
| (●, V, ●) | → | (〇, ●, 〇) | \({}_3 \mathrm{C }_2\) の仲間 |
| (●, V, V) | → | (〇, ●, ●) | \({}_3 \mathrm{C }_1\) の仲間 |
| (●, V, 〇) | → | (△, △, △) | |
| (●, 〇, ●) | → | (●, 〇, ●) | \({}_3 \mathrm{C }_1\) の仲間 |
| (●, 〇, V) | → | (△, △, △) | |
| (●, 〇, 〇) | → | (●, 〇, 〇) | \({}_3 \mathrm{C }_2\) の仲間 |
| ⇒ | (〇, ●, ●)(●, 〇, ●)(●, ●, 〇)は、1例〈〇, ●, ●〉の並び替え数(\({}_3 \mathrm{C }_1\))といえる ∴ 「誰か1人勝ち」= \({}_{人数} \mathrm{C }_\color{red}{1}\) |
| ⇒ | (〇, 〇, ●)(〇, ●, 〇)(●, 〇, 〇)は、1例〈〇, 〇, ●〉の並び替え数(\({}_3 \mathrm{C }_2\))といえる ∴ 「誰か2人勝ち」= \({}_{人数} \mathrm{C }_\color{red}{2}\) |
途中に点在する(△△△)→\({}_3 \mathrm{C }_3\)=1通りや(V, ●, 〇)は数えていないということ
| ⇒ | 全通り-誰か1人勝ち-誰か2人勝ち =あいこ |
| ・ | 同手あいこは、1山につき1通りしかない → 3山に3通り → 何人でも3通り |
| ・ | バラバラあいこ = あいこ-同あいこ3通り |

〈4人のじゃんけん〉
| → | 人数が増えても、考え方は同じ、という確認になります |
| → | 樹形図は大きすぎるので、Aのグーの山だけでいきますね |

ほとんど同じことですね
| → | 「特定の1人」が勝つ手は、1山につき1通りしかない |
| → | 「誰か1人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{1}\))通りしかない |
| → | 「特定の2人」が勝つ手は、1山につき1通りしかない |
| → | 「誰か2人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{2}\))通りしかない |
| → | 「特定の3人」が勝つ手は、1山につき1通りしかない |
| → | 「誰か3人」が勝つ手は、1山につき(\({}_{人数} \mathrm{C }_\color{red}{3}\))通りしかない |
| → | Aのグーだけの山を考えて、3倍すればよい |
| → | 人数が増えるとあいこが爆発的に増えてくる |
| → | 全通り-誰か1人勝ち-誰か2人勝ち-誰か3人勝ち=あいこ |

じゃんけん
・ 名指し組の勝つ確率 =
・ 誰か〇人勝ちの確率 =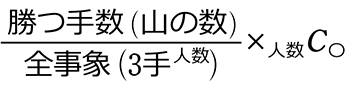
《 例 》
| ・ | 2人でじゃんけんをして、「Aさんがグーで」(1人)勝つ確率は? |
| → | A(名指し)がグー(1山)で勝つ
\(\large{\frac{(グーの)\color{red}{1}(手)}{3^2}}\)×(Aさんの)1(人) = \(\large{\frac{1}{3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{9}}\) |
| ・ | 2人でじゃんけんをして、「Aさんがグーかチョキで(2山)」(1人)勝つ確率は? |
| → | A(名指し)がグーかチョキで勝つ
\(\large{\frac{(グーチョキの)\color{red}{2}}{3^2}}\)×1 = \(\large{\frac{2}{3\ \cdot \ 3}}\)×1 = \(\large{\frac{2}{9}}\) |
| ・ | 2人でじゃんけんをして、「Aさんが」(1人)勝つ確率は? |
| → | A(名指し)が全手で勝つ
\(\large{\frac{(グーチョキパーの)\color{red}{3}}{3^2}}\)×1 = \(\large{\frac{3}{3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{3}}\) |
| ・ | 2人でじゃんけんをして、「どちらかが」勝つ確率は? |
| → | 誰か1人が全手で勝つ( \(\large{\frac{3}{3^2}}\)×\({}_2 \mathrm{C }_1\)= \(\large{\frac{3}{3\ \cdot \ 3}}\)×2 = \(\large{\frac{2}{3}}\) |
| ・ | 2人でじゃんけんをして、「Aさんが」負ける確率は? |
| → | 2人なのでAが全手で1人負け=1人勝ちと同じ確率
\(\large{\frac{(グーチョキパーの)3}{3^2}}\)×1 = \(\large{\frac{3}{3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{3}}\) |
| ・ | 3人でじゃんけんをして、「Aさんが」「グー」で1人勝ちする確率は? |
| \(\large{\frac{1}{3^\color{red}{3}}}\)×(名指しの)1 = \(\large{\frac{1}{3\ \cdot \ 3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{27}}\) |
| ・ | 3人でじゃんけんをして、「Aさんが」1人勝ちする確率は? |
| \(\large{\frac{\color{red}{3}}{3^3}}\)×(名指しの)1 = \(\large{\frac{3}{3\ \cdot \ 3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{9}}\) |
| ・ | 3人でじゃんけんをして、「Aさんが」勝つ確率は? |
| → | Aの1人勝ちではなく、とにかくAが勝っているですね |
| Aの1人勝ち( |
Aを含む誰か2人勝ち=(
| \(\large{\frac{3}{3^3}}\)×(A1人勝ちの1 +(A決定の)1×(残りの2人の1人)\({}_2 \mathrm{C }_1\)) = \(\large{\frac{3}{3^3}}\)×(1通り+2通り) =\(\large{\frac{9}{3\ \cdot \ 3\ \cdot \ 3}}\) = \(\large{\frac{1}{3}}\) |
| ・ | 3人でじゃんけんをして、「AさんとBさんが」勝つ確率は? |
| =「Cさんが1人負け」→ ( \(\large{\frac{3}{3^3}}\)×1 = \(\large{\frac{3}{3\ \cdot \ 3\ \cdot \ 3}}\)×1 = \(\large{\frac{1}{9}}\) |
| ・ | 3人でじゃんけんをして、「(誰か)2人が」勝つ確率は? |
| → | (〇〇●)の\({}_3 \mathrm{C }_2\) (\({}_3 \mathrm{C }_1\)でも同じことでしたね) (\({}_n \mathrm{C }_r\)=\({}_n \mathrm{C }_{n-r}\))
\(\large{\frac{3}{3^3}}\)×\({}_3 \mathrm{C }_2\)= \(\large{\frac{3}{3^3}}\)×\({}_3 \mathrm{C }_1\) = \(\large{\frac{3}{3\ \cdot \ 3\ \cdot \ 3}}\)×3 = \(\large{\frac{1}{3}}\) |
\({}_〇 \mathrm{C }_\color{red}{1}\)は簡単ですね
\({}_3 \mathrm{C }_\color{red}{1}\)は3通り、\({}_5 \mathrm{C }_\color{red}{1}\)は5通り、\({}_8 \mathrm{C }_\color{red}{1}\)は8通り
| ・ | 3人でじゃんけんをして、「(誰か)2人が」負ける確率は? |
| → | 「負ける確率」は「勝つ確率」と全く同様でしたね
\(\large{\frac{3}{3^3}}\)×\({}_3 \mathrm{C }_2\) = \(\large{\frac{3}{3\ \cdot \ 3\ \cdot \ 3}}\)×3 = \(\large{\frac{1}{3}}\) |
《 例 》
A, B の2人がじゃんけんをして、Aさんが勝つ確率は?
ただし、答を求めるまでの過程も書け
| → | このような問題は、じゃんけんに関わらず、複数特徴系、1特徴系でも、中学では |
| ① | 簡単な条件設定(自分のやりやすいように) |
| ② | 樹形図 |
| ③ | 条件に合ったものを数えて、結論 というのが書き方の定番ですね |
たとえば、
| ① | ・ | 3つの白玉をそれぞれ1, 2, 3 と区別する |
| ・ | 大きいサイコロの目が2、小さいサイコロの目が3のとき、(2, 3)と表すとする (等々、自由に設定) |
→ Aがグー、Bがパーのとき、(グー, パー)と表すとする
② 2人の手の出し方を樹形図で表すと
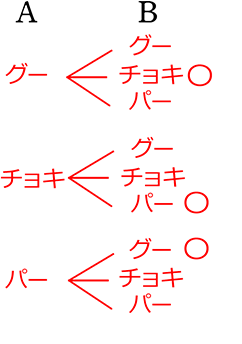
全ての場合は、(末端を数えて)9 通りあり
このうち、Aが勝つのは〇をつけた (グ、チ)(チ、パ)(パ、グ)の3通りである
③ したがって、求める確率は \(\large{\frac{3}{9}}\) = \(\large{\frac{1}{3}}\)
(もちろん①②③のような番号は不要です)
解答欄が答のみなら、中学生でも公式OKですね
名指し組の勝つ確率 = \(\large{\frac{「何手」 }{全事象}}\)×1 → \(\large{\frac{「全手で」}{全事象}}\)×1 = \(\large{\frac{3}{3^\color{red}{2}}}\)×1 = \(\large{\frac{1}{3}}\)
《 例 》
ABCDの4人がじゃんけんをして、誰か1人が勝つ確率は?
→ \(\large{\frac{全手の3}{3^4}}\)×\({}_4 \mathrm{C }_1\) = \(\large{\frac{1}{27}}\)×4 =\(\large{\frac{4}{27}}\)
| → | \({}_4 \mathrm{C }_1\)の内訳(〇●●●)(●〇●●)(●●〇●)(●●●〇)計4通り |
《 例 》
ABCDの4人がじゃんけんをして、Aが勝つ確率は?
→ とにかくAが勝っていればよい
| → | Aの1人勝ち(〇●●●) +Aを含む2人勝ち{〇┃(〇●●), 〇┃(●〇●), 〇┃(●●〇)}+Aを含む3人勝ち{〇┃(〇〇●), 〇┃(〇●〇), 〇┃(●〇〇)} |
| → | \(\large{\frac{全手の3}{3^4}}\)×(1人勝ちの1通り+(1×\({}_3 \mathrm{C }_1\))+(1×\({}_3 \mathrm{C }_2\) ))
=\(\large{\frac{1}{27}}\)×(1+(3)+(3)) |
《 例 》
ABCDの4人がじゃんけんをして、ABの2人だけが勝つ確率は?
→ AB(名指し)の2人勝ち
→ 名指し = \(\large{\frac{全3手}{3^4}}\)×1 = \(\large{\frac{1}{27}}\)
(ABの2人が勝つなら)
| → | AB2人勝ち(〇〇●●)+ABを含む誰か3人勝ち(〇〇┃〇●)(〇〇┃●〇) |
= \(\large{\frac{全手3}{3^4}}\)×(1通り+1×\({}_2 \mathrm{C }_1\))
= \(\large{\frac{1}{27}}\)×(1+2)
= \(\large{\frac{1}{9}}\)
あいこ
「あいこ」は、余事象というのは、
参加人数が増えてくると、「あいこ」の場合の数が数えきれないほど
たくさんの種類があるからですね
例えば5人のあいこは、 (〇〇〇〇〇) (△△△△△) (□□□□□) (〇〇〇△□) (〇〇〇□△)・・・重複順列の「空室2つはOK(全員グーの部屋など)、空室1つはNG(全員グーかチョキの部屋など)」分→(全部屋選ぶ-2部屋選ぶ) ←これを計算すると153通りもありますね
そこで余事象!

あいこの確率
| ・ | 2人じゃんけん、3人じゃんけんのあいこの確率はともに=\(\large{\frac{1}{3}}\) ←よく出てくるので憶えてしまうのがお得 |
・4人以上のあいこは、余事象
| → | あいこの数 = 全通り-(誰か1人勝ち +誰か2人勝ち +誰か3人勝ち+・・・) (全員勝ちの手前まで) |
| ・ | 同手あいこは、人数に関わらず1手(1山)につき1通り、全手(3山)につき3通り |
| ※ | 誰か1人は\({}_n \mathrm{C }_1\)、誰か2人は\({}_n \mathrm{C }_2\)ですね |
| ※ | 全員勝ち…それは「同手あいこ」ですね。 → \({}_n \mathrm{C }_\color{red}{{n-1}}\)まで! |
《 例 》
5人でじゃんけんをして、「あいこ」になる確率は?
あいこの確率= 1-誰かが〇人勝ちの確率 = 1-(誰かが1人勝ち +誰かが2人勝ち +誰かが3人勝ち +誰かが4人勝ち)
= 1-(\(\large{\frac{3}{3^5}}\)・\({}_5 \mathrm{C }_1\)+\(\large{\frac{3}{3^5}}\)・\({}_5 \mathrm{C }_2\)+\(\large{\frac{3}{3^5}}\)・\({}_5 \mathrm{C }_3\)+\(\large{\frac{3}{3^5}}\)・\({}_5 \mathrm{C }_4\)) cf. 5人が勝つ?それは「あいこ」ですね!(4人まで)
= 1-\(\left(\large{\frac{{}_5 \mathrm{C }_1+{}_5 \mathrm{C }_2+{}_5 \mathrm{C }_3+{}_5 \mathrm{C }_4}{3^4}}\right )\) 3を先に約分した
= 1-\(\left(\large{\frac{5+10+10+5}{3^4}}\right )\)
= 1-\(\large{\frac{30}{81}}\)
= \(\large{\frac{81-30}{81}}\)= \(\large{\frac{51}{81}}\)
= \(\large{\frac{17}{27}}\)
《 例 》
4人でじゃんけんをしてあいこになる確率は?
・ あいこの余事象は→「誰かが勝つ」
| → | 誰かが勝つ=誰か1人勝ち+誰か2人勝ち+誰か3人勝ち |
=3手×\({}_4 \mathrm{C }_1\)+3×\({}_4 \mathrm{C }_2\)+3×\({}_4 \mathrm{C }_3\)
=3×4+3×6+3×4
=12+18+12
=42通り
・ 全事象=34=81通り
∴ 本事象の「あいこ」=81-42=39
∴ \(\large{\frac{39}{81}}\)=\(\large{\frac{13}{27}}\)
b 1特徴系 (カード、玉、くじ、人など)
再確認
| ・ | 区別のないものはこちらで区別をつける(番号をふる) |
| ・ | 1特徴系とは、1つにつき1つの番号しか持たないものですね ex. 1と書かれたカード、4と書かれた玉、2と書かれたはずれ、ゼッケン3をつけた人 → ただし、人は無条件で区別がある |
・ 全事象(分母)は普通順列  (階段状に下がっていく)
(階段状に下がっていく)
→ 自分は1つしかないのでマスに自分を入れたら、次のマスは自分を除いた個数になる (1つのマスにしか入れない)

樹形図の枝は減っていく(最後は自然に決まる)
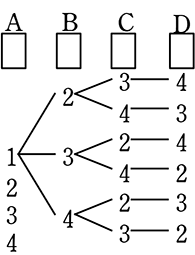
↑
Aの2以下は省略しています
→ とにかく系の分子(白玉1, →白玉2)ではなく(白玉, と白玉)のときは組合せでもよい
(
(そのときは分母も組合せ数えで)
1特徴系はすべて同じ問題
1特徴系には、カード、玉、くじ、人などがありますが
すべて同じ問題といってもよいですね
〈区別がある問題では〉
ex. 1~6までの数字が1つずつ書かれたカードがある
123456 などは
〇で囲めば、①②③④⑤ 玉の問題
カードにひもをつければ、くじの問題
ゼッケンと見れば、人の問題 ですね
〈区別がない(同じものを含む)問題では〉
1が書かれたカードが4枚、2が書かれたカードが2枚ある
111122 などは
〇〇〇〇●● 白玉4個、赤玉2個な、玉の問題
外れ4本、当たり2本な、くじの問題
両親、子4人な、人の問題と同じことですね
⇒ これらは、新たに区別をつけるだけですね!

傾向
「同じこと」ということは、どのようなタイプの問題でも、カードや玉や人で同じような問題が作れるということになりますが…
| ・ | カード、玉は、選んだ2つが~、という問題(普通順列) |
| ・ | くじは、~番目に当たる という問題 |
| ・ | 人は、並べたときに誰々がどこに という問題(全順列)が、多いですね |
① カード・玉・くじ・人
● 1個とる
《 例 》
1から9までの整数を1つずつ書いた9枚のカードから1枚を引くとき、それが3の倍数のカードである確率を求めましょう
123456789
→ 3の倍数を列挙すると、(3, )(6, )(9, ) の3通り
・全事象= 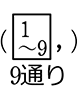 = 9通り
= 9通り
∴ \(\large{\frac{3}{9}}\)=\(\large{\frac{1}{3}}\)
《 例 》
赤玉2個、白玉4個が入った袋から1個の玉を取り出すとき、それが赤玉である確率を求めましょう
また、1回で赤玉を取り出したときの残りの玉の状態を図で示しましょう
●●○○○○
・ ●●○○○○を
→ 赤玉を列挙すると、(1, )(2, ) の2通り
・ 全事象=6通り
∴ \(\large{\frac{2}{6}}\)=\(\large{\frac{1}{3}}\)
残りの状態図は、●○○○○
「1個をとる」くらいなら区別をつけなくても、6個中2個が赤 → \(\large{\frac{2}{6}}\)とわかりますね
《 例 》
総数6本のくじがある。そのうち1等は1本、2等は2本あり、それ以外はからくじである。この6本のくじから1本ひくとき、2等に当たる確率を求めましょう
122
・ 1つ取るときは、もう区別をつけなくても見ただけで数えられるので
→ 全6本中、2等は2本 → ∴ \(\large{\frac{2等は2本}{6本につき}}\)=\(\large{\frac{1}{3}}\)
《 例 》
男子3人、女子2人からクラス委員を1人選ぶとき、男子が選ばれる確率を求めましょう
・ 「人」は絶対的に区別がある →
→ 男を列挙すると、(1, )(2, )(3, ) の3通り
・ 全事象 = 5通り
∴ \(\large{\frac{3}{5}}\)
最初から区別のある問題もありましたが、すべて同じ問題ですね
| → | カード\(\leftrightarrow\)玉\(\leftrightarrow\)くじ\(\leftrightarrow\)人、で入れかえても問題を作ることができる |
【 区別がある 】
〈1〉 「戻して」系
「戻して」系
| ⇒ | 「戻して」系は、カードや玉ではありますが、実は『袋が基準』なので 「複数特徴系」の『サイコロ』になります |
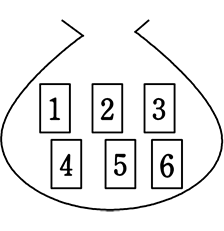

例えば、すごろくを、サイコロ1つの代わりに、1つの袋に1~6の数字が書かれたカード(玉)(上図)で、引いたカードを毎回『戻して』次の人が引いても、面倒ではありますが成立しますね、誰もが「6出ろ~、6出ろ~」と思いますが、「6はもうないから、5出ろ~」とはなりませんものね
| ⇒ | サイコロがないとき → 1~6のカード(玉)が入ったこの袋セットで代用できる = サイコロ ですね! |
「戻して」系まとめ
・ 袋に注目して → 複数特徴系
・ 「1回目2回目」より → 順列数え
| ・ | ぞろ目ラインあり(同様に確かのため) → 絶対順列数え |
| ・ | 基準名は( |
・ 全事象 = (袋の中の個数)2
結局、
《 例 》
袋の中に3, 4, 5, 6, 7 の数字が1つずつ書かれた5枚のカードが入っています。袋の中からカードを1枚取り出し、そのカードに書かれた数をaとします。取り出したカードを袋の中にもどして、もう1回袋の中からカードを1枚取り出し、そのカードに書かれた数をbとするとき、10a+b の値が3の倍数となる確率を求めましょう
| ・ | 「戻して」というフレーズより → =サイコロ → 順列数え |
| ・ | 片方だけ10倍 → 親中数えダメ |
| → | 34567 → 10a+bが3の倍数(各位の和が3の倍数:倍数判定)になるものを列挙すると、 |
(3, 3 6)(4, 5)(5, 4 7)(6, 3 6)(7, 5) =8通り
| ・ | 全事象=5面体のサイコロ2つ=(5面)2 =52 =25通り |
∴ \(\large{\frac{8}{25}}\)
ではなく○で囲めば玉の問題にできますね
〈2〉 「袋2つ」系
「袋2つ」系
⇒ 「袋2つ」系も、カードや玉ではありますが、実は『袋が基準』なので 「複数特徴系」の『サイコロ』になります
| ① | 2つの袋(箱)の中身が同じ(数字も枚数も)ときは、
「戻して」系と全く同じ状態になりますね = サイコロ |
ですが、問題では9分9厘
| ② | 中身(数字や枚数)が異なる = 目の違うサイコロ |
| ア | :枚数が異なれば |
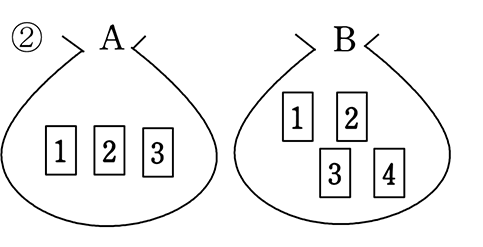

| → | ぞろ目ラインが「不完全」か「ない」
確かに、( |
| ⇒ | ぞろ目ラインが不完全でもあれば、絶対順列数え(同様に確かのため) |
| ⇒ | ぞろ目ラインがなければ(対になるもが全くない)、実は組合せ数えをしても、実は順列数えと同じ結果になります → ですが、A からの→ Bという基準名があるので、原則順列数えで! |
イ:数字が異なれば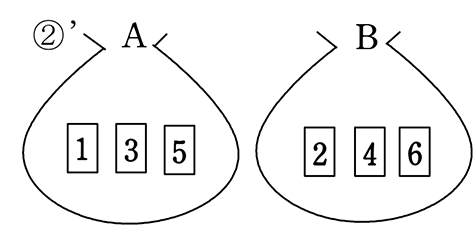
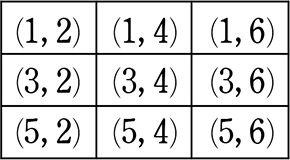
| → | ぞろ目ラインが「ない」
確かに、( |
見たことはありませんが、袋も見た目区別がなく、それぞれから「同時に」1つずつの場合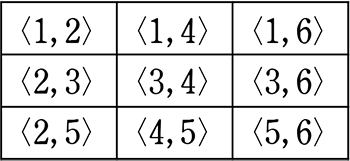
すべての組み合わせに、元々対になるものがなかったので
| → | 結局、上の順列数えと同じ結果で、9通り |
| ⇒ | 中身がすべて異なれば、 順列数え数 = 組合せ数え数 |
「袋2つ」系のまとめ
・ 袋に注目して → 複数特徴系
・ 「袋A袋B」より → 順列数え
・ ぞろ目ラインが少しでもあれば → 絶対順列数え
・ 目が違えば → 親中数えダメ
| ・ | 基準名は ( |
| ・ | 全事象 = (袋Aの中の個数)×(袋Bの中の個数) |
結局、
| ① | 中身が同じ → =サイコロ → 順列数え → 親中数えOKの可能性あり |
| ② | 中身が違う → ≒サイコロ → 順列数え → 目が違う → 親中数えダメ |
《 例 》
箱Aには12, 13, 14, 15, 16 の数字が1つずつ書かれた5個の玉が入っており、箱Bには2, 3, 4 の数字が1つずつ書かれた3個の玉が入っています。箱Aと箱Bのそれぞれから玉を1個ずつ取り出すとき、箱Bから取り出した玉に書かれた数が、袋Aから取り出した玉に書かれた数の約数である確率を求めましょう
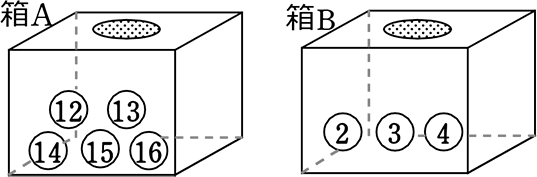
| ・ | 「箱2つ」より → ≒サイコロ → 順列数え →目が違う → 親中数えダメ |
→ Bが約数を列挙すると、 (12, 2 3 4)(13, …ない)(14, 2)(15, 3)(16, 2 4) =3+0+1+1+2 =7通り
| ・ | 全事象=サイコロもどき2つ=5通り×3通り=15通り |
∴ \(\large{\frac{7}{15}}\)
〈3〉 「続けて」系
「続けて」系
| ⇒ | 「続けて」系は、玉やカードに注目しますので、正真正銘『1特徴系』になります |
| ・ | 「続けて」を正確にいうと、「(戻さずに)続けて」ですね |
| ・ | 「続けて」より → 基準名「1回目」「2回目」…が自動発生! → 並びにこだわる → 順列数え |
〔「続けて」の列挙 〕
《 例 》
6個から「続けて」2個とる全事象は何通り?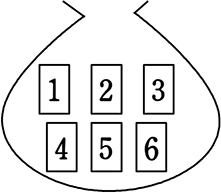
まずは、与えられた数字
「1 2 3 4 5 6」を書いて
(比較:サイコロの列挙イメージ)
⇒ 「続けて」系の列挙は
・ 見本の数字と
・  なフサフサが右に動いていくイメージでOKですね
なフサフサが右に動いていくイメージでOKですね
「続けて」系まとめ
・ 1特徴系
・「続けて」より → 「1回目、2回目…」が自動発生 → 順列数え → 問題により親中数えOK (親中数えの可否)
(親中数えOKな場合、実は組合せ数えでも同じ答えになる ←ぞろ目ラインがないので)
・ 基準名は (
・ 列挙のイメージは「左あり、自分なしフサフサ( )
)
・ 全事象は、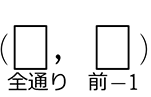 や
や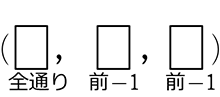 → 階段状に下がる → 普通順列 → \({}_{全個数} \mathrm{P }_{取る個数}\)
→ 階段状に下がる → 普通順列 → \({}_{全個数} \mathrm{P }_{取る個数}\)
(当該事象を、ずるをして組合せ数えで数えたときは、全事象も組合せ数えで! → \({}_{全個数} \mathrm{C}_{取る個数}\)) → 解く過程も書け、なら面倒でも順列数え)
《 例 》
1から6までの数字が書かれた6枚のカードをよくきり、続けて2枚を取り出す。これらを並べて、2けたの整数をつくるとき、素数となる確率を求めましょう
123456
| ・ | 「続けて」というフレーズより → 順列数え |
| ・ | 「並べて」というフレーズより → 絶対順列数え |
| ・ | (2, 3)と(3, 2) で意味が異なる(対は当然に成立しない) → 親中数えダメ |
→ 並べて2桁が素数を列挙すると、
(1, 3)(2, 3)(3, 1)(4, 1 3)(5, 3)(6, 1) =1+1+1+2+1+1 =7通り
・ 全事象 = 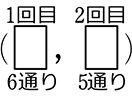 =\({}_6\mathrm{P }_2\) = 6!の前2つ = 30通り
=\({}_6\mathrm{P }_2\) = 6!の前2つ = 30通り
∴ \(\large{\frac{7}{30}}\)
《 例 》
1, 2, 3, 4, 5 の数が1つずつ書かれた5枚のカード(玉)から、
もとに戻さずに続けて2枚のカードを取り出す。
取り出したカードに書かれた数の和が奇数となる確率は?
12345
・「続けて」より → 順列数え
・「和」より → 親中数えOK
→ 和が奇数を列挙すると、
(親中数え) 〈1, 2 4〉〈2, 3 5〉〈3, 4〉〈4, 5〉 =4+4+2+2 =12通り
(順列数え) (1, 2 4)(2, 1 3 5)(3, 2 4)(4, 1 3 5)(5, 2 4) =2+3+2+3+2 =12通り
もう少し規則性を考えて列挙すると、
(親中数え) 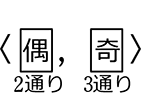 =12通り
=12通り
(順列数え) 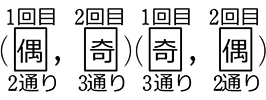 =6+6 =12通り
=6+6 =12通り
| ・ | 全事象=\({}_5 \mathrm{P }_2\) =5!の前2つ =5×4 =20通り |
∴ \(\large{\frac{12}{20}}\)=\(\large{\frac{3}{5}}\)
(組合せ数えでずる) 〈1, 2 4〉〈2, 3 5〉〈3, 4〉〈4, 5〉 =2+2+1+1 =6通り
・ 全事象 = 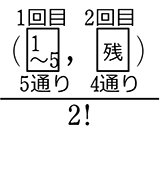 =\({}_5 \mathrm{C }_2\)=5!の前2つ÷2!=20÷2=10通り ←かぶりをなくすための÷2!
=\({}_5 \mathrm{C }_2\)=5!の前2つ÷2!=20÷2=10通り ←かぶりをなくすための÷2!
∴ \(\large{\frac{6}{10}}\)=\(\large{\frac{3}{5}}\) (答えは同じですね)
後ろのマスが前のマスと無関係なときの組合せ数えの全事象 としますね
としますね
→ 組合せ数は、4×3=12通り
後ろのマスが前のマスと関係があるときの組合せ数えの全事象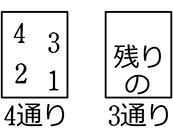 としますね
としますね
→ 組合せ数は、\(\large{\frac{4×3}{\color{red}{2!}}}\) = 6通り
上にはない(3, 4)などを含んでしまっているということですね
〈4〉 「同時に」系
「同時に」系
| ・ | 「同時に」系も、玉やカードに注目しますので、正真正銘『1特徴系』になります |
| ・ | 「同時に」2つ取ると、(1, 2)も(2, 1)も…「組合せ的に同じ」だ! ⇒ 組合せ数え(数学ルール) → 〈1, 2〉の1通り となります |
例えば、
司会者「袋の中の玉を同時に両手で2つ取ってください!」 → すると、左手が2、右手が1だった(
⇒ 順列数えのイメージ(〇, → 〇)、 組合せ数えのイメージ〈〇, と〇〉
〔「同時に」の列挙 〕
《 例 》
6個から「同時に」2個とる全事象は何通り?
与えられた数字
「1 2 3 4 5 6」を書いて
(比較:サイコロの列挙イメージ)
(比較:「続けて」の列挙イメージ
⇒ 「同時に」系の列挙は
・ 見本数字と
・  なフサフサが右に動いていくイメージでOKですね
なフサフサが右に動いていくイメージでOKですね
「同時に」系まとめ
・ 1特徴系
| ・ | 「同時に」より → 「組合せ数え」(数学ルール) |
・ 基準名は ない → 〈2, 1〉→〈1,
・ 列挙のイメージは「自分なし、右のみフサフサ( )
)
・ 全事象は、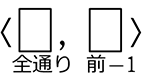 ÷マス数の!(階乗) → 順列数えを÷マス! → \({}_{全個数} \mathrm{C }_{取る個数}\)
÷マス数の!(階乗) → 順列数えを÷マス! → \({}_{全個数} \mathrm{C }_{取る個数}\)
(マス数の階乗で割ると「かぶり」がなくなる)
《 例 》
袋の中に数字2, 3, 4, 5, 6 を書いた玉がそれぞれ1個ずつある。この5個の玉から同時に2個を取り出すとき、
書かれている数の積が、4の倍数である確率を求めましょう
・ 図がないときは自分で図を書きますが、袋や箱は不要ですし、分かりやすいように並べて書きます
 23456
23456
| ・ | 「同時に」より → 組合せ数え(数学ルール) |
| → | 積が4の倍数(因数に2が最低2個あればよい)を列挙すると、( ) ) |
〈
・ 全事象=組合せ数えで数えたので組合せ数え= ÷2!= \({}_5 \mathrm{C }_2\) = 10通り
÷2!= \({}_5 \mathrm{C }_2\) = 10通り
∴ \(\large{\frac{5}{10}}\) = \(\large{\frac{1}{2}}\)
・ マスの並びに意味があるために、当該事象(分子)を順列数えしたら
→ 分母も順列数え!
確率 = 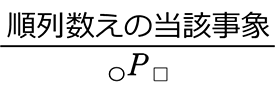
・ マスの並びに意味がないために、当該事象(分子)を組合せ数えしたら
→ 分母も組合せ数え!
確率 = 
実は下段の は
は 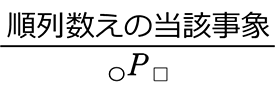 としても答は同じですね
としても答は同じですね
ex. 例えば2個選ぶとき、\({}_〇 \mathrm{C }_□\) の□は2なので、\({}_〇 \mathrm{C }_2\)ですね
分母と分子の□が同じとき、 =
= 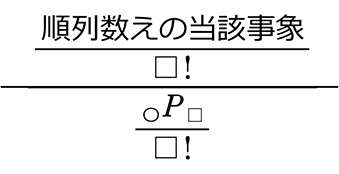 = \(\large{\frac{□!}{□!}}\)という「1」をかけて
= \(\large{\frac{□!}{□!}}\)という「1」をかけて 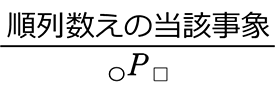 ですね
ですね

同じなら、全部 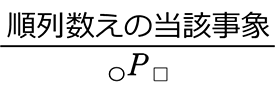 ですればよいのでは?
ですればよいのでは?
→ やめておきましょうね
ex. 1, 2, 3, 4, 5 の数が1つずつ書かれた5枚のカード(玉)から、
「同時」に2枚のカードを取り出す。
取り出したカードに書かれた数の和が奇数となるのは何通り?
→ 6通りです!(12通りではなかったですね)
→ 質問に合った答えは 組合せ数え(「同時に」のときは「組合せ数え」という数学ルール)の当該事象
「結局同じだから」が通用するのは「計算途中」だけですね
また、 のようなとき、すなわち
のようなとき、すなわち 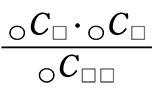 のようなときは使えないですね
のようなときは使えないですね
→ □に入る「階乗」は、1!×1!=1 ≠ 2! ですものね
〈5〉【 区別がない(同じものを含む) 】
⇒ 区別がないものは、こちらで区別をつけて1特徴系に昇格させれば、 → 今まで学んできた「戻す」「袋2つ」「続けて」「同時に」系と全く同じように解けますね
ついでですので、「乗法定理」や「PやC」での考え方も載せておきますが、まずは「列挙で」ですね!
《 例 》
| 1と書いたカードが2枚、2と書いたカードが4枚ある | ||
 |
→ | 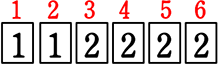 |
赤玉が2個、白玉4個ある |
||
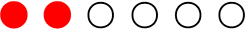 |
→ |  |
6本のくじがあり、その中に当たりくじが2本ある |
||
 |
→ | 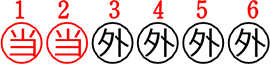 |
女子が2人、男子が4人いる |
||
 |
→ |  |
↑はすべて同じ題材ということですね
慣れるまでは、「完全に区別」した方が混乱しにくいですね → 1a, 1b, 2a, 2b、赤1, 赤2, 白1, 白2 という「最低限区別」は思ったより混乱しやすいですね
〔1-1, 戻して系 (親中数えOK)〕
112222
このカードから1枚カードを取り出し、数字を記録してから、取り出したカードをもどし、再び1枚カードを取り出し、数字を記録する。このとき、1回目の数字と2回目の数字の和が3以上になる確率を求めましょう
=赤と白が出る確率、当たりと外れが出る確率、女子と男子である確率
(樹形図なら)  → 「戻し」より → =サイコロ2つ → 樹形図は62
→ 「戻し」より → =サイコロ2つ → 樹形図は62
2枚の1と書かれたカードを1, 2、4枚の2と書かれたカードを3, 4, 5, 6として
2枚のカードの取り出し方を樹形図で表すと
全ての場合は36通りあり、このうち和が3以上になるものは32通りである
したがって、求める確率は、\(\large{\frac{32}{36}}\)=\(\large{\frac{8}{9}}\)
(列挙なら) 
 ありありフサフサ
ありありフサフサ
・ 「戻し」より → =サイコロ → 順列数え
・ 余事象は → 「和が3未満」 → 整数より「和が2以下」でよい
→ 和が2以下を列挙すると、(1, 1)(1, 2)(2, 1)(2, 2)の4通り 「和」より親中数えでもOK  左なしフサフサ
左なしフサフサ
・ 全事象=サイコロ2つ=62=36通り
・ 本事象=36-4=32通り
∴ \(\large{\frac{32}{36}}\)=\(\large{\frac{8}{9}}\)
(Pなら) 
・ 和が3以上は、1+2、2+1、2+2
・ \(\large{\frac{(1, → 2)(2, → 1)(2, → 2)}{全事象}}\) =\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ {}_4 \mathrm{P }_1)+({}_4 \mathrm{P }_1 \ , \ {}_2 \mathrm{P }_1)+(4^2)}{6^2}}\) =\(\large{\frac{2通り×4通り+4通り×2通り+16通り}{36通り}}\) =\(\large{\frac{8+8+16}{36}}\) =\(\large{\frac{32}{36}}\) =\(\large{\frac{8}{9}}\)
(親中数えOKなのでCで) 
・ 和が3以上は、1+2、2+2
・ \(\large{\frac{〈1, と2〉〈2, と2〉}{全事象}}\) =\(\large{\frac{〈{}_2 \mathrm{C }_1 \ , \ {}_4 \mathrm{C }_1〉×並びにこだわる2!+〈4通り×4通り〉}{6^2}}\) =\(\large{\frac{8×2+16}{36}}\) =\(\large{\frac{32}{36}}\) =\(\large{\frac{8}{9}}\)
(乗法定理なら) 
・ 和が3以上は、(1, →2) (2, →1) (2, →2)
∴ (\(\large{\frac{2}{6}}\), \(\large{\frac{4}{6}}\))(\(\large{\frac{4}{6}}\), \(\large{\frac{2}{6}}\))(\(\large{\frac{4}{6}}\), \(\large{\frac{4}{6}}\)) ←(1回目1を引く確率, 2回目2を引く確率)(1回目2を引く確率, 2回目1を引く確率)(1回目2を引く確率, 2回目2を引く確率) =\(\large{\frac{8}{36}}\)+\(\large{\frac{8}{36}}\)+\(\large{\frac{16}{36}}\) =\(\large{\frac{32}{36}}\) =\(\large{\frac{8}{9}}\) ←まとめて分子を数えて全事象で割るのか(今まで)、その都度確率を求めて足すのか(乗法定理)の違いですね
〔1-2, 戻して系 (親中数えダメ)〕
この玉から1個の玉を取り出し、玉の色を記録してから、取り出した玉をもどし、再び1個の玉を取り出し、玉の色を記録する。このとき、1回目が赤、2回目が白になる確率を求めましょう
=1回目のカード<2回目のカード、すなわち(1, → 2)となる確率、1回目が当たり2回目が外れ(当, →外れ)の確率、1回目が女子、2回目が男子(女, →男)の確率
(樹形図なら)  →「戻し」より → サイコロ2つ → 樹形図は 62
→「戻し」より → サイコロ2つ → 樹形図は 62
2つの赤玉を1, 2、4つの白玉を3, 4, 5, 6 として
2個の玉の取り出し方を樹形図で表すと
全ての場合は36通りあり、このうち1回目が赤、2回目が白になるものは8通りである
したがって、求める確率は、\(\large{\frac{8}{36}}\)=\(\large{\frac{2}{9}}\)
(列挙なら) 
 ありありフサフサ
ありありフサフサ
・ 「戻し」より → =サイコロ → 順列数え
→ (赤, → 白)を列挙すると、(1, 3 4 5 6)(2, 3 4 5 6)=4+4=8通り 対は当然に成り立たないので親中数えダメ
・ 全事象=サイコロ2つ=62=36通り
∴ \(\large{\frac{8}{36}}\)=\(\large{\frac{2}{9}}\)
(Pで) 
・ 赤 → 白の確率=\(\large{\frac{(赤 \ , \ → 白)}{6^2}}\)=\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ {}_4 \mathrm{P }_1)}{6^2}}\)=\(\large{\frac{8}{36}}\) =\(\large{\frac{2}{9}}\)
(親中数えダメ(対は当然に成り立たない)よりCは不可)
(乗法定理で) 
・ 赤 → 白の確率=(\(\large{\frac{2}{6}}\), \(\large{\frac{4}{6}}\))=\(\large{\frac{8}{36}}\) =\(\large{\frac{2}{9}}\)

確率の乗法定理 (確率どうしのかけ算)
例えば、(複数特徴系で) 2つのサイコロを投げて、1個目が1の目、2個目が2の目になる確率は?
・ 当該事象= ( )= 1×1=1通り (
)= 1×1=1通り (
・ 全事象=62=36通り
∴ \(\large{\frac{1}{36}}\)
この\(\large{\frac{1}{36}}\) は、1個目1の出る確率\(\large{\frac{1}{6}}\)×2個目2の出る確率\(\large{\frac{1}{6}}\)=\(\large{\frac{1}{36}}\) と同じですね!
⇒ 独立した事象の確率は、かけ算してもよいということになります!
『独立』とは、確率の場面では「無関係」ということですね
2つの試行において、2回目の試行(2個目の試行)「2の目が出る確率(事象)」は、1回目の目に「関係」なく2が出てますものね
→ 1回目の試行が2回目の試行に影響を与えない、2回目の試行は1回目の試行に影響を受けない⇒2回目の試行は『独立』ですね(当然1回目も「独立な試行」)
逆に『従属』なら、「関係あり」ということですね
例えば、赤玉2個、白玉3個から玉を戻さずに2回続けて玉をとる
●●〇〇〇
・ 1回目が赤の確率は\(\large{\frac{2}{5}}\)
・ 2回目が赤の確率は・・・
1回目が赤のときは、(①残りは●○○○)赤1、白3で\(\large{\frac{1}{4}}\)
1回目が白のときは、(②残りは●●○○)赤2、白2で\(\large{\frac{2}{4}}\)
・・・2回目の試行は1回目の試行の影響を受けているので「独立」ではないですね
ですが!2回目のそれぞれの試行を個別に見ると
| ① | は赤1、白3から1個とるという ある意味「独立」な試行 |
| ② | は赤2、白2から1個とるという ある意味「独立」な試行 |
実際、このあとの「前提のある事象の確率」もかけ算していますね
| ⇒ | 結局、2つセットの事象で「独立か」「そうでないか」を考える意味はないですね! |
| ⇒ | 2つセットの事象では「確率が同じか、変わるか」だけ注意すればよいということですね |
次に、例えば、(1特徴系で)
12345から続けて2個とるとき1個目が〇、2個目が〇になる確率は?
・ 当該事象= ( ) =3通り×2通り=6通り
) =3通り×2通り=6通り
・ 全事象= (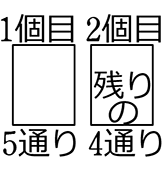 ) =5通り×4通り=20通り
) =5通り×4通り=20通り
∴ \(\large{\frac{6}{20}}\) = \(\large{\frac{3}{10}}\)
この\(\large{\frac{3}{10}}\)は、1回目の赤の確率\(\large{\frac{3}{5}}\)×2回目の(赤が1つ減った)白の確率\(\large{\frac{2}{4}}\) = \(\large{\frac{6}{20}}\) = \(\large{\frac{3}{10}}\) と同じですね!
| ⇒ | 前提のある事象の確率は、かけ算してもよいということになります! |
2回目の状態●●〇〇を、別の「独立した」Bの袋(●●〇〇)から1個とる とみなしているのですね
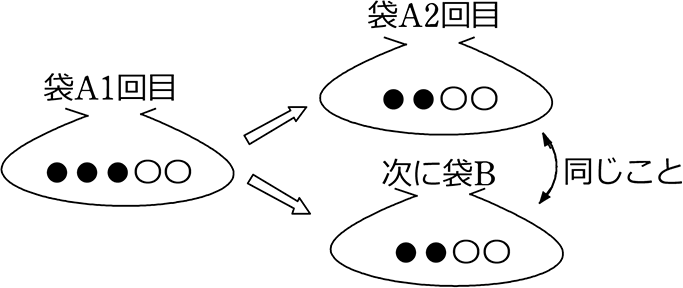
確率の乗法定理
| ① | 独立した事象の確率は、かけ算してもよい |
| ② | 前提のある事象の確率は、かけ算してもよい |
ただし、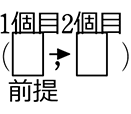 や
や 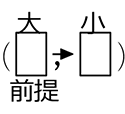 のようにマスの並びにこだわった順列数えの確率であることを忘れない
のようにマスの並びにこだわった順列数えの確率であることを忘れない
正式には
① P(A
(ただし、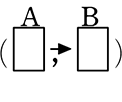 マスの並びにこだわっていることを忘れない。「かつ」といえば両方向カバーしていそうですが(A,
マスの並びにこだわっていることを忘れない。「かつ」といえば両方向カバーしていそうですが(A,
② P(A∩B)=P(A)×PA(B) 「AかつBの確率は、Aの確率×Aが起こった前提のBの確率」
(ただし、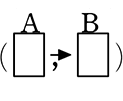 マスの並びにこだわっていることを忘れない。「かつ」といえば両方向カバーしていそうですが(Aが起こって,
マスの並びにこだわっていることを忘れない。「かつ」といえば両方向カバーしていそうですが(Aが起こって,
すなわちここでの ∩ (俗読み:かつ、正式読み:キャップ)は「ABの順の(並びにこだわっている → 順列数えの)」確率となります
決して、とにかく(1と2)、とにかく(赤と白)のような(  ,と
,と  ) 系や
) 系や
とにかく 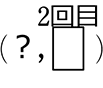 型のような、とにかく2回目に当たり系にはそのまま使えません、これらはあともう1処理必要になりますね
型のような、とにかく2回目に当たり系にはそのまま使えません、これらはあともう1処理必要になりますね
〔2-1、続けて系(親中数えOK)〕
このくじから先にAが1回引き、続けてBが1回引く。このときAとBの結果が異なる確率を求めましょう
=1回目のカードの数+2回目のカードの和が奇数(1, と2)となる確率、1回目と2回目で異なる色玉になる確率、委員長副委員長で異性が選ばれる確率
(樹形図なら)  → 「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
→ 「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
2本の当たりを1, 2、4本の外れを3, 4, 5, 6 として
2本のくじの取り出し方を樹形図で表すと
全ての場合は30通りあり、このうち結果が異なるものは16通りである
したがって、求める確率は、\(\large{\frac{16}{30}}\)=\(\large{\frac{8}{15}}\)
(列挙なら) 
 自分なしフサフサ
自分なしフサフサ
・ 「続けて」より → 順列数え
→ 結果が異なるを列挙すると、(1, 3 4 5 6)(2, 3 4 5 6)(3, 1 2 )(4, 1 2)(5, 1 2)(6, 1 2) =4+4+2+2+2+2 =16通り 結局、対も当然に成り立つ〈当, と外〉より親中数もOK  右のみフサフサ
右のみフサフサ
・ 全事象=\({}_6 \mathrm{P }_2\)=30通り
∴ \(\large{\frac{16}{30}}\)=\(\large{\frac{8}{15}}\)
(Pなら) 
・ 結果が異なる → (当, → 外)(外, → 当)
・ \(\large{\frac{(当, → 外)(外, → 当)}{全事象}}\) =\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ {}_4 \mathrm{P }_1)({}_4 \mathrm{P }_1 \ , \ {}_2 \mathrm{P }_1)}{{}_6 \mathrm{P }_2}}\) =\(\large{\frac{2通り×4通り+4通り×2通り}{30通り}}\) =\(\large{\frac{8+8}{30}}\) =\(\large{\frac{16}{30}}\) =\(\large{\frac{8}{15}}\)
(親中数えOKなのでCで) 
・ 結果が異なる → 〈当, と外〉
・ \(\large{\frac{〈当 \ , \ 外 〉}{全事象}}\) =\(\large{\frac{〈{}_2 \mathrm{C }_1 \ , \ {}_4 \mathrm{C }_1〉×並びにこだわる2!}{{}_6 \mathrm{P }_2}}\) =\(\large{\frac{(2通り×4通り)×2}{30}}\) =\(\large{\frac{16}{30}}\) =\(\large{\frac{8}{15}}\)
(親中数えOK+ぞろ目ラインがないので組合せ数えでズル) 
・ 結果が異なる → 〈当, と外〉
・ \(\large{\frac{〈当 \ , \ 外〉}{全事象}}\) =\(\large{\frac{〈{}_2 \mathrm{C }_1 \ , \ {}_4 \mathrm{C }_1〉}{{}_6 \mathrm{C }_2}}\) =\(\large{\frac{2通り×4通り}{15通り}}\) =\(\large{\frac{8}{15}}\)
(乗法定理で) 
結果が異なる → (当, → 外)(外, → 当)
∴ (\(\large{\frac{2}{6}}\), \(\large{\frac{4}{5}}\))(\(\large{\frac{4}{6}}\), \(\large{\frac{2}{5}}\)) ←(1回目当を引く確率, 2回目当が1本減った5本から外を引く確率)(1回目外を引く確率, 2回目外が1本減った5本から当を引く確率)
=\(\large{\frac{8}{30}}\)+\(\large{\frac{8}{30}}\) =\(\large{\frac{16}{30}}\) =\(\large{\frac{8}{15}}\)
〔2-2,続けて (親中数えダメ)〕
このくじから先にAが1回引き、続けてBが1回引く。このときAが当たりBが外れる確率を求めましょう
=Aのカード<Bのカード、すなわち(1, → 2)となる確率、Aが赤玉Bが白玉(赤, → 白)となる確率、委員長が女子副委員長が男子(女子, → 男子)の確率
(樹形図なら)  → 「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
→ 「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
2本の当たりを1, 2、4本の外れを3, 4, 5, 6 として
2本のくじの取り出し方を樹形図で表すと
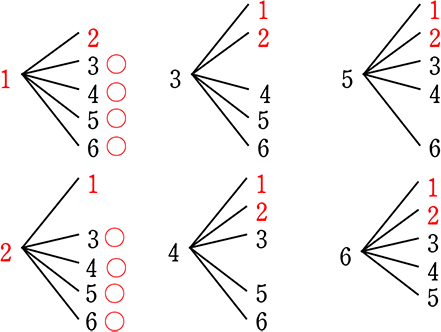
全ての場合は30通りあり、このうち1回目が赤、2回目が白になるものは8通りである
したがって、求める確率は、\(\large{\frac{8}{30}}\)=\(\large{\frac{4}{15}}\)
(列挙なら) 
 自分なしフサフサ
自分なしフサフサ
・ 「続けて」より → 順列数え
→ (赤, → 白)を列挙すると、(1, 3 4 5 6)(2, 3 4 5 6)=4+4=8通り 対は当然に成り立たないので親中数えダメ
・ 全事象=\({}_6 \mathrm{P }_2\)=30通り
∴ \(\large{\frac{8}{30}}\)=\(\large{\frac{4}{15}}\)
(Pなら) 
・ (当, → 外)の確率=\(\large{\frac{(赤, → 白)}{全事象}}\) =\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ {}_4 \mathrm{P }_1)}{{}_6 \mathrm{P }_2}}\) =\(\large{\frac{8}{30}}\) =\(\large{\frac{4}{15}}\)
(親中数えダメ(対は当然に成り立たない)よりCは不可)
(乗法定理で) 
・ (当, → 外)の確率=(\(\large{\frac{2}{6}}\), \(\large{\frac{4}{5}}\)) =\(\large{\frac{8}{30}}\) =\(\large{\frac{4}{15}}\)
【 日本語の解明 】
① ② ③ ④ ⑤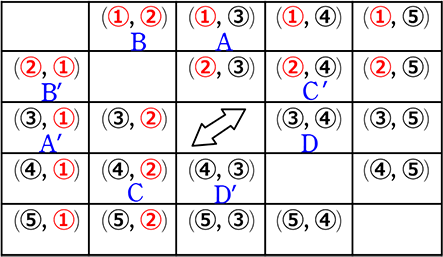
| 「続けて」引いて → 原則 順列数え | ||||
|---|---|---|---|---|
| 1回目は~、 2回目は~ | ~と~ | |||
|
1回目は赤、 |
1回目は赤、 |
赤と白 の確率 |
赤と赤 の確率 |
同じ色 の確率 |
| =( |
=( |
=( |
=( |
=( |
|
「対」不成立 |
「対」自動成立 |
それぞれで、「対」自動成立 |
||
| AとA’は違う | BとB’(対も成立) |
AとA’もCとC’も |
BとB’(対も成立) |
BとB’もDとD’も |
| ( |
〈●, と●〉 |
〈●, と〇〉 |
〈●, ●〉 |
〈●, ●〉+〈○, ○〉 |
〔3, 同時に系〕
この6人から代表を2人選ぶとき、男女となる確率を求めましょう
=同時に2枚取って数字が異なる〈1, と2〉の確率、同時に2個取って色が異なる〈赤, と白〉の確率、同時に2本引いて当たりと外れ〈当, 外〉になる確率
(樹形図なら)  → 「代表」≒「同時に」より → 組合せ数え(数学ルール) → 樹形図は \({}_6 \mathrm{C }_2\)
→ 「代表」≒「同時に」より → 組合せ数え(数学ルール) → 樹形図は \({}_6 \mathrm{C }_2\)
2人の女子を1, 2、4人の男子を3, 4, 5, 6 として
2人の代表の選び方を樹形図で表すと
全ての場合は15通りあり、このうち男女となるものは8通りである
したがって、求める確率は、\(\large{\frac{8}{15}}\)
(列挙なら) 
 右のみフサフサ
右のみフサフサ
・ 「代表」より → 並びにこだわらない → 組合せ数え 代表, 副代表などなら順列数え
→ 〈女子, と男子〉を列挙ですると、〈1,3 4 5 6〉〈2, 3 4 5 6〉=4+4=8通り
・ 全事象=\({}_6 \mathrm{C }_2\)=15通り
∴ \(\large{\frac{8}{15}}\)
(Cなら) 
〈女, と男〉の確率=\(\large{\frac{〈女, と男〉}{全事象}}\) =\(\large{\frac{〈{}_2 \mathrm{C }_1 \ , \ {}_4 \mathrm{C }_1〉}{{}_6 \mathrm{C }_2}}\) =\(\large{\frac{2通り×4通り}{15通り}}\) =\(\large{\frac{8}{15}}\)
(Pなら) 
〈女, と男〉の確率 =(女, → 男)+(男, → 女)の確率 =\(\large{\frac{(女, → 男)(男, → 女)}{全事象}}\) =\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ {}_4 \mathrm{P }_1)({}_4 \mathrm{C }_1 \ , \ {}_2 \mathrm{P }_1)}{{}_6 \mathrm{P }_2}}\) =\(\large{\frac{8通り+8通り}{30通り}}\) =\(\large{\frac{16}{30}}\) =\(\large{\frac{8}{15}}\)
(乗法定理で) 
・ 〈女, と男〉の確率 =(女, → 男)の確率+(男, → 女)の確率
∴ (\(\large{\frac{2}{6}}\), \(\large{\frac{4}{5}}\))(\(\large{\frac{4}{6}}\), \(\large{\frac{2}{5}}\)) =\(\large{\frac{8}{30}}\)+\(\large{\frac{8}{30}}\) =\(\large{\frac{16}{30}}\) =\(\large{\frac{8}{15}}\)
【 日本語の解明 】
① ② ③ ④ ⑤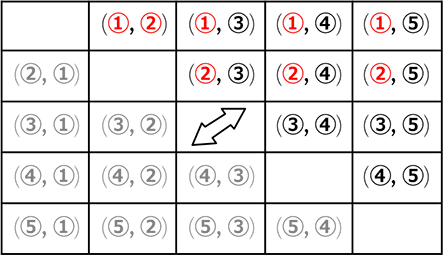
「対」達も昇順に並び替えたら同じだ!
→ 対は不要 → 対がない
| 「同時に」引いて → 組合せ数え (数学ルール) | |||
|---|---|---|---|
|
1回目は~、 |
~と~ | ||
|
赤と白 の確率 |
赤と赤 の確率 |
同じ色 の確率 |
|
|
〈●, と〇〉 |
〈●, ●〉 |
〈●, ●〉+〈○, ○〉 |
|
〔4, とにかく○番目〕
この6本のくじからAさんが1本引き次にBさんが1本引くとき、Bさんが当たる確率を求めましょう
=2回目にひくカードが1である確率、2回目に取る玉が赤の確率、委員長副委員長を選ぶとき副委員長が女子である確率
(樹形図なら)  → ≒「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
→ ≒「続けて」より → 順列数え → 樹形図は \({}_6 \mathrm{P }_2\)
2本の当たりを1, 2、4本の外れを3, 4, 5, 6 として
2本のくじの取り出し方を樹形図で表すと
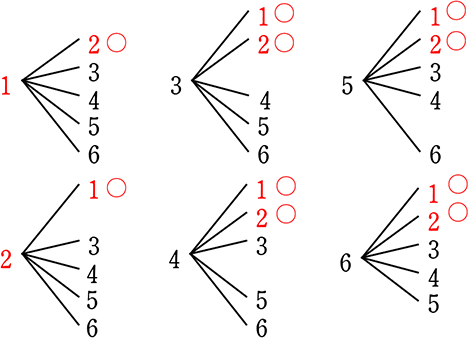
全ての場合は30通りあり、このうちBが当たるのは10通りである
したがって、求める確率は、\(\large{\frac{10}{30}}\)=\(\large{\frac{1}{3}}\)
(列挙なら) 
 自分なしフサフサ
自分なしフサフサ
・ 「続けて」より → 順列数え
→ (?, 当)=(当, 当)(外, 当)を列挙すると、(1, 2)(2, 1)(3, 1 2)(4, 1 2)(5, 1 2)(6, 1 2)=1+1+2+2+2+2=10通り
・ 全事象=\({}_6 \mathrm{P }_2\)=30通り
∴ \(\large{\frac{10}{30}}\)=\(\large{\frac{1}{3}}\)
(Pなら) 
・ (当, 当)(外, 当)の確率 =\(\large{\frac{(当, 当)(外, 当)}{全事象}}\) =\(\large{\frac{({}_2 \mathrm{P }_1 \ , \ 残りの1通り)({}_4 \mathrm{P }_1 \ , \ {}_2 \mathrm{P }_1)}{{}_6 \mathrm{P }_2}}\) =\(\large{\frac{2通り+8通り}{30通り}}\) =\(\large{\frac{10}{30}}\) =\(\large{\frac{1}{3}}\)
(親中数えダメ(対は当然に成り立たない)よりCは不可)
(乗法定理なら) 
・ (当, 当)(外, 当)の確率 =(\(\large{\frac{2}{6}}\), \(\large{\frac{1}{5}}\))(\(\large{\frac{4}{6}}\), \(\large{\frac{2}{5}}\)) =\(\large{\frac{2}{30}}\)+\(\large{\frac{8}{30}}\) =\(\large{\frac{10}{30}}\) =\(\large{\frac{1}{3}}\)
実は、くじを引くときの『どこかで当たる当たりやすさ』は、引く順番とは無関係!
⇒ すべて等しい
ex. 例えば、6回引いたときの当たりはずれの全並び方は
(1回目, 2回目, 3, 4, 5, 6回目)の順で
または(Aさん, Bさん, C, D, E, Fさん)の順で
全通りは…
(●●〇〇〇〇)
(●〇●〇〇〇)
(●〇〇●〇〇)
(●〇〇〇●〇)
(●〇〇〇〇●)
(〇●●〇〇〇)
(〇●〇●〇〇)
(〇●〇〇●〇)
(〇●〇〇〇●)
(〇〇●●〇〇)
(〇〇●〇●〇)
(〇〇●〇〇●)
(〇〇〇●●〇)
(〇〇〇●〇●)
(〇〇〇〇●●)
↓ ↘
5通り↓
5通り
→ 縦で見るとすべての人が5通り
1回目に当たる(Aが当たる)確率は、\(\large{\frac{5}{15}}\) = \(\large{\frac{1}{3}}\)
2回目に当たる(Bが当たる)確率は、\(\large{\frac{5}{15}}\) = \(\large{\frac{1}{3}}\)
結局は
(?, ○) や (?, ?, ○)などの確率 =1回目に○の確率
ex)
このくじをA, B が引いたあとに、Cが3番目に引いたときの当たりの確率を求めましょう
・ (?, ○)の型
∴ 1回目のAが当たる確率と同じより、(○, ) =\(\large{\frac{2}{6}}\) =\(\large{\frac{1}{3}}\)
(確認)
→ Cがとにかく当たりを列挙すると、
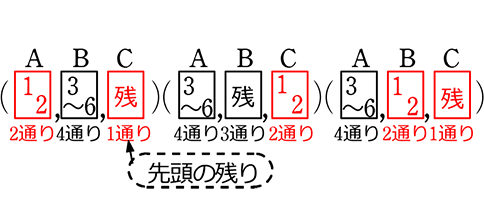 =8通り+24通り+8通り =40通り
=8通り+24通り+8通り =40通り
・ 全事象=\({}_6 \mathrm{P }_3\)=6×5×4 =120通り
∴ \(\large{\frac{40}{120}}\)=\(\large{\frac{4}{12}}\)=\(\large{\frac{1}{3}}\)
《 例 》
赤玉,青玉,白玉がそれぞれ2個ずつ入った袋から、同時に2個の玉を取り出すとき、異なる色が出る確率は?
・区別をつけて、123456
・「同時に」より → 組合せ数え
| ・ | 2個で異なる組合せは〈赤, と青〉〈赤, と白〉〈青, と白〉の3パターン |
→ これらを列挙すると、〈1 2, 3 4 5 6〉〈3 4 , 5 6〉=8通り+4通り=12通り
→ 全事象=\({}_6 \mathrm{C }_2\)=15通り
∴ \(\large{\frac{12}{15}}\)=\(\large{\frac{4}{5}}\)

排反とは
なんとなく、再び分子がどういうとき「足し算?」「かけ算?」??になってきているかもしれませんね
まず「事象」について、
定義
| 排反である… | 同時に起こりえない事象 |
| 排反でない… | 同時に起こりえる事象 |
イメージが湧かないので、もう少し丁寧に
もう少し丁寧に
・ 排反事象…同時に起こりえない事象のくくり名 
→ くくり名がかぶらない関係
・ 排反でない…同時に起こりえる事象のくくり名 
→ くくり名がかぶっている関係
ex.
サイコロを1回投げて、2または3の目が出る確率は?
→ \(\large{\frac{2の目の1通り\color{red}{+}3の目の1通り}{6}}\)=\(\large{\frac{2}{6}}\) でしたね
| → | 2の目というくくり名に注目すれば、3の目も、4の目も同時に起こらない → 排反 |
| → | 3の目のくくり名は、問題文には適している → 「排反な事象は足す」ですね → 正確には『問題文に適した排反な事象(適合排反(親中用語))は足す』ですね |
| → | 2の目のくくり名と3の目のくくり名は、適合排反(親中用語)⇒単純に足せる |
| → | 4, 5, 6 は不適合排反(親中用語)⇒足さない → 余事象である |
ex.
サイコロを1回投げて、偶数の目が出る確率は?
→ (2 4 6, )の3通り → \(\large{\frac{1+1+1}{6}}\)=\(\large{\frac{3}{6}}\) でしたね
→ 偶数の目というくくり名に注目すれば、1, 3, 5 の目は排反
→ 1, 3, 5は問題文にも適していない → 不適合排反 → 余事象
ex. サイコロを1回投げて、2の倍数または3の倍数が出る確率は?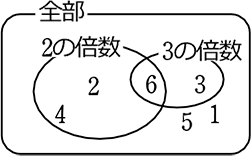
→ くくり名がかぶっている=「排反ではない(同時に起こり得る)」 → 単純には足せない
2の倍数+3の倍数-6の倍数=3通り+2通り-1通り=4通り
列挙なら、(2 3 4 6, )の4通り ∴ \(\large{\frac{4}{6}}\)
cf.
サイコロを1回投げて、2の倍数かつ3の倍数が出る確率は?
→ 「かつ」より → かぶった部分 → 6 の1通り ∴ \(\large{\frac{1}{6}}\)
2の倍数かつ3の倍数 → 2の倍数であり3の倍数でもある
● 3個とる
《 例 》
赤玉3個、青玉2個、白玉1個が入った袋から、同時に3個の玉を取り出すとき、3個とも異なる色になる確率は?
| ・ | 区別をつけて、 123456 |
(列挙なら)
| ・ | 「同時に」より → 組合せ数え(数学ルール) |
| ・ | 3個とも色が異なるのは、〈赤, と青, と白〉の1パターン |
| → | 〈赤, 青, 白〉を列挙すると、〈1 2 3, 4 5, 6〉=3通り×2通り×1通り=6通り |
| → | 真面目に列挙すると、〈1, 4, 6〉〈1, 5, 6〉〈2, 4, 6〉〈2, 5, 6〉〈3, 4, 6〉〈3, 5, 6〉 |
・ 全事象=\({}_6 \mathrm{C }_3\)=6×5×4÷3!=20通り
∴ \(\large{\frac{6}{20}}\)=\(\large{\frac{3}{10}}\)
(Cなら) \(\large{\frac{〈{}_3 \mathrm{C }_1 \ , \ {}_2 \mathrm{C }_1 \ , \ {}_1 \mathrm{C }_1〉}{{}_6 \mathrm{C }_3}}\) =\(\large{\frac{3×2×1}{20}}\) =\(\large{\frac{3}{10}}\)
《 例 》
赤玉4個、白玉2個が入った袋から、同時に3個の玉を取り出すとき、赤玉が2個、白玉が1個になる確率は?
・ 区別をつけて、 123456
(列挙なら)
| ・ | 「同時に」より → 組合せ数え(数学ルール) |
→ 〈赤, 赤, 白〉を列挙すると、 =12通り
=12通り
・ 全事象=\({}_6 \mathrm{C }_3 \) = 20通り
∴ \(\large{\frac{12}{20}}\) = \(\large{\frac{3}{5}}\)
(Cなら) \(\large{\frac{〈{}_4 \mathrm{C }_2 \ , \ {}_2 \mathrm{C }_1〉}{{}_6 \mathrm{C }_3}}\) = \(\large{\frac{12}{20}}\)=\(\large{\frac{3}{5}}\)
(乗法定理なら) 〈●, と●, と○〉=(●→●→〇)+(●→〇→●)+(〇→●→●) =\(\large{\frac{4}{6}}\)×\(\large{\frac{3}{5}}\)×\(\large{\frac{2}{4}}\)+\(\large{\frac{4}{6}}\)×\(\large{\frac{2}{5}}\)×\(\large{\frac{3}{4}}\)+\(\large{\frac{2}{6}}\)×\(\large{\frac{4}{5}}\)×\(\large{\frac{3}{4}}\) =\(\large{\frac{24}{120}}\)+\(\large{\frac{24}{120}}\)+\(\large{\frac{24}{120}}\) =\(\large{\frac{72}{120}}\) =\(\large{\frac{3}{5}}\)
《 例 》
赤玉4個、白玉5個が入った袋から、同時に3個の玉を取り出すとき、
(1) 色がそろう確率は?
・ 区別をつけて、123456789
・「同時に」より → 組合せ数え(数学ルール)
→ 列挙すると、 → 〈●と●と●〉〈〇と〇と〇〉=\({}_4 \mathrm{C }_3\)+\({}_5 \mathrm{C }_3\) = \({}_4 \mathrm{C }_1\)+\({}_5 \mathrm{C }_2\) = 4+10=14通り (nCr=nC(n-r))
・ 全事象=\({}_9 \mathrm{C }_3\)=\(\large{\frac{9\ \cdot \ 8\ \cdot \ 7}{3\ \cdot \ 2\ \cdot \ 1}}\)=84通り
∴ \(\large{\frac{14}{84}}\)=\(\large{\frac{7}{42}}\)=\(\large{\frac{1}{6}}\)
(2) 赤と白が混ざっている確率は?
→ 余事象は…「混ざっていない」=「そろっている」=(1)の答
∴ 1-\(\large{\frac{1}{6}}\)=\(\large{\frac{5}{6}}\)
〈7〉 人
【 全員の並び方 】
《 例 》
両親と子供3人合わせて5人が、横1列に並ぶとき
(1) 5人の並ぶ方法は何通り?
・ 人は区別がある →
・「並べる」より → 絶対順列数え
・ 全事象=5人の全順列 =\({}_5 \mathrm{P }_5\) =5! =5×4×3×2×1 =20×6 =120通り
cf
人は絶対的に区別がありますね、「異なる~」ですね
1年生の「割合」で、クラス40人に鈴木さんが2名
鈴木さんの割合は? → \(\large{\frac{2}{40}}\) でしたね
40としたということは、40名の生徒を本能的に「区別をつけて数えた」ということですね
そもそも割合的なもの(\(\large{\frac{△}{〇}}\))、確率もそうですが区別をつけて数えなければ正確な割合など求められるわけがないということですね
→ 学び始めの「確率は、すべてに区別をつけて」は当然のことを言っていたということですね
(2) 両親が両端にいる確率は?
→ 両親が両端を列挙すると、
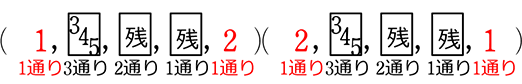 =6通り+6通り =12通り
=6通り+6通り =12通り
(ワンランク上の列挙だと)
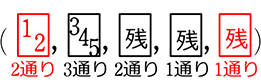 =2通り×6通り =12通り
=2通り×6通り =12通り
∴ \(\large{\frac{12}{120}}\)=\(\large{\frac{1}{10}}\)
(3) 両親と子が交互に並ぶ確率は?
→ 交互を列挙すると、
( , , , , )のパターンしかない
赤がもう1人多ければ、
( , , , , , ) ( , , , , , )の2パターンですね
 =6通り×2通り=12通り
=6通り×2通り=12通り
∴ \(\large{\frac{12}{120}}\)=\(\large{\frac{1}{10}}\)
(4) 両親が隣り合って並ぶ確率は?
→ 両親が隣り合うを列挙すると、
-2a.png) =12+12+12+12 =48通り
=12+12+12+12 =48通り
(ワンランク上の列挙だと)
両親を1つと見て、-2b.png) =∧∧∧∧は4つから1つ(箇所)を選ぶこと=\({}_4 \mathrm{C }_1\)=4通りの場所
=∧∧∧∧は4つから1つ(箇所)を選ぶこと=\({}_4 \mathrm{C }_1\)=4通りの場所
∴ 子の並び(3!)×∧の選び方(4通り)× ボックス内の並び(2!) =6×4×2 =48通り 原理は上と同じですね、見比べて、「確かに同じことだな」と思っていただければ、2歩前進ですね!
ボックス内の並び(2!) =6×4×2 =48通り 原理は上と同じですね、見比べて、「確かに同じことだな」と思っていただければ、2歩前進ですね!
∴ \(\large{\frac{48}{120}}\)=\(\large{\frac{12}{30}}\)=\(\large{\frac{2}{5}}\)
(5) 両親の間に少なくとも1人の子供がいる確率は?
・「間に少なくとも1人いる」の余事象は、 → 「間にいない」=(4)の「両親が隣り合わせ」
∴ 1-\(\large{\frac{2}{5}}\)=\(\large{\frac{3}{5}}\)
もちろん正統に列挙もOK、
-2d.png)
=2!×3!×6パターン=2×6×6=72通り
∴ \(\large{\frac{72}{120}}\)=\(\large{\frac{12}{20}}\)=\(\large{\frac{3}{5}}\)
【 1部を選ぶ 】
《 例 》
男子A, B, C、女子D, E の5人グループがいる
(1) この5人から、委員長, 副委員長, 書記長 の選び方は何通り?
・ 並びに「こだわる」3人の選び方は → \({}_5 \mathrm{P }_3\)=5×4×3=60通り
(
(2) この5人から代表3人を選ぶ選び方は何通り?
・ 並びに「こだわらない」3人の選び方
→ \({}_5 \mathrm{C }_3\)=\(\large{\frac{5×4×3}{3!}}\)=10通り
(
(3) この5人の中から3人の当番を選ぶことにした。3人の中にAとDがともに選ばれる確率を求めよ
| ・ | 「当番」より → 並びにこだわらない → 組合せ数え |
| → | AとDが含まれる3人を列挙すると |
| ・ | 〈A, D, B C E〉=1×1×3=3通り |
| ・ | 全事象=組合せ数えで数えたので組合せ数え=\({}_5 \mathrm{C }_3\)=5×4×3÷3÷2=10通り |
∴ \(\large{\frac{3}{10}}\)
c いろいろな問題
《 例 》
図のようなマスを、赤,青,黄,白の4色のうち、3色を使って塗るとき、中央に青がくる確率を求めましょう

・ 赤 青 黄 白 を
| ・ | マスに場所がある → 並びにこだわる → 順列数え |
・  と区別して
と区別して
→ 中央が青を列挙すると、 =6通り
=6通り
・ 全事象=\({}_4 \mathrm{P }_3\)=4×3×2=24通り
∴ \(\large{\frac{6}{24}}\)=\(\large{\frac{1}{4}}\)
《 例 》
図のような円周を6等分する点A, B, C, D, E, F がある。
これらの中から3点を選んで、それらを頂点とする三角形をつくるとき、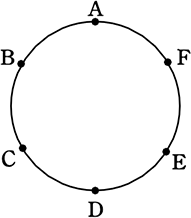
(1) 三角形は全部でいくつできますか
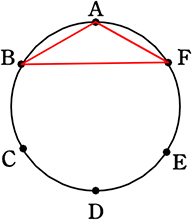
6点から3点を「(並びにこだわらずに)選べば」
よいですね
\({}_6 \mathrm{C }_3\)=\(\large{\frac{6×5×4}{3×2×1}}\)=20個
ex. 〈A, B, F〉 → 組合せ数えなので(A, F, B)
などのかぶりが排除できてますね
(2) それが直角三角形である確率を求めましょう
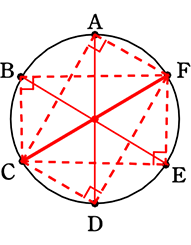
直角三角形になるには、
辺の1つが直径であればよいですね (円周角の定理)
→ 直径は〈A, D〉〈B, E〉〈C, F〉の3通り
→ 1つの直径につき、4通りの直角三角形がある
∴ 3通り×4直角三角形=12個
・ 全事象=(1)の20個
∴ \(\large{\frac{12}{20}}\)=\(\large{\frac{3}{5}}\)

最短経路の確率 (同じものを含む全順列か反復試行か)
「反復試行」は、高校で学びますね
「反復試行」とは、「同じ条件」で「同じ試行」を繰り返す ことですね
「同じ条件」とは
| ・ | コインは、何回投げても1回1回の確率は、表の確率\(\large{\frac{1}{2}}\)、裏の確率\(\large{\frac{1}{2}}\) |
| ・ | サイコロも同様に、1の目の確率は\(\large{\frac{1}{6}}\)、1以外の目の確率は\(\large{\frac{5}{6}}\) |
| ・ | 3個の白玉、2個の赤玉も毎回袋に戻せば、白玉の確率\(\large{\frac{3}{5}}\)、赤玉の確率\(\large{\frac{2}{5}}\) |
cf. 玉を戻さなければ「同じ条件」ではないですね
《 例 》
コインを3回投げて、「表」が2回出る確率は?
〈今までの求め方〉
「3枚を同時に投げて表が2枚に」置き換えて、\(\large{\frac{当該事象}{全事象}}\)としていましたね
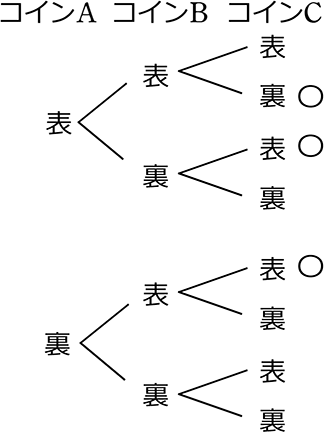
・全事象 2×2×2 = 8通り
・当該事象 図より 3通り
計算で求めるなら
・当該事象 = 〈表, 表, 裏〉の並び数
「同じものを含む全順列」なら、\(\large{\frac{3!}{2!}}\) = 3通り
「組合せ」なら、\({}_3 \mathrm{C }_2\) = 3通り
∴ 確率は \(\large{\frac{3}{8}}\)
〈反復試行での求め方〉
①まずは、表が2回の並びの「1

← コインは毎回、「互いに独立(一方の結果が
もう一方(次の試行)に影響を及ぼさない)」ので
→ 確率どうしを掛け合わせてよい ですね!

横の問題
よって、この並びになる確率は…
②そして、実際は、表2回 裏1回はどこで起こってもよいので

→どういうパターンがあるか?
すなわち、「何通りの並び方があるか」ということですね
| ・ | 「同じものを含む順列」で求めるなら、\(\large{\frac{3!}{2!}}\) = 3通り |
| ・ | 「組合せ」で求めるなら、\({}_3 \mathrm{C }_1\) = 3通り |
③よって、「同じ条件下」で求めた「\(\large{\frac{1}{8}}\)の確率」が、「同じ試行」として「3通り分」あるので
→ \(\large{\frac{1}{8}}\)×3 = \(\large{\frac{3}{8}}\) ですね

前提:同じ条件(毎回「同様に確か」)
反復試行 = 1
《 例 》
サイコロを5回振って、「最後に1の目」が出る確率は?
① 1例は→ (
よって、14×\(\large{\frac{1}{6}}\) = ただの\(\large{\frac{1}{6}}\)
② 並び方は→ 最後の「1の目」は固定されているので→前の4つの並び替え数ですね
よって、\({}_4 \mathrm{C }_4\) = 1通り
∴ \(\large{\frac{1}{6}}\)×1 = \(\large{\frac{1}{6}}\) ←前4回は全く関係ないですね!(どうでもよいという問題でした)
《 例 》
サイコロを5回振って、「最後に2回目の1の目」が出る確率は?
① 1例は→ (1, 他, 他, 他, 1)
よって、\(\large{\frac{1}{6}}\)×\(\left(\large{\frac{5}{6}}\right )^3\)×\(\large{\frac{1}{6}}\) = \(\large{\frac{125}{7776}}\)
② 並び方は→ 最後の「1の目」は固定されているので→前の4つの並び替え数ですね
よって、\({}_4 \mathrm{C }_1\) = 4通り
∴ \(\large{\frac{125}{7776}}\)×4 = \(\large{\frac{125}{1944}}\)
《 例 》
袋に白玉3個、赤玉2個、1つ取っては戻すを5回繰り返す、白玉を2月回引く確率は?

←「戻す」ということは
またこの形になりますね
→「条件が同じ」といえる
① 1例は → (白, 白, 赤, 赤, 赤) → \(\left(\large{\frac{3}{5}}\right )^2\)×\(\left(\large{\frac{2}{5}}\right )^3\) = \(\large{\frac{72}{3125}}\)
② 並び方は→ \({}_5 \mathrm{C }_2\) = 10通り
∴ \(\large{\frac{72}{3125}}\)×10 = \(\large{\frac{144}{625}}\)
それでは、「反復試行」もなんとなく解ったという前提で、
本題の「最短経路の確率」を見ていきますね
《 例 》
AからFの最短経路で、Pを通る確率は?
● aさんの解答:
・全事象\({}_3 \mathrm{C }_1\) = 3通り
・Pを通る事象 = (A→D→E→Fの)1通り
∴ \(\large{\frac{Pを通る}{全事象}}\) = \(\large{\frac{1}{3}}\)
● bさんの解答:
Aを出発点として、
Bに向かう「右」の確率\(\large{\frac{1}{2}}\)、
Dに向かう「上」の確率\(\large{\frac{1}{2}}\)、
∴ 上を選べばPを通るので \(\large{\frac{1}{2}}\)
どちらが正解なのでしょうか?
・・・実は問題文が悪いのです!
| ・ | AからFの最短経路で、Pを通る確率は?
ただし、「経路全体の選び方」が「同様に確からしい」とする |

「経路全体の選び方」が
「同様に確からしい」
このようであれば、 aさんの答えが正解ですね!
| ・ | AからFの最短経路で、Pを通る確率は?
ただし、「分岐点では上右の選び方」が「同様に確からしい」とする |
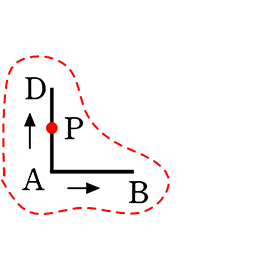

このようであれば、 bさんの答えが正解ですね!
そういえば、サイコロもコインも学び始めの頃は、
「同様に確からしいサイコロ、コイン」と言ってくれてましたが、
今では当たり前のように、サイコロ\(\large{\frac{1}{6}}\) 、コイン\(\large{\frac{1}{2}}\)で計算してますね!
いわゆる「社会通念」「常識」ということでしょうが、
この「最短経路」の問題では、
何をもって「同様に確か」かをはっきりさせてもらわないと困りますね!
よって、AからF最短経路で、Pを通る確率は? の解は…
A. 何が「同様に確か」であるかが不明なので、確率は不明
または
A. 経路全体の選び方が「同様に確か」な場合は\(\large{\frac{1}{3}}\)
分岐点での上右の選び方が「同様に確か」な場合は\(\large{\frac{1}{2}}\)
こうであっても、問題集によって「分岐点の選び方が同様に確か」と言いつつ、解答は「経路全体の選び方が同様に確か」で計算したものがありますので
「ああ~っ、もうどっち~!?」となってしまいますね!
⇒ 問題集も間違えることはある
《 例 》
「経路全体の選び方」が「同様に確からしい」場合、
SからGの最短経路で、Pを通る確率は?
〈計算で求める場合〉
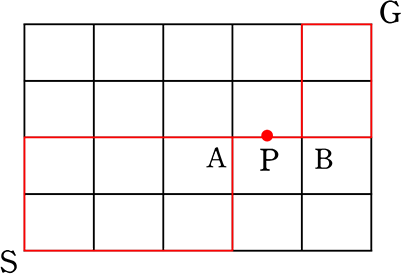
・全事象 = \({}_9 \mathrm{C }_4\) = 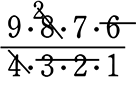 = 126通り
= 126通り
・Pを通る事象 = (S→A)×(A→B)×(B→G)
= \({}_5 \mathrm{C }_2\)×1×\({}_3 \mathrm{C }_1\) = \(\large{\frac{5\ \cdot \ 4}{2\ \cdot \ 1}}\)×1×3 = 30通り
∴ \(\large{\frac{30}{126}}\) = \(\large{\frac{5}{21}}\)
〈図形から求める場合〉

・全事象は、図より 126通り

・Pを通らない事象は図より 96通り
・Pを通る事象 = 全126-Pを通らない事象
= 126-96 = 30 通り
∴ \(\large{\frac{30}{126}}\) = \(\large{\frac{5}{21}}\)
《 例 》
「分岐点での進路の選び方」が「同様に確からしい」場合
SからGの最短経路で、Pを通る確率は?

〈計算から求める場合〉
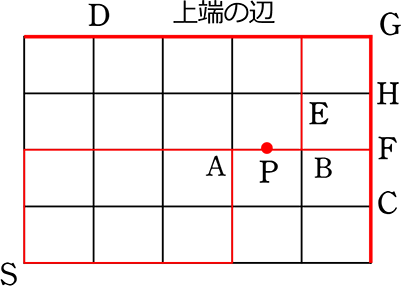
(注意) 上or右を選べる場合は、
上\(\large{\frac{1}{2}}\)、右\(\large{\frac{1}{2}}\) ですが、
上端、右端に達したら選択枝がないですね
例えば、上辺にあるDまで行くとその後は「↑」の選択肢はなく、 「→」の1択
→確率「1(100%)」
(100%右に行くしかない)
右辺にあるCまで行くとその後は「→」の選択肢はなく、「↑」の1択 →確率「1」
ですね!
というわけで、点Aは、上端にも右端にも達していませんので、
分岐点での「条件」が同じ (どの → も、 どの↑も\(\large{\frac{1}{2}}\)ですので、「反復試行」が使えますね!
・S → Aに行く確率は、
① 1例 は (→ → → ↑ ↑) → \(\left(\large{\frac{1}{2}}\right )^3\)×\(\left(\large{\frac{1}{2}}\right )^2\) = \(\large{\frac{1}{32}}\)
② その並び方は \({}_5 \mathrm{C }_2\) = 10通り
よって \(\large{\frac{1}{32}}\)×10 = \(\large{\frac{5}{16}}\)
・A→Bに行く確率は、
Aから「上」の\(\large{\frac{1}{2}}\) か、「右」の\(\large{\frac{1}{2}}\) なので、
よって 右の\(\large{\frac{1}{2}}\)
∴ Pを通る確率は \(\large{\frac{5}{16}}\)×\(\large{\frac{1}{2}}\) = \(\large{\frac{5}{32}}\) (= S→A→Bの確率)
ちなみに
・B→Gに行く確率は・・・実は「1」ですね!!
実はGoalが絡むと確率は「1(100%)」なのです
当然と言えば当然ですね、必ず(100%)Goalにたどり着くのですから!
(山に降った雨は必ず(100%)海にたどり着く感じ)
さらに、実はPを通った後の確率なんてどうでもよいですね!
(念のため証明)
B→Eの「↑」とF→Hの「↑」は、同じ「↑」でも、確率が違いますね!
B→Eの「↑」は(右もあるので)\(\large{\frac{1}{2}}\)
F→Hの「↑」は選択肢がないので1
よって、「条件」が異なるので「反復試行」が使えませんね!
( → ↑↑は\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)?\(\large{\frac{1}{2}}\)×1×1?などなど)
よって、経路ごとに確率を求めていきます
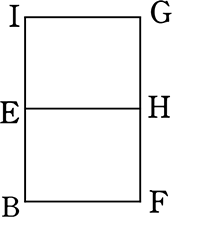
 BFHGの経路 → \(\large{\frac{1}{2}}\)×1×1 = \(\large{\frac{1}{2}}\)
BFHGの経路 → \(\large{\frac{1}{2}}\)×1×1 = \(\large{\frac{1}{2}}\) BEHGの経路 → \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×1 = \(\large{\frac{1}{4}}\)
BEHGの経路 → \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×1 = \(\large{\frac{1}{4}}\) BEIGの経路 → \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×1 = \(\large{\frac{1}{4}}\)
BEIGの経路 → \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×1 = \(\large{\frac{1}{4}}\)
よって、 \(\large{\frac{1}{2}}\)+\(\large{\frac{1}{4}}\)+\(\large{\frac{1}{4}}\) = 1
別れて確率が低くなっていたものが、Goal付近では「集約」されて
「1」にどんどん近づいてきますね!
よって「左からの援護(合流)」、「下からの援護(合流)」というイメージで ・・・足し算ですね!
∴ (S→Aの確率)×(A→Bの確率)×(B→G)の確率 B→Gは本来不要ですが念のため = \(\large{\frac{5}{16}}\)×\(\large{\frac{1}{2}}\)×1 = \(\large{\frac{5}{32}}\)
〈図形から求める場合〉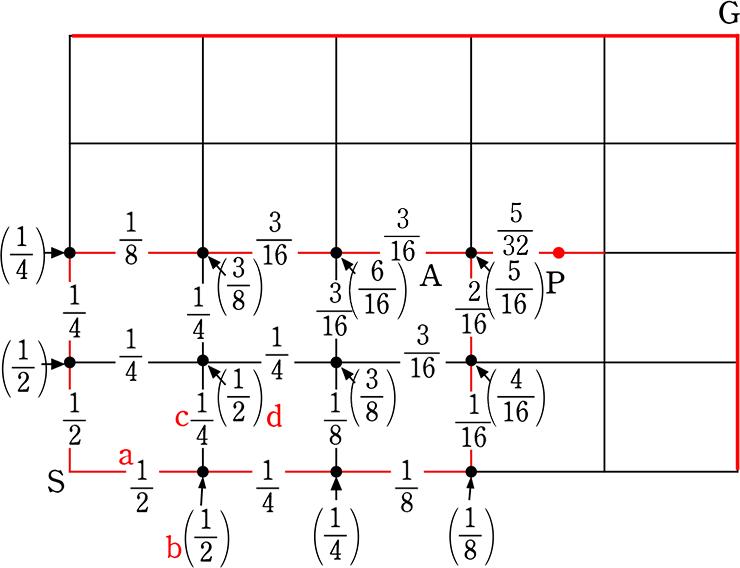
Pまでの図を切り出してみると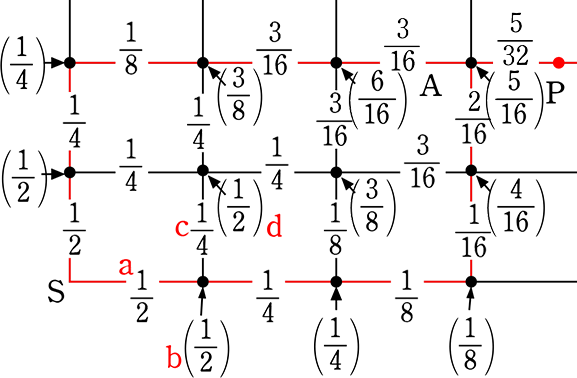
(手順)
a経路は、「上(\(\large{\frac{1}{2}}\))」か「右(\(\large{\frac{1}{2}}\))」かの、「右」の\(\large{\frac{1}{2}}\)
b地点は、合流してくるものがないので、そのままa経路の\(\large{\frac{1}{2}}\)
c経路は、b地点がすでに\(\large{\frac{1}{2}}\) で、さらに「上(\(\large{\frac{1}{2}}\))」か「右(\(\large{\frac{1}{2}}\))」かの、「上」の\(\large{\frac{1}{2}}\)を掛けた\(\large{\frac{1}{4}}\)
d地点は、下からの\(\large{\frac{1}{4}}\)と 左からの\(\large{\frac{1}{4}}\)が 合流した(\(\large{\frac{1}{4}}\)+\(\large{\frac{1}{4}}\)の)\(\large{\frac{1}{2}}\)
・
・
・
∴ 図より、Pを通る確率は \(\large{\frac{5}{32}}\)
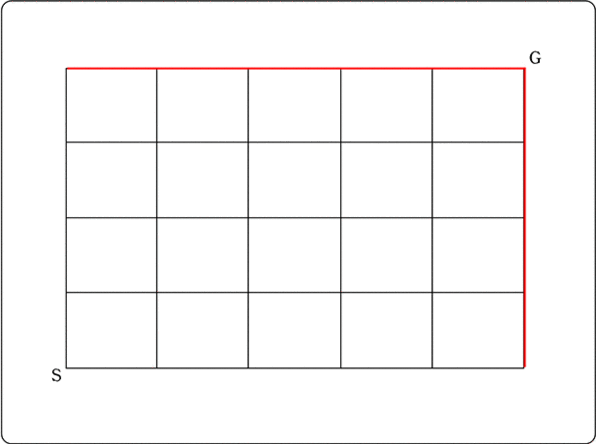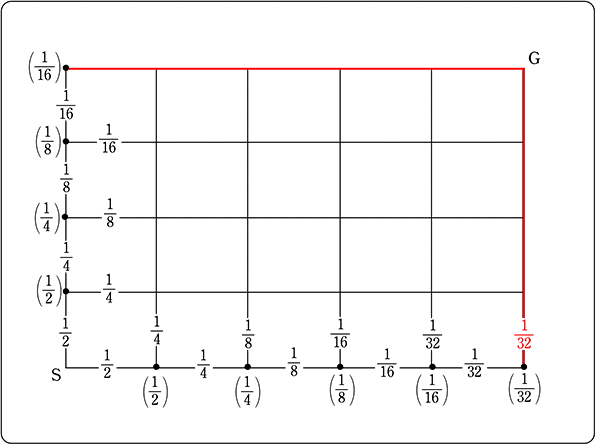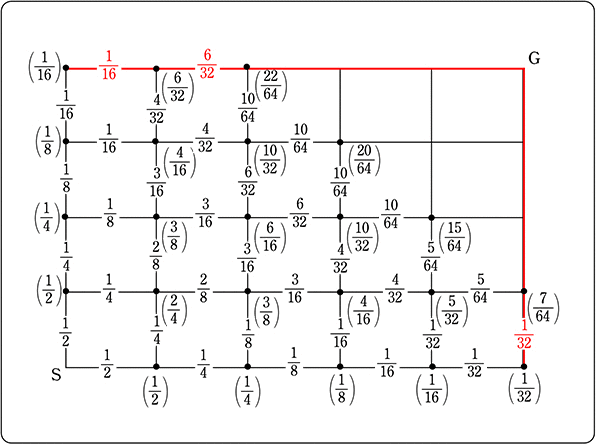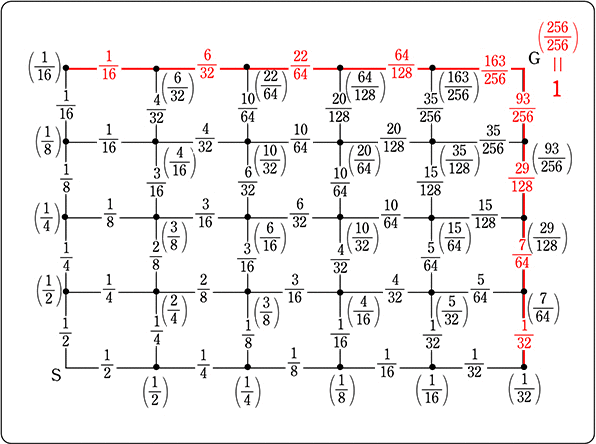

宝くじの確率
ジャンボ宝くじは、1ユニットにつき必ず1等が1本、前後賞、2等何本…と全てが含まれていますね
それらが、売れ行きにより、30ユニット、40ユニットと発売されますね
そして、1ユニットの枚数は…1000万枚
1ユニットを買い占めるために必要な金額は、30億円!
ジャンボくじの期待値は、145円
1枚300円ですので、単純計算155円ずつ損していきますね!
買い占めた場合に戻ってくる金額は、1~6等まで全て含まれているのですが、
13億5000万!
外れた16億5000万は公共のために役立っていきますね!
では1等の確率は? 1ユニットにつき1000万枚ですので…
\(\large{\frac{1}{1000万}}\)!
10枚買えば、 \(\large{\frac{1}{1000万}}\)×10 = \(\large{\frac{1}{100万}}\)と、確率が1枚より10倍上がりますね!
よく、10枚のうち、 1枚目の確率は\(\large{\frac{1}{1000万}}\)、 2枚目の確率は\(\large{\frac{1}{999万9999}}\) 、 3枚目は\(\large{\frac{1}{999万9998}}\)…10枚目は\(\large{\frac{1}{999万9990}}\)で、
「1枚買うのも、10枚買うのもほとんど変わらない!」と言いますが、これは
1枚目~9枚目は100%外れるという前提で、10枚目が当たる確率ですね、
よって、10枚買えば確率は10倍(\(\large{\frac{1}{100万}}\))、100枚買えばちゃんと100倍(\(\large{\frac{1}{10万}}\))ですね!
では、10枚(3千円分)購入した場合の確率\(\large{\frac{1}{100万}}\)とは、どのくらいなのでしょうか?
よく「雷に直撃される確率」「25mプールに米粒を敷き詰めて1粒選ぶ確率」
などに例えられますが、せっかく数学で確率を学んだのですから
サイコロで!
1回目に1の目が出る確率は\(\large{\frac{1}{6}}\) 、2回目
…7.7回目も1の目が出る確率は\(\large{\frac{1}{1000000}}\) (\(\large{\frac{1}{6^x}}\) = \(\large{\frac{1}{100万}}\))
「1の目を出す!」と宣言して、
およそ8回連続「1の目」が出るような確率ですね!悪くないかも!
では、「毎年1枚購入を10年間続ける」と
「毎年の購入金額を10年分貯めて10年目にまとめて10枚購入」
ではどちらに分があるのでしょう? (1回でも当たればよい)
・毎年1枚は…「反復試行」を流用して
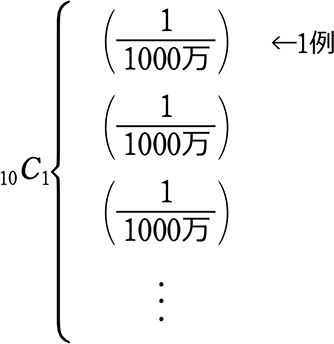
\(\large{\frac{1枚}{1000万}}\)×10年間のチャンス = \(\large{\frac{1}{100万}}\)
・10年目に全てを懸けるは… \(\large{\frac{1枚}{1000万}}\)×10 = \(\large{\frac{1}{100万}}\) 同じですね…
なぜか、10年に絞ってドンと買った方が確率が上がるイメージがあるのですが(1~9年間は外れる!という先入観ですね)、
全体として見れば同じ! それなら毎年楽しみたい!
最後に、宝くじ購入は「あり」か「なし」か?!
・・・「あり」と思います…
外れても痛くもかゆくもない範囲内ならですけど…
③ 確率の問題文の読み方まとめ
| 複数特徴系 | 1特徴系 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| じゃんけん | コイン | サイコロ | カード ・ 玉 ・ くじ ・ 人 | ||||||
|
注意する |
じゃんけん |
コイン |
サイコロ |
戻して |
袋2つ | 続けて |
1番目の 結果が「?」 →(?, 〇)の型 |
同時に |
|
| 中身同じ | 中身異なる | ||||||||
|
フレーズによる |
順列数え | 組合せ数え | |||||||
| 理由 | 基準名がある(1回目2回目、AさんBさん、袋A袋Bなど) | 数学ルール | |||||||
| 絶対順列数え(ぞろ目ラインがある) | |||||||||
| 列挙の方法 |
不要 |
1 |
|
|
|
|
|||
|
数え方の |
公式 |
「対」も成立→親中数えOK |
分配法則 |
「対」も成立→組合せ数えでズル |
1番目に |
||||
| 全事象 | 3人数乗 | 2枚数乗 | 面数個数乗 や 袋の中身2 | 袋A×袋B | \({}_{全数} \mathrm{P }_{並べる数}\) | \({}_{全数} \mathrm{C }_{選ぶ数}\) | |||
「場合の数」、「確率」は習得するのに時間のかかる単元だと思います
| ・ | よく似た問題文であるのに、全く違う問題であったり |
| ・ | <ということは>~、は知っていないと、時間内では考えつかないでしょうし |
| ・ | 答えが出ても、答の確かめ算がなかったり |
他の単元より時間がかかると割り切って
じっくり頑張っていきましょうね!
当2年生問題集では、「確率を分かりきる!」「確率の鬼になる!」を目標に
本問題(312問)とは別に
ほぼ全国の公立高校入試2014~2019の確率過去問221問も解説しています
よろしければご利用くださいね