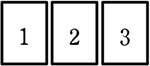
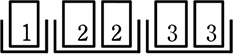
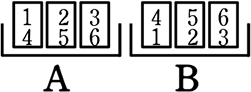
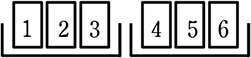
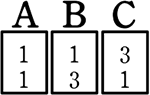| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 場合の数 | (2) 確 率 |
| ア | 場合の数 |
|---|---|
| ・ | ものの数え方の基本 |
| a | 和の法則・積の法則 |
| ・ | 場合の数の数え方の種類 |
| b | 順列 |
| ・ | 普通順列 |
| ・ | 全順列 |
| ・ | 順列の樹形図の書き方のコツ |
| ・ | ! (階乗) や P(パーミュテーション) の意味 |
| ・ | 普通順列の応用 |
| ① | 重複順列 |
| ② | 同じものを含む全順列 |
| ・ | (例題) ローマ字の並び |
| ・ | (例題) 最短経路(P) |
| ・ | 「同じものを含み」、かつ、「何枚か」を取り出す順列 |
| ③ | 円順列 |
| ・ | 円順列の別解 |
| ④ | じゅず順列 |
| ・ | 同じものを含む円順列・じゅず順列 |
| c | 組合せ |
| ・ | nCr = nC(n-r) |
| ・ | 組合せの樹形図の書き方のコツ |
| ・ | 組合せ C(コンビネーション) の意味 |
| ① | 重複組合せ |
| ・ | 選ばれないOKの重複組合せ |
| ・ | 組合せ(C)の3つのイメージ |
| → (最短経路(C)) | |
| ・ | 選ばれないNG( = 1つは選ぶ)の重複組合せ) |
| ・ | 重複組合せの公式 |
| ・ | 重複組合せの記号 \({}_n \mathrm{H }_r\) |
| d | 組分け |
| ① | 分けはめ |
| ② | 組分け |
| ・ | 何が違うのか、比較しながら解いてみる |
| → 重複順列(選ばれないNG) | |
| ・ | ただただ3つに分ける問題は? |
| c’ | 同じものを含む組合せ |
| ・ | 正しい順序は「PからC」? 「CからP」? |
| ・ | (場合の数まとめ表) |
場合の数
もしかしたら、
数学は得意なほうだけど・・・
「どうしても『資料の活用』、
その中でも特に「場合の数」、「確率」は
苦手という人は多いのではないでしょうか?
では どうしてそうなってしまうのでしょうか
他の単元は
問題文を読んだらすぐに「〇〇〇の問題だな!」
例えば「二次関数の直線が囲む面積の問題だな!」とわかるのですが
「場合の数」「確率」の場合は 問題文を読むと・・・
「何の問題だったっけ・・・」
「似ているけれど、何かが微妙に違うんだよな~」
となりがちですね
確かに「似てます」が「ちゃんと違います!」
逆を言えば「微妙に違うんだよな~」を
「完全に違う!」と理解できればOKということですね
練習を一通り終えたら
次は「問題文」を読んだら、
「区別がある!ない!」
「並びにこだわる!こだわらない!」
「個数指定がある!ない!」
「普通の順列!全順列!重複順列!」
「同じものを含む全順列!」
「選ばれないNGの重複組合せ!」
のように、「題名だけ答える練習」をするのがよいのかなと思います
(大まかな区別)
それさえわかれば あとは「一本道」なのですから
他の単元同様、
場合の数も確率も数学であるからには・・・
答えは「ただ一つ!」ですね
ア 場合の数
「場合の数」は2009年度より小学校6年で習っているようですね!
ですが、念のため、「場合の数」の復習をしますね
場合の数
「場合の数」とは、何パターン(何通り)あるか?というその数ですね
それだけです。

クリック・タップで答え (反応が遅い場合があります)
ものの数の数え方の基本
例えば、たくさんあるものを数えるとき、
途中で混乱しないように
必ずといっていいほど『基準を決めて』数えますね
ex. 1~10までが本当に10個か数えましょう
「1, 2, 3, 4…10で、10個!」ですね
「4, 7, 3, 5, 9,…まだ言ってないのは…2…6,あとは…」とは数えないですね
→ 『小さいものを基準にした(昇順に数えた)』
⇒ 昇順、または降順に数える
番号の分からない  ダイヤルロックを何回試してもよい(=
ダイヤルロックを何回試してもよい(=
「000, 001, 002…997, 998, 999」と試していきますね
「367, 851, 442…あと試してないのは…545…」とは試行しませんね
→ 『3つののダイヤルの位置を固定して、昇順に数えた』
ex. 2つのサイコロの目の出方は何通り?
「1つを左手に1、もう1つを右手に1, 2,…6で6通り(1につき6通り)
左手を2の目にして、右は同様に1, 2…6で6通り(2につき6通り)
ということは左の1通りにつき6通り…左は全部で6通り…
6通り×6通り=36通り」
(
「(
| → | 『左手、右手を固定して、数えた』 |
| ⇒ | 種類ごとに位置を固定する (マスの位置を固定する) |
| ➡ | 合わせて、種類ごとに位置を固定して、昇順に数える (これだけで、飛ばしで数えたり、だぶって数えたりを防げますね!) |

ものの数の数え方のまとめ
樹形図、表うんぬんの前に、まず何マス使うのかをイメージする、ですね!
(その下に必要なら樹形図、表を書く(イメージする)ですね)
・ サイコロ2つ、コイン2枚、カード2枚、玉2個、2回取り出す、なら、
→ 2マスですね ( , )
・ サイコロ3つ、コイン3枚、カード3枚、玉3個なら、
→ 3マスですね ( , , )
次に、マスの順序が途中で入れかえられないように、
マスの上に『基準名』を書きます
→ マスの順が『基準』です。基準は1度決めたら『固定』です!
・ 大サイコロ
・ 1回目のサイコロ
・ コインA
・ 1枚目にひいたカード

・ 小サイコロ
・ 2回目のサイコロ
・ コインB
・ 2枚目にひいたカード・玉
次に、マスの中はイメージBOXです、書き込まずに
頭の中で 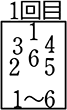 や
や  などが入るな。など想像BOXですね。
などが入るな。など想像BOXですね。
もちろん、問題によっては (ex. 2つのサイコロの出目の積が奇数となるのは何通り? などは、
奇数=奇数× 奇数しかないので 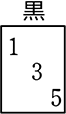 と書き込んでもよいですね)
と書き込んでもよいですね)
→ 絞りこめて固定できそうなら書き込んでもよいですね
次に、問題にしたがって「何通り」かをマスの下にを書きます や先ほどの奇数なら
や先ほどの奇数なら 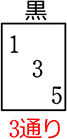 などですね
などですね
1行のマス ( , )だけで答が分かればラッキーで、中学の問題は
大体は「複数行のマス(場合分け)」
( , )
( , ) や
マスをもとに「列挙(頭の中で、順に、適合・不適合を考えて、適合するものを書きだしていく)」か「樹形図」か「表」になっていきますね
ex. 2つのサイコロの目が和が10以上になるのは何通り?
(第1段階の思考)
→ (

(第2段階の思考)
ということは → あとは小しだいだな
「列挙」なら
→ (4のときは…, 6でOK)、
(5のときは…, 5も6もOK)、
(6のときは…, 4も5も6もOK)
すなわち、
(4, 6)(5, 5 6)(6, 4 5 6) → 6通り
解答に書く場合は、
(4, 6) (5, 5) (5, 6) (6, 4) (6, 5) (6, 6)の6通りですね
→ マスの中のイメージ力が大事
(第2段階の思考)
ということは
→ あとは小しだいだな
「列挙」なら
→ (4のときは, 6でOK)
(5のときは, 5も6もOK)
(6のときは, 4 5 6もOK)
すなわち、
(4, 6)(5, 5 6)(6, 4 5 6)
→ 6通り
解答に書く場合は、
(4, 6) (5, 5) (5, 6) (6, 4)
(6, 5) (6, 6)
の6通りですね
⇒ マスの中の
イメージ力が大事
「樹形図」なら
適合するものに〇をつけて、 ∴ 〇が6個で6通り
→ マスの下にそろえて書くと間違えにくい
→ マスがあると余分な部分をカットできる可能性がある
「表」なら
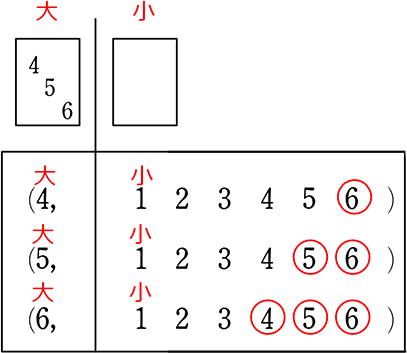
∴ 〇が6個で、6通り
→ マスがあると途中、混乱しがちになることを防げる
ちなみに、2つのサイコロの出目をまじめに書くと…
(大, 小)の順で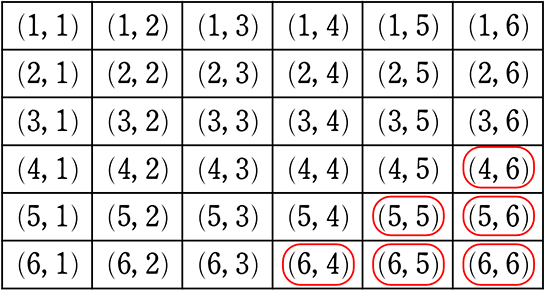
ですね
→ 丸6個のために全部書くのはイヤですね
数え方の基本のまとめ
・ マスをイメージ
・ 基準を動かさない
なんなら、(
(  ) ダイヤルのように、イメージしておくのもよいですね
) ダイヤルのように、イメージしておくのもよいですね
→ cf. これなら「12」と「21」が別物であるというように、サイコロの目の(1, 2)と(2, 1)も別物とわかりますね
⇒ ここまでの『並びにこだわる』数え方を → 『順列』に数える といいます(基本)
後々、『並びにこだわらない数え方』 → 〈 , 〉 → マスに基準名がない → 『組合せ』で数える をお話ししますね
《 例 》
3つの整数1, 2, 3 を並べる方法は何通り?
| → | 「並べる」より「並びにこだわる」 → 順列数え |
| → | サイコロ(複数特徴系)とは異なり、2マス目は1マス目で選んだものが選べませんね(1特徴系) = 樹形図の枝が減っていく |
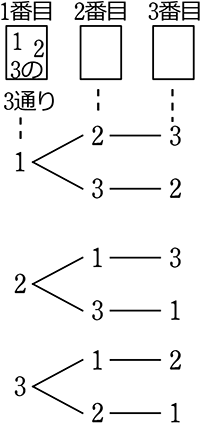
→ 「樹形図」なら
末端を数えて
6通り
cf
樹形図の枝は
ただの棒と思わずに
「につき」と読むと
よいですね
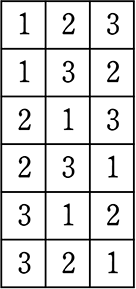
| → | 「表」なら、6通りですが、
3マスのときの表は、 |
→ 「列挙」なら、 (頭の中で…先頭が1のとき…, 2があるな, 残りは3か)
ということは、(1, 3, 2) (2のとき, 1, 3) (2, 3, 1) (3のとき, 1, 2) (3, 2, 1)で6通り
→ 実は、「全通り」は「計算」で…

→ 3通りにつき2通りずつ
3×2=6通り、その6通り
につき1通り、6×1で6通り
⇒ 3通り×2通り×1通 = 3! = 6通りですね
→ (後述) 「 ! (階乗)」

今後 問題を解くときは、表や樹形図を書いて、あてはまるものを数えるより、 「列挙」で数えられるようになるのが目標ですね!
和の法則 ・ 積の法則
場合の数を求める途中段階に「積の法則」、最終段階に「和の法則」が出てきますね
ですが、「法則」というわりには、この「法則」を用いて解く というものではなく
解き終わってみれば「結果」、
「積の法則を使っていた、和の法則を使っていた」という
「後付け命名的」な、法則とは名ばかりの法則ですね
一般的な定義
| 積の法則 | … | 事象A と事象B が同時に起こる場合の数は、 m×n 通り |
| 和の法則 | … | 事象A と事象B が同時に起こり得ない場合の数は、 m+n 通り |
実際はこれで十分
| 積の法則 | … | 「〇通りにつき〇通り」なら、〇通り×〇通り |
| 和の法則 | … | 「あとは数えるだけ!」なら、〇通り+〇通り |
ex. 2つのサイコロの目が和が10以上になるのは何通り?(2つ前と同じ問題)
(マスなら)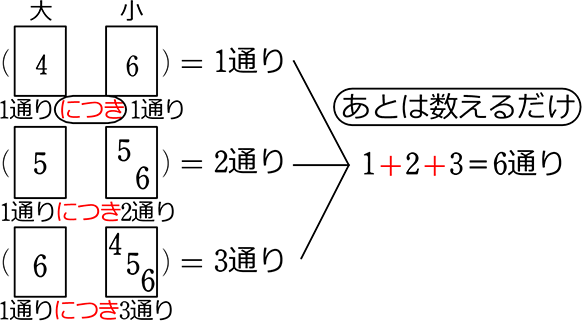
(樹形図なら)
(列挙なら)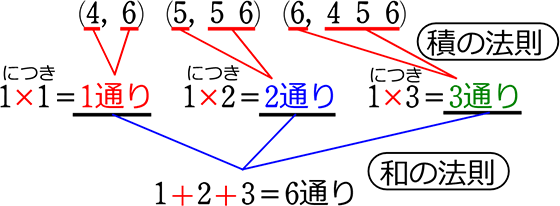
(2つの法則の存在場所)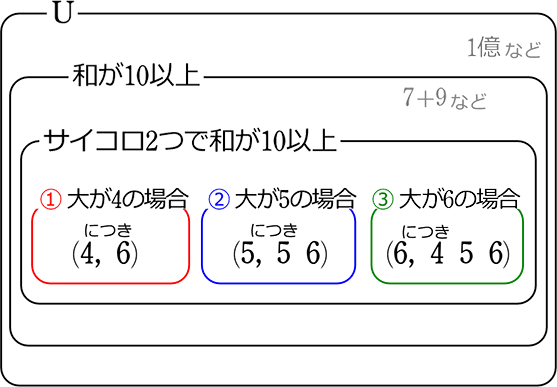
①+②+③ = 1通り+2通り+3通り = 6通り
(①と②と③は同時に起こらない)
例え話②
2つのサイコロを投げて、目の積が奇数、または偶数になるのは何通り?
(2つの目の積は必ず奇数か偶数なので、体感的に36通りとわかりますが、例として)
(まじめ列挙)
| ・ | 奇数になるのは → (1(の目)(の1通り)につき, 1(の目)(の1通り)) (1, 3) (1, 5) (3, 1) (3, 3) (3, 5) (5, 1) (5, 3) (5, 5)
同様に |
||||||||
| ・ | 偶数になるのは① → (1(の目)(の1通り)につき, 2(の目)(1通り)) (1, 4) (1, 6) (3, 2) (3, 4) (3, 6) (5, 2) (5, 4) (5, 6)
|
||||||||
| ・ | 偶数になるのは② → (2(の目)(の1通り)につき, 1(の目)(1通り)) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (4, 1)~(4, 6) (6, 1)~(6, 6) = 18通り
∴ 9+9+18 = 36通り |
(もう少しまとめた列挙)
| ・ | 奇数になるのは → (1, 1 3 5) (3, 1 3 5) (5, 1 3 5) = (1通り → 3+3+3を3×3とする「×」は九九の「 |
| ・ | 偶数になるのは① → (1, 2 4 6) (3, 2 4 6) (5, 2 4 6) = (1通り |
| ・ | 偶数になるのは② → (2, 1 2 3 4 5 6) (4, 1 2 3 4 5 6) (6, 1 2 3 4 5 6) = (1通り ∴ 9+9+18 = 36通り |
(最高にまとめた列挙)
| ・ | 奇数になるのは → (1 3 5, 1 3 5) = (3通り |
| ・ | 偶数になるのは① → (1 3 5, 2 4 6) = (3通り |
| ・ | 偶数になるのは② → (2 4 6, 1 2 3 4 5 6) = (3通り ∴ 9+9+18 = 36通り |
(まとめ)
| ⇒ | 列挙時、(カッコ)の中の者たちは「積の法則」、(カッコ)どうしは「和の法則」 |
| ⇒ | 樹形図なら、代表(先頭)の山の下位は「積の法則」、代表(先頭)の山どうしは「和の法則」 |
| → | どうしても代表の山が複数になる = 「場合分け」をしているということ = 「同時に起こらない」ということ = 各代表の山の値は「和の法則」 |
※「和の法則」「積の法則」という言葉はまったくこだわる必要はないですね!
「〇通りにつき〇通り」なら「掛ける」、
「場合分け(樹形図)」をして末端を数えたような結果は「足す」、で十分ですね
(cf. 排反とは)
場合の数の数え方の種類
場合の数の数え方の種類は、大きく分けて2つですね
今まで見てきた「順列」的な数え方と、新たに「組み合わせ」的な数え方 ですね!
| ・順列数え | … | 並び方にこだわる数え方 |
| ・組合せ数え | … | 並び方にこだわらない数え方 |
ex.
1233枚のカードがあります
・ 3枚の並べ方は?
→ 「並べ方」 → 「並びにこだわる」 → 基準名がある →  → 3×2×1=6通り
→ 3×2×1=6通り
→ 内訳は (1→2→3) (1, 3, 2) (2, 1, 3) (2, 3, 1) (3, 1, 2) (3, 2, 1) の6通り
・ 3枚の選び方は?
→ 「選び方」 → 「並びにこだわらない(選ぶだけ)」 → 基準名なし → 〈123〉 → 1通り
→ 内訳は〈1, 2, 3〉の1通り
⇒ (1, 3, 2)も(3, 2, 1)も〈1と2と3〉を選んだことと同じだ!
以後、親中ではどちらで数えたか判別できるように
順列で数えた場合は、( マルカッコ )
組合せで数えた場合は、〈 クカッコ 〉
でいきますね
簡単なイメージ
(順列主義の)順列母さん「今日は鍋に 砂糖 → 醤油→ 酢 の順で調味料を入れて下さい」
子「砂糖 → 醤油 → 酢っと!」
…昨日は 醤油 → 酢 → 砂糖 の順だったな…
(組合せ主義の)組合せ母ちゃん「鍋に 砂糖、醤油、酢 入れておいて」
子「何から入れるの?」
組合せ母ちゃん「なんでもいいわよ!とにかく砂糖と醤油と酢が入っていればいいの!」
→ 鍋に 砂糖、醤油、 酢 を入れる方法の 数え方の違いですね
順列母さんの数え方なら、6通り (〇,→ 〇,→ 〇)
組合せ母ちゃんの数え方、1通り 〈〇と〇と〇〉
今後勉強が進むにつれて、順列にも色々な数え方があるような…
枝が減っていくもの、減らないもの…
と混乱してきた場合は
順列
基本「順列」というワードがあれば「数え方」を指します
⇒ 「並びにこだわって数える」
「マスに基準名がある → 順列数え」ということですね
そこから、
| 1部(r個)を並べる順列 | → | 普通順列 |
| 全部を並べる順列 | → | 全順列 |
| 同じものを含む順列 | → | 同じものを含む全順列 同じものを含み1部並べる順列 |
| 「重複順列」 | → | 重複順列 |
| 「円順列」 | → | 円順列 |
と親中では区分けしていきますね
| ● 順列数え … | 並びにこだわる数え方 |
| | 〈1, 2〉は、( |
| | ( |
| ● 組合せ数え … | 並びにこだわらない数え方 |
| | ( |
| → | 1と2が〈クカッコ〉の中で勝手に小さいもの順に整列してしまう!イメージ 〈2, 1〉 → 〈1 |
この先、当分の間 順列のお話になります
b ~ 順列 ~
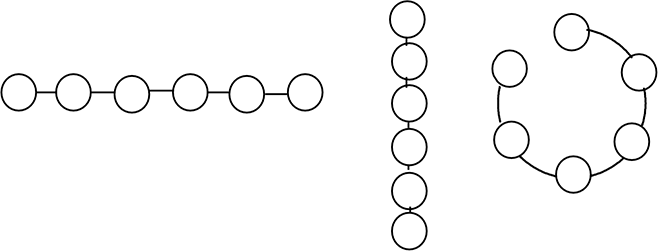
・順列は、「並びにこだわる」と言いましたが、横でも縦でも円でも構いませんね
それでは、個別に見ていきますね
【 普通順列 】
| 前提: | (1特徴系で) 選ばれる元はすべて異なり、異なるものを(r個)選び、並びにこだわる (一特徴系・複数特徴系とは) |
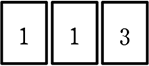
番号0~5の赤白の図のようなカードがあったとします
012345
● 「3」を取り出して並べる、何通り?
 ←「3」と指定されてしまいましたね、当然に「1通り」ですね
←「3」と指定されてしまいましたね、当然に「1通り」ですね
(注:マスの上の基準名が省略されていることがありますが、基準名は絶対あります)
● 1枚を取り出して
012345
並べる = 並びにこだわる
 ←0でも1でも…6でもよい、あるのは6枚のカードだから、6通り
←0でも1でも…6でもよい、あるのは6枚のカードだから、6通り
→ (1 2 3 4 5 6) の6通り
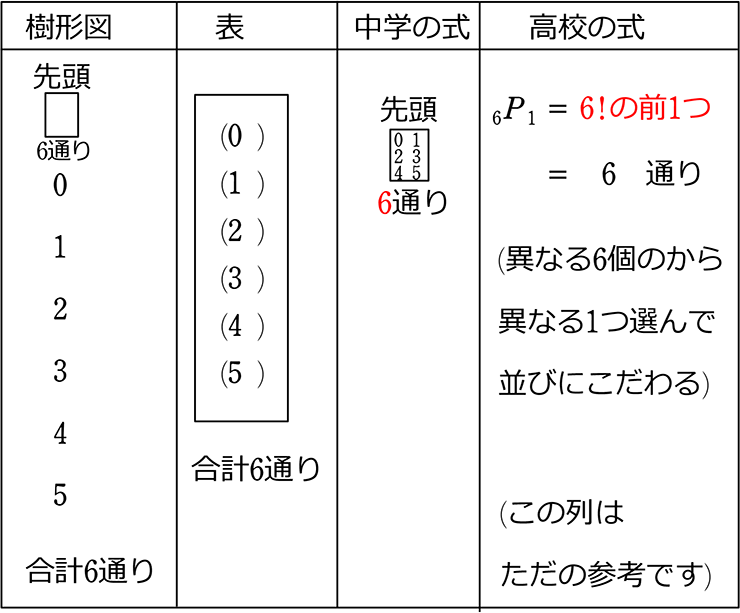
● 2枚を取り出して(選んで)、並べる、何通り?
012345
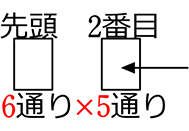 先頭で、何か1枚使っているので、残りのカードは5枚 →5通り
先頭で、何か1枚使っているので、残りのカードは5枚 →5通り
∴ 6×5 = 30通り
・サイコロ、コインは2個目(回目)も、
1~6の6通りを選べるので「普通順列」ではない!ということですね
→ 後にお話しする『重複順列』です (複数特徴系は重複順列)
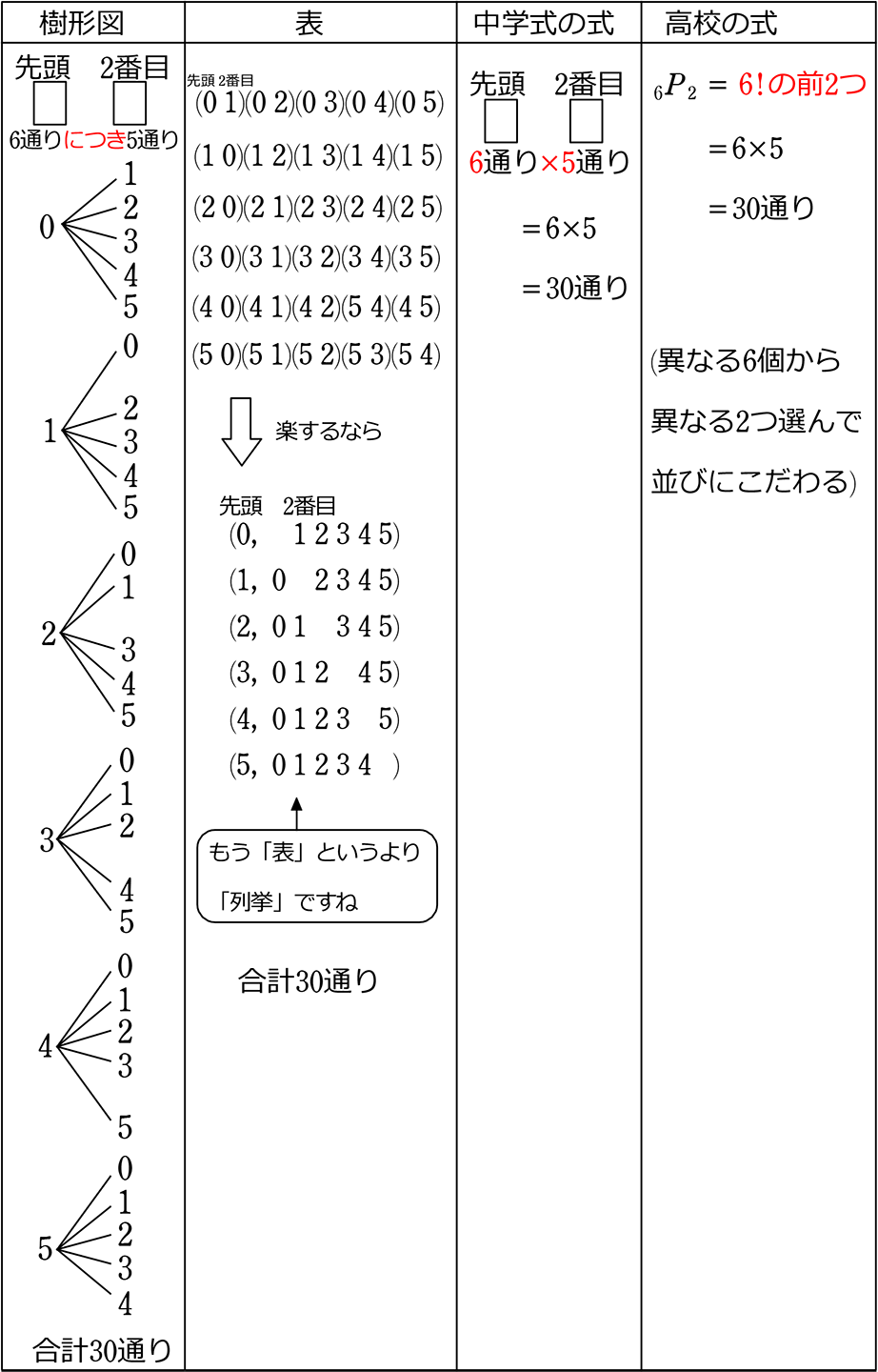
● 3枚を取り出して並べる、何通り?
012345
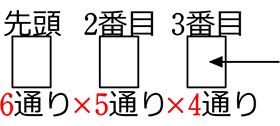 先頭と2枚目で2枚使っているので、残りのカードは4枚
先頭と2枚目で2枚使っているので、残りのカードは4枚
∴ 6×5×4 =120通り

● 4枚を取り出して並べる、何通り?
012345
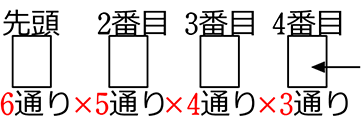 3枚使用済みで、残りのカードは3枚(3通り)
3枚使用済みで、残りのカードは3枚(3通り)
∴ 6×5×4×3 =360通り
| 樹形図 | 表 | 中学の式 | 高校の式 |
| (省略します) | (省略します) | 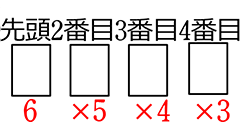 = 6×5×4×3 = 360 通り | \({}_6 \mathrm{P }_4\) = 6!の前4つ = 6×5×4×3 = 360 通り (異なる6個から 異なる4つ選んで 並びにこだわる) |
● 5枚を取り出して並べる、何通り?
012345
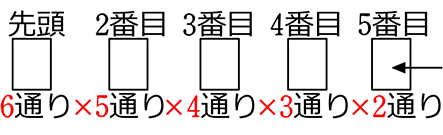 4枚使用済みで、残りのカードは2枚(2通り)
4枚使用済みで、残りのカードは2枚(2通り)
∴ 6×5×4×3×2 = 720通り
| 樹形図 | 表 | 中学の式 | 高校の式 |
| (省略します) | (省略します) | 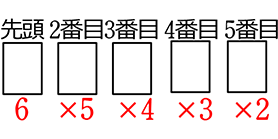 = 6×5×4×3×2 = 720 通り | \({}_6 \mathrm{P }_5\) = 6!の前5つ = 6×5×4×3×2 = 720 通り (異なる6個から 異なる5つ選んで 並びにこだわる) |
【 全順列 】
● 6枚を「全て」取り出して並べる、何通り?
012345
→ 全てを使う順列ということで、親子中学では「全順列」と呼ばしてもらいますね! 残り最後は自然に決まる → 1通り
残り最後は自然に決まる → 1通り
∴ 6×5×4×3×2×1 = 720通り
| 樹形図 | 表 | 中学の式 | 高校の式 |
(省略します)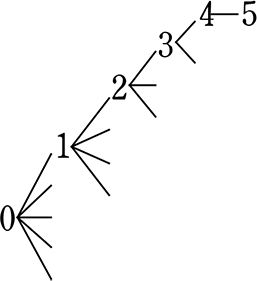 → 自動で決まるとは 最後は枝分かれ できずに 横棒1本 ということですね | (省略します) | 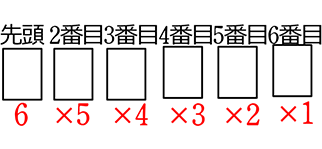 = 6×5×4×3×2×1 = 720 通り → 最後のマスは自動で 決まるので 1つ上と同じですね | \({}_6 \mathrm{P }_6\) = 6!の前6つ =6×5×4×3×2×1 ( = 6!) = 720 通り (異なる6個から 異なる6つ選んで (全部選んで) 並びにこだわる) |

普通順列の樹形図の書き方のコツ
「普通順列」の樹形図の書き方のコツは、
・「数字の小さいものから書く」「アルファベットの小さいものから書く」など
『 規則性のある自分ルール 』を持つことですね!当然と言えば当然ですね
《 例 》
4人の男子から3人「選んで」「並べる」方法は何通り?
→ キーワード「並べる」 → こだわる → 順列
⇒ 「人」は区別があるので番号があります
→ 1234
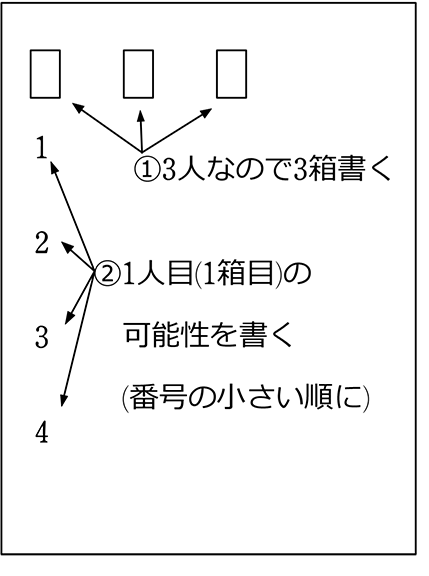


!(階乗) や P(パーミュテーション) の意味
私学中学では学ぶのかわかりませんが、公立中学では学びませんね
ですが、いずれは学びますのでここで!
「 ! 」の読み方は、PCキーボードの「エクスクラメーションマーク」ではなく、感嘆符の「ビックリ」でもなく、
数学では「階乗(かいじょう)」といいますね
6! なら「6の階乗」や「6階乗」と言いますね
使い方は
6!= 6×5×4×3×2×1 となります (階段状の乗算(かけ算)ですね)
3! = 3×2×1 ですね、1×2×3でもOKですが、どちらでもOKなら小さくしていく方が使いやすいですね!
n! なら、n (n-1) (n-2) ・・・×1 ですね
nに0を代入する、0! は「1」となります、これはいわゆる「数学ルール」です
cf.
012345の6枚のカードから、1枚も並べないのは何通り?
| ⇒ | 1枚も並べないという『1通り』ですね |
→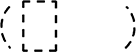 = 0! = 『1通り』 = 0! = 『1通り』 |
|
| ∴ | nに0を代入と考えるより、「1枚も並べない通り数」と考えればよいですね |
では次に
\({}_6 \mathrm{ P }_2\) や \({}_6 \mathrm{ P }_3\) や \({}_n \mathrm{ P }_r\) ですが
読み方は、「6P2 (ろくピーに)」「6P3 (ろくピーさん)」となりますね
意味は、「
となりますね
心の中では「nコ(6コ)から、rコ(3コ)選んで
計算方法は、\(\small{{}_6 \mathrm{ P }_2}\) であれば、
「6!の前2つ」→ 6×5 = 30 通り ですね
中学の をかっこよく
をかっこよく
表現しただけですね!
公式風なら
\(\large{\frac{6!}{(6-2)!}}\) = \(\large{\frac{6!}{4!}}\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4\ \cdot \ 3\ \cdot \ 2\ \cdot \ 1}{4\ \cdot \ 3\ \cdot \ 2\ \cdot \ 1}}\)
= 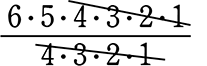 ←計算の前に約分! ← この約分が「〇階乗の
←計算の前に約分! ← この約分が「〇階乗の
\({}_6 \mathrm{ P }_3\) → 6×5×4 = 120 通りですね
中学の をかっこよく
をかっこよく
表現しただけ
ですね!
公式風なら、
\(\large{\frac{6!}{(6-3)!}}\) = \(\large{\frac{6!}{3!}}\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4\ \cdot \ 3!}{3!}}\) = 6×5×4 = 120 通り
\({}_6 \mathrm{ P }_r\) = \(\large{\frac{6!}{(6-r)!}}\)
\({}_n \mathrm{ P }_r\) = \(\large{\frac{n!}{(n-r)!}}\)
↑すべて、意味ありげな分母ですが、
「ただ分子の階乗の尻尾を切りたい」
という意味だけの分母ですね!
→ 公式は不要!「n! の前r個」で十分!
結局、
\({}_6 \mathrm{ P }_2\) = 「6! の前2つ」 = 6×5 (普通順列)
\({}_n \mathrm{ P }_r\) = 「n! の、前 r個」 (普通順列)
\({}_6\mathrm{ P }_6\) = 「6! の前6個」 =6! の全部 = 6! (全順列)
\({}_n \mathrm{ P }_n\) = 「n! の前n個」=n! の全部 = n! (全順列)
で十分ですね
(文字より、適当な数字の方が憶えやすいですね!)
(\(\large{\frac{n!}{(n-r)!}}\)は不要!)
(階乗的な公式の考え方)
| ・ | 数字やマスで意味を理解してから → では文字で表してみましょう(=一般化してみましょう)(=公式化してみましょう)の順ですね! → 「n!の前r個」をあらわすには・・・\(\large{\frac{n!}{(n-r)!}}\) とするしかないのか・・・ |
| ・ | 公式を憶えてから → 数値を当てはめて解きましょう の順だといつまでも何となく場合の数 ・ 確率は???ですね |
\({}_6 \mathrm{ P }_2\) =  = 6! の前2つ で十分!
= 6! の前2つ で十分!
(\({}_6 \mathrm{ P }_2\) は新しい記号ではなく、 を速く書きたいと思っただけ)
を速く書きたいと思っただけ)
P自体は 「公式」ではなく「意味」になりますね
ですから、
授業などで 先生が
「ここは〇P△、ここは 〇P△、よって、・・・」
などと 当たり前のように進めていくことがありますが
「ここは〇個から△個選んで並べるということ、
ここは〇個から△個選んで並べるということ、よって、・・・」
というように Pは「短縮語」のようなものと思って下さいね
決して、
「ここは24通り、ここは12通り、よって・・・」
というように、計算結果まで望んでいる訳ではありませんので!
先生が計算結果まで望んでいると思ってしまうと
「高校の授業・・・ムズッ!(=難)」
というふうになってしまいますね
【 普通順列の応用 】
カードは同様なものを使いますね
012345
● 3
<ということは>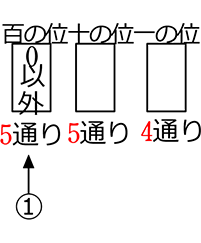
①先頭が「0」はダメ
(∵ 2桁になってしまう)
∴ 先頭は6通りではなく5通り
∴ 5・5・4 = 100 通り
● 4
012345
<ということは>
①一の位が「0」「2」「4」、パターン3つ (∵ 場合分け)
②千の位が「0」はダメ (∵ 3桁になってしまう)
∴ (5・4・3)+(4・4・3) +(4・4・3) = 156 通り
↑場合分けの結果→和の法則
| ×4 | マスの下の~通りはどのマスから決めてもよいですね → どのみち「積」だから! |
● 3枚を選んで
012345
<ということは>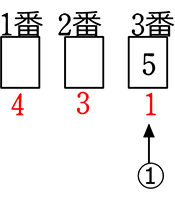
因数5の場所はどこでも
よいですね
どのみち積だから
● 両端が赤で、5枚を
012345
<ということは>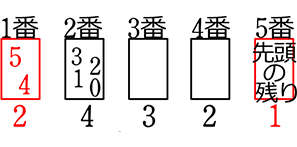
→ 赤から考えて → 2・1×4・3・2 = 48 通り
または

→ 1・1×4・3・2 + 1・1×4・3・2
↑場合分けの結果 → 和の法則
= 24+24 = 48 通り ←同じですね!
cf. 男女の並べ方も同じ考え方ですね
● 黒が隣合わせの
012345
<ということは>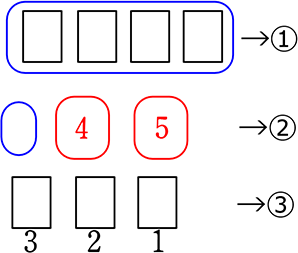
①第1段階として、黒4つを1つと見れば
②カードは3枚扱いになる
③カード3枚の順列は、3・2・1 = 6通り
④実は  のカードは内に24通り(4!)を持っていますね
のカードは内に24通り(4!)を持っていますね
∴ 3・2・1
= 6×24 = 144 通り
cf. 男女の並べ方も同じ考え方ですね
または
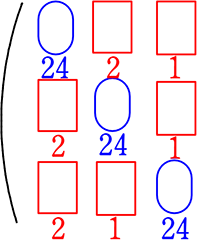
24・2・1+24・2・1+24・2・1
↑場合分けの結果 → 和の法則
= 48+48+48 = 144 通り
● 赤が隣合わせにならない並べ方、何通り?
012345
<ということは>
→① ∧の5か所から2か所を選んで、並べる
その2つを赤に置き換えることと同じ通り数
(=abcdeの5文字から
2文字「選んで」「並べる」ことと同じ)
ポイント
今後の説明でも
<ということは> 「~と同じこと」
とでてきますが、「同じこと」と言うのですから
カードのことは『切り離して』、 だけに専念してくださいね
だけに専念してくださいね
カードなどのことは忘れる!切り離す!
ですね!
abcdeの5文字から2個選んで並べる …① 5×4 = 20通り
5×4 = 20通り
ex. (
②元の黒の並び→ 0 1 2 3 から4個(全部)選んで並べる…②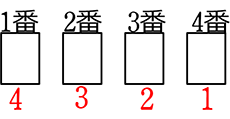 4・3・2・1 = 24 通り
4・3・2・1 = 24 通り
∴ ①
① 重複順列
読み方は、「ちょうふくじゅんれつ」「じゅうふくじゅんれつ」どちらでもOKのようです。
本来は、下図のように「複数特徴系 (サイコロ、コイン、じゃんけん)」を数える場合に用いる数え方ですが、
ex)
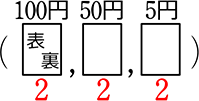

少し工夫すれば重複順列は「1特徴系」にも応用できますね
普通順列は、取り出した(選んだ)カードは、次のマスに使えませんでしたが、
元に戻して(袋に戻して)、2回目を選べば… → 重複順列ですね!
= 重複順列は、1度選んだカードを『何回でも』使える!
それだけの違いですね
前提は、「全て異なるもの」を「(基準のあるマスに)並べる」
(どちらも「異なる」ということですね
| ・ | 選ばれる元が異なる → 同じものを含まない → ずべて異なる |
| ・ | 選ぶ方も異なる → マスに基準名がある → 並びにこだわる → 順列数え) |
同じカードを使いますね
012345
● 
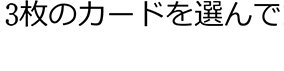
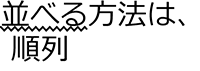
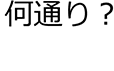
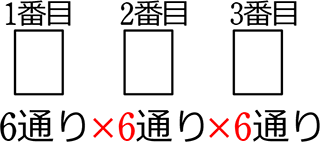
| → | 先頭で使った何かのカードが、何度でも使えるので、2つ目も 3つ目も 6通りとなります |
| ∴ | 6・6・6 = 63 = 216 通り |
| (0~5の6通りの目のサイコロを3回投げる と考えてもよいですね) |
普通順列なら、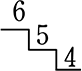 階段状でしたが、 (→ \({}_6 \mathrm{ P }_3\) → 6×5×4 → \({}_n \mathrm{ P }_r\))
階段状でしたが、 (→ \({}_6 \mathrm{ P }_3\) → 6×5×4 → \({}_n \mathrm{ P }_r\))
重複順列は、 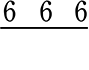 下がりませんね! ( 63 → 6×6×6 → nr )
下がりませんね! ( 63 → 6×6×6 → nr )
(キーワード)
「重複を許して」、「(袋に)戻して」、
「さいころ・コイン・じゃんけん(複数特徴系)」、「2進法」、
などがあれば、『重複OKかな?』 となりますね
⇒ 2マス目も1マス目と同じ数字が入ってもおかしくないな
今までの \({}_6 \mathrm{ P }_3\) が 63となるから、単純な感じがしますが、
何気に、日本語にすると「???」 となりがちですね
例えば、
《 例 》
3人に
(↑本当に重複順列の問題?と感じますね)
3人 → 人は区別します → 異なる3人
Aさん、Bさん、…となっていなくても、AさんBさんCさんです
 → 63 = 216 通り?
→ 63 = 216 通り?
「配る」という言葉から、人がマスのようにイメージしてしまいがちですが、ダメですね!
| → | Aさんに、お菓子1が入ったら、お菓子1を次のマスにも使うのはおかしいですね (Aさんも、Bさんもお菓子1を持っているという列挙 → ×) |
| → | 許されない重複 |
| → | しかも最終的にお菓子が余りますね |
正しいイメージは…お菓子達がマスです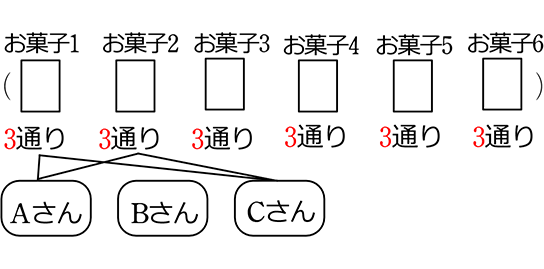 → 36 = 729通りですね!
→ 36 = 729通りですね!
(お菓子たちが、A~Cの3つの目のサイコロをそれぞれ振っていくイメージもありですね)
ex. 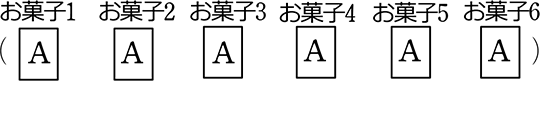
↑この1例列挙を整理して見やすくすると
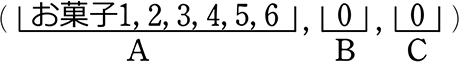
という意味ですね
各お菓子達が、全部Aさんを選んだなら、Aさん全種6個、BさんCさんは0個
| ・ | 「お菓子が配られる」というより「それぞれのお菓子が人を選ぶ」イメージですね!
→ 重複順列をうまいこと応用利用していますね |
| ・ | 「普通順列」では、カード(A, B, Cさん)が減っていくので、4フレーム目以降には何も入れることができないですね! |
| (普通順列) | 元(選ばれる方) ≧ マス(選ぶ方)
ex.(3枚のカードから3枚選んで並べる) |
| (重複順列) | 元(選ばれる方) < マス(選ぶ方)も可能
ex.(3枚のカードから重複をゆるして4回選んで並べる) |
・実際、「どっちがマス?」となってしまった時は・・・
→ 2マス程の1例を書いてシミレーションしてくださいね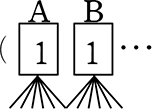 → Aさん, Bさんマスにお菓子1を入れると …2人がお菓子1を持つ → 重複使用はおかしい
→ Aさん, Bさんマスにお菓子1を入れると …2人がお菓子1を持つ → 重複使用はおかしい
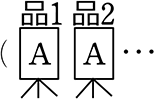 → お菓子1, 2マスにAさんを入れると…Aさんがお菓子1, 2を持つ → 重複に矛盾がない
→ お菓子1, 2マスにAさんを入れると…Aさんがお菓子1, 2を持つ → 重複に矛盾がない
よって、お菓子がマス!
cf.
「3人に異なる6個のお菓子を配る方法は何通り? ただし1個ももらえない人がいてもよい」を
(日本語訳ならぬ数訳すると)
「異なる(基準名のある)」お菓子たちが、「異なる」ABC達を「重複を許して選ぶ」方法は何通り?(自然に重複OK)ただし1個ももらえない人がいてもよい
それでは再度!
3人に異なる6個のお菓子を配る方法は何通り? ただし1個ももらえない人がいてもよい
→ 「異なる、異なる(W異なる)」 → 普通順列系か円順列系か重複順列 → 円順列ではないな → 「もらえる ・ もらえないの但し書き」 → 重複順列だな → どっちがマスかな → 簡単な2マスシミレーション → お菓子がマス → 36 → 729通り
(定義) 重複順列 nr
「異なるn種のものを、重複を許してr回選んで、並びにこだわる」 (基本)
↓ ↑
異なるn種のものを、基準名のあるr個マス達がそれぞれ選ぶ
↓ ↑
基準を持って並んでいるr個マス達がそれぞれ、異なるn種のものを、選ぶ
↓ ↑
(並んでいるr個マス達(お菓子達)がそれぞれ、異なるn種のもの(3人)を、選ぶ)
② 同じものが含まれるときの全順列
(前提)カード全てを使います(= 同じものを含む全順列)
cf. 後で学びますが、「同じものが含まれて」そこから「何枚か」を取り出す場合は、「場合分け」をになります難
同じカードを使いますが、黒のカードに番号がありません( = 同じものを含む)
56
● 6枚の全順列は、何通り?
① いきなり式を立てることはできません。まずは全パターンを求めます
② 全パターンを求めるために、まずは黒のカードを区別して数えます
56を
↓
123456としますね
まず、全パターンを求めてみますね
(中学全順列)
6×5×4×3×2×1 =720通り
(高校全順列)
\({}_6 \mathrm{ P }_6\) = 6! = 6×5×4×3×2×1 = 720 通り
では、次に、かぶり ですね
(123546)
(124536)
(132546)
(134526)
・
・
・
も、黒を区別しなければ(黒から番号を消せば)、「同じ並び」にすぎないですね!
5 6
すなわち、「内部的に」1234の4マス分の
全順列分、かぶりが存在するということですね
1, 2, 3, 4 の全順列、すなわち4マス分の全順列は、 4×3×2×1= 4! = 24 通りのかぶりがあるということですので、それを「1通り」とするためには…4!で割ればよいですね!
かぶりをなくす方法
同じものを使用しているマス数の階乗で割る
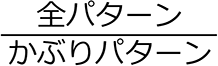 =
= 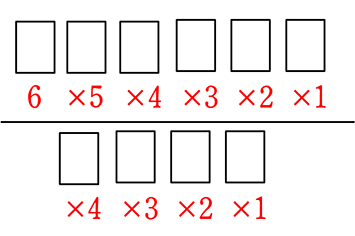 =\(\large{\frac{全順列}{同じものの全順列}}\) = \(\large{\frac{6!}{4!}}\) =
=\(\large{\frac{全順列}{同じものの全順列}}\) = \(\large{\frac{6!}{4!}}\) = 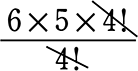 = 30通り ですね
= 30通り ですね
(6! は720通りなので、690通りもかぶりがあったのですね)
では
黒のカードだけでなく、赤のカードにも番号がありません
● 6枚の全順列は、何通り?
もうわかりますね!
どこかにある
123546 と
123645 なども 「かぶり」ということになりますね
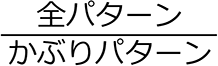
= 
= 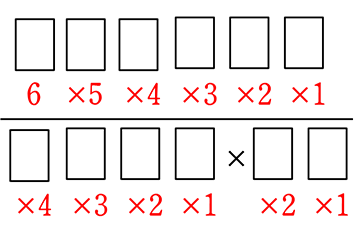
= \(\large{\frac{6!}{4!\ \cdot \ 2!}}\) =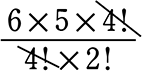 =
= 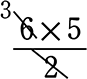 = 15 通り ですね
= 15 通り ですね
ちなみに、15通りを書き出してみますと
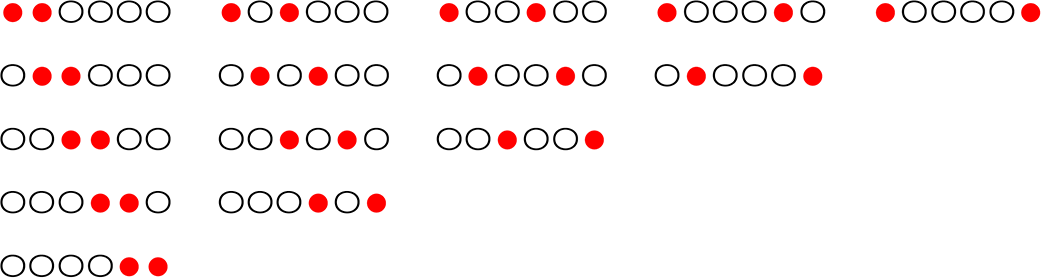
後で学ぶ \({}_6 \mathrm{ C }_2\)と全く同じこになります
cf. 逆算もできるということですね
56の並べ方は何通り?
→ 赤も区別がないとすれば → \({}_6 \mathrm{ C }_2\) = 15通り
→ 実は2つの赤は異なる → \({}_6 \mathrm{ C }_2\)×2! = 30通り ですね

同じものを含む全順列 =  =
= 
《 例 》
(1) YOKOHAMA の8字を並び替えると何通りの
(綴り → 当然並びにこだわる →順列)
・全部…8文字
・かぶり…Oの2文字、Aの2文字
同じものを含む全順列
= 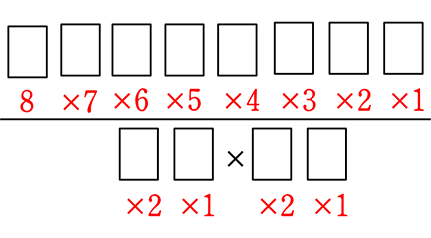
= 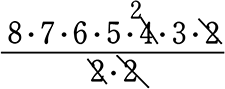
= 56・30・6
= 10080 通り
(2) 子音(Y, K, H)が隣り合わない並び方は、何通り?
(母音) A, I, U, E, O
(子音) それ以外
<ということは>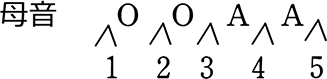
→ 母音の並び数(かぶりあり)
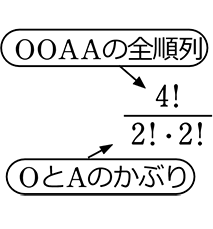
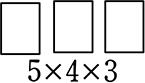 =
= 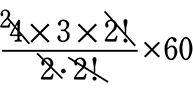 = 6×60 = 360 通り
= 6×60 = 360 通り
(3) 母音が偶数番目に入る並び方は、何通り?
<ということは>
① 
必ず偶数番目 → 奇数番目無視 → 偶数番目4マスの「同じものを含む全順列」
→ \(\large{\frac{4!}{2!\ \cdot \ 2!}}\) = 6通り
② 残りの4マスに、子音YKHMを並べる「普通全順列」
→ 4! = 24通り
∴ ①6通り
(4) YKHM が、
(「この順番」とは、YKHM がくっついている必要はありませんね!
ex. □Y□KH□□Mなどでもよい)
<ということは>
① 〇 〇〇 〇 でまずは異なるYKHMを区別のない(〇)として、母音を区別のない( として、「同じものを含む順列」で〇と の並び方は何通りかを求めます
→ \(\large{\frac{8!}{4!×4!}}\) = \(\large{\frac{8×7×6×5×4!}{4!×4×3×2}}\) = 70通り
② さらに4つの〇の並びにこだわれば、×4!ですが(H, K, M, Y)(H, K, Y, M)…(Y, M, K, H) → (Y, K, H, M)の並びだけでよいので×4!は不要ですね → そのままでよい → 選ばれた4マスは勝手にYKHMの並びになっている
イメージ
(1, 2, 3) を順列数えすると、3!で6通り (123)(132)(213)(231)(312)(321)でしたね
(1, 2, 3) を組合せ数えすると、 3!÷3! = 〈1, 2, 3〉の1通り
これは順列数えの昇順になっている先頭(123)を「代表」にした感じですね
別に代表となる「1通り」は(123)でなくても(321)でも(231)でも何ら問題はないですね
ということは
(HKYM)の並び方の代表はアルファベット順に並んだ〈HKYM〉でなくても〈YKHM〉としてもよいということですね
∴ 〇〇〇〇はどこにいても「組合せ数え」または「同じもの」とみなせば代表YKHMの並びになっているということですね
これを4! してしまうとどこにいても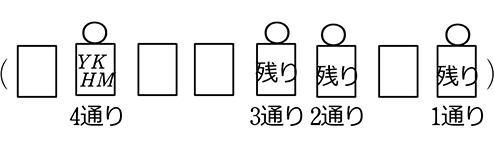 になってしまいますね
になってしまいますね
③ の並びは実はOOAAの並びなので
→ \(\large{\frac{4!}{2!×2!}}\) = 6通り
∴ ①8場所から4場所「選んだ」70通り
〔 別解 〕
というほどではありませんが
① YKHMを「同じもの」とみなせば → 並び方は1通り → その1通りはYKHMとしてよいという理屈さえ分かれば
OOAAの並び方何通り?ということ = 同じものを含む順列 = \(\large{\frac{8!}{4!×2!×2!}}\) = 420通り
② 組合せ3つのイメージの内の「型」で\({}_8 \mathrm{C }_4\)で選ばれた4つは必ず「昇順」になっているを「必ずYKHM順になっている」とみなして
\({}_8 \mathrm{C }_4\)
(↑理屈はすべて同じですね!)
《 例 》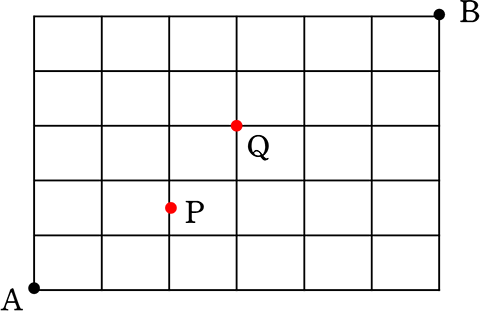
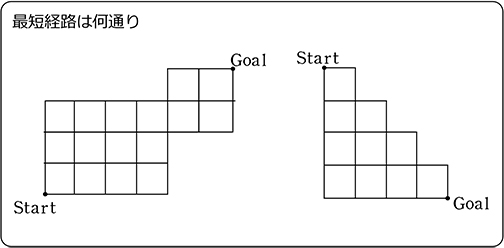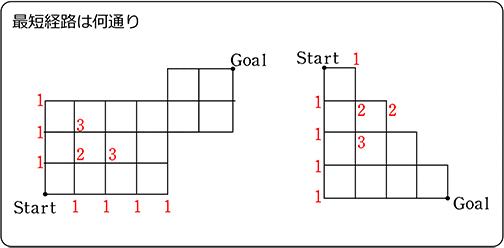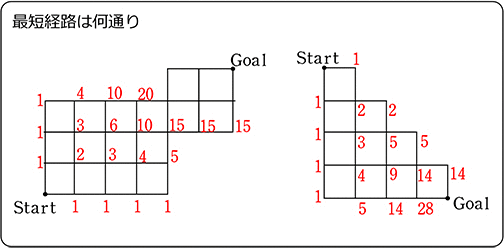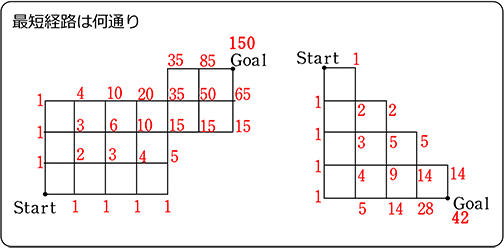
(1) AからBに行くための最短経路は、何通り?
(いわゆる「最短経路」の問題ですね!
あみだくじでたどって数えるのは、厳しいですね!)
<ということは>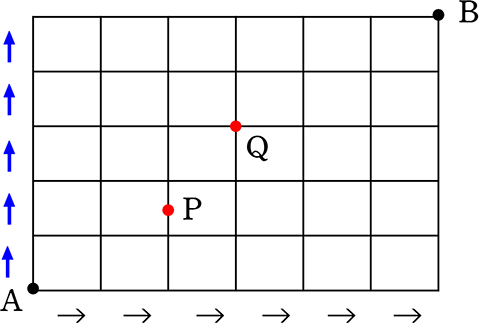
Aから(→)6個と( )5個の計11回でBに行けますね
)5個の計11回でBに行けますね
「同じものを含む全順列」ということですね
かぶり6!・5! で割ればよいですね!
(→→→→→→↑↑↑↑↑) の並べ方は何通り?という問題ですね
→ \(\large{\frac{11!}{6!\ \cdot \ 5!}}\) = 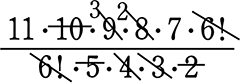 = 11・42 = 462 通り
= 11・42 = 462 通り
この場合の「かぶり」とは、たとえば
(→)をそれぞれ E1E2E3E4E5E6
( )をそれぞれ N1N2N3N4N5
)をそれぞれ N1N2N3N4N5
とします
東:east → E
北:north → N
(\(\large{\frac{→}{E_1}}\) \(\large{\frac{↑}{N_1}}\) \(\large{\frac{→}{E_2}}\) \(\large{\frac{→}{E_3}}\) \(\large{\frac{↑}{N_2}}\) \(\large{\frac{→}{E_4}}\) \(\large{\frac{↑}{N_3}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{↑}{N_4}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{↑}{N_5}}\))も
(\(\large{\frac{→}{E_2}}\) \(\large{\frac{↑}{N_2}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{→}{E_5}}\) \(\large{\frac{↑}{N_5}}\) \(\large{\frac{→}{E_1}}\) \(\large{\frac{↑}{N_3}}\) \(\large{\frac{→}{E_3}}\) \(\large{\frac{↑}{N_4}}\) \(\large{\frac{→}{E_4}}\) \(\large{\frac{↑}{N_1}}\))も
↑矢印だけ見れば「同じ経路」ですね(マス基準名一筆目、二筆目、三筆目…11筆目は省略しています)
順列は並びを区別しますから、結果同じ経路でも〇筆目に入るものが異なるとカウントしてしまいます
よって、
(\(\large{\frac{→}{E_1}}\) \(\large{\frac{↑}{N_1}}\) \(\large{\frac{→}{E_2}}\) \(\large{\frac{→}{E_3}}\) \(\large{\frac{↑}{N_2}}\) \(\large{\frac{→}{E_4}}\) \(\large{\frac{↑}{N_3}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{↑}{N_4}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{↑}{N_5}}\))も
(\(\large{\frac{→}{E_2}}\) \(\large{\frac{↑}{N_2}}\) \(\large{\frac{→}{E_6}}\) \(\large{\frac{→}{E_5}}\) \(\large{\frac{↑}{N_5}}\) \(\large{\frac{→}{E_1}}\) \(\large{\frac{↑}{N_3}}\) \(\large{\frac{→}{E_3}}\) \(\large{\frac{↑}{N_4}}\) \(\large{\frac{→}{E_4}}\) \(\large{\frac{↑}{N_1}}\))も
(\(\large{\frac{→}{E}}\) \(\large{\frac{↑}{N}}\) \(\large{\frac{→}{E}}\) \(\large{\frac{→}{E}}\) \(\large{\frac{↑}{N}}\) \(\large{\frac{→}{E}}\) \(\large{\frac{↑}{N}}\) \(\large{\frac{→}{E}}\) \(\large{\frac{↑}{N}}\) \(\large{\frac{→}{E}}\) \(\large{\frac{↑}{N}}\))にすべく
\(\large{\frac{11\ \ !}{Eのかぶり階乗\ \cdot \ Nのかぶり階乗}}\)ですね
【 イメージ 】
●左右を両方上げている この『形』は何通り?
この『形』は何通り?
・組合せ君:「 〈1, 2〉の1通り (\({}_2 \mathrm{ C }_2\))」!
〈1, 2〉の1通り (\({}_2 \mathrm{ C }_2\))」!
→ 正解!!
・順列君:「まず①を上げて 、次に②を上げた
、次に②を上げた と
と
まず②を上げて 、次に①を上げた
、次に①を上げた (1, 2)(2, 1)の2通り (\({}_2\mathrm{ P }_2\))」!
(1, 2)(2, 1)の2通り (\({}_2\mathrm{ P }_2\))」!
→ 『形』って言ったでしょ! それはこの「形」になるための『方法数』でしょ!
順列君:「あっそうだ!『形』ということは、①②の順番は関係ない、
すなわち同じものあつかい、すなわち「かぶり」かぁ~、
「かぶり」で割って(\(\large{\frac{{}_2 \mathrm{ P }_2}{2!}}\))で…「1通り!」
→正解!
●ではこの形  は何通り?
は何通り?
・組合せ君: の1通り〈1, 2, 3〉
の1通り〈1, 2, 3〉
→ 正解!!
・順列君:まず ①書いて→次に
①書いて→次に ②書いて→最後に
②書いて→最後に  ③書いた「1通り(1, 2, 3)」と・・・
③書いた「1通り(1, 2, 3)」と・・・
まず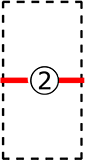 ②書いて…
②書いて…
「順列君っ!」
・順列君:「ハイハイ、『形』ですね、1通りでしょ!」
→ 正解…(わざとか…)
(2) 点Pを通る最短経路は、何通り?
<ということは>
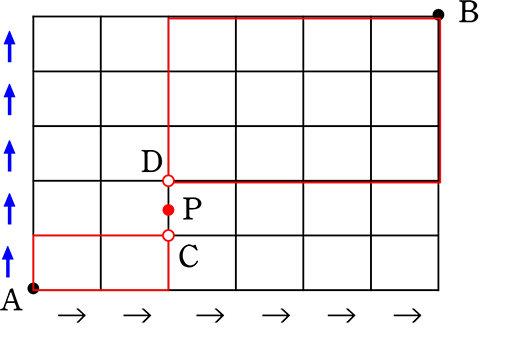
最短経路範囲を、
目立つように(図は赤線使用)
すれば分かりやすいですね
A→C 合計矢印3、右2上1
C→D 1通り
D→B 合計矢印7、右4上3
cf. 赤線枠の外を通ると、Pを通らなかったり、
最短経路ではなかったりするということですね
→ AからCまでの最短経路×CからDの1通り×DからBまでの最短経路ですね
→ \(\large{\frac{3!}{2!\ \cdot \ 1!}}\)×1×\(\large{\frac{7!}{4!\ \cdot \ 3!}}\) = 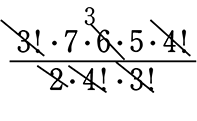 = 21・5 = 105 通り
= 21・5 = 105 通り
(3) 点Pを通らない最短経路は、何通り?
<ということは>
全体-通る = 通らない
ですね!いわゆる「余事象」ですね
全体462通り-通る105通り = 通らない357 通り
(4) 点Qを通る最短経路は、何通り?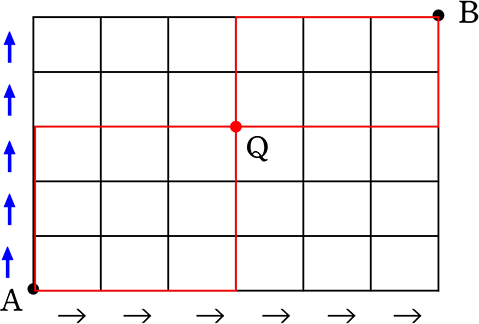
\(\large{\frac{6!}{3!\ \cdot \ 3!}}\)×\(\large{\frac{5!}{3!\ \cdot \ 2!}}\) = 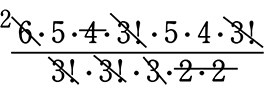 = 10・20 = 200 通り
= 10・20 = 200 通り
〔 書き込み方式 〕 (樹形図の和の法則利用)でも解けますね
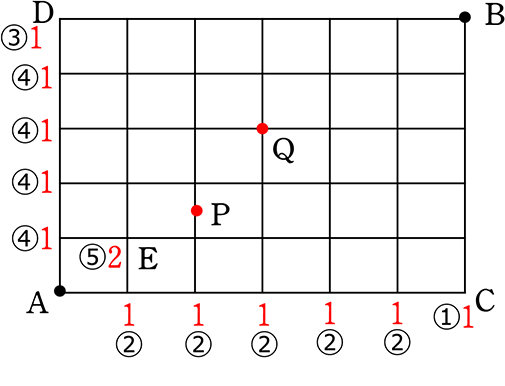
① A→Cに行くには何通り? →1通り
② といことは、途中のT字路も →1通り
③ 同様にA→Dは? →1通り
④ 同様に、途中のT字路も →1通り
⑤ AからEに行くには? →2通り
→2通り
ということは、Eは
⑥あとは、これをBまで続けると

かなりの手間にはなりますが
経路が長方形でない場合に使えますね!
「同じものを含み」、かつ、「何枚か」を取り出す順列
それでは、次に「同じものを含み、さらに、全部ではなく、何枚かを取り出す」パターンです
45
● 上の6枚のカードから、4枚を並べる、何通り?
→ 難しいパターンですね! その都度「場合分け」をするしかありませんね
考えられる4枚のパターンは…
①(全部黒) 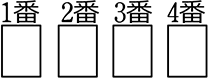 →
→
②(1枚赤) 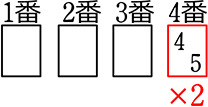 → \(\large{\frac{4!}{3!}}\)×
→ \(\large{\frac{4!}{3!}}\)×
③(2枚赤)  → \(\large{\frac{4!}{2!\, 2!}}\)×
→ \(\large{\frac{4!}{2!\, 2!}}\)×
∴ 1+8+12 = 21 通り
● この6枚のカードから、1枚を並べる、何通り?
45
考えられる1枚のパターンは…
①(全部黒)  → 1通り (黒には区別がないから)
→ 1通り (黒には区別がないから)
②(全部赤)  → 2通り
→ 2通り
∴ 1+2 = 3 通り
● この6枚のカードから、2枚を並べる、何通り?
45
考えられる2枚のパターンは
①(全部黒) 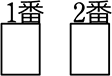 → 1通り
→ 1通り
②(黒・赤)  →
→
③(全部赤) 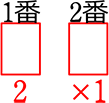 → 2通り
→ 2通り
∴ 1+4+2 = 7 通り
● この6枚のカードから、3枚を並べる、何通り?
45
考えられる3枚のパターンは
①(全部黒) 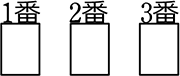 → 1通り
→ 1通り
②(赤1枚) 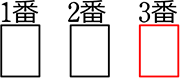 → \(\large{\frac{3!}{2!}}\)×2通り = 6通り
→ \(\large{\frac{3!}{2!}}\)×2通り = 6通り
③(赤2枚) 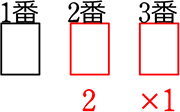 → 全部バラバラ → 3! = 6通り
→ 全部バラバラ → 3! = 6通り
∴ 1+6+6 = 13通り
● 上の6枚のカードから、5枚を並べる、何通り?
45
考えられる5枚のパターンは
①(赤1枚) 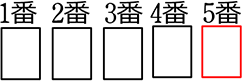 → \(\large{\frac{5!}{4!}}\)×2通り = 10通り
→ \(\large{\frac{5!}{4!}}\)×2通り = 10通り
②(赤2枚) 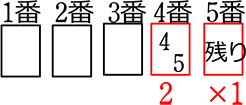 → \(\large{\frac{5!}{3!\, 2!}}\)×2\(!\) = 10通り×2通り = 20通り
→ \(\large{\frac{5!}{3!\, 2!}}\)×2\(!\) = 10通り×2通り = 20通り
∴ 10+20 = 30 通り
● 上の6枚のカードから、6枚を並べる、何通り?
45
6枚のパターンは・・・全部を使うということ → 「同じものを含む全順列」ですね!
(念のため)
6枚のパターンは
①(黒4赤2) 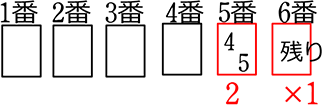 → \(\large{\frac{6!}{4!\, 2!}}\)×2\(!\) =\(\large{\frac{6!}{4!}}\) = 30 通り
→ \(\large{\frac{6!}{4!\, 2!}}\)×2\(!\) =\(\large{\frac{6!}{4!}}\) = 30 通り

同じものを含み、かつ、何枚かを取り出す順列 = 場合分け
③ 円順列
順列は、「1列に並べること」 とありましたが、
「円形に1列」に並べると、「直線に1列」に並べる時とは変わった現象が起こりますね!
円順列は前提として、
・与えられたカードは全て異なる
・与えられたカードを「全て使って」並べます
cf. 「10枚から6枚を選んで、円形に並べる」 →少し難しいですね
「6枚があります、それを円形に並べます」→今回はこれですね!
同じカードを「人」に置き換えますね
● この6人を、円卓に座らせる方法は、何通り?
その前に、「円形は変わった現象が起こる」とありましたね、
ある「6通り」を円形に並べてみると…






父「せっかくの外食だから、家とは違う並び方にするぞ!」
自分「・・・変わってないんですけど・・・」
そうです
(自分, 姉, 妹, 父, 母, 祖母)も (姉, 妹, 父, 母, 祖母, 自分)も、
(0, 1, 2, 3, 4, 5)も (1, 2, 3, 4, 5, 0)も、
(1, 2, 3)も (2, 3, 1)も、
違う並べ方ではありますが、円形に並べると、「位置関係」は同じですね!
円順列では このような「かぶり」を『同じ』と
→ まとめて「1通り」です
というわけで、円形に並べると、
6人いれば「6通りづつ かぶりが存在」します
5人なら「5通りづつ かぶりが存在」します
4人なら「4通りづつ かぶりが存在」します
「6通り」を「1通り」とみなす方法は、その数である「6」で割ればよいですね
→「6通り」÷6 = \(\large{\frac{「6通り」}{6}}\) = 1通り
cf. 実際は、全ての並び方に「6通り」づつ「かぶり」があるので
→ \(\large{\frac{ある「6通り」}{6}}\)+\(\large{\frac{ある「6通り」}{6}}\)+\(\large{\frac{ある「6通り」}{6}}\)+・・・\(\large{\frac{ある「6通り」}{6}}\) = \(\large{\frac{「全通り」}{6}}\)
= 円順列ですね!

(前提:全て使い、全て異なる)
〔 かぶり排除 方式 〕
円順列
= 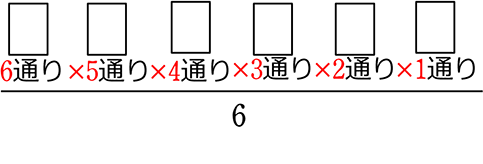 = \(\large{\frac{全順列}{6}}\) = \(\large{\frac{6!}{6}}\) = \(\large{\frac{{}_n \mathrm{ P }_n}{n}}\) = \(\large{\frac{n!}{n}}\)
= \(\large{\frac{全順列}{6}}\) = \(\large{\frac{6!}{6}}\) = \(\large{\frac{{}_n \mathrm{ P }_n}{n}}\) = \(\large{\frac{n!}{n}}\)
問題に戻って、再度
この6人を、円卓に座らせる方法は、何通り?
→ \(\large{\frac{6!}{6}}\) = 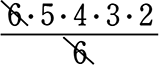 = 120 通り
= 120 通り
円順列には、もう一つの導き方があります!
先頭を固定してしまい、その後続を「残りの全順列」とする考え方です
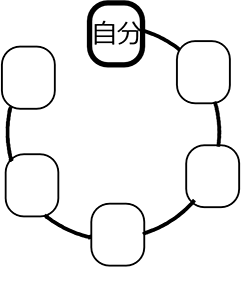
1、先頭を(誰でもよい)個定してしまいます
2、残りの「祖父 父 母 姉 妹」5人の並び方
が何通りあるか? ですね!
(もう円順列ではなく、普全順列の問題に
なっていますね!)

(前提:全て使い、全て異なる)
〔 先頭固定 方式 〕
円順列
(全員-1)の全順列 = (n-1)! = \({}_{(n-1)} \mathrm{ P }_{(n-1)}\)
こちらで解くと、
円順列 = (全員-1)の順列 = 6-1の順列 = 5人の全順列 = 5! = 5・4・3・2 = 120 通り (上の公式と同じ答ですね)
「かぶり排除方式」
「先頭固定方式」
= 5・4・3・2
途中式が結局同じですね!
円順列は、「先頭固定方式」の方が使いやすいと思いますが、
「かぶり排除方式」も大切な考え方ですね!
それでは問題に戻りますね

● この6人を、円卓に座らせる方法は、何通り?
(かぶり排除) \(\large{\frac{6!}{6}}\) = 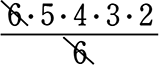 = 5・4・3・2 = 120 通り
= 5・4・3・2 = 120 通り
(先頭固定) (6-1)! = 5! = 5・4・3・2 = 120 通り
● 「父」と「母」が隣り合う座り方は、何通り?
<ということは>
父と母を1人とみなして の5人扱いの円順列
の5人扱いの円順列
5人の円順列 = (5-1)! = 4! = 4・3・2 = 24 通り
内に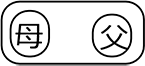 の並びもあるので、 24通り×2 ∴ 48 通り
の並びもあるので、 24通り×2 ∴ 48 通り
● 「父」と「母」が隣り合わない座り方は、何通り?
<ということは>
「父」「母」以外を先頭に固定すると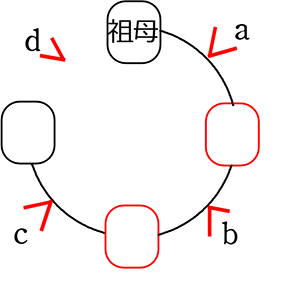

a b c d の4か所から 2か所に父母を座らせること、
すなわち、(父母のために) 4か所から2か所を選ぶ順列と同じですね!
よって、
= (4-1)!× (=(4-1)!×\({}_4 \mathrm{ P }_2\))
(=(4-1)!×\({}_4 \mathrm{ P }_2\))
= 3!×12= 6×12 = 72 通り
(または余事象で)
(1)の全座り方120-(2)の隣り合う48 = 72通り
● 父と母が向かいあう座り方は、何通り?
<ということは>
父を「先頭固定」、母を「向かいに決めて」、残り4席の 「普通の順列」
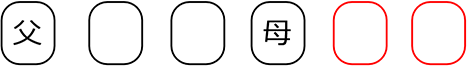
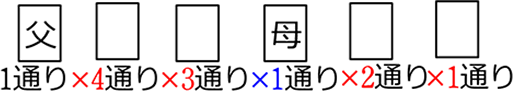 = 24 通り
= 24 通り
cf.
→母が「向かい」=母を「どこかに決める」順列と同じことですね
ex. 3桁の数字が5の倍数→因数に5を含む→5の場所は先頭でも、真ん中でも、1の位でも、どこでもよいのと同じ考えですね
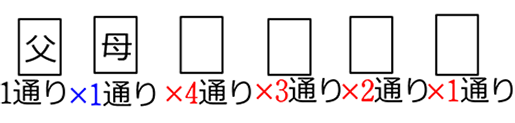 = 24 通り
= 24 通り
 = 24 通り
= 24 通り
「父と母が向かいあう 座り方は何通り?」
=「父を固定、母を右ななめに決める 座り方は何通り?」
=「父を固定、母をどこでもいいから1か所に決める 座り方は何通り?」
→ 真向かいという言葉にがんじがらめにならなくてもよいということですね
→ 母の×1通りは、どこにあってもどのみち「積」
よって全て、 4×3×2 = 24 ∴ 24 通り
④ じゅず順列 ( 数珠順列 )
法事などで使う じゅず、ですね
じゅず、ですね
「円卓の座席」は円順列でしたが、
「座席」の代わりに「石」や「玉」であった場合、円順列とはまた違った現象が起こりますね!
同じカードを「石」に置き換えますね
● この6石を、糸でつないで首輪を作る方法は、何通り?
その前に、「円順列とは変わった現象が起こる」とありましたね、
ある「2通り」を円形に並べて、首輪のようにしますね

確かに違う並び方ですが・・・
座席と違って、持ち上げて「裏から見ることができる」ですね!
では、自分の右手の甲を見て、(爪を宝石と思って)
それを向こう側から見てください
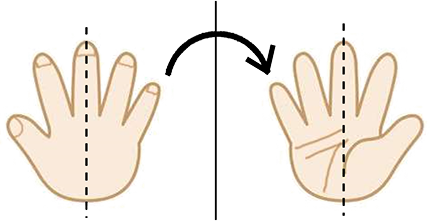
実線で「折り返し」た感じになりますね!
同じ感じで、「12通り目」を裏から見ると(折り返すと)…
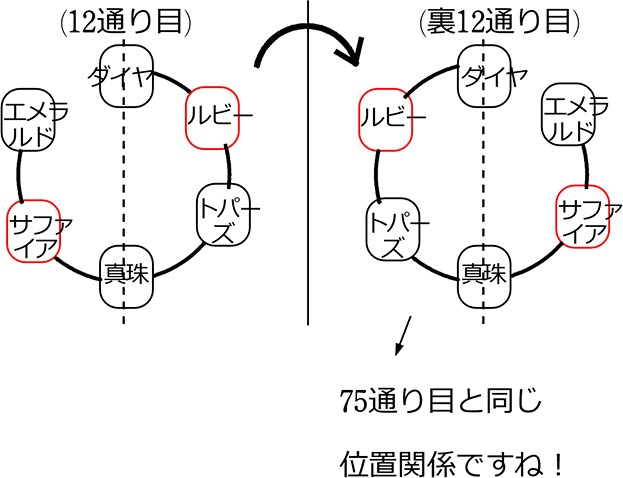
というわけで、75通り目は12通り目と同じとみなして数えません
これが、円順列の「全通り」に存在しますので

(前提:全て使い、全て異なる)
数珠順列 = \(\large{\frac{円順列}{2}}\)
もちろん、円順列は偶数通りですのでちゃんと割り切れます
〇〇.5通りなどにはなりませんので安心して下さい
ex. (5-1)!= 4!= 4・3・2
(4-1)!= 3!= 3・2
↑必ず因数に「2」を含むので、「偶数」
さらに、元が奇数個でもちゃんと「2通りづつ」同じものが存在しますので、
安心して「2」で割って下さいね!
ex.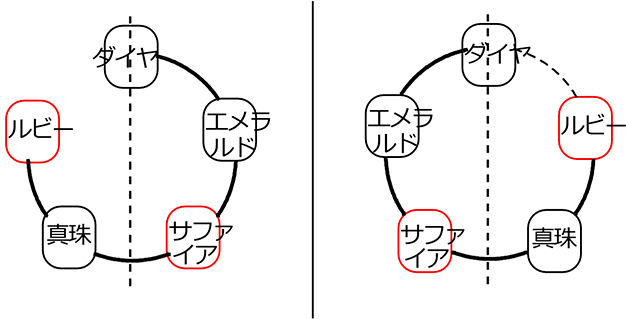

ポイントは、問題文の日本語ですね
「つなぐ」「じゅず状にする」「ネックレス」など
「並べる」「円にする」だけでなく「つなぐ」「持ち上げられる」という意味が見て取れたら、
「じゅず順列」ですね
【 同じものを含む円順列・じゅず順列 】
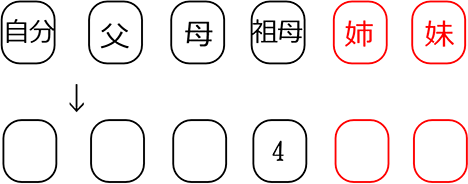 に変えますね
に変えますね
● 黒カード3枚、「4」、赤カード2枚 を円形に並べる方法は、何通り?
<ということは>
1枚しかないカードを固定して、
後は「普通の順列」→「同じものを含む順列」に変えて考えるだけですね!
「4」のカードを固定 → あとは黒3枚、赤2枚の「同じものを含む順列」
→ (6-1)!= 5! が \(\large{\frac{5!}{3!\ \cdot \ 2!}}\) になるだけですね
∴ 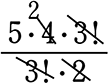 = 10 通り
= 10 通り
● じゅず状に並べる方法は、何通り?
同じものを含む場合、単純に2で割ることができません
なぜなら、2で割る理由は
「違う並びであるのに、裏から見ると同じである」並びを排除するためでしたね
逆をいうと、「ある並びを裏返すと、違うものになる」という必要がありますね
ということは
「左右対称」の並びは、裏返しても 違う並びになりませんね
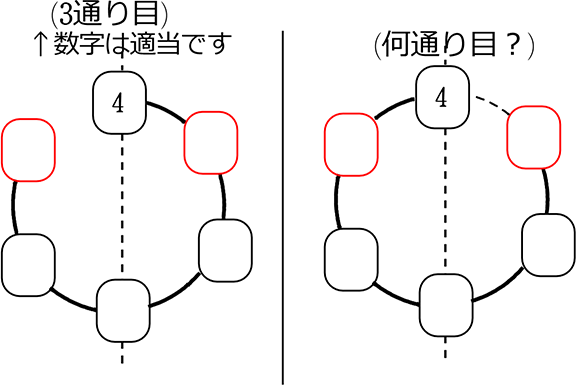
ということは、右の並びは、全10通りの中で元々「かぶり」として排除されていますね!
それなのに「2」で割るということは、(3通り目)の「1通り」を「2」で割る
→「0.5通り」となってしまいますので、
こういう左右対称なものは、「2」で割る前に「よけておきます」
では次に、
あとは、「左右対称なもの」が何個あるか?ですね
1つ目は自力で見つけ出すにしても、それに付随する「左右対称なもの」は
「右半分の順列」ということになりますね
例えば
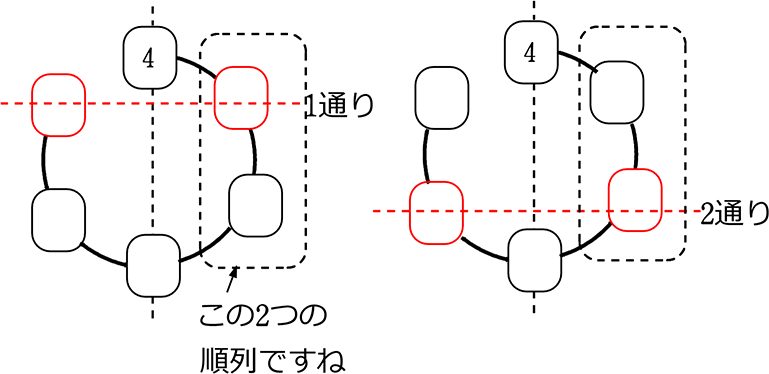
よって、
「同じものを含む全順列」(今回は2つですので同じものを含んでいません)
= 2! = 2通り ですね!
ex.
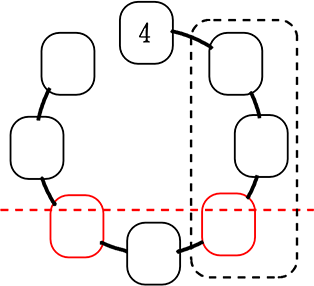
この場合は
\(\large{\frac{3!}{2!}}\) = 3通り
ですね

同じものを含むじゅず順列 = 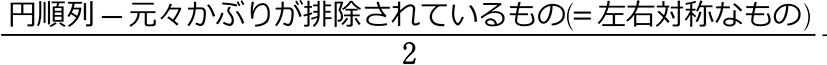 +左右対称なもの ←取り除いておいたものを戻す意味
+左右対称なもの ←取り除いておいたものを戻す意味
= 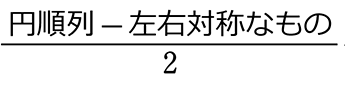 +左右対称なもの
+左右対称なもの
問題に戻りまして、再度
● じゅず状に並べる方法は、何通り?
→ 同じものを含むじゅず順列 =\(\large{\frac{円順列-左右対称なもの}{2}}\)+左右対称なもの = \(\large{\frac{10-2}{2}}\)+2 = 4+2 = 6 通り
上のex.の なら
なら
・円順列= \(\large{\frac{7!}{5!\ \cdot \ 2!}}\) = 21通り
・左右対称なもの= \(\large{\frac{3!}{2!}}\) = 3通り
∴ 同じものを含むじゅず順 = \(\large{\frac{円順列-左右対称なもの}{2}}\)+左右対称なもの = \(\large{\frac{21-3}{2}}\)+3 = 12通り
【 1枚しかないカードがない場合 】
・・・いい考え方がありませんね!
よって、全てのパターン図を書き出すしかないと思われます!
〔円順列〕
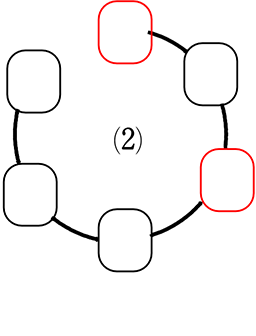
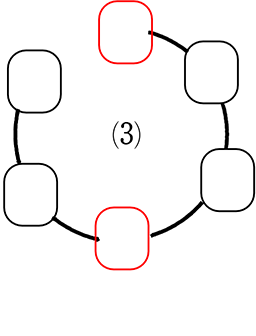
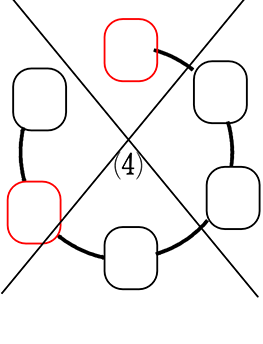
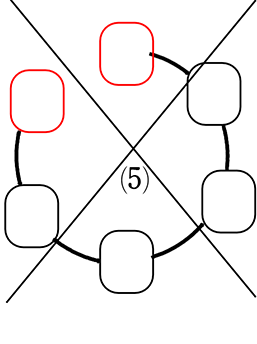
(1)と(5)、(2)と(4)は「位置関係」が同じですね ∴ 3 通り
〔じゅず順列〕
裏返すと違うものが もう排除されてしまってますね(してくれてますね)
言い換えれば、「裏から見たら同じだ というかぶり」がないですね ∴ 3 通り
c ~ 組合せ ~
順列は選んだ後の「並び方」にまでこだわりましたが、
組合せは選んだ後の「並び」はこだわりませんね!選ぶだけです
(前提) 異なる(n個)ものから、異なる(r個)ものを、選ぶ
組合せ:選ぶだけ
順列:選んで、選んだものの並びにこだわる
\({}_{10}\mathrm{ P }_4\)÷4! = \({}_{10}\mathrm{ C }_4\)
\({}_{10}\mathrm{ C }_4\)×4! = \({}_{10}\mathrm{ P }_4\)
「組合せ」は「同じものを含む順列」と同じように、「だぶり」で割るということですね
「だぶり」のイメージは「内部」「2層目」という感じでしょか
「だぶり数」は選んだ数の個数の階乗分(マス数分)ありますね(=選んだ個数の全順列分)
ex.
456の3数から3つ(全部)を「選ぶ」(=並びにこだわらない)、何通り?
→ 本能的に〈4, 5, 6〉の「1通り」ですが
→ どういう計算を行ったのでしょうか?
⇒ 実は、まずは並びにこだわる順列数えをしています
3マス 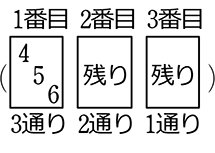 なので、 3通り
なので、 3通り
→ これを、〈1, 2, 3〉の1通りとするには、分子と同じもの(今回は3マスの階乗)で割ればよいということですね!
∴ 1, 2, 3 の3数から3つを「選ぶ」 → \(\large{\frac{{}_3 \mathrm{P }_3}{3!}}\) → \(\large{\frac{3!}{3!}}\) = 1通り ですね
ex. では次に
4567の4数から3つを「選ぶ」(=並びにこだわらない)、何通り?
→ まずは順列数えでしたね → 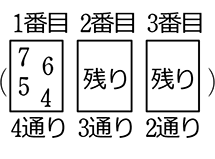 = \({}_4 \mathrm{P }_3\) = 4!の前3つ = 4×3×2 = 24通り でしたね
= \({}_4 \mathrm{P }_3\) = 4!の前3つ = 4×3×2 = 24通り でしたね
→ これを整理して列挙すると
〈4, 5, 6〉の並びにこだわったもの
の6通り → これを組合せは1通りにしたい → 3マスの階乗で割ればよい → 6通り÷3! = 1通り
〈4, 5, 7〉の並びにこだわったもの
の6通り → これを組合せは1通りにしたい → 3マスの階乗で割ればよい → 6通り÷3! = 1通り
〈4, 6, 7〉の並びにこだわったもの
の6通り → これを組合せは1通りにしたい → 3マスの階乗で割ればよい → 6通り÷3! = 1通り
〈5, 6, 7〉の並びにこだわったもの
の6通り → これを組合せは1通りにしたい → 3マスの階乗で割ればよい → 6通り÷3! = 1通り
∴ 組合せ数え = (\(\large{\frac{6通り}{3!}}\))+(\(\large{\frac{6通り}{3!}}\))+(\(\large{\frac{6通り}{3!}}\))+(\(\large{\frac{6通り}{3!}}\)) = \(\large{\frac{6通り+6通り+6通り+6通り}{3!}}\) = \(\large{\frac{24通り}{3!}}\) = \(\large{\frac{順列数え}{同じマス数の階乗}}\) = \(\large{\frac{{}_4 \mathrm{P }_3}{3!}}\) = 4通り
〔リアルなイメージ〕
泥棒さんが、自転車を盗もうとしています
さらに、盗んだキャッシュカードで現金を引き出そうとしています
1回の試行でロックを解除する確率は?
ただし、数字は4つであることは知っているようです


二者の10キーから4つを「選ぶ」場合の数は?
→ \({}_{10}\mathrm{ C}_4\) = \(\large{\frac{10\ \cdot \ 9\ \cdot \ 8\ \cdot \ 7}{4!}}\) = 210 通り
(4つへこますパターン数は210通り)
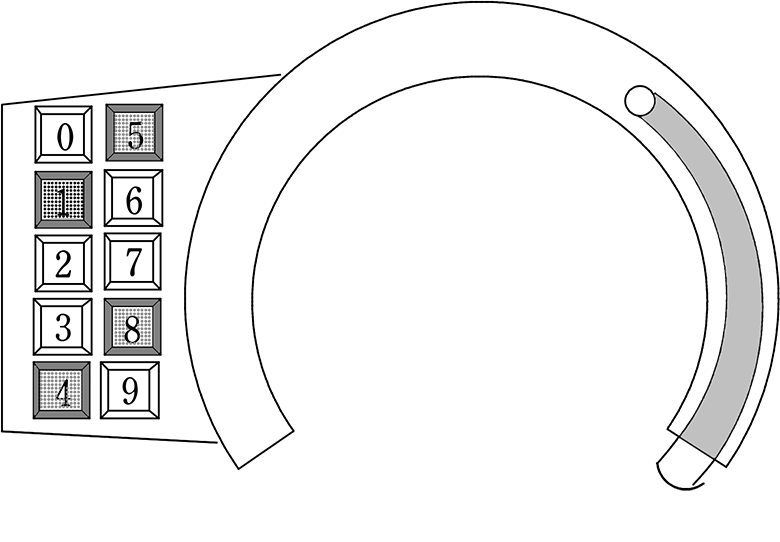
自転車のカギは「\(\large{\frac{1}{210}}\)の確率で1回で開きますね!
→ 1と4と5と8 さえ「選ばれ」ていればよい(組合せ)
(何から押してもよい)
→ 1と4と5と8 さえ「へこんで」いればよい
→ 1と4と5と8 さえ「へこんで」いる『形』であればよい
(↑この『形』ということを意識すると「組合せ」の勉強がstep upしますね!)
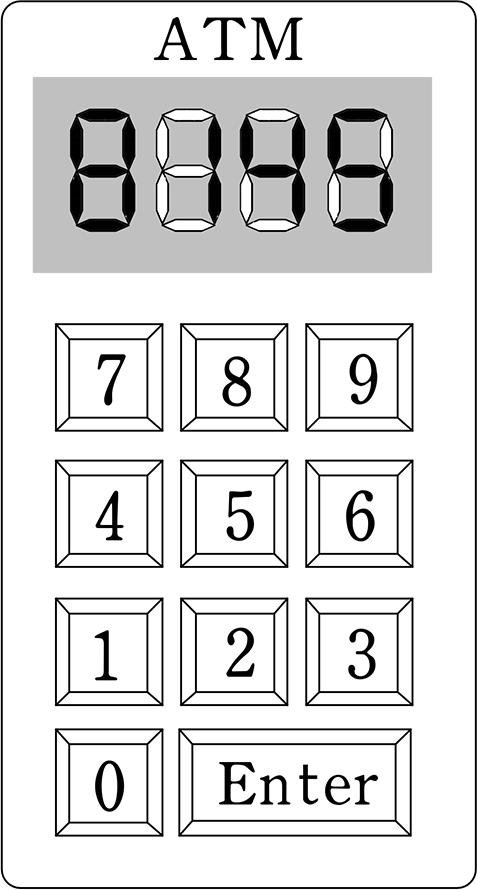
対してATMは 「1→4→5→8」では解除しませんね
\({}_{10}\mathrm{ C}_4\)×4! = すなわち \({}_{10}\mathrm{ P}_4\) = 10・9・8・7 = 5040通り
ATMは「\(\large{\frac{1}{5040}}\)の確率で1回で解除しますね!
→ 選んだ後の順番に「こだわる」(順列)
→ 8→1→4→5 のときだけ開錠!
●順列 ≒ ATM ≒ 〇→〇→〇→〇 ≒ \({}_{10}\mathrm{ P}_4\)
●組合せ ≒ 自転車のカギ ≒ 〇と〇と〇と〇 ≒ \({}_{10}\mathrm{ C}_4\)
前提:すべて異なり、異なるものを選び、並びにこだわらない
012345
● 「3」を選ぶ方法は、何通り? ←「3」と指定されてしまいましたね、当然に「1通り」ですね
←「3」と指定されてしまいましたね、当然に「1通り」ですね
● 1枚を ←0でも1でも…6でもよい、あるのは6枚のカードだから、6通り
←0でも1でも…6でもよい、あるのは6枚のカードだから、6通り
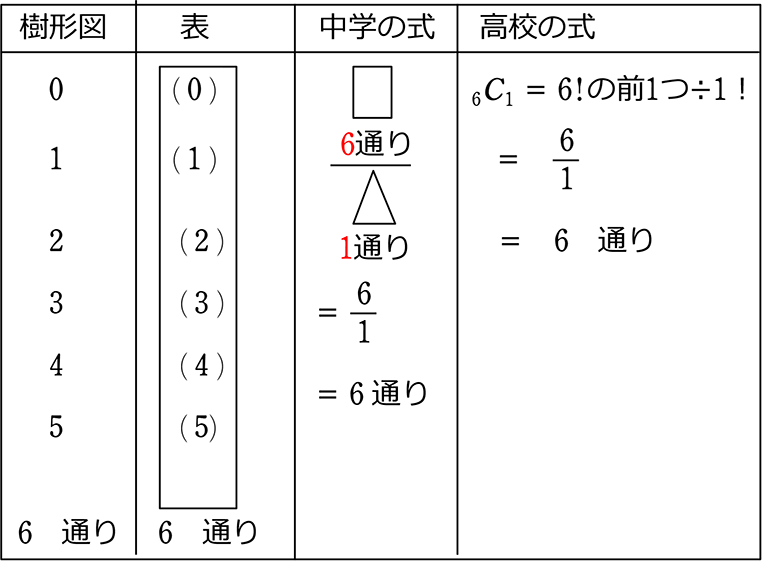
ここまでは、「順列」と同じ結果ですね (だぶりがないから)
ダブりは  にしますね
にしますね
● 2枚を
012345

● 3枚を
012345

● 4枚を選ぶ方法は、何通り?
012345
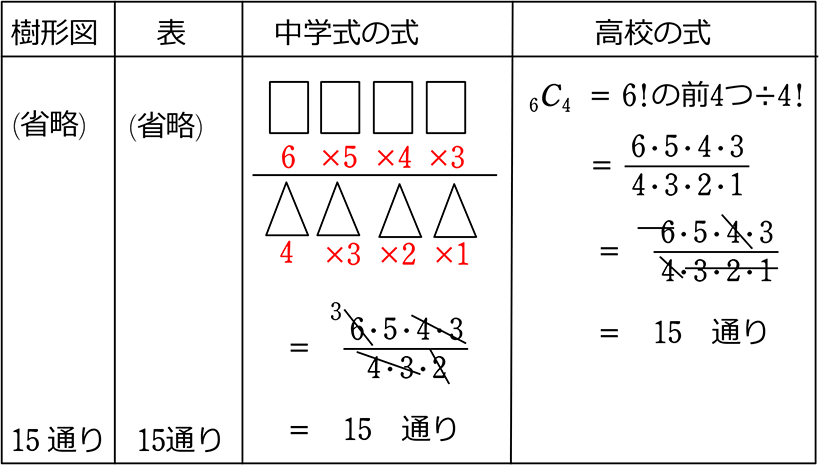
ここで、6枚から4枚選ぶ通り数は、
先に出てきた6枚から2枚選ぶ通り数と
(\({}_6 \mathrm{ C }_2\)=\(\large{\frac{6\ \cdot \ 5}{2!}}\)=15通り)
同じであると気づいたかもしれませんね!
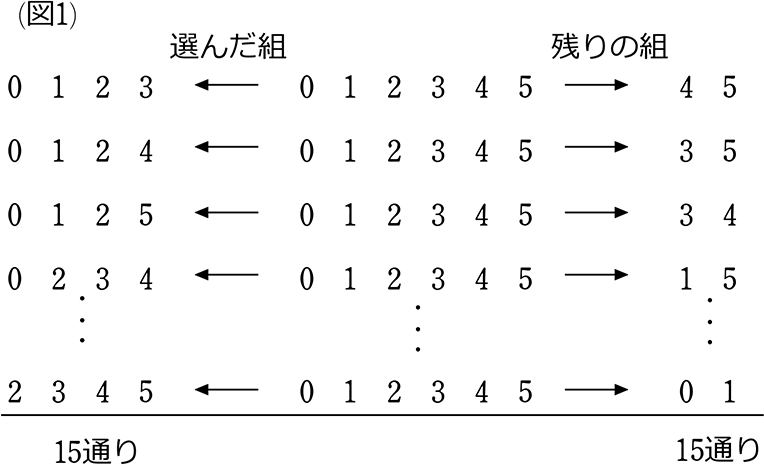
となりますものね!
よって、4枚を選ぶ通り数 = 残りの通り数(6-4 = 2枚を選ぶ通り数)
すなわち、4枚を選ぶ場合、残り(2枚)の方を選んでも同じ
\({}_6 \mathrm{C }_4\) = \({}_6 \mathrm{C }_{6-4}\) = \({}_6 \mathrm{C }_2\)
\({}_n \mathrm{C }_r\) = \({}_n \mathrm{C }_{(n-r)}\)
ex.
自転車のカギで例えるならば
「1458」をへこます型をつくるということは
「023679」を浮かび上げる型をつくるということ同じですね

完成形から見た人は
「023679を選んだのかな?」
と思うかもしれませんね!
少しだけ計算が楽になりますね
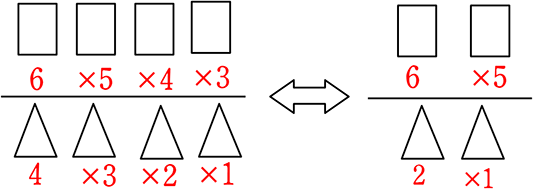
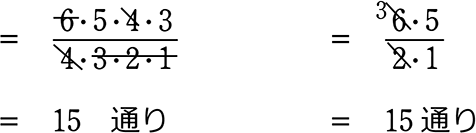
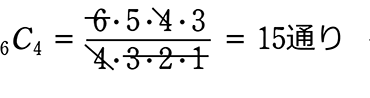
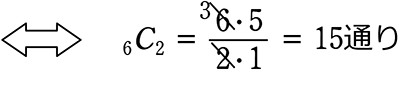
さらに、4枚の組と2枚の組の、2つの組に分ける方法は何通り?
と同じということにもなりますね!
ex. 上の(図1)を見ながら
\({}_6 \mathrm{ C }_4\) は「異なる6個から4個を選ぶ方法は何通り?」ではありますが、
=「異なる6個を、4つの組と2つの組、2つに分ける方法は何通り?」
ということにもなりますね
\({}_6 \mathrm{ C }_4\) は「4に注目」しているようで、実は「2にも注目」している!
というわけで、次の「5枚を選ぶ方法は、何通り?」は
「1枚を選ぶ方法は、何通り?」と同じになるのですが、念のため。
● 5枚を選ぶ方法は、何通り?
012345
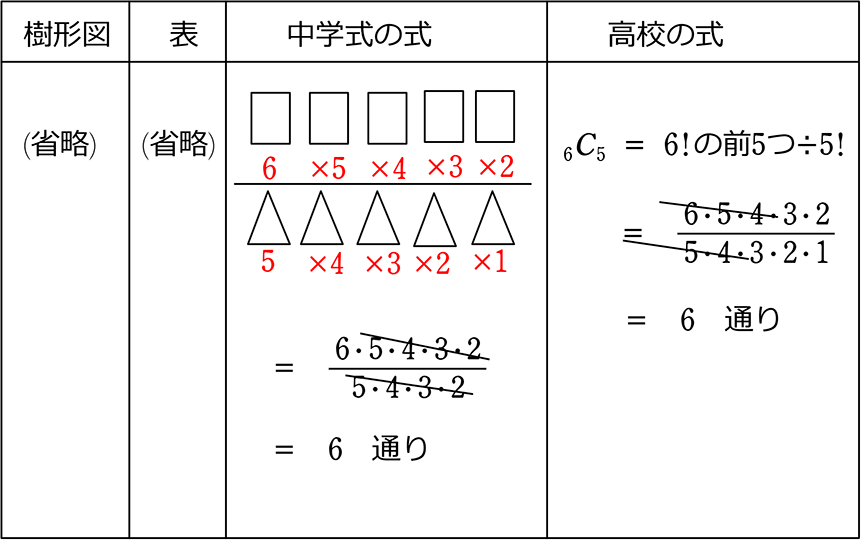
● 6枚を選ぶ方法は、何通り? → 全部選ぶ → 1通り ですね
012345

組合せの樹形図の書き方のコツ
「組合せ」の樹形図の書き方のコツは、
・「数字の小さいものから書く」 「アルファベットの小さいものから書く」
ここまでは、「順列」と同じですね! さらに
・左より小さいものを書かない!昇順だけが許される ですね!
(もちろん、すべて逆にした「左より大きいものを書かない」「降順だけが許される」でもOK)
→ 左より小さい数字を書いてしまいますと、
同じ意味の並びをすでに書いているはずですので、
ダブルカウントになってしまいますね!
ex. 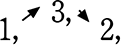 は先に書いた
は先に書いた 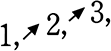 と同じ→ ダブルカウント!
と同じ→ ダブルカウント!
《 例 》 1, 2, 3, 4 から3つを
→ キーワード「選ぶ」 → こだわらない → 組合せ



組合せ C(コンビネーション) の意味
\({}_6 \mathrm{ C }_2\) や \({}_6 \mathrm{ C }_3\) や \({}_n \mathrm{ C }_r\) ですが、
・読み方は、
「6C2(ろくシーに)」「6C3(ろくシーさん)」となります
・意味は、
「
となりますね
心の中では「nコ(6コ)から、rコマス分(3コ)
・計算方法は、
\({}_6 \mathrm{ C }_2\) であれば、
「6! の前2つをだぶり(2マスの階乗)で割る」
→ 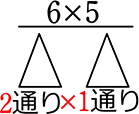 = 15 ですね
= 15 ですね
・公式風なら、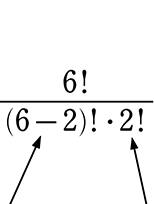
6!の尻尾を切る
ためのもの
だぶりを無くす
ためのもの
→ \(\large{\frac{6!}{4!\ \cdot \ 2!}}\) → \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4!}{4!\ \cdot \ 2}}\) →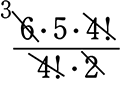 → 15
→ 15
中学の をかっこよく
をかっこよく
表現しただけですね!
\({}_6 \mathrm{C }_3\)→ 「6!の 前3つを 3!で割る」→\(\large{\frac{6×5×4}{3!}}\) = 20 ですね
公式風なら、\(\large{\frac{6!}{(6-3)!\ \cdot \ 3!}}\) → \(\large{\frac{6!}{3!\ \cdot \ 3!}}\) → 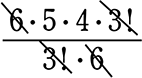 → 20
→ 20
\({}_6 \mathrm{C }_3\) → \(\large{\frac{6!}{(6-r)!\ \cdot \ r!}}\)
\({}_n \mathrm{C }_r\)
→ 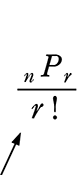
\(\large{\frac{順列}{だぶり}}\)
→ 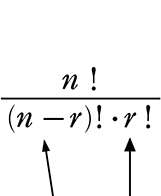
意味ありげな分母ですが、
「ただ分子の階乗の尻尾を切りたい
という意味だけの分母」×「だぶりを
無くすと言う意味の分母」ですね!
Cの計算方法は、 「n! の前 r 個 を、 マス数の階乗 で割る」で十分ですね
(例) \({}_7 \mathrm{C }_4\)
= \(\large{\frac{7\ \cdot \ 6\ \cdot \ 5\ \cdot \ 4}{4!}}\)
= \(\large{\frac{7\ \cdot \ 6\ \cdot \ 5\ \cdot \ 4}{4\ \cdot \ 3\ \cdot \ 2\ \cdot \ 1}}\) 尻尾を切ったあと、階乗をばらすと、必ず分母と分子の個数が同じ(幅が同じ)になりますね
\({}_6 \mathrm{C }_6\) = 1 (全部を選ぶという選択)
\({}_n \mathrm{C }_n\) = 1 (全部を選ぶという選択)
\({}_n \mathrm{C }_0\) = 1 (何も選ばないという選択)
\({}_n \mathrm{C }_r\) = \({}_n \mathrm{C }_{(n-r)}\) (反対を選んでもよい)
(Pの時同様、公式 \(\large{\frac{n!}{(n-r)!\ \cdot \ r!}}\) は不要!)
⇒ n階乗の前r個 ÷ r(マス数)の階乗 で十分
「C」も「P」もそれ自体は「公式」ではなく、「短縮語」ですね!
→ \({}_6 \mathrm{C }_3\)「6個から3個選ぶ」、\({}_6 \mathrm{P }_3\)「6個から3個選んで並びにこだわる」という「意味」

《 例 》
男子3人、女子3人がいます

● 人は、「絶対的に区別があります!」 → 実は 1,2,3,4,5,6、a,b,c,d,e,f である → 「異なる~」である
→ あとは数え方の問題
| ① | 並びにこだわる(= 順列数え) ex. 男子・女子を「並べる」 委員長、副委員長を「選ぶ」 |
| ② | 並びにこだわらない(= 組合せ数え) ex. 男子・女子を「選ぶ」 役員を「選ぶ」 |
| ● | 「人」、数字・アルファベットが書かれた「もの」以外は、「区別できません」 (みかん3個、赤玉2個、などですね) |
| 白玉 → 仮に区別をつけて選ぶ → 戻す(区別をなくす) (=組合せ数え) |
再度、男子3人、女子3人がいます
(1) 委員長、副委員長、書記長の3人を選ぶ方法は、何通り?
<ということは>
「人」→「区別します」、「選ぶ」という文言ですが、組合せ数えではないですね、マスに基準名があるので 「並び」→「こだわる」 → 順列
123456
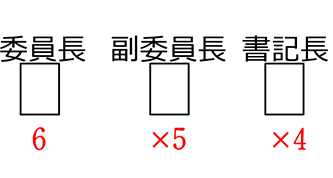 = \({}_6 \mathrm{P }_3\) = 6・5・4 = 120 通り
= \({}_6 \mathrm{P }_3\) = 6・5・4 = 120 通り
(2) 3人の代表を選ぶ方法は、何通り?
<ということは> → 基準名が同じ →
→ 基準名が同じ → 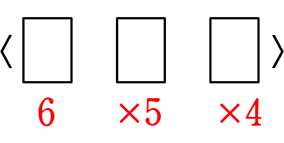 基準名がないのと同じ → 並びにこだわらない → 組合せ
基準名がないのと同じ → 並びにこだわらない → 組合せ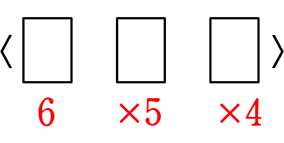 ÷3! =
÷3! = 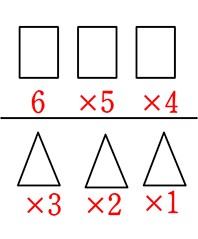 = \({}_6 \mathrm{C }_3\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\) = 20 通り
= \({}_6 \mathrm{C }_3\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\) = 20 通り
(3) 男子2人、女子2人を選ぶ方法は、何通り?
→「選ぶ」→「男子どうしの並び、女子どうしの並びにはこだわらない」→ 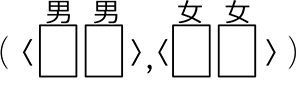 ← 「分けはめ」の応用利用ですね
← 「分けはめ」の応用利用ですね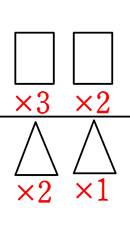 ×
× 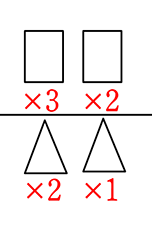 = \({}_3 \mathrm{C }_2\)×\({}_3 \mathrm{C }_2\) = 3通り
= \({}_3 \mathrm{C }_2\)×\({}_3 \mathrm{C }_2\) = 3通り
(4) 少なくとも 女子が1人 入るように3人を選ぶ方法は、何通り?
(「少なくとも」というキーワードがあれば、余事象ですね)
<ということは>
少なくとも女子が1人 = 全ての3人の選び方 - 女子が0の3人の選び方(=全て男子)
= 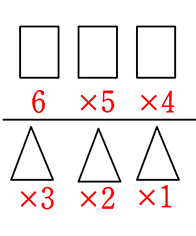 -
- 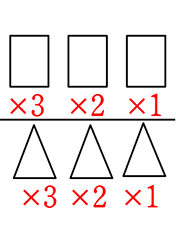
= \({}_6 \mathrm{C }_3\)-\({}_3 \mathrm{C }_3\) = 20-1 = 19 通り
〔正当に「場合分け」でも大丈夫です〕
考えられるパターンは・・・
| ① | 女子1男子2 → \({}_3 \mathrm{C }_1\)×\({}_3 \mathrm{C }_2\) = 3×3 = 9 通り |
| ② | 女子2男子1 → \({}_3 \mathrm{C }_2\)×\({}_3 \mathrm{C }_1\) = 9通り |
| ③ | 女子3 → \({}_3 \mathrm{C }_3\) = 1 通り |
∴ (場合分けは「和の法則」でしたね) 9+9+1 = 19 通り
《 例 》
(1) 八角形の対角線は、何通り? (=何本?)
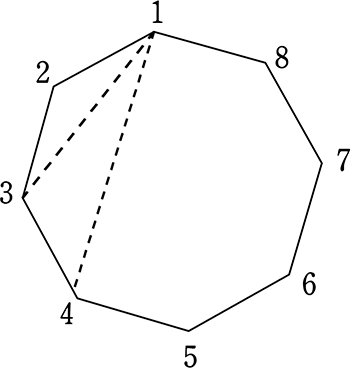
1、2本ほど対角線を引けば、なんとなく分かりますね!
| → | 8頂点から2頂点「選べ」ばよいですね (1, → 3) (3, → 1)は「だぶり」なので 〈1, 3〉で1通りと数えたい ⇒ 組合せ数えだな |
| → | 隣どうしの2頂点を選んだ場合は「対角線」ではないな →「辺」→ そういう2点の選び方(辺の数)は8通り |
| ∴ | 1 2 3 4 5 6 7 8 頂点から 2頂点「選ぶ」こと - 辺となる2点を「選ぶ」こと ですね
∴ \({}_8 \mathrm{C }_2\) - 8 = \(\large{\frac{8\ \cdot \ 7}{2\ \cdot \ 1}}\)-8 = 28-8 = 20 通り |
辺の8通りの内訳は、\({}_8 \mathrm{C }_2\)の中にある〈1, 2 3 4 5 6 7 8〉〈2, 3 4 5 6 7 8〉〈3, 4 5 6 7 8〉〈4, 5 6 7 8〉〈5, 6 7 8〉〈6, 7 8〉〈7, 8〉
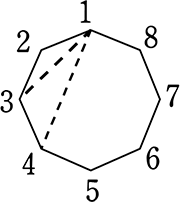
全28通りの中の赤ですね
抜き出すと
〈1, 2〉〈1, 8〉〈2, 3〉〈3, 4〉〈4, 5〉〈5, 6〉〈6, 7〉〈7, 8〉の8通り
→ この8通りを選んだ場合は「対角線」ではなく「辺」だ
もちろん、先に学んだ平面図形の「多角形の対角線の本数(2年)」の公式で求めてもかまいませんね
(2) n角形の対角線は、何通り? (=何本?)
\({}_8 \mathrm{C }_2\) - 8 の 8をnに換えるだけですね
∴ \({}_n \mathrm{C }_2\) - n = \(\large{\frac{n\ \cdot \ (n-1)}{2\ \cdot \ 1}}\) - n = \(\large{\frac{n\ \cdot \ (n-1)}{2}}\) - \(\large{\frac{2n}{2}}\) = \(\large{\frac{n\{(n-1)-2\}}{2}}\) = \(\large{\frac{n(n-3)}{2}}\) ←図形のときの公式と同じですね
(3) 八角形の頂点を結んでできる三角形の個数は、何個?
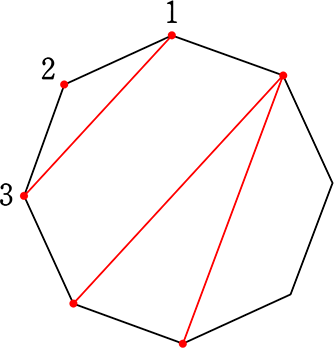
8個の頂点のうち、3個を「選べば」三角形ができますね
(1,→ 2,→ 3) (1, 3, 2) (2, 1, 3) (2, 3, 1) (3, 1, 2) (3, 2, 1) な順列数えではかぶって数えていますね
∴〈1, と 2, と 3〉のような組合せ数えですね
∴ \({}_8 \mathrm{C }_3\) = \(\large{\frac{8\ \cdot \ 7\ \cdot \ 6}{3\ \cdot \ 2\ \cdot \ 1}}\) = 56 個
(4) (3)の三角形で、八角形と「辺を共有する」三角形は、何個?
| ・ | (3)の左上の三角形などは、
八角形と「2辺を共有する」三角形ですね |

∴ 8 個 …①
| ・ | (3)の中程の三角形などは、
八角形と「1辺を共有する」三角形ですね |

∴ 4個×8辺 = 32 個 …②
∴ 八角形と(何かしら)辺を共有する三角形の数 = ①+② = 40 個
cf.
全56通り-40通り = 16通りは
辺を共有しない三角形ということですね

| → | この三角形は数え挙げるのは難しい |
| ∴ | このように余事象がよいですね |
《 例 》
の8人から5人を選んで円形に座らせる方法は、何通り?
(第1段階) 8人から5人を選ぶ \({}_8 \mathrm{C }_5\) = 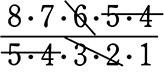 = 56 通り
= 56 通り
(第2段階) あとは5人の円順列×56通り
5人の円順列 = (5-1)! = 4・3・2 = 24 通り
∴ 24通り×56通り = 1344 通り
① 重複組合せ
重複組合せとは(異なる)n種類のものから重複を許して r個(r回)選ぶ(選んだ後の並びにはこだわらない) ことですね
( = 区別のない r個マス達が、区別のあるn種類のものを、各々選ぶ! で十分ですね!)
重複とは、例えば、全て異なる a b c d e f の6個から3個取るとき、
普通の「組合せ」では、〈 a b c 〉 ・・・ 〈 d e f 〉のように〈カッコ〉内は
全て異なっていましたが
「重複組合せ」では、〈 a a a 〉〈 a a b 〉 ・・・ 〈 c c c 〉も可能
「重複順列」ではさらに( a a b) なら( a b a ) ( b a a )も違うものとしていましたね
ですが、結局は「C」を使いますので、「重複組合せ」の定義は意識せず
〇の間を┃(仕切り棒)が動く問題に出会えば、「ああ重複組合せか」と
思うくらいで十分ですね!
《 例 》
10個のみかんを、Aさん、Bさん、Cさん に分ける
(1) 1つももらえない人がいてもよい場合、何通り(の分け方)?
本当に「重複組合せ」の問題?と思ってしまいますね
| → | AさんBさんCさん(n種)を、10(r)回選ぶ、選んだ後の並びはこだわらない
(選んだ後の並びにこだわらない = マスに基準名がないことをいいことに、そこを「みかん」としている) |
| → | (区別のない)みかん10個が、それぞれ1回づつ合計10回選ぶ |
<ということは>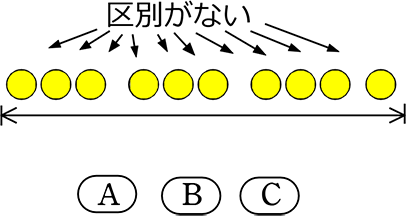 の10個のみかんが
の10個のみかんが
(区別のある)ABCをそれぞれ選んでいくのですが・・・ ←マスの基準名が同じ = マスに基準名がない = 選び終わった10文字の並びに『こだわらない』 → 組合せ数え → 重複組合せ
←マスの基準名が同じ = マスに基準名がない = 選び終わった10文字の並びに『こだわらない』 → 組合せ数え → 重複組合せ
重複順列では、区別のないみかんではなく、区別のあるお菓子1お菓子2…でしたね → マスに基準名があった → 順列数え → 重複順列
みかんに区別がないので、組合せ数えをした結果は、Aを選んだみかんは「左に集めてしまう」、Bを選んだみかんは「真ん中に集めてしまう」、Cを選んだみかんは「右に集めてしまう」、という意味と同じですね
<ということは>
(┃) 仕切り棒2本を みかんと「合体」させて、動かすこと と考えられますね!
=みかんを2つ増やして、12個のみかんのうちの2つを「選ぶ=それを(┃)とみなす」ということですね
例えば、仕切り棒(┃)がそれぞれ自由に動いて、
 なら、Aさん3個・Bさん2個・Cさん5個の形と見ることができますね
なら、Aさん3個・Bさん2個・Cさん5個の形と見ることができますね
┃┃〇〇〇〇〇〇〇〇〇〇 なら、Aさん0個・Bさんも0個・Cさん10個と見れますね
〇〇〇〇〇┃┃〇〇〇〇〇 なら、Aさん5個・Bさん0個・Cさん5個と見れますね
┃〇〇〇〇〇〇〇〇〇〇┃ なら、Aさん0個・Bさん10個・Cさん0個と見れますね
・
・
・
というわけで、10個のみかんと仕切り2本の合計12から、2個選ぶ形ということと同じ意味ですね!
12個から2個選ぶ → 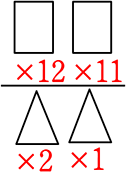 = \({}_{12}\mathrm{C }_2\) = \(\large{\frac{12\ \cdot \ 11}{2\ \cdot \ 1}}\) = 66 通り
= \({}_{12}\mathrm{C }_2\) = \(\large{\frac{12\ \cdot \ 11}{2\ \cdot \ 1}}\) = 66 通り
ex. 66通りの中身は、

組合せ(C)の3つのイメージ
C (コンビネーション)は
「ただ選ぶ」というイメージは持てていたとは思いますが、
さらに2つ、全部で3つのイメージを持っていると今後の勉強の理解に
とても役立ちますね!
それでは
● 1つ目のイメージは 「ただ選ぶ」でしたね
すなわち、順列で並べたものを並びに「こだわらなくした」イメージ
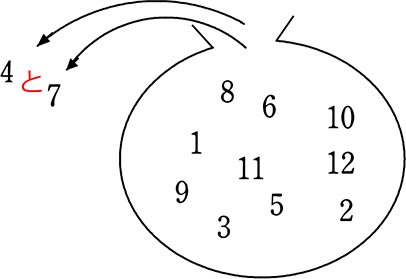
cf. (4, →7) (7, →4)は
違うから「2通り」とする
のは『順列』でしたね
→ 12個から2つ「選ぶ」 → \({}_{12} \mathrm{C }_2\) → \(\large{\frac{12\ \cdot \ 11}{2}}\) = 66 通り

● 2つ目のイメージは 「残りが勝手に決まる」、
すなわち、「2つに分ける」イメージですね
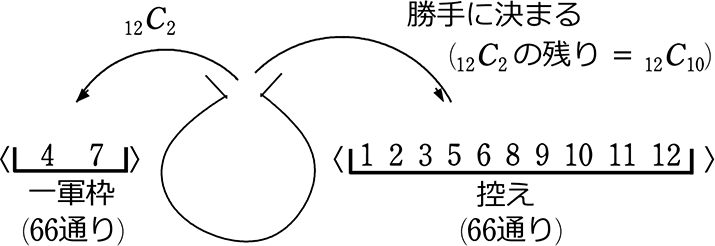
→ 12個から2つ「選ぶ」、残りの「選び方」→ \({}_{12} \mathrm{C }_{10}\) = 66通り
(「残りの選び方」といっても、最初の「2つの選び方」しだい
ですので「残りの選ばれ方」ですね 「袋から出さなければ袋に残っている方の 通り数」とも言えますね)
→ 12個から2つ「選ぶ」 = 12個から自動的に10個「選ばれる」
→ \({}_{12} \mathrm{C }_{10}\) = \({}_{12} \mathrm{C }_2\) につながりますね \({}_n \mathrm{C }_r\) = \({}_n \mathrm{C }_{n-r}\)でしたね

結果、「2個の組枠」と「10個の組枠」に「2つに分ける通り数」と言えますね
● 最も重要な、3つ目のイメージは「型の通り数」ですね
例えば、1~12の数字が書かれた12枚の札などがあるとします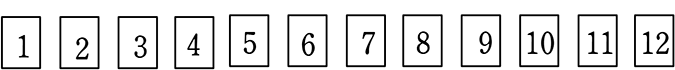
今回は、選んだものを手元に取出さずに「その場」で選びます
(選んだものを指で押さえる感じでしょうか、赤く同時に光るイメージでいきますね
・4と7 を選んだ場合 …型No33
…型No33
これは、選んだ2つのマスを、(┃)に置きかえれば、
〇〇〇┃〇〇┃〇〇〇〇〇 という型を表しているとみなせますね
他にも、選んだ2つのマスを、(/)赤色に置きかえれば、
/ / / / / / / / / / / / という型を表していますね!
他にも、 ∧∧∧∧∧∧∧∧∧∧∧∧ を
他にも、 → → →↑→ →↑→ → → → → を
他にも、○○○●○○●○○○○○ (コインを12回投げて2回裏が出る「型」の1場面) を表していますね
( \({}_{12} \mathrm{C }_2\) = 66通りの型パターンのうちの1つ、型No33 ですね)
・1と2 を選んだ場合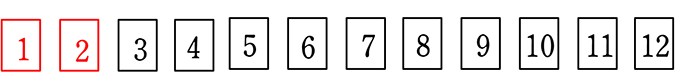 …型No1
…型No1
これは、┃┃〇〇〇〇〇〇〇〇〇〇 を
他には、 / / / / / / / / / / / / を
他にも、 ∧∧∧∧∧∧∧∧∧∧∧∧ を
他にも、↑ ↑→ → → → → → → → → → を表していますね!
・6と7 を選んだ場合 …型No46
…型No46
これは、 〇〇〇〇〇┃┃〇〇〇〇〇 を
他には、 / / / / / / / / / / / / を
・11と12 を選んだ場合 …型No66
…型No66
これは、 〇〇〇〇〇〇〇〇〇〇┃┃ を
他には、 / / / / / / / / / / / / を
・1と12 を選んだ場合 …型No11
…型No11
これは、┃〇〇〇〇〇〇〇〇〇〇┃ を
他には、 / / / / / / / / / / / / を
他にも、 ∧∧∧∧∧∧∧∧∧∧∧∧ を
他にも、↑→ → → → → → → → → →↑ を
他にも、●○○○○○○○○○○● を表していますね
→ どれ一つ同じ「型」はないですね
全部で型が\({}_{12} \mathrm{C }_2\) = 66パターンあるということですね
すなわち \({}_{12} \mathrm{C }_2\) は、
→「型 のパターン数」ともなりますね!
パソコンも同じ原理ですね、
パソコンは「0」と「1」の並び方(形)で
「文字」を表現していますね!
1001 の並び(型)であれば → 9 を表す
1010 の並び(型)であれば → A を表す
1011 の並び(型)であれば → B を表す
1100 の並び(型)であれば → C を表す
1101 の並び(型)であれば → D を表す
1110 の並び(型)であれば → E を表す
【 まとめ 】
\({}_{12} \mathrm{C }_2\) の意味
| ● | 2個を「ただ選ぶ通り数」(順列のこだわりをなくす) |
| ● | 2個組と10個組の「2つに分ける通り数」 |
| ● | 12のうちの2つを選ぶ「型(位置関係)のパターン数」(その場で選ぶ) |
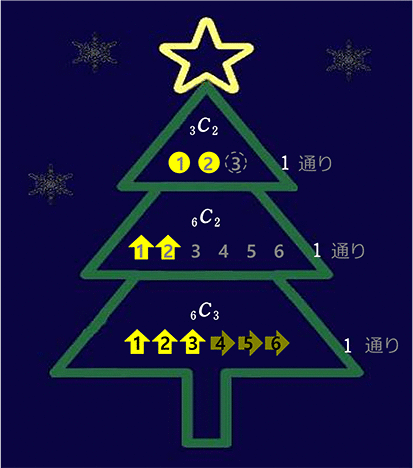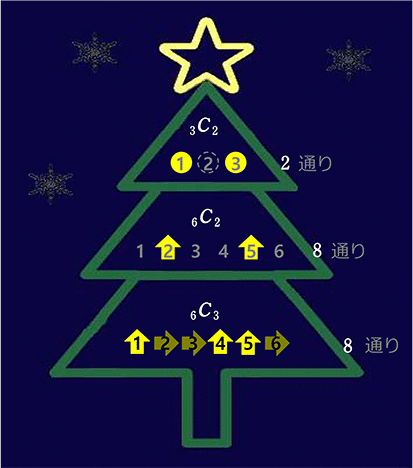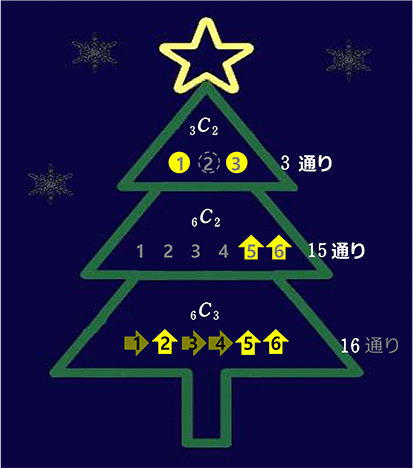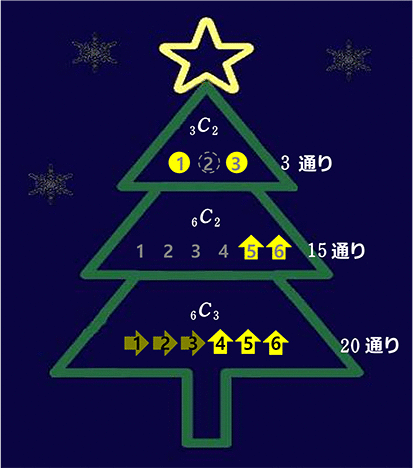
上段(3通り)、中段(15通り)、下段(20通り)ともに
同じ「光り方(形)」はないですね!
全体として 3
《 例 》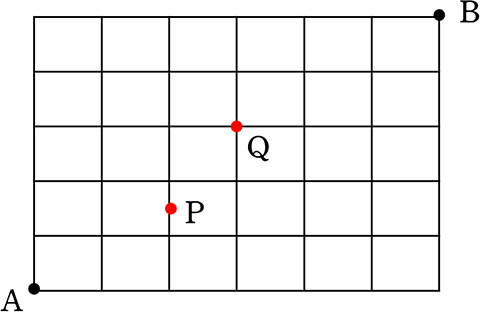
(1) AからBに行くための最短経路は、何通り?
「同じものを含む全順列」で解いていますね
(別解)として、Cの方がシンプルに考えられるというお話です。
上の「位置関係のパターン数」を利用します
図は右に「6」、上に「5」の合計「矢印11個」で最短経路ですね
これを「上」と「右」の「位置関係のパターン数」にすると

この11マスから5個を選んで、
それを「上↑」とみなせばよい ということですね
ex. 
ですね、「型のパターン数」の利用ですね
∴ \({}_{11} \mathrm{C }_5\)= 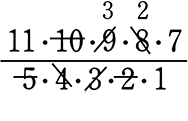 = 11・42 = 462 通り
= 11・42 = 462 通り
(どれ1つ同じ「型」はない = どれ1つ同じ経路はない = すべて異なる経路)
《 例 》
下図のような、横に6本の線と縦に4本の線によって作られる
平行四辺形は何個あるでしょうか?
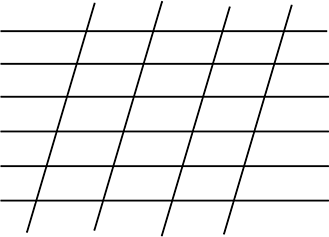
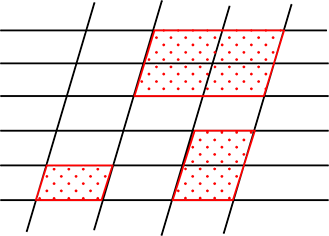
たくさんありそうですね
ですが、どの平行四辺形も結局は 「縦2本と横2本の線」
によってできていますね
これも、「型のパターン数」の利用ですね
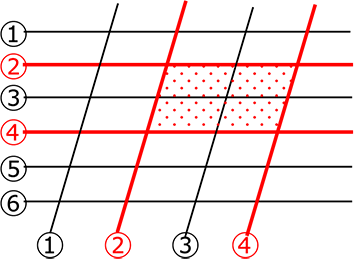
というわけで、
横6本のうちの2本が赤の組み合わせ × 縦4本のうちの2本が赤の組み合わせ
ですね
= \({}_6 \mathrm{C }_2\)×\({}_4 \mathrm{C }_2\) = \(\large{\frac{6\ \cdot \ 5}{2\ \cdot \ 1}}\)×\(\large{\frac{4\ \cdot \ 3}{2\ \cdot \ 1}}\) = 15×6 = 90 個 通り
【 イメージ 】
●左右を両方上げている この『形』は何通り?
この『形』は何通り?
・組合せ君:「 〈1, 2〉の1通り (\({}_2 \mathrm{ C }_2\))」!
〈1, 2〉の1通り (\({}_2 \mathrm{ C }_2\))」!
→ 正解!!
・順列君:「まず①を上げて 、次に②を上げた
、次に②を上げた と
と
まず②を上げて 、次に①を上げた
、次に①を上げた (1, 2)(2, 1)の2通り (\({}_2\mathrm{ P }_2\))」!
(1, 2)(2, 1)の2通り (\({}_2\mathrm{ P }_2\))」!
→ 『形』って言ったでしょ! それはこの「形」になるための『方法数』でしょ!
順列君:「あっそうだ!『形』ということは、①②の順番は関係ない、
すなわち同じものあつかい、すなわち「かぶり」かぁ~、
「かぶり」で割って(\(\large{\frac{{}_2 \mathrm{ P }_2}{2!}}\))で…「1通り!」
→正解!
余談が長くなってしまいましたので
再度、問題文です
《 例 》
10個のみかんを、Aさん、Bさん、Cさん に分ける
(1) 1つももらえない人がいてもよい場合、何通り? → 済
(念のため再度)
→ 10+仕切り棒2本 = 12
<ということは>
→ 12個の〇から2つを選んで、その2つを┃に変えることと同じ
∴ \({}_{12} \mathrm{C }_2\) = \(\large{\frac{12\ \cdot \ 11}{2\ \cdot \ 1}}\) = 6・11 = 66 通り
〈CCCCCCCCCC〉 〈BCCCCCCCCC〉 〈BBCCCCCCCC〉 〈BBBCCCCCCC〉 〈BBBBCCCCCC〉 〈BBBBBCCCCC〉 〈BBBBBBCCCC〉 〈BBBBBBBCCC〉 〈BBBBBBBBCC〉 〈BBBBBBBBBC〉 〈BBBBBBBBBB〉 〈ACCCCCCCCC〉 〈ABCCCCCCCC〉 〈ABBCCCCCCC〉 〈ABBBCCCCCC〉 〈ABBBBCCCCC〉 〈ABBBBBCCCC〉 〈ABBBBBBCCC〉 〈ABBBBBBBCC〉 〈ABBBBBBBBC〉 〈ABBBBBBBBB〉 〈AACCCCCCCC〉 〈AABCCCCCCC〉 〈AABBCCCCCC〉 〈AABBBCCCCC〉 〈AABBBBCCCC〉 〈AABBBBBCCC〉 〈AABBBBBBCC〉 〈AABBBBBBBC〉 〈AABBBBBBBB〉 〈AAACCCCCCC〉 〈AAABCCCCCC〉 〈AAABBCCCCC〉 〈AAABBBCCCC〉 〈AAABBBBCCC〉 〈AAABBBBBCC〉 〈AAABBBBBBC〉〈AAABBBBBBB〉 〈AAAACCCCCC〉 〈AAAABCCCCC〉 〈AAAABBCCCC〉 〈AAAABBBCCC〉 〈AAAABBBBCC〉 〈AAAABBBBBC〉 〈AAAABBBBBB〉 〈AAAAACCCCC〉 〈AAAAABCCCC〉 〈AAAAABBCCC〉 〈AAAAABBBCC〉 〈AAAAABBBBC〉 〈AAAAABBBBB〉 〈AAAAAACCCC〉 〈AAAAAABCCC〉 〈AAAAAABBCC〉 〈AAAAAABBBC〉 〈AAAAAABBBB〉 〈AAAAAAACCC〉 〈AAAAAAABCC〉 〈AAAAAAABBC〉 〈AAAAAAABBB〉 〈AAAAAAAACC〉 〈AAAAAAAABC〉 〈AAAAAAAABB〉 〈AAAAAAAAAC〉 〈AAAAAAAAAB〉 〈AAAAAAAAAA〉
の66通り
| ↑ | 仕切り棒2本の場所をイメージしてみてくださいね |
〈CCCCCCCCCC〉 →〈┃┃CCCCCCCCCC〉
(2) 1つはもらえる場合は、何通り?
<ということは>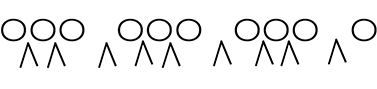 のみかん10個のすき間の9個の∧のうち どれか2つを選んで、赤(∧)に換えれば、
のみかん10個のすき間の9個の∧のうち どれか2つを選んで、赤(∧)に換えれば、
ex. なら
なら
必ず1つはもらえていることになりますね!
↑Aさん1個、Bさん4個、Cさん5個とみれますね
∴ \({}_9 \mathrm{C }_2\) = \(\large{\frac{9\ \cdot \ 8}{2\ \cdot \ 1}}\) = 36 通り
〔考え方2〕
3人に先に(もらえない防止のため)1つづつ分けておきます
残り 〇〇〇 〇〇〇 〇 7個+仕切り棒(┃)2本 =9
∴ \({}_9 \mathrm{C }_2\) ←全く同じですね = 36 通り
〈ABCCCCCCCC〉 〈ABBCCCCCCC〉 〈ABBBCCCCCC〉 〈ABBBBCCCCC〉 〈ABBBBBCCCC〉 〈ABBBBBBCCC〉 〈ABBBBBBBCC〉 〈ABBBBBBBBC〉 〈AABCCCCCCC〉 〈AABBCCCCCC〉 〈AABBBCCCCC〉 〈AABBBBCCCC〉 〈AABBBBBCCC〉 〈AABBBBBBCC〉 〈AABBBBBBBC〉 〈AAABCCCCCC〉 〈AAABBCCCCC〉 〈AAABBBCCCC〉 〈AAABBBBCCC〉 〈AAABBBBBCC〉 〈AAABBBBBBC〉 〈AAAABCCCCC〉 〈AAAABBCCCC〉 〈AAAABBBCCC〉 〈AAAABBBBCC〉 〈AAAABBBBBC〉 〈AAAAABCCCC〉 〈AAAAABBCCC〉 〈AAAAABBBCC〉 〈AAAAABBBBC〉 〈AAAAAABCCC〉 〈AAAAAABBCC〉 〈AAAAAABBBC〉 〈AAAAAAABCC〉 〈AAAAAAABBC〉 〈AAAAAAAABC〉
の36通り
《 例 》
x+y+z = 10 を満たす「0以上の整数」x、y、zの組は、何通り?
(整数:-2、-1、0、1、2… 「0」OK!)
実は上の(1)(もらえないOK)と 同じ問題、全く同じ原理、と分かりますか?
<ということは>
10は、1+1+1+1+1+1+1+1+1+1
(1と┃は似ているので1を〇にしますね)
ex. ┃┃〇〇〇 〇〇〇 〇〇〇 〇 →
∴ 10+仕切り棒2= 12
\({}_{12} \mathrm{C }_2\) ∴ 66 通り みかんのときと同じですね
もちろん、全列挙でもかまいませんが…
(
数えて合計66通り … 大変ですね
《 例 》
x+y+z = 10 を満たす「自然数」x、y、zの組は、何通り?
(自然数:1、2、3… 「0」OUT!)
<ということは>
もうわかりますね、実は上の(2)と 全く同じ原理、 同じ問題ですね! (1つはもらう)ですね
∧ (「すき間三角」と呼ばしてもらいますね)は…
∧の数 = 〇-1 = 10-1 = 9
ex) 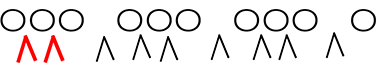 →
→
∴ \({}_9 \mathrm{C }_2\) = 36 通り
《 例 》
りんご、みかん、ぶどう を合わせて9個の詰め合わせを作る
(1) 1つも使わないフルーツがあってもよい場合、何通り?
→ 重複してよいものが、「人」から「りんご、みかん、ぶどう」になっただけですね
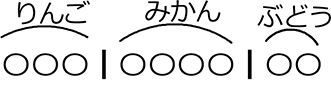 の「C(コンビネーション)」ですね
の「C(コンビネーション)」ですね
簡単にイメージするならば、
区別のないフルーツの素(〇)9個達が、
りんごを選んだら、フルーツがりんごに変身!
みかんのを選んだら、みかんに変身!するイメージですね
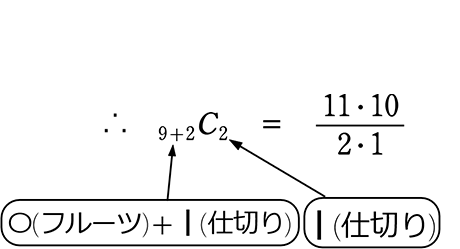 = 11・5 = 55 通り
= 11・5 = 55 通り
ex.
〈RRRRRRRRR〉←フルーツ:りんごを選んでりんごになりました!次のフルーツ:僕もりんごになりました!
〈RRRRRRRRM〉←フルーツ:みかんを選びました!そして並びにこだわらないみたいなので、1番後ろに並びました
・
・
・
〈BBBBBBBBB〉の55通り
(2) 少なくとも1つは使うような分け方は、何通り?
<ということは>
→ 8個の∧のどれか2つを選んで∧に換えれば、
必ず1つは使っていることになりますね!
∴ \({}_8 \mathrm{C }_2\) = \(\large{\frac{8\ \cdot \ 7}{2\ \cdot \ 1}}\) = 28 通り
(または)
先に各フルーツを先に1個づつ入れておきます。
残りの6個+┃2本
→ 〇〇〇〇〇〇+┃┃
∴ \({}_8 \mathrm{C }_2\) = 28 通り

重複組合せのまとめ
| ① | 選ばれない/もらえない/入らないOK → 仕切り棒┃ |
| ② | 選ばれない/もらえない/入らないNG (1つは入る) → すき間三角 ∧
または、 |
重複組合せの定義
「(異なる)n種類のものから重複を許して r個(r回)(r個マス分)選ぶ(選んだ後の並びにはこだわらない)」
重複順列の定義
「異なるn個のものを、重複を許してr個選んで、並べる」
などは、問題を解く前にnとrを問題にあてはめるより、
問題を「解いて」、「理解」できれば
何がn (選ばれる方)で、何がr (選ぶ方 = マス)かが解りやすくなりますね
∴ まずは、定義について深く考えない!ですね!
個別に理解が進んだら・・・
(普通順列)
異なるものから、異なるものを、選んで、並びにこだわる
〈普通組合せ〉
異なるものから、異なるものを、選んで、並びにこだわらない
(重複順列)
異なるものから、
〈重複組合せ〉
異なるものから、
| ・ | 異なるものを、選んで → n個 ≧ r回 |
| ・ | 同じものを、選んでもよく → n個 < r回 |

重複組合せ、一言で 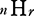 (Homogeneous polynomial)
(Homogeneous polynomial)
「重複組合せ」には、無理やり作ったような「公式」がありますね
《 例 》 10個のみかん を、4人に分ける方法は、何通り?
ただし、もらえない人がいてもよい
→ これは「重複組合せ」「もらえない/入らないOK」パターンで、
→「仕切り棒タイプ」でしたね!
〇┃┃〇〇〇〇┃〇〇〇〇〇
→ みかん10個 → 10○が
→ 4人を選ぶ → 仕切り棒3本
で、\({}_{10+3} \mathrm{C }_3\) = \({}_{13} \mathrm{C }_3\) で解いていましたね
ですが、問題文には「10」と「4」という数字しかありませんね
この「10」と「4」から、\({}_{13} \mathrm{C }_3\) を導こうとしているのが「公式」です
実際的には
| ① | もらえない/入らないOK → 仕切り棒┃ |
| ② | もらえない/入らないNG → すき間三角∧ |
で十分なのですが・・・
「\({}_4 \mathrm{H }_{10}\) の値を求めましょう」という計算問題で、
せっかく「重複組合せ」を理解しているのに、解けないのではもったいないですからね
\({}_4 \mathrm{H }_{10}\) = 異なる4種から、重複を許して10回選び、(出来上がった10個のものの)並びにこだわらない
→ \({}_4 \mathrm{H }_{10}\) = \({}_{4種} \mathrm{H }_{〇10個}\) =「(異なる)4種に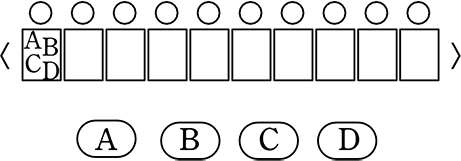
文字にすると
\({}_n \mathrm{H }_r\) = \({}_{n種} \mathrm{H }_{〇r個(回)}\) = 「(異なる)n種にHん化する、r個の(区別のない)○(マス)たち」
おそらくですが、\({}_n \mathrm{H }_r\) の
| n → | number → 数字がふられている → 区別がある |
| H → | Homogeneous (ホモジーニアス) → 同次的 |
| r → | round → 回数(ボクシングなどの12ラウンドなど) → マスの数 |
でしょうか
\({}_n \mathrm{H }_r\) →「区別のあるものを(n)」「重複的に(同次的に)、並びにこだわらずに(H)」「rマス回選ぶ(r)」
\({}_4 \mathrm{H }_{10}\) はそのままでは計算できません! 結局「Cに変身させます」

= \({}_{13} \mathrm{C }_{10}\) 〇を選んでいますね
= \({}_{13} \mathrm{C }_{3}\) ┃を選んだほうが計算も楽 = \(\large{\frac{13\ \cdot \ 12\ \cdot \ 11}{3\ \cdot \ 2\ \cdot \ 1}}\) = 286 通り
cf
問われることはないとは思いますが…
「もらえないNG」の場合は、先に〇を配っておくので、 〇は10-4=6
| → | \({}_4 \mathrm{H }_6\) ということですね → \({}_{4+6-1} \mathrm{C }_6\) = \({}_9 \mathrm{C }_6\) = \({}_9 \mathrm{C }_3\) = 84通り |
逆に、\({}_4 \mathrm{H }_{10}\)で「もらえないNG」なら
→ 〇は14あったということですね
14-最初に4種 = 〇10)
「もらえない」「1個はもらえる」の文言がないときは
原則「もらえないOK」となります
→ 「1個はもらえる」のほうが『ただし~』がお似合い
「H」は公式と言うには・・・ちょっと・・・残念・・・ですね
やはり「公式」ではなく、「記号」「短縮語」ですね
「\({}_4 \mathrm{H }_{10}\) の値を求めましょう」のような計算問題のためだけに
知っていないといけない・・・益々残念な「記号」ですね・・・
\({}_n \mathrm{H }_{r}\) = \({}_{n+r-1} \mathrm{C }_{r}\) と公式風に憶えるのもありですが
\({}_4 \mathrm{H }_{10}\) = (適当に1例を挙げて) 〇┃〇┃〇〇〇┃〇〇〇〇〇 = これは \({}_{13} \mathrm{C }_{3}\)
でも十分ですね
d 組分け
次は、言葉の順番的に
「同じものを含む組合せ」なのですが、
先に、「組分け」に行きますね
① 分けはめ
「分けはめ」という言葉は当然正式な名称ではありません(親中造語)
本来は次に学ぶ「組分け」に属するものとなります
(組合せ(C)の3つのイメージのうちの1つ「分ける」ですね)
親中ではあえて分類させていただきますね
一般的な定義
| 組分け | … | 異なるもの(区別のあるもの)を、「個数指定」にしたがって分けて、区別のある枠や、区別のない枠にはめ込む |
親中
| 分けはめ | … | 異なるもの(区別のあるもの)を、「個数指定」にしたがって分けて、区別のある枠にはめ込む → ( 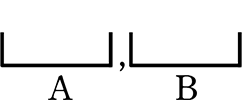 ) や ( ) や (  ) )→ 枠の並びにこだわって数える |
| 組分け | … | 異なるもの(区別のあるもの)を、「個数指定」にしたがって分けて、区別のない枠にはめ込む → 〈 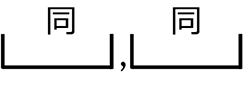 〉 〉 → 枠の並びにこだわらずに数える |
《 例 》
8人の部員を一軍に3人、二軍に3人、三軍に2人に分ける方法は何通り
→ 人は区別(名前)がある ABCDEFGH
→ 枠にも区別がありますね 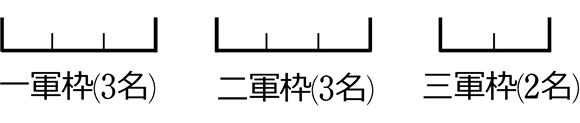
まずは\({}_8 \mathrm{C }_3\)で一軍に3人 → \(\large{\frac{8\ \cdot \ 7\ \cdot \ 6}{3\ \cdot \ 2\ \cdot \ 1}}\)=56通り ┃
┃  このような状態ですね (当然現時点控えも56通り)
このような状態ですね (当然現時点控えも56通り)
↑「分ける」なので当然 枠内の並びにはこだわっていない → \({}_8 \mathrm{C }_3\)でOK
次に控え5人から\({}_5 \mathrm{C }_3\)で二軍に3人 → \(\large{\frac{5\ \cdot \ 4\ \cdot \ 3}{3\ \cdot \ 2\ \cdot \ 1}}\)=10通り ┃
┃  現時点 56
現時点 56
最後の控え2人は自動的に三軍枠へ入るので1通り (「最後は1通り」でも「\({}_2 \mathrm{C }_2\)で1通りでもどちらでもOK)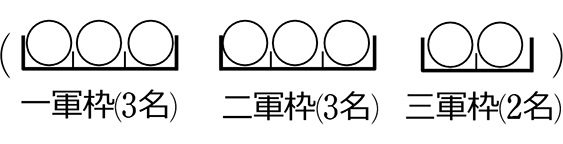
∴ 56通り×10通り(×1通り)=560通り
↑「分けはめ」ですね
| ・ 元 | … | 区別がある |
| ・ 個数指定 | … | あり |
| ・ 枠 | … | 区別がある (枠の並びにこだわる) |
(枠内の並びには)
《 例 》
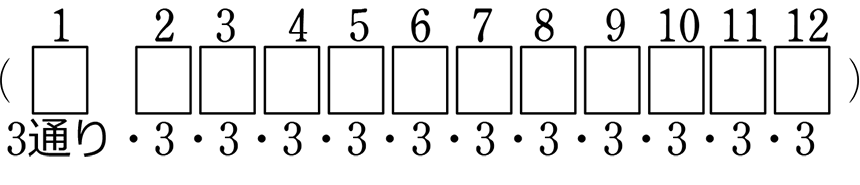
12冊の異なる本を、Aさんに5冊、Bさんに4冊、Cさんに3冊ずつ分ける方法は何通り?
| → | 元 → 区別あり (異なる~より) |
| → | 個数指定 → あり |
| → | 枠の区別 → あり(Aさん、Bさん、Cさん)(枠の並びにこだわる (枠内の並びにはこだわらない) |
⇒ 分けはめ
→ \({}_{12} \mathrm{C }_5\)×\({}_7 \mathrm{C }_4\) =\(\large{\frac{12\ \cdot \ 11\ \cdot \ 10\ \cdot \ 9\ \cdot \ 8}{5\ \cdot \ 4\ \cdot \ 3\ \cdot \ 2\ \cdot \ 1}}\)×\(\large{\frac{7\ \cdot \ 6\ \cdot \ 5}{3\ \cdot \ 2\ \cdot \ 1}}\) =792×35 =396×70 =27720通り
cf
| ・「異なる」が なければ | → | 1通り (AAAAABBBBCCC) (↑重複組合せのある1場面) |
| ・「異なる」がなく 「個数指定」もない =「変動枠」 ならば | → | 重複組合せ |
| ・「異なる」で 「個数指定」がない =「変動枠」 ならば | → | 重複順列 |
《 例 》
6人を2人ずつ部屋A、部屋B、部屋Cに分ける方法は何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠の区別 → あり(部屋A、部屋Bさん、部屋C)(枠の並びにこだわる) |
⇒ 分けはめ
→ \({}_6 \mathrm{C }_2\)×\({}_4 \mathrm{C }_2\)=15×6=90通り
② 組分け
「組分け」のイメージは、個数指定に従って、「ただ分ける」ですね!
全体的なイメージなら
123456
→ 3人選べば当然、 枠が発生しますね
枠が発生しますね
→ 次に選んだ組にも当然  枠が発生!
枠が発生!
→ そして実は、この枠には潜在的な名前が付いていたのです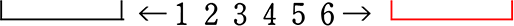
 の名は
の名は
「1番目に選んだ3個組」
分けはめではこれを、
「Aの部屋」「Aの箱」
「A君(に3冊)」
という区別のある
「枠」に入れてましたね
 の名は
の名は
「2番目に選んだ3個組」
分けはめではこれを、
「Bの部屋」「Bの箱」
「B君(に3冊)」
という区別のある
「枠」に入れてましたね
ex)
 や
や
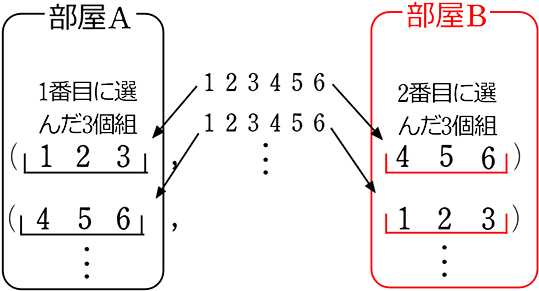
● そして、「組分け」は、この潜在的な名前を「消去」します
すなわち「枠名がない!」
→よって、「組合せ数えをすると」 →「 組合せ的に同じ」といえるものが発生する場合があります!
上のex)から枠名(部屋名)をなくすと
区別のない部屋になりますね
部屋A → 部屋
部屋B → 部屋
潜在的な枠名の方も、
「1番目に選んだ3個組」「2番目に選んだ3個組」は
実は「ただの3個組」「ただの3個組」だったとなります
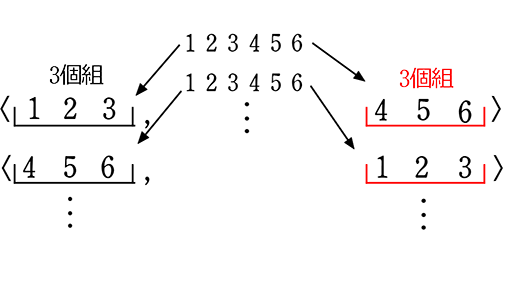 や
や
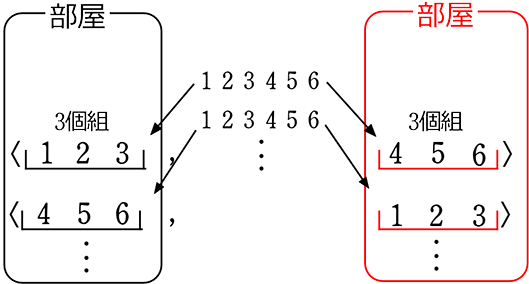
「ダブってますね!」
バスケ監督が頭の中で考えています…
選手ABCDEF6人を、3人3人に分けて3on3したら何ゲームできるんだ…
最初の3人を選べば、残りは勝手に決まるから
最初の3人を選ぶことに集中すればいいか…
〈ABC, vs 残り(DEF)〉 の1ゲーム!
次っ!
〈DEF, vs 残り(ABC)〉 の1ゲーム・・・
…さっき あったな!
というわけで、
1 2 3 をX、4 5 6 をYとおくと
(X, Y) (Y, X) → 〈X, Y〉
枠単位で組合せ数えをするということですね
ということは、
「同じ大きさの枠の個数の階乗」で割れば、ダブりが解消されるということですね
(枠を、組合せのときのマスのように思えばよいですね → マスに基準名があれば順列数え、なければマス数の階乗で割った組み合わせ数え でしたね))
(上の場合なら、枠レベルで組合せ数えをするとダブりになってしまうものが2つ → \(\large{\frac{2通り}{\color{red}{ 2!}}}\) = 1 通り ですね)
ex.
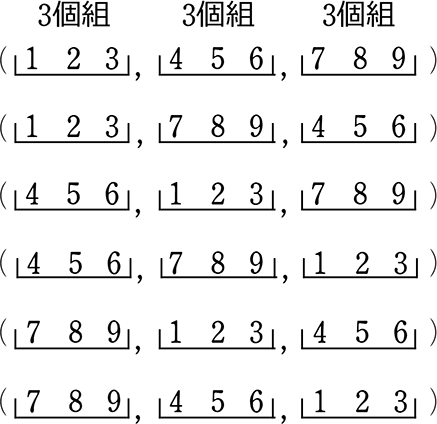
1,2,3 の枠名を1、
4,5,6 の枠名をを 2
7,8,9 の枠名をを 3 とすると
↓
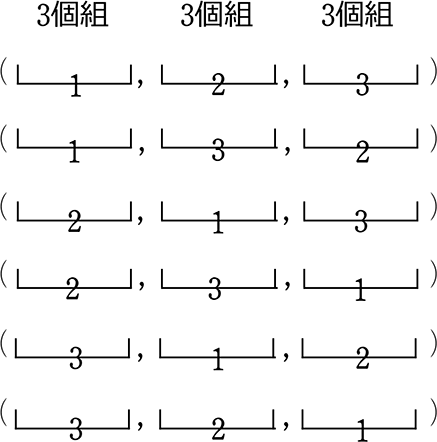
部屋名がない(枠名がない) → 区別しない = 並びにこだわらない数え方
→ ただの組み合わせのときに、かぶりをなくすために「マス数の階乗」で割ったように、「枠数の階乗」で割る ということですね
この場合なら、\(\large{\frac{6通り}{\color{red}{3!}}}\) = 1 通り 〈1, 2, 3〉ですね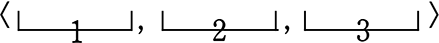 → 1通りだ!
→ 1通りだ!
● 枠名がなくても、枠の大きさが違うと
→ かぶりは発生しない → 枠に区別があるということ → 分けはめだ!
ex.
「1番目に選んだ4個組」「2番目にに選んだ2個組」が
「4個組」「2個組」になります…が!別物ですね!
列挙していくと

ここに2桁の数字が来る列挙は絶対にない = ダブりとなる組合せは出てこない ですね
よって、階乗で割る必要がないですね
| → | 枠名がなくても枠の大きさが違えば「別物(区別がある)」 |
| → | 分けはめだ! |
バスケ監督が頭の中で考えています…
選手ABCDEF6人を、4人2人に分けてハンデ戦したら何ゲームできるんだ…
最初の4人を選べば、残りは勝手に決まるから
最初の4人を選ぶことに集中すればいいか…
〈ABCD, vs 残り(EF)〉 の1ゲーム!
次っ!
〈ABCE, vs 残り(DF)〉 の1ゲーム!
・
・
・
最後(15ゲーム目)!
〈CDEF, vs 残り(AB)〉 の1ゲーム!
… 考えどおり!(\({}_6 \mathrm{C }_4\)(×\({}_2 \mathrm{C }_2\)) = 15ゲーム)
組分け (親中)
| (前提) | 枠名がない かつ、 枠の大きさが同じ |
| (処理) | 同じ大きさの枠数の階乗で割る → 〈 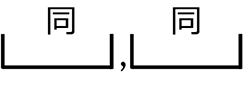 〉 枠の並びにこだわらないということ 〉 枠の並びにこだわらないということ |
「同じ大きさのフレーム数の階乗」ということは、同じ大きさのフレームが
なければ「フレーム数の階乗」で割る必要はないということ
それでは例題です
「組分け」の前提は、「全て異なるものを」「全部または1部使い(選び)ます」(出題では99%「全部使う(分けきる)」ですね)
《 例 》
123456の6人がいます
(1) 部屋Aに3人、部屋Bに3人に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → あり (部屋A、部屋B)(枠の並びにこだわる) |
⇒ 分けはめ
\({}_6 \mathrm{C }_3\)×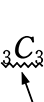
最後の残りの選び方ですね
今後は「×1」や省略している場合があります
= \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\)・1 = 20 通り
(2) 3人、3人に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → なし → 枠の大きさ → 「2つとも同じ」 =「枠の区別なし」 |
⇒ 組分け
∴ \(\large{\frac{{}_6 \mathrm{C }_3}{\color{red}{ 2!}}}\) = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1×2!}}\) = 10 通り
(3) Aに3人、Bに2人、Cに1人 に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → あり (A、B、C) |
⇒ 分けはめ
∴ \({}_6 \mathrm{C }_3\) ×  ×
× 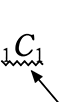
残りの3人から2人を選ぶ 最後の残り
= \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\)・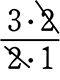 ・1 = 60 通り
・1 = 60 通り
(4) 3人、2人、1人 に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → なし 枠の大きさ → 「異なる」=「枠の区別あり」 |
⇒ 分けはめ
∴ (3)と同じ 60 通り
(5) 2人、2人、2人 に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → なし 枠の大きさ →「3つとも同じ」=「枠の区別なし」 |
⇒ 組分け 〈  ,
,  ,
,  〉
〉
∴ \(\large{\frac{{}_6 \mathrm{C }_2×{}_4 \mathrm{C }_2×1}{\color{red}{3!}}}\) = 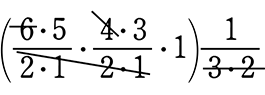 = 15 通り
= 15 通り
(6) 2人、2人、1人、1人 に分ける方法は、何通り?
| → | 元 → 区別あり (人より) |
| → | 個数指定 → あり |
| → | 枠名 → なし 枠の大きさ →「2つ2つで同じ」=「枠の区別部分的になし」 |
⇒ 分けはめ、組分け (〈  ,
,  〉,〈
〉,〈  ,
,  〉)
〉)
∴ \(\large{\frac{{}_6 \mathrm{C }_2×{}_4 \mathrm{C }_2×{}_2 \mathrm{C }_1×1}{\color{red}{2!}×\color{red}{2!}}}\) = 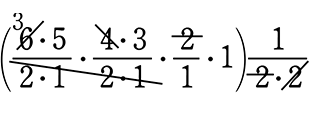 = 45 通り
= 45 通り
何が違うのか、比較しながら解いてみる
同じ意味の問題を2種類並べて見ていきますね
《 例 》
● W異なる
(1)
| ア | 8個の異なる品物を、3人(=異なる3人)に1つずつ分ける方法 |
| イ | 8人(=異なる8人)を、3つの異なる部屋に1人ずつ分ける方法 |
(全く同じ問題です。「品」が「人」、「人」が「部屋」になっただけですね)
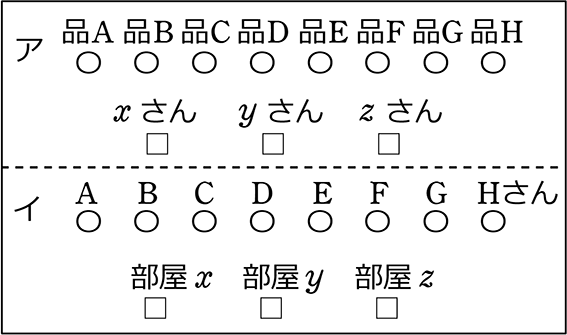
| ・ | W異なる(マスになる方も、選ばれる方も区別がある) → 絶対順列数え系(どちらがマスになっても必ず基準名があるから) → 普通順列系か円順列系か分けはめか重複順列 |
| ・ | 個数指定あり → 「1つずつ/1人ずつ」より |
→ 「1マス限定枠 ( 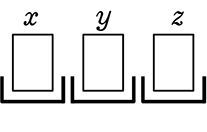 ) 」 → 普通~系
) 」 → 普通~系
| ・ | 「W異なる」「1マス限定枠」より、普通順列系か円順列系 →「円状」的なワードなし → 円順列ではない ⇒ 『普通順列』 |
| ・ | xyz がマス(選ぶ方) |
→ (どちらがマスかな?な時は → 1例シミレーション)
( 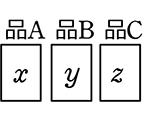 ) or (
) or (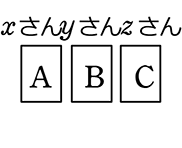 )?
)?
→ DEFが使えるのは… xyz がマスだな
∴ 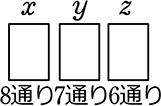 = \({}_8 \mathrm{P }_3\) = 8×7×6 = 336通り
= \({}_8 \mathrm{P }_3\) = 8×7×6 = 336通り
1例:(
(2)
| ア | 8個の異なる品物を、xさんに3個 yさんに3個 zさんに2個ずつ分ける方法 |
| イ | 8人(=異なる8人)を、部屋xに3人 部屋yに3人 部屋zに2人ずつ分ける方法 |

| ・ | W異なる → 絶対順列数え系 → 普通順列系か円順列系か分けはめか重複順列 |
| ・ | 個数指定あり → 「指定枠」発生 → 分けはめ系 → 枠名 → あり → 基準名があるということ → 枠レベルの順列数え ⇒ 『分けはめ』 |
| ・ | 少ない方が枠 → xyz が枠(選ぶ方) |
| (・ | マス → 個数指定のため → 枠内にある →「分ける」より、並びにこだわらない) |
∴ \({}_8 \mathrm{C }_3\)
1例: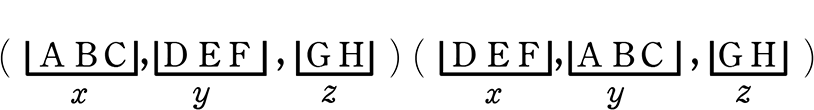
(3)-①
| ア | 8個の異なる品物を、3人(=異なる3人)に分ける方法 ただし、もらえるない人がいてもよい |
| イ | 8人(=異なる8人)を、3つの異なる部屋に分ける方法 ただし、空室があってもよい |

| ・ | W異なる → 絶対順列数え系 → 普通順列系か円順列系か分けはめか重複順列 |
・ 個数指定なし → 「変動枠 (1枠につき1マス 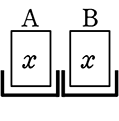 → 出来上がったものごとに後付けで 枠を連結 するということ
→ 出来上がったものごとに後付けで 枠を連結 するということ 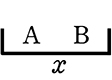 )」 → まずはマスだけで勝負 → 重複~系
)」 → まずはマスだけで勝負 → 重複~系
| ・ | 「W異なる」「変動枠」より ⇒ 『重複順列 (もらえない/空室OK)』 |
・ ABCの方がマス(選ぶ方)
→ (どちらがマスか?な時は → 2マスシミレーション)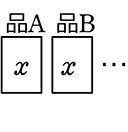 or
or 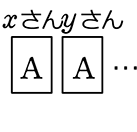 ? → xさんyさんともにAを持つ?!→ ABC がマスだな
? → xさんyさんともにAを持つ?!→ ABC がマスだな
∴ 38 = 94 = 812 = 6561通り
1例:(
(3)-②
| ア | 8個の異なる品物を、3人(=異なる3人)に分ける方法 ただし、少なくとも1個はもらえる |
| イ | 8人(=異なる8人)を、3つの異なる部屋に分ける方法 ただし、少なくとも1人は入る |

同様な絞り込みで
⇒ 『重複順列 (もらえない人/空室はNG)』 → 場合分け
重複順列のもらえない/空室NGは「場合分け」になります!!難です、高校入試ではまず出題されないと思われます
(考え方) 「少なくとも」とくれば、「余事象」ですね!
〈1個はもらえる/1人は入る〉 = 全通り -〈もらえない人がいる/入らない部屋がある〉
 = 全通り-
= 全通り- 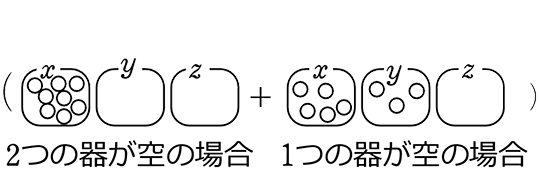
= 全通り-みんなが同じものを選んだ場合 (結果:もらえない人2人/空室2部屋)-みんなが2種類のどちらかを選んだ場合(結果:もらえない人1人/空室1部屋)
ⅰ) もらえない2人/空室2部屋
みんなx を選んだ 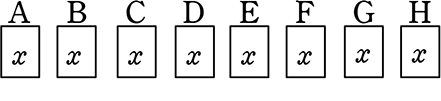 → 1通り
→ 1通り
みんなy を選んだ 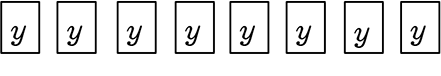 → 1通り
→ 1通り
みんなz を選んだ  → 1通り
→ 1通り
= 計3通り
ⅱ) もらえない1人/空室1部屋
・みんなが x か y を選んだ (結果 z のみ空 の場合) - みんながx を選ぶ1通り - みんながy を選ぶ1通り みんながx、またはみんながy を選ぶとⅰと同じく空が2つになってしまいますので = 28-1-1 = 256-2 = 254 通り(結果z のみ空)
- みんながx を選ぶ1通り - みんながy を選ぶ1通り みんながx、またはみんながy を選ぶとⅰと同じく空が2つになってしまいますので = 28-1-1 = 256-2 = 254 通り(結果z のみ空)
・同様に、みんなが x か z を選んだ(結果y のみ空) → 254 通り
・同様に、みんなが y か z を選んだ(結果x のみ空) → 254 通り
∴ 空が〈1人/1部屋〉の場合 254+254+254 = 計762 通り
∴ 何かしらの空がある場合 = ⅰ+ⅱ = 3+762 = 合計765 通り
∴ 少なくとも1個はもらえる/少なくとも1人は入る 分け方は
6561-765 = 5796 通り
1例:(
● シングル異なる(バージョン1)
(4)-①
| ア | 8個の区別のない品物(8個のみかん等)を、3人(=異なる3人)に分ける方法 ただし、もらえない人がいてもよい |
| イ | 8人を区別しない(人を区別しないとは変な話ですが)で、3つの異なる部屋に分ける方法 ただし、空室があってもよい |
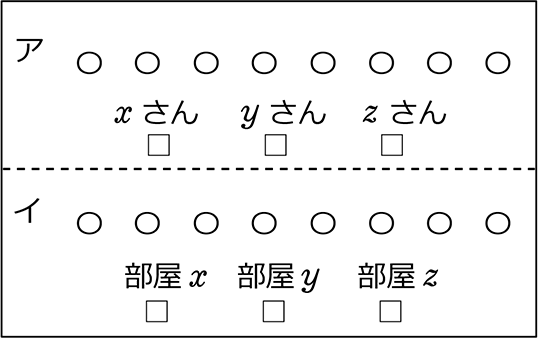
| ・ | シングル異なる → 順列系か組合せ系か不明(どちらがマスかによる) |
| ・ | 個数指定なし → 「変動枠」→ 重複系 |
・ マスシミレーション
→ 〈 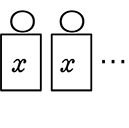 〉 or (
〉 or ( 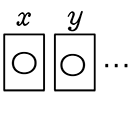 ) ? → (〇〇〇) 〇が3並んでも意味がない → 〇達がマスだな
) ? → (〇〇〇) 〇が3並んでも意味がない → 〇達がマスだな
| ⇒ 『重複組合せ(もらえない/空室OK)』 |
cf
「重複順列」のある3場面
(  )や
)や
( 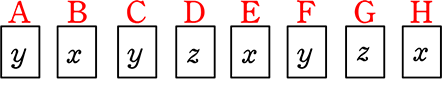 )や
)や
( 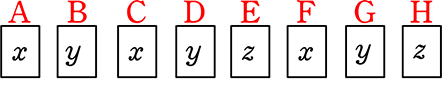 )は、
)は、
どれも x 3つ、y 3つ、z 2つ ですが、
「マス名がある」=「並びにこだわる」ので別物ですね!3通りですね!
ですが、「重複組合せ」では、マス達に名前がない(区別しない)のですから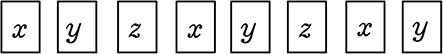 も
も も
も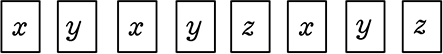 も
も
結局は
〈 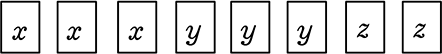 〉と自動整列されて1通りに集約されてしまいますね ⇒ 重複組合せ
〉と自動整列されて1通りに集約されてしまいますね ⇒ 重複組合せ
というわけで、
重複順列÷かぶり= 重複組合せ
のはずですが、かぶりを求めるために膨大な場合分けが必要になりますね
そこで、「重複組合せ」には、よい考え方がありましたね !!
| ① | 空がOKな場合 → 「仕切り棒(┃)」 |
| ② | 空がNGな場合 → 「すき間三角(∧)」 または、「先配り」 でしたね |
∴ 今回は 「空がOK」ですので、「仕切り棒(┃)タイプ」!
3つに分けるので、仕切り棒は、2本
〇〇┃〇〇〇〇┃〇〇
\({}_{8+2} \mathrm{C }_2\) = \({}_{10} \mathrm{C }_2\) = \(\large{\frac{10\ \cdot \ 9}{2\ \cdot \ 1}}\) = 45 通り
1例:〈
(4)-②
| ア | 8個の区別のない品物(8個のみかん等)を、3人(=異なる3人)に分ける方法 ただし、1つはもらえる |
| イ | 8人を区別しない(人を区別しないとは変な話ですが)で、3つの異なる部屋に分ける方法 ただし、1人は入る |

・ 同様な絞り込みで
⇒「重複組合せ(もらえない/空室NG)」
・ 空がNGな場合 → すき間三角∧
→ 3つに分けるので、∧を2つ選べばよいですね
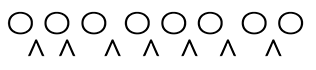
確かに、どの2つの∧を選んでも、
1つは入りますね!
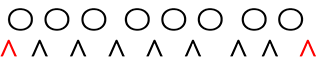
はダメですね! 両端の2つを選んだ場合に
xさん/部屋x、zさん/部屋zが空ですね
∴ 〇より外側に∧は作らない
∧の数は、(〇-1)個 ですね
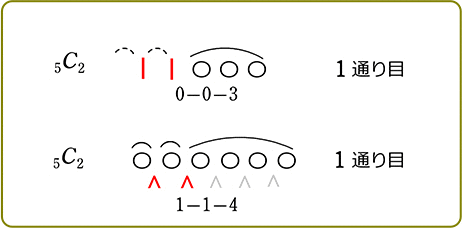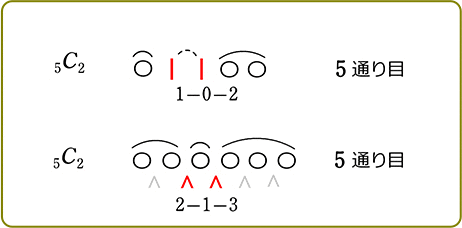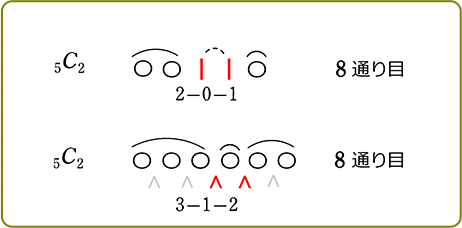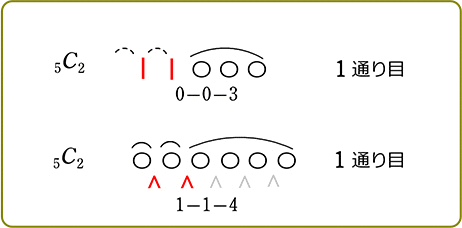
∴ \({}_7 \mathrm{C }_2\) = \(\large{\frac{7\ \cdot \ 6}{2\ \cdot \ 1}}\) = 21 通り
または、あらかじめ3人/3部屋に、1つずつ/1人ずつ 分配しておいて、残りの5個/5人(← 8-3)の〇達で仕切り棒┃でもOKでしたね
∴ \({}_{5+2} \mathrm{C }_2\) = \({}_7 \mathrm{C }_2\) (上と全く同じですね) = 21通り
1例:〈
(5)
| ア | 8個の区別のない品物(8個のみかん等)を、xさんに3個 yさんに3個 zさんに2個分ける方法 |
| イ | 8人を区別しない(人を区別しないとは変な話ですが)で、部屋x に3人 部屋y に3人 部屋z に2人に分ける方法 |

・ 個数指定あり、枠名あり ⇒ 分けはめ
ですが、
枠内の並びが1通りということ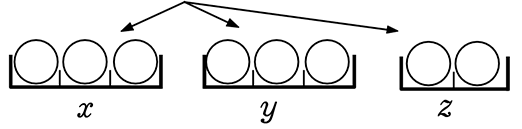 = (1通り, 1通り, 1通り) = 1通り
= (1通り, 1通り, 1通り) = 1通り
⇒ 重複組合せでも考えられますね
〈xxx yyy zz〉 の1通りしかない(重複組合せのある1場面)
1例しかありませんが:
( 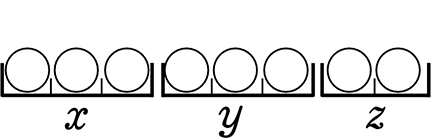 ) または 〈xxx yyy zz〉
) または 〈xxx yyy zz〉
● シングル異なる(バージョン2)
(6)
| ア | 8個の異なる品物を、区別のない3人(人を区別しないとは変な話ですが)に1個ずつ分ける方法 |
| イ | 8人(=異なる8人)を、区別のない3部屋に1人ずつ分ける方法 |
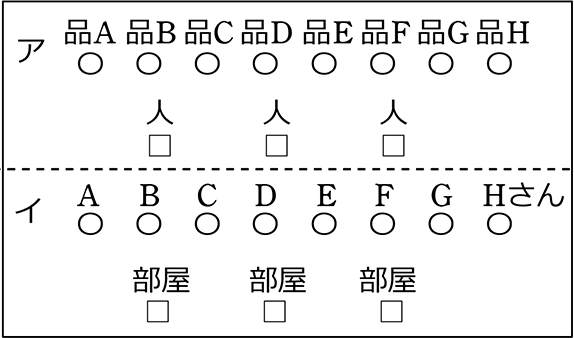
| ・ | シングル異なる → 順列系か組合せ系か不明(どちらがマスかによる) |
| ・ | 個数指定あり → 「1個ずつ・1人ずつ」より →「1マス限定枠 ( 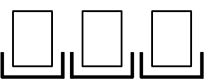 ) 」 → 普通~系 ) 」 → 普通~系 |
| ・ | マス → シミレーション |
( 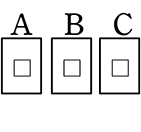 ) or〈
) or〈 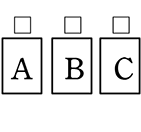 〉→ □が3つ並んでも意味がない … □がマスだな
〉→ □が3つ並んでも意味がない … □がマスだな
| ・ | マス名がない → マスの並びにこだわらない ⇒ 『普通組合せ』 |
∴ 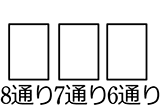 ÷3! = \({}_8 \mathrm{C }_3\) = \(\large{\frac{8×7×6}{3×2×1}}\) = 56通り
÷3! = \({}_8 \mathrm{C }_3\) = \(\large{\frac{8×7×6}{3×2×1}}\) = 56通り
1例:〈 A, B, F 〉
(7)
| ア | 8個の異なる品物を、区別のない3人に3個、3個、2個ずつ分ける方法 |
| イ | 8人(=異なる8人)を、区別のない3部屋に3人、3人、2人に分ける方法 |

| ・ | シングル異なる → 順列系か組合せ系か不明(どちらがマスかによる) |
| ・ | 個数指定あり → 「指定枠」 → 分けはめ系 |
| ・ | 枠 → 少ない方が枠 → □が枠(選ぶ側) → 枠名がない → 同じ大きさの枠は並びにこだわらない ⇒ 『分けはめ』『組分け』 |
| (・ | マス → 個数指定のため → 枠内にある →「分ける」より、並びにこだわらない) |
∴ 2枠が同じ大きさより → \(\large{\frac{{}_8 \mathrm{C }_3×{}_5 \mathrm{C }_3×{}_2 \mathrm{C }_2}{2!}}\) = \(\large{\frac{8\ \cdot \ 7\ \cdot \ 6×5\ \cdot \ 4\ \cdot \ 3}{3\ \cdot \ 2\ \cdot \ 1×3\ \cdot \ 2\ \cdot \ 1×2\ \cdot \ 1}}\) = 280通り
1例:(〈 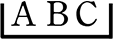 ,
, 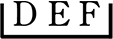 〉,
〉,  )
)
| ア | 8個の異なる品物を、区別のない3人(人を区別しないとは変な話ですが)に分ける(3組に分ける)方法 ただし、少なくとも1つはもらえる |
| イ | 8人(=異なる8人)を、区別のない3部屋に分ける(3組に分ける)方法 ただし、少なくとも1人は入る |

| ・ | シングル異なる → 同じものを含む順列系か組合せ系か不明(どちらがマスかによる) |
・ 個数指定なし → 「変動枠」 → 重複系
⇒ 重複組合せ? → ~組合せなので区別のない方がマス
シミレーション 〈
⇒ では重複順列? → ~順列なので区別のある方がマス
シミレーション (
・ 枠名はないけど3つの枠はある → 「個数指定」があれば、分けはめ・組分けなのに……
考え方1)
個数指定のバリエーションを自分で考えて「分けはめ・組分け」とする
→ 3つの枠になる個数指定は、

の5パターン
枠名がない → 枠単位の組み合わせ数えなので〈3マス3マス2マス〉などは⑤〈2マス3マス3マス〉のダブりとなりますね → 先頭枠 ≦ 中枠 ≦ 右枠 と基準づけて列挙すればダブりを防げますね
∴ 個数指定のパターンはこの5パターン
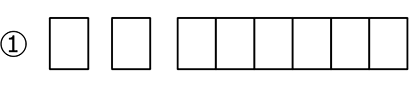
\(\large{\frac{{}_8 \mathrm{C }_1×{}_7 \mathrm{C }_1×{}_6 \mathrm{C }_6}{2!}}\) = \(\large{\frac{8\ \cdot \ 7\ \cdot \ 1}{2\ \cdot \ 1}}\) = 28 通り
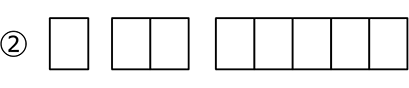
\({}_8 \mathrm{C }_1\)×\({}_7 \mathrm{C }_2\)×\({}_5 \mathrm{C }_5\) = 8・21・1 = 168 通り
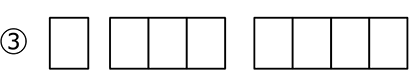
\({}_8 \mathrm{C }_1\)×\({}_7 \mathrm{C }_3\)×\({}_4 \mathrm{C }_4\) = 8・35・1 = 280 通り

\(\large{\frac{{}_8 \mathrm{C }_2×{}_6 \mathrm{C }_2×{}_4 \mathrm{C }_4}{2!}}\) = \(\large{\frac{28\ \cdot \ 15\ \cdot \ 1}{2\ \cdot \ 1}}\) = 210 通り

\(\large{\frac{{}_8 \mathrm{C }_2×{}_6 \mathrm{C }_3×{}_3 \mathrm{C }_3}{2!}}\) = \(\large{\frac{28\ \cdot \ 20\ \cdot \ 1}{2\ \cdot \ 1}}\) = 280 通り
∴ 28+168+280+210+280 = 966 通り
1例:〈 A, D, BCEFGH 〉
考え方2)
□に名前を付けて(区別をつけて)「重複順列」とする、その後〈人名/部屋名〉を除く処理(かぶり排除)をする
(3)-② 重複順列(1つはもらえる/1人は入る)の解は「5796通り」でしたね
枠名をなくすために、3つの枠分の「かぶり」である3! で割れば「組分け」と同じ効果ですね
例えば、
上のパターン の28通りのうちの1つに
の28通りのうちの1つに 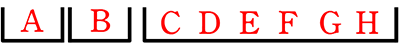 があります。
があります。
重複順列の  を
を 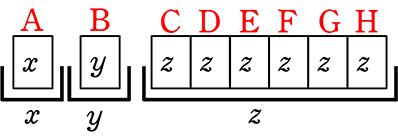 まとまった枠に入ったとみなし(個々の枠を連結し)、見やすくした
まとまった枠に入ったとみなし(個々の枠を連結し)、見やすくした 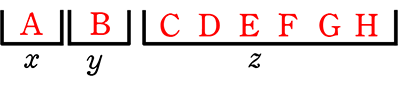 から枠名をなくしたものは、
から枠名をなくしたものは、 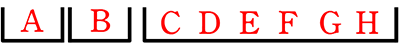 と同じですね
と同じですね
そして重複順列はあらゆるパターンを持っていますので、中には




も含まれています
ということは、枠x, y, z の並びにこだわらない数え方をすれば枠名がなくなるということ
⇒ x, y, z の枠数の階乗でわればよい → 3! で割ればよいということですね!
重複順列のどこかにある  などは、枠を基準にすれば
などは、枠を基準にすれば 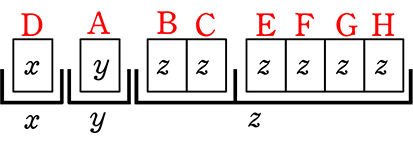 となりますね(枠内はちゃんとアルファベット順ですねBC…)
となりますね(枠内はちゃんとアルファベット順ですねBC…)
これも3!で割れば  の28通りのうちの1つ
の28通りのうちの1つ  ですね → 安心して枠数の階乗で割ってOK
ですね → 安心して枠数の階乗で割ってOK
∴ \(\large{\frac{5796}{3!}}\) = 966 通り
1例は同じく:〈 A, D, BCEFGH 〉
(8)-②
| ア | 8個の異なる品物を、区別のない3人(人を区別しないとは変な話ですが)に分ける(3組に分ける)方法 ただし、もらえない人がいてもよい |
| イ | 8人(=異なる8人)を、区別のない3部屋に分ける(3組に分ける)方法 ただし、1人も入らない部屋があってもよい |

考え方1)
同様に、個数指定のパターンをリストアップして「分けはめ ・ 組分け」とすると、
上のパターン+1人占めパターン+2人占めパターン
\({}_8 \mathrm{C }_8\) = 1 通り(空が2つの場合)

\({}_8 \mathrm{C }_1\)×\({}_7 \mathrm{C }_7\) = 8×1 = 8 通り
\({}_8 \mathrm{C }_2\)×\({}_6 \mathrm{C }_6\) = 28×1 = 28 通り
\({}_8 \mathrm{C }_3\)×\({}_5 \mathrm{C }_5\) = 56×1 = 56 通り
\(\large{\frac{{}_8 \mathrm{C }_4×{}_4 \mathrm{C }_4}{2!}}\) = \(\large{\frac{70\ \cdot \ 1}{2\ \cdot \ 1}}\) = 35 通り
∴ (7)-①の966+ 1+8+28+56+35 = 1094 通り
1例:
〈 ABCDEFG 〉〈 D, ABCEFGH 〉〈 A, D, BCEFGH 〉
考え方2)
同様に、区別をつけて重複順列(1つもらえない/空室OK)の解(6561通り)から、かぶりを除く方法ですね
ただし、〈もらえない人/空室あり〉の部分は、単純に「3!」で割れないですね、
(もらえない2人/空室2つ)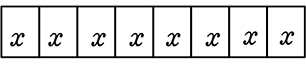 1通り
1通り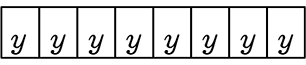 1通り
1通り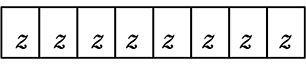 1通り
1通り
ただの「3」で割って、1通りですね
→ 重複順列の列挙の中に、2人もらえない/空室2つを表す  はあっても、
はあっても、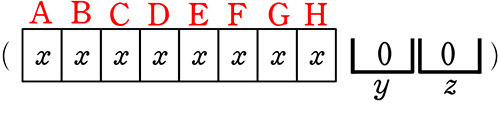 のようなものはないですね
のようなものはないですね
∴ 重複順列には元々1マスにつき1つの枠しかなく、
マスがx, y, z を選んだ後に後付けで枠を連結とみなしているので
「ある、空、空」は、「文字数から1つを並べた通り数」
すなわち、今回なら \({}_3 \mathrm{P }_1\) = 3通りで存在している
∴ 最終段階として、x, y ,z の区別をなくすには \({}_3 \mathrm{P }_1\)で割ればよいということですね
同様に、
(1人もらえない/空室1つ)を表すものは などですね
などですね のようなものはないですね
のようなものはないですね
∴ 「ある、ある、空」は、「文字数から2つを並べた通り数」
すなわち、今回なら \({}_3 \mathrm{P }_2\) = 6通りで存在している
例えば、 の8通りの内の1つ 〈A, BCDEFGH〉になるものは
の8通りの内の1つ 〈A, BCDEFGH〉になるものは
(
(x, zzzzzzz) (z, xxxxxxx)
(y, zzzzzzz) (z, yyyyyyy) の6通りで存在
∴ 最終段階として、x, y ,z の区別をなくすには \({}_3 \mathrm{P }_2\)で割ればよいということですね
という訳で
\(\large{\frac{2つ空のとき}{{}_3 \mathrm{P }_1}}\)+\(\large{\frac{1つ空の時}{{}_3 \mathrm{P }_2}}\)+\(\large{\frac{空がない時}{3!}}\)
= \(\large{\frac{3}{3}}\)+\(\large{\frac{762}{6}}\)+\(\large{\frac{(6561-3-762)}{6}}\)
= 1+\(\large{\frac{6561-3}{6}}\)
= 1+1093
= 1094 通り
1例は同じく:
〈 ABCDEFG 〉〈 D, ABCEFGH 〉〈 A, D, BCEFGH 〉
● どちらも区別がない
(9)-①
| ア | 8個の区別のない品物を、区別のない3人(人を区別しないとは変な話ですが)に分ける(3組に分ける)方法 ただし、もらえない人がいてもよい |
| イ | 区別のない8人(人を区別しないとは変な話ですな)を、区別のない3部屋に分ける(3組に分ける)方法 ただし、1人も入らない部屋があってもよい |
もうここまでくると、「列挙」するしかないですね!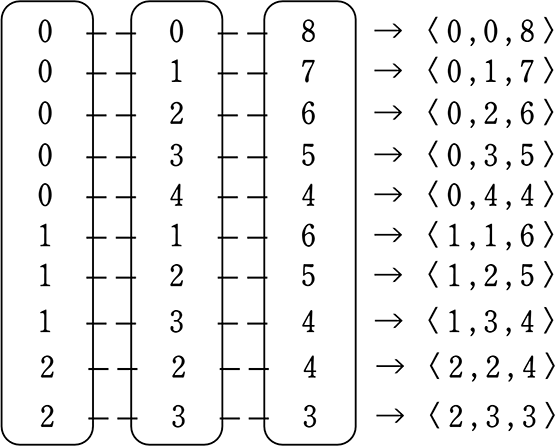
∴ 10 通り
(9)-②
| ア | 8個の区別のない品物を、区別のない3人(人を区別しないとは変な話ですが)に分ける(3組に分ける)方法 ただし、1つはもらえる |
| イ | 区別のない8人(人を区別しないとは変な話ですな)を、区別のない3部屋に分ける(3組に分ける)方法 ただし、1人は入る |
→ (9)-① の答えから「0」を含むものを除けばよいですね
∴ 5 通り

ただただ3つに分ける
(異なる)8人を、ただ3つのグループに分ける方法は 何通り?
という、「入らない部屋OK」「入らない部屋NG」を
示してくれていない「個数指定もない」問題に出会った時は、
どのようにすればよいのでしょうか?
当然に、
→「入らない部屋NG」で「枠パターンを制作」
→「かぶり処理(組分け)」
で考えていくのかなと感じますね (上の(8)-①の問題)

なぜなら、「入らない部屋」があるということは・・・
「2つのグループ」や「1つのグループ(かたまり?)」があるということで
それは、問題文の「3つのグループに」に分けていない!とも考えられるからです。
この点、「入らない部屋OK」「入らない部屋NG」を
示していない問題に出会ったことはありませんが、
もし出会ってしまった場合は・・・・
① 賭けに出て…「入らない部屋NG」で進める
② 無難に…「0人のグループOK」「0人のグループNG」の場合分けでいく
やはり、「組分け」は、
「区別を作る」→「区別をとる」という原則のような
ものがありますので…②なのかな…
出会ったら報告しますね
c 同じものを含む組合せ
同じものを含む場合は、もう単純に「C」は使えせんね!
ご想像通り …「場合分け →考えられるパターンは?」となります
《 例 》
aaabbc
● 1枚を取り出す「組合せ」は、何通り? マスには abcの3種類全て可能性がありますね
マスには abcの3種類全て可能性がありますね
∴ 3通り 〈a〉〈b〉〈c〉
〇 1枚を取り出す「順列」は、何通り? ∴ (同様)に 3通り (a)(b)(c)
∴ (同様)に 3通り (a)(b)(c)
● 2枚を取り出す「組合せ」は、何通り?
aaabbc
考えられるマスパターンは ←(場合分け)
① 2枚同じ 
← 3枚あるaと2枚あるbに可能性がありますね
→ 2通り 〈a a〉〈b b〉
② バラバラ 
← abcの3文字から2つ選ぶことと同じですね
→ 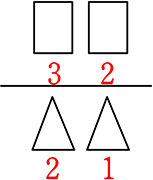 = \({}_3 \mathrm{C }_2\) = \(\large{\frac{3\ \cdot \ 2}{2\ \cdot \ 1}}\) = 3 通り 〈a b〉〈a c〉〈b c〉
= \({}_3 \mathrm{C }_2\) = \(\large{\frac{3\ \cdot \ 2}{2\ \cdot \ 1}}\) = 3 通り 〈a b〉〈a c〉〈b c〉
場合分け←和の法則でしたね ∴ 2通り+3通り= 5 通り
〇 2枚を取り出す「順列」は、何通り?
考えられるマスパターンは ←(場合分け)
① 2枚同じ 
← 3枚ある a と2枚あるbに可能性がありますね
→ 2通り(a a)(b b)
② バラバラ 
← abcの3文字から2つ選び+並べることと同じですね
→ \({}_3 \mathrm{C }_2\)×2!= \({}_3 \mathrm{P }_2\)= 3・2= 6 通り
(a b)(a c)(b a)(b c)(ca)(c b)
∴ 2 通り+6 通り= 8 通り

正しい順序は「PからC」? 「CからP」?
「日本語の流れ」や「イメージ」から言いますと、CからPが自然ですね
例えば
・abcdef から3個「
・abcdefから3個「
\({}_6 \mathrm{C }_③\)×3! = 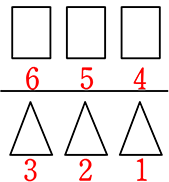 ×
×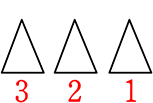 = \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\)×3・2・1 = \({}_6 \mathrm{P }_③\)
= \(\large{\frac{6\ \cdot \ 5\ \cdot \ 4}{3\ \cdot \ 2\ \cdot \ 1}}\)×3・2・1 = \({}_6 \mathrm{P }_③\)
\({}_6 \mathrm{P }_③\)÷3!=  ×
×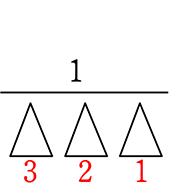 = 6・5・4×\(\large{\frac{1}{3\ \cdot \ 2\ \cdot \ 1}}\)= \({}_6 \mathrm{C }_③\)
= 6・5・4×\(\large{\frac{1}{3\ \cdot \ 2\ \cdot \ 1}}\)= \({}_6 \mathrm{C }_③\)
確かに、教科書の手順上、「順列」から学びますし、
計算上、「異なるものを選ぶ」ために番号をつける→「順列」が先に出現→だぶりで割ると「組合せ」
すなわち、Pに何かをして→ Cですね
ですが
「場合の数」の理解が進んできたら、「C」から考えていく ということを
おすすめしたいかなと思います
| 選ぶ (C) | |
| ↓ | |
| 並びにこだわるのかこだわらないのか? | |
 |
|
| こだわる | こだわらない |
| ↓ | ↓ |
| 掛ける 〇!(P) | そのまま (C) |
● 3枚を取り出す「組合せ」は、何通り?
aaabbc
考えられるマスパターンは
① 3枚同じ
→ aのみ可能性あり → \({}_1 \mathrm{C }_1\) = 1 通り 〈a a a〉
② 2枚同じ
・前マスは aかbのみ可 → \({}_2 \mathrm{C }_1\) → 2 通り
・後マスは 残った2種類から1つ → \({}_2 \mathrm{C }_1\) → 2 通り
よって、 \({}_2 \mathrm{C }_1\)×\({}_2 \mathrm{C }_1\) = 4 通り 〈aab〉〈aac〉〈bba〉〈bbc〉
③ バラバラ
→ \({}_3 \mathrm{C }_3\) = 1 通り 〈abc〉
∴ 1通り+4通り+1通り = 6 通り
〇 3枚を取り出す「順列」は、何通り?
→ おおよそ、上のC×〇!でP(順列)ですが…
① \({}_1 \mathrm{C }_1\)×1! = 1 通り (aaa)
②
さすがに、CからPを求めましょうと言いましても、
C自体が段階を踏んでますので、全体像に戻りまして、 で同じものを2つ含む順列は? ですね!
で同じものを2つ含む順列は? ですね!
→ 4通り×\(\large{\frac{3!}{2!}}\) = 4通り×3通り = 12 通り
〈aab〉×\(\large{\frac{3!}{2!}}\) +〈aac〉×\(\large{\frac{3!}{2!}}\) +〈bba〉×\(\large{\frac{3!}{2!}}\) +〈bbc〉×\(\large{\frac{3!}{2!}}\)
③ \({}_3 \mathrm{C }_3\)×3! = 6 通り 〈abc〉×3!
∴ 1通り+12通り+6通り = 19通り
● 4枚を取り出す「組合せ」は、何通り?
aaabbc
考えられるマスパターンは
① 3枚同じ
・前マスは aのみ可 → 1 通り
・後ろマスは → 残った2種類から1つ → \({}_2 \mathrm{C }_1\) → 2 通り
よって、\({}_1 \mathrm{C }_1\)×\({}_2 \mathrm{C }_1\) = 1×2 = 2 通り 〈aaab〉〈 aaac〉
② 2枚同じ、次も2枚同じ
・前マスは aかbのみ可 → \({}_2 \mathrm{C }_1\) → 2 通り
・後マスは 残った1種類から1つ → \({}_1 \mathrm{C }_1\) → 1 通り
よって、\(\large{\frac{{}_2 \mathrm{C }_1×{}_1 \mathrm{C }_1}{\color{red}{ 2!}}}\) = 1 通り 〈aabb〉
そもそもは4文字の組合せですので の中の並びはこだわりませんね
の中の並びはこだわりませんね
すなわち、「組分け」の考え方をお借りします
フレームの大きさが同じ場合は要注意です!
③ 次はバラバラ
・前マスは aかbのみ可 → \({}_2 \mathrm{C }_1\) → 2 通り
・後マスは \(\large{\frac{{}_2 \mathrm{C }_1×{}_1 \mathrm{C }_1}{\color{red}{2!}}}\) = 1 通り
よって、\({}_2 \mathrm{C }_1\)×\(\large{\frac{{}_2 \mathrm{C }_1×{}_1 \mathrm{C }_1}{\color{red}{2!}}}\)= 2通り×1通り= 2 通り 〈aabc〉〈
④ 全部バラバラ は…ないですね→ 0 通り
は…ないですね→ 0 通り
∴ 2通り+1通り+2通り+0通り = 5 通り
※ 同じ大きさの枠を個別に見ると、「組分け」に注意となりますが
同じ大きさのフレームをまとめて見てあげると、「組合せ」だけで大丈夫ですね
というわけで、再度!
aaabbc
● 4枚を取り出す「組合せ」は、何通り?
考えられるフレームパターンは
① 3枚同じ
・前マスは aのみ可 → 1 通り
・後ろマスは → 残った2種類から1つ → \({}_2 \mathrm{C }_1\) → 2 通り
よって、\({}_1 \mathrm{C }_1\)×\({}_2 \mathrm{C }_1\) = 1×2 = 2 通り 〈aaab〉〈 aaac)
② 2枚同じ、次も2枚同じ
・2か所に、候補 a, b を入れる → \({}_2 \mathrm{C }_2\) = 1 通り 〈aabb〉
当然と言えば当然ですね!
元々は  4枚の「組合せ」を考えていたのですから!
4枚の「組合せ」を考えていたのですから!
2つ2つに勝手に分けて考えたのは自分ですから! と
と は、かぶりですね!
は、かぶりですね!
③ 次はバラバラ
・前マスは aかbのみ可 → \({}_2 \mathrm{C }_1\) → 2 通り
・後ろマス2つは、 2か所に、「残りの2つ」を入れる → \({}_2 \mathrm{C }_2\) = 1通り
よって、\({}_2 \mathrm{C }_1\)×\({}_2 \mathrm{C }_2\) = 2 通り 〈aabc〉〈bbac〉
④ 全部バラバラ は…ないですね→ 0 通り
は…ないですね→ 0 通り
∴ 2通り+1通り+2通り+0通り = 5 通り
〇 4枚を取り出す「順列」は、何通り?
①  で
で
例〈aaab〉
3枚同じものを含む順列は→ \(\large{\frac{4!}{3!}}\)= 4 通り
→ 4通りが2通り←上の組合せで求めたものある
= 4×2 = 8 通り
②  で
で
例〈aabb〉
2枚、2枚で同じものを含む順列は → \(\large{\frac{4!}{2!\ \cdot \ 2!}}\) = 6 通り
→ 6通りが1通りある = 6×1 = 6 通り
③  で
で
例〈aabc〉
2枚同じものを含む順列は → \(\large{\frac{4!}{2!}}\) = 12 通り
→ 12通りが2通りある = 12×2 = 24 通り
∴ 8+6+24 = 38通り
● 5枚を取り出す「組合せ」は、何通り?
aaabbc
考えられるマスパターンは
①
・前マスは aのみ可 → \({}_1 \mathrm{C }_1\)
・後マスは bのみ可 → \({}_1 \mathrm{C }_1\)
よって、 1×1 = 1 通り 〈aaabb〉
②
・前マスは aのみ可 → \({}_1 \mathrm{C }_1\)
・中,後2マスは 2か所に「残りの2つ」を入れる → \({}_2 \mathrm{C }_2\)
よって、 1×1 = 1 通り 〈aaabc〉
③
・前,中2マスは 2か所に、 候補 a,bを入れる → \({}_2 \mathrm{C }_2\) → 1 通り
・後マスは残りの c ←余った aは入れてはいけない
aは先に「2つ使う」として使用済み→ aabbaは①と同じ! →\({}_1\mathrm{C }_1\)
よって \({}_2 \mathrm{C }_2\)×\({}_1 \mathrm{C }_1\) = 1×1 = 1 通り 〈aabbc〉
∴ 1+1+1 = 3 通り
最後の1個を残して、他の全部を「選ぶ」ということは
「他の全部」の中に同じものが含まれていても、いなくても
「1通り」×「種類数」ですね
なぜなら、\({}_6 \mathrm{C }_5\) = \({}_6 \mathrm{C }_1\) → 1つを選ぶことと同じ
aaabbcから「1つ」を選ぶことは、 「文字の種類数通り」 → 3通りですね
〇 5枚を取り出す「順列」は、何通り?
① 〈aaabb〉の順列 = \(\large{\frac{5!}{3!\ \cdot \ 2!}}\) = 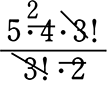 = 10 通り
= 10 通り
② 〈aaabc〉の順列 = \(\large{\frac{5!}{3!}}\) = 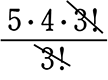 = 20 通り
= 20 通り
③ 〈aabbc〉の順列 = \(\large{\frac{5!}{2!\ \cdot \ 2!}}\) = 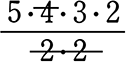 = 30 通り
= 30 通り
∴ 10+20+30 = 60 通り
aaabbc
● 6枚を取り出す「組合せ」は、何通り? → 1 通り ですね
〇 6枚を取り出す「順列」は、何通り?
aaabbcの「同じものを含む全順列」ですね
→ \(\large{\frac{6!}{3!\ \cdot \ 2!}}\) = 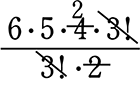 = 60 通り
= 60 通り
《 例 》
a,a,a, b,b,b c,c, d,e から4つを取り出す 組合せは何通り?
→ 同じものを含む → 何個かを取り出す → 場合分け
考えられるマスパターンは
①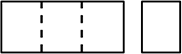
・前マスは 1か所に a, bの可能性 → \({}_2 \mathrm{C }_1\) = 2 通り
・後マスは 1か所に残りの4つが候補→ \({}_4 \mathrm{C }_1\)通り = 4 通り
よって、2×4 = 8 通り
②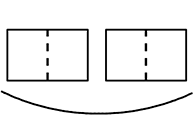
・2か所に a b c の可能性 → \({}_3 \mathrm{C }_2\) = 3 通り
③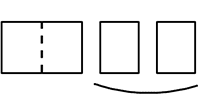
・前マスは 1か所に a b c の可能性 →\({}_3 \mathrm{C }_1\) = 3 通り
・中、後ろ2マスは 2か所に残りの4つが候補 → \({}_4 \mathrm{C }_2\) = 6 通り
よって、3×6 = 18 通り
④
4か所にa b c d e の5つが候補 → \({}_5 \mathrm{C }_4\) = 5 通り
∴ 8+3+18+5 = 34 通り
場合の数まとめ
は難です、高校入試でまず出ることはありません
| 元 (n) | 選び方 | マスの並びに | 枠 | 名前 |
|---|---|---|---|---|
|
全て異なる
ex. |
全部を
(使う) |
マスの並びに |
1枠につき1マス |
全順列 (\({}_n \mathrm{ P }_n\) = \(n!\) ) |
| 円順列 ( \((n-1)!\) or \(\large{\frac{{}_n \mathrm{ P }_n}{n}}\)) | ||||
| じゅず順列 (\(\large{\frac{円順列}{2}}\)) | ||||
|
整理すると結果 |
選ばれないOKな 重複順列 (\(n^r\)) |
|||
| 選ばれないNGな 重複順列 (場合分け) |
||||
|
マスの並びに |
全部を選ぶ組合せ (\({}_n \mathrm{ C }_n\) = \(1\)) | |||
|
整理すると結果 |
||||
|
・枠の大きさ指定あり |
|
|||
|
・枠の大きさ指定あり |
||||
|
1部を
(取り出す) |
マスの並びに |
1枠につき1マス
|
(普通の) 順列 (\({}_n \mathrm{ P }_r\)) |
|
|
マスの並びに |
1枠につき1マス
|
(普通の) 組合せ (\({}_n \mathrm{ C }_r\)) |
||
|
同じものを
ex. |
全部を
(使う) |
マスの並びに |
同じものを含む |
|
|
マスの並びに |
||||
|
1部を
(取り出す) |
マスの並びに |
|||
|
マスの並びに |
| 元 (n) | 選び方 | マスの並びに | 名前 | 枠 |
|---|---|---|---|---|
|
全て異なる
ex. |
全部を
(使う) |
マスの並びに |
全順列 (\({}_n \mathrm{ P }_n\) = \(n!\) ) |
1枠につき1マス |
| 円順列 ( \((n-1)!\) or \(\large{\frac{{}_n \mathrm{ P }_n}{n}}\)) | ||||
| じゅず順列 (\(\large{\frac{円順列}{2}}\)) | ||||
| 選ばれないOKな 重複順列 (\(n^r\)) |
整理すると結果 |
|||
| 選ばれないNGな 重複順列 (場合分け) |
||||
|
マスの並びに |
全部を選ぶ組合せ (\({}_n \mathrm{ C }_n\) = \(1\)) | |||
|
整理すると結果 |
||||
|
|
・枠の大きさ指定あり |
|||
|
・枠の大きさ指定あり |
||||
|
1部を
(取り出す) |
マスの並びに |
(普通の) 順列 (\({}_n \mathrm{ P }_r\)) |
1枠につき1マス
|
|
|
マスの並びに |
(普通の) 組合せ (\({}_n \mathrm{ C }_r\)) |
1枠につき1マス
|
||
|
同じものを
ex. |
全部を
(使う) |
マスの並びに |
同じものを含む
・全順列 (\(\large{\frac{n!}{かぶり!×かぶり!}}\)) |
|
|
マスの並びに |
||||
|
1部を
(取り出す) |
マスの並びに |
同じものを含む順列 (場合分け) |
||
|
マスの並びに |
同じものを含む組合せ (場合分け) |
「場合の数」のお話はここまでですが、
かなり長くなってしまいましたね!
中学生には「難しい」と感じたと思いますが、
あえて「小学、中学レベルの場合の数」と「高校レベルの場合の数」の中間レベルのお話をさせていただきました
そうすることで、「2つ効果」があると期待したからです
| ① | 「小学、中学レベルの場合の数」が簡単に感じる |
| ② | 高校生になった時、すんなりと「高校レベルの場合の数」に入っていける |
②に関しては、「場合の数」の難しさレベルが「小、中」と「高校」では
ギャップが大きすぎると感じていたからです。
「中間レベル」が必要では?と感じていたのでした!!
頑張っていきましょう!
その他の問題は、「問題集」で !!