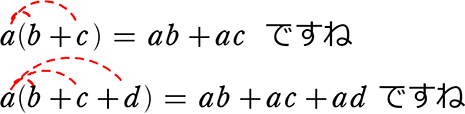| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 正の数・負の数 | (2) 文字を用いた式 | (3) 一元一次方程式 |
正の数・負の数
ア 正の数と負の数の必要性と意味
(登場人物)
 神 神 | : | はるか上空から、「自然の道理」でものを見る |
.png) 人間 人間 | : | 地上で、「人間独自の基準」でものを考える |
 中学生 中学生 | : | 素朴な疑問を持つ |
 神:はるか上空から、「自然の道理」でものを見る
神:はるか上空から、「自然の道理」でものを見る.png) 人間:地上で、「人間独自の基準」でものを考える
人間:地上で、「人間独自の基準」でものを考える 中学生:素朴な疑問を持つ
中学生:素朴な疑問を持つ
.png) 「人間は、人々が生活しやすいように、共通の『基準』をつくりました」
「人間は、人々が生活しやすいように、共通の『基準』をつくりました」
「例えば、100円硬貨は日本全国で 100円の価値がありますね。」
「北海道では、100円の価値。沖縄では 10円の価値。ではありませんね。」
「人間は共通した『基準』を作りたがるのです」
「そして、『 0 』を基準としたために、『-』(マイナス)という概念が生まれたのです。」
 「わしら神や自然に『マイナス』なんてないのじゃ!」
「わしら神や自然に『マイナス』なんてないのじゃ!」
「人間は勝手に『基準』なんか作りおって!勝手にせい!」
それでは、
例で「人間の考え方」と「神の上空からの目線」を比較しましょう。
・・・
●(水が氷りだしました).png) 「0℃!」
「0℃!」
 「全ての物質が凍りつく「絶対零度(人間の基準で、「-273.15℃」)」を基準にしたら、水が氷る温度は+273.15℃となるの~」
「全ての物質が凍りつく「絶対零度(人間の基準で、「-273.15℃」)」を基準にしたら、水が氷る温度は+273.15℃となるの~」
「沸騰するのは、+373.15℃かいな~」
⇒ そうです、「水が氷りだす温度を 『0℃』にしましょう!と「基準付けた」のは人間なのです。
●(リンゴ3個-リンゴ5個=?).png) 「-2個!」
「-2個!」
 「はぁ~?-2個?「-2個」なんて自然界に存在しないでしょ!」
「はぁ~?-2個?「-2個」なんて自然界に存在しないでしょ!」
「答えは、「3から5は引けない!」または「無くなるから0個」でしょ!」
⇒ そうです、神は「0=無い」、
人間は「0=無い、0=『基準』の二つの意味を持たせたのです」
●(運動会で、スタートラインから後ろに3m走り、気づいて前に5m走りました。何m進んだ?)
.png) 「0(基準)-3+5で、2m!」
「0(基準)-3+5で、2m!」
 「上空から見てたけど、「元の場所から」8mでしょ!ちゃんと8m分のカロリー消費してるでしょ!」
「上空から見てたけど、「元の場所から」8mでしょ!ちゃんと8m分のカロリー消費してるでしょ!」
⇒ そうです、スタートラインを「基準」にしたのも人間、
後ろを「-」、前を「+」としたのも人間でした。
●(10時の2時間前は?).png) 「8時!」
「8時!」
 「存在しない! 過ぎた時はもう無いのじゃ!」
「存在しない! 過ぎた時はもう無いのじゃ!」
⇒ そうです、時間は「有限」なのです!
などなど、
実際、自然界に『マイナスなもの』は存在しませんね!
目に映るものは…「ある」のです
コピー機で縮小コピーをする場合でも、
82%(1(そのもの)×0.82)、50%(1×0.5)、10%(1×0.1)、・・・1%(1×0.01)はできますが、
0%なんてボタンはないし、もしあっても何も出てこないということですね!
ましてや、-10%なんて・・・
神様いわく「ないものはないのじゃ!」ですね。
ただの「コピーボタン」は1倍(×1)(100%)で「そのもの」ですね。
| -(マイナス) |
-「引く」と |
0 |
1 |
1より大きい数 |
|
 |
無い |
引けるなら |
・無い |
そのものがある |
いっぱいある |
.png) |
あると考える | 「あり」 |
・無い |
1個ある
(数える) |
8個ある |
 |
.png) |
|
|
-(マイナス) |
無い |
あると考える |
|
-「引く」と |
引けるなら |
「あり」 |
| 0の意味 | ・無い |
・無い |
| 1の意味 |
そのものがある |
1個ある
(数える) |
|
1より大きい数 (例8) |
いっぱいある |
8個ある |


.png)

ここに、
「小学生の「算数」と、中学生以降の「数学」の違いは?」
のヒントがありますね!
お父ちゃんが、思うのは・・・
「-」を、「引く」ではなく「マイナス」と読んだ時、
もう数学という学問がはじまっていると !!
そして、「基準」をつくり、「マイナス」という概念をつくったことで、
人類は発達したのでしょうね !! (神様がびっくりするほどに!)
イ 正の数と負の数の四則計算の意味
四則 … +、-、×、÷
| + | 足し算 (加法)「かほう」 ←で求められた値(答)を「和」 |
| - | 引き算 (減法)「げんぽう」 ←で求められた値を「差」 |
| × | 掛け算 (乗法)「じょうほう」 ←で求められた値を「積」 |
| ÷ | 割り算 (除法)「じょほう」 ←で求められた値を「商」 |
まとめて、「加減乗除(かげんじょうじょ)」と言います。
ウ 正の数と負の数の四則計算

( )カッコの外しかた
(+)×(+)、(-)×(-) のように、同符号どうしの掛け算は、+
(+)×(-)、(-)×(+) のように、異符号どうしの掛け算は、 -
短すぎて、逆に意味がわかりませんね! では例を、
《 例 》 ( )カッコを外しましょう!
+(3) = +(+3) = +3 = 3
+(-4) = -4
-(7) = -(+7) = -7
-(-9) = +9 = 9
もっと正確にいうと、全ての「字(数字/文字)」には、「そのものがある」という意味の『×1』が含まれているのです。省略されていますが。
の外し方②.png)

クリック・タップで答え (反応が遅い場合があります)

『 0 』と『 1 』は特別な数字
前項で少し触れましたが、
『0』と『1』はとても特別な数字です。
『数』というよりも『意味のある文字』と考えることができますね。
『0』・・・『ない』
『1』・・・『そのものがある』
例えば、
0×リンゴ、(数字と文字の組み合わせは「×」を省略できますので、)
0リンゴ →「ないリンゴ」→(リンゴがない)
0×6 →「ない6」→ (6がない)
0x →「ないx」→ (xがない)
1×リンゴ →「そのものがあるリンゴ」 → (リンゴそのものがある)
1×x →「そのものがあるx」→ (xそのものがある)
2×リンゴ=2×1×リンゴ →「2、ある、リンゴ」→ (リンゴが、2、ある)
2x=2×1×x →「2、ある、x」→ (xが、2、ある)
.png) 「0と1はそんなに特別? 2×リンゴは?」
「0と1はそんなに特別? 2×リンゴは?」
.png) 「0の『ない』と、1の『ある』は、神と人間共通だけど、
「0の『ない』と、1の『ある』は、神と人間共通だけど、
2、3、4、5、……は人間独自なものといえるよ」
「たまたま人間の指が10本だから『10進法』を採用しているけど、
もしカニのつめのように、両手で指が4本だったら
きっと『4進法』だったと思うよ。
1、2、3、10、11、12、13、20、21、22、23、30、31、32、33、100、101、……のように4、5、6、7、8、9、のない世界!
( cf. コンピュータの世界は『2進法』で『0』と『1』しかない世界ですね。)
「関係はないですが、2×リンゴは、
『リンゴ2個』なのか『大きさ2倍のリンゴ』か『重さ2倍リンゴ』なのか
分かりませんね)
その点、「1」はまさしく『そのものがある』という意味で特別だよ。
だけど当たり前すぎて逆に「省略」されますね、
「1リンゴ」→「リンゴ」
「1x」→「x」
「1×(x+y )」→「x+y 」のように
『 1 』は、「数多くある数字の中の一つ」ではなく、
特別な、『そのものがある』という意識をもっておけば、
「分数」や今後の「割合」なども理解しやすくなりますね!
お父ちゃんが学生の頃、
「問題集の解説によく出てくる『1』 !! この「1」は何?どこからきたの?」
と苦しんだものです。

マイナス×マイナス はどうして「+」?
結論から言いますと、「数学の『ルール』だからです」
人間が作った「-(マイナス)」は、自然界には存在しないものですね、
自然界にはないものを、自然界にあるもので無理やり説明しようとすると、
逆に「???」となってしまいますね。
数学では、
「( )の中から先に計算する」
「+-×÷の混ざった式は 『×÷ から先』に計算する」
「分数や比はできる限り簡単な形にする」
といったような「ルール」がかなりありますね。
その「ルール」の理由は、
「みんなが同じ答えを導けようにするため」であったり、
「計算に矛盾がないようにするため」であったりというものです。
今回の、
『 -×- =「+」』については、例えば、

⑤ の符号は「+」でないと 右辺の「0」にならない
ということになってしまう
⑥ ということは・・・
「-」×「-」は、「+」にしよう!
というわけで
「-」×「-」は「+」にしよう! という数学ルール
ですね
※ ここでも、「+- よりも ×÷ を先に計算する」
という数学ルールを使っているので、説得力に欠けますが、
お許しを!
数の大きさ
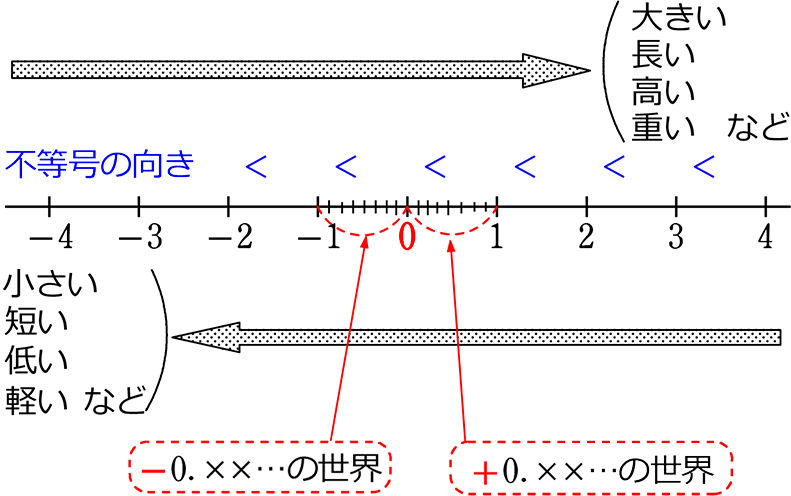
グラフの右にあるものほど大きい!以上!
と言いたいところですが・・・
念のため、
0.02は、-0.2より大きいですよ。
0.02は、(0+0.02)で(+0.02)ですので「0」より大きい(0より右にある)、
「1(そのもの)」はないけれども、「ほんの少しあることはある!」
-0.2は、(0-0.2)で(-0.2)ですので「0(ない)」より小さい(0より左にある)、
「極小」でもなく (→極小はあることはある)、
「ない、より小さい」→「ないより0.2小さい」と考えます。
数の大きさだけを見て錯覚しないように、
ちゃんと +-の符号から見てくださいね!

加法・減法 (足し算・引き算)

「+」と「-」は方向が逆
・+と+はどちらも正の方向へ足すだけ
・-と-はどちらも負の方向へ足すだけ
・+と-、-と+は、数字の大きい方が勝つ!
それでは、言葉より例題で
《 例 》 5+2 = 2+5
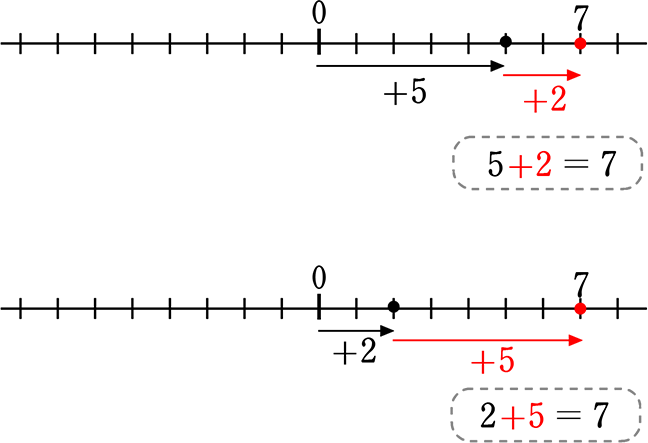
(イメージ)
0を「起点」に、「+」なら右に、「-」なら左に移動
これは今までよく見た計算ですね
説明はいりませんね
A. 7
《 例 》 -5-2 = -2-5
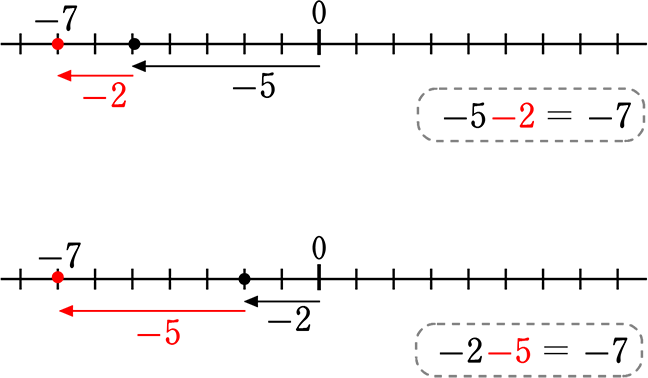
(イメージ)
0を「起点」、「+」なら右に、「-」なら左に移動
A. -7
ですが……結局は、慣れてくると
符号が同じ「-」、ということは「-」は決定、あとは-(5+2) = -7
(符号が決定した後は → 足し算!ですね)
《 例 》 5-2 = -2+5
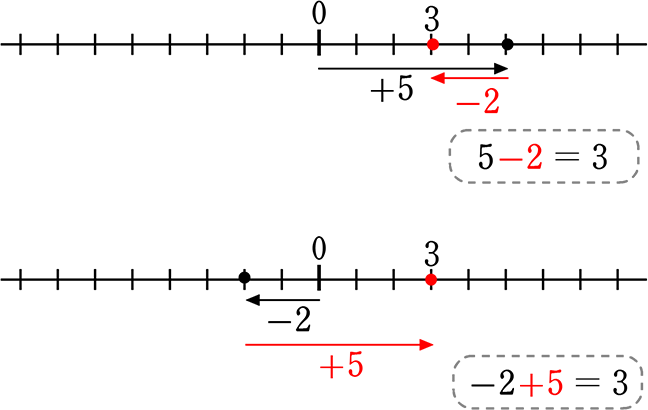
(イメージ)
0を「起点」に、「+」なら右に、「-」なら左に
A. 3
ですが…結局は、慣れてくると
符号が違うときは数字の大きい方の符号が勝つ、
ということは「+」は決定、
あとは +(大-小) = +(5-2) = +3 = 3
(符号が決定した後は → 引き算!ですね)
《 例 》 -5+2 = 2-5
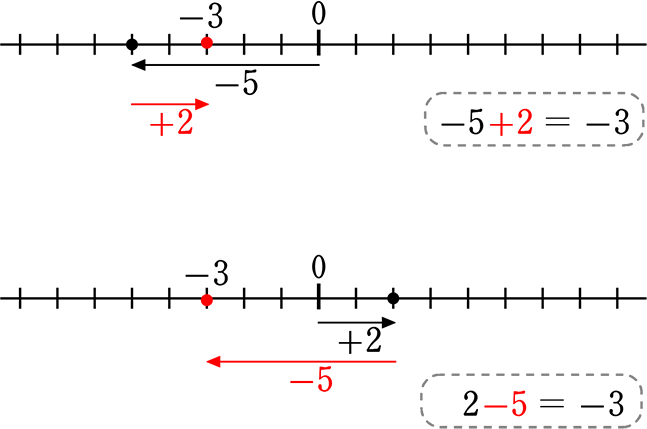
(イメージ)
0を「起点」、「+」なら右に、「-」なら左に
A. -3
ですが…結局は、慣れてくると
符号が違うときは数字の大きい方の符号が勝つ、
ということは「-」は決定、
あとは -(大-小) = -(5-2) = -3 = -3
(符号が決定した後は → 引き算!ですね)
加減のまとめ
まず、( )を外して、
ex. (-3)-(-7)=-3+7
| ・同符号のとき → | 協調 (同方向に足し合わす) |
3+7=10
-3-7=-10
| ・異符号のとき → | けんか (数字の大きい方の符号が勝つ) |
-3+7 → +7が勝って → =4
3-7 → -7が勝って → =-4
《 例 》
+(\(\large{\frac{1}{3}}\))-(-\(\large{\frac{3}{2}}\)) = \(\large{\frac{1}{3}}\)+\(\large{\frac{3}{2}}\) = \(\large{\frac{2+9}{6}}\) = \(\large{\frac{11}{6}}\) //
↑(カッコ)を外して通分しただけですね
中学数学では仮分数(分母より分子が大きい形の分数)の形で終了です。
\(1\large{\frac{5}{6}}\)のように帯分数(整数+真分数)の形にしなくてもよいですね
cf.
| 真分数 … | 分母より分子が小さい形の分数、普通の分数 (\(\large{\frac{3}{4}}\)など) |
帯分数の読み方
ex.
| 2\(\large{\frac{3}{5}}\) … | 現在は「2と5ぶんの3」 30年くらい昔は「2箇(か)5ぶんの3」でもOKでしたね |

加減の計算、暗算、はできる限り頭からしましょう
63+78=?
小学生の頃は、

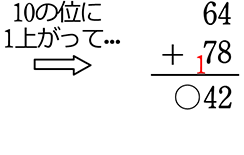
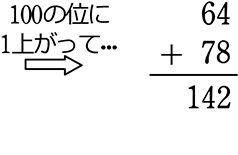
「2, 4, 1」 前から読みなおして「142!でしたね!」
ですが・・・ できる限り前から(先頭から)計算しましょう
1. 6+7は、1上がることは確かだから、「百・・」(確定)
(2上がることは絶対にない、最大の9+9でも18で、1しか上がらない)
2. 6+7だけに注目した場合の1の位は「3」、だけど、
次の4+8が「1」上がってくるのは確かだから、
「百(すでに確定)・・・40(確定)・・・最後、1の位が2!」「142!!」
(後ろから計算するひっ算のように「それを前から読むと」という
並び替え作業がないのでミスが減りますね!
頭の中では「百・・・2、3、40・・・2」ですね!
たしか、「そろばん」も前からでしたよね!

加減だけでつながるものは、並び替えは自由です
《 例 》
-4+8
= 8-4 でもよいですね
《 例 》
-4+6-5+7
=7+6-5-4 (=13-9=4) (+グループ-グループ)
=7-5+6-4 (=2+2=4) (途中で大きい数をできる限り作らない)
《 例 》
3-(+4) = -(+4)+3
などなど、並び替えは自由ですので、
1番楽に計算できる方法を、いつも探しましょうね!
(問題によって、楽に計算できる並び方があるものです。)
※ 数学は、
いかに『楽』に『間違えず』に『早く』解けるかが
最大のテーマであると感じますね!

『通分』する意味は何?


そうです!「目盛り(規格)」が違うのです!

この「1を\(\large{\frac{1}{2}}\) できる定規」と「1を\(\large{\frac{1}{3}}\) できる定規」の2つの定規を使って
家を建てたら、おそらく「ガラクタオブジェ」が出来上がることでしょう!
「分母をそろえる」ということは
「目盛りをそろえて統一定規で図る」ということですね。
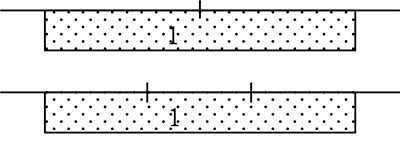
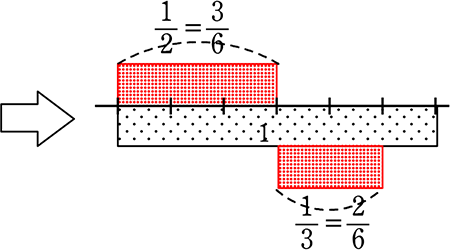
よって、\(\large{\frac{1}{2}}\)+\(\large{\frac{1}{3}}\) = \(\large{\frac{3}{6}}\)+\(\large{\frac{2}{6}}\) = \(\large{\frac{3+2}{6}}\) = \(\large{\frac{5}{6}}\)

最後の答えは『約分』していないと間違いなの?
数学の暗黙のルールで
「計算できるものは計算しましょう!」
「簡潔にできるものはできる限り簡潔にしましょう!」
みたいなルールがあります。
だから、「約分」していないと、
答え的には間違いではないけれど、
数学ルール的に足りていないという意味で
「
\(\large{\frac{6}{8}}\)=\(\large{\frac{3}{4}}\) 〇
\(\large{\frac{3}{4}}\)のように「最も約分された分数」を「
→ 「


乗法 (掛け算)
● 掛けることを「乗じる」といいます。
ex)
1,000円に1.25を乗じたものを時間外時給とする
→ 1000 × 1.25=1250
● 掛け算をして出てきた答えを「積」といいます。
ex)
・1000と1.25の積を求めよ
=「1000×1.25の答えを求めよ」
ex.
・面積
・体積
では、本題
( )カッコの外しかた でも話しましたが、
(+)×(+)、 (-)×(-) のように、同符号どうしの掛け算は、 +
(+)×(-)、 (-)×(+) のように、異符号どうしの掛け算は、 -
それだけでしたね。
《 例 》

分数の掛け算、割り算は通分しなくてもいいの?
それでは、① \(\large{\frac{1}{2}}\)+\(\large{\frac{1}{3}}\)と ② \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{3}}\) の根本的な違いから説明しますね。
①を正確に表すと、
1×\(\large{\frac{1}{2}}\) +1×\(\large{\frac{1}{3}}\) ( 1を\(\large{\frac{1}{2}}\)したものと、1を\(\large{\frac{1}{3}}\)したものを足す)
②を正確に表すと、
1×\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{3}}\) ( 1を\(\large{\frac{1}{2}}\)して、さらにそれを\(\large{\frac{1}{3}}\)する) ですね。
①は「元」が2つ、目盛りをそろえないと(通分しないと)足したり引いたりできない



というわけで、「通分」すると、
\(\large{\frac{3}{6}}\)+\(\large{\frac{2}{6}}\)= \(\large{\frac{3+2}{6}}\) というふうに「一つの分数」で表すことができますね。
②は「元」が1つ、その「元」をどう変形させているのか、ということですね。

「元」を\(\large{\frac{1}{2}}\)して、
さらにそれを\(\large{\frac{1}{3}}\) するですね
(結局、\(\large{\frac{1}{6}}\) ですね)
というわけで、いきなり
1×\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{3}}\) = \(\large{\frac{1×1}{2×3}}\) というふうに「一つの分数」(元々1つ)で表すことができますね
確認のため、「通分」してみると、
\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{3}}\) = \(\large{\frac{3}{6}}\)×\(\large{\frac{2}{6}}\) = \(\large{\frac{1}{6}}\) で「通分」は「約分」されて、「意味のないもの」とわかりますね
(まとめ)
| ① | 「+-」でつながっているものと、「×÷」でつながっているものは、根本的に違う (「元」の数が違う) |
| ② | 「×÷」でつながっているものは、いきなり「一つの分数」で表すことができる |

●「×÷」でつながっている

「元」は1つ
(「元」がどのように 「変形」したのか
イメージ:横に大きくなって、次に縦に大きくなって、次は全体的に小さくなって・・・ )
ex.
3 → 1×3
xy → 1×x×y
\(\large{\frac{1}{2}}\)xyz → 1÷2×x×y×z
●「+-」でつながっている
![]()
「元」は 複数 ある
(「元」に「何がくっついてきたのか」
「何が引かれてしまったのか」 )
ex.
1+2
x+y
\(\large{\frac{1}{2}}\)+x+y+z
分配法則
8(3-20) = +8×(3-20) = 8×(-17) = -136 ですね。
これを、分配法則で行うと、
8(3-20)

= (+8)×3+8×(-20)
= 24-160
= -136
となります
文字ですると、
分配法則の目的は、
| ① | 数学的には、(カッコ)を外すことが大目的です!
(逆が、3年生で習う因数分解ですね!) |
| ② | 普段的には、計算を簡単にするためですね! |
例えば、
コミック360円を12冊買うといくら?
360×12=4320 (円)ですが、
分配法則を使うと
360×12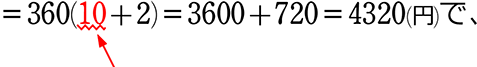
ここを自由な数字に設定できるのが便利ですね(100、10、など)
360×10は「暗算」できますし
3600は「頭の片隅」に置いておけますね
残りの 360×2 =360+360 =720
よって、
720+3600 =3600+720 =4320円
少し暗算がしやすくなりますね。
を外す.png)
そうです、最後の-(-5)は、
「正の数と負の数の四則計算」で出てきた( )を外しましょうですね!
分配法則の、『( )の中が、元がひとつ』バージョンだったんですね!
累乗
2×2×2×2×2×2×2×2×2×2 = 210
「2の10乗」で 1024 ですね
憶えておきたい
210 = 1024
×2 をいっぱい書くのは無駄ですものね、
「同じ数」を何回か掛けることを「累乗(るいじょう)」といいます。
この右上の小さい数字が「指数(しすう)」といって
「〇を10回掛ける」という意味になります。
2×2×2×2×2×2×2×2×2×2 = 25×25= 210
2×2×2×2×2×2×2×2×2×2 = 23 ×27= 210
ということは・・・
2m×2n = 2m+n が導けますね
→ am×an= am+n (2年:指数法則)



二乗を「平方」、三乗を「立方」と言うことがありますね
● 面積でよく使った「cm2」 (平方センチメートル)ですね
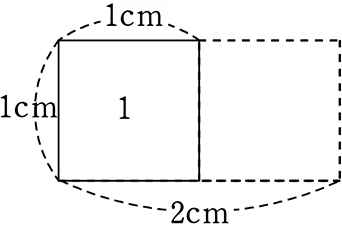
1(cm)×1(cm)
= 1×1×(cm)×(cm)
= 12×(cm)2
= 1(cm)2
・1(cm)×1(cm)×2(倍)= 1cm×2cm= 2cm2
● 体積でよく使った「cm3」(立方センチメートル)ですね
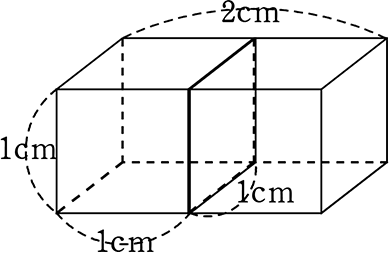
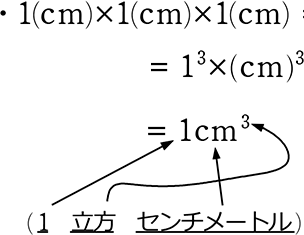
・1(cm)×1(cm)×2(倍)= 2(cm)2×1(cm) = 2cm3 // ですね!
徐法 (割り算)
割ることを「徐する」といいます。
ex) 10,000円を8で除したものを基本時給とする
→ 10,000÷8 = 1250 円/時
割り算をして出てきた答えを「商」といいます。
ex) 10,000を8で除した商を求めよ
=「10000÷8の 答えを求めよ」
では、本題
数学では、「÷」という記号はほとんど使いません!
その上で・・・

除法のポイント
もう一度確認しておきますね
●「×÷」でつながっている

「元」は1つ
(「元」がどのように「変形」したのか
イメージ:横に大きくなって、次に縦に大きくなって、次は全体的に小さくなって・・・ )
ex.
3 → 1×3
xy → 1×x×y
\(\large{\frac{1}{2}}\)xyz → 1÷2×x×y×z
●「+-」でつながっている
「元」は 複数 ある
( 「元」に「何がくっついてきたのか」
「何が引かれてしまったのか」 )
ex.
1+2
x+y
\(\large{\frac{1}{2}}\)+x+y+z
⇒「÷〇」は、「× \(\large{\frac{1}{〇}}\)」というふうに、
分数の分母にもってくれば 掛け算になりますね!
⇒「÷\(\large{\frac{〇}{●}}\)」は、「×\(\large{\frac{●}{〇}}\)」というふうに、
「×逆数」にすれば 掛け算になります!
実は、上の2つは同じことを言っていますね
「÷〇」は、実は「÷ \(\large{\frac{〇}{1}}\) 」ですものね
《 例 》
3÷7 = \(\large{\frac{3}{7}}\) これで答えです!
・3÷7 →「3を7で割る」という意味
・\(\large{\frac{3}{7}}\) →「3を7で割る」、「1を7で割ったものが3つ」、「7につき3」 という意味も見えてきますね。
ただし、問いに「少数第何位まで求めよ」とあれば、
ミチミチと小数に計算しなければなりませんね・・・
\(\large{\frac{3}{7}}\) = 0.4285・・・と。
その他、
(+)×(+)、 (-)×(-) のように、同符号どうしの掛け算は、 +
(+)×(-)、 (-)×(+) のように、異符号どうしの掛け算は、 -
ですし、÷のままでも
(+)÷(+)、 (-)÷(-) のように、同符号どうしの割り算は、 +
(+)÷(-)、 (-)÷(+) のように、異符号どうしの割り算は、 -
→ まったく同様ということですね

逆数 とは
「逆数」とは、= その数に掛けたら、「 1 」になるような数。
簡単に言いますと
| ① | 整数なら、分母にするだけ |
| ② | 分数なら、上下を逆にするだけ |
| ③ | 符号は変わりません |
《 例 》
・ 2の逆数は \(\large{\frac{1}{2}}\)
(確かに、2×\(\large{\frac{1}{2}}\)=1)
・ \(\large{\frac{1}{3}}\)の逆数は 3
(確かに、\(\large{\frac{1}{3}}\)×3=1)
・ -3の逆数は \(-\large{\frac{1}{3}}\)
(確かに、-3×(-\(\large{\frac{1}{3}}\))=1)
・ 0.25の逆数は
| →① | \(\large{\frac{1}{0.25}}\)(機械的に分母にした) = \(\large{\frac{100}{25}}\) = 4 |
| →② | =\(\large{\frac{1}{4}}\)の逆数 → 4 (先に分数にしてから、逆数にした) |
《 例 》
-\(\large{\frac{3}{4}}\)÷\(\left(-\large{\frac{3}{2}}\right )\)×\(\left(-\large{\frac{9}{8}}\right )\)
= -\(\large{\frac{3}{4}}\)×\(\left(-\large{\frac{2}{3}}\right )\)×\(\left(-\large{\frac{9}{8}}\right )\) … 逆数を利用して全て掛け算の形にした
= -\(\large{\frac{3×2×9}{4×3×8}}\) … -が3つなので先に-を確定させて、まとめた
= 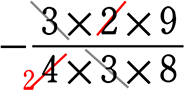 … 約分できる者どうしで約分した
… 約分できる者どうしで約分した
= -\(\large{\frac{9}{16}}\)


( )の意味
( )の意味は
| ① | ( )の中から先に計算する、ですね |
数学ではもう一つ!
| ② | ( )で囲むと…それで「一つのグループ」「一つの文字」になるという意味もありますね! |
(a+b+c+d+e+f+g)といくら長くてもこれで「一つの文字」です
掛けるでつながる (a×b×c×d×e×f×g)は、元々「abcdefg」の一文字ですから、( )は不要ですね
そういう意味で、「+-×÷の混ざった式は×÷から先に計算する」の意味になりますね!
(3+4+5)もこれで、「一つの文字」ですが、
文字は文字でも、中が「数字」ですので、計算ができてしまいますね!
そういう意味で、( )の中から計算しましょう!の意味になりますね!
(読む+書を)を「一文字」とはイメージしにくいと思いますが、
(読書)とすれば「一文字」とイメージできてしまいますね、
(読む+書を)も、( )で囲まれているからには、これで「一文字」とイメージできるように なりたいですね。
ex.
3(a+b+c+d+e)+4(a+b+c+d+e)= 7(a+b+c+d+e)
→ 3x+4x = 7x と同じ考え方ですね
(カッコ)を「1文字」と見れることに慣れると、
「計算間違い防止」や「因数分解」などに役立ちます。
先ほどの問題で
・ 5÷(2+4) = \(\large{\frac{5}{(2+4)}}\) = \(\large{\frac{5}{2+4}}\) = \(\large{\frac{5}{6}}\)
においても、(2+4) を「一文字」とイメージできれば、
機械的に、(2+4) を分母にもってくることができますね!
・・・イメージできない場合は、
(2+4) = X (←ラージエックスなど)
「本当に1文字」に置き換えみて、
5÷X = \(\large{\frac{5}{X}}\)
(X = 2+4 より)
\(\large{\frac{5}{X}}\) = \(\large{\frac{5}{2+4}}\)
というふうに「2段階」踏むことになってしまいますね
「置きかえる」→「戻す」 …できれば省きたい作業ですね!

「0÷」(0を割る)、「÷0」(0で割る)
0÷3=? (0を3で割ると・・・)
 「ないものを3で割っても、『ない』じゃろ?人間で言う「0」じゃ!」
「ないものを3で割っても、『ない』じゃろ?人間で言う「0」じゃ!」.png) 「0円を3人で分けたら・・・一人0円・・・答えは0 !?」
「0円を3人で分けたら・・・一人0円・・・答えは0 !?」
そうです、0÷3=0 です。「0は割ることができます」
では次に、3÷0 は?
 「3÷『ない』=?じゃな?・・・『ない』は書かなくていいから・・
「3÷『ない』=?じゃな?・・・『ない』は書かなくていいから・・
3÷ となるの、ということは「÷」も書く意味がないから、3・・・イコールまでたどりつかぬの~、
『答え、「書くことができない!」じゃ』」.png) 「そこを何とか『 ÷0= 』まで書いてほしいのですが!」
「そこを何とか『 ÷0= 』まで書いてほしいのですが!」
 「書けないものは書けぬ!」
「書けないものは書けぬ!」.png) 「そこをなんとか…」
「そこをなんとか…」 「魔閃光 !!!」
「魔閃光 !!!」
すいませんでした・・・
では、人間の番です.png) 「3÷0」…「3円を0人で分けたら、一人あたり…あれ?0人あたり…
「3÷0」…「3円を0人で分けたら、一人あたり…あれ?0人あたり…
あれ?
う~ん、次の考え方!
「÷」を「×」にしてみよう、0の逆数は・・・ 0×□=1 で□のような数字は…あれ?ない!…????
それでは、解答です…
「÷0」、「\(\large{\frac{}{0}}\)」は…『 定義しない』 でした。
イメージ的には、「数学では(そのようなものは)扱わない」という感じでしょうか。
もし、数学では考えないはずの 「÷0 (分母0)」 がテストにでたら、
答えは、「定義しない」と書いてくださいね
自然数とは
自然数の定義:正の 整数 ( 1、2、3、4、5、6…)
イメージは、
| ① | まず、「ある(自然界に存在する)」こと →「マイナスではない」 |
| ② | そして「個数を数える」ときに使う
(1.3個、そんなものは自然界にはありませんね) |
1個、2個、3個…、
1人、2人、3人…ごくごく、自然界ですね。(だから自然数)

実数の種類

エ 具体的場面における表現や処理
《 例 》
標高が100m高くなるにつれて、気温が0.6℃下がります。
地上が20℃の時、富士山頂(3776m)は何℃?
20+3776÷100×(-0.6)
=20+\(\large{\frac{3776×(-0.6)}{100}}\) ×÷の一体化
=\(\large{\frac{2000+(-2265.6)}{100}}\) 通分、分子計算
=\(\large{\frac{-265.6}{100}}\) 分子計算
= -2.656 (℃)

摂氏と華氏 (せっしとかし)
温度には2つの標準がありますね
ほとんどの国が採用している 摂氏(せっし)
20℃ → 摂氏20度
アメリカとほんの1部の国で採用されている 華氏(かし)
68℉ → 華氏68
この2つは、「目盛りの価値」だけではなく「始点」も異なります
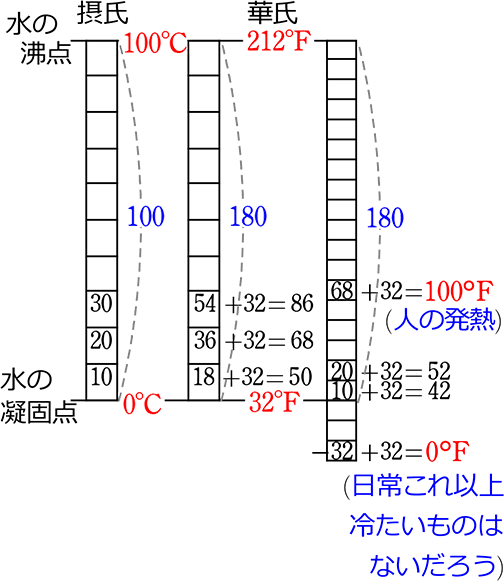
摂氏の基準 → 水の状態
華氏の基準 → 人の体温 ・ 身近な自然
| 摂氏の価値感 → | 小数、マイナスおかまいなし |
| 華氏の価値感 → | できる限り整数、できるかぎりプラス |
基準は一度慣れると改変するのは大変ですね
円の1周は360°(360や180は細かく分けても整数が多い)に慣れてしまっていることと同じですね
明日から1周100°に改変します!と言われても慣れるのに大変ですね
直角は…100°×\(\large{\frac{1}{4}}\)…25°!?
では、
● 36.5℃は何 ℉?
1目盛りの価値が1.8倍(\(\large{\frac{18}{10}}\))になるので → 36.5×1.8 = 65.7
℉はスタート地点ですでに32を持っているので → 65.7+32 = 97.7 ℉ (平熱)
● 100 ℉は何 ℃?
℃はスタート地点で32を持っていないので → 100-32 = 68
1目盛りの価値が\(\large{\frac{10}{18}}\)になるので → 68×\(\large{\frac{10}{18}}\) = 37.777…℃ (発熱)
● 0 ℉は何 ℃?
℃はスタート地点で32を持っていないので → 0-32 = -32
1目盛りの価値が\(\large{\frac{10}{18}}\)になるので → -32×\(\large{\frac{10}{18}}\) = -17.777…℃ (氷枕)
(身近にある最も冷たいものが氷枕だった)
(ちなみに日本の家庭用冷蔵庫の冷凍庫は大体 -21℃、よくテレビでみる船上げされたばかりのカチンコチンのマグロは -60℃ ですね)
℃ と ℉、起点まで違うのはちょっと辛いですね!
《 例 》
パー5のゴルフコースを3打でまわった、スコアは?

∴ -5+3=-2
《 例 》
中学生が、おこずかいを使い果たしたので、
母に3,000円借りました。中学生の財産は?
・返す気の全くない悪い中学生の場合
0+3000=3000 ∴ 財産3,000円
・返す気のある普通の中学生の場合
+3,000円、だけど借金(負債)も3,000円(=-3,000円)
3000-3000=0 ∴ 財産0
・先を読む中学生の場合
使うことが決定しているから3,000円を借りた、
ということは、使った後は借金(負債)が3,000円(=-3,000円)
0-3000=-3000 ∴ 財産(-3,000円)になるのか・・・
《 例 》
クラスの平均点が70点でした。
Aさんは62点でした。平均点より何点低い?
70-62=8 ∴ 8点低い
Bさんは70点でした。Bさんの偏差値は?
→ 偏差値50
(偏差値は複雑な計算式です、
ですが、平均点だけは、必ず偏差値50ですね)
(偏差値の求め方)
このように、人が作った「基準」というものは、
「環境」により結構「変動」しますね。
「大人」は自分たちの都合のいいように、「基準」を変えますね!
子供たちが大人を嫌いになる最大の理由といえるかもしれませんね。
「今回の場合は、・・・」と、大人が言い出せば、
大体「基準」が変わると思っていいと思います。
話がそれてしまいましたね。
この単元は、
「基礎の基礎だから、『正確に』『早く』計算できるように
「繰り返し」「何度も」練習しましょう!・・・ とは言いません !!
今後の課程の計算の中で、勝手に「繰り返し」「何度も」しますので、
ここでは、「正確に」できれば十分です。
「正確に」できれば、次に行きましょう !!
お疲れ様でした !!
その他の問題は、「問題集」で !!