| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平面図形 | (2) 空間図形 |
| ア | 基本的な作図とその活用 |
|---|---|
| ・ | 図形の各部名称 |
| ・ | 2大根本作図 |
| ・ | ひし形・たこ形の性質 |
| A | 4つの基本的な作図 |
| ① | 垂線の作図 |
| ・ | 垂線の特徴 |
| ・ | 本当に直角? |
| ・ | 三角形の面積公式の1/2とは |
| ・ | ひし形の面積の有効活用 |
| ① | 点Pを通る垂線の作図 |
| ・ | 点Pを通る垂線の特徴 |
| ・ | 50点な点Pを通る垂線の作図 |
| ② | 垂直二等分線の作図 |
| ③ | 角の二等分線の作図 |
| ・ | 角の二等分線の特徴 |
| ・ | 正三角形の作図 |
| ・ | 色々な作図 |
| イ | 平行移動、回転移動、対称移動 |
| ① | 平行移動 |
| ② | 回転移動 |
| ・ | コンパスで回転移動の作図 |
| ・ | 点対称移動 |
| ③ | 対称移動 | ・ | コンパスで(線)対称移動の作図 |
| ウ | 図形の面積 |
| ① | 平行四辺形系の面積 |
| ② | 三角形の面積 |
| ③ | 底辺共有2三角形の面積 |
| ・ | 四角形の分類表 |
| ④ | 円の面積 と円周 |
| ・ | 円周率とは |
| ・ | 道路標識の「R」の意味 |
平面図形
ア 基本的な作図とその活用
「図形」は、「数と式」「関数」「資料の活用」と比較して、
最も理解しやすい分野といえますね!
なぜなら、自然の摂理と同じだからです、イメージがしやすいのです!
「-(マイナス)」なんて人間の考えた基準は出てきません!
点数の稼ぎどころと言えますね!
図形のポイントは、1、2、3年生を通じて、
| 1. | その図形の特徴(性質)を、知っていること! |
| 2. | その図形の特徴(性質)を、見つけ出せること!(練習あるのみ!) |
| 3. | その図形の特徴(性質)を、利用できること!(練習あるのみ!) |
です!
図形の各部名称
まずは、憶えるとこは憶えておきましょう!

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)



.png)
sp.png)
2大根本作図
数学での「作図」においては、「コンパス」と「定規」しか使いません。
しかも、定規は「直線を引くだけのためのもの」であって、目盛りは使ってはいけません。
距離を測る手段は「コンパス」です。
作図は、「書き方」で憶えると、いずれ忘れてしまいます。
「特徴(性質)」を憶えておけば、「書き方」を忘れても、なんとか書けますね!
その中でも、「考え方」の「根本」になる 2大根本作図が・・・
① ひし形 と② たこ形 ですね!
① ひし形
《 例 》
1点から「ひし形」を2個ほど書きましょう


①適当に開いたコンパスで
円弧を書きます

①と「同じ開き」で
円弧上の適当な2点から
交わるように円弧②を書く

「点」と「交点」を結んで
「ひし形」の完成ですね
《 例 》
2点から「ひし形」を書きましょう


2点を支点に「同じ開き」で
交わるように円弧①を書いて

「点」と「交点」を結んで
「ひし形」の完成ですね
② たこ形
《 例 》
1点から「たこ形」を2個ほど書きましょう

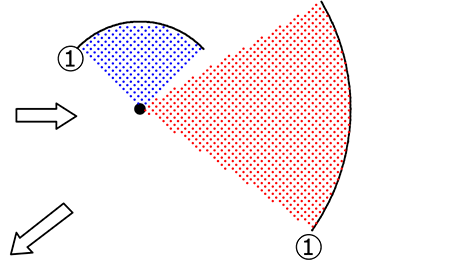
①適当に開いたコンパスで
円弧を書きます

①と「違う開き」で
円弧上の適当な2点から
交わるように円弧②を書く

「点」と「交点」を結んで
「たこ形」の完成ですね
《 例 》
2点から「たこ形」を書きましょう


①適当に開いたコンパスで
円弧を書きます

①と「違う開き」で
交わるように円弧②を書く

「点」と「交点」を結んで
「たこ形」の完成ですね

「ひし形」「たこ形」の性質
2つの図形はたくさんの性質を持ちますが
作図で役立つ性質を太字にしますね
【 ひし形 】
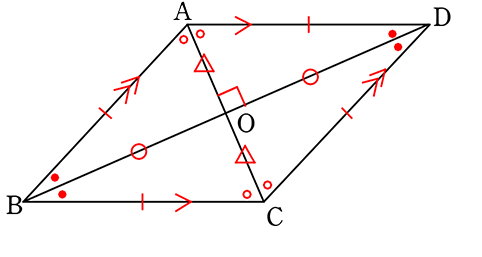
・対辺がそれぞれ平行
(AD//BC、AB//DC)
・4辺が全て等しい
(同じ開きのコンパス⇔同じ半径)
・対角がそれぞれ等しい
(∠A = ∠C、∠B = ∠D)
・対角線が「中点」で「直角」に交わる
(ACはBDの垂直二等分線、
BDはACの垂直二等分線)
・2本の対角線は「角の二等分線」
(∠ABD = ∠CBD など)
【 たこ形 】
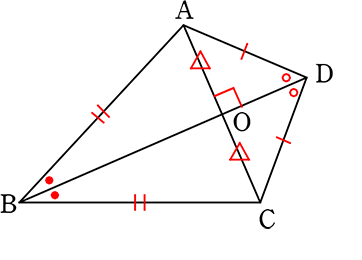
・2辺がそれぞれ等しい
(2つの開きのコンパス⇔それぞれは同じ半径)
・対角線がACの「中点」で「直角」に交わる
(ACはBDの垂線、
BDはACの垂直二等分線)
・1本の対角線は「角の二等分線」
(∠ABD = ∠CBD ∠ADB = ∠CDB)
これら「ひし形、たこ形の書き方」と「ひし形、たこ形の性質」を知っていれば 作図の7割はカバーできますね!
すなわち
与えられた問題に、まずは薄っすらと「ひし形」や「たこ形」を 「どう配置すればよいか」をイメージすれば作図も進みやすいですね!
4つの基本的な作図
1-① 垂線
直線lに垂線(直角に交わる線)を引きましょう
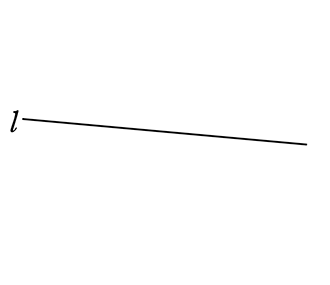
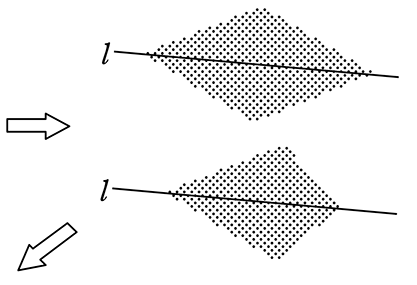
「ひし形」か「たこ形」を想像して・・・
「たこ形」でいきますね

①適当に開いたコンパス(  )の支点を、
)の支点を、
直線lの適当な場所に置いて円を描く

②適当に開きを変えた(変えなくてもよい)コンパスの支点を、
直線lの別な場所に置いて円を描く
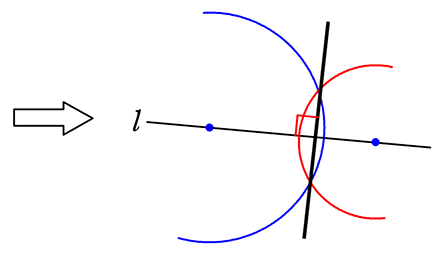
③2つの交点を通る
直線を引いて完成

垂線の特徴
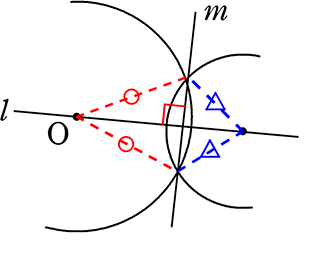
① m⊥l
② 〇=〇、 △=△ (半径より)
言葉で憶えられなくても、
図に、直角マーク「 」や
」や
長さが同じマーク「 、〇、△、」など
、〇、△、」など
を書き込むことができれば十分です
付随知識として、
① 〇=〇(△=△)の二等辺三角形
② m⊥lより、mやlは点線三角形の
「底辺」や「高さ」と見ることができる
たこ形の性質を知っていれば当たり前のことですね!

直線上の2点を中心とした円弧の交点を結んだ線は本当に直角?
上の図で、最後に「![]() 」(直角マーク)を書き込むとき、
」(直角マーク)を書き込むとき、
「本当にこれは直角?」「なぜ直角と言えるの?」
となりますね。
本当に直角なのでしょうか?
下図は、上の図の点で切り出して、各点に名前を付けたものです
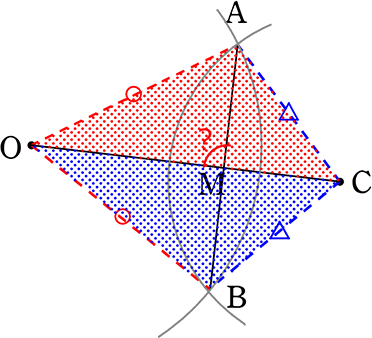
(証明1)
△OACと△OBCにおいて、
\(\small{\begin{cases}
OA = OB (半径より)\\
CA = CB (半径より)\\
OC = OC (共通)
\end{cases}}\)
よって、「3つの辺がそれぞれ等しい」ので △OAC≡△OBC …①
(2年生の「合同」です、のちほど 学びましょうね)
次に、△OMAと△OMBにおいて
\(\small{\begin{cases}
OA = OB (半径より)\\
∠AOM = ∠BOM (①より)\\
OM = OM (共通)
\end{cases}}\)
よって、△OMA ≡ △OMBより
∠OMA=∠OMB…②
∠OMA+∠OMB=180°…③
②を③に代入して、
∠OMB+∠OMB=180° → 2∠OMB=180° → ∠OMB=90°
(または、MはAB上にあるから、 ∠OMA=∠OMB=90°とさらっと言ってもOKですね)
(または、△BOCは△AOCの「線対称」の図 (Oが共通より
また、△AOCは△BOCの「線対称」の図
よって、「線対称」ということは、対応する点(AB)を結んだ線は、
「対称の軸(折り目OC)」に直交(直角に交わる)するでもOKですね)
∴ OC⊥ AB
(証明2)
\(\small{\begin{cases}
OA= OB \\
CA = CB
\end{cases}}\)
∴ 四角形AOBCは「凧型四角形」である
∴ 凧型四角形の対角線は直交するので
OC⊥AB //
●「ひし形」の場合は明らかに「垂直」に交わっているといえますね
∵ ひし形は「4辺が全て等しい」 (ひし形の性質)
∴ ひし形は同じ二等辺三角形が2つくっついたもの
∴ 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する
(二等辺三角形の性質)
∴ 対角線が直交する

三角形の面積
三角形の面積は、底辺×高さ÷2ですね
少し数学風に言えば、S(面積) = \(\large{\frac{1}{2}}\)(底辺)(高さ) ですね
・\(\large{\frac{1}{2}}\) とは?
→ 三角形はひっくり返してくっつけたら「平行四辺形」になる
その平行四辺形の面積の
半分の面積という意味の「\(\large{\frac{1}{2}}\) 」ですね or
or 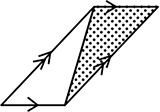
・底辺とは?→ そのまま「底辺」ですね
・では、「高さ」とは?

頂点から底辺に下した
「垂線」ということになりますね
垂線が三角形の中にあれば、
イメージしやすいですが、

垂線が三角形からはみ出て、
イメージしにくくても、
底辺の延長上に下した垂線が「高さ」です!

長方形にするとイメージしやすですね
平行四辺形の面積が、(底辺)×(高さ)の理由
(直角三角形の合同条件:2年)

ひし形の面積の有効活用
余談が続いてすいません
ひし形の定義、定理(特徴・性質)は、
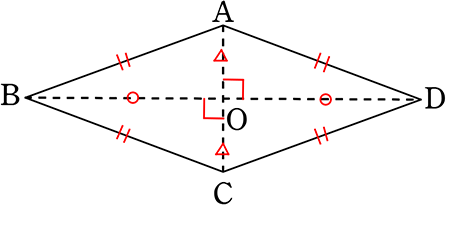
① 平行四辺形の全性質 プラス
② 4辺が全て同じ長さ
③ 対角線が直交する ですね。
そして、
① ひし形の面積 = 底辺×高さ
または
② ひし形の面積 = \(\large{\frac{1}{2}}\)(対角線)(対角線) でしたね
下は四角形の定番の (底辺)(高さ) は出てこないし、
四角形なのに「\(\large{\frac{1}{2}}\) 」がつくって、なにか気持ち悪いですね。
そうです、この公式は、2つの三角形の面積を足した式 ですね!
共にACを底辺とする
高さBOの三角形と、高さDOの三角形を足したものですね
(BDを底辺と見るなら、高さはそれぞれAO、CO)
ひし形の面積
= △ABC+△ADC
= \(\large{\frac{1}{2}}\)AC・BO+\(\large{\frac{1}{2}}\)AC・DO
= \(\large{\frac{1}{2}}\)AC(BO+DO)
= \(\large{\frac{1}{2}}\)(AC)(BD)
= \(\large{\frac{1}{2}}\)(対角線)(対角線)
難しい!ので 数字で行きましょう!
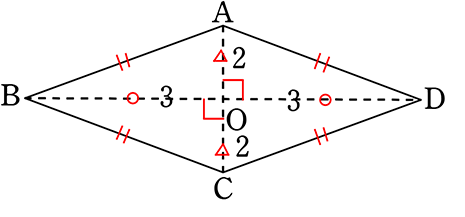
●ひし形の公式だと
\(\large{\frac{1}{2}}\)(対角線)(対角線) = \(\large{\frac{1}{2}}\)×4×6 = 12
●△ABC+△ACDだと
= \(\left(\frac{ 1 }{ 2 }・4・3 \right )\)+\(\left(\frac{ 1 }{ 2 }・4・3 \right )\)
= 6+6 = 12 ですね!
この、
①「底辺を共有」していて、
②「高さ」がわかっている 2つの三角形の面積の和を、
ひし形だけで済ますのはもったいないです。
例えば、次の図の面積を求めるとき、第一感(直感)は?
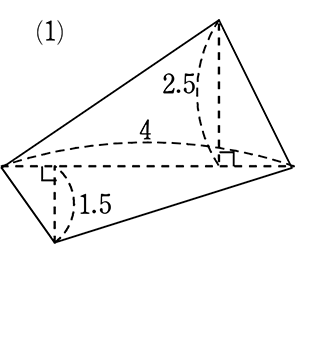
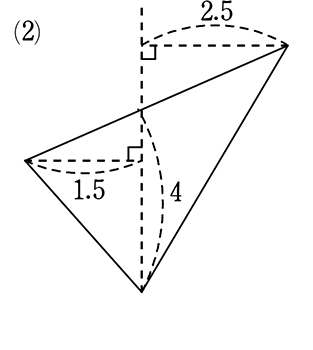
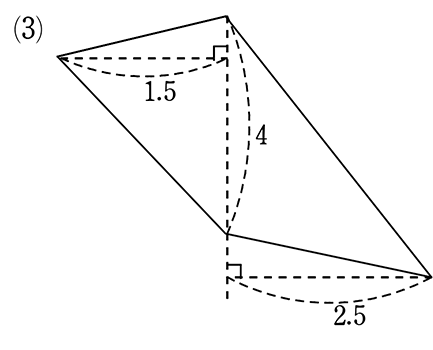
「四角形・三角形というより、三角形が2つだな」と思ったと、思います。
底辺に直交していれば「高さ」ですからね。
そして、2つの三角形をそれぞれ求めて、足し合わせますね。
(1)は、\(\left(\frac{ 1 }{ 2 }・4・2.5 \right )\)+\(\left(\frac{ 1 }{ 2 }・4・1.5 \right )\) = 5+3 = 8
・・・ですが・・
ひし形の面積のようにまとめてしまいましょう!
\(\large{\frac{1}{2}}\)・4・(2.5+1.5) = \(\large{\frac{1}{2}}\)・4・4 = 8

「底辺共有2三角形」の面積 = \(\large{\frac{1}{2}}\)(底辺)(合計高さ)
↑お父ちゃんが勝手に名付けました、皆様で自由に名付けてくださいね!
(2)も(3)も全く同じです。
(2)は少し「2つの三角形」とはイメージしにくいかもしれませんが、同じです。
まだまだ先の話になりますが、
「2次関数」と「図形」の複合問題などで役に立ちますね!

図の赤い部分は、底辺共有2三角形ですね
共有底辺は、0~4の「4」ですよ~
合計高さは-2~3の「5」ですよ~
共有底辺を見つけることもポイントですね!
ちなみに、共有底辺を「共有高さ」とイメージするほうが楽なら、
それでも全く問題なしですね! (全く同じ結果ですので)
話が飛び過ぎてしまいましたが、
2つの三角形は、「底辺が共有」なら「高さ」を「足した」三角形の面積と
同じということです。
ここに当然、
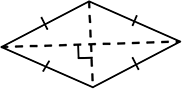
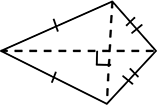
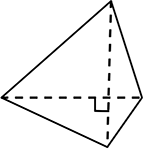
(対角線がたまたま直交する)
変形たこ形も
含まれてくるわけですね!

①-2 点Pを通る垂線
点Pを通る、lの垂線を描きましょう
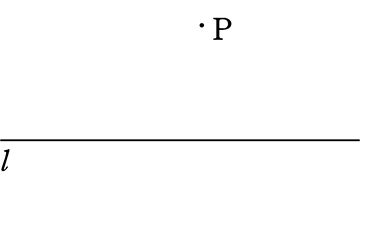

①Pを支点に
適当なABを決める
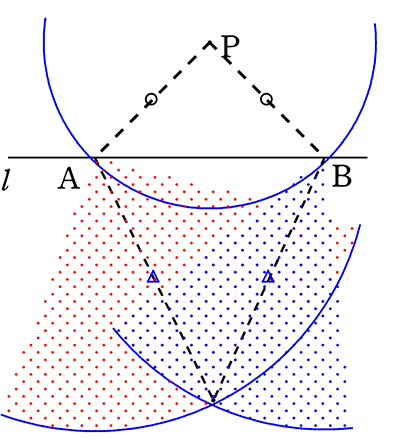
②適当に開きなおしたコンパスを
(開きが同じならひし形 OKです)
Aを支点に円を描く
開きはそのままに、今度は
を支点に円を描く

③交点とPを結んで完成
最初に「ひし形かたこ形」を
イメージすると楽ですね

点Pを通る垂線の特徴 (= 垂直二等分線の特徴)
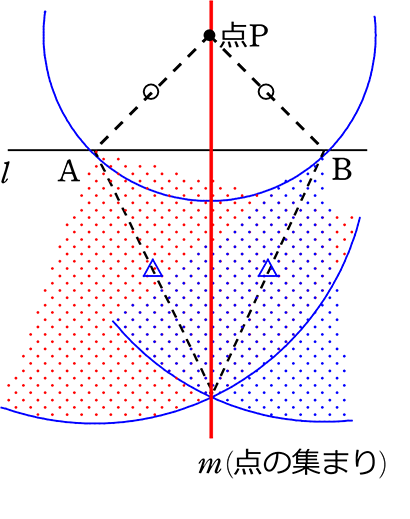
① m⊥l
② 〇=〇、 △=△ (半径より)
③ (Pがm上を動いても)常に AP=BP
言葉で憶えられなくても、
図に、直角マーク「 」や
」や
長さが同じマーク「 、〇、△、など」
、〇、△、など」
を書き込むことができれば十分です
付随知識として、
④ 〇=〇(△=△)の二等辺三角形
⑤ m⊥lより、mやlは点線三角形の
「底辺」や「高さ」と見ることができる
③は、直線mは点Pの集まりということですね
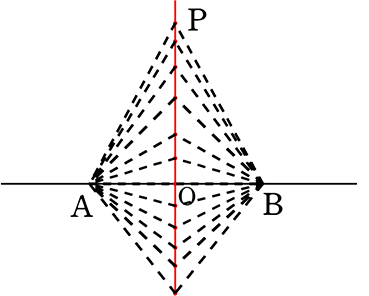
常にPA = PBより
Pが直線AB上に来た時、
Pは、当然A点 と点Bの 中点 になりますね
これで
点Pが直線上にある場合の垂線も同様に描けますね


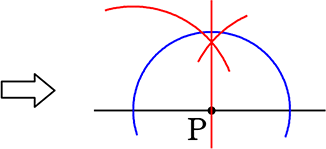

50点な点Pを通る垂線の描き方
点Pを通る垂線は、常にPを頂点とする二等辺三角形なのだから、
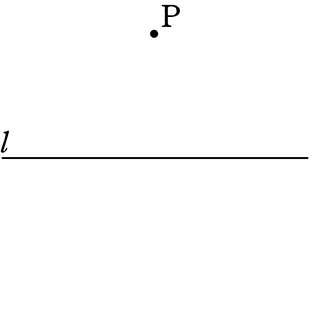

①適当なl上にコンパスの針を置き
コンパスの鉛筆側をPに合わせて
円を描く
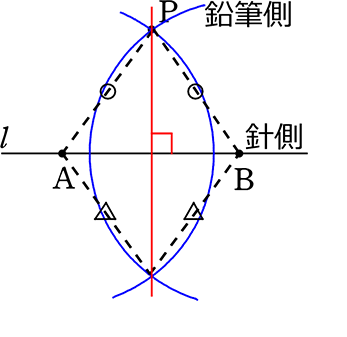
②コンパスの開き具合はそののまま、
今度は、Pに鉛筆側を合わせて×
針がl上になる点を探して、円を描く
これは、確かに理論上は PA = PBで 点Pを通る垂線なのでしょうが、
コンパスを定規のようにして「距離を予測している」 ということで
×(バツ)なんでしょうね。
「すでにある点と点」にコンパスの開き具合を調整するのはアリですが、
やはり与えられた点にはまず「針」を刺すものなのでしょうね
② 垂直二等分線
もう垂直二等分線なんてわかっちゃいますね
最初から、点Aと点Bが与えられているのですから!

垂直二等分線というからには、
ABの中点を通りますね
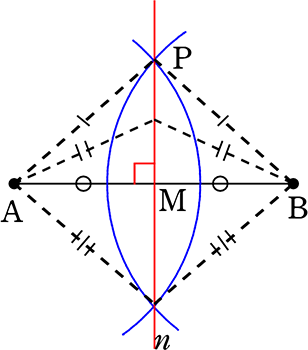
(薄っすら「ひし形」をイメージして)
①Aを支点に、適当な円を描き
②コンパスの開きはそのままに
Bを支点に円を描く
③交点を結んで完成です!
特徴は繰り返しになりますが、
① AB⊥ n
② 常に AP = BP
③ MはABの中点
(M : middle、mannnakaでもいいかも)
③ 角の二等分線
角を2等分する線です
90°の角があれば45°と45°に分けることができるということですね
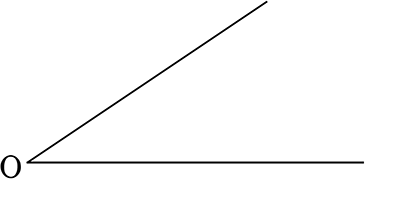

①ひし形かたこ形をイメージして

②(Ot = Osをイメージしながら)
Oにコンパスの針をあてて、適当な円を描く

③tを支点に適当な円を描き、
開きはそのままに、sを支点に円を描いて完成です
【 二等分線である証明 】
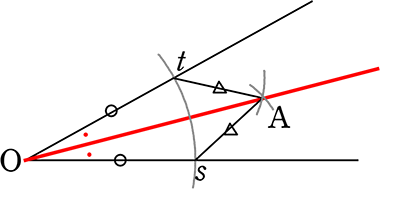
△OtAとOsAにおいて
\(\small{\begin{cases}
Ot = Os \\
At = As \\
OA = OA (共通)
\end{cases}}\)
3辺がそれぞれ等しいので
∴ △OtA≡ △OsA
∴ ∠tOA = ∠sOA (確かに二等分線)

角の二等分線の特徴
角の二等分線の特徴(性質)はかなり役立ちます!
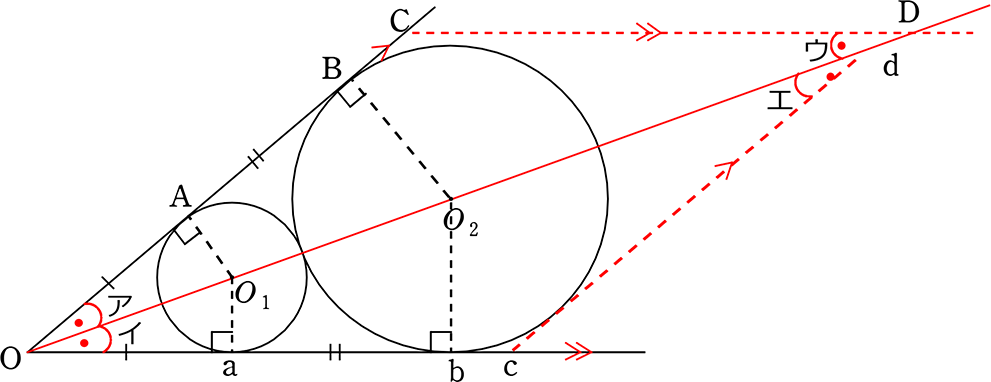
特徴(性質)
① ∠ ア=∠ イ
② OA = Oa (△OAO1≡△OaO1 より)
③ OA⊥ O1A (接線の性質より)
付随特徴として、
④ 二等分線は、挟んだ円の中心の集まりである
(ピースサインの指にピンポン玉を挟んで指先方向に
⑤ 適当な平行線CDを引くと、△CODは二等辺差角形
(∠ ア=∠ イ、∠ イ=∠ ウ(錯角) ∴∠ ア = ∠ ウ、→ 底角が等しい)
適当な平行線cdも同様に、△cODは二等辺三角形
⑥ OAが2倍になると、O1Aも2倍になる。3倍なら3倍。\(\large{\frac{1}{2}}\) 倍なら\(\large{\frac{1}{2}}\)倍
文字にすると難しくなってしまいますが、
ゆっくり、図の該当場所を鉛筆で押さえながら確認すれば、
なんとなくわかるかと思います。⑤⑥はなんとなくでかまいません。
④ 正三角形の作図
描けそうな気がしますね!

①コンパスをABの長さに広げて、
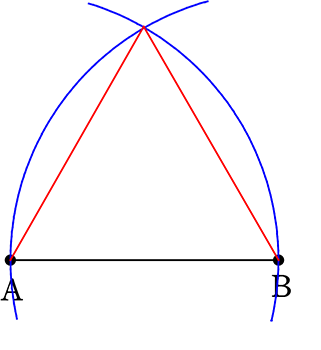
②Aを支点に円をえがき、
開きはそのままに、次に
Bを支点に円を描いて 完成です
【 正三角形の性質 】
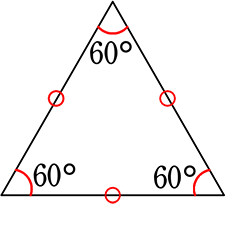
① 3辺が等しい
② 全ての角が等しい (全て60°)
以上が基本の4作図で、今後使える「ツール」となります。
①垂線 が引けますね(90°が書ける)!
②垂直二等分線 が引けますね(中点を見つけられる)!
③角を二等分 できますね(半角にできる)!
④正三角形 が描けますね(60°が書ける)!
「作図」は少しひねられると、できそうでできない…
読めるけど書けない「漢字」のような難しさがあります
できる限り実際に描いてみてくださいね。
《典型例 》


イ 平行移動、回転移動、対称移動
主に方眼紙と定規だけ使う分野です。
当たり前と言えば、当たり前の分野ですね!
① 平行移動
・ 平行移動・・・図形を、「一定の方向」に「一定の距離」だけずらす移動。
・ 一言、「マウス」
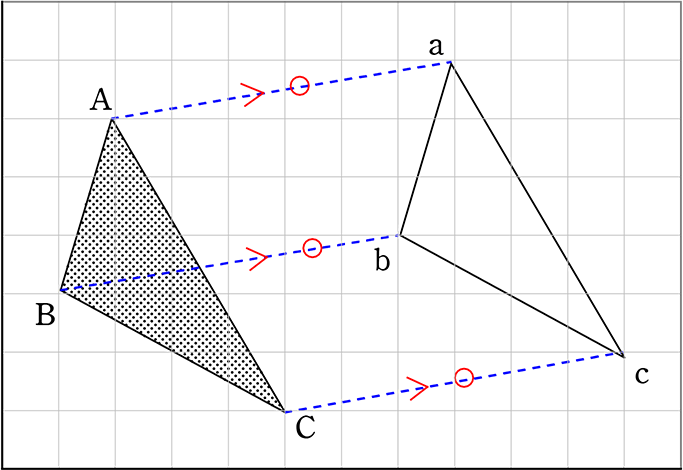
(性質)
① 軌跡(きせき…点が動いた跡)が、同じ長さ (Aa=Bb=Cc)
② 軌跡が、平行 (Aa//Bb//Cc)
(イメージ) は、パソコンのマウスですね 

【 平行移動をコンパスと定規だけで作図 】
《 例 》
△ABC を、点Aを点aに移すように平行移動した図を作図しましょう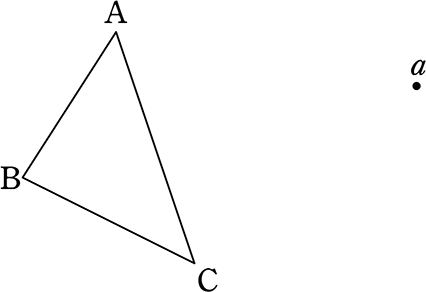
①

背景に平行四辺形をイメージすれば
c の位置がわかりますね
(平行四辺形の性質)
②

AC の開きで、aを支点にc付近
Aa の開きで、Cを支点にc付近
cの確定 (=平行四辺形の完成)
③
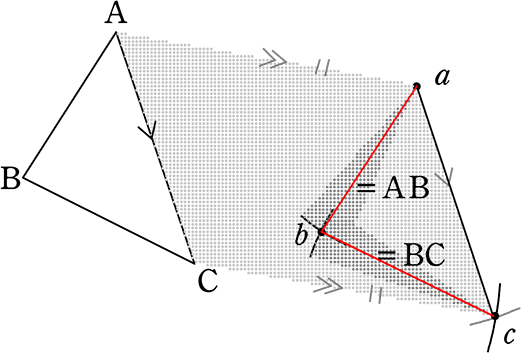
あとは辺acが決まったので
三角形を完成させる ですね
ABの開きで、aを支点にb付近
BCの開きで、cを支点にb付近
→ bの確定
③’ 点bも平行移動で決めるなら(正統?)

再び平行四辺形をイメージ
bはあそこですね
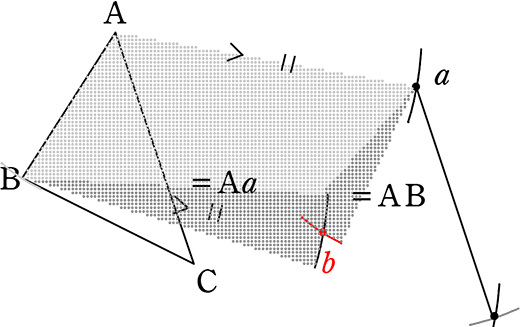
ABの開きで、aを支点にb付近
Aaの開きで、Bを支点にb付近
→ bの確定
cf.
①’何も考えず作図できるのはひし形ですね
→ 開きを何回も変えずに平行線がひける

背後にひし形をイメージして
Aaと平行な線が見えましたね
(ひし形の性質)
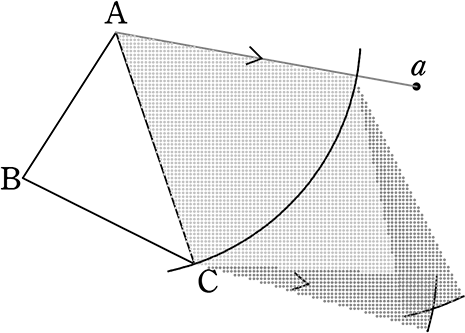
ACの開きで、Aa上の点
そのままの開きで
Aa上の点を支点に平行付近
Cを支点に平行付近
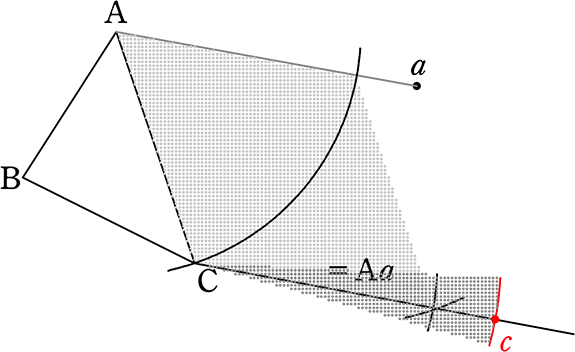
Cと交点を通る線は
Aaに平行ですね
Aaの開きで、Cを支点にすれば
→ cの確定ですね
後は同様に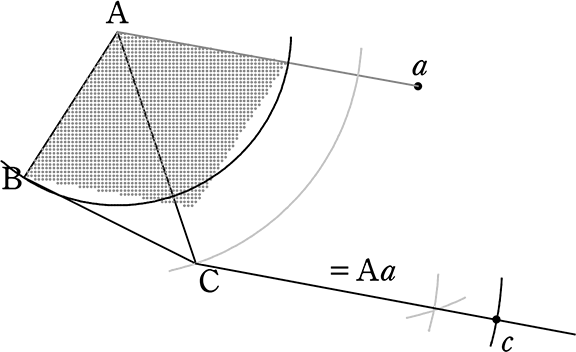
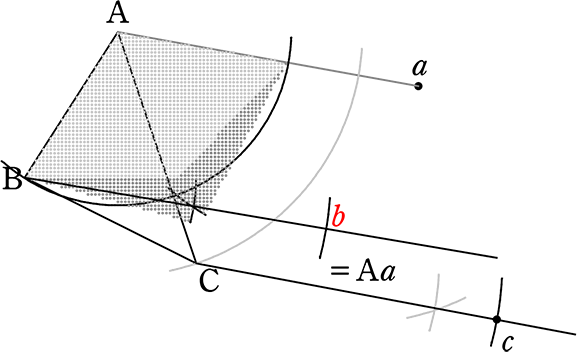
結局は
平行四辺形の作図ですね
② 回転移動
・ 回転移動・・・「ある1つの点を中心」に「一定の角度だけ回転」させる移動。
・ 一言、「太陽系」「風車」
△ABCを時計回りに「90°」回転させた図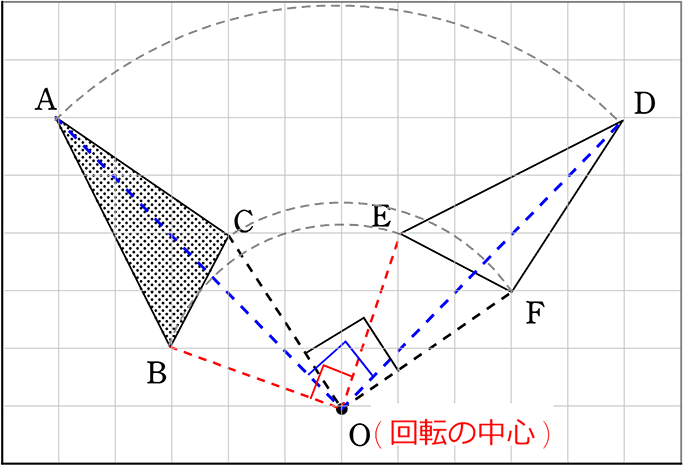
(性質)
① 角度が同じ (∠AOD = ∠BOE = ∠COF = ~°)
② 対応する長さが同じ ( OA = OD、 OB = OE、 OC = OF)
(イメージ) は、風車ですね 
(時計周りに90°の場合の「点」の求め方)
例えば、 Oから左に2、上に3の点C(上図)の場合、
①座標化します…O( 0 , 0 )で…Cは、( -2 , 3 )
②C点を分数化します… \(\large{\frac{上下}{左右}}\)…-\(\large{\frac{3}{2}}\)
③逆数にします…-\(\large{\frac{3}{2}}\) → -\(\large{\frac{2}{3}}\)
④「-1」を掛けます… -\(\large{\frac{2}{3}}\)×(-1) = \(\large{\frac{2}{3}}\)
⑤座標に戻して完成です… \(\large{\frac{2}{3}}\) → F( 3 , 2 )
これは、1次関数の、「傾き」に対する「垂線の傾き」の利用ですが、
今、難しければ、
「2行って、3」は「3行って、2の、90°ぽい所」、
「3行って、1」は「1行って、3の、90°ぽい所」 でOKです!

【 回転移動をコンパスと定規だけで作図 】
《 例 》
三角形 abc は三角形 ABC をある点 O を中心として回転移動したものである。点 O を作図しましょう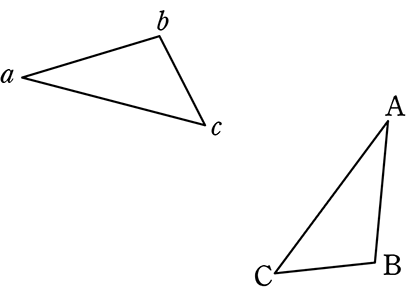
まず、前提知識として1つの円周上での弦の垂直二等分線はどのような弦であっても必ず中心を通りましたね (典型作図)
この原理は、「二等辺三角形の頂角の二等分線は、底辺の垂直二等分線」になります (二等辺三角形の条件)
どの点と中心を結んでもそれは半径なので同じ長さ
→ どんな長さの弦であってもOを頂角とする二等辺三角形の底辺
→ どの二等辺三角形もOが頂点(当然)
→ 二等辺三角形の底辺の垂直二等分線は頂角の二等分線
⇒ ∴ 弦の垂直二等分線は中心Oを通る(集まる)
またこれらは同心円上の円でも成り立ちますね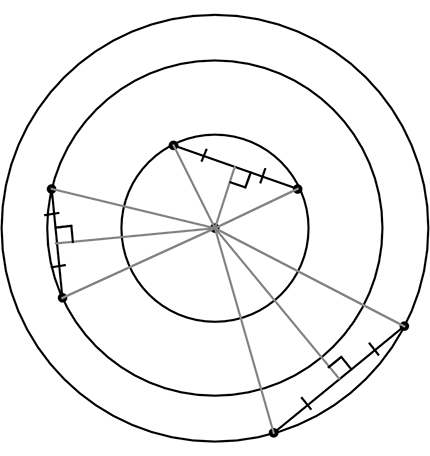
では、問題に戻りまして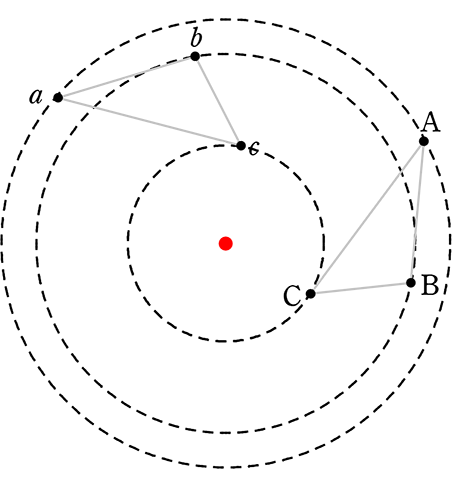
Aとa(地球)、Bとb(金星)、Cとc(水星)はそれぞれ同心(太陽)円周上の点ですね
ということは、弦Aaの垂直二等分線上のどこかにOがある
また弦Bbの垂直二等分線上のどこかにOがある
交わったところが共通のO → 中心ですね
2つで十分「決まる」ので別にCとcの垂直二等分線は省略可ですね
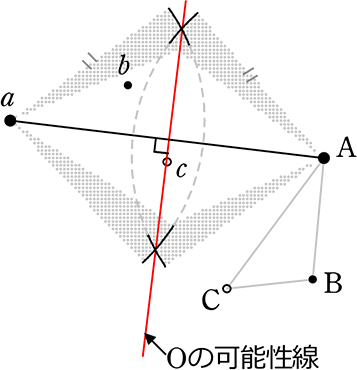
① 弦Aaの垂直二等分線の作図
(垂直二等分線の作図)
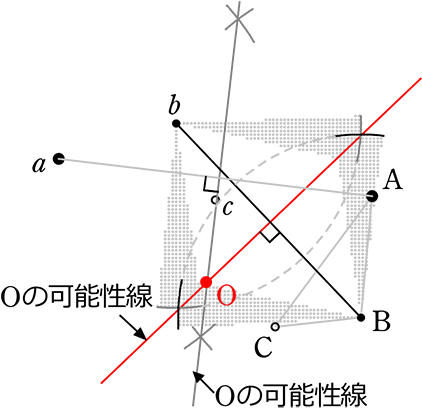
② 弦Bbの垂直二等分線の作図
③ 2つの垂直二等分線の交点が
中心O ですね
確認図で、ポイント確認 → 「対応する点は同じ円周上」「各弦の垂直二等分線の交点が中心」「確かに△OAaは二等辺三角形」
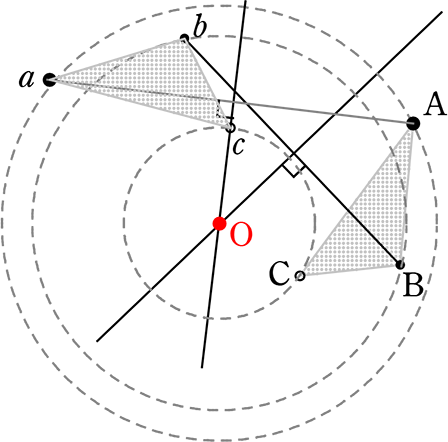
作図の「仕方」で覚えると
線が重なって混乱してしまいますが、
「ポイントの理解」でいつでも描けますね
《 例 》
図の△ABC を、点 O を回転の中心として、反時計回りに (1) 180°、(2) 60°、(3) 30°、(4) 90°、(5) 45° 回転移動して得られる△abc を作図しましょう
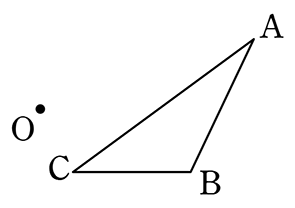
分かりやすいように、各点が動く円を全部書いてしまいますね。
実際は、必要な実線部分だけの円弧を書くと思います
(1) 180°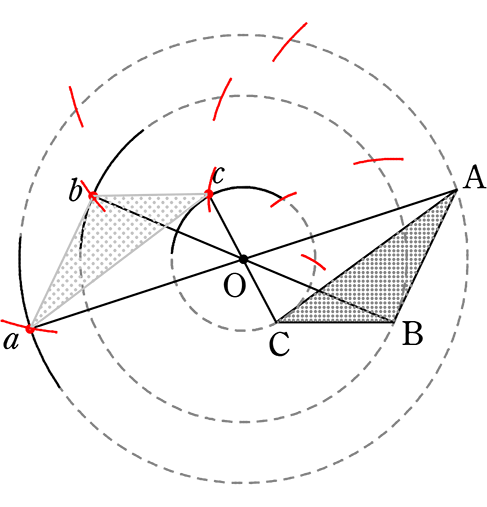
① およそ180°と思われる円弧をそれぞれ書く(黒実線円弧)
② AOを延長した線とAが動く円との交点がa、同様に、BO, COを延長してb, c を決める
②’ (定規による2点の「延長線」を認めない厳しい先生の場合(すべてコンパス)は
コンパスを半径の開きで円周を区切っていけば3つ目が180°ですね
半径の開きで円周を順次区切れば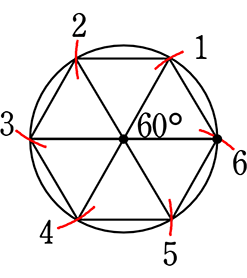
・ 内接正六角形 ・ 正三角形ぴったり6個
・ 円周6等分 でしたね
③ 3点abc を結んで完成
(三角形を動かすというよりも、点を動かすイメージ)
(2) 60°
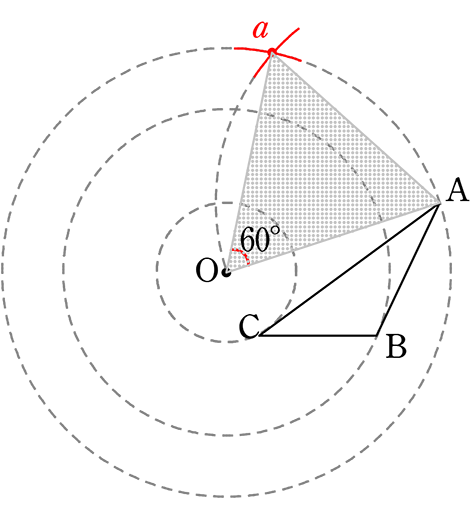
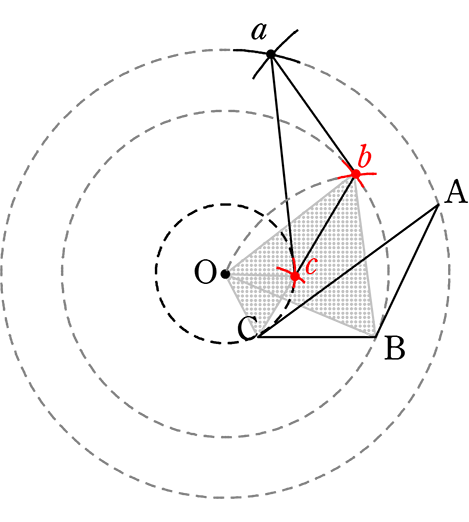
② 同様にBO, COを1辺とする正三角形を
作図して、点b, c を決める
③ 3点abc を結んで完成
(3) 30°
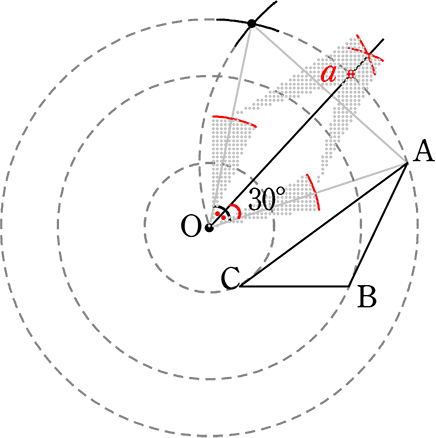
① (2)の正三角形の二等分線と
Aが動く円との交点で、∠AOa=30°ですね
(角の二等分線の作図)
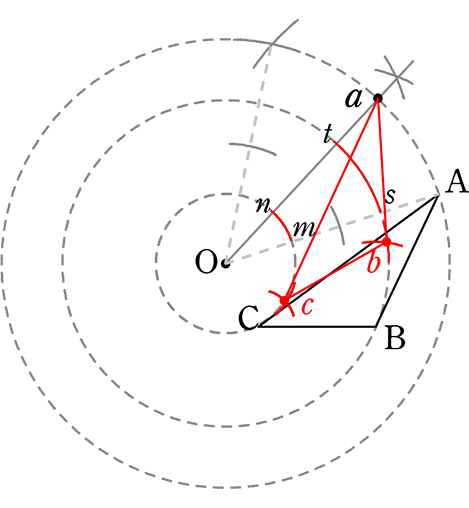
② 当然、st, mn も30°
→ st にコンパスを開いて、その開きのまま
Bを支点にBの動く円との交点がb
同様にmnを利用してc
(もちろん、b, cも a同様
正三角形からの二等分線でもOK)
③ 3点abc を結んで完成
(4) 90°
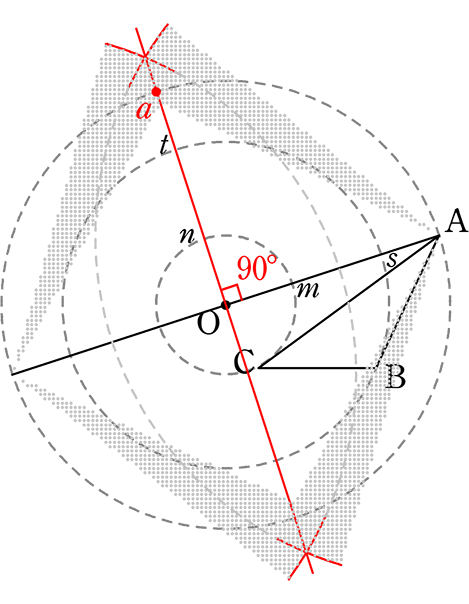
① (1)の180°の点との垂直二等分線と
Aが動く円との交点が90°ですね
② 同様にB, Cの90°の点を決める
③ 3点を結んで完成
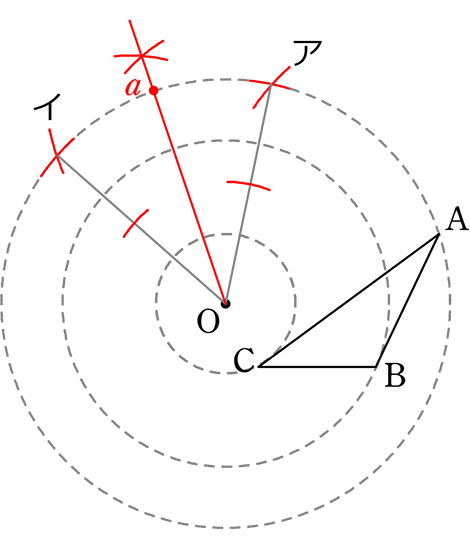
(または)
①コンパスをAOに開いてAを支点にア、
アを支点にイでAア、アイ間はそれぞれ60°
→ その二等分線は
AOからすると60°+30度=90°ですね
② 同様にB, C
③ 3点を結んで完成
(5) 45°
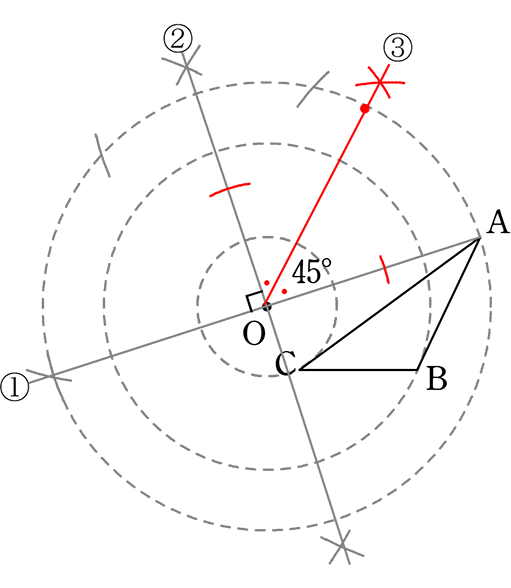
① (1)の180°
② (4)の90°
③ 90°の二等分線は → 45°
④ 同様にB, Cを作図
→ 3点a, b, cを結んで完成
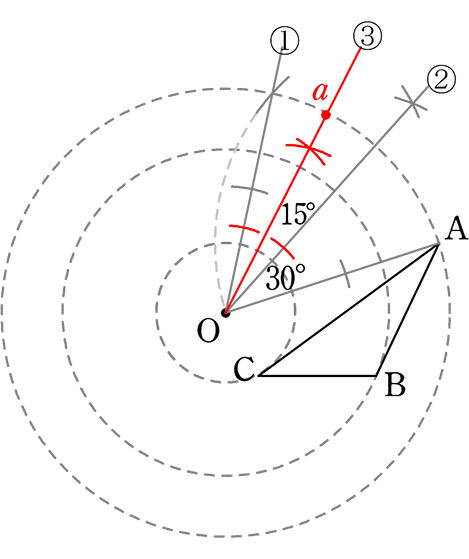
(または)
①’(2)の60°
②’60°の二等分線は30°
③’30°の二等分線は15°
AOからすると、30°+15°=45°
④’同様にB, C を作図
→ 3点a, b, cを結んで完成
作図の方法は他にもいろいろ考えられますが
結局は
① 辺AOから何度の線を引くか(今までの作図)
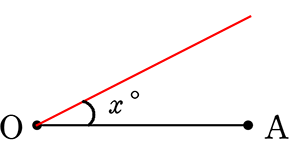
と
② Aの動く円との交点を求めるということですね

(回転移動の作図=今までの作図+長さをそろえる)
・ 点対称移動・・・回転移動の180°バージョン
・ 一言、「2枚羽プロペラ」
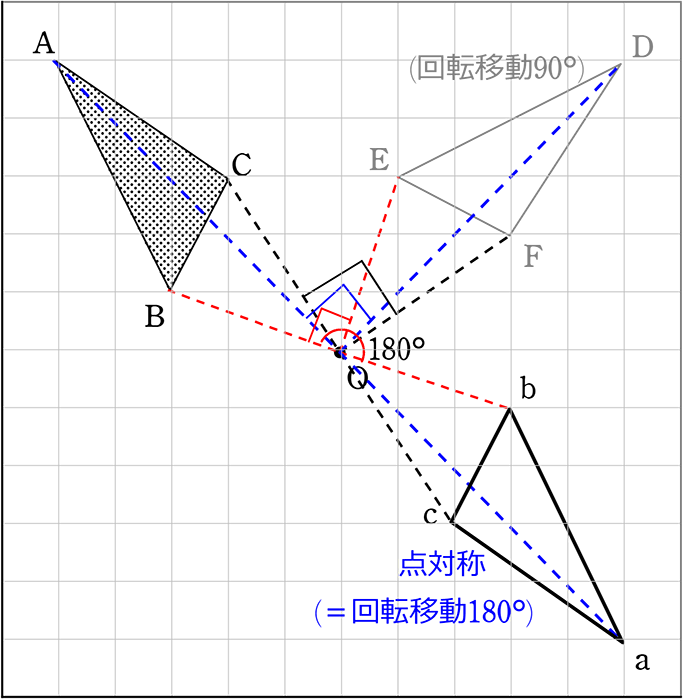
(性質)
① 角度が同じ (∠AOa = ∠BOb = ∠COc = 180°)
② 対応する長さが同じ (OA = Oa、OB = Ob、OC = Oc )
↑当然、先ほどの「回転移動」と同じ性質ですね
(イメージ) は、2枚羽プロペラ 

【 点対称移動をコンパスと定規だけで作図 】
回転移動の180°バージョンと同じでしたね

③ 対称移動
・ 対称移動・・・「対称の軸」(折り目)で折り返す移動
・ 一言、「ノート」
普段、「対称移動」と言えば、「点対称移動(180°回転移動)」ではなく、この「線対称移動」を指します。
△ABCを、直線lを「対称の軸」として対称移動させた図
(性質)
① 垂直に交わる (Aa⊥l、Bb⊥l、Cc⊥l)
② 対応する長さが同じ ( Al1 = al1、Bl2= bl2、Cl3 = cl3)
③ 結果、l は垂直二等分線になる
(イメージ) は、そのまんま「ノート」ですね 

【 対称移動をコンパスと定規だけで作図 】
《 例 》
△ABCを直線lを対称の軸として、(線)対称移動させた図を作図しましょう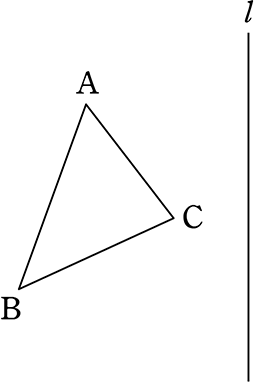
①
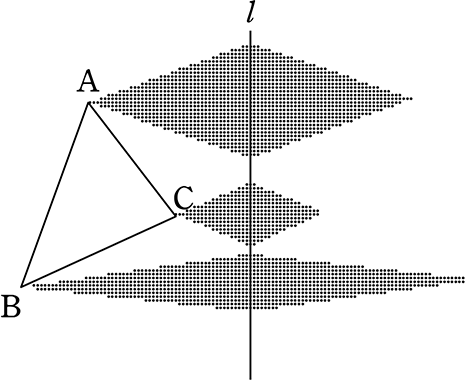
背景に適当なひし形をイメージ
点a, b, c が見えましたね 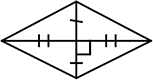
②
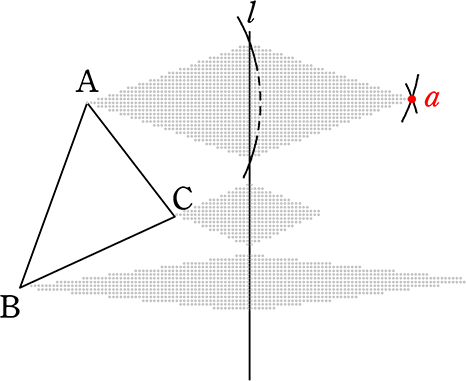
Aを支点に、lを越えるくらいの開きで2点
そのままの開きで2点を支点にa付近
→ 交点で aの決定 ですね
同様にb, c もすればOKですね
ウ 図形の面積
おさらいとなります
① 平行四辺形系の面積
長方形の面積 = (底辺)×(高さ) でしたね

大前提の 1×1 ですね
単位は、cmなら 1cm2、mなら 1m2、
μm(マイクロメーター)なら 1μm2、
単位ナシなら、単位ナシで、ただの「1」
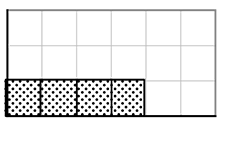
「1」×4コ で 4
結局は、4(底辺)×1(高さ)で 「4」ですね

「4」が3段 で 12
結局は、4(底辺)×3(高さ)で 「12」ですね
平行四辺形(どんな平行四辺形)も「底辺」と「高さ」を変えずに
「長方形」に変形できますので・・・↓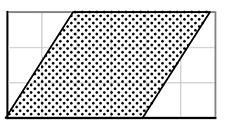
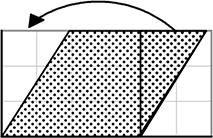
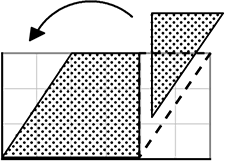
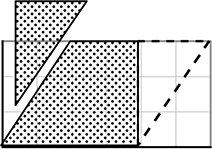

結局は、平行四辺形も長方形同様 4(底辺)×3(高さ)で 「12」ですね
② 三角形の面積
三角形の面積 = \(\large{\frac{1}{2}}\)×(底辺)×(高さ)
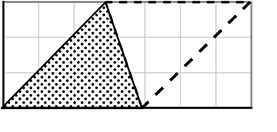
→ 2つ合わせると必ず「平行四辺形」
→ その半分という「\(\large{\frac{1}{2}}\) 」がつきますね
\(\large{\frac{1}{2}}\) ×4(底辺)×3(高さ) = 6
③ 底辺共有2三角形の面積
底辺共有2三角形の面積 = \(\large{\frac{1}{2}}\)×(底辺)×(
または \(\large{\frac{1}{2}}\)×(
(ひし形)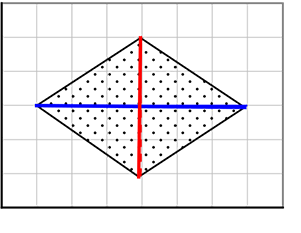
青:底辺 赤:高さ
\(\large{\frac{1}{2}}\)×6×(2+2) = 12
(たこ形)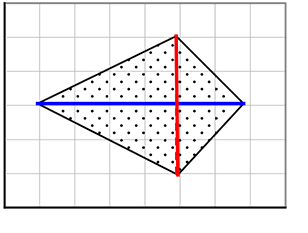
\(\large{\frac{1}{2}}\)×6×(2+2) = 12
(変形たこ形)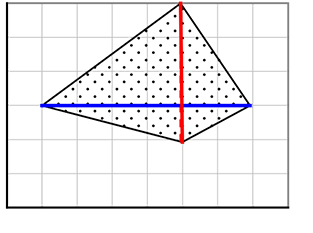
\(\large{\frac{1}{2}}\)×6×(3+1) = 12
(底辺共有2三角形)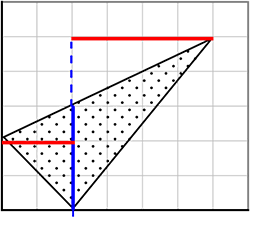
\(\large{\frac{1}{2}}\)×3×(2+4) = 9
(高さ共有2三角形)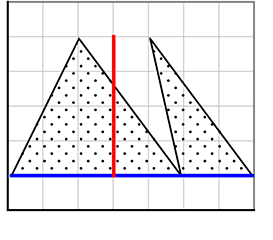
\(\large{\frac{1}{2}}\)×(5+2)×4 = 14
(台形)(=高さ共有2三角形)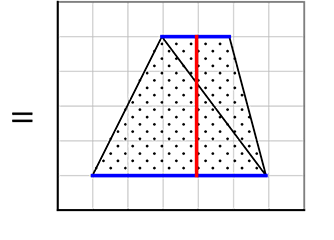
\(\large{\frac{1}{2}}\)×(5+2)×4 = 14
「上底+下底」の意味が
はっきりしましたね
原理は同じですので、個別に「公式」を憶える必要はないということですね!

四角形の分類
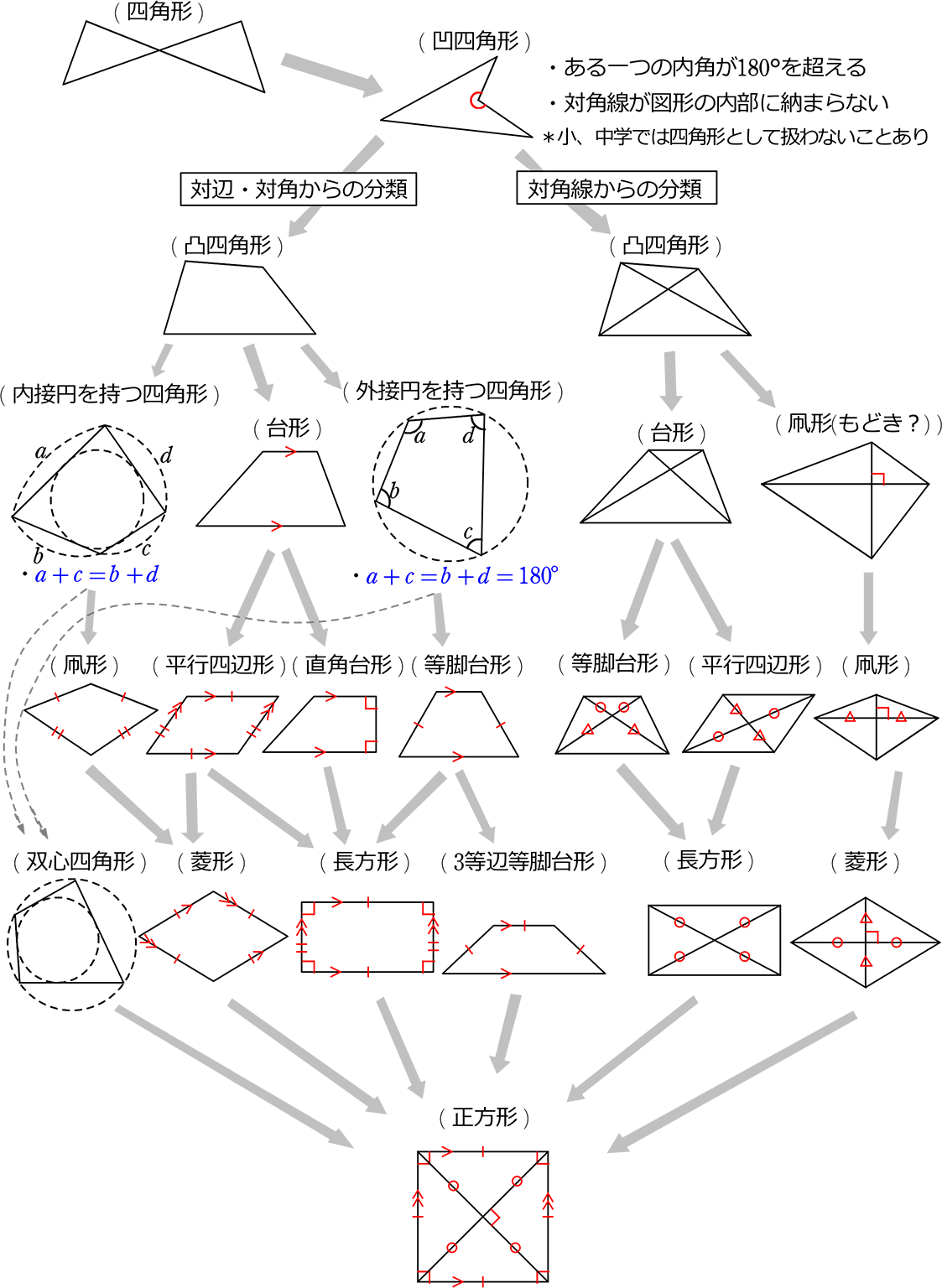
④ 円の面積と円周
円の面積は
半径×半径×円周率(およそ 3.14) でしたね
ですが、数学では
・半径は、「r」 (radius)
・直径は、半径の2倍ということで、「2r」
・円周率は、3.14を使わず「 π(パイ)」とします
よって、
円の面積 = r2π = πr2 でOKです。楽ですね!
↑並び順は何でも構いません。
ゴロがいいからこの並び順なのでしょうね「パイアールのにじょう」
ということは、円周 (直径×円周率3.14)は
円周 = (r+r)π = 2rπ = 2πr ですね!
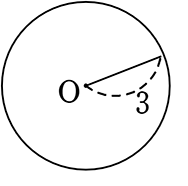
円の面積は、3×3×3.14 = 28.26 としなくても、
3×3×π =9π // でいいのです!
円周は、3×2×3.14 = 18.84 としなくても
3×2×π = 6π でいいのです!
楽でいいですね!

円周率とは
「円周率」とは、「直径」に対する円周の「比」ですね
(簡単に言うと、直径を まる~く包むための倍率)
どんな長さの直径に対しても、円周率を掛ければ
その直径に対する円が描けるということですね!
イメージ的には
①

を 3.14倍 したら
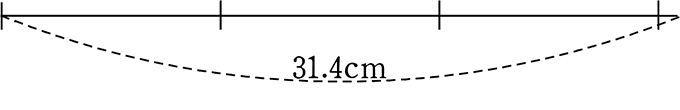
になる
そして、10cmを、この 31.4cmで丸く包むと・・・
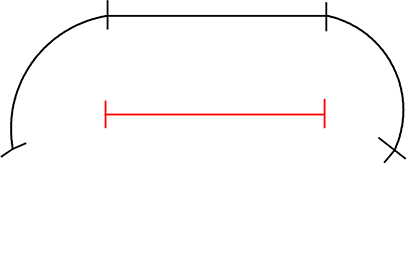
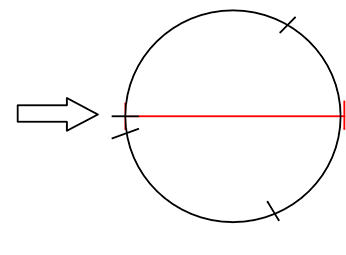
直径10cmの「円」になる
という感じでしょうか。
② または、直径10cmの円を転ばせば、1周で31.4cmの地点にある、という感じでしょうか。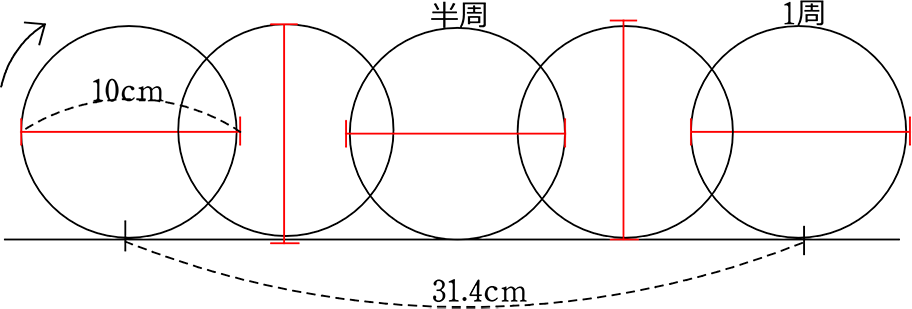
そして、円周率は「循環しない無限小数」です。
「π」 = 3.141592・・・・永遠に続きます(現在、2000兆桁目を超えています)
ということは、一時期話題になった「円周率は3で計算」、
正確には「手計算においては円周率を3とする(電卓計算なら3.14)」
の「3」においても、「3.14」においても、「3.14159」においても、
必ず直径より、ほんの、ほんの少しだけ小さい円ができるということですね。
例えば、直径3cm があります
・円周率「2」とすれば
3×2 = 6 (= 3cmの往復)
直径に全然届きませんね
・「3」の場合
3×3=9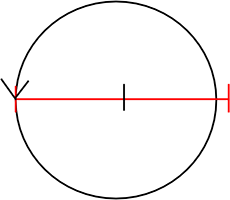
・「3.14」の場合
3×3.14 = 9.42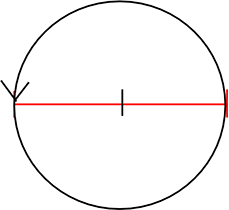
・「3.14159」の場合
3×3.14159 = 9.42477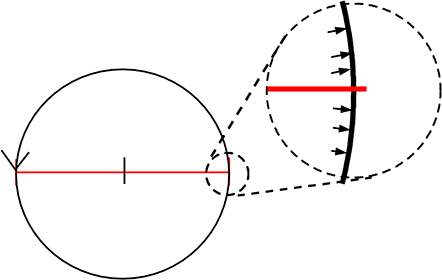
ミクロン単位で、円が直径の端に届かない
というふうに、桁数が多いほど「正確」に近づきますね!
= 円の縁が直径の端に限りなく近づきますね!
だけど、絶対に届きはしないのです・・・
そして どこかで「切り上げ」た瞬間、直径を超えてしまいます
超精密工業製品などの製造は「3.14159……」と何桁目まで掛けるのでしょうね?

道路標識の「R」

すなわち「国道16号線」という意味ですね。
今回の「R」は、こちら


道路のカーブを半径で表示してますね
半径が小さいほど「急」カーブになりますので、
カーブの手前で「十分に減速するように」と注意しています
カーブ中に減速すると、外側の前タイヤに
「遠心力のG」+「ブレーキのG」がダブルでかかりますので
タイヤの滑り出しが早くなりますね、危険です!
カーブ中はできる限り、同じ速度か、少し加速が安定しますので、
カーブの手前で十分に減速を終わらせておきましょう。
タイヤの接地力が、遠心力に負けると、外側に滑り出して、
ガードレールとあいさつすることになりますね!
とは言いましても、実際の運転中に、R(半径)120m の標識が出てきても
「急カーブ?緩いカーブ?」「わかりませ~ん」ですね
まだ直径の方がイメージできるかなとは思いますが・・・
限界速度のデータがあります
「車種」「タイヤの性能」「重さ」など、色々な要素で
変化するとは思いますが、
| 半径 | 乾燥路面 | 濡れた路面 |
|---|---|---|
| r = 20m | 40km/h | 30km/h |
| r = 40m | 60km/h | 45km/h |
| r = 60m | 70km/h | 55km/h |
| r = 100m | 90km/h | 70km/h |
のようですが、憶えておくことは不可能ですので、
「今の速度より、20km/h 落としておく」くらいでよいのではないでしょうか。
ちなみに、
| ・ | 東名高速の最小半径Rは、300m (神奈川県と静岡県の県境あたり、下り左ルート右ルートで分かれている区間内に R300カーブがあります。 実際の恐怖心は「勾配」も関係してきますので、その付近の上り車線(東京向き)、「坂を下りながらの緩いカーブの方が10倍怖いですね!) |
| ・ | 新東名高速の最小半径Rは、3000m 以上! (カーブよりも たくさんあるトンネルを抜けた瞬間の横風(谷風)に注意ですね! |
お疲れ様でした !!
その他の問題は、「問題集」で !!















