| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平面図形 | (2) 空間図形 |
| ア | 空間における直線や平面の位置関係 |
|---|---|
| ① | 平面と点 の関係 |
| ② | 直線と直線 の関係 (ねじれの位置とは) |
| ③ | 直線と平面 の関係 |
| ④ | 平面と平面 の関係 |
| イ | 空間図形の構成や表現 |
| ① | 立体の名称 |
| ② | 立体の各部名称 |
| ③ | 正○○柱、正○○錐とは |
| ④ | 正多面体 |
| ⑤ | 平面の回転 (回転体) |
| ⑥ | 投影図 |
| ⑦ | 展開図 |
| ⑧ | 図形の切断 |
| ウ | 扇形の弧の長さと面積、基本的な柱体、錐体、球の表面積と体積 |
| ① | 表面積 |
| ② | 扇形 |
| ・ | 円錐の側面積πlr |
| ・ | 扇形の面積S=1/2lr |
| ③ | 球の表面積 |
| ④ | 体積 (体積の公式) |
空間図形
ア 空間における直線や平面の位置関係
平面図形が「2次元の図形」なら、
空間図形は「3次元の図形」、すなわち「立体」ですね！
① 平面と点 の関係
・平面に、点が「1つ」のとき、
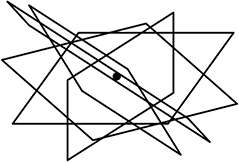
平面は、「自在」に「無限」に位置がある
イメージは、一本足の椅子に座った感じ
またはウエイターさんが お盆を指1本でトレイを支える感じ
・平面に、点が「2つ」のとき、
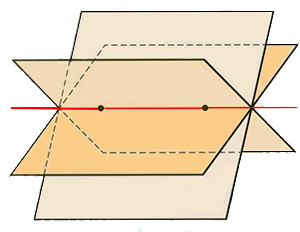
平面は、「回転軸を軸」に「無限」に位置がある
イメージは、2本足の椅子に座った感じ
またはウエイターさんが お盆を指2本でトレイを支える感じ
・平面に、点が「3つ」のとき、
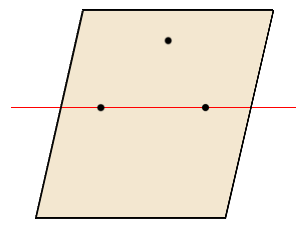
平面が、「1つ (１か所)に決まる」
ただし、その3点が一直線上な配置な場合は
上の点が「2つ」と同じことですね →1か所に決まらない
イメージは3本足の椅子に座った感じ、初めてカチッと「安定」しますね
またはウエイターさんが お盆を指3本でトレイを支える感じ
グラグラしないということですね
「決まる」 とは
「(1つに)決まる」とは…
・「ピタッとなる !」
・「グラグラしない !」
・「それしかない !」
・「そこしかない !」
・「それ以外考えられない !」
という状況、状態
② 直線と直線 の関係 (ねじれの位置とは)
直線は、直線の両端を(にょい棒のように)永遠に延ばし続けたら
①交わる
②交わらない
の2通りですね。
②の交わらない理由は、
1.平行だから
2.「ねじれの位置」にあるから
の2通りですね。
平行 とは
同一の平面上にあって、
両方向に限りなく延長しても、
いずれの方向においても互いに交わらない直線
ねじれの位置 とは
2直線が(延長しても)交わらない位置関係で、
「平行の場面」を除いたもの
また、
「交わる」場合と、「平行」の場合の2つは、「同一平面上」にあると言えますね
《 例 》
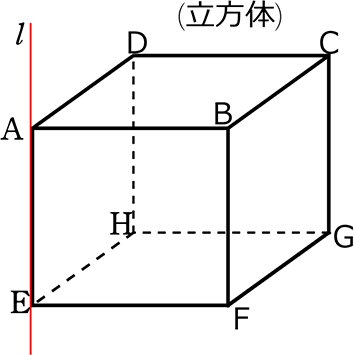
ADは 直線lと、交わる
ABも、EHも、EFも、同様に交わる
DHは 直線lと、交わらない (平行なので)
CGも、BFも、交わらない (同じく平行なので)
DCは 直線lと、交わらない (ねじれの位置にあるので)
BCも、HGも、FGも、交わらない (同じくねじれの位置にあるので)
クリック・タップで答え (反応が遅い場合があります)
クリック・タップで答え (反応が遅い場合があります)
③ 直線と平面 の関係
先ほどまでは
「平面」と「点」、「直線」と「直線」の関係でしたね
次は
「平面」と「直線」、
その関係は 3通り ですね
(平面を拡大し続ける、直線を延長し続けるイメージを頭の片隅に持っておいてくださいね)
① 直線が平面上にある
② 交わる
この時、必ず一か所は「90°」の箇所がある
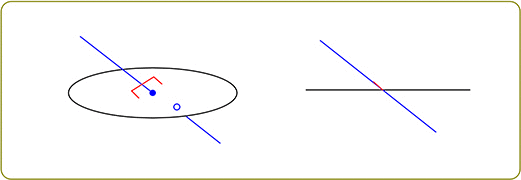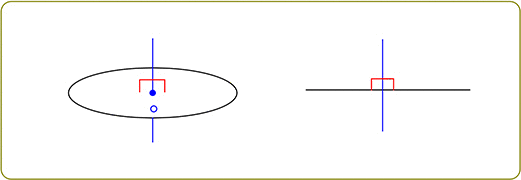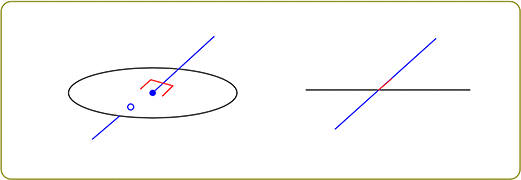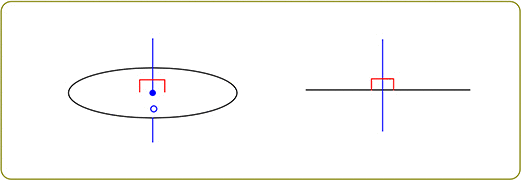
イメージは、電車のアクセルでしょうか
ということは、他にもう１か所(合計2か所) 垂直な場所がある場合には、
Pとlは、「垂直」に交わっているということになりますね
(上図のレバーを垂直に立てるように)
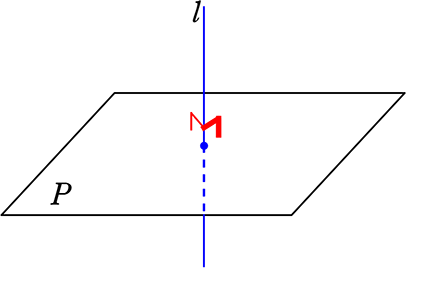
2か所垂直であることを
証明できれば、
P⊥l といえますね
③ 交わらない
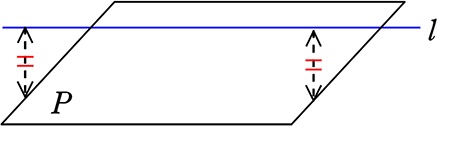
→ 平行の場合だけですね
平面P//直線l → P//l
少しでも傾いていれば、
いずれ必ず、交わる！
④ 平面と平面 の関係
平面と平面の関係は 2通り ですね
2つの平面をそれぞれ拡大し続ければいずれ・・・
①交わる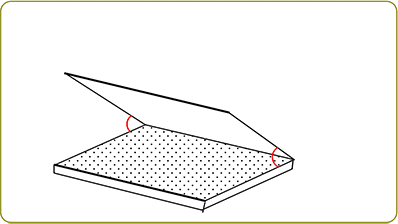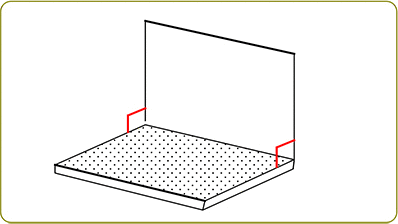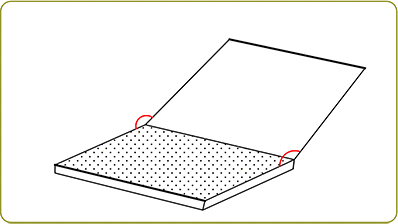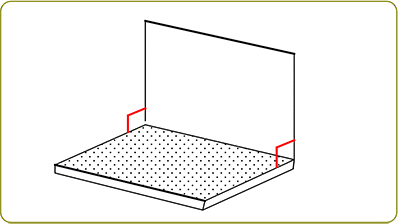
→ ノートパソコンの折り目部分が 2つの平面の交わる部分ですね
→ 2平面が平行でない場合は 必ずこの部分が発生しますね
②交わらない (平行のときだけ)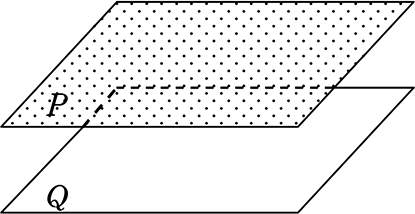
イ 空間図形の構成や表現
① 各立体の名称
まずは名前を憶えてしまいましょう
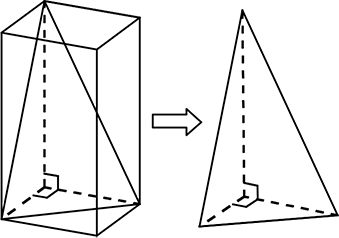
頂点が、中心からずれていても「三角錐」です。
とにかく とがっていれば「～
② 立体の各部名称
③ 正○○柱、正○○錐とは
① 底面が、「正三角形」「正方形」、「正～角形」の場合で、
② 側面の面たちが、全て同じ形の場合
「正三角柱、正三角錐」、「正四角柱、正四角錐」、「正～角柱、正～角錐」と言いますね。
では、「ピラミッド」は、正～錐でしょうか？
答え． 正四角錐ですね！
正多面体
正多面体の条件
1. すべての面が同じ形
2. 頂点に集まる面の数が全て同じ
2. へこみがない
ですね
この世に5種類しかありませんので、
(数学っぽくはないのですが) 英単語のように憶えてしまいましょう
→「辺の数」は、例えば、正十二面体の場合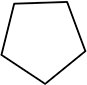
一つの面には5つの辺
ですが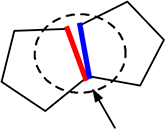 
となりの面もその辺を持つ！
他の辺に関しても同様なので…
ダブり防止のため「2」で割るですね！
→「頂点の数」は、例えば、正十二面体の場合
1つの頂点をつくるのに
3つの辺が必要なので
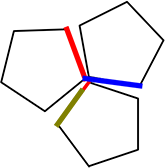
「3」で割れば
辺のダブりが解消されますね
ちなみに、
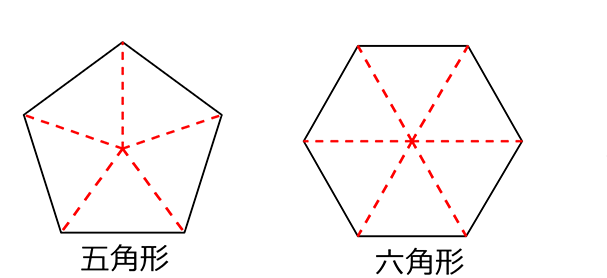
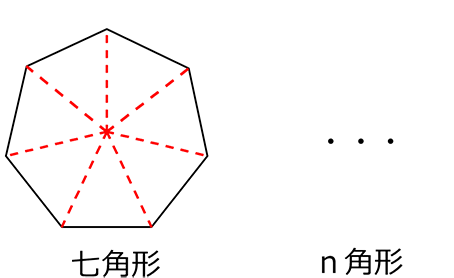
・サッカーボールは、
五角形と六角形でできていますから
正多面体ではないですね！
・正四面体を2つ合わせた多面体は
全ての面が正三角形ですが…
3つの面が集まる頂点と、4つの面が集まる頂点がありますので、
正多面体ではないですね！
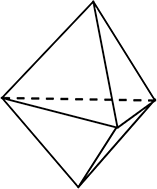
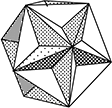
・図は、全ての面が同じ形、
全ての頂点には同じ数(10個)の面が集まりますが、
「へこみ」部分があるので
正多面体ではないですね！
⑤ 平面の回転 (回転体)
「点」を動かすと「線」が 
「線」を動かすと「面」が 
「面」を動かすと「立体」ができますね！
そして、「平面」をある軸で、回転させても立体ができますね、
これを「回転体」と言います。
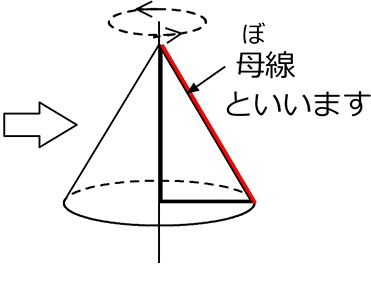
「円錐」ができました
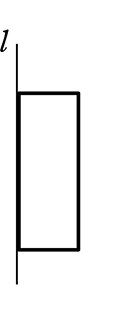
「円柱」ができました
【 回転体の特徴 】
・ 回転体を、「軸に垂直な平面」で切った「切り口」は、
切る位置に関係なく必ず『円』である。
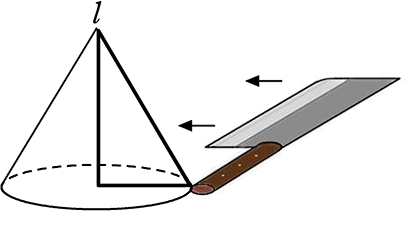
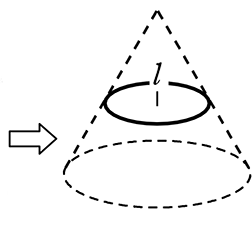
・ 回転体を、「軸を含む平面」で切った「切り口」は、
「軸を対称軸」とする『線対称』な図形である。
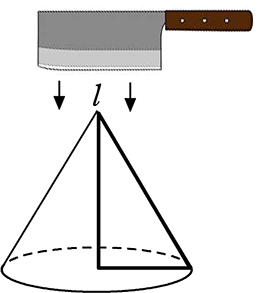
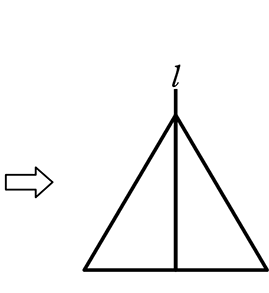
・ 回転体は、「軸を含む平面(ガラス)」について、
「面を対称面」とする『面対称』な図形である。
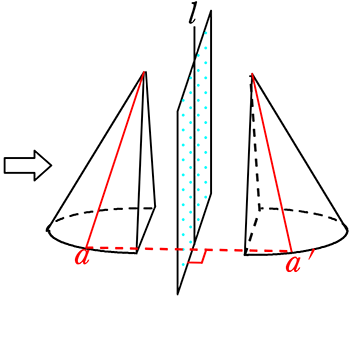
【 軸に接する三角形の回転体体積 】
《 例 》
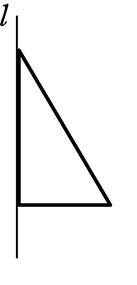
次の3つの△ABCをl軸を回転軸として1回転させた立体の体積を求めましょう
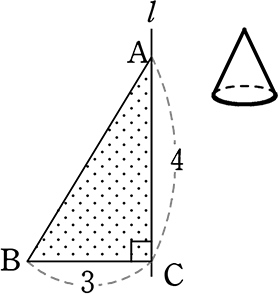
体積 ＝ \(\large{\frac{1}{3}}\)・底面積・高さ
＝ \(\large{\frac{1}{3}}\)・9π・4
＝ 12π
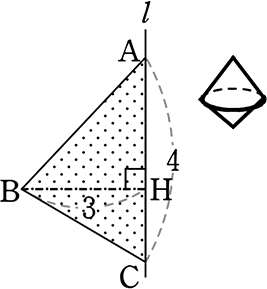
体積 ＝ 上円すい+下円すい
＝ \(\large{\frac{1}{3}}\)・底面積・高さ+\(\large{\frac{1}{3}}\)・底面積・高さ
＝ \(\large{\frac{1}{3}}\)・9π・AH+\(\large{\frac{1}{3}}\)・9π・CH
＝ 3π(AH+CH)
＝ 12π
体積 ＝ 大円すい-小円すい
＝ \(\large{\frac{1}{3}}\)・底面積・高さ-\(\large{\frac{1}{3}}\)・底面積・高さ
＝ \(\large{\frac{1}{3}}\)・9π・AH-\(\large{\frac{1}{3}}\)・9π・CH
＝ 3π(AH-CH)
＝ 12π
どれも同じ体積ですね！
すなわち、結局は
回転軸に接する三角形の回転体の体積 ＝ \(\large{\frac{1}{3}}\)・最大回転面積・軸に接する長さ
ですね
《 例 》
回転体の体積を2通りで求めてみましょう
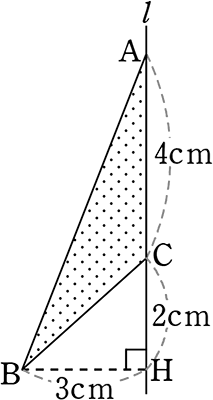
(方法①)
体積 ＝ 大円すい-小円すい
＝ \(\large{\frac{1}{3}}\)・9π・6-\(\large{\frac{1}{3}}\)・9π・2
＝ 18π-6π
＝ 12π cm3
(方法②)
体積 ＝ \(\large{\frac{1}{3}}\)・最大円面積・軸に接する長さ
＝ \(\large{\frac{1}{3}}\)・9π・4
＝ 12π cm3
⑥ 投影図
投影図は、
「真上」から見た図(平面図)と、
「真正面」から見た図(立面図)で表す方法ですね
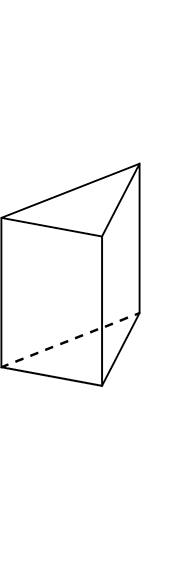
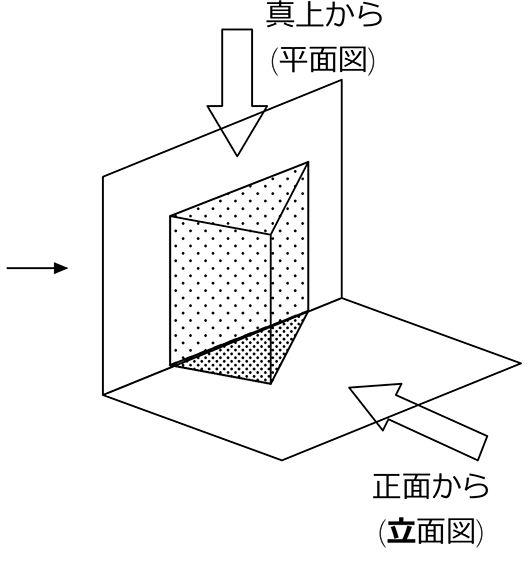
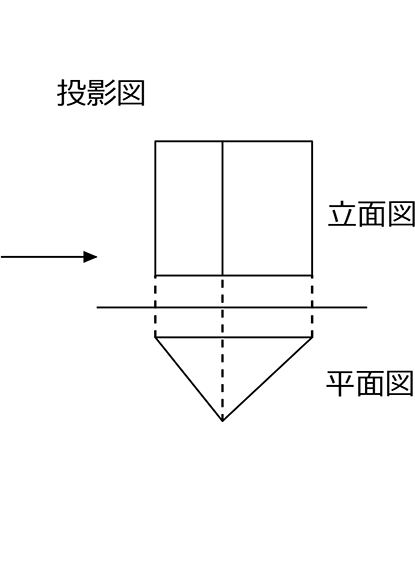
立面図、平面図、どっちが上だったっけ？ となったら…
適当に立てた三角柱などを描いて
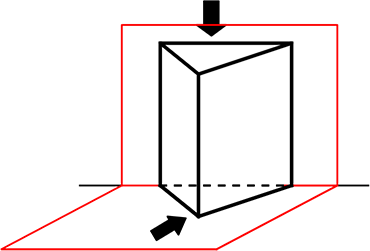
背後に2つ折りの台紙を描いて
●
● 上空から見て立体感がなくなってしまって、
平面化したものが描かれる「平面図」が「下」
ですね
⑦ 展開図
立体をばらした図ですね、設計図みたいなものです
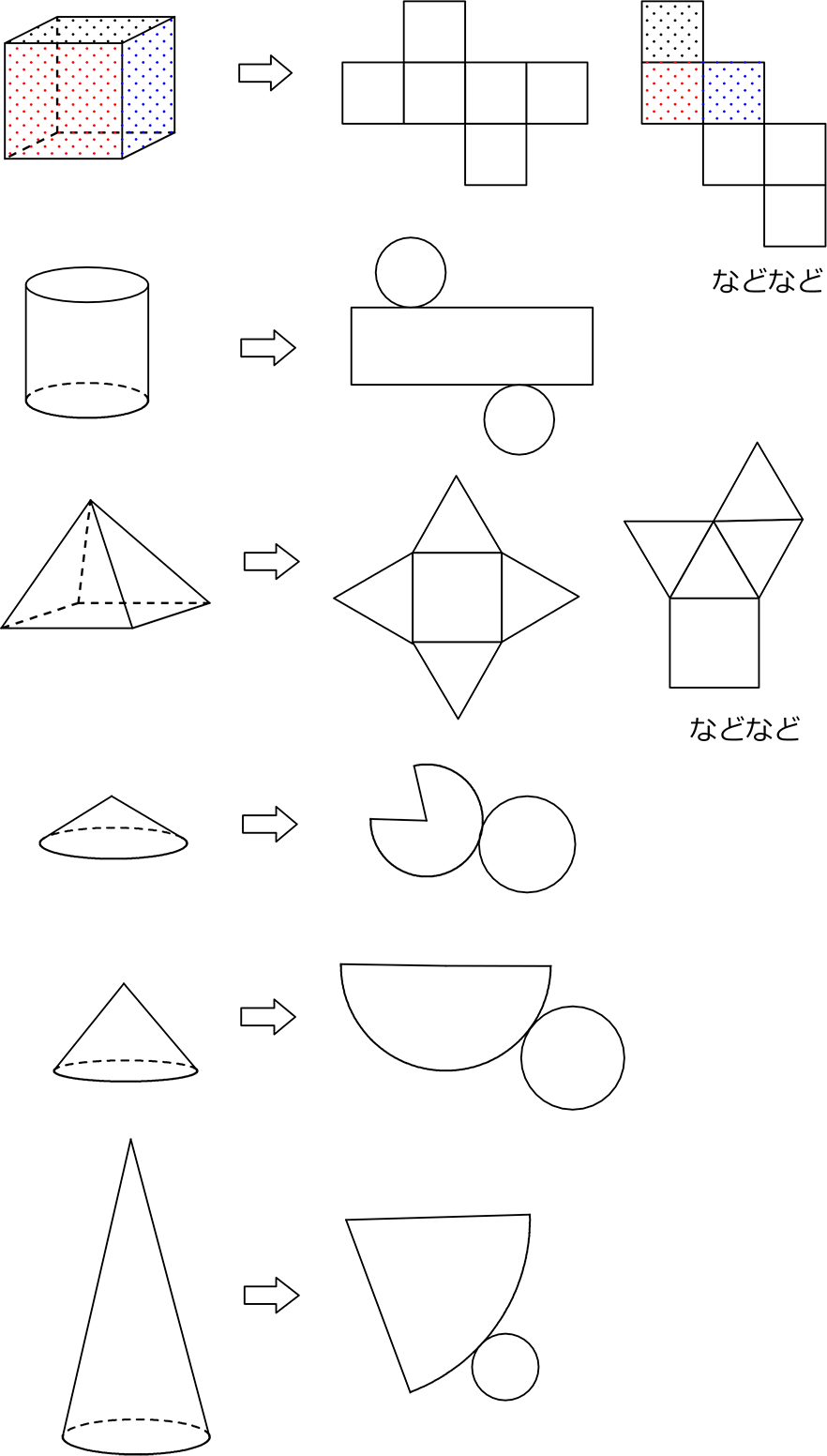
【 立方体の展開図の見分け方 】
(前提) 6面からなる
(基本形) 位置を 
として、
展開図の基本形を 
や 
としますね
そして、面は『同じ線上なら転がってもよい』ので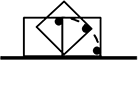
同じ線上〇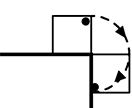 
同じ線上でない×
や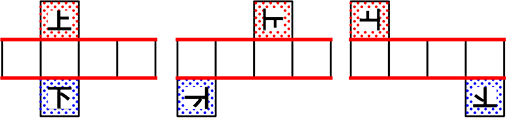 
も基本形ということができますね！
逆を言えば、「同じ線上で転がして、基本形になれば展開図としてOK」ということですね！
《 例 》
図は立方体の展開図になりますか
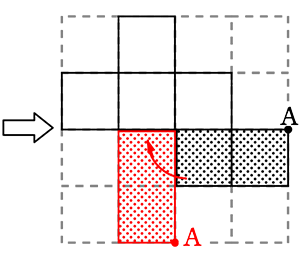
2ついっしょに転がしても
OKです
→ 基本形になったので
→ 展開図になる
図形の切断
立体を包丁で切断すると、
切り口がいろいろな形になりますね
《 例 》
立方体ABCD‐EFGHがあります
M、Nはそれぞれの辺の中点です
MNをふくむ平面で切るとき、考えられる切り口の形は？
直線MNは決定ですね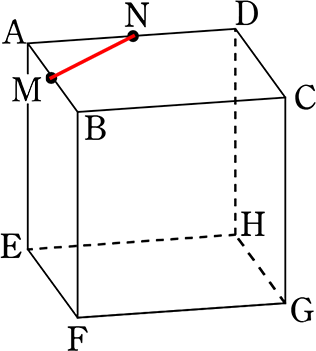 
2点を含む平面では平面は「決まり」ませんでしたね (平面と点)
正三角形
二等辺三角形
長方形
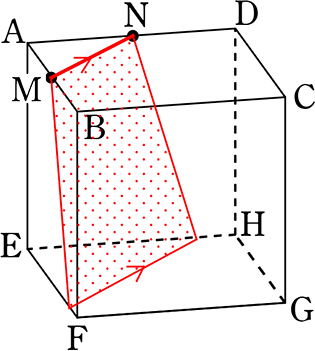
台形
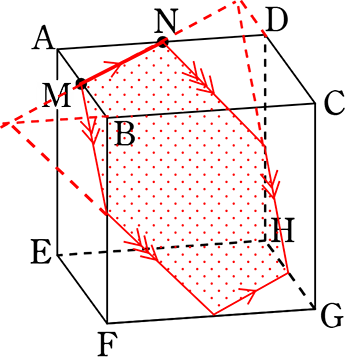
六角形
(全て中点を選べば正六角形)
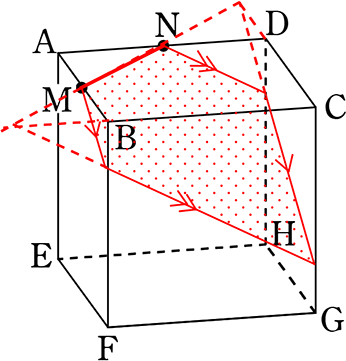
五角形
2点を含む平面では平面は「決まり」ませんので
大きく分けて、「三角形」「四角形」「五角形」「六角形」の
4つも考えられますね
この点、M、N、Gの(一直線上にない) 3点を指定されていたら・・・
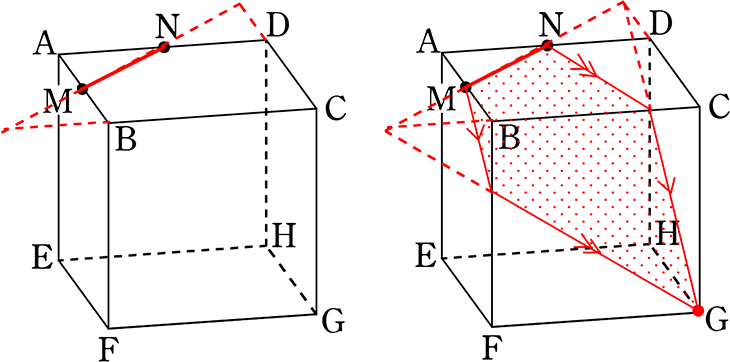
五角形の一つに「決まって」いましたね
豆腐の味噌汁をつくっているときに
豆腐だけ切らしてもらいましょうね！
立方体を何個かつくって、いろいろ試してみてくださいね
〔 切り口の書き方の要点 〕
① 切り口の線は必ず立体の表面上にある
(立体の内部を通って点をつないではいけない)
② 立体の 平行な面にある切り口どうしは必ず平行
③ 辺を延長した交点と遠い点(上のGなど)をつなぐと1平面がイメージできる
【 直方体(立方体)を二等分する平面 】
対角面 ←造語です(対角線を含む平面)は直方体や立方体を二等分しますね
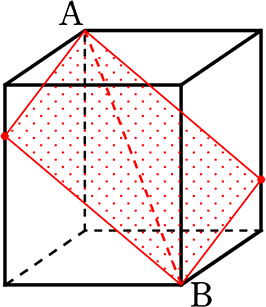
これら対角面(対角線を含む平面)で分けられた立体は、すべて体積が同じですね！
例えば(ウ)を完全に分けてみると…
このように分けられて、
そして、(ウB)を手前に1回転させると
左右対称な図形とわかりますね
すなわち、「同じ体積」「二分する」ですね！
対角面は直方体(立方体)を二等分する
《 例 》
図は、1辺の長さ6cmの立方体である。
点I, Jはそれぞれ辺BC、辺AD上の点で、BI ＝ DJ ＝ 2cmである。
この立方体を、3点F, I, Jを通る平面で切って2つに分けるとき、
点Cを含む側の立体の体積を求めよ
切断面をいれると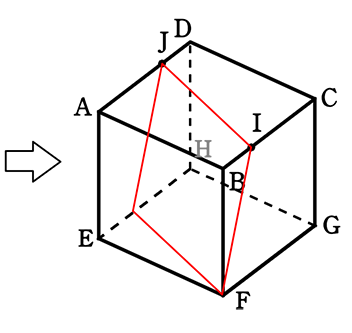
対角面を利用したいですね
JがFの対角になるように
直方体ABKJ‐EFLMで考えると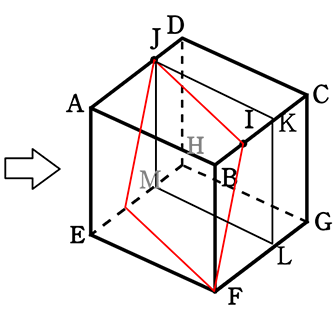
・ABKJ‐EFLMはJKCD‐MLGHの2倍
・対角面はABKJ‐EFLMを二等分する
すなわち、
点Cをを含む側の立体の体積は、全直方体の\(\large{\frac{2}{3}}\)とわかる
∴ 点C側体積 ＝ \(\large{\frac{2}{3}}\)・全直方体
＝ \(\large{\frac{2}{3}}\)・6・6・6
＝ 144 cm3
ウ 扇形の弧の長さと面積、基本的な柱体、錐体、球の表面積と体積
① 表面積
立体の『表面積』は、それぞれの面の面積を足し合わせるだけですね。
展開図を書く必要は、そんなにはないかなと思いますが、
慣れるまでは書いた方がいいのかな、とも思います。
他方、
立体を構成する「面」は、
円を除いて、全て三角形で構成されていますね。
というわけで、「面積の求め方」はすでに勉強済みですので
「表面積」は、各面積を足す、それだけですね！
② 扇形
それでは、本題の「扇形(おうぎがた)」です
円錐の展開図の側面部分は必ず「扇形」になりますね
も扇形ですね。円が少しでも欠ければ「扇形」です
扇形で問題になるのは
「中心角の大きさ」
「弧の長さ」
「面積」
の3つだけです
そして、実は『割合』の問題ともいえますね
割合の公式は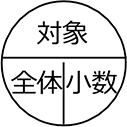
だけでしたね
これを扇形に当てはめると、
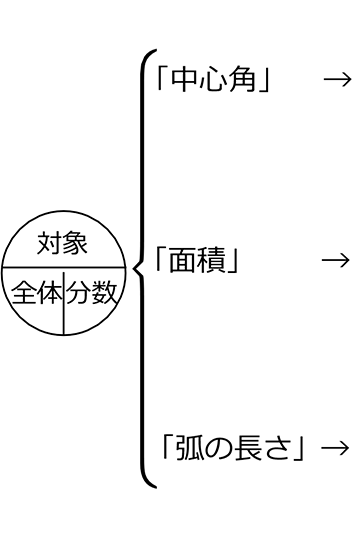
扇形は、この「分数(割合)」が必要なのです！「分数」を求めたいのです！
そして、「同じ半径の円」なら、
この「割合」は
「中心角」「面積」「弧の長さ」 全てに共通なのです
例えば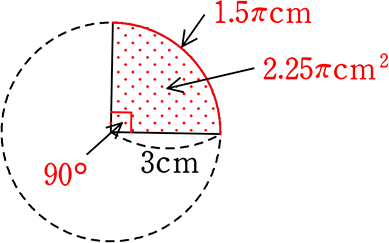
の扇形の場合、
・中心角は、\(\large{\frac{対象}{全体}}\) ＝ \(\large{\frac{90°}{360°}}\) 
＝ \(\large{\frac{1}{4}}\)
・面積は、\(\large{\frac{対象}{全体}}\) ＝ \(\large{\frac{2.25\pi cm^2}{9\pi cm^2}}\) 
= \(\large{\frac{1}{4}}\)
・弧の長さは、\(\large{\frac{対象}{全体}}\) ＝ \(\large{\frac{1.5\pi cm}{6\pi cm}}\) 
= \(\large{\frac{1}{4}}\)
この「\(\large{\frac{1}{4}}\) (0.25 = 25％)」という「割合」を求めたいのです
この「\(\large{\frac{1}{4}}\)」さえ解れば、
あとは「全体 360° や 全面積 や 全円周」に「\(\large{\frac{1}{4}}\) 」を掛ければ、
それぞれ、「対象」(扇形の「中心角・面積・弧の長さ)が求まりますね！！
なんとなく気づいたとは思いますが、
角度の「全体」は、円の大きさに関係なく、常に「360°」ですね！
一番楽に「割合」を出せるということですね！ \(\large{\frac{60°}{360°}}\) = \(\large{\frac{1}{6}}\) !みたいに！
そして、この「\(\large{\frac{1}{6}}\) 」という「割合」を利用して、
扇形の「面積」や「弧の長さ」を求めたりしていたのですね。
ということは、中心角が解らない時は、
ミチミチと「面積」や「弧の長さ」から「割合」を求めればよい。
ということですね！
円錐の側面積
これでもう「円錐の側面積」も求められますね！
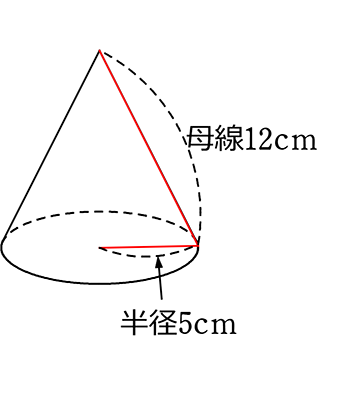
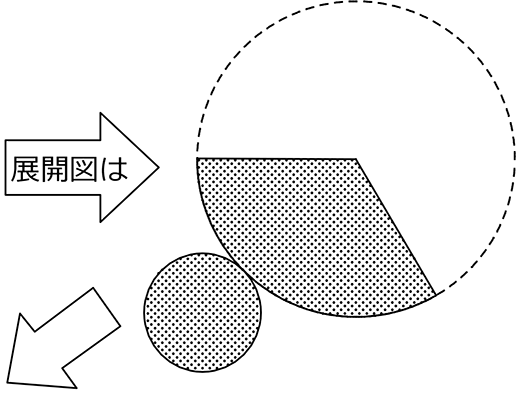
データを書き込むと、
底面の半径は、扇形の「弧の長さ」のヒントだったんですね！
もう、みなまで解くな！という感じですが、念のために、
扇形の「中心角」も「面積」も解らない、
→「弧の長さ」から「分数(割合)」を求めるのだな！
割合 ＝ \(\large{\frac{対象}{全体}}\) ＝ \(\large{\frac{扇形の弧の長さ}{大円の円周}}\) ＝ \(\large{\frac{小円の円周}{大円の円周}}\) = \(\large{\frac{10\pi }{24\pi }}\) 
= \(\large{\frac{5}{12}}\) (=0.416…=≒41.6％)
扇形の面積 = 全面積×\(\large{\frac{5}{12}}\) = πr2×\(\large{\frac{5}{12}}\) 
= 60π A. 60π cm2
ちなみに、表面積は、 側面積+底面積 = 60π+25π = 85π A. 85π cm
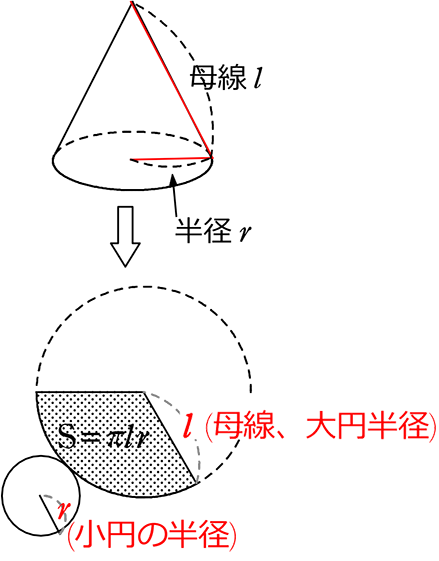
円錐の側面積の公式 πlr
公式集でよく見る「円錐の側面積 S＝πlr」
これはどういう意味なのでしょうか？
360など、数字が一つも出てこないけど・・・？？
もう、すぐに理解できると思います！
繰り返しになるようで申し訳ないのですが、
上の問題で、数字を文字に置き換えてみますね
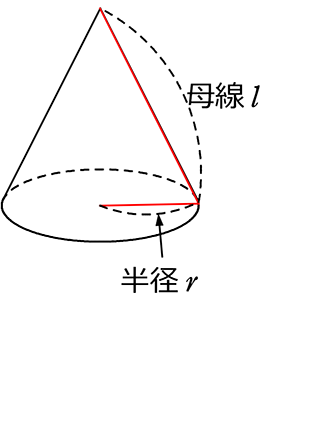
データを書き込むと、
扇形の「中心角」も「面積」も解らない、
→「弧の長さ」から「分数(割合)」を求めるのだな！
割合 = \(\large{\frac{対象}{全体}}\) = \(\large{\frac{扇形の弧の長さ}{大円の円周}}\) = \(\large{\frac{小円の円周}{大円の円周}}\) = \(\large{\frac{2r\pi}{2l\pi}}\) 
= \(\large{\frac{r}{l}}\) ← イメージしにくいですがこれが「分数(割合)」です
扇形の面積 = 全面積×割合 = l2π×\(\large{\frac{r}{l}}\)
= πlr ですね
「証明」されましたので、今後は公式として利用可能です！
円錐の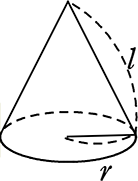
扇形の面積公式 S = 1/2lr
まったくの余談公式で憶える必要はありませんが
扇形の面積公式 S = \(\large{\frac{1}{2}}\)lr
初めて見ると「何…これ?」となってしまいますので、
念のため触れておきますね
(問) 扇形の面積を求めましょう
(中心角が90°に見えますが、正方形に収まっている訳でなく…不明！ですね)
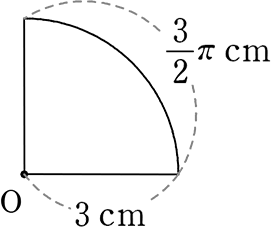
解① 扇形の面積
= 全円面積×割合
= πr2×\(\large{\frac{弧}{全弧}}\)
= πr2×\(\large{\frac{弧}{円周}}\)
= πr2×\(\large{\frac{弧}{2\pi r }}\) …ア
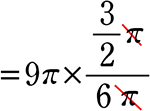
= 9π×\(\large{\frac{1}{4}}\)
= \(\large{\frac{9}{4}}\)π cm2 ですね
解② 扇形の面積 = \(\large{\frac{1}{2}}\)lr (l = 弧の長さです)
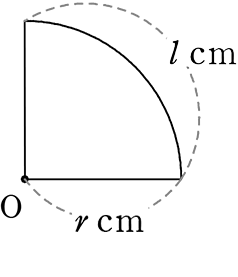
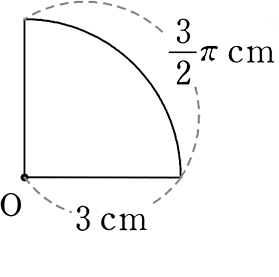
= \(\large{\frac{1}{2}}\)・\(\large{\frac{3}{2}}\)π・3
= \(\large{\frac{9}{4}}\)π cm2 となります
(原理) 解①のアですね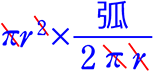
= \(\large{\frac{1}{2}}\)弧r = \(\large{\frac{1}{2}}\)lr ですね
いつもの公式のただの「ショートカット」バージョンですね！
よって、憶える必要はないですね、なぜなら
→①割合を求める場合、
・扇形の「弧の長さ」を与えられた問題…0.1％
・扇形の「面積」を与えられた問題…0.1％
・扇形の「中心角」を与えられた問題…99.8％
→②円錐の側面積の公式 S = πlr のlやrと混乱してしまう
よって、
扇形の「面積」や「弧の長さ」はやはり
「全面積」×割合、 「全弧(円周)」×割合
で十分ですね！
憶えるのであれば、日本語で
扇形の面積 = \(\large{\frac{1}{2}}\)・弧・半径 ですね！
【 イメージ 】
ペタン ペタンと落としていくと・・・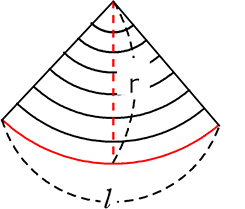
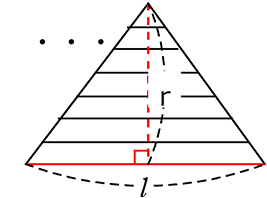
・・・三角形になります
これを超超超薄紙で行うと、斜辺もツルツルですね！
③球の表面積
球の表面積は、公式で憶えてしまいましょう。
なぜなら、その証明は高校レベルの、それもかなり深い部分だからです。
その割に、公式自体は簡単ですので、中学で扱うのでしょうね！
球の表面積の公式
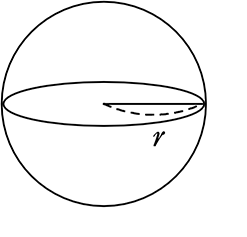
球の表面積 S = 4πr2
なぜか、中の円の面積を「4倍」すると球の表面積になりますね！
中学ではこれで十分です！
球の表面積 = 
×4
④ 体積
とうとう１年生数学 図形の終盤ですね！
「難しくはありません！」・・・大人のような言い回しですいません！
「簡単です！」と言いたいのですが、なぜか、そう言うのが怖いのです・・・
・柱体( 
)…「底面積」×「高さ」
・錐体( 
)…\(\large{\frac{1}{3}}\)×「底面積」×「高さ」
・球( 
) …\(\large{\frac{4}{3}}\)πr3 (これも表面積と同様の理由で、憶えてしまいましょう)
以上です！
ここで、「高さ」とは、
「上底」や「頂点」から「底面のある面」に下した「垂線」になります
「垂線」が「底面」から外れていてもかまいません。
「底面」のある平面までの「最短距離」が「高さ」です。
「底面」は、必ず床にくっついている面、である必要は全くありません。
自分が、「最もイメージしやすい」「最も計算がしやすい」面を
見つけてくださいね！自由です！
3年「三平方の定理」を学んだ後には、
この「空間図形」の応用問題はグッと難しくなりますね！
正確には「難しくなる」ではなく→「空間認識力が
お疲れ様でした !!
その他の問題は、「問題集」で !!
