| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 資料の散らばりと代表値 |
| ア | ヒストグラムや代表値の必要性と意味 |
|---|---|
| ① | 値の種類(名前)とその意味 |
| ・ | 調整平均の必要性 |
| ② | 度数分布表 |
| ・ | 未満の対義語は何? |
| ③ | 度数分布表での代表値 |
| ④ | 相対度数 ・ 累積相対度数 |
| ⑤ | 統計的確率 |
| ⑥ | ヒストグラム |
| ・ | グラフの種類 |
| ⑦ | 度数折れ線 (度数分布多角形) |
| ・ | ヒストグラム・度数折れ線での代表値 |
| ⑧ | 四分位数 |
| ・ | 四分位範囲 |
| ⑨ | 箱ひげ図 | ・ | 三角グラフの読み方 |
| ・ | 行と列の覚え方 |
| ・ | ボクシングの体重別階級表 |
| ・ | ~の…に対する〇〇 |
| イ | ヒストグラムや代表値による資料の傾向の把握と表現 |
| ・ | 彼を知り己を知れば百戦殆うからず |
| ・ | 各代表値の長所と短所 |
| ウ | 近似値 |
| ・ | 四捨五入…正確には |
| ・ | 誤差 |
| ・ | 真の値の範囲 |
| ⑩ | 有効数字 |
| ・ | 大人は「有効数字」を理解しやすい |
資料の散らばりと代表値
ア ヒストグラムや代表値の必要性と意味
① 値の種類とその意味
この単元は、たくさんの名詞が出てきます。
内容自体は、難しい計算もありませんので、
シミレーションしながら、「専門用語(名詞)」と「その意味」を憶えてしまいましょう
「面積、あれね!」くらいのレベルになるくらいに!
「階級値、あれね!」 みたいに!
専門用語が出てきたら、赤い字にしますね!
では、あなたは「クラス男女39人を受け持つ先生」です。
(0点~100点の)テストをしました。
生徒の点数は、次のようでした。

まさに「ただのデータ(資料)」ですね
「最大値」、「最小値」すら
探すのが大変ですね!
辛うじて「100点」が目立つので
「男子の最大値は100」と分かりますか…
あと、「点数の合計(
「平均値 (代表値の1つ)」は分かりますね
平均値
平均値 = 
・男子の平均値 = \(\large{\frac{1388(点)}{20(人)}}\) = 69.40(点)
・女子の平均値 = \(\large{\frac{1324(点)}{19(人)}}\) = 69.68(点)
・全体(男女)の平均値 = \(\large{\frac{1388+1324}{20+19}}\) = 69.54(点)
ただのデータ
| ・ | 「平均値」がわかる |
| ・ | かろうじて「最大値」、「最小値」が分かる |
では、次に、もう少し意味のあるデータ(資料)にするために、
点数の「
ここでは、「昇順 (低い順)」に並び替えますね。
「ただのデータ(資料)」が「昇順 (低い順)のデータ」になりました!
かなり個別データの取り出しやすいデータになりましたね!
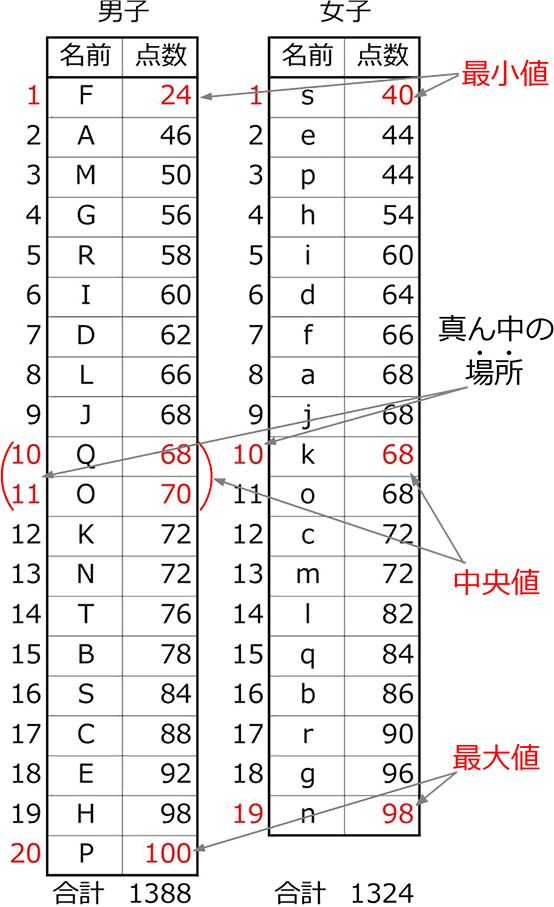
最小値
1番小さい値
・男子の最小値 = 24
・女子の最小値 = 40
・全体の最小値 = 24
最大値
1番大きい値
・男子の最大値 = 100
・女子の最大値 = 98
・全体の最大値 = 100
真ん中の場所
真ん中の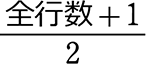
・男子の真ん中の場所 = \(\large{\frac{20+1}{2}}\)= 10.5 (行目)
・女子の真ん中の場所 = \(\large{\frac{19+1}{2}}\) = 10 (行目)
→このように
偶数行の場合、2つの行の間にある
奇数行の場合、1つの行に決まる
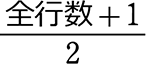 も憶える必要はありません、その都度、左手を見て→「5本指は奇数行」→「真ん中は中指」→「左から数えても右から数えても3番目」→「3を出すためには…1を足して2で割ればいいのか」で十分ですね
も憶える必要はありません、その都度、左手を見て→「5本指は奇数行」→「真ん中は中指」→「左から数えても右から数えても3番目」→「3を出すためには…1を足して2で割ればいいのか」で十分ですね
偶数行なら親指を折って → 4本指の真ん中は2.5 → ということは…と同様にするだけですね
行数の少ない表なら計算しなくても、見ただけで真ん中の場所が分かりますね!
中央値 (メジアン) ( = 第2四分位数)
中央値 = 真ん中の場所にある値
(真ん中の場所が行の境目の場合 → 境目の前後の平均
| ・ | 偶数行の場合 → 「真ん中の場所」の前後2つの値を足して2で割ったもの |
| ・ | 奇数行の場合 → 「真ん中の場所」の値 |
※ 中央値(メジアン)は「平均値」ではありません、あくまで表の「真ん中に位置する」値です(場所の問題です)
・男子の中央値 = \(\large{\frac{68+70}{2}}\) = 69
・女子の中央値 = 68
もう一度同じ表です
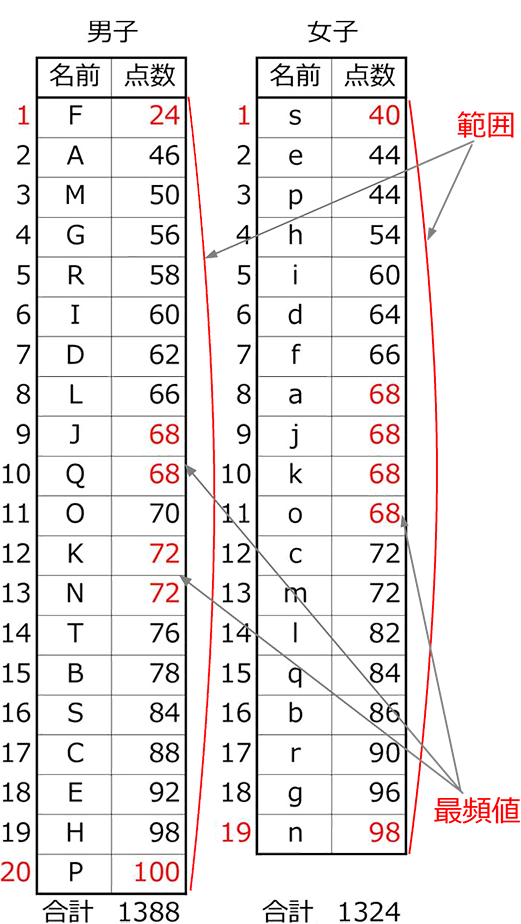
範囲 (レンジ)
範囲 = 最大値-最小値
range:ある範囲内のもの
※ テストの点数の範囲は0~100点
ですが、このときの「範囲」とは
表に収められている値を対象
にします
・男子の範囲 = 100-24 = 76
・女子の範囲 = 98-40 = 58
→ 76>58 男子の値の方が
ばらつきがあると言える
最頻値 = 1番よく出てくる値
(最も
| ・ | 男子の最頻値 = 68と72 (2人) (今回は2つですが、テスト問題では1つのはずですね) |
| ・ | 女子の最頻値 = 68 (4人) |
その他、「調整平均」(最も低い値、最も高い値から同数個除いた平均)
というものがあります。
ex.

調整平均 = \(\large{\frac{52+54+56+58+60}{5}}\) = 56

調整平均 = \(\large{\frac{54+56+58+58}{4}}\) = 56
こういった平均を「調整平均」といいますね。
上にでてきた、「平均値」「中央値」「最頻値」(「調整平均」)をまとめて、
代表値 (そのデータから『標準を知ろうとする値』) といいます。(何のために代表値を調べるの?)
代表値 
平均値
中央値
最頻値
(調整平均)
↑調整平均は中学ではあまり出てきませんね
よって
並び替えただけで
| ・ | 「最大値」、「最小値」が一目で分かる |
| ・ | 「範囲」がすぐに分かる |
| ・ | 「中央値」「最頻値」などの『代表値』がすぐに分かる |
| (・ | 調整平均を求めやすくなる) |

調整平均の必要性
どうして、「調整平均」というものがあるのでしょうか?
例えば、人が点数をつける競技がありますね。
スケート、体操、ボクシング、モーグル…たくさんありますね!
スケート、体操などは点数をつける審判はおよそ「9名」います。
このとき、ないとは思いますが、
嫌いな選手には0点、好きな選手には10点をつける「ひいき審判A」がいたとします。
x選手の演技点数が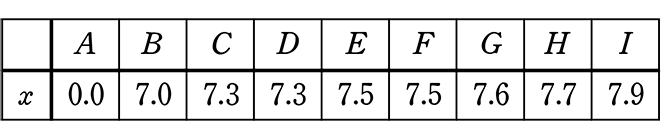 だとしたら、
だとしたら、
点数 = 平均点数 = \(\large{\frac{総点数}{総(人)数}}\) = \(\large{\frac{59.8点}{\color{red}{9人}}}\) = 6.64点ですね!
「大体どの審判も7点以上つけているのに、A審判のせいで6.64…」
不公平な平均点 = 正確でない平均点 という気持ちになりますね!
→ このような平均値から遠く外れた(平均値を乱す?)値を「
そこで、かけ離れた小さな値を除いて、その代わりに(反対側の)最高点も除いて出す平均点を「調整平均」といいます。

→ \(\large{\frac{7.0+7.3+7.3+7.5+7.5+7.6+7.7}{\color{red}{7人}}}\) = 7.41点 が調整平均となります。
「より正確といえる平均値」なのでしょうね。
A, B 2人の点数を除いた場合は、反対側の I, H 2人の点数も除きます(マイナス両端同数)です。
人の価値観が入ると難しいですね。人の気持ちの調整(調整平均?)
さて、
次に思うことは、おそらく…
「表が大きい! もう少しコンパクトにしたい」、でしょう。
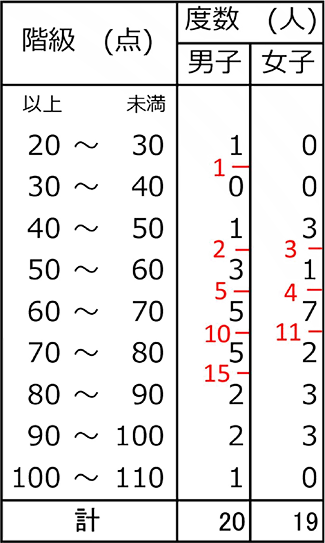
② 度数分布表
ボクシングや柔道のように、個別的な値(点数、体重など)を階級別にすれば、
表がコンパクトになりますね!
上の表を、例えば10点刻みの表にすると…
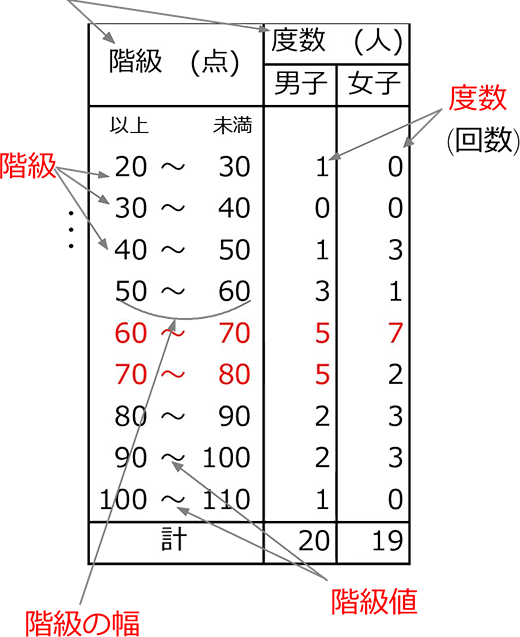
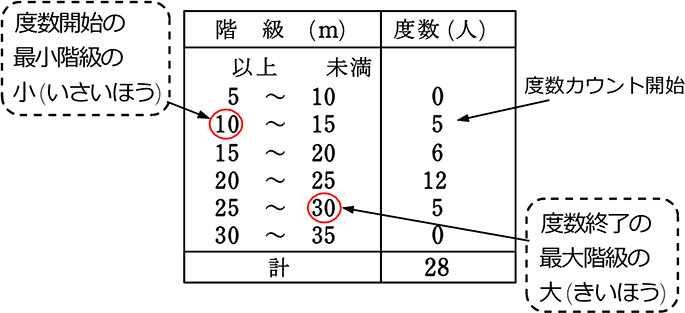
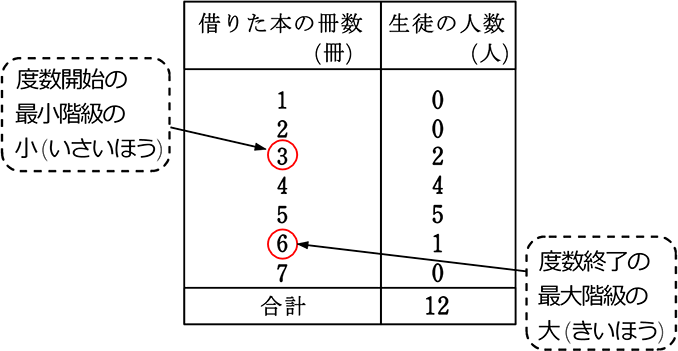
度数分布表 (「階級」と「度数」、最低この2つのデータがあれば「度数分布表」です)
階級
区間(区間名)ですね
柔道でいえば
20キロ級、30キロ級…
ボクシングでいえば
ミドル級、バンタム級…
今回の表なら
「20~30点」や
「70~80点」ですね
・女子が7人の階級は?
→ 60~70
階級の幅
階級の大きさですね
階級の幅 = 大ー小
・60-50 = 10
・90-80 = 10
10点刻みで表を作ったのですから、当然どこも「10」ですね
階級値
階級の幅の真ん中の値ですね
階級値 = \(\large{\frac{小+大}{2}}\)
その階級の「目安」となる数値ですね
・50~60の階級の階級値 = \(\large{\frac{50+60}{2}}\) = 55
・20~30の階級の階級値 = \(\large{\frac{20+30}{2}}\) = 25
→ 今後、度数分布表やヒストグラムから代表値を求めていく場合、
50~60にいる男子3人は全員「55点扱い」ということになります
もっと言えば3人全員「55点」です!
もう一度同じ表です

累積度数
最小の階級から指定階級
(教育改定により、平成31(令和元年)に1年生の方は入試範囲になります)
| ・ | 男子の60~70の階級までの累積度数は? → 1+0+1+3+5 = 10 |
| ・ | 女子の70~80の階級までの累積度数は? → 0+0+3+1+7+2 = 13 |
⇒ 当然、最後の階級までの累積度数 = 全度数 ですね
〈 階級の幅がある度数分布表での
階級の幅がない度数分布表の階級は真の値ですので
範囲 = 最大値-最小値 ですね
階級の幅がある度数分布表の範囲は
作成元のデータがない限り
最大値、最小値の真の値が分かりませんので
まず出題されることはありませんが念のため
階級の幅がある度数分布表の範囲
・範囲 = 度数終了最大階級の大 -度数開始最小階級の小
・範囲 = 最大値のある階級値-最小値のある階級値 という説もあります
男子の範囲は
(上の場合なら) 110-20 = 90
(下の場合なら) 105-25 = 80
(元データありなら) 100-24 = 76
→ 異なりますね
テストでは明らかに違う問題しかでませんね
ex.
ア. 範囲は100より大きい → ×
イ. 範囲は70より小さい → × など
後述、度数分布表・ヒストグラムでの「代表値」は 「概数」ですが
度数分布表・ヒストグラムでの「範囲・四分位範囲」は「概数」-「概数」、概数を2つも使うそのような値はどうなの??という意味で、テスト問題で見ることはないのでしょうね
《 例 》
範囲は?
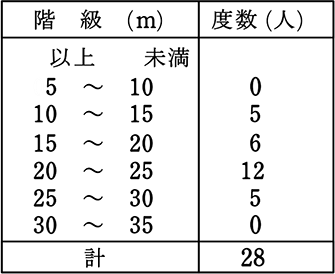

範囲 = 30-10 = 20
このあと出てくるヒストグラムでも全く同様です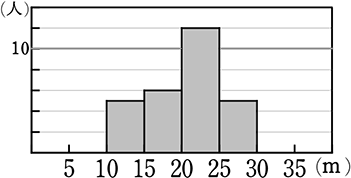

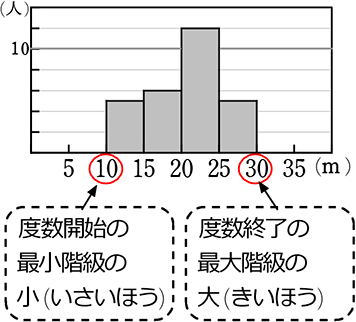
範囲 = 30-10 = 20
また、階級に幅がないときも同様に

範囲 = 6-3 = 3

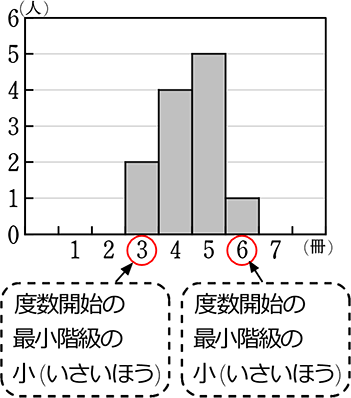
範囲 = 6-3 = 3
→ 階級に幅がないということは、真の値ですね
ということは、最小値3、最大値6 ですね
最初の階級に幅のある例題では、最小値・最大値はわかりませが
便宜上、
範囲 = 度数終了最大階級の大 -度数開始最小階級の小
ですね
このあたりで、「階級の幅」、「階級値」において、
表は「〇以上~□
20以上~30未満の階級の
・階級の幅 = 29.9999… -20 = 9.9999…では?
・階級値 = \(\large{\frac{20+29.9999\cdot\cdot\cdot}{2}}\) = 24.9999…では?
と疑問に思うかもしれませんが、
この度数分布表にした時点で、言葉は悪いかもしれませんが、
「かなり適当化」されています。
例えば、70点の人と78点の人を同じ75点(階級値)扱いにしてしまうくらいに。
すなわち、「未満」と「以下」のような「厳密性」より、
「データの傾向」という「イメージ性」に重きを置いている分野といえますね!
「60点台が5人」→「60点台が多い、少ない」のように。
よって、未満であっても、その数字を入れて計算してもかまわない、くらいに思っていい分野としか説明できないですね!(理数系というより文系ぽい?)

「未満」の対義語
「以下」の対義語は「以上」
では、「未満」の対義語は?
⇒「超」「超過」「~より大きい」ですね!
| ・ | 「以上」「以下」は、その数字を「含む」 →「5以上」なら「5」も「含みます」ね |
| ・ | 「超」「未満」は、その数字を「含まない」 →「5超」なら「5」は「含まない」、イメージとしては「5.00000000…1~」のような感じですね →「5未満」なら「5」は「含まない」、「~4.99999…」のような感じですね |
例えば、労働基準法 第32条第2項には、
「使用者は、1週間の各日については、労働者に、休憩時間を除き1日について8時間を超えて(こえて)、労働させてはならない。」 とあります。
「以上」ではなく「超」ですので「8時間(ちょうど)」を含んでいませんね
8時間労働はOK、8時間1秒労働はOUT! ですね!
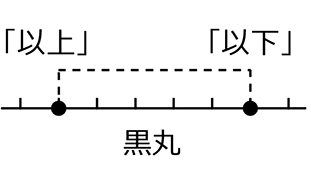

で表現しましたね

「以上」と「以下」の組み合わせでは、「重複部分」ができてしまいますね
「3はどっちに入るの?」のように。
→ どっちにも入る

「超」と「未満」の組み合わせでは、「空白部分」ができてしまいますね
同じく「3はどっちに入るの?」
→ どっちにも入らない
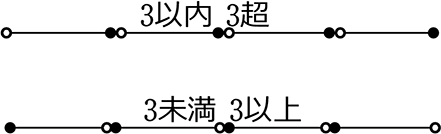
「超」と「以内」や、 「以上」と「未満」の組み合わせで 漏れや重複のない
「1本のつながった線」になりましたね!
③ 度数分布表での代表値(平均値、中央値、最頻値)
度数分布表にしたとたんに、各代表値(平均、最頻、中央)の扱いが今までと少し異なってきますね。
(考え方は同じです、「値」の代わりに「階級値」を利用するだけです)
もう一度同じ度数分布表です。
毎回、階級値を求めるのは面倒ということで、表の横に、「階級値」の1列を書き加えると、後々楽ですね!
「~」の上に、書き込むのもありですね  のように
のように

平均値
平均値 = 
・男子の平均値
= \(\large{\frac{25×1+\cdot\cdot\cdot+65×5+\cdot\cdot\cdot105×1}{20}}\) = 70.0
・女子の平均値
= \(\large{\frac{45×3+\cdot\cdot\cdot+65×7+\cdot\cdot\cdot95×3}{19}}\) = 70.26
(昇順データのときは、
男子「69.40」、女子「69.68」でしたね)
最頻値
最頻値 = 度数の最も多い階級の階級値
・男子の最頻値は、 5人の60~70の階級と、同じく5人の70~80の階級の、各階級値ですね
\(\large{\frac{60+70}{2}}\) = 65 (点)と \(\large{\frac{70+80}{2}}\) = 75 (点)
(昇順データのときは、「68点」と「72点」の2つでしたね)
・女子の最頻値、7人の60~70の階級、の階級値
\(\large{\frac{60+70}{2}}\) = 65 (点)
(昇順データのときは、「68点」でしたね)
中央値
| 中央値 = | 真ん中の場所が所属する階級の 階級値 |
・男子の中央値
→ 20人の真ん中の場所は、\(\large{\frac{20+1}{2}}\) = 10.5
∴ 10番目と11番目が所属する階級の、
階級値が中央値となります。
地道に上から足し算をします。(表のように)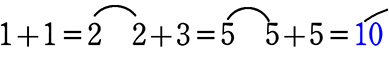
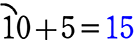
10番目は、60~70の階級に
11番目は、70~80の階級に ありますね
またがっている場合は・・・ でしたね
でしたね
ここでも「値」がないので、やはり「階級値」を使います
男子の中央値 = \(\large{\frac{65+75}{2}}\) = 70
(昇順データのときは69でしたね)
・女子の中央値
→ 19人の真ん中の場所は、 \(\large{\frac{19+1}{2}}\) = 10
∴ 10番目が所属する階級の、階級値が中央値となります。
同じく、地道に足し算をして所属する階級を調べます。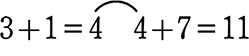 → 4<10番目<11
→ 4<10番目<11
10番目は60~70の階級の中にありますね
女子の中央値 = 60~70の階級値 = 65
(昇順データのときは68でしたね)
以上のように、度数分布表での代表値(平均、最頻、中央)は
昇順データのときの代表値よりかなりぼけていますが、かけ離れてはいませんね
度数分布表にすると
| ・ | 表がコンパクトになるが、各代表値がぼける |
| ・ | 「値」がないので「階級値」を用いる |
| ・ | 最大(小)値がわからなくなる |
| ・ | 最頻値 → 一目でわかる |
| ・ | 平均値 → 求めにくさはあまり変わらない |
| ・ | 中央値 → 求めにくくなる |
| ・ | 分布イメージはつかみやすい |
④ 相対度数 ・ 累積相対度数
せっかく度数分布表で、大体の「分布イメージ」、
この階級が多い、少ないというイメージがつかめたのですから、
もう少し正確な「多い、少ない」をイメージしたいですね!
まだ、39人の先生ですよ~!
先の「男子の最頻値65点が2人、75点が2人」は、
男子全体からしてどのくらいなのでしょうか?
そうです「割合」です。
相対度数 = 割合 ですね!
割合で使えるものは、 だけでしたね!
だけでしたね!

相対度数
指定階級の
(全体に対する)度数の割合
・(男子全体に対する)
階級20~30の男子1名の割合は?
→ 割合=対象÷全体
=1÷20=0.05 (5%) ですね!
・階級60~70の女子7名の割合は?
→ 7÷19 = 0.368…≒0.37 (37%)
ただそれだけですが…
「相対度数は?」といえば、「小数のまま」です。
(もちろん、問題が、何%?なら%で !)
(食塩水のときは「~%」、値段のときは「~割、~%」
…統一してほしいものですね。)
それでは、他の階級も計算してみると、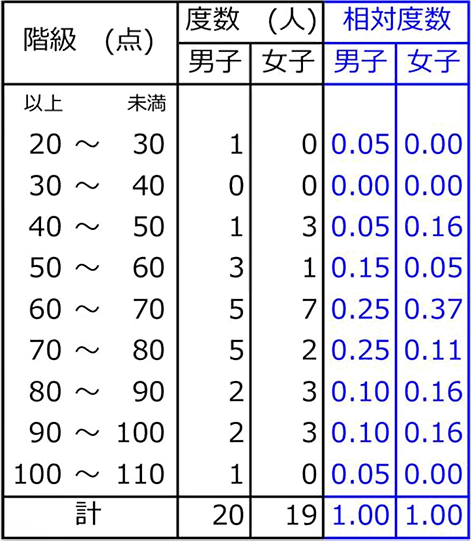
ですね
〈 累積相対度数 〉

累積相対度数
| ・ | 最小の階級から指定階級 または |
| ・ | 最小の階級から指定階級 |
(教育改定により、平成31(令和元年)に1年生の方は入試範囲になります)
| ・ | 男子の50~60の階級までの累積相対度数は?
(方法1) その階級までの相対度数を足していく |
| ・ | 女子の60~70の階級までの累積相対度数は?
(方法1) 0+0+0.16+0.05+0.37 = 0.58 |
〈 相対度数 ・ 累積度数の端数の処理 〉
| ・ | 割り切れない場合、大体小数第3位を四捨五入します → %にしたとき歯切れがよい |
| ・ | 四捨五入された数値の集まりなので、相対度数の合計が「1.00 (100%)」にならない場合があります。 → 2つの処理があります |
| ① | 合わないままにして、合計だけは「1.00」にする。(=調整しない) |
| ② | (ア)度数が多く、しかも(イ)表内に同じ度数がない階級 の相対度数を改変して「1.00」になるように調整する。 |
| ① | 実社会の資料は大体これですね
→ 役所の資料では表の下あたりに、「四捨五入のため合計が1にならない場合があります」と一言注意書きが添えられていますね |
| ② | (ア) 度数の少ないところに0.01などを付け加えるよりも、度数の大きい所で0.01などを付け加える方がデータに与える影響が少ない。
(イ) 同じ度数であるのに、相対度数が異なることを防ぐ |
実は、学者にも統一見解のないところです。
マル付けに困るテスト問題は作らないと思いますっ!
なにか、歯切れが悪くなってしまいましたが、
単語の意味さえ解れば、全体的に難しい計算はありませんね!
⑤ 統計的確率
(教育改定により、令和2年に1年生の方は入試範囲になります)
統計的確率
「多数の観察(1000人で1回)」や「多数回の試行(10人で100回)」によって得られる確率
⇒ 多数回調べたなら、相対度数を「確率」とみなしてもよいということ
対して、中2の確率は「数学的確率」と言いますね
《 例 》
下の表は、ジュース瓶のふたを100回投げて表裏を調べるシミレーションを3回行ったものです
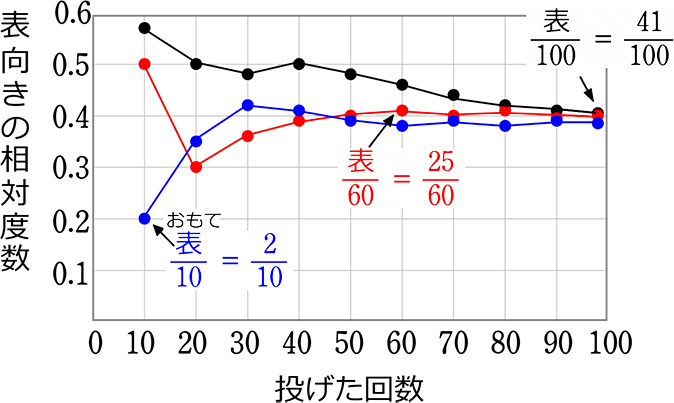
グラフを見て、次の文の正誤を答えましょう
| 1. | ふたを投げる回数が多くなるにつれて、表の出る相対度数のばらつきは小さくなり、その値は1に近づく → 誤:ばらつきは小さくなるが、値は0.4 に近づいている(1は100%表ということ) |
| 2. | ふたを投げる回数が多くなるにつれて、表の出る相対度数のばらつきは小さくなり、その値は0.4に近づく → 正 |
| 3. | ふたを投げる回数が多くなっても、表の出る相対度数のばらつきはなく、その値は0.4で一定である → 誤:ばらつきは小さくはなるが、あることはある(一定ではない)、0.44(80回)、0.43(90回)、0.41(100回) |
| 4. | ふたを投げる回数が多くなっても、表の出る相対度数の値は大きくなったり小さくなったりして、一定の値には近づかない → 誤:大きくなったり小さくなったりはするがその振れ(ばらつき)幅は小さくなっていく → 一定の値(0.4)に近づいているということ ex. 2人でじゃんけん3回勝負をして3連勝もあり得ますが、続ければ3連敗もありますね、100回1000回とすると、なんだかんだ 勝ち\(\large{\frac{1}{3}}\)、負け\(\large{\frac{1}{3}}\)、あいこ\(\large{\frac{1}{3}}\)、という値に近づくとイメージできますね |
| 5. | 裏が出る相対度数は0.6に近づくので、101回目は必ず裏が出る 誤:必ずではない、相対度数を確率とみなせば、表は\(\large{\frac{4}{10}}\), 裏\(\large{\frac{6}{10}}\)で、「若干裏が出やすい」にとどまる |
それでは、クラスの先生に戻って
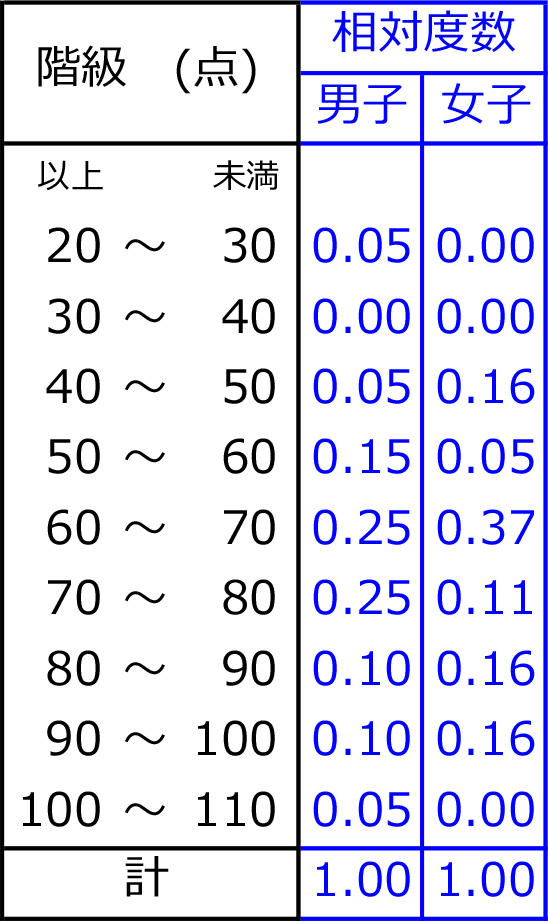
この表は、1クラスで1回のテストでしたが、
仮に、
1クラスで100回行った結果(多数回の試行)や
100クラスで1回行った結果(多数の観察)で
あった場合は
⇒ 相対度数を「確率」とみなしてよいということですね
ex.
ある男子15人, 女子15人のクラスで同様のテストを行いました
① 男子が60~70点をとる確率は?
→ 0.25 = \(\large{\frac{25}{100}}\) = \(\large{\frac{1}{4}}\)
| ② | 何人の女子が60点未満になると予想されますか → 60までの累積相対度数は、0+0+0.16+0.05 = 0.21 ∴ 15人×0.21 = 3.15 ≒ およそ3人 |
(先の女子19人のクラスでは、 19人×0.21 = 3.99 ≒ 4人 でしたね)
(イメージ)
女子
円グラフにしてルーレットにするイメージ
まとめ
多数(回)調べた結果なら
(たまたま感がなくなるので)
相対度数を確率とみなしてもよい
↑統計的確率
⑥ ヒストグラム
では、次に思うことは、
もっと「直感的に、視覚的にイメージを把握したい!」
ではないでしょうか?
そこで、データのグラフ化ということになりますね
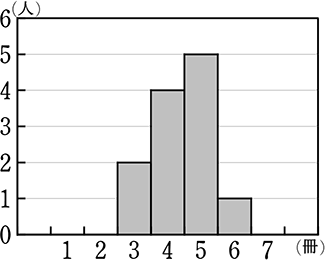
「度数分布表」は「ヒストグラム」という「棒グラフ」が描けますね!
(ヒストグラムは 柱状グラフ ともいいますね)

グラフの種類
棒グラフ 
折れ線グラフ 
帯グラフ 
ヒストグラム
(柱状グラフ)
散布図 
→ グラフから、数学がよければ大体理科もよい と読みとれますね
cf.
散らばりの楕円が細くなって( = 散らばりが小さくなって)、「直線」にまでなったら
「関数」ということですね
⇒ xの値を決めれば、yの値がただ1つ決まる関係
レーダーチャート 
三角グラフ 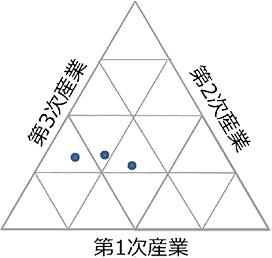
円グラフ 
cf. 箱ひげ図 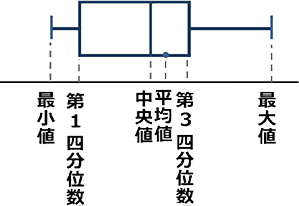
(後述:箱ひげ図)
上の余談のように、
「ヒストグラム」は「棒グラフ」の一種ですね
| ・ | 棒グラフは、横軸、縦軸に何をとってもよい |
| ・ | ヒストグラムは、横軸に階級、縦軸に度数、という決まりがある(定義) |
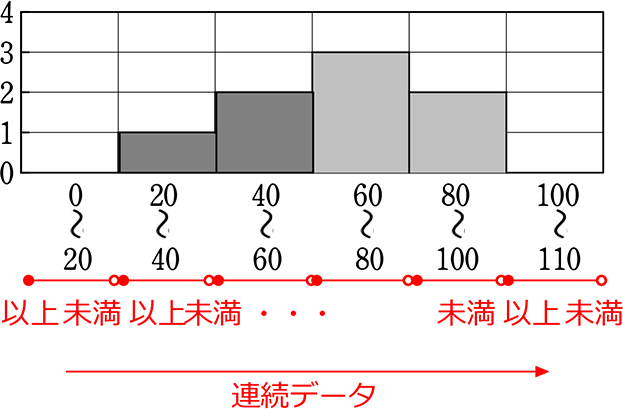
さらに、暗黙の了解で、ヒストグラムのグラフは
| ① | 横軸は「階級」であるから、当然に連続データになる |
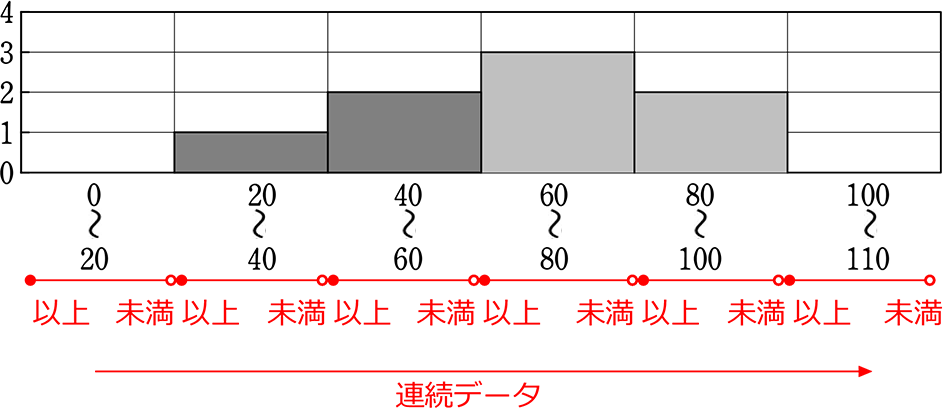
ということは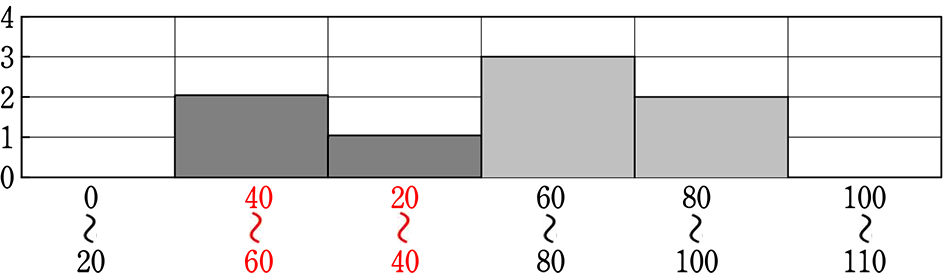
ということは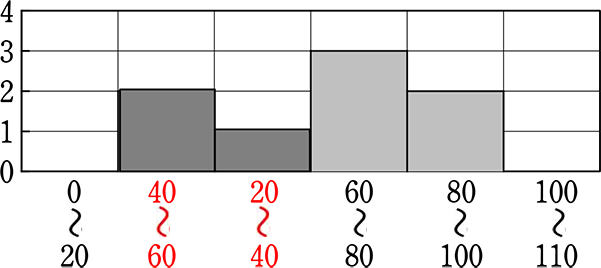
のように、「20~40の階級」と「40~60の階級」を入れ替えてはいけません。
入れ替えたら、「ヒストグラム」ではなく、「ただの棒グラフ」ということになりますね。
つまり、ヒストグラムの目指すところは、
「一目で、全体の、散らばり具合 がわかる」ということになりますね !!
| ② | 連続データであるということを示すという意味で、
グラフの棒が、隣とくっついていますね! |
ただの棒グラフ
離れてもかまわない
ヒストグラム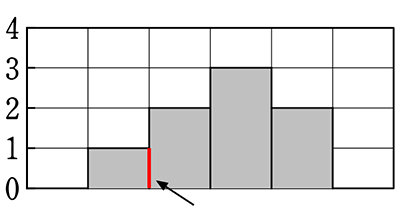
くっついている
| ③ | ヒストグラムのグラフでは、「棒の面積比」で散らばり具合を表している |
どうしても「20~40」「40~60」の度数を(理由はともかく)、
「20~60」という階級にまとめたい場合、
棒(長方形)の面積 = 縦(度数)×底辺(階級)
底辺は、皆同じ長さですので、「1」でも「2」でも「文字」でも何でもかまいません、
ここでは、「1」としますね
「60~80」=3×1=3
「40~60」=2×1=2
3÷2=1.5 →「60~80」は「40~60」の1.5倍いる(ある)
2÷3=0.67 →「40~60」は「60~80」の0.67倍いる(ある)
このように、面積比で視覚的な散らばりを表現しているのです。
それでも、どうしても一部の階級を結合したい場合は、
面積を変えてはいけませんので、
① 高さだけで面積調整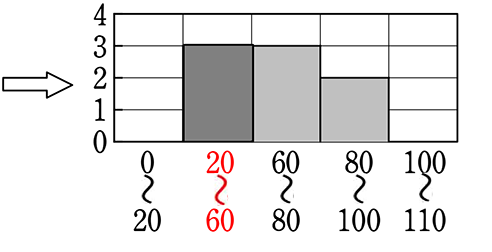
→「間違ったイメージ」を与え
てしまうので「ヒストグラム」
の役目を果たしていませんね!
② 底辺と高さで面積調整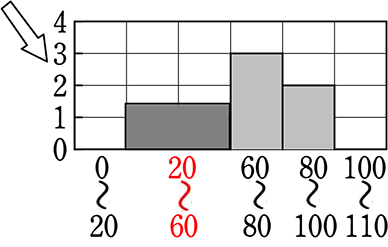
→ ①よりはイメージが崩れて
いませんが、同じ幅をとるので
あれば結合しなくてもよいので
は? となりますね。
ヒストグラムで、「階級を結合しなさい」という問題は、
見たことがありませんが、
ここでは、ヒストグラムは「棒の面積に意味がある」棒グラフと
いうことだけ、わかっていてくださいね!
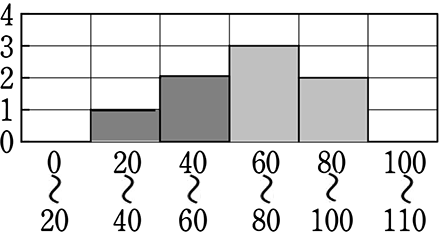
それでは、本題に戻りまして、男女39人のヒストグラムを作成してみましょう。

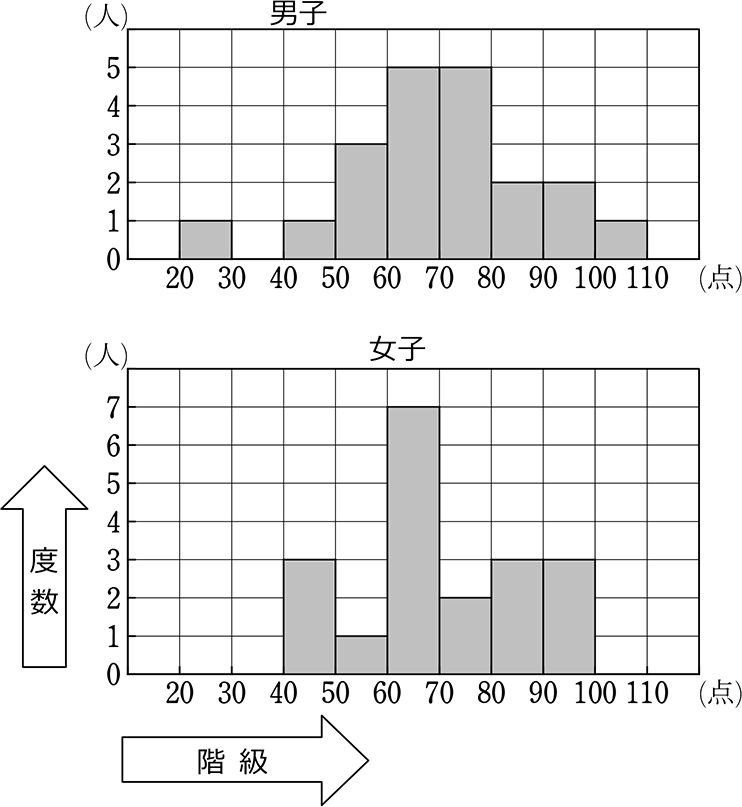
横軸の表示方法は、どちらでもOKです!
⑦ 度数折れ線 (度数分布多角形)
棒の上底の中点を結んだものを、
度数折れ線 または 度数分布多角形 といいます
それだけです
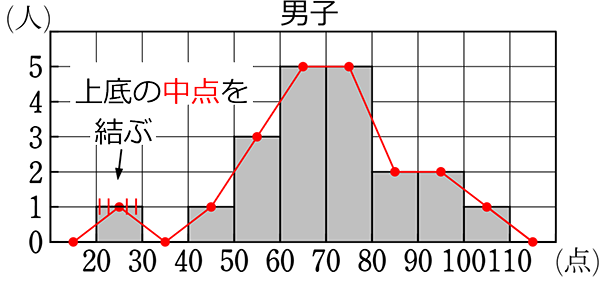
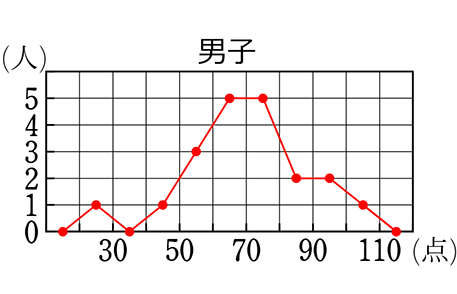
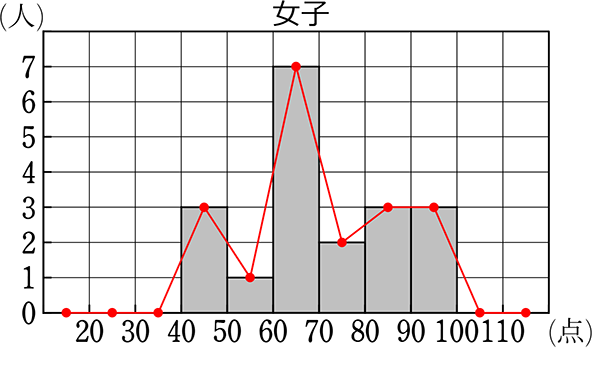
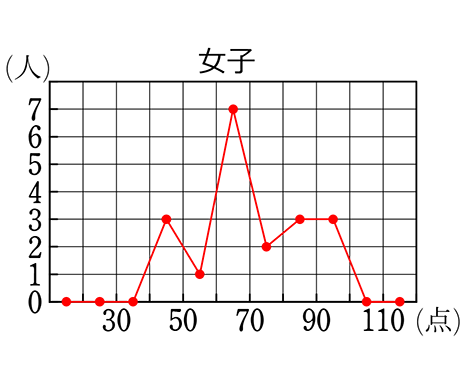
左は、「ヒストグラム」+「度数折れ線」、右(小)は「度数折れ線」のみになります
下は、男子の「度数折れ線」と女子の「度数折れ線」を重ねたものです
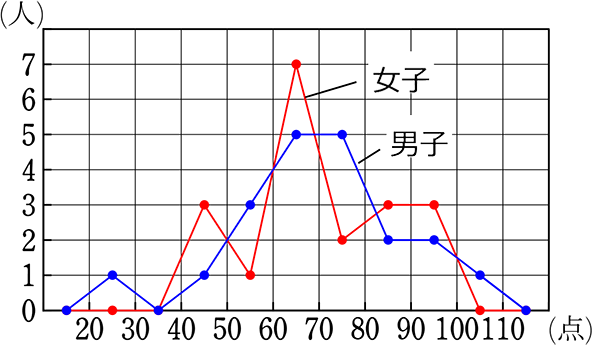
比較がしやすくなりますね!
【 ヒストグラム・度数折れ線での代表値 】
ヒストグラム・度数折れ線での代表値は
「度数分布表での代表値」と全く同じです
なぜなら、資料(データ)を「表」にするか「グラフ」にするかの違いだけで
中身(使われる数字)は全く同じだからです!
よって、同様に「階級値」を利用して計算します
《 例 》
ヒストグラム・度数折れ線から代表値を求めましょう
→ グラフに、図のように「度数(または累積度数)」や「階級値」を書き込むのもありですね
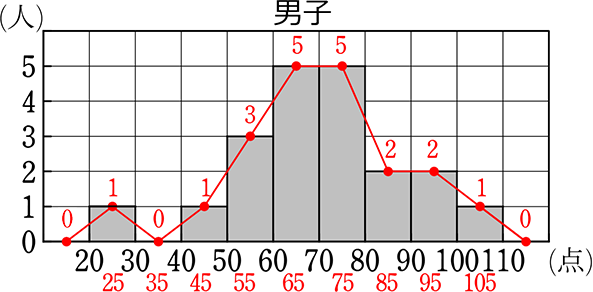
① グラフから男子の人数を求めましょう
→ 1+1+3+5+5+2+2+1 = 20 (人〉
② グラフから平均値を求めましょう
→ 平均値
= \(\large{\frac{各階級値×度数、の合計}{総(人)数}}\)
= 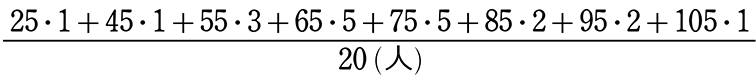
= 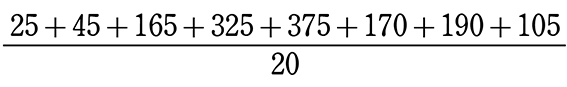
= 70 (点)
③ グラフから最頻値を求めましょう
→ 一目で60~70、70~80が多いと分かる
→ 最頻値 = 度数の最も多い階級の階級値 = 65と75
④ グラフから中央値を求めましょう
→ 20の真ん中の場所= \(\large{\frac{20+1}{2}}\)= 10.5
→ 1人+0人 =1+1人=2+3人 =5+5人=10+5人=15
∴ 10人目は60~70の階級に、11人目は70~80の階級にいる
→ 中央値 = \(\large{\frac{65+75}{2}}\) = \(\large{\frac{140}{2}}\) = 70(点)
イメージとして 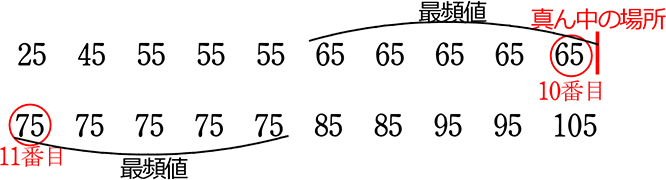
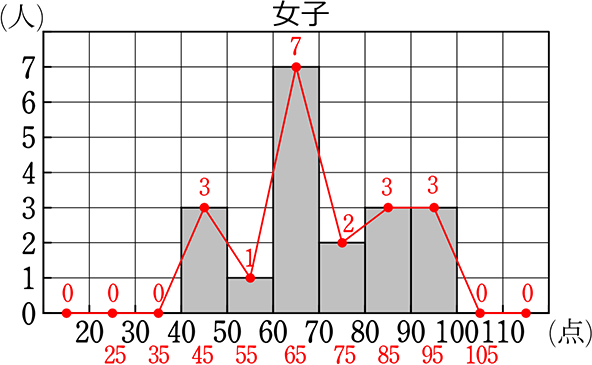
① グラフから女子の人数を求めましょう
→ 3+1+7+2+3+3 = 19 (人)
② グラフから平均値を求めましょう
→ 平均値
= \(\large{\frac{各階級値×度数、の合計}{総(人)数}}\)
= 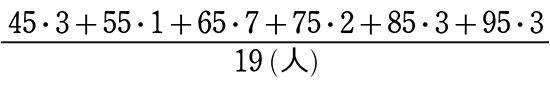
= 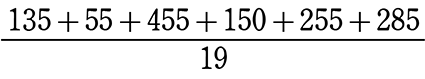
= 70.26 (点)
③ グラフから最頻値を求めましょう
→ 一目で60~70が多いと分かる
→ 最頻値 = 度数の最も多い階級値 = 65
④ グラフから中央値を求めましょう
→ 19の真ん中の場所 = \(\large{\frac{19+1}{2}}\) = 10
→ 3人+1人=4+7人=11
∴ 10人目は60~70の階級にいる
→ 中央値 = 65 (点)
イメージとして 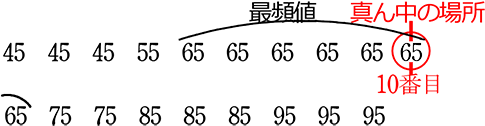
(当然、すべて度数分布表での代表値と同じ値ですね)

クリック・タップで答え (反応が遅い場合があります)


クリック・タップで答え (反応が遅い場合があります)

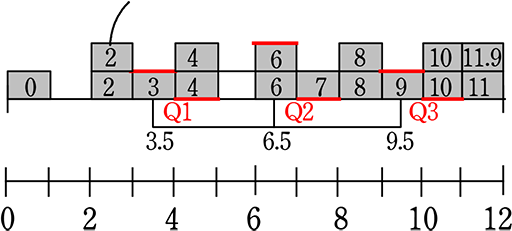
⑧ 四分位数
(教育改定により、令和2年に2年生の方は入試範囲になります(高校数Ⅰから移行)
(中学2年課程になりますが、中2確率は手強いと思いますので、親中ではここ1年で学びますね)
昇順に並べたデータを4等分して
1/4のところを、第1四分位数 (Q1)
2/4のところを、中央値(第2四分位数) (Q2)
3/4のところを、第3四分位数 (Q3) と言います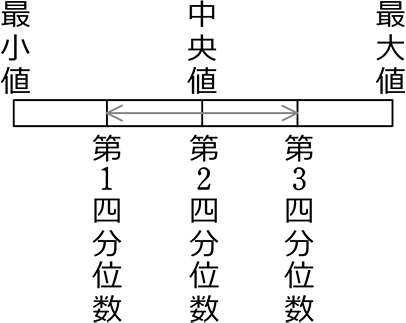
(イメージ)
→ 中央値までの中央値、中央値後の中央値
⇒ 「中央値の次の中央値」で十分ですね
Q:quartile:四分位数
(cf. quarter:4分の1)
hinge:
〈 四分位数の求め方 〉
中央値を求めるとき、「真ん中の場所」に
値があれば、それが中央値
値がなければ、前後の平均が中央値でしたね
→ 第1, 第3四分位数も同様です
⇒ あればそれ、なければ前後の平均です
では、具体的に
(手順①)
| ・ | まずは、単独中央値を含まずに真っ二つに分けます
→ 含もうとすると「どっちに含むの~?」となりますね |
| ・ | なければ普通に真っ二つ |
| ア | 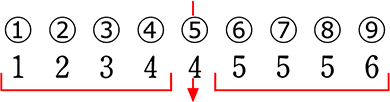 (単独)中央値:4 (第2四分位数) |
| イ | 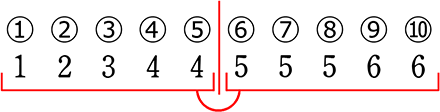 (合成)中央値:4.5 (第2四分位数) |
| ウ | 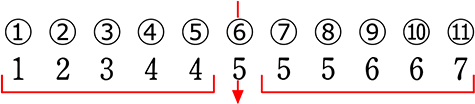 (単独)中央値:5 (第2四分位数) |
| エ | 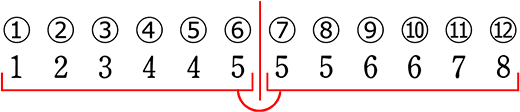 (合成)中央値:5 (第2四分位数) |
.png)
(手順②)
あとはそれぞれの次の中央値を求めるだけですね
| ア | 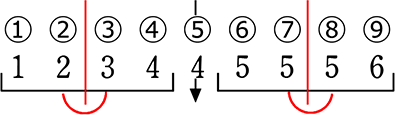 第1四分位数:2.5 第3四分位数:5 |
| イ | 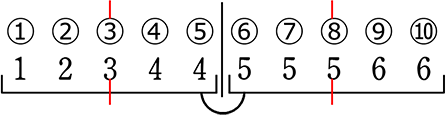 第1四分位数:3 第3四分位数:5 |
| ウ | 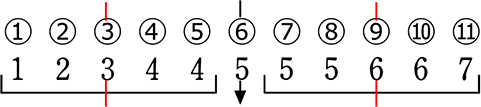 第1四分位数:3 第3四分位数:6 |
| エ | 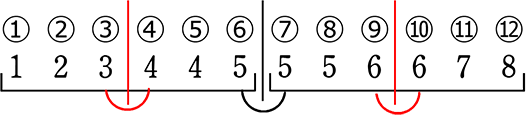 第1四分位数:3.5 第3四分位数:6 |
→ 全部で4パターンですね (全部単独~全部合成)
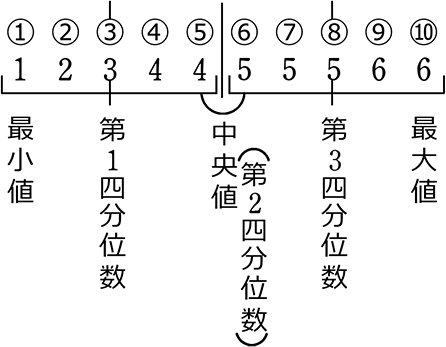
↑ これら5つの値を『五数要約』と言います
(↑後述、箱ひげ図の元データになりますね)
では先生に戻って
↓面倒なので「行の境目」を0.5としています
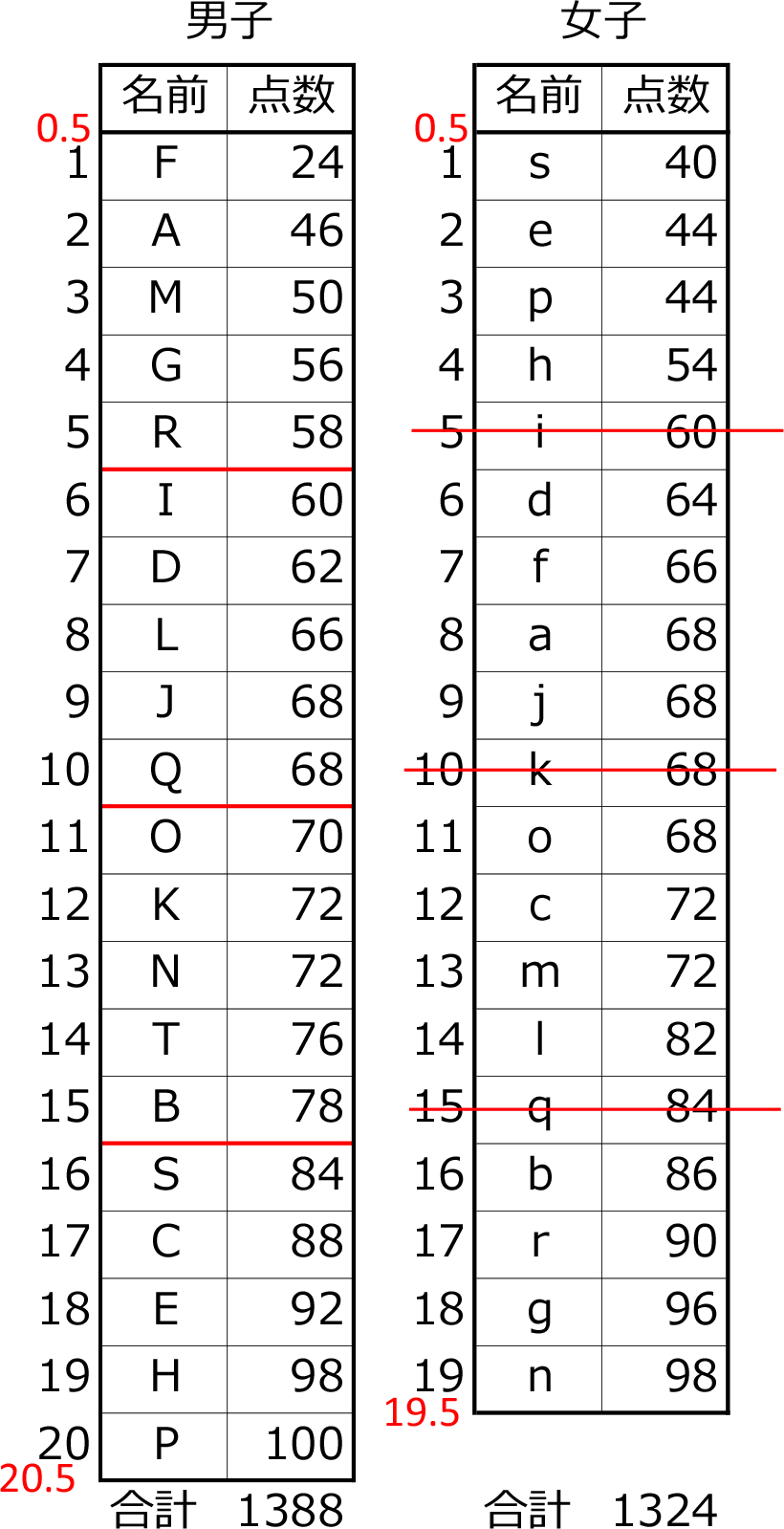
・男子の第1四分位数は?
→ まずは普通の中央の場所
\(\large{\frac{20.5+0.5}{2}}\) = 10.5行目 (場所は足す)
→ 前半の中央の場所
\(\large{\frac{10.5+0.5}{2}}\) = 5.5行目
∴ \(\large{\frac{58+60}{2}}\) = 29+30 = 59
・男子の第3四分位数は?
→ 後半の中央の場所
\(\large{\frac{20.5+10.5}{2}}\) = 15.5行目
∴ \(\large{\frac{78+84}{2}}\) = 39+42 = 81
・女子の第1四分位数は?
→ 普通の中央の場所
\(\large{\frac{19.5+0.5}{2}}\) = 10行目
→ 前半の中央の場所
単独中央値は含まないので
\(\large{\frac{9.5+0.5}{2}}\) = 5行目
∴ 60
・女子の第3四分位数は?
→ 後半の中央の場所
\(\large{\frac{19.5+10.5}{2}}\) = 15行目
∴ 84
中央値, Q1, Q3の求め方
方法① 上のように「計算」で求める
方法② シンプル4パターンを書く
 | 4マスは全合成 |
 | 5マスはQ1Q3合成 |
 | 6マスはQ1Q3単独 |
 | 7マスは全単独 |
8マス(行)なら上に戻って、全合成
19マス(行)なら同様にぐるぐる数えて、7マスでstop → 全単独
20マス(行)なら同様にぐるぐる数えて、4マスでstop → 全合成
⇒ 2つの合わせ技で求めれば安心ですね
四分位範囲
四分位数を単体で求めても、何のための値?? でしたが
ここで少しは存在意義がわかりますね
四分位範囲
| ・四分位範囲 = | 第3四分位数-第1四分位数
→ 度数全部の内、中央値を挟む50%の度数がこの範囲内にいますよ~ |
| ・ただの範囲 = | 最大値-最小値
→ 度数全部の範囲ですよ~ |
| ・四分位 | \(\boldsymbol{\large{\frac{四分位範囲}{2}}}\)
→ (イメージ) 両翼の片翼の幅 |

資料の価値基準
「資料の散らばり」を学んでいると、何のためにそんな値を求めるの?
と思うことが多々あるかと思います
そんなとき、資料の散らばりを扱う専門家がとにかく何を知りたいのか
という根本を意識できれば、少しはその値に納得できるのではないでしょうか
人や環境がからむデータを集めると…
ほとんどが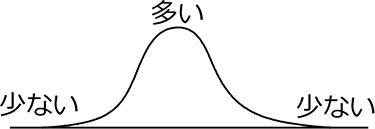
このような形になります
そして、データを扱う人は「最も膨らんだ場所付近(代表値)」や「そこから左右にどのように広がっているか」をすごく知りたいのです
何かを設定する材料(製造数設定・価格設定・税率設定・志望校合格率設定等々)につながったり、ビジネスにつなっがったり、社会の進歩につながったり、するのでしょうね
四分位偏差も、度数が多いだろうと踏んだ場所の片方ずつのの翼の幅を知りたいのでしょうね
(四分位範囲の幅のイメージ)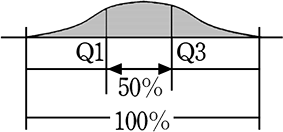

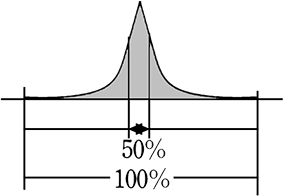
→ 同じ50%でも 幅の割合が違いますね
cf. 偏差値の求め方
それでは先生に戻って、
男子の第1四分位数は 59
第3四分位数は 81

女子の第1四分位数は 60
第3四分位数は 84

でしたね
では
男子の四分位範囲は?
→ 81-59 = 22
男子の四分位偏差は?
→ \(\large{\frac{22}{2}}\) = 11 (片翼の幅)
女子の四分位範囲は?
→ 84-60 = 24
女子の四分位偏差は?
→ \(\large{\frac{24}{2}}\) = 12 (片翼の幅)
⑨ 箱ひげ図
(四分位数同様、高校数Ⅰから中2に移行、親中ではここで学びますね)
先に出てきた「五数要約」を視覚的にとらえようとする図ですね
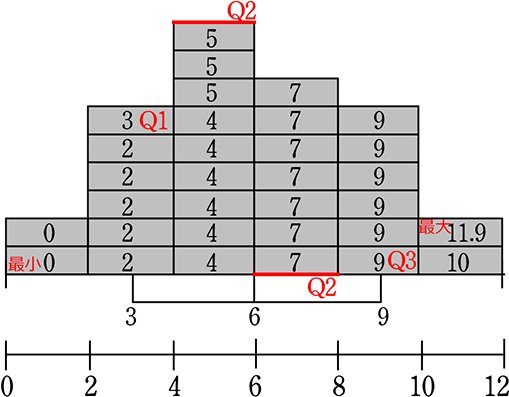
男子の五数要約 → 最小値24、最大値100、第1四分位数59、第3四分位数81、中央値69 から箱ひげ図を作ってみると
男子
「範囲」の中の「四分位範囲」(  )を強調した図を考えたら、自然に このような図(
)を強調した図を考えたら、自然に このような図(  )になったんだろうなと想像できますね
)になったんだろうなと想像できますね
そして、その図が箱にひげが生えたように見えるので『箱ひげ図』ですね!
⇒ 箱ひげ図の利点、「シンプル」
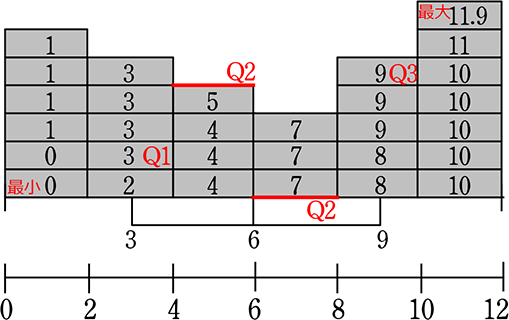
リアルには
のように書きたかったのでしょうね
必要に応じて「平均値」を「+」印で書き込むこともあります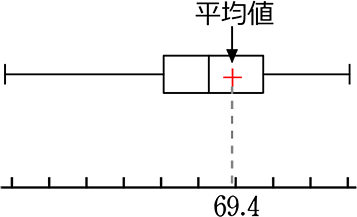
〈 箱ひげ図から分かること 〉

→ 4つに分けた部分で、短い部分ほど度数が上に伸びる!
ということは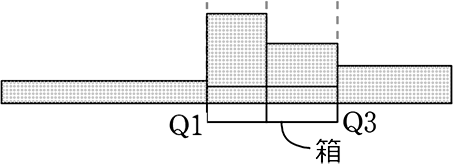
大体このようなヒストグラムと想像できますね
なぜなら、
長方形の面積は25ですべて同じで、底辺が指定されているならば、あとは「高さ」で調整するしかないですものね
反比例のイメージですね
a = xy → 25 = 底辺×高さ

上の練習で、実際には…
4区分には それぞれ階級が刻まれているはずなので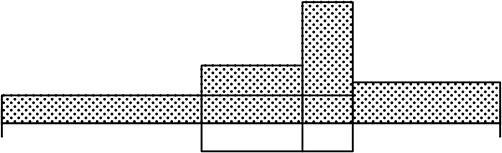
は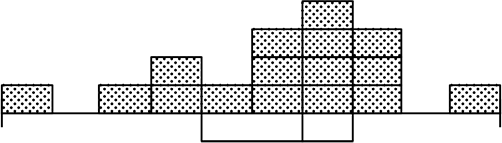
このようであるかもしれませんね
→ マスを氷と思えば、溶ければ上図ですね
次に、4区分に分けるQ1などの区切り線(箱の左縦線)は、実際には目盛とずれているはずです
例えば、上の練習の2番目の問題では
「大体平らなヒストグラム」を予想しましたね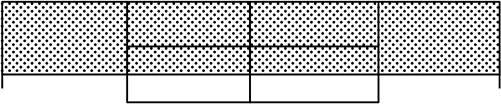
ですが「階級に幅がある」ヒストグラムでは必ずしも「平らっぽく」なるとは限りませんね
例えば、以下の3つは4範囲均等箱ひげ図から考えられるヒストグラムです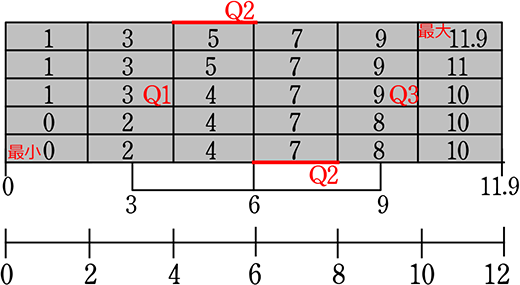
「平ら型( )」ばかりか「山型(
)」ばかりか「山型( )」「谷型(
)」「谷型( )」まで考えられますね
)」まで考えられますね
| ⇒ | 箱ひげ図の4範囲の比から、必ずしも「平ら型」「山形」「谷型」が決まるわけではない |
先ほどの「長方形の考え方」は何だったの? となりますね
では、「4範囲の間が細かく刻まれている」または「階級に幅がない」場合の考えられるヒストグラムは…
階級の幅がないので、1つの列には1種類の値
| → | 4範囲のそれぞれに1氷ずつ合計4氷足しても、2氷ずつ合計8氷足しても、「山形」「谷型」は作りにくいですね |
| ⇒ | 「階級に幅がない」場合は「長方形の考え方」は有効 と言えますね
(実社会では このとらえ方の方が多いですし、素直ですし、箱ひげ図の価値も高くなりますが、なぜか中学数学ではおおまかな階級の幅をとって 必ずしも想像どおりのヒストグラムにはならないということを強調して教えられますね) |


マスの数え方 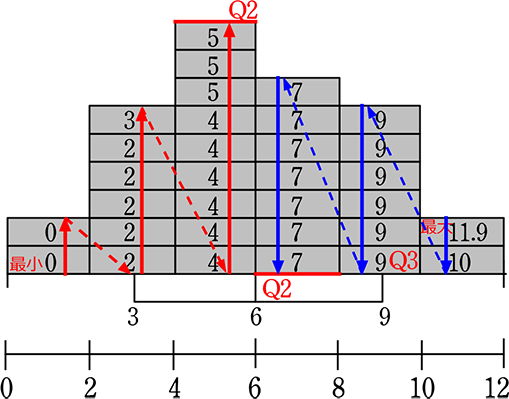
| → | 最小値から上へ、最大値から下へ |
| → | マス数により、Q2, Q1, Q3 は単独, 合成が決まってましたね (Q2Q1Q3の求め方) |
箱ひげ図とヒストグラムの関係
| ・ | 長方形のイメージを持ちつつ |
| ・ | 必ずしも「山・平・谷型」は決まらないという意識 |
| ・ | 面倒でもグラフのマスを数えなければならない時がある |
あなたが先生シミレーションはここまでです!
お疲れ様でした!
「資料の散らばりと代表値」をたくさん扱った問題集は少ないと思いますので
当1年生無料問題集では
ほぼ全国の2014~2019の高校入試過去問の「資料の散らばりと代表値」を集めた問題(157問(60ページ))を解説しています
よろしければご利用くださいね!

三角グラフの読み方
三角グラフには2種類あります。
① 割合の多さを、垂線の高さで表すもの (垂線目盛り)
② 割合の多さを、斜辺の高さ(の割合)で表すもの (斜辺目盛り)
どちらのグラフも「割合」しか扱えず、
さらには「三分された割合」しか扱うことができません。
例えば、50%、30%、20%など、計100%なものですね
それ以上「項目」があれば、「円グラフ」等を用いますね。
具体的な値を扱いたい場合は、(カッコ)で扱うことになります。
例えば、46%(7161万件) のように。
この点は「帯グラフ」や「円グラフ」と同じですね。
もし具体的な「値」を用いれば、
突き抜けてしまったりしてしまいますね!
では、まず、前提として
「三角形の性質」から、斜辺でも高さを表すことができますね
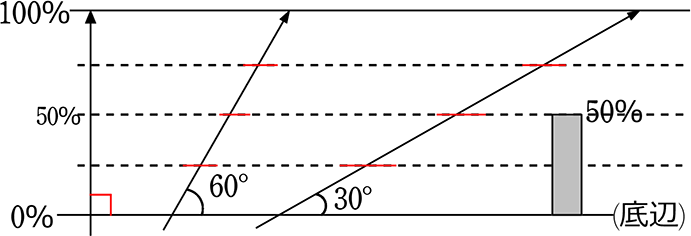
面積を求めるための正確な「高さ」ではありませんが、
斜辺でも、「高さの割合」は同じですね!!(高さにあたるもの)
以後「高さ」と言ってしまいますね!
それでは本題、
ここでは、②の「斜辺目盛り」の三角グラフ、
地理の「産業推移」の三角グラフを扱いますね(三角グラフはここしか出てきませんので)
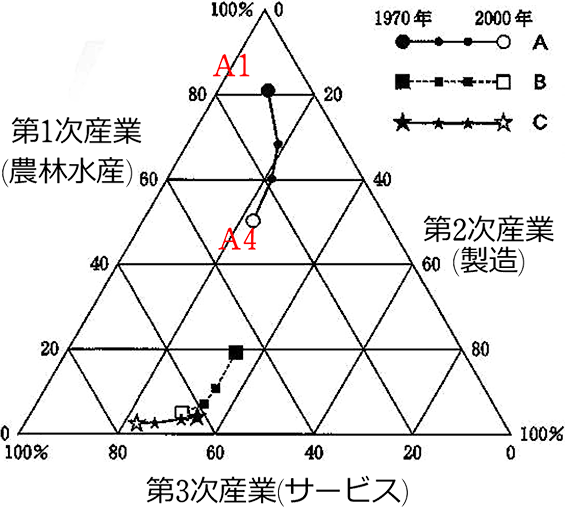
2013年センター試験地理の問題です
(問)
A、B、C はアメリカ、中国、日本のいずれかです。対応させましょう
(先進国ほど第3次産業の割合が多くなりますね)
三角グラフは、1つの目盛りから2本の線が出ていますので、
「この目盛りはどっちのためのもの?」となりがちです
そこで、先ほどの「底辺」と「高さ」で把握していきます
A1の第1次産業の割合は? 「高さ」はすぐ横にある  ですね
ですね
ということは、「底辺」は  ですね
ですね
ということは、「目盛り」は  ですね (底辺に平行)
ですね (底辺に平行)
 ではないですね!
ではないですね!
ということで、第1次産業の割合は、81%くらい
同様にA1の第2次産業の割合、
「高さ」はすぐ横にある 
ということは、「底辺」は、 
ということは、「目盛り」は  (底辺に平行)
(底辺に平行)
ということで、第2次産業の割合は、10%くらい
同様にA1の第3次産業の割合、
「高さ」はすぐ横にある 
ということは、「底辺」は、 
ということは、「目盛り」は  (底辺に平行)
(底辺に平行)
ということで、第3次産業の割合は、9%くらい
ちなみに、以上A1(1970年時点)を帯グラフで表してみると、
以上のように、三角グラフの読み方は
「高さ」→「底辺」→「目盛り(底辺に平行)」の順で読むと
間違いがなくなるのかなと思います。
よく「時計回りに読む」などありますが、お父ちゃんの頭では難しすぎです。
問題の解答は、
A-急激に第3次産業の割合が増えてきた中国
B-日本
C-日本の10年先を行くアメリカ でした
「垂線目盛り三角グラフ」は、「斜辺目盛り三角グラフ」の理解まで混乱させ
てしまうと思われますので、省略しますね!

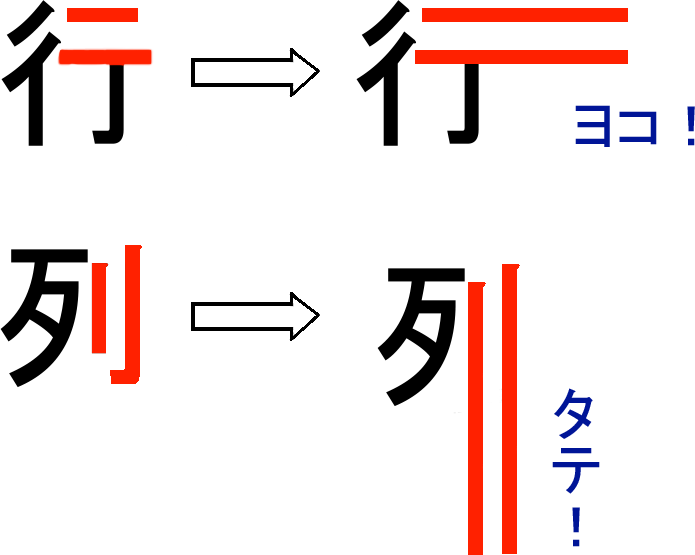
行と列、縦?横?
Excelなどの表計算ソフトを使うと、
「行の追加、削除」「列の追加、削除」を行う場面がありますね、
その時、行…横?縦?となることがありませんか?
それでは、すぐに思い出す方法を…
行列という漢字には、それぞれ2本の「平行棒」がありますね!
失礼しました…

ボクシングの階級
| 階級 (kg) | 階級名 | |
| 1 | ミニマム級 (WBA・WBC) ミニフライ級 (IBF・WBO) |
|
| 2 | 47.62 ~ 48.98 | ライトフライ級 (WBA・WBC) ジュニアフライ級 (IBF・WBO) |
| 3 | 48.98 ~ 50.80 | フライ級 |
| 4 | 50.80 ~ 52.16 | スーパーフライ級 (WBA・WBC) ジュニアバンタム級 (IBF・WBO) |
| 5 | 52.16 ~ 53.52 | バンタム級 |
| 6 | 53.52 ~ 55.33 | スーパーバンタム級 (WBA・WBC) ジュニアフェザー級 (IBF・WBO) |
| 7 | 55.33 ~ 57.15 | フェザー級 |
| 8 | 57.15 ~ 58.96 | スーパーフェザー級 (WBA・WBC) ジュニアライト級 (IBF・WBO) |
| 9 | 58.95 ~ 61.23 | ライト級 |
| 10 | 61.23 ~ 63.50 | スーパーライト級 (WBA・WBC) ジュニアウェルター級 (IBF・WBO) |
| 11 | 63.50 ~ 66.67 | ウェルター級 |
| 12 | 66.67 ~ 69.85 | スーパーウェルター級 (WBA・WBC) ジュニアミドル級 (IBF・WBO) |
| 13 | 69.85 ~ 72.57 | ミドル級 |
| 14 | 72.57 ~ 76.20 | スーパーミドル級 |
| 15 | 76.20 ~ 79.37 | ライトヘビー級 |
| 16 | 79.37 ~ 90.71 | クルーザー級 (WBA・WBC・IBF) ジュニアヘビー級 (WBO) |
| 17 | 90.71 ~ | ヘビー級 |
階級ごとに、『個別の名称』をつけていますね
セクハラではありませんが、皆様は、何級でしたか?
数学の度数分布表では、色々な場面がありますので、
『個別の名称』はつけずに、「52.16~53.52の階級」などといいますね。
その他、度数分布表では大体「以上~未満」でしたが、
ボクシングの階級では、「超~以下」となっていますね!
軽い階級目指して減量していますので
「53.52kgになりさえすれば、
バンタム級でセーフ!」
ということで、はっきりさせるために上限が黒丸(以下)ということですね

~の…に対する〇〇
お父ちゃんが子供の頃、この 「~の…に対する〇〇」というフレーズが、とても「???」だったのです。
今はさすがに解りますが。
「彼の彼女に対する想い」
「鈴木さんという苗字のクラス全体に対する割合」
分解すると 3つのパートからできていますね
「①彼の ②彼女に対する ③想い」
「①鈴木さんという苗字の ②クラス全体に対する ③割合」
①と②は順番を替えても大丈夫で、どちらかというと替えた方が、
スーと頭に入ってくると思います。
「②彼女に対する ①彼の ③想い」
「②クラス全体に対する ①鈴木さんという苗字の ③割合」
並び替える前も、後も、要は、
①彼の③思い +補足として②(彼女に対する) なんですね
①鈴木さんという苗字の③割合 +補足として②(クラス全体に対する) なんですね!
「の」を強く、「…に対する」に( )をつければ、
どちらの並びでも、スーと頭に入ってきますね
彼の(彼女に対する)想い
鈴木さんという苗字の(クラス全体に対する)割合
それにしても、自分で口にすると、なんかカッコよくなった気持ちになるフレーズですね!
「わが部署の前年度に対する利益は…」…かっこいいですね!
「前年度に対する我が部署の利益は…」…普通ですね
つまらないお話を失礼しました!
イ ヒストグラムや代表値による資料の傾向の把握と表現
ここまで「資料」を勉強してきて、
「結局、資料から何を知りたいの?」となっているのかなと思います。
お父ちゃんも含めて、「ものを受け取る側」「情報を(テレビなどから)受け取る側」は、
どちらかと言うと、最高(値)、最低(値)に興味を持ちがちです。
ですが、「ものを作る側、売る側」「情報を発信する側」は、
代表値(平均、中央、最頻)が表す『標準』を知りたいのです。
例えば、皆さまが「靴(くつ)づくり職人」になったとします。
よく売れるように、
おそらく、25~27cmサイズの靴から作り出すと思います(男子)。
いきなり 22cm や 30cmからは作らないですよね(男子)。
Tシャツ作りでも同じです。
MやLサイズから作ると思います。
いきなり、Sや3Lからは作らないですよね。
テレビ番組作成でも同様です。
「視聴率を高くしたい」→「大衆受けするテーマ」を取り上げると思います。
いきなり「マニアックなテーマ」は取り上げないですよね。
テスト問題作りでも同じです。
「0点、100点の少ない、すなわち5, 60点の多いテストを作ると思います。
いきなり、0点だらけ、100点だらけになりそうなテストは作らないですよね。
そうです
「売れ筋」「大衆受け」 ≒ 代表値付近なのです!
という訳で、
今、中学生の皆様も、年齢とともに
「受け取る側」から「与える側、作る側」になっていくのですから、
『標準』を知っていかなければいけない、ということになりますね。
(もちろん、皆様に「標準になりましょう!」と言っているわけではありません、
他人とは違う個性は大切にしつつ、「標準、一般」、すなわち他人(ひと)の気持ちや考えも分かれば、鬼に金棒ということですね!)

彼を知り己を知れば百戦殆うからず
『彼を知り己を知れば百戦殆(あや)うからず。彼を知らずして己を知るは一勝一負す。彼を知らず己を知らざれば戦う毎に殆うし。』
孫子の兵法の1節ですね。
「彼」→「相手」「敵」
「己(おのれ)」→「自分」「味方」
「殆うし」は、「危うし」でもよいですね
孫子の兵法の解釈の仕方、用い方は常に1つではないとは思いますが、
上記を簡単にいうと、
「相手(の実力)を知り、自分(の実力)を知っていれば、百戦百勝できる」
「相手を知らず、自分を知っていれば、勝ったり負けたりする(百戦50勝くらいにとどまる)」
「相手のことも、自分のことも知らなければ、常に危ない(百戦百敗するかもしれない)」
今は、中学数学・高校受験という場面ですので、
・彼 → 志望校
・己 → 自分の数学の実力
というところでしょうか?
| 彼(志望校)の実力? | → 難易度(偏差値) → 試験問題の傾向 → 過去問研究、などで知ることができますね! |
| 己(自分)の実力? | → 今は太刀打ちできなくても、本番までに準備ができますね! ⇒ 実力を上げていくことができますね! |
ちなみに、海音寺潮五郎の歴史小説「孫子」は面白いと思いますので
お時間があるときにでも、読んでみてほしいかなと思います。
それで歴史が好きになるきっかけや、国語力UPにつながれば、
なお お得ですね!
それでは、具体例です。
ヒストグラムから、どのようなことを読み取ることができるでしょうか?
下の3つのヒストグラムは、ある中学校3校の模擬テストの結果だとしますね
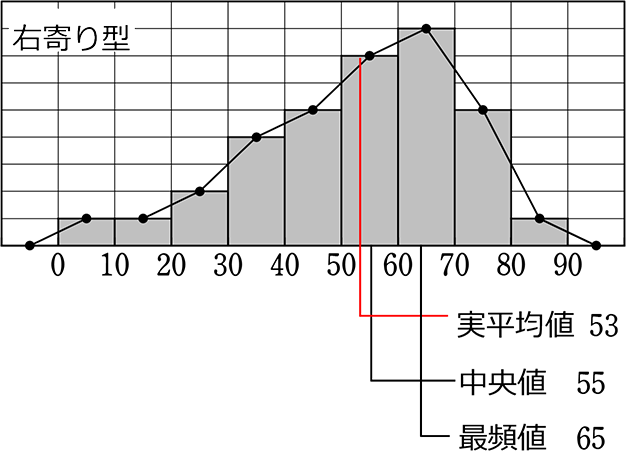
→ 「平均値」の目盛りで2分すれば、左右で同じ面積ですね
→ 「最頻値」はグラフにすると一目で分かる 代表値ですね(1番長い)
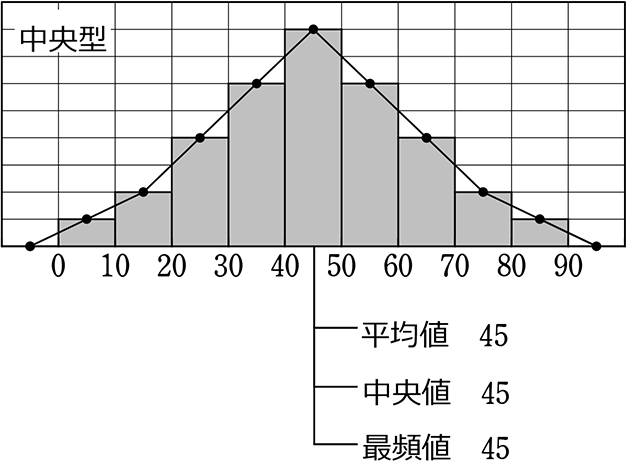
きれいな中央型は、
平均、中央、最頻の位置がほぼ
一致しますね!
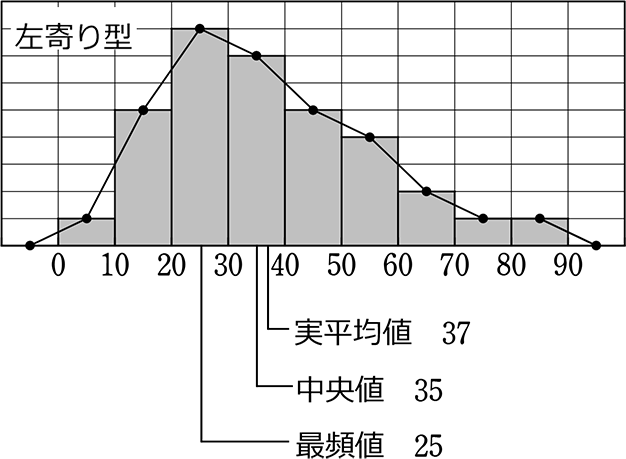
3つのグラフから考えられることは、
・右寄り型は、進学校かな…
・左寄り型の学校の次の目標は、中央型、その次に右寄り型になることかな…
・テストを受けた本人目線なら、同じ50点でも3校で価値が違いますね!
逆に、これらのグラフが、軽犯罪~重犯罪の発生件数であるならば、
・左寄り型の方が優れているといえますね!(軽犯罪は多いが重犯罪は少ない)
次です、ある職場の従業員の年収としますね
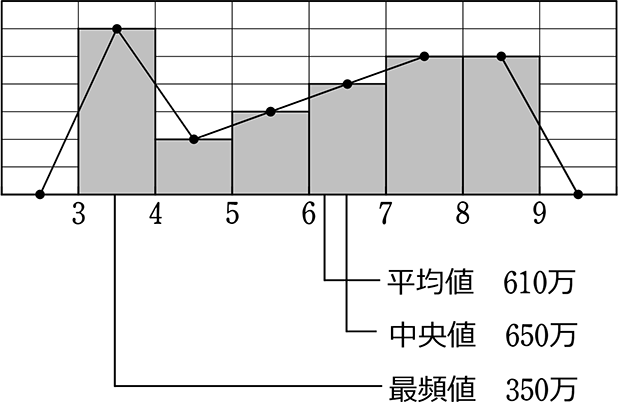
人員を採用したい職場では、もしかしたら、
中央値や平均値をもって従業員の「平均年収」のように宣伝するかもしれませんね
「平均650万くらい稼いでますよ~」
逆に、高給取りがたくさんいると世間から批判を受けるような職場では、
最頻値をもって「平均年収」のように公表するかもしれませんね
「最も多い年収層は350万くらいですよ~」
「平均値」は、かけ離れた「大きい値」、または「小さい値」があると
「中央値」「最頻値」に比べて、かなり影響を受けますね!
次です、2山型
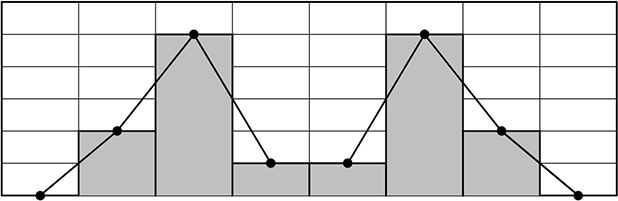
2山型は、2種類の対象があるといえますね
例えば、
日本人と外国人、
大人と子供、
男子と女子、など
先のグラフも「2山型」といえますね、
規制緩和後採用人員と規制緩和前採用人員というところでしょうか…
次です、中学生7人の1ヶ月のお小遣いのヒストグラムとします

グラフを見た第1感は、「ばらつきがある」だと思います。
ここで、最頻値だけを見て「中学生のお小遣いは大体7000~8000である」
と言われては… それは違うでしょ感がありますね
・最頻値は、対象者が少ないと「信憑性が低い」(たまたま感)
→ 1万人を対象にしたアンケートなど、対象数が多い場合は信憑性がありますね
以上のように、グラフを見る者の立場や、注目したいことの違いによって、
感じることは異なりますが、おおまかなイメージを感じられれば十分ですね!
(各代表値まとめ)
| 長所 | 短所 | |
| 平均値 |
全ての値を利用して算出される |
極端に小さい値、大きい値の |
| 中央値 |
極端に小さい値、大きい値の |
小さい側、または大きい側に変化があった場合も変化しない |
| 最頻値 |
・一目で見つけ出せる |
対象が少ない場合、信憑性が低い |
| 長所 | 短所 | |
| 平均値 |
全ての値を利用して算出される |
極端に小さい値、大きい値の |
| 中央値 |
極端に小さい値、大きい値の |
小さい側、または大きい側に変化があった場合も変化しない |
| 最頻値 |
・一目で見つけ出せる |
対象が少ない場合、信憑性が低い |
⑦ 近似値
まずは、小学数学の「概数(がい数)」を確認しますね
| ●「概数」… | 「切り上げ」、「切り捨て」、「四捨五入」などによって表される、概(おおむ)ねの数。 |
| 「切り上げ」… | 該当している数字が、「0でなければ、次の位(上の位)に入れてしまう」こと |
| 「切り捨て」… | 該当している数字を、「スパーン!と切り捨てる」こと |
| 「四捨五入」… | 該当している数字が、「5未満(数<5)ならば切り捨て、5以上(5≦数)ならば切り上げる」こと |
「切り上げ」、「切り捨て」、「四捨五入」は→「方法」であって、
「概数」は→「その方法で得られた数字」(結果)ですね!

四捨五入…正確には
「四捨五入」、言葉からは「4は捨て、5は入れる」ですね
図で表すと
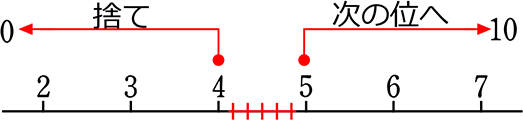
ですが、空白部分がありますね。「4.2はどっち?」「4.987はどっち?」
一の位に注目して四捨五入すれば、「4.2」も「4.987」も「0」ですね
注目している位の、「次の位」も「その次の位」も「その次の次の位」も
注目している位に付随しているのです。
ということは、「四捨五入」をもう少し正しくいうと、
「5未満捨5以上入」ですね!
これで 数直線上の全ての数字をカバーできますね

小学生で習う、
「4以下(数 ≦4) ならば切り捨て、5以上(5≦ 数) ならば切り上げる」
は「個数もの」では十分適応できますが、
「数値」「長さ」「重さ」などの「連続もの」では、
「5未満(数<5) ならば切り捨て、5以上(5≦ 数) ならば切り上げる」でないと
適応できませんね!




もう少し小学生の復習です
「概算」というものがありましたね
例えば、1980円の服を4着購入しました。合計金額は?
(Aさんの方法)
1980×4 = 7920 →  → 8000円(結果の概数化ですね)
→ 8000円(結果の概数化ですね)
(Bさんの方法)
1980×4 =  → 2000×4 = 8000円 (概算ですね)
→ 2000×4 = 8000円 (概算ですね)
「概算」の目的は、
「答えを簡単にするのではなく、 計算を簡単にする!」ですね!
では本題に戻りまして、
「近似値」とは何なのでしょうか?

近似値 =「真の値」に近い値
「概数」=「近似値」なのか?という疑問が湧くかと思います。
| ・ | 「切り捨て」、「切り上げ」、「四捨五入」→「方法」 |
| ・ | 「概数」→「結果」 でしたね、そして、 |
| ・ | 「近似値」は → 「扱い方」 ですね |
例えば、
円周率の「真の値」は → π
「概数」は → 3.14
そして、
| ・ | 「紙コップ製作所」の場面では、3.14(概数)は「近似値だ!」 |
| ・ | 「精密機器製作所」の場面では、3.14(概数)は「近似値ではない!」 「3.1415926535(概数)が近似値だ!」 |
| ・ | 「数学研究機関」の場面では、「3.1415926535(概数)は近似値ではない!」 「3.14159265358979323846(概数)が近似値だ!」 |
となるのかもしれませんね!
扱う場面で、「概数」にとどまったり、「近似値」になったりしますね
では、
「中学・高校数学」の場面では、3.14(概数)は?…そうです「近似値」ですね!
ということは、「中学・高校数学」の場面では、全て、
「概数」=「近似値」 となってしまいますね!
実社会にある数値は、ほとんどが「近似値」です。
「真の値」で表されている数値はほとんどない!ですね!
「重さ」「長さ」「温度」「時間」…
…ほとんど、ミクロン単位で「△△.□□□□□…」と続いているはずですから。
この点
「個数」は「真の値」ですね!
誤差

「誤差」 =「近似値」-「真の値」
この単元でしか使わない公式ですので、
時間が経てば、「どっちから、どっちを引くんだっけ?」となると思います。
そういう時は、適当に具体例を自分で作りましょう
「真10.5cm、近似10cm、誤差は…-0.5cm」
(なぜか、公式がなくても、「真の値」が基準で、それよりどれくらい大きいか小さいかが「誤差」…と、なりませんか?)
ということは、
-0.5 = 10-10.5 → 「誤差」=「近似値」-「真の値」 ですね!
そんな時間がもったいない人は、ゴロ合わせで
誤差 = 近藤さん-真彦さん ですね。
《 例 》
中学校の生徒数294人を、概数300人と表すとき、誤差は何人か。
誤差 = 近似値-真の値 = 300-294 = 6 人
真の値が分からない場合の誤差 (真の値の範囲)
《 例 》
(1) 近似値5.8、真の値の範囲は?
(「範囲」を求める場合は、必ず「略図」を書く、数学のコツでしたね!)
→ 5.7の次の位、5.7□を四捨五入して切り上がったものと、
5.8の次の位、5.8□を四捨五入して切り捨てたものがあるな!

 を四捨五入 → 5.8
を四捨五入 → 5.8 を四捨五入 → 5.8
を四捨五入 → 5.8
「真の値」は、「5.750」かもしれないし「5.7532」かも「5.849」かも…
すなわち、「真の値」は、5.75~5.84999……の間に無数に考えられる
すなわち、「線」だな。
よって、真の値の範囲は A. 5.75≦真の値<5.85
(2) このとき、「誤差の絶対値は?」
→「絶対値」とは「距離」、「距離」は「必ず
よって、5.8から5.75は「-0.05の地点」であるが、「距離」は「0.05」
他方、5.8から5.84999…は「+0.04999…の地点」で、「距離」は「0.04999…」
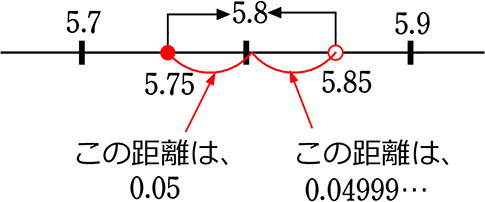
「誤差」は大きい方を採用するので、
A. 0.05 以下
このとき、「0.4999…」を、教科書では「0.05」としていますね
中学数学資料の分野では細かいことは気にしないから「0.05」なのか
高校数学の「極限」から、「0.05」としているのかは分かりませんが
「0.4999…」を「0.05」としても間違いではないのでしょうね!
ただし白丸、黒丸はしっかりお願いします!




⑩ 有効数字
2017(平成29年)1月1日現在の福岡県の人口は5,108,372人でした。
これを、千の位で「四捨五入」して 近似値511万としたとします。
(人口を概数で表す場合は、千の位で四捨五入することが多い)
① いじられて
② 位取りするだけの0群になってしまった数字
(位取り = 位を表す)
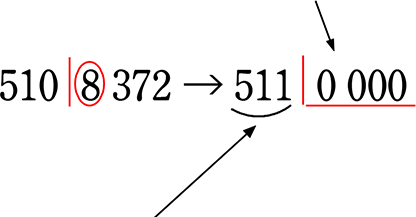
③ それ以外の数字を
「有効数字 (信頼できる数字)」
という
(510から511に
下の位から繰り上がっていてもかまわない)
上の場合、
・有効数字は、 5、1、1
・有効数字の桁数(有効桁数)は、 3桁
【 小数バージョン 】
| ① | いじられて |
| ② | 無表示になってしまった0
(小数点より右にある いじられた数字は無表示に!) |
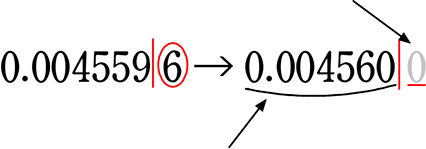
③ それ以外の数字(いじられていない数字)は
「有効数字?」
→ 本来、0.004560は、いじられていないのですから
「有効数字」なはずですが、
0.00は「有効数字」とはしません!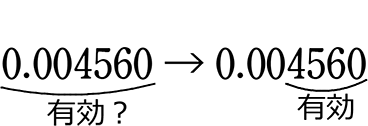 となります
となります
(理由)
「有効数字」とは
| ① | 0でない数字 (1~9)と数字に挟まれた0 |
| ② | 他の0は、小数点より最も右にある0まで
=いじった0か、いじっていない0か不明な場合の0で、いじっていない0! |
0.004560 の 0.00 は、いじってはいませんが、「元々位取りの0」ということですね
ex. 0.0000050km は 5.0mm とできますものね
 :神 「0.00000 は人間の基準の問題、新たな単位(ナノ)などを作ればいくらでも整数で表せるじゃろ!」
:神 「0.00000 は人間の基準の問題、新たな単位(ナノ)などを作ればいくらでも整数で表せるじゃろ!」
上の場合、
・有効数字は、4、5、6、0
・有効数字の桁数(有効桁数)は、 4桁
(まとめ)
「1~9の数字」と、「小数点」が
有効数字をはっきりさせてくれる





有効数字は大人になるほど理解しやすい分野
例えば、お米屋さんが、

ここに新米が、『8000粒』ありま~す!
今なら300円ですよ!
とふれ込んでいた場合。
| 小学生: | 「8000粒かぁ~!」 |
| 中学生: | 「本当に8000粒かな~?」 |
| 大 人: | 「ちょうど8000粒なわけないでしょ!およそ8000粒でしょ!」 |
と、大人になればなるほど、「0」に怪しさを持ちます。
「0」が「0000」のように増えればなおさらです。
これは、現実社会には「ちょうど」というものが本当に少なく、
その割には「0000」はゴロゴロと目につくからです。
「0000」は何か処理 ( 切り上げ、切り捨て、四捨五入) されていると
「経験則」という「直感」で感じるようになってしまっているのですね。
ですから、練習43などは大人は「経験則」で当然の話と思うことでしょう。
ということは、逆に中学生は「0000は社会にはほとんどない!」と
意識していれば、理解が進む分野なのかなと思います。
「8000粒ですよ!」 大人:「そんなわけないでしょ!」
「8001粒ですよ!」 大人:「本当に数えたんだ!」
「8000.0粒ですよ!」 大人:「本当に数えたんだ!」
本題に戻りまして、
上の問43の「9000」のように、いきなり「9000」と出てくると、
どこまでが有効数字か分かりませんね!
そこで、「ここが有効数字ですよ!」と分からせる表示方法があります。
 ←(大きい数値用)
←(大きい数値用) ←(小さい数値用)
←(小さい数値用)
言葉で表すと「??」ですので、形でイメージできればよいです
〇×10〇 〇.〇×10〇 〇.〇〇×10〇 〇.〇〇〇×10〇 などです
〇×\(\large{\frac{1}{10^〇}}\) 〇.〇×\(\large{\frac{1}{10^〇}}\) 〇.〇〇\(\large{\frac{1}{10^〇}}\) 〇.〇〇〇×\(\large{\frac{1}{10^〇}}\) などです
青〇が有効数字になります。
(小数点より左(整数部分)は、皆、1桁ですね!)
10〇 や \(\large{\frac{1}{10^〇}}\) が位取り数字です



.png)



sp.png)
「資料の散らばりと代表値」をたくさん扱った問題集は少ないと思いますので
当1年生無料問題集では
ほぼ全国の2014~2019の高校入試過去問の「資料の散らばりと代表値」を集めた問題(157問(60ページ))を解説しています
よろしければご利用くださいね!
お疲れ様でした !!















