| 中学1年生 | 中学2年生課程へ | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 正の数・負の数 | (2) 文字を用いた式 | (3) 一元一次方程式 |
| ア | 文字を用いることの必要性と意味 |
|---|---|
| ・ | 文字にxを選んだ訳 |
| ・ | 文字式の基礎ルール |
| ・ | 代入とは |
| ・ | 0乗が「1」の理由 |
| イ | 文字を用いた式における乗法・除法 |
| ・ | 項とは、係数とは、定数項とは |
| ・ | 絶対値とは |
| ・ | 1次式の計算方法 |
| ウ | 簡単な一次式の加法・減法 |
| エ | 文字を用いた式による表現や読み取り |
文字を用いた式
ア 文字を用いることの必要性と意味
一言で言うと
「数学っぽいからです」「かっこいいからですね!」
例えば、
6+□ = 9 より 6+x = 9、
\(\large{\frac{24}{□}}\) = 8 より \(\large{\frac{24}{x}}\) = 8
の方が、数学っぽいですね。それだけです。
文字は、xでもいいし、y、□、〇、△、( )、?、あ、山、何でもいいですね。
( )で囲まれたらそれで「一文字」とイメージできるなら、
(x+y) でも(山+海)でも (xy)でも (山海)でも、かまわないということですね。
6+(山+海)=9のとき、 山+海は? → 山+海 = 9-6 = 3
ただ、数学では、わからないものは「 x 」と置くことが多いですね!

未知なるもの
西欧では昔から、「未知なるもの」を「 x 」と表すことが多かったようです。
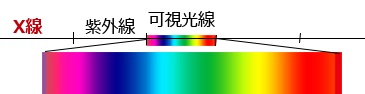
例えば、昔、ドイツの物理学者ヴィルヘルム・レントゲンは、
「紫 (可視光線)」の外側の「紫外線 (不可視光線:目に見えない線)」の さらに外側に何か未知なる「線」を発見し、
「X線 ( エックス線) 」と名付けました。
現在では「レントゲン線」とも言いますね

文字式の基礎ルール
●「
ex) 3×a → 3a
(「元は1つ」とさらにイメージしやすくなりましたね)
● 数字は文字の前です
ex) y3 → 3y
●「 1 」を省略します
ex) 1z → z, -1b → -b
(zを書くときは「2」と間違えないように工夫しましょう。 、←斜め線を入れるなど)
、←斜め線を入れるなど)
●「 ÷ 」は、「
(「÷」という記号は数学ではほとんど使いません)
ex) x÷3 →\(\large{\frac{x}{3}}\)か\(\large{\frac{1}{3}}\)x, 3÷x → \(\large{\frac{3}{x}}\)
● 原則 アルファベット順です
ex) 2bac → 2abc、 yx2→ x2y
●
● 明らかに単体になったら、( )は不要
ex) 3÷(x+1) → \(\large{\frac{(3)}{(x+1)}}\) → \(\large{\frac{3}{x+1}}\)
(2)(x+7) → 2(x+7)
(逆に単体でなくなったら、( )を忘れずに! 上で、 3÷x+1は (3÷x)+1です!別物になってしまいます!)
● ( )の、( の直後は、+(プラス)が望ましい
ex) +(-3x+2) → -(+3x-2) → -(3x-2)
● 分母は+(プラス)が望ましい
ex) \(\large{\frac{x+y}{-3}}\) (←「\(\large{\frac{-1}{-1}}\)」という「1」を掛けて) → \(\large{\frac{-x-y}{3}}\)
または分母全体の「-」や分子全体の「-」を前に出すだけ
・ \(\large{\frac{-x-y}{3}}\) = \(\large{\frac{-(x+y)}{3}}\) = -\(\large{\frac{x+y}{3}}\)
・ \(\large{\frac{x+y}{-3}}\) = -\(\large{\frac{x+y}{3}}\)

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)
代入
文字を「数」や「他の文字」や「式」に置きかえることですね。
《 例 》
6x+1 において
x
→ 6(y+3)+1 代入ですね
《 例 》
(y+1)2+3(y+1)+2 において
y+1=xと判明しました
→ (x)2+3(x)+2 代入ですね



0乗はなぜ 1
全ての「項」には「そのものがある」という意味の「1」が隠されていますね (「ある」という意味の1)
x3 = 1×x×x×x (1にxを3回掛ける)
x2 = 1×x×x (1にxを2回掛ける)
x1 = 1×x (1にxを1回掛ける)
x0 = 1 「1にxを、1回も掛けない」
→「1にxは掛けない」という意味ですね!
「じゃあ1に0を掛けよう」ということにはつながらない!ですね
「0乗」と「×0」とは根本的に違うということですね
ちなみに、マイナスの指数は…
x-1 = 1×\(\large{\frac{1}{x}}\)
x-2 = 1×\(\large{\frac{1}{x^2}}\)
x-3 = 1×\(\large{\frac{1}{x^3}}\) ですね
イ 文字を用いた式における乗法・除法
項、係数
8x+3 という数式があるとします
今までは、
「+-でつながっているものは、『元』がその数の分だけある」
と言ってましたが、数学的には『元』のことを『項(こう)』といいます
![]()
そして、文字を含む項の数字の部分を「係数」といいます
上の例であれば、8x の係数は?→ 「8」となりますね
ex. 2xyの係数は? → 2
2xyでyの係数は? → yが基準 → 係数は 2x
そして、8xは「文字の掛け合わせが1つ」なので、8xは「1次の項」といいます
「2つの文字のかけ合わせ(x2 、xy など)」であれば「2次の項」ですね
「+3」は項は項でも文字を含んでいませんので
特別に「定数項」といいます
(中学では問われることはありませんが、
3の係数は? → 3 となります)
「1次の項」だけでできている数式を「1次式」といいます
ex. 3x, x+4=0, 2x+3y=12


絶対値
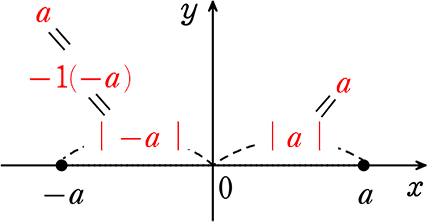
絶対値とは「距離」ですね ただそれだけです
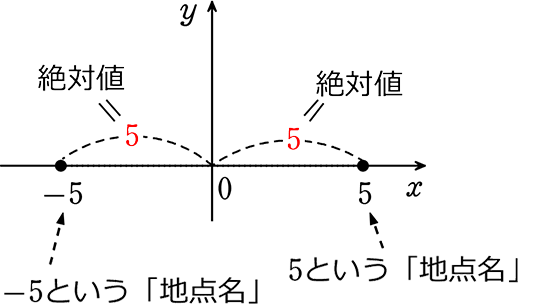
![]() は「距離」を表すときによく使われますね
は「距離」を表すときによく使われますね
∴ -5 の絶対値は 5 記号で表すと |-5|(読み:絶対値-5)= 5
5 の絶対値は5 記号で表すと |5|= 5
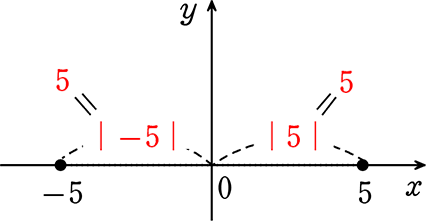
∴ 逆に 絶対値が 5 のとりうる値(地点名)は -5と5
絶対値が 5 のとりうるマイナスの値(マイナスの地点名)は -5
(問) |-5+2| = |-3| = 3
|-5|+|2| = 5+2 = 7
絶対値記号(||)の外し方まとめ
| ① | ||の中が「+」のとき、 ||をそのまま外すだけ |
| ② | |0|は、0 |
| ③ | ||の中が「-」のとき、 中身に -1 を掛けて外す |
③において「符号を取るだけ」「符号をプラスにするだけ」との案内もあるかとは思いますが、
親子中学では「-1を掛けて外す」でいきますね
ex ) |\(\small{\sqrt{3}}\)-2|の値を求めましょう (= 絶対値を求めましょう。=||を外しましょう。
→ 「符号を取るだけ」「符号をプラスにするだけ」では対応できませんね
|1.732…-2| = |-0.267…| = 0.267… これでは「概数」ですね
→ \(\small{\sqrt{3}}\) =1.732…なので ∴ まず||の中は「マイナス」と判明
∴ |\(\small{\sqrt{3}}\)-2| = -1(\(\small{\sqrt{3}}\)-2)= -\(\small{\sqrt{3}}\)+2 //
( 「0.267…」と「-\(\small{\sqrt{3}}\)+2」では、 「-\(\small{\sqrt{3}}\)+2」の方が正しく数値を表している!
cf. 「3.14…」と「π」では、「π」の方が正しく数値を表している )
いつか
① a>0のとき、|a|= a
② a = 0のとき、|a|=0
③ a<0 のとき、|a|= -a
という「まとめ」を見る時が来るとは思いますが (高校?)、その時に
|a| =-a だけを見て…
「ん!? |a| = -a? 絶対値は外したら「+」じゃないの?」と
変に混乱してしまった場合には…
次のように読み替えて下さいね
⇒ a<0 のとき (すなわち絶対値記号の中のaが負のとき)、
= a (そのまま出さずに)
= aに(-1)をかければ||が外れるのですよ~
a<0 という前提を忘れないでね~
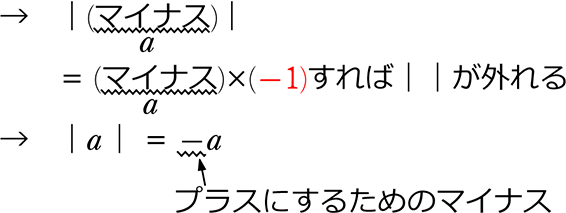
最初のまとめの③を 文字で表現すると後の③になってしまうのです
③ ||の中が「-」のとき、 中身に-1 を掛けて外す

③ a<0 のとき、 |a|= -a
1次式の計算

| 1. | ( )を外す 分配法則を用いて |
| 2. | 同じ文字の項をまとめる(同類項をまとめる) |
| 3. | 数字は計算する |
これだけです

= y-6x+4

= x-3x-2
= -2x-2 同類項はまとめることができる
・3a×6 = 18a
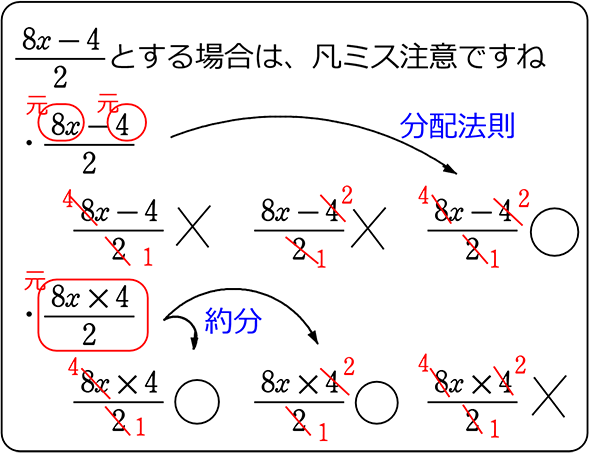
・(8x-4)÷2
= \(\large{\frac{1}{2}}\)(8x-4)
= 4x-2


ウ 簡単な一次式の加法・減法の解法と活用


エ 文字を用いた式による表現や読み取り


お疲れ様でした !!
その他の問題は、「問題集」で !!

.png)














