| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 一次関数 |
| ア | 事象と一次関数 |
|---|---|
| イ | 一次関数の特徴 |
| a | 一次関数の4ポイント |
| ① | 直線の式 |
| ・ | 変化の割合 (傾き) |
| ・ | 変化の割合で傾き具合をイメージする |
| ・ | y切片 |
| ② | 直線とy軸の交点 |
| ③ | 直線とx軸の交点 |
| ・ | 直線の式のまとめ | ・ | 「決まる」とは |
| ④ | 直線と直線の交点 |
| ・ | 高校生の1次関数の求め方 |
| ・ | 直線の平行移動 |
| b | 変域 |
| ・ | 傾きの範囲 |
| c | 中点の座標 |
| ・ | 重心の座標 |
| d | 対称な直線や点 |
| ・ | y=xに対称な直線 |
| ・ | 平行な傾き |
| ・ | 垂直な傾き |
| ・ | 対称な点 |
| ・ | 対称な直線、垂直な直線・対称な点のまとめ |
| ・ | 折り返す最短距離 |
| e | 座標上の面積 |
| ・ | 平行四辺形を2分する直線 |
| ・ | 三角形を2分する直線(等積変形) |
| ウ | 二元一次方程式と関数との関係 |
| エ | 一次関数を用いた具体的な事象の説明 |
| ・ | 動点 |
| ・ | ダイアグラム (2016過去問) |
| ・ | 電車、バスの時刻表 |
一次関数
ア 事象と一次関数
関数とは、xが決まれば、yの値がただ一つ決まる関係でしたね。
yがxの「1次関数である」とは
y =ax+b の形になるということですね
1年生で学んだ「比例式」
y = ax に 「b」が付いただけです
「a」「b」には、「定数」すなわち「数字」が入って固定されます
例えば、
y = 2x (比例式であり、1次関数)
y = 2x+3 (1次関数)

上の式で
・比例は 毎月2冊づつ本を買えば、xか月後にy冊貯まる という感じ
3か月なら (
・1次関数は 元々3冊持っている上で、毎月2冊買うという感じ
3か月なら (


比例の式を上下に「ずらしただけ」ですね!
ただそれだけの違いです
比例式 同様「×(かける)でつながっている公式(〇=△・□・◇・▽)」のようなものは、すべて「1次関数」になれる可能性があるということですね!
→右辺の文字のうち、1つだけが文字(変数)として残り、それ以外は数字(定数)になれば 1次関数ということですね!
例えば
・距離 = 速さ・時間

ここ(z)が「数字で、決まれば」、「一次関数」ですね
・面積 = 横×縦
・体積 = 底面積×高さ
・(角、円)
・対象=全体×割合
・・・などなどたくさんありますね
《 例 》
・縦5cm、横xcmの長方形の面積yは、1次関数でしょうか
y = 5x → y = ax の形 → 1次関数 (比例関数でも可)
・縦5cm、横xcmの長方形の周囲の長さyは、1次関数でしょうか
y= 2(x+5) → y = 2x+10 → y = ax+b の形 → 1次関数
・x円の服を3割引きで買った時の代金yは、1次関数でしょうか
y = 0.7x → y = ax+0 の形 → 1次関数(比例関数でも可)
・15%の食塩水xgの塩の重さyは、1次関数でしょうか
y = \(\large{\frac{15}{100}}\)x → y = ax+0 の形 → 1次関数 (比例関数でも可)
イ 一次関数の特徴
一次関数の4ポイント
一次関数のポイントは下の4つだけですね!

これだけですね!
上のグラフに値を入れてみると


それでは 個別に見ていきますね
① 直線の式
y = ax+b
この形が全ての始まりになります
yとxは、「変数( 色々な数字を試し入れするための箱のような文字) 」ですので そのまま さわらずに残しておきます
aとbは、「定数(定まった数字)」ですので、その場面、その問題において決まった数字が入ります
ex) y = 3x+1
・ 変化の割合 ( 傾き)
「a」を「変化の割合」や「傾き」と言います
比例式では「比例定数」と呼びましたね!
この3つの呼び方は、名前が違うだけで、内容は全く同じですね
→ どれも・・・ (底辺に対する) 高さの割合です(割合とは)
◎ 傾き(a)の求め方

傾き(斜辺の角度)が同じなら、
直角三角形の大きさに関わらず、
高さの(底辺に対する)割合は同じ!↓

a = \(\large{\frac{高さ}{底辺}}\) = \(\large{\frac{yの長さ}{xの長さ}}\)=\(\large{\frac{yの増加量}{xの増加量}}\)=\(\large{\frac{y_{1}-y_{2}}{x_{1}-x_{2}}}\) ですね
(※ 座標上ですので「マイナス」の高さもあります)
・xとy、どっちが分母?分子?となってしまった場合は…
大基本形 y = ax を aの式(a= の式) にするだけでしたね
y = ax → a = \(\large{\frac{y}{x}}\) → xが分母! yが分子! でしたね
・どうしてxが分母? という根本疑問には
「yを高さにしたから」「xを横軸にしたから」
「高さの(y)割合だから」
「横からスタートすると基準付けたから(ルール)」としか 言えませんね…
イメージとして

原点を出発!
→ ①人は空を飛べないから
まずは横に歩きますね!
②すると、実は上に(下に)これだけ
上がっていたというイメージでしょうか
∴ 横からスタート、横(x)が分母!

図の直角三角形で傾き具合\(\large{\frac{1}{2}}\) は、その三角形で
「最も約分された比」ですね
横の目盛り2、縦の目盛り1 が、
それぞれ 4と2、 8と4、 7と3.5、なども
\(\large{\frac{2}{4}}\) \(\large{\frac{4}{8}}\) \(\large{\frac{3.5}{7}}\)
→ 約分すれば当然「\(\large{\frac{1}{2}}\)」ですね
(グラフなら、y軸から最初の
格子点になるということ)
∴ 斜辺の角度が同じなら、どこの目盛りを読んでもよい! となりますね
→ \(\large{\frac{2}{4}}\) = \(\large{\frac{3}{6}}\) = \(\large{\frac{1}{2}}\)
格子点

格子点とは、 → 線と線の交差点 ですね ですので
ですので
目盛りは必ず整数や1とは限りません
各問題により必ず図や目盛りなどで
格子点の基準(1目盛りの大きさ)は示してくれていますね
(中学ではほぼ、2つの線の目盛りは1ですね)

←このような目盛りのグラフでは、
(0, 0)から最初の格子点は(4, 2) ですね
《 例 》2点(-2,3) (6,-1)を通る直線の傾き(変化の割合)を求めましょう
→ 2点が決まれば、直線が決まりますね
→ 座標は便利ですね

どっちでも同じですね
① 右に歩くと、下に落ちていた
a = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{-1-3}{6-(-2)}}\) = \(\large{\frac{-4}{8}}\) = -\(\large{\frac{1}{2}}\)
② 左に歩くと、上に上がっていた
a = \(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{3-(-1)}{-2-6}}\) = \(\large{\frac{4}{-8}}\) = -\(\large{\frac{1}{2}}\)
結果が同じなら、1つのやり方に慣れた方が間違いが少なくなりますね
おすすめとして、
「分母がマイナスは気持ち悪い」「右にしか歩かない」という意味で
a = \(\large{\frac{高さ}{底辺}}\) = \(\large{\frac{yの長さ}{xの長さ}}\) = \(\large{\frac{yの増加量}{xの増加量}}\)

上の例、2点(-2,3) (6,-1)なら


という感じで、「自分ルール」を作るのもよいのではないでしょうか
そして、2点の座標が解れば、実は「b」も解る、
すなわち、「直線の式」全てが解るのですが
次で、お話しますね

変化の割合で傾き具合をイメージする
小学生では、傾きといえば「分度器」を使って角度を表示していましたね
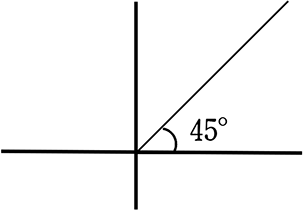
このようであれば、直線の傾きが「イメージ」しやすいかもしれませんね

対して1次関数では、45°なら y = \(\large{\frac{1}{1}}\)x → y = 1x で傾き「1」ですね
「傾きが 1って? 何?」と感じているかもしれませんね
以前「余談」で話した「勾配(こうばい)」を表す「%」はイメージできるようになっているでしょうか?
例えば、「20%」の上り坂なら
勾配 = \(\large{\frac{高さ}{底辺}}\) = \(\large{\frac{高さ20m}{横100m}}\) ( =\(\large{\frac{高さ2m}{横10m}}\)) = 0.2 = 20% でしたね

「分数」をイメージするためには
100mぶんの20mと読まずに
100mにつき20m、10mにつき2m と読めばイメージがしやすくなりましたね!
角度なら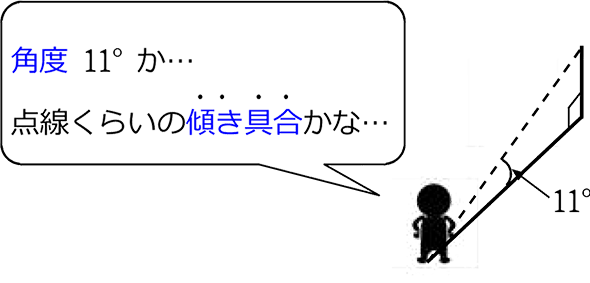
1次関数の「傾き( =変化の割合)」なら
傾き( =変化の割合)= \(\large{\frac{高さの増加量}{横の増加量}}\) =\(\large{\frac{yの増加量}{xの増加量}}\) = \(\large{\frac{20}{100}}\)=\(\large{\frac{1}{5}}\)


どれも「傾き具合」の表現方法ですね
「角度表示」も慣れてきたように「分数表示」でも傾き具合がイメージ
できるように必ずなります!ご安心ください
・ \(\large{\frac{1}{1}}\) → 1 → 45°→ (イメージとして)標準の傾き
・ 分母が大きくなる→ \(\large{\frac{1}{1}}\) → \(\large{\frac{1}{2}}\) →\(\large{\frac{1}{3}}\) → \(\large{\frac{1}{4}}\) →「傾き」がなだらかになる
・ 分子が大きくなる→ \(\large{\frac{1}{1}}\) → \(\large{\frac{2}{1}}\) →\(\large{\frac{3}{1}}\) → \(\large{\frac{4}{1}}\) →「傾き」が急になる
・「勾配」は分数を\(\large{\frac{〇〇}{100}}\)にして%表示したものですね
・「傾き (変化の割合)」は分数をただ約分したものですね
全くの余談になりますが
傾き1 → 45° → 標準の傾き とは言ってみましたが
実際45°の斜面の上に立つと「断崖絶壁」のように感じますね!
スキー場の上級者コースで、たまに「最大斜度35°」とかありますが
実際、上から斜面を見ると足がすくみますね!!

クリック・タップで答え (反応が遅い場合があります)
・ y切片
y =ax+b の基本形で、「b」を「y切片(せっぺん)」と言いますね
b すなわちy切片とは、「y = ax+b の直線」と「 y軸との交点 」ですね
座標なら ( 0, b)、y軸の目盛り読みならb となりますね
例えば
y切片は -2 となりますね
座標表示なら →(0, b) → (0, -2) ですね
すなわち、直線の式で xが「0」の時の yの値ですね
= xに0を代入したときの yの値
→ y = 2x-2 → y = 2・(0)-2 → y = -2 ですね
《 例 》
2点 (-1, -4) (3, 4) を通る直線の b(y切片)を求めましょう
(方法①) 傾きを求めて、次にbを求める (順次方式)
y = ax+b の4文字のうち (2点が明らかなので)aは求められるな…
a = \(\large{\frac{4-(-4)}{3-(-1)}}\) = \(\large{\frac{8}{4}}\) = 2 ∴ y = 2x+b まで判明
次に、yとxが解れば、残り1つになる「b」が解るな…
→ 与えられた座標を代入するだけですね!
(-1, -4) (3, 4)どちらでも大丈夫ですが、
楽そうな「+」ばかりの(3, 4) の方で行ってみますね
yに4、xに3を代入
y = 2x+b → (4) = 2・(3)+b → b = -2
A. y切片は-2 (y = 2x-2)
(方法②) 解らない4文字のうち、2つが2回解っているので、連立方程式
→ 元 y=ax+b、 2点 (-1, -4) (3, 4)
\(\small{\begin{cases}
-4 = a(-1)+b …①\\
4 = a(3)+b …②
\end{cases}}\)
\(\small{\begin{cases}
-4 = -a+b \\
4 = 3a+b
\end{cases}}\)
①-②
-8 = -4a → a = 2 …③
③を②に代入
4 = 6+b → b = -2
A. y切片は-2 (y = 2x-2)
基本的には、1次関数では解らないものを「徐々に」求めていくという
場面が多いので、方法①を多用することにるのかなと思います
② 直線とy軸の交点
これは、すなわち上の「y切片」と同じ話ですので、上を参照願います
③ 直線とx軸の交点
「x切片」…もう想像がつきますね!
直線と x軸 の交点ですね すなわち、yが「0」の時のxの値ですね

y = ax+b の式で、
y切片は「
x切片は直接、式に現れていませんので、x切片を求めるには
直線の式に(?, 0)を代入、すなわち y =0 を代入して求めます
上の y = 2x-2 のx切片は?
→ 0 = 2x-2 → x = 1
A. 1 (1, 0) ですね!
そして、
ただの「切片」と言った場合には、それは「y切片」を指しますね!

直線の式のまとめ
1. 2点がわかれば、直線の式が解る(決まる)
1点しか分からないと…
y=a(x+1)+1という
無数の直線が考えられる
もう1点あると (2点あると)…
y=\(\large{\frac{4-1}{5+1}}\)(x+1)+1
これしかない!(1つに決まる)
2. 傾きがわかっていれば、あとは 1点で、直線の式が解る(決まる)
傾きしか分からないと…
y=\(\large{\frac{2}{3}}\)x+b という
無数の直線が考えられる
1点あると
y=\(\large{\frac{2}{3}}\)x+1
これしかない!(1つに決まる)
決まる
数学で「決まる」とは、直線においても図形においても
『それ以外考えられない!』ということですね
その形 であったり、その位置 であったり、その大きさ であったり、その傾き具合 であったり
→ 一言、それ以外考えられない!
3. 直線が、プラスの場合(a(傾き)>0の場合)は、「右肩上がり」
マイナスの場合(a<0の場合)は、「右肩下がり」

4. y = ax+b の直線はy = axの直線を bの分だけ上下にずらしたもの


④ 直線と直線の交点
直線と直線が交わる座標ですね!
交点の求め方は、2つの直線の式を「連立方程式」として解けばよいだけですね!
なぜ、連立方程式で解けば「交点の座標」が求まるのかは
先に学んだ「連立方程式」の「連立方程式の解が1つに決まる理由」で少し話しましたね
そうです、それぞれの直線を「2元1次方程式」と考えれば、
それぞれの式の解は、例えば、
①の式の解・・・
\(\small{\begin{cases}
x = 1 のとき \\
y = -1
\end{cases}}\)
\(\small{\begin{cases}
x = 2 のとき \\
y = -3
\end{cases}}\)
\(\small{\begin{cases}
x = 3 のとき \\
y = -5
\end{cases}}\)
・・・無数
②の式の解・・・
\(\small{\begin{cases}
x = 1 のとき \\
y = 4
\end{cases}}\)
\(\small{\begin{cases}
x = 2 のとき\\
y = 6
\end{cases}}\)
\(\small{\begin{cases}
x = 3 のとき\\
y = 8
\end{cases}}\)
・・・無数
共に無数の解を持ちましたね
そして、2つの方程式の解が、「共通のx、かつ、共通のy」であるために
「
「連立」 → 「共に成り
よって、2直線の「交点」を求めるには、
2直線を連立方程式として解けばよい ということになりますね
《 例 》
直線 y = 2x-3 と 直線 y = -x+3 の交点Pを求めましょう
\(\small{\begin{cases}
y = 2x-3 \\
y = -x+3
\end{cases}}\)
∴ x = 2 , y = 1
A. P (2, 1)
以上
① 直線の式
② y切片
③ x切片
④ 交点
が 1次関数のポイントですね!
そして、この後 お話していくことは、付随的なポイントということになります

高校の1次関数の求め方
● 2点( p, q )、( r , s )を通る直線の式を、高校では
(y-s) = \(\large{\frac{s-q}{r-p}}\)(x-r)
または、
(y-q) = \(\large{\frac{s-q}{r-p}}\)(x-p)
と、いっぺんに求めてたりしますね
「傾き」の求め方は、中学と全く同じ ですね(\(\large{\frac{s-q}{r-p}}\)、 その後どちらかの点を
x-〇、y-〇に入れるだけですね、y-〇はどの道、「移項」しますので、
→ (矢印)の右側のような形から始めれば楽ですね
● 中学同様に、「傾き」が解っていれば、あと「1点」わかればよいですね
(回っている2本羽のプロペラに指を突っ込んで止めるイメージ、「止まった!」=「決まった!」)
y = a(x-p)+q や y = a(x-r)-s
となりますね
《 例 》
2点(-2, -7)、(4, 5) を通る直線の式を求めましょう
y = \(\large{\frac{5-(-7)}{4-(-2)}}\)(x-4)+5 (4, 5)の点を利用してみました
y = 2(x-4)+5
y = 2x-8+5
y = 2x-3
A. y = 2x-3
《 例 》
傾き2の直線が点(4, 5)を通るとき、直線の式を求めましょう
y = 2(x-4)+5 …上の《 例 》の途中から始まっただけですね!
y = 2x-8+5
y = 2x-3
A. y = 2x-3
これらは、中学では学びませんが、途中式の不要なテストでは使えそうですね!

傾きa、1点(x1, y1)を通る直線の式
y = a(x-x1)+y1
ex. 傾きa, 点(-2, 3)を通る直線の式は?
y=a(x-(-2))+3 → y=a(x+2)+3 ←ここまでで十分ですね、傾きが判明したらこの先も計算ですね
この先は完全な余談です! 読み流すだけで大丈夫です!
この公式の原理は…実は「平行移動」です
直線(y-5) = 2(x-4)は、直線(y) = 2(x)をx軸方向に(+4)、y軸方向に(+5)
平行移動させたものという意味になります
点で言えば、直線(y) = 2(x)上の点(0, 0)などを
x軸方向に(+4)、y軸方向に(+5)平行移動させたものという意味になります
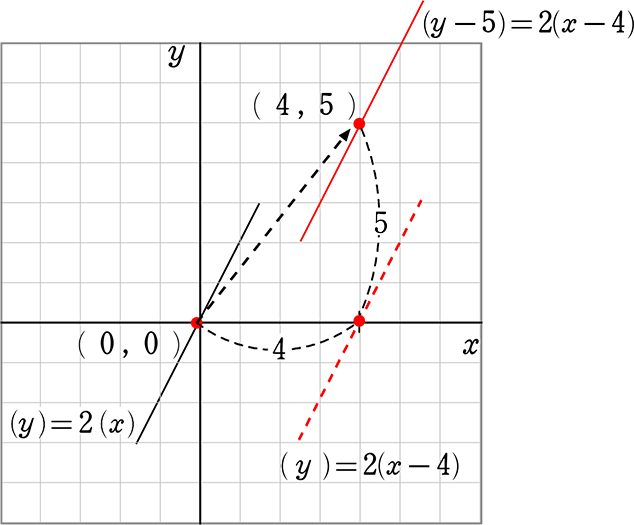

直線 y = ax を
x軸方向にp、y軸方向にq移動した直線
(y-q) = a(x-p)
(他例) y = 2x を、
x軸方向に0、y軸方向に0 移動すると
(y-0) = 2(x-0)
y-0 = 2x-0
y = 2x … 当然、移動していない
x軸方向に4、y軸方向に5 移動すると
(y-5) = 2(x-4)
y-5 = 2x-8
y = 2x-3
ふと疑問が湧きますね … 平行移動しているということは何となく解ったけど、
プラス方向の移動なのに、どうして、
(y+5)や(x+4) ではなく
(y-5)や(x-4)なの? 符号が逆では?
直線 y = 2x を、x軸に+4、y軸に+5移動した新直線を l2 としますね
l2上のある点を(X, Y)、y = 2x 上の点を(x, y)とします
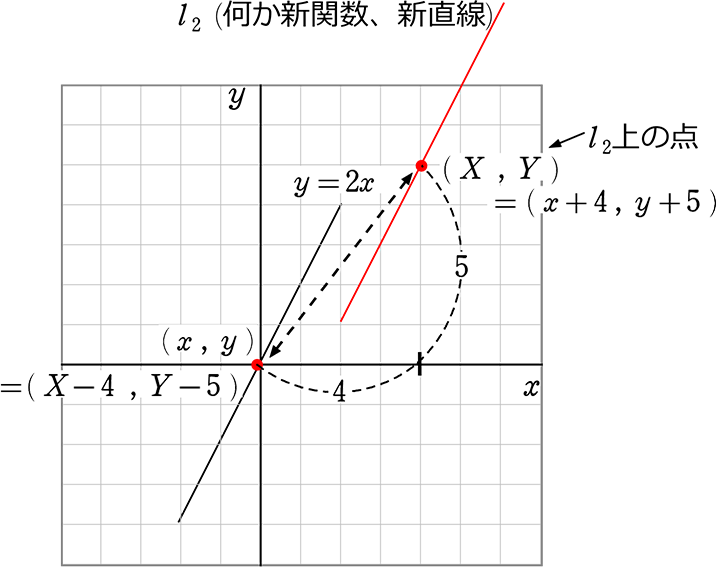
X = x+4 → x = X-4
Y = y+5 → y = Y-5
y = 2x に x = X-4 と y = Y-5 を代入すれば、新関数ですね
→ (Y-5) = 2(X-4) の完成ですね
→ あとは小文字にしてもかまいません → (y-5) = 2(x-4)
(イメージ的には) …あくまでイメージです!
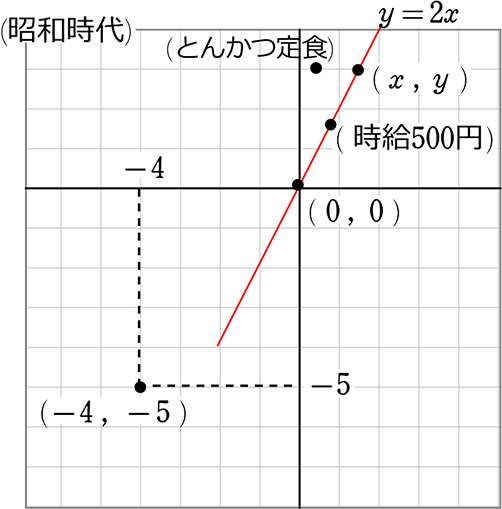
① y = 2x上に 左図のような
3点が乗っているとします
② 左下の方のある点は
(-4, -5) ですね
③ これを「昭和時代」とします
④ そして、平成時代になりました、
政府:「物価が上がったので新基準を採用します!
今までの最低時給500円を、最低時給900円にします!
今までの (-4, -5) を原点 (0, 0) にします!
皆様の価値が上がります!」
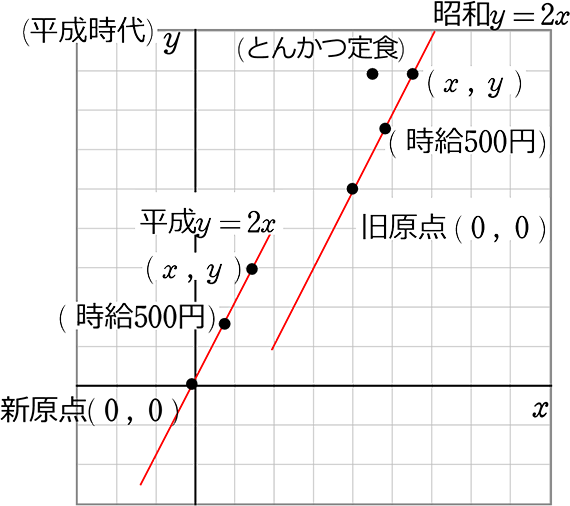
昭和 y = 2x:「僕たちは
今後どうなるの?」
 政府「こうなります!」
政府「こうなります!」
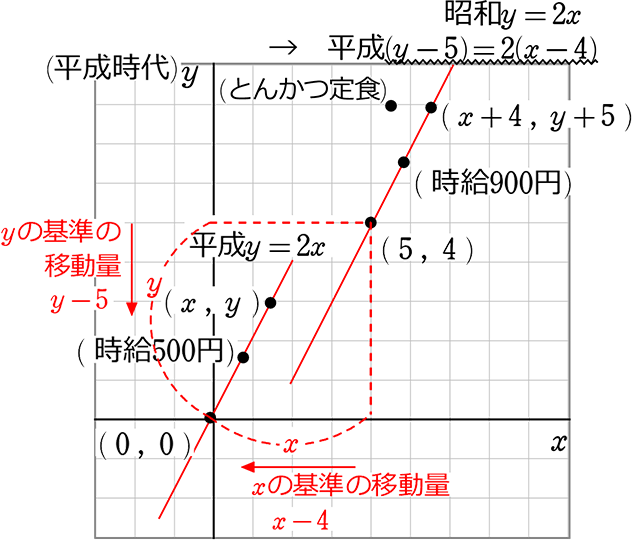
平成(\(\underbrace{ y-5}_{yの基準の移動量}\)) = 2(\(\underbrace{x-4}_{xの基準の移動量}\))
結果、「直線」や「点」が
増えたように、
平行移動したように、見える
(x+4, y+5):「やったー!(x, y)から僕の価値が勝手に上がったー!」
(5, 4):「やったー!(0, 0)から僕の価値が勝手に上がったー!」
(時給900円):「やったー!(時給500円)から僕の給料が勝手に上がったー!」
政府:「クックックッ…騙されおって、上がったのは『数字(物価)』だけなのに!
『価値』は上がってないのに、喜んじゃって!
隣の『とんかつ定食』の位置関係を考えたらわかるだろうに!」
昭和 y=2x: 「あれ、僕の身体が何か変わってる〔(y-5) = 2(x-4)〕…
まっ いいかっ! 価値が上がったんだし!」
政府: 「その(x-4)と(y-5)は『ICチップ』じゃ~!
「ぬか喜びするように」というプログラムのICチップじゃ~」
以上はイメージです! イメージですよお~!
しかし、実際 貨幣価値は時代とともに下がっていますね
明治時代の10円は、公務員の月給とほぼ同等
平成時代の10円は、うまい棒1本とほぼ同等
b 変域
1年で学んだ比例の変域と全く同じですね!
xの値に対するyの値が「1つ」あるように、
xの変域に対するyの変域が「範囲」としてありますね
xの変域を「定義域」、
yの変域を「値域」と言ったりしますね
xの区
「範囲」を求める場面では、本当に簡単でいいから「略図を書く」のがポイントでしたね!
《 例 》
1次関数 y = -2x+5 で、定義域 ( = xの変域)が -1≦x<6のとき
値域( = yの変域)を求めましょう
x = -1 のときの yの値 → 7
x = 6 のときの yの値 → -7
(凡ミス防止用略図)
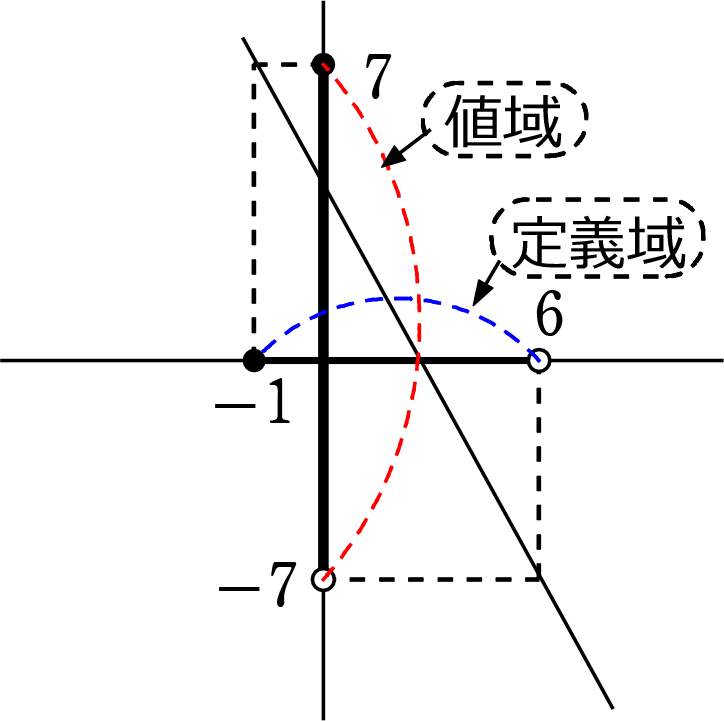
定規なんかいりません!手書きでOKです
① y切片が
② 傾きが
③ 傾きが-2 → 結構、急斜面
④ yの●〇は xの ●〇に対応させる
あとは yの範囲を読むだけですね!
A. -7<y≦7
《 例 》
① 関数 y = ax+b において、x の変域が -2<x≦3 のとき、
y の変域が -3≦y<7 である。この関数を求めよ
→ 不等号から「-2」に対応するのは「7」と分かりますね
( < → 〇、 ≦ → ● でしたね)
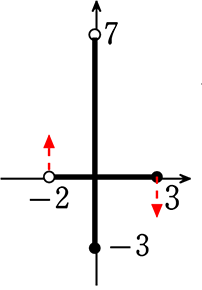
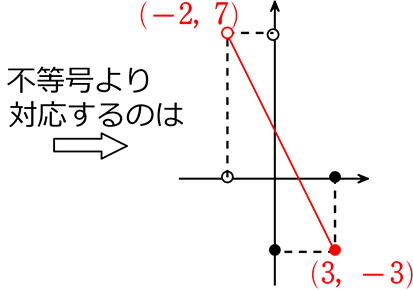
→ あとは、2点(-2, 7)、(3, -3)を通る直線を求めるということ
(順次方式で解いてみると)
a = \(\large{\frac{-3-7}{3+2}}\) = -2
∴ y = -2x+b まで確定
y = -2x+b が (3, -3) を通るので
(-3) = -2(3)+b → b=3
∴ y = -2x+3
② 関数 y = ax+b において、x の変域が -2≦x≦3 のとき、
y の変域が -3≦y≦7 である。この関数を求めよ
→ -2に対応するのは、-3? 7?
→ どちらもあり得る → どちらも求めなければならない
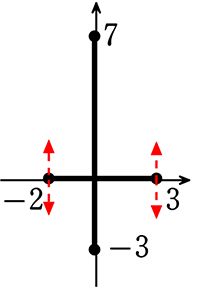
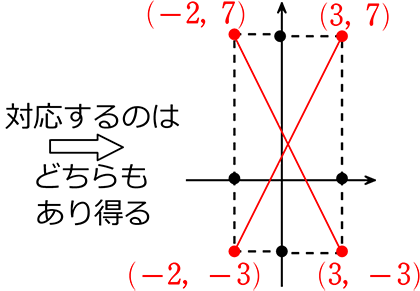
→ 2点(-2, 7)、(3, -3)を通る直線と
2点(-2, -3)、(3, 7) を通る直線を求めるということ
((-2, 7)、(3, -3)は連立方式で解いてみると)
\(\small{\begin{cases}
(7)=a(-2)+b \\
(-3)=a(3)+b
\end{cases}}\)
→ \(\small{\begin{cases}
7=-2a+b \\
-3=3a+b
\end{cases}}\)
(上-下で) 10 = -5a → a = -2
(a = -2 を上へ) 7 = -2(-2)+b → b = 3
∴ y = -2x+3
((-2, -3)、(3, 7)は高校方式で解いてみると)
y=傾き(x-x座標)+y座標
y=\(\large{\frac{7+3}{3+2}}\)(x-3)+7
y=2(x-3)+7
y=2x-6+7
y=2x+1
∴ y = -2x+3, y = 2x+1 の2式
・ 傾きの範囲
《 例 》
2点A(1, 4)、B(3, 1) がある。直線y=ax-2 (aは定数)が線分AB(両端の点A, B を含む)上の点を通るとき、a のとることのできる値の範囲を求めましょう
→ 図のイメージは

最小の傾きは、(0, -2)(3, 1)を通るとき
y=\(\large{\frac{1+2}{3-0}}\)(x-0)-2
y=1(x)-2 → y=x-2 ∴ a=1
最大の傾きは、(0, -2)(1, 4)を通るとき
y=\(\large{\frac{4+2}{1-0}}\)(x-0)-2
y=6x-2 ∴ a=6
∴ a のとることのできる値の範囲は、 1≦a≦6
aの値の大小をそのまま〇≦a≦〇に当てはめると、
当然(aの値小≦a≦aの値大)ですね
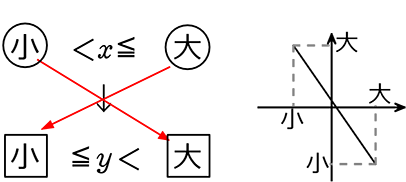
これをグラフでイメージすると
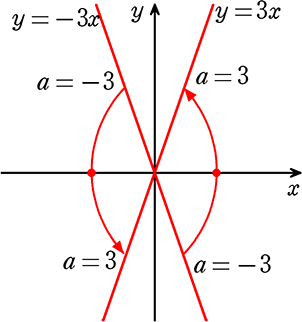
(第1象限、第4象限で)
右下がり≦a≦右上がり
→ 反時計回り → 下から上
(第2象限、第4象限では)
→
最大に範囲を広げると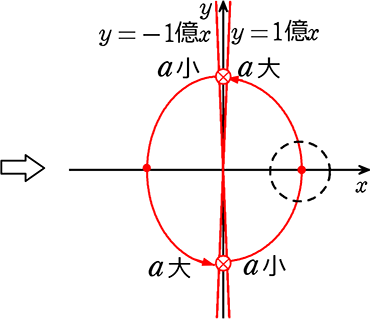
右側(第1、第4)は下から上
左側は、上から下で、
どちらもy軸上は
《 例 》
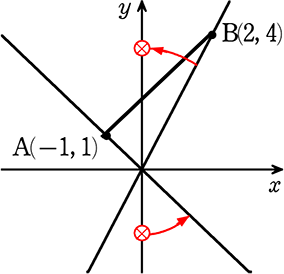
2点A, B の座標を(-1, 1)、(2, 4)とする、
直線y=ax が線分ABと交わるとき、aの範囲を求めましょう
→ 略図は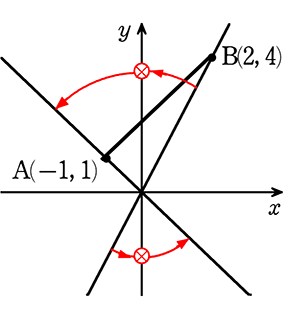
→ (0, 0)(2, 4)の式の傾きaは
y=\(\large{\frac{4-0}{2-0}}\)(x-0)+0
y=2x (↑傾きaの値さえ分かればよいので赤部分だけでよかったですね)
→ (0, 0)(-1, 1)の傾きaは
a=\(\large{\frac{0-1}{0+1}}\)=- 1
反時計回りなので、赤矢印の部分の範囲ですね
どのように不等号で表現すればよいのでしょうか
→ 2≦a<× (2以上×未満:×は定義できない傾き →
→ 第2象限の×<a≦-1 の部分は、第4象限で考えるとイメージしやすいですね
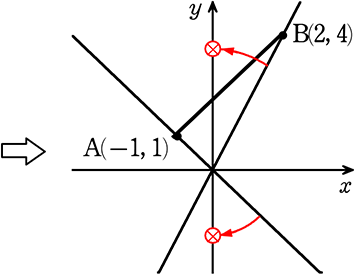
⇒ 答えに「
∴ 2≦a, a≦-1
気持ち悪いですが、これが答ですね 
イメージ


どうしてy軸上は白丸ではなく×? (●と〇の意味)
×ということは、「傾きが90°」のようなものは「ない(定義できない)」ということですね
傾きをきつくしていく(=底辺が0に近づく)と…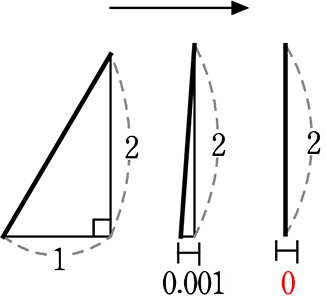
傾きは、底辺に対する高さの割合ですので、
傾き=\(\large{\frac{高さ}{底辺}}\) でしたね、ということは
図の三角形の傾きは左から…\(\large{\frac{2}{1}}\)、\(\large{\frac{2}{0.001}}\)、\(\large{\frac{2}{\color{red}{0}}}\)
→ 分母が「0」!はダメでしたね → 定義できない (0を割る、0で割る)
ということで、原点とy軸上の点を結ぶ直線の傾き具合は、「定義できない」
→ × ですね 
では、x軸と重なる線はOK?
→ OKです、黒丸です
同じように三角形で考えると
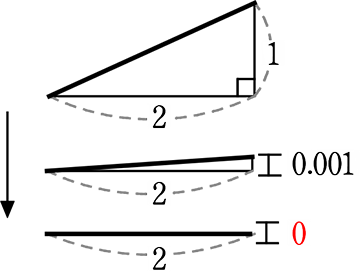
傾きは上から、\(\large{\frac{1}{2}}\)、\(\large{\frac{0.001}{2}}\)、\(\large{\frac{\color{red}{0}}{2}}\)
→ 「0を割る(分子が0)」はOKでしたね
 ではなく⇒
ではなく⇒ 
ということで、原点とx軸上の点を結ぶ直線の傾きは「0」
直線の式は、y=0x+0 → y=0 ですね
(ちなみに先の×の直線の式は、 → いきなり x=0)
以下は中学生には全く関係ありません、読み飛ばしてOKです
直線を「極細三角形」と見立てるこの考え方は
高校生になったとき少し役立ちますね。図は半径1の円です
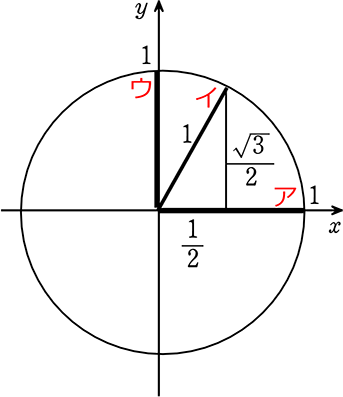
ということは
| |
→ \(\large{\frac{高さ}{斜辺}}\) 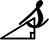 |
=高さ具合 |
| |
→ \(\large{\frac{底辺}{斜辺}}\) 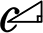 |
=底辺具合 |
→ \(\large{\frac{高さ}{底辺}}\)  |
=傾き具合 |
| θ |
ア |
イ |
ウ |
|---|---|---|---|
| sin |
sin0° |
sin60° |
sin90° |
| cos | \(\large{\frac{1}{1}}\)=1 | \(\large{\frac{\large{\frac{1}{2}}}{1}}\)=\(\large{\frac{1}{2}}\) | \(\large{\frac{0}{1}}\)=0 |
| tan | \(\large{\frac{0}{1}}\)=0 | \(\large{\frac{\large{\frac{\small{\sqrt{3}}}{2}}}{\large{\frac{1}{2}}}}\)=\(\small{\sqrt{3}}\) |
\(\large{\frac{1}{\color{red}{0}}}\) → × |
⇒ 90°の傾き具合=tan90°は「値なし」ですね
c 2点の中点の座標
2つの点の「中点」とは
2つの点「最短距離の真ん中」 → 2つの点を結ぶ線分上で2つの点から等しい距離の点
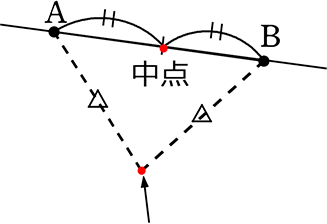
ココは中点ではないですね、ただA、Bから距離が等しい点ですね
(ABの垂直二等分線上の点の1つ、向こう側にも点をとれば、たこ型やひし形ができましたね)
図のイメージだけで十分ですね
2つの座標の「中点」の座標は…

・ 2点の座標を 足して 2で割る だけです
・ 文字で表すと
2点 (x1, y1) (y1, y2) の中点の座標は
( \(\large{\frac{x_1+x_2}{2}}\), \(\large{\frac{y_1+y_2}{2}}\) ) ですね!
《 例 》
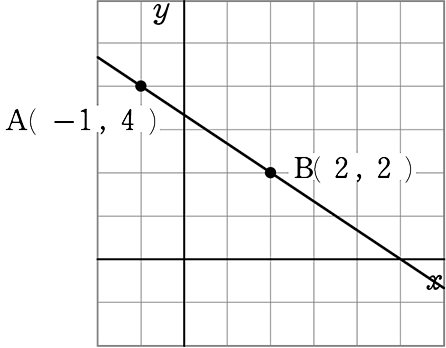
2点ABの中点Mを求めましょう
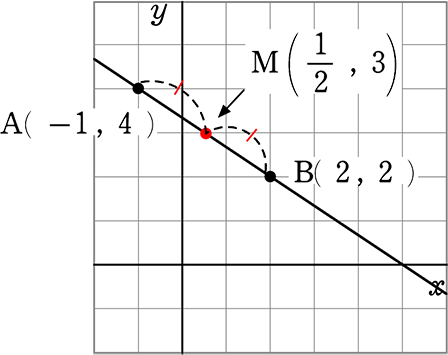
中点 = ( \(\large{\frac{-1+2}{2}}\) , \(\large{\frac{4+2}{2}}\) )
= ( \(\large{\frac{1}{2}}\) , 3 )
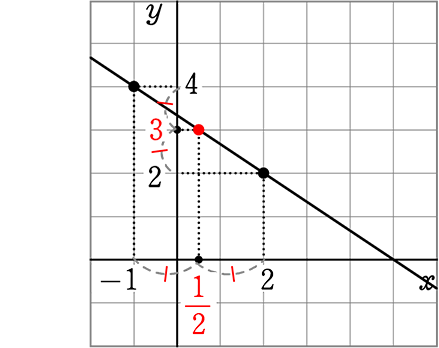
個別に見れば当たり前ですね
x座標だけなら中点は
\(\large{\frac{2+(-1)}{2}}\) = \(\large{\frac{1}{2}}\) (\(\large{\frac{1}{2}}\), 0)
y座標だけなら中点は
\(\large{\frac{4+2}{2}}\) = 3 (0, 3)
2つをたどると・・・(\(\large{\frac{1}{2}}\) , 3)

中点は 足して2で割る
「足して」2で割るというのは解ったのですが、
なんとなく「引いて」2で割るというイメージがあるのですが、
どういうことなのでしょか?
→ 引いて2で割るというのは、「距離的なものですね!
→ 足して2で割るというのは、「位置的なもの」」ですね!
たとえば、長男のお小遣いは1000円、3男500円、次男はその中間、
次男のお小遣いは?
→直感的に750円と解りますね
(250円ではないですよね)
これを、座標を用いて表現すると

となりますね
言葉で言えば、長男-3男の500は「差」という「距離」ですね、
250は その半分の「距離」ですね
したがって「引いて」2男の「位置」を求めるには、もう一段階、
「長男の位置-250」 か「 3男の位置+250」 が必要ですね
・「傾き(変化の割合)」は「距離」が解ればよかったので「引いて」の方でしたね
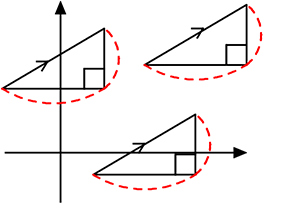
a = \(\large{\frac{高さ}{底辺}}\) =\(\large{\frac{yの長さ\color{red}{(距離)}}{xの長さ\color{red}{(距離)}}}\) =\(\large{\frac{y_1\color{red}{-}y_2}{x_1\color{red}{-}x_2}}\)
・「資料の活用の平均値」は「位置」」が必要ですので「足して」の方でしたね
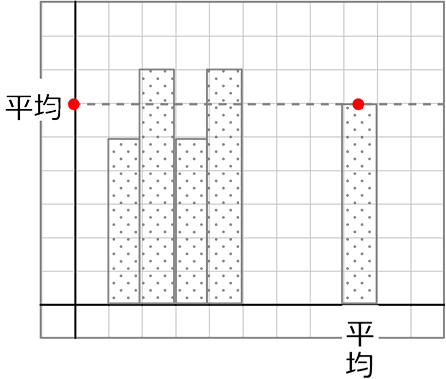
平均 = \(\large{\frac{値の合計}{客体数}}\)=\(\large{\frac{5\color{red}{+}7\color{red}{+}5\color{red}{+}7}{4}}\) =\(\large{\frac{24}{4}}\) = 6


重心の座標
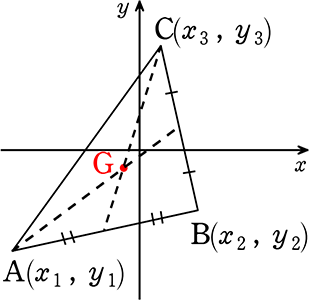

重心Gの座標(x, y) = (\(\large{\frac{x_1+x_2+x_3}{3}}\) , \(\large{\frac{y_1+y_2+y_3}{3}}\))
《 例 》
3点A(-3, -2) 、B(4, -1) 、C(5, 6) を頂点とする
△ABC の重心G(x, y) の座標を求めましょう
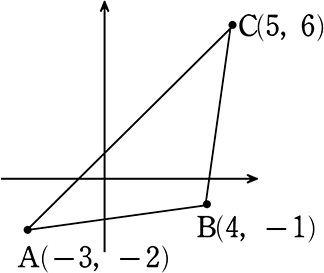
G = (\(\large{\frac{-3+4+5}{3}}\) , \(\large{\frac{-2+(-1)+6}{3}}\))
= (\(\large{\frac{6}{3}}\) , \(\large{\frac{3}{3}}\))
= (2, 1)
(原理)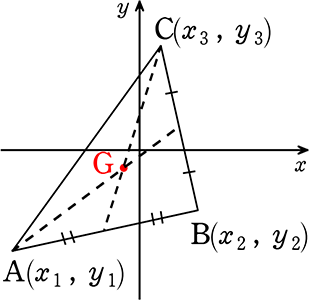
まず、ABの中点Mの座標は?
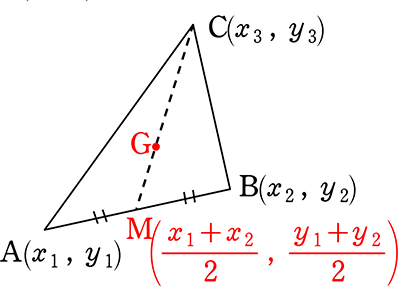
M = (\(\large{\frac{x_1+x_2}{2}}\) , \(\large{\frac{y_1+y_2}{2}}\))
重心は 2:1 でしたね
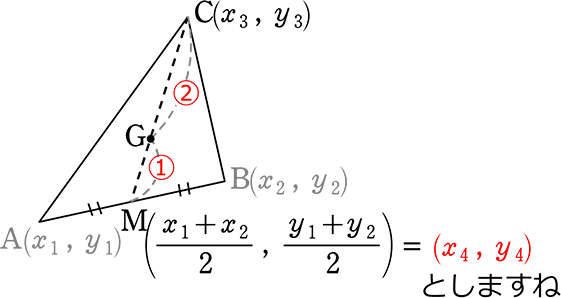
内分点G = (\(\large{\frac{mx_4+nx_3}{m+n}}\) , \(\large{\frac{my_4+ny_3}{m+n}}\))
= (\(\large{\frac{2\ \cdot \ x_4+1\ \cdot \ x_3}{2+1}}\) , \(\large{\frac{2\ \cdot \ y_4+1\ \cdot \ y_3}{2+1}}\))
= (\(\large{\frac{2x_4+x_3}{3}}\) , \(\large{\frac{2y_4+y_3}{3}}\)) (内分点の求め方)
x4, y4 を元に戻して
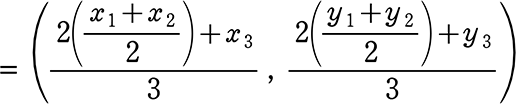
= (\(\large{\frac{x_1+x_2+x_3}{3}}\) , \(\large{\frac{y_1+y_2+y_3}{3}}\))
《 例 》 先と 同じ問題です
3点A(-3, -2) 、B(4, -1) 、C(5, 6) を頂点とする
△ABC の重心G(x, y) の座標を求めましょう

ABの中点 = (\(\large{\frac{4+(-3)}{2}}\) , \(\large{\frac{-1+(-2)}{2}}\))
= (\(\large{\frac{1}{2}}\) , -\(\large{\frac{3}{2}}\))
CMを2:1に内分する点G
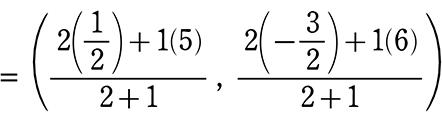
= (\(\large{\frac{1+5}{3}}\) , \(\large{\frac{-3+6}{3}}\))
= (\(\large{\frac{6}{3}}\) , \(\large{\frac{3}{3}}\))
= (2 , 1) 同じですね!
d 対称な直線
《 例 》
y = \(\large{\frac{2}{3}}\)x-1 が x軸に対称である直線は?

・「右辺全体」に「-1」を掛けただけですね!
→ 憶える必要はありませんね、
略図を書ければ、すぐにわかること
ですから!
→ y= -(\(\large{\frac{2}{3}}\)x-1)= -\(\large{\frac{2}{3}}\)x+1
《 例 》
y = \(\large{\frac{2}{3}}\)x-1 が y軸に対称である直線は?

・「傾き」に「-1」を掛けただけですね!
→ 同じく略図から毎回考えればOKです!
→ y = -(\(\large{\frac{2}{3}}\)x)-1= -\(\large{\frac{2}{3}}\)x-1
《 例 》
y = \(\large{\frac{2}{3}}\)x-1 が y =xに対称である直線は?
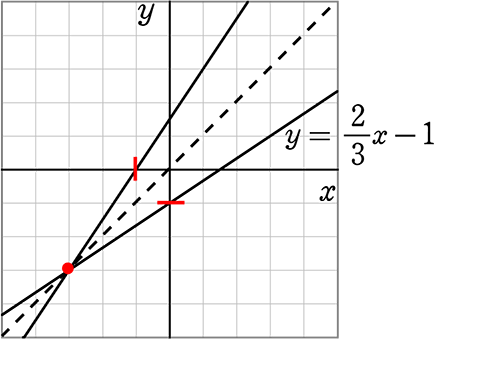
・y = x (=45°)に対称は頻出ですね!
→ 傾きの「逆数」が「新傾き」です!
・あとは位置ですね →「傾き」がどういう点を通るのか?ですね
〔方法①〕 y切片がx切片になりますね
→ y = \(\large{\frac{3}{2}}\)x+b が (-1, 0) を通る
→ 0 = \(\large{\frac{3}{2}}\)(-1)+b → b = \(\large{\frac{3}{2}}\)
∴ y = \(\large{\frac{3}{2}}\)x+\(\large{\frac{3}{2}}\)
〔方法②〕 y = \(\large{\frac{2}{3}}\)x-1 と y = x の交点座標を求める
→ 連立方程式 → 交点は(-3, -3)
→ y = \(\large{\frac{3}{2}}\)x+b が (-3, -3) を通る
→ b = \(\large{\frac{3}{2}}\)
∴ y = \(\large{\frac{3}{2}}\)x+\(\large{\frac{3}{2}}\)
◎なぜ、逆数が「新傾き」?
→ これは物理的現象ですので説明が難しいのですがイメージとして
① 図のような直角三角形と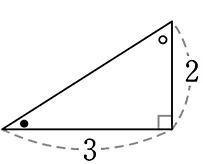
② 合同な三角形を、
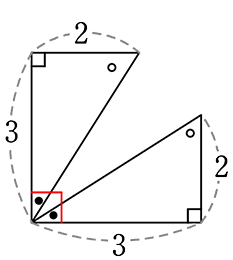
図のように配置すると
③ 必ず 正方形(全90°、全辺同じ)になる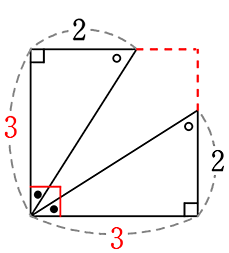
④ ということは
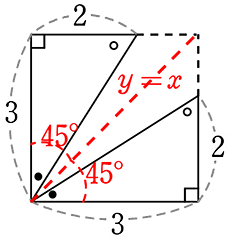
対角線が45°
ということは、対角線は、y=x
⑤ ということは
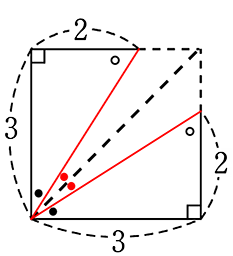
●=● (∵ともに45°-●)
→ ということは、
2つの斜辺は、y=x に対称
→ 背面に座標をイメージすると
下の斜辺の傾きは\(\large{\frac{2}{3}}\)
上の斜辺の傾きは \(\large{\frac{3}{2}}\)
⇒ 「逆数」ですね!
∴ y=x に対称な新傾きは…『逆数』
平行な傾き
《 例 》
y=\(\large{\frac{1}{3}}\)x+1 に平行で
点(-3, -3) を通る直線の式を求めよ
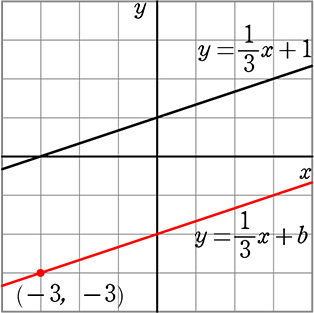
平行な傾きは、当然 元の傾きと同じですね
一言『同じ傾き』ですね!
→ 平行より、y=\(\large{\frac{1}{3}}\)x+b まで確定
→ これが(-3, -3) を通るので、(-3)=\(\large{\frac{1}{3}}\)(-3)+b
→ -3=-1+b → b=-2
∴ y=\(\large{\frac{1}{3}}\)x-2
垂直な傾き
《 例 》
y = \(\large{\frac{2}{3}}\)x-1 に 垂直な傾きは?
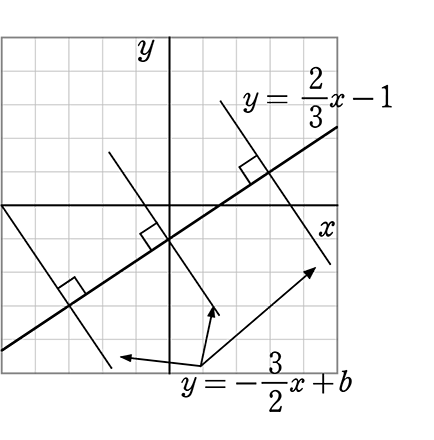
・「垂直な傾き」も大切ですね!
→ 傾きの「逆数×(-1)」が「新傾き」です
→ ①y = xに対称 +②x軸またはy軸に
対称させたという意味ですね
→ y = -\(\large{\frac{3}{2}}\)x+b ですね!
・あとは、通る1点を指定してくれれば、
直線の式が解りますね!
(イメージ)
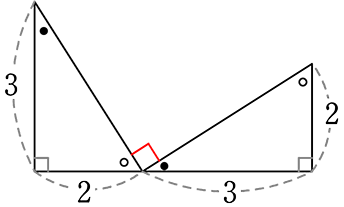
2つの合同な直角三角形を
図のように配置すると
三角形内部で、●+〇=90°
真ん中部分で、直線180°-●-○=90°ですね!
背面に座標をイメージすると
右の斜辺は \(\large{\frac{2}{3につき}}\)
左の斜辺は \(\large{\frac{-3}{2につき}}\)
→ -・逆数は、垂直な傾きになる!
(三平方の定理:ガーフィールドさんの証明
のイラストに似ていますね)
対称な点
《 例 》
点(3, 2)が対称
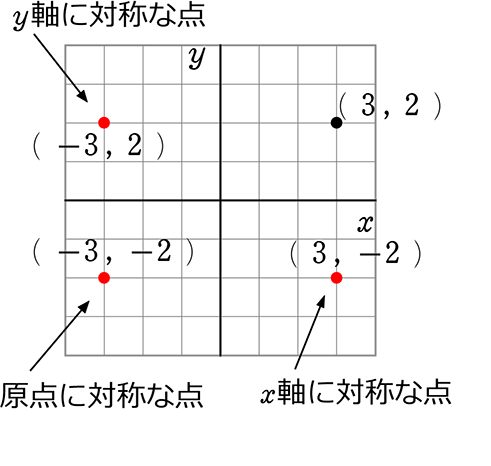
・ 何も憶えることはことはないですね!
→ 略図を書けば、自ずと解りますね!
《 例 》
y = x に対称な点
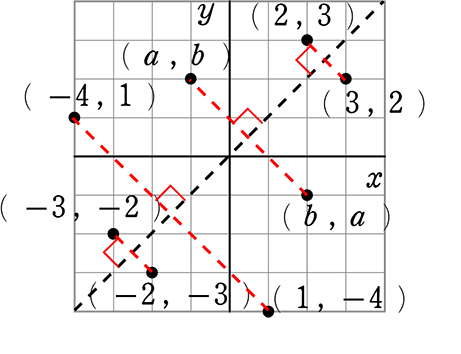
・「x座標とy座標を取り換えたもの」ですね!
(a, b) ⇔ (b, a)
〔付随特徴〕
→ y = x との交点は 「中点」ですね
→ y =x への「垂線」ですね

対称・垂直まとめ
y = x に対称な
線の「傾き」は
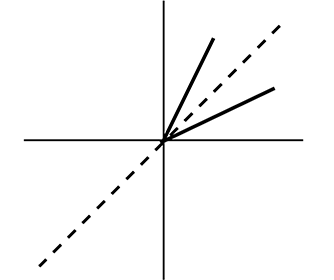
逆数
垂直な傾きは
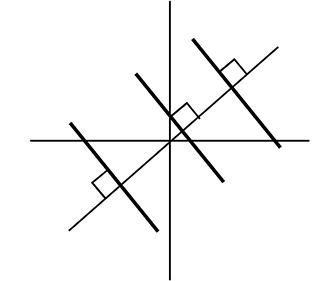
-・逆数
(傾きa×新傾きa’ = -1)
y = x で対称な
点の「座標」は

x座標 ⇔ y座標 とっかえ
・中点
・垂直
・最短距離




e 座標上の面積
座標上の図形の面積は、升目が利用できるので求めやすいですね!
《 例 》 座標上の図形の面積を求めましょう
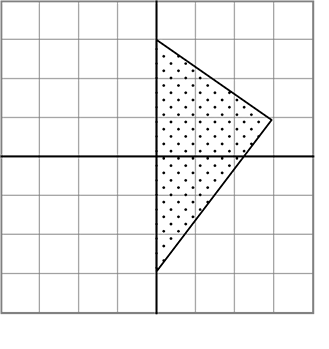
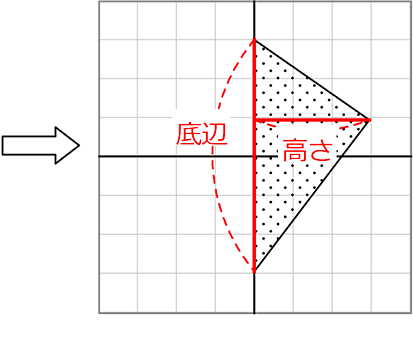
と見れますね
面積 = \(\large{\frac{1}{2}}\)・6・3 = 9
→ ・升目は90°ですので、上手く利用ですね
・「底辺と見れる線」、「高さと見れる線」を図形から見つけ出せることが大切ですね
《 例 》 面積を求めましょう

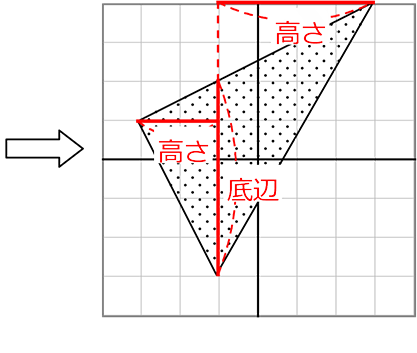
と見れますね
面積 = \(\large{\frac{1}{2}}\)・底辺・(高さ+高さ) = 15
→ 底辺共有2三角形ですね
《 例 》 点Pを通って平行四辺形の面積を2等分する直線を求めましょう


平行四辺形系の面積を2等分する直線
( 平行四辺形系: 平行四辺形、ひし形、長方形、正方形 )
→ 平行四辺形の定義、定理の利用ですね
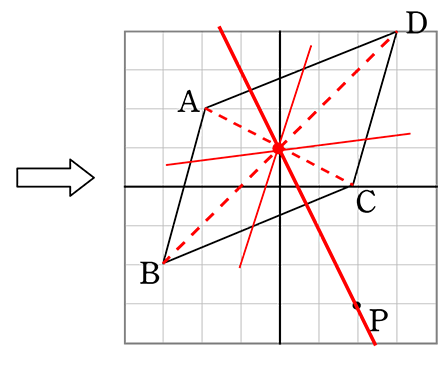
ACの中点は
BDの中点でもあるので、
どちらかでよいですね
点Pが、平行四辺形の内部・辺の上、にあっても同様に考えてOKですね
→ (点Pの座標)と(点の座標)の2点が解れば、中点の座標が解りますね
・ 点Pの座標 → グラフより P(2, -3)
・ 頂点の座標 → A(-2, 2)、 C(2, 0)より
→ 中点(x1, y1) = \(\left(\large{\frac{-2+2}{2}},\large{\frac{2+0}{2}} \right )\) = (0, 1)
・ P(2, -3)と中点(0, 1)を通る直線は
y = \(\large{\frac{-3-1}{2-0}}\)(x-0)+1
y = -2x+1
《 例 》 Oを通る直線で三角形の面積を2等分しましょう

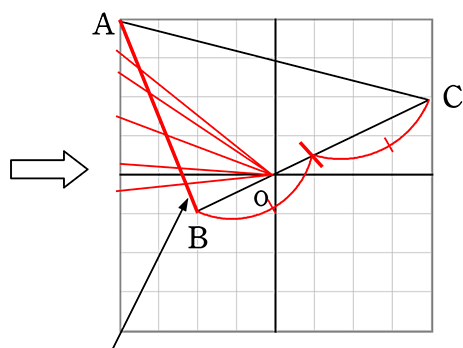
ABを横切る直線で、半分にすることは
無理ですね、なぜなら、三角形の面積を
半分にする場面は、大きく分けて
① 底辺が半分 (高さはそのまま) 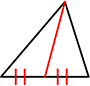
② 高さが半分 (底辺はそのまま) 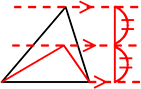
→ oはBCの中点よりC側でないと無理ですね!
というわけで ACを横切るはずですね
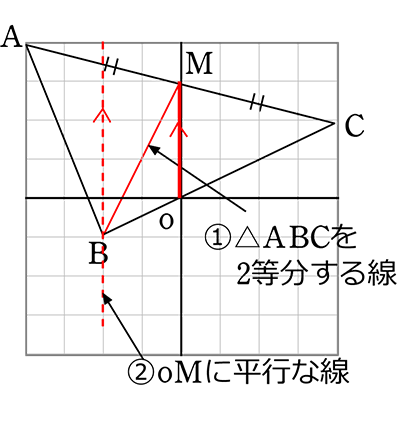
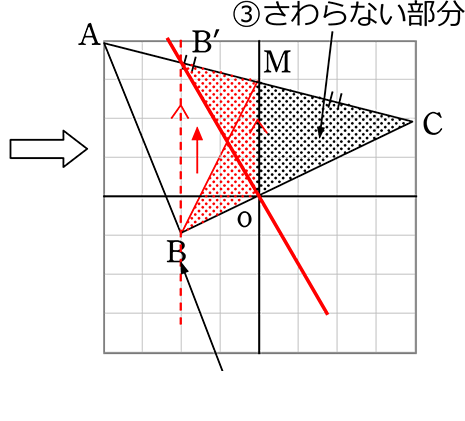
④△oBMの頂点Bを平行移動させても
面積は変わりませんでしたね!
(平行線の性質 の利用ですね)
確かに、△BAM = △BCM = △oB’Cですね
あとは B’(-2, ?)と o(0, 0)の2点を通る直線を求めるだけですね
ACの直線は? → A(-4, 4)と C(4, 2)の2点を通る直線
y = \(\large{\frac{2-4}{4-(-4)}}\)(x-4)+2
y = -\(\large{\frac{2}{8}}\)(x-4)+2
y = -\(\large{\frac{1}{4}}\)x+1+2
y = -\(\large{\frac{1}{4}}\)x+3
B’のy座標は
y = -\(\large{\frac{1}{4}}\)(-2)+3 =\(\large{\frac{1}{2}}\)+3 = \(\large{\frac{7}{2}}\)
∴ B’(-2, \(\large{\frac{7}{2}}\))
最後に、o(0, 0)とB’(-2, \(\large{\frac{7}{2}}\))の2点を通る直線を求めると
y = \(\large{\frac{0-\large{\frac{7}{2}}}{0-(-2)}}\)x
y = -\(\large{\frac{\large{\frac{7}{2}}}{2}}\)
\(\large{\frac{2}{2}}\)という「1」をかけて
y = -\(\large{\frac{7}{4}}\)x
ウ 二元一次方程式と関数との関係
二元一次方程式とは、文字が2文字で、文字の掛け合わせがない方程式でしたね
例えば、
x+2y = 3 などですね ( 〇元〇次の意味)
二元一次方程式は、yの式(左辺がyだけの式)にすると、「1次関数」ですね
よって、① yの式にする → ② 1次関数として扱う それだけですね
《 例 》
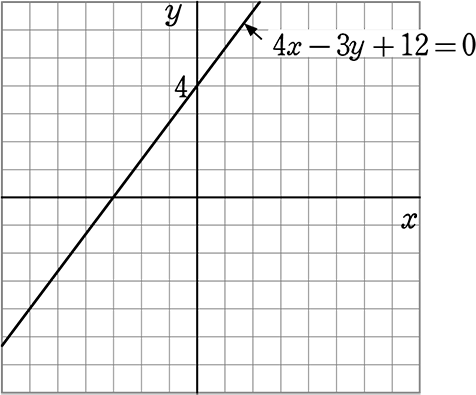
4x-3y+12 = 0 のグラフを描きましょう
→ yの式にすると
→ -3y = -4x-12
y = \(\large{\frac{4}{3}}\)x+4 のグラフを描いて
名前だけは 4x-3y+12 = 0 とするだけですね
《 例 》
y = 3 、 x = 5 、 y = 0x-3 のグラフを描きましょう
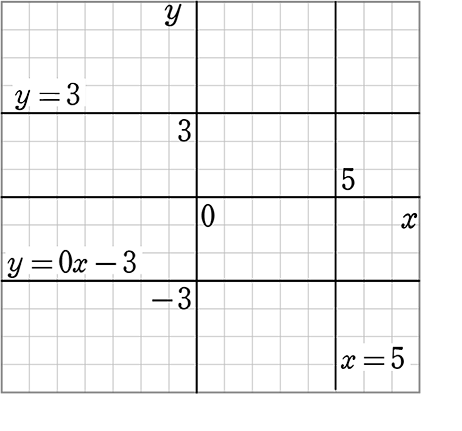
→ y = 3 → 「xの値に関わらず常に3」という感じですね
x軸が無くてもよいくらいですね
そうすれば
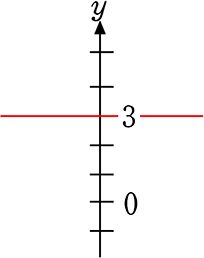
→ x = 5 → 「yの値に関わらず常に5」という感じですね
同じく y軸がなくてもよいくらいですね、 そうすれば
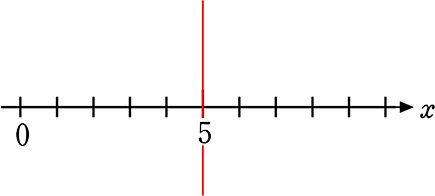
→ y = 0x-3 → y = -3
エ 一次関数を用いた具体的な事象の説明
1次関数で文章問題的なものはあまりないですね
定期テスト用という感じでしょうか
文章問題風にしてみても、実際のグラフ・求める値などは、文章の長さの割に単純なものとなってしまいますね!
やはりメインどころは、上で学んだ「グラフ操作」から、直線・傾き・交点・面積などを求めるというところが、
実力テスト・入試テストで扱われるということになりますね!
動点
動点のポイントは
動点Pと図形の頂点との「距離」の表現ですね

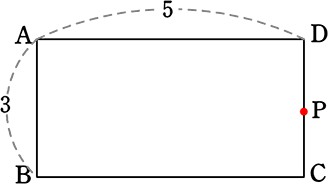
図の長方形ABCDは縦3、横5である。
点Pは毎秒1の速さでAを出発してB, C, D を通りAまで戻る点とします
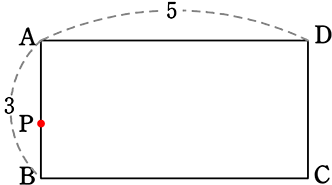
① APの距離は?
Pの動いた「距離」=「速さ」×「時間」
=1×x=x
② BPの距離は?
BAの距離-Pの動いてきた「距離」
=(3)-(1×x)=3-x

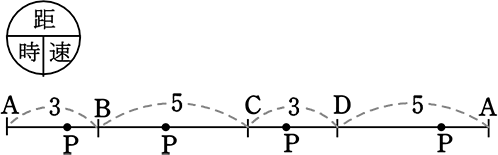
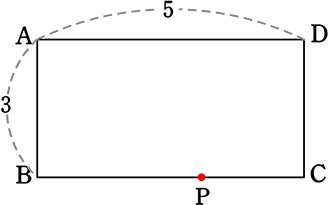
③ BPの距離は?
Pの動いてきた「距離」-不要なABの「距離」
=(1×x)-(3)=x-3
④ CPの距離は?
全行程ABCの「距離」-Pの動いてきた「距離」
=(3+5)-(1×x)=8-x
⑤ CPの距離は?
Pの動いてきた「距離」-不要なABCの「距離」
=(1×x)-(3+5)=x-8
⑥ DPの距離は?
全行程ABCDの「距離」-Pの動いてきた「距離」
=(3+5+3)-(1×x)=11-x
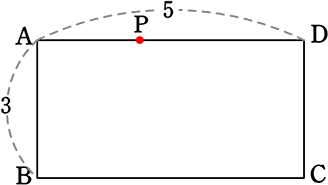
⑦ DPの距離は?
Pの動いてきた「距離」-不要なABCDの「距離」
=(1×x)-(3+5+3)=x-11
⑧ APの距離は?
全行程ABCDAの「距離」-Pの動いてきた「距離」
=(3+5+3+5)-(1×x)=16-x
《 例 》
図ように、1辺の長さが20cmの正方形の頂点Bから
点Pが毎秒4cmの速さで辺上を矢印の方向に進み、
C, Dを通ってAまで進むものとする。
点PがBを出発してからx秒後に、APまたはBPを
結んでできる△ABPの面積をycm2とするとき

① xの変域が次のような場合、yをxの式で表しましょう
ア. 0≦x≦5
→ PはBC上より、
面積y=\(\large{\frac{1}{2}}\)×底辺AB×高さBP = \(\large{\frac{1}{2}}\)×20×(4・x) = 40x ∴y=40x
イ. 5≦x≦10
→ PはCD上より、
面積y=\(\large{\frac{1}{2}}\)×底辺AB×高さ常に20 = \(\large{\frac{1}{2}}\)×20×20 = 200 ∴y=200
ウ. 10≦x≦15
→ PはDA上より、
面積y=\(\large{\frac{1}{2}}\)×底辺AB×高さPA = \(\large{\frac{1}{2}}\)×20×(60-(4・x)) = 10(60-4x) =-40x+600 ∴y=-40x+600
ダイアグラム
《 例 2016過去問 》
ある鉄道路線があり、A駅、B駅、C駅、D駅の順に駅がある。
A駅とB駅の間の道のりは3km、B駅とC駅の間の道のりは6km、
C駅とD駅の間の道のりは3kmである
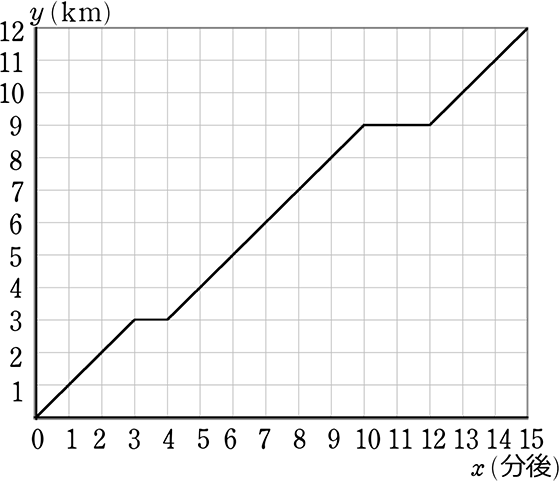
また、この路線を走行する普通列車は各駅に停車し、
特列車はA駅とD駅に停車する。
右の図は、この路線において、普通列車Pが、
午前9時にA駅を出発してからD駅に到着するまでの、
午前9時からx分後A駅からの道のりをykmとして、
xとyの関係を表したグラフであり、原点はOである。
このとき、次の問いに答えなさい。ただし、列車の長さは考えないものとし、
列車は各駅間において一定の速さで走行するものとする
(1) 普通列車PはC駅で何分間停止したかを求めなさい

y軸(距離の軸)に地点名(~駅、小学校、自宅等)を書いておくと
イメージが具体的になりますね!
右上がりは離れていく!
右下がりは戻ってくる!
→ 駅間の距離データから、このような関係ですね
→ 「時間」が経過しているのに「距離」が増えていない、
グラフが横線の部分が「停止状態」=駅ですね
∴ (C駅では) 12分-10分 = 2分間停車した
(2) 特急列車Qは、午前9時5分にA駅を出発してD駅に向かい、
D駅に到着するまで時速90kmで走行した。
このとき、特急列車Qが、A駅を出発してからD駅に到着するまでの、
午前9時からx分後のA駅からの道のりをykmとして、xとyの関係を表したグラフを図にかき入れなさい。
→ ちなみに普通列車Pの走行中の平均
3km/3分 = 60km/60分 = 60km/時
(Qの傾きの方が急とわかる)
→ 特急列車Qの
90km/時 = 90km/60分 = \(\large{\frac{3km}{2分につき}}\) → 傾き\(\large{\frac{3}{2}}\)、A駅を9:05分発 = x切片が(5, 0)
(念のため式は y=\(\large{\frac{3}{2}}\)(x-5)+0 → y=\(\large{\frac{3}{2}}\)x-\(\large{\frac{15}{2}}\)
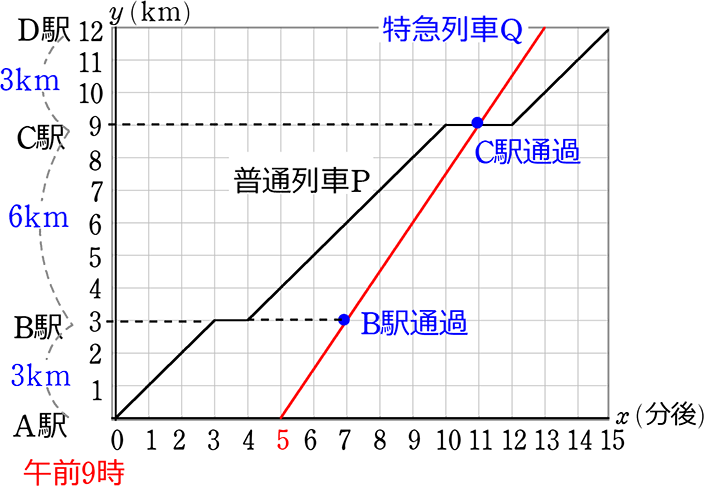
(3) 特急列車Rは、午前9時にD駅を出発してA駅に向かい、A駅に到着するま
で時速90kmで走行したところ、途中で普通列車Pとすれ違った。
このとき、すれ違ったのは特急列車RがD駅を出発してから何分後かを求めなさい
→ Rは9時にD駅にいて、
マイナスのスピード(傾きが-\(\large{\frac{90km}{60分につき}}\) = -\(\large{\frac{3}{2}}\))で走行していると考えることができますね
式は y切片D駅の(0, 12)と傾き-\(\large{\frac{3}{2}}\)で、y=-\(\large{\frac{3}{2}}\)x+12
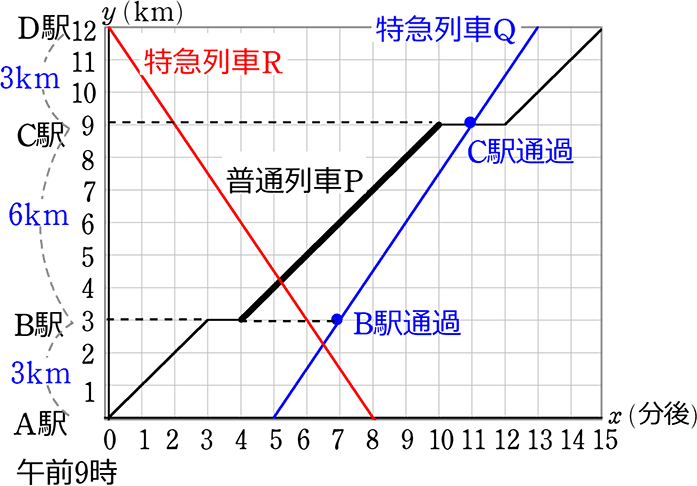
→ 「折れ線」と「直線」の交点は求めることができませんので
「直線」と「直線」の式にする ということですね
交差している直線の部分だけの式(太線の式)を求めると…
傾き「1」で点(4, 3)を通る
→ y = 1x+b → 3 = 4+b → b = -1
∴ 太線部分は y = x-1
交点は \(\small{\begin{cases}
y = x-1 \\
y = -\large{\frac{3}{2}}\small{x+12}
\end{cases}}\)
x-1 = -\(\large{\frac{3}{2}}\)x+12 → 2x+3x = 24+2 → 5x = 26 → x = 5.2
(時間だけを問われているので、yを求めることが省けますね)
∴ 5.2分後 = 5分+60秒・0.2 = 5分+12秒
A. 5.2分後にすれ違う
・問いが何分何秒後か?なら A. 5分12秒後にすれ違う
・普通列車PがA駅を出発してから何分後か? なら
→ 交差するまでPがどんな走り方をしようが、 交点のx座標は(5.2, ) A. 5.2分後にすれ違う

時刻表
上の過去問に使われているグラフは、実際に電車やバスの現場で使われていますね
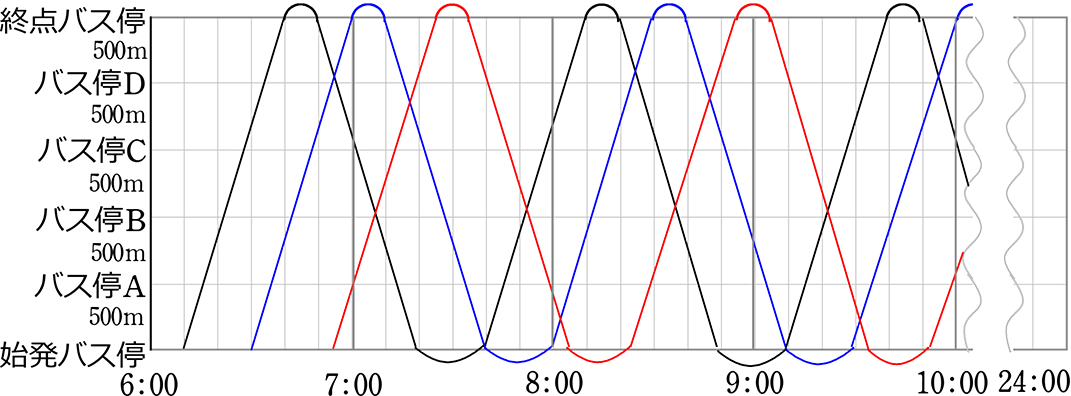
「まき」「まきダイヤ」と言っていましたね (巻物みたいに長いから?)
主に事務所用ですね 色々読み取れますね
・片道所要時間は30分
・終点バス停折り待ち時間は10分
・始発バス停折り待ち時間は20分
・この路線は3台のバスで回している 等々
※「折り待ち時間」「余裕時分」「待機時間」、呼び名は各社によるのでしょうね

電車はもっと複雑ですね!
〇〇駅で特急に抜かれる、
連結する、切り離す など
当然、途中駅の停車時間も
表現しているでしょうね
・・・ですが、複数人でダイヤを作成するわけではなく
「スジ屋」と呼ばれるたった一人の社員が作成していることが多いようですね
大勢で作成するとごちゃごちゃになって、1つの電車が2か所で走っている
みたいな、不思議ダイヤができあがるのかもしれませんね!
戻りまして、
「まきダイヤ」の黒線、青線、赤線のダイヤを個別に取り出したものが
それぞれ乗務員に渡されますね 「スターフ」と言ってましたね
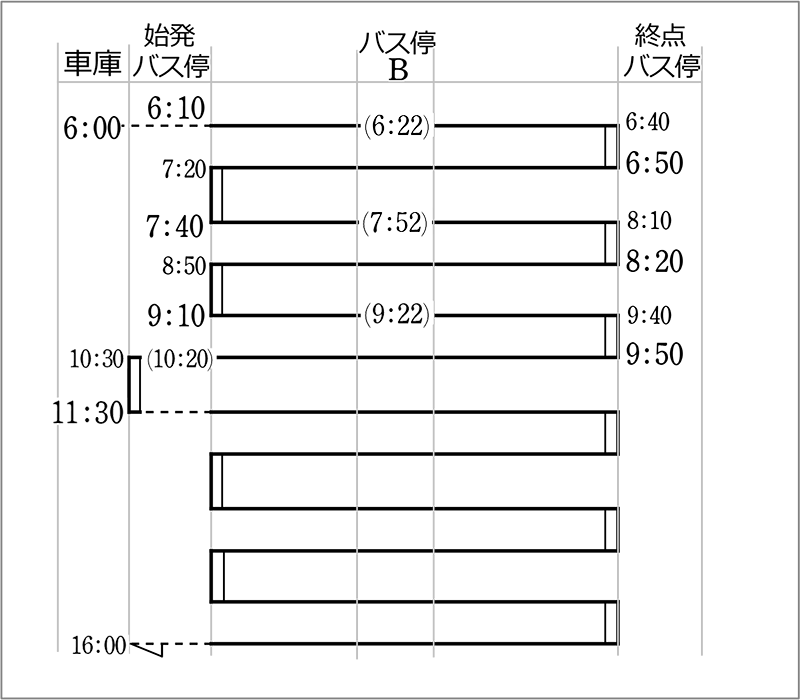
各乗務員は、自分に渡されたスターフどおりに運行すれば間違いはない
ということですね
各社によって、縦向きであったりしますね
そして、「まきダイヤ」のy軸の各バス停のx方向の時間を取り出したものが
利用客のための、各バス停の「時刻表」になりますね
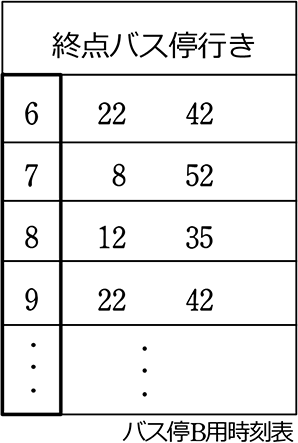
このように、「関数」は普通に実社会で役立っていますね
先の過去問では y軸は「距離」のみでしたが
→バス停間の距離は定まっているので「まきダイヤ」では「バス停名」の方が目立つように書かれていますね
先の過去問においても y軸の目盛りに B駅 C駅と書き足せば
理解しやすくなりましたね!

《 例 》
聡君は、Sグレードのガソリン車か、Gグレードのハイブリッド車の購入で
迷っています。ガソリンは1リットルあたり125円とします

(優遇税制、優遇保険料率、車検費用、ローン利率等、その他諸経費は無視します)
(1) 年間ガソリン代を、それぞれ求めましょう
S → 9600km÷12km×125円 = 100000円
G → 9600km÷24km×125円 = 50000円

(2) 略グラフを描きましょう


(3) S 、Gの直線の式を求めましょう
S: y = 10万x+200万
G: y = 5万x+260万
(4) 何年乗ればGの方がお得といえるでしょうか
→ SとGの交点ですね
\(\small{\begin{cases}
y = 100000x+2000000\\
y = 50000x+2600000
\end{cases}}\)
∴ x = 12 y = 320万
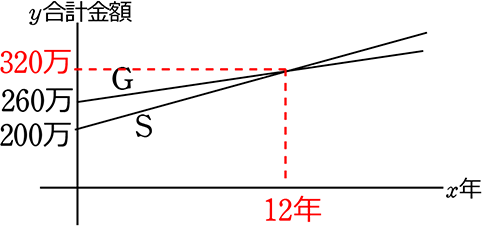
A. 12年より長ければGがお得
お疲れ様でした !!
その他の問題は、「問題集」で!!