| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 文字を用いた式の四則計算 | (2) 連立方程式 |
| ア | 二元一次方程式とその解の意味 |
|---|---|
| ・ | 二元一次方程式の解の表現方法 |
| イ | 連立方程式とその解の意味 |
| ① | 連立方程式の解法 |
| ・ | 加減法 |
| ・ | 代入法 |
| ② | 3つの式がつながる連立方程式 (A=B=C) |
| ・ | 解が1つに決まる理由 |
| ③ | 連立方程式 (3つの式) |
| ④ | 連立方程式 (4つの式) |
| ウ | 連立方程式の解法と活用 |
| ・ | 連立方程式の文章問題を解くポイント |
| ・ | 連立方程式を利用した例題文章問題 |
| a | 値段 |
| ・ | ~は…より〇〇多いの表現方法 |
| b | 距離 |
| ・ | 出会う、追い越すのポイント |
| c | 食塩水 |
連立方程式 ( 2つの二元一次方程式 )
ア 二元一次方程式とその解の意味
二元一次方程式とは、 「文字が2種類」で「文字の掛け合わせは 1乗まで」でしたね!
(○元○次の意味)
例えば、
x-y = 2 などでしたね
(この点、x2 やy2がある式は「2次式」ですね、
間違いやすいところで、xyでも「二次式」ですね!
x-y=2 は・・・
「文字どうしの掛け合わせ」が「ない」ので → 1次式
そして「使っている文字」が「2種類」 → 2元
よって2元1次方程式 ですね)
そして、「方程式」とは、「xやyなどの文字の値や解を求めるための等式」でしたね。
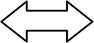
では、上の 二元一次方程式 x-y = 2 の xの解とyの解は求められるのでしょうか?
→ 1つには求められませんね!
引いて「2」のxやyの「関係」なんて無数にありますね
x= 6 の時は y= 4、 x= -3 の時は y= -5、 x= 5.5 の時は y=3.5
そうです、「二元一次方程式」と言いつつ・・・
xの値が決まれば、yの値がただ一つ決まる関係、すなわち
「関数」ですね!
確かに、x-y= 2 を yについて解くと、
y= x-2 「←1次関数」の形ですね!
よって
二元一次方程式
x-y = 2
・ xやyの解を求めたい
という気持ち
・ yの式(y=の式)で
なくてもよい
・ xとyの組
1次関数
y = x-2
・ xとyの関係性を知りたい
という気持ち
・ yの式なら1次関数
・ xが決まればyが決まる
では、x-y = 2 をグラフで表してみます (→ 結局 y = x-2 の形にして作成)
x-y=2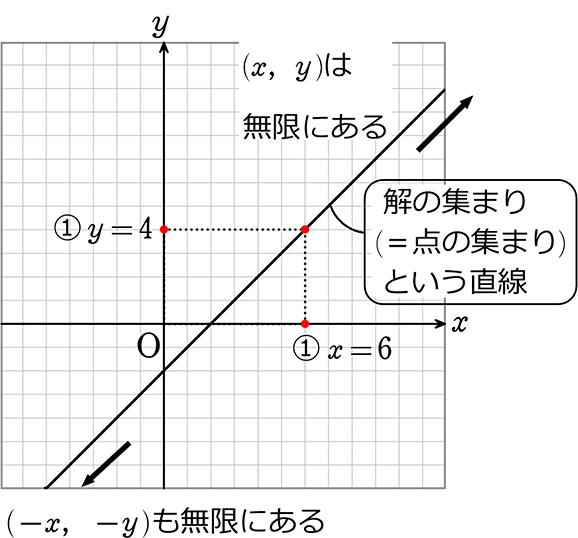
y=x-2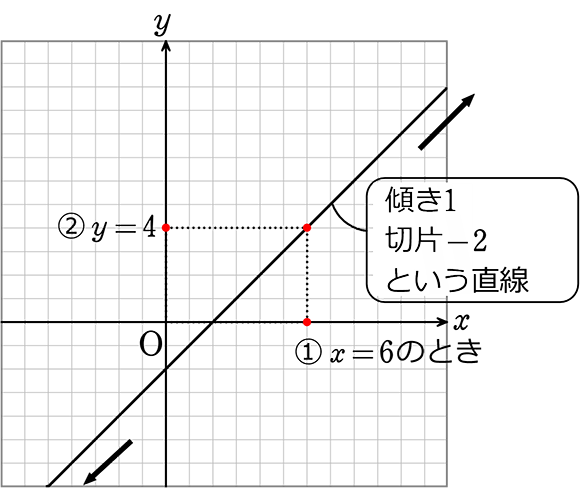
ですが、こだわる場面ではありません!
二元一次方程式 は 1次関数として考えるとわかりやすい!
まったく「同じ」とは言いませんが、
「同じ
二元一次方程式 = 1次関数 でOKです!!
このように、二元一次方程式では xの値(解)が無数にあるように、
それに対する y の値(解)も無数にあるということになります。
でありますので、二元一次方程式の問題では、必ず
xに、「条件づけ」や「範囲指定」があります。
《 例 》
x-y = 2 において、xが2から5までの整数のとき、yの値を求めましょう。
→ xは2~5の整数という範囲指定ですね
xの条件は、2~5までの整数 → 2、3、4、5
| ① | 計算を楽にするために、 x-y = 2 を y = x-2 にして |
| ② | y = x-2 の xにそれぞれ値を代入して、yを求める |
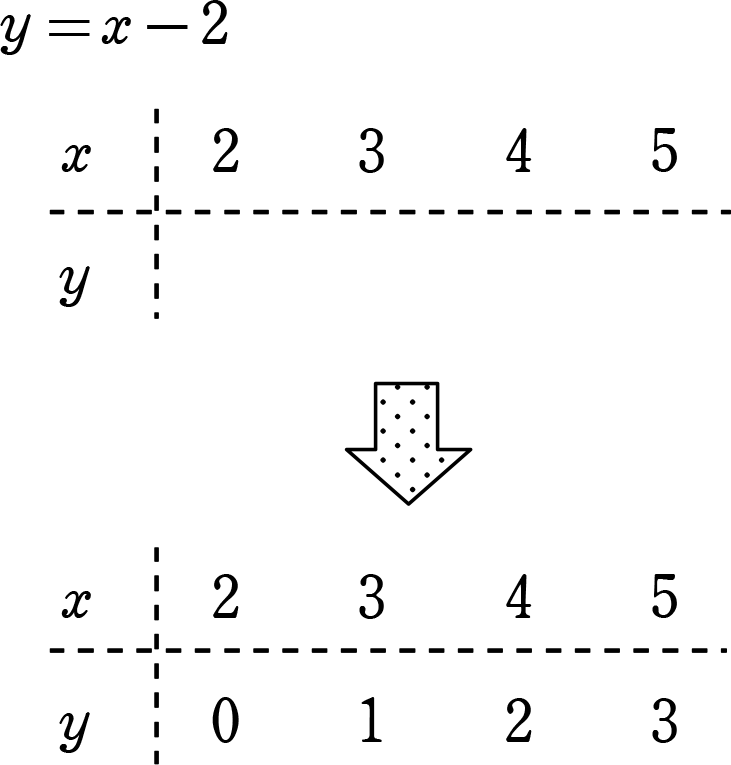
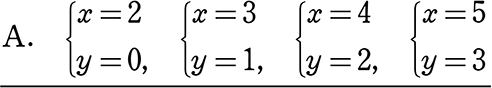
A. x=2のときy=0 x=3のときy=1 x=4のときy=2 x=5のときy=3
A. (x , y) = (2, 0) (3, 1) (4, 2) (5, 3)
解答の表現方法はどれでもOKです (1番下が最もポピュラーですね)
これらは、「場合分けの解答」ですね! 初見参ですね!
「~のときは~、 ~のときは~」 今後たまに出てきます!
長くなってしまいましたが、ここでは原則として、
| ● | 文字が1つなら、式は1つ で解が1つに決まる (1年生 一元一次方程式) |
| ↓ | |
| 〇 | 文字が2つなら、式が1つでは 解が1つに決まらない (2年生 二元一次方程式) |
| ↓ | |
| ● | 文字が2つなら、式は2つ で解が1つに決まる (2年生 連立方程式) |
| ↓ | |
| 〇 | 文字が3つなら、式が2つでは 解が1つに決まらない |
| ↓ | |
| ● | 文字が3つなら、式は3つ で解が1つに決まる |
というイメージを持っていて下さいね!
イ 連立方程式とその解の意味
「連立方程式を解く」とは
| → | 同じ未知数(x, yなど)についての方程式が2つ以上あるとき、それらすべてを同時に満たす未知数の値を決定すること ですね |
簡単にいえば
| → | それぞれ無数の解を持つ方程式達の共通解を求めることですね (関数的に言えば、交点を求めること) |
① 連立方程式の解法
連立方程式 … 難しくはありません!
式が2つあるだけです
(正確には、ここでは二元一次方程式が2つあるだけです)
先に軽くふれましたが、文字が2種類なら、等式が2つあれば、
解が1つに決まる というものですね。
では解き方です
《 例 》
次の連立方程式を解きましょう
\(\small{\begin{cases}
2x + 8y = 18 \scriptsize{…①}\\
x + y = 3 \scriptsize{…②}
\end{cases}}\)
2つの解法があります、 (1)ひっ算方式 (2)代入方式
まずは、(1) ひっ算方式(加減法) で解いてみますね。
加減法
xの係数、またはyの①係数を上下で同じにして、引いたり足したりして
②どちらかの文字をなくしてしまいます
できる限り小さい数字を掛けて (後の計算を楽にするため)、
xの係数かyの係数をそろえます。
\(\small{\begin{cases}
2x + 8y = 18 \scriptsize{…①}\\
x + y = 3 \scriptsize{…②}
\end{cases}}\)
xの係数を「2」でそろえよう!とねらいをつけてみました。
②×2 → 2x+2y = 6 …②’ (読み:まる2ダッシュ)
xの係数がそろったので、①-②’ (②’-①でも可) をします
2x+8y=18 …①
-) 2x+2y=6 …②’
0+6y=12
よって、y=2
あとは、y=2を ①か②か②’の楽なものに代入して、xも求めます
②に代入してみますね
x+(2) = 3 → x = 1
A. x= 1, y= 2
親御さんは、②×2ではなく、①×\(\large{\frac{1}{2}}\)(=①÷2) だろう!
と途中でお子さんを叱らないで下さいね!
「面倒かも」「無駄かも」を経験して、「もっといい方法はないのか?」
を「考えるようになる」と思いますので(数学でも実社会でも)。
ミチミチ計算も途中で止めず、最後までやってから
「正解! でも、こういう方法もあるかも」
と言ってほしいかなと思います。
(なるほど感も違うと思いますし、方法(手段)も1つではないと体感もできますし)
えらそうを申してすいみません…
では、(2) 代入方式 (代入法)です
\(\small{\begin{cases}
2x + 8y = 18 \scriptsize{…①}\\
x + y = 3 \scriptsize{…②}
\end{cases}}\)
代入法
2つの式のどちらかを、xの式、または yの式 にして、
他方の式に代入して、一元一次方程式にしてしまいます。
②の式を、xの式にしようと!とねらいをつけてみました。
x+y= 3 → x= -y+3 …②’
②’を①に代入する前に、①の整理が楽ですね
2x+8y = 18 → x+4y = 9 …①’
ここで、②’を①’に代入
| (-y+3)+4y= 9 … | (一元)一次方程式になった |
→ 3y=6
→ y=2
あとは、「ひっ算方式」同様、y= 2 を、①②①’②’の楽そうなものに代入
②’に代入してみますね
x= -y+3 = -(2)+3 = 1
A. x= 1, y= 2
【 確かめ算 】
x= 1, y=2を、①②にそれぞれ代入します
\(\small{\begin{cases}
2x + 8y = 18 \scriptsize{…①}\\
x + y = 3 \scriptsize{…②}
\end{cases}}\)
↓
\(\small{\begin{cases}
2(1) + 8(2) = 18 \scriptsize{…①}\\
(1) + (2) = 3 \scriptsize{…②}
\end{cases}}\)
↓
\(\small{\begin{cases}
2 + 16 = 18 \scriptsize{…①}\\
1 + 2 = 3 \scriptsize{…②}
\end{cases}}\)
↓
\(\small{\begin{cases}
18 = 18 \scriptsize{…①}\\
3 = 3 \scriptsize{…②}
\end{cases}}\)
2つの式で、ともに成り立っていますね! →
② 連立方程式 (A=B=C)
《 例 》
次の連立方程式を解きましょう
\(\large{\frac{x-1}{2}}\)-\(\large{\frac{y+1}{3}}\) = \(\large{\frac{x-2}{10}}\)+\(\large{\frac{y-3}{4}}\) = \(\large{\frac{x+y}{12}}\)
A = B = C の形のときは、A = B 、A = C、B = C
の 3通り に分けてもよいですね
そのうちの楽そうな2つを、今まで通り「連立」させましょう
\(\small{\begin{cases}
A = C \\
B = C
\end{cases}}\)で行ってみますね
\(\small{\begin{cases}
\large{\frac{x-1}{2}}-\large{\frac{y+1}{3}} = \large{\frac{x+y}{12}}\scriptsize{…①}\\
\large{\frac{x-2}{10}}+\large{\frac{y-3}{4}} =\large{\frac{x+y}{12}}\scriptsize{…②}
\end{cases}}\)
「係数そろえ」「代入」うんぬんの前に、「整理」が必要ですね
| ① | 分数が嫌なので、①には「12」、②には「60」をかけた |
\(\small{\begin{cases}
6(x-1)-4(y+1) = x+y \\
6(x-2)+15(y-3) = 5(x+y)
\end{cases}}\)
| ② | (カッコ)を1文字と見ても、いい案がなさそうので、「展開」 |
\(\small{\begin{cases}
6x-6-4y-4 = x+y \\
6x-12+15y-45 = 5x+5y
\end{cases}}\)
③「移項」+「計算」
\(\small{\begin{cases}
5x-5y = 10 \\
x+10y = 57
\end{cases}}\)
④「簡素化」
\(\small{\begin{cases}
x-y =2 \scriptsize{…①’}\\
x+10y = 57 \scriptsize{…②’}
\end{cases}}\)
| ⑤ | あとは、いつもの「連立方程式」ですね! |
x - y = 2
-) x+10y = 57
-11y=-55 → y = 5
y = 5 を①’に代入
x-y = 2 → x-(5) = 2; → x = 7
A. x = 7, y = 5

連立方程式の解が1つに決まる理由
どうして式が2つあると解が1つに決まるのでしょうか?
一言で言えば、
「同一平面上の2直線は、『重なっている場合』と『平行の場合』を除けば、必ずどこかで交わる」からです。
そして2元1次方程式の解は直線でしたね
→ 2本あれば必ず共通解(交点)がある!
例えば
\(\small{\begin{cases}
-2x+y = -4 \scriptsize{…①}\\
-x+2y = 7 \scriptsize{…②}
\end{cases}}\) を解くと A. x= 5, y= 6
この2つの式をグラフ上に表すと、
それぞれの式は、無数に解を持ちますね
そして、解の集まりが「直線」ですね
例えば
x= 9のとき、 ①式では y= 14、 ②式では y= 8
x= -3のとき、 ①式では y= -10、 ②式では y= 2
解が共通ではありませんね↓
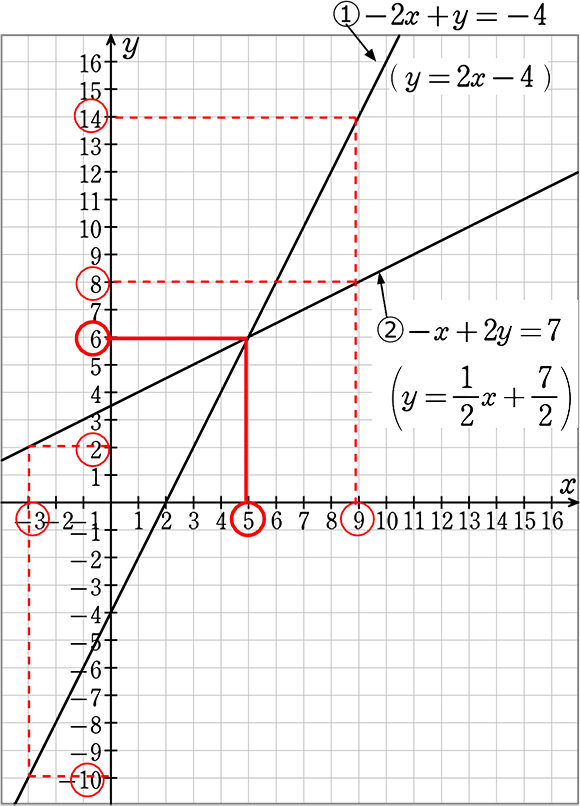
①式では成り立つけど②式では成り立たない、
②式では成り立つけど①式では成り立たない、これでは連立方程式を解けていませんね。
というわけで、①の式、②の式ともに成り立つxの解、yの解は…
そうです、2直線が交わる所ですね!!
A. x=5, y= 6 ですね!
| 「連立」… | 性質のちがう別々のものが、一緒になって成り立っているもの = 共に成立 |
この「共通の解のある場所」は、今後学ぶ「1次関数」では「交点」といいます
ということは、「交点の座標」の求め方は、
| ⇒ | 2直線の式を、「連立方程式」で解けばよいということになりますね! |
他方、2直線が「重なっている」場合や「平行」な場合は…
●「重なっている」…
\(\small{\begin{cases}
x+y = 2 \scriptsize{…①}\\
2x+2y = 4 \scriptsize{…②}
\end{cases}}\) などですね
②式を「2」で割ると①式と全く同じですね!
\(\small{\begin{cases}
x+y = 2 \scriptsize{…①}\\
x+y = 2 \scriptsize{…②’}
\end{cases}}\)
x+2 = 2
-) x+y = 2
0-0 = 0
文章問題で、自分の作った2式がこのような事態になるということは、
「全く同じ意味の式」を2つ作った
すなわち
「二元一次方程式」を1つ作っただけ ということになります
ということは、解は、~の時は~、~の時は~ … となります
A. 解は無数
考え直しですね!
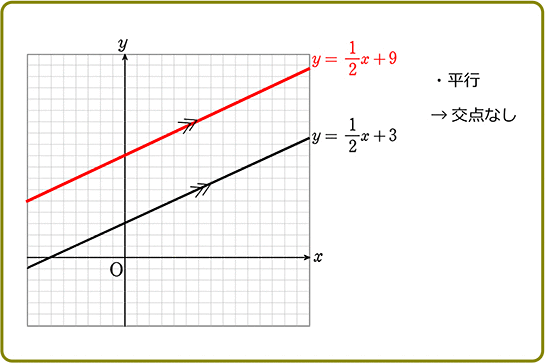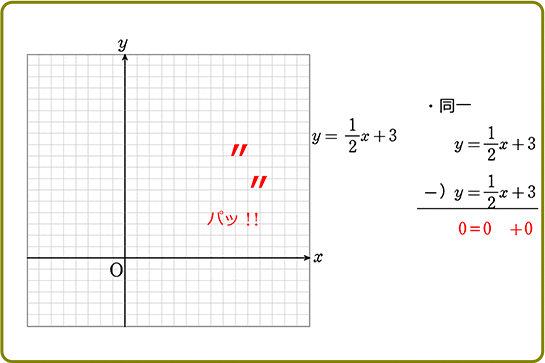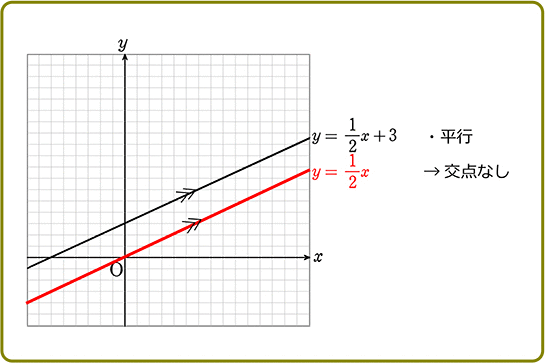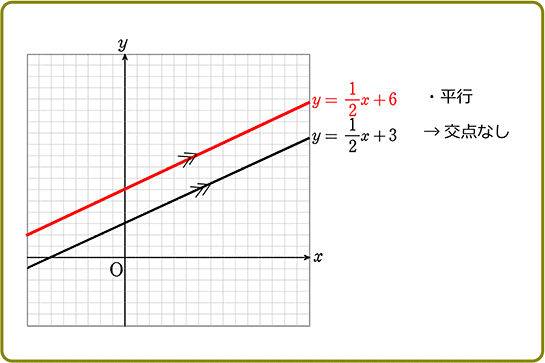
●「平行」…
\(\small{\begin{cases}
x-y = -4 \scriptsize{…①}\\
x-y = 2 \scriptsize{…②}
\end{cases}}\) などですね
①②を yの式にすると
\(\small{\begin{cases}
y = 1x+4 \scriptsize{…①’}\\
y = 1x-2 \scriptsize{…②’}
\end{cases}}\) 「傾き」がどちらも「1」
→「平行」
→「交点なし」ですね!
y = x+4
-) y = x-2
0 = 0+6 → 0 = 6 ???ですね!
A. 解なし (ともに成り立つ解はない)
※「重なっている」「平行」などの問題は出ません。
文章問題で、自分の立てた2式が、このような(消えちゃった!)感じのときは、
「同じ意味」か「どちらかが間違っている」ので、
せっかくですが、どちらかの式を「考え直し」ましょうね!
(大体1つは合っていますので…)
③ 連立方程式 (3つの式)
《 例 》
次の連立方程式を解くと、xの値がyの2倍になるという。
連立方程式の解と、aの値を求めましょう
\(\small{\begin{cases}
x+2y=a+6 \scriptsize{…①}\\
-x+3y=a \scriptsize{…②}
\end{cases}}\)
パッと見、文字が3つで式が2つ
→ 解が1つに決まらず、解に文字が残りそう ですが、
「xの値がyの2倍」という文言より
x=2y という関係式もありますね
ということは、結局
\(\small{\begin{cases}
x+2y=a+6 \scriptsize{…①}\\
-x+3y=a \scriptsize{…②}\\
x=2y \scriptsize{…③}\\
\end{cases}}\)
あとは この「3つの式の連立方程式」を解くだけです

連立方程式の解法の根本
いかにして文字を消去して減らすか
これだけです!!
③を①、②に代入するとyとaだけの式になりますね
\(\small{\begin{cases}
(2y)+2y=a+6 \scriptsize{…①’}\\
-(2y)+3y=a \scriptsize{…②’}\\
\end{cases}}\)
整理して
\(\small{\begin{cases}
4y-a=6 \scriptsize{…①’’}\\
y=a \scriptsize{…②’’}\\
\end{cases}}\)
②’’を①’’に代入(代入法)して
4(a)-a=6 ∴ a=2
②’’より yも2 (y=2)
-x+3y=a …② に求めたyとa値を代入して
-x+3(2)=(2) ∴ x=4
A. 解は x=4, y=2 aの値はa=2
④ 連立方程式 (4つの式)
《 例 》
2つの連立方程式\(\small{\begin{cases}
x-y=3 \scriptsize{…①}\\
ax+y=5 \scriptsize{…②}
\end{cases}}\) と \(\small{\begin{cases}
3x-by=-1 \scriptsize{…③}\\
2x+3y=1 \scriptsize{…④}
\end{cases}}\) の解が同じであるとき、a、bの値を求めましょう
「解が同じ」ということは・・・
4つの直線は「1点で交わる」ということですね
(イメージ)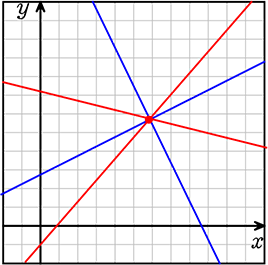
ということは、どの2直線を選んで連立させてもよいということ
→ 文字を打ち消しあえる2式を選んで
\(\small{\begin{cases}
x-y=3 \scriptsize{…①}\\
2x+3y=1 \scriptsize{…④}
\end{cases}}\)
これを解くと、x=2、y=-1
これらを②、③にそれぞれ代入すると
a=3、b=-7 ですね
ウ 連立方程式の解法と活用
方程式の活用といえば、「文章問題」!
1年生では「(1元)1次方程式(文字が1つ)」で、式を立てていましたね
そして、2年生では「連立方程式」で式を立ててもよいのです!
文字を2つ使ってもよいのです!
解らないものが2つまで許してくれるのです!
決して、
| ① | 「1年生より難しいのだろうな~」とか |
| ② | 「2文字使わないといけないのか~」とか |
| ③ | 「これからは、1次方程式の文章問題か連立方程式の文章問題か、見抜かなければいけないのか~」 |
とか心配しないでくださいね!
①はすっきり考えられる分、ある意味簡単になったと思うはずです
②は2文字使ってもよいのです (使わなければいけません、といことではないのです)
(あまりにも簡単な問題、「縦5mで面積15㎡の長方形、横は?」などは、
2文字目を使う余地がありませんが…)
③は見抜く必要は全くありません!どういう式を立てるかだけを考えればよいです。
「これも解らないな~、2文字目使うかぁ」という感じです。
論より証拠ですね
「鶴(足2本)と亀(足4本)が合わせて、15匹います。
足の合計は48本でした。鶴と亀はそれぞれ何匹?」
〈小学生〉 武器は 鶴亀算 (「もし全部が」から始める技)
①もし全部が鶴だったら、足数は 2本×15匹=30本
→ 18本足りない
②1匹亀に入れ替えると、鶴足28+亀足4=32本
→1匹入れ替えると、足が2本増えるのだろう
③ ①のときより18本増やしたい
→18÷2=9 亀は9かな?
④ 確認
→足4本×亀9匹+足2本×鶴6羽=36+12=48本
答え. 鶴6羽 亀9匹
グラフで言えば、2直線の交点の近くから、交点に近づけていくイメージですね!
「鶴(足2本)と亀(足4本)が合わせて、15匹います。
足はの合計は48本でした。鶴と亀はそれぞれ何匹?」(全く同じ問題です)
〈中学1年生〉 新武器は 1次方程式
①鶴をx羽とおく、すると亀は、 (総数-x)匹、すなわち、 (15-x)匹と表すことができる
②足の総合計数は、
(2本×x羽)+〔4本×(15-x)匹〕=48本
→ 2x+4(15-x)=48 …式を立てた
③後は解くだけ。 A. 鶴6羽 亀9匹
〈中学2年生〉 新武器は 連立方程式
①鶴をx羽、亀をy匹とおく
② x+y=15 …(匹数)
2x+4y=48 …(足数) …式を立てた
③後は連立で解くだけ。 A. 鶴6羽 亀9匹
すっきりしてますね! イメージしやすいですね!
では、問題を解いていきましょう
やはり代表的な問題は、1次方程式同様、
「金額」「距離」「割合」ですね。

連立方程式の文章問題を解くポイント
連立方程式は、式を2つ作ることになるのですが、ポイントは、
① 横をそろえる
例えば、
「A合計」+「B合計」 =「全合計」…合計でそろえた
「A金額」+「B金額」 =「全金額」…金額でそろえた
マル図  で言えば
で言えば
 の部分が「物理的に存在するもの」なので、よく使いますね、
の部分が「物理的に存在するもの」なので、よく使いますね、
「A距離」+「B距離」 =「全距離」
「A時間」+「B時間」 =「全時間」
「A対象」+「B対象」 =「全対象」
「A全体」+「B全体」 =「全全体」
 の部分は、「割合的なもの」なので、 単純には足せません!!
の部分は、「割合的なもの」なので、 単純には足せません!!
「A速さ」+「B速さ」 =「全速さ」 ダメです!
正しくは、
「\(\large{\frac{A距離+B距離}{A時間+B時間}}\)」 = 「\(\large{\frac{全距離}{全時間}}\)」 ですね!
「A割合」+「B割合」 =「全割合」 ダメですね!
正しくは、
「\(\large{\frac{A対象+B対象}{A全体+B全体}}\)」= 「\(\large{\frac{全対象}{全全体}}\)」 ですね!
ex)
10%-10%=0% → ダメですね
「何の」10%かを問題文から確認すると
1000円と100円の10%だった
1000円の10% → 100円
100円の10% → 10円
→ 割合はそれぞれ「個別の基準」を持っている
⇒ 単純に加減乗除できない
② 1次方程式同様 「掛け算の形」、「分数の形」が、何を表しているのか が 確実に「見えるように」 ですね!
例えば、(時間)・(速さ)は・・・「距離」ですね!
よって、(時間)・(速さ)の形のままでも、それは、
「距離」を
ex)
・ 3時間×速さ60km/h

・ x時間×速さ60km/h
![中学数学 連立方程式[二元一次] |](../img/2021連立ポイント-2b.png)
「距離」ですね!
分数の形も同様です
・ 120km ÷ 時速60km/h
![中学数学 連立方程式[二元一次] |](../img/2021連立ポイント-2c.png)
・ xkm ÷ 時速60km/h
![中学数学 連立方程式[二元一次] |](../img/2021連立ポイント-2d.png)
| ・ | 「時間を表している、 |
| ・ | 「塩を表している、すなわち塩」ではなく、一言で「これは塩!」
と言えるように、一目で見れるように練習していきましょうね! |
そして、最後に、
問題集の解答例の「式立て」と「自分の式立て」が違っていても
答えが同じなら「自分の式立て」はマル! ですので!
解答例は「食塩水」をxとおいていた
自分は「塩」をxとおいた
考え方が間違っていなければ、答えは同じはずですね!!
《 例 》
ある銭湯の入浴料は大人300円、子供200でした
ある日の入浴料の売り上げ(=合計金額)は77,000円でした
子供の入場者数は大人の2倍より35人多かった
大人の入場数、子供の入場者数を求めましょう
(「鶴亀系」の問題ですね
本体自体が特徴を持つ
・本体自体が、4本の「足」を持つ
・本体自体が、300円の「値段」を持つ)
大人の人数を x 、 子供の人数を y とおいてみます
( 復習 ) 料金
| (円)・(人) | ||
| 1人なら | 300・1 | → 300 (円) |
| 2人なら | 300・2 | → 600 (円) |
| 3人なら | 300・3 | → 900 (円) |
・ ・ ・ ・ | ||
| x 人なら | 300・x | → 300x (円) |
合計料金 → 300x+200y = 77000 (円)
合計人数(の関係) → y = 2x+35
\(\small{\begin{cases}
300x+200y = 77000 \scriptsize{…①}\\
y = 2x+35 \scriptsize{…②}
\end{cases}}\)
①/100に②を代入(←①式を100で割った式に②を代入)
3x+2(2x+35) = 770 ∴ x = 100
x = 100 を②に代入
y = 2(100)+35 ∴ y = 235
A. 大人100人 子供235人
《 例 》
ある店は、ボールペン1本は100円、シャーペン1本は150円で売っていました
先月は、シャーペンの売上金額が、ボールペンの売り上げよりも22000円多かった
今月の売り上げ本数(≠売上金額)は、先月に比べて、ボールペンは3割減、シャーペンは4割増だったので、
ボールペンとシャーペンの売り上げ本数の合計は2割増えました
今月のボールペンとシャーペンの売り上げ本数をそれぞれ求めましょう
(「先月・今月」「去年・今年」「前回・今回」などの「比較系」は、
どっちを「基準」にしたかをしっかり意識しておきましょう!
基準さえブレなければ、どちらを基準にしても答えは同じですね!)
(「売上」というと金額的なものだけを想像しますが、
「売上金額」=「合計金額」、 「売上総数」=「合計数」
ただの「売上」=「売上金額」=「合計金額」
となりますね)
先月のボールペンの売り上げ本数を x、シャーペン売り上げ本数をyとおく
先月の売り上げ金額
→ 150y-100x = 22000
今月の売り上げ本数
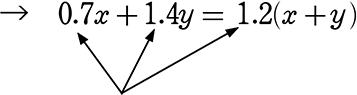
「裏対象」

「AはBより10多い」を式で表してみましょう・・・
おそらく、
6割の人が 「A-B=10」 …ア
2割の人が 「B+10=A」 …イ
2割の人が 「A-10=B」 …ウ
と表現するのかなと思います
| ア | は、「Aの方が大きい、だから、 大ー小=10」 |
| イ | は、「Aの方が10多い、ということは、 小に10足したら、=大」 |
| ウ | は、「Aの方が10多い、ということは、 大から10引いたら、=小」 |
どれも表現は違えど、「内容は全く同じですね!」
ア、イ、ウの数式をそれぞれ「移項」してみれば、皆同じとわかりますね
よって、どれでもOKです!
矯正する必要はありませんね!
\(\small{\begin{cases}
150y-100x = 22000 \scriptsize{…①}\\
0.7x+1.4y = 1.2(x+y) \scriptsize{…②}
\end{cases}}\)
①/10、②×10で
\(\small{\begin{cases}
-10x+15y = 2200 \scriptsize{…①’}\\
-5x+2y = 0 \scriptsize{…②’}
\end{cases}}\)
①’ -10x+15y = 2200
②’×2 -) -10x+4y = 0
11y = 2200

y = 200 を②’に代入
-5x+2(200) = 0 → -5x = -400 → 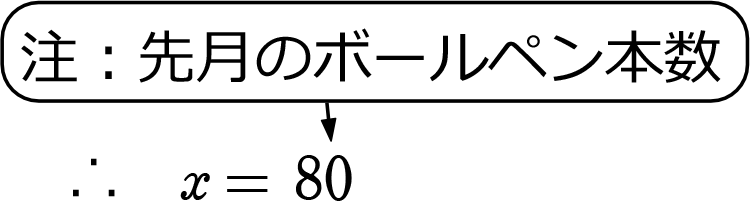
(今後の問題では途中計算は省かせてもらいますね)
最後に何を求めるのかを確認!問題は、今月の本数を問いていますので、
ボールペン3割減 → 80×0.7 = 56
シャーペン4割増 → 200×1.4 = 280
A. ボールペン56本、 シャーペン280本

本番入試試験では、「式立て」と「答え」だけでOKですね!
学校の定期テストでは、「途中計算」も要求してくるかもわかりませんが
「途中計算」に決まった「書き方」はありませんので、
「こんな感じで計算を進めましたみたいな解答」で十分だと思います
先生も、
「係数合わせたのか → ひっ算方式か → これが問いにあった単位計算か」
と分かりますので! プロですから!
《 例 》
周囲が2100mの池をAさんとBさんが走ります
2人が同時出発で、反対方向に回りだすと、7分後に出会いました
次に、Aさんが出発し2分後にBさんが、同じ方向に回ると5分後に追いつきました
AさんBさんそれぞれの走る速さは毎分何mでしょう
「距離問題」ですね → まずは「図」を書いて問題のイメージ化ですね!
問題から明らかにBさんの方が早いので、Bさんの距離を長くしました
(できる限りでいいので、イメージ図の位置関係はリアルがいいですね)
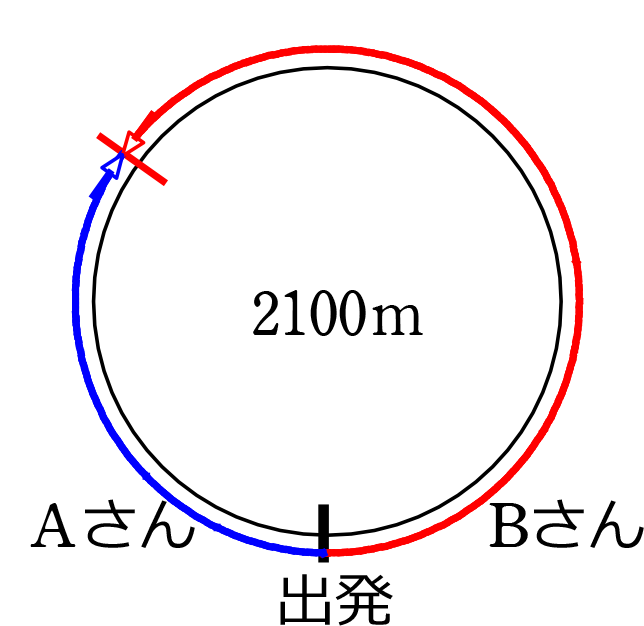
Aさんの「速さ」をxm/分、 Bさんの「速さ」をym/分としてみますね
・Aさんの 「距離」=「速さ」×「時間」 = x×時間ですね
7分なので、Aさんの「距離」は → 7x
・Bさんの「距離」も同様に → 7y
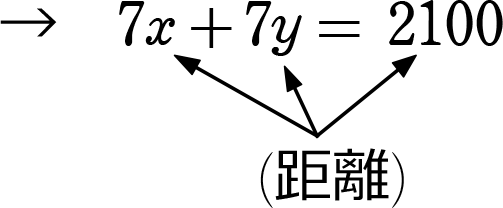
よって、「出会う」ということは、
Aさんの「距離」+Bさんの「距離」=池の1周の「距離」
後段、「追いついた」は、池も関係ないですね。直線でもよいですね
・Aさんの走った「時間」 → 2+5 = 7 分間
Aさんの走った「距離」 → 7x m
・Bさんの走った「時間」 → 5 分間
Bさんの走った「距離」 → 5y m
よって、「追いつく」ということは、
Aさんの「距離」= Bさんの「距離」
→ 7x = 5y
\(\small{\begin{cases}
7x+7y = 2100 \\
7x = 5y
\end{cases}}\)
∴ x = 125, y = 175
A. Aさん125m/分、 Bさん175m/分
《 例 》 (まわりもの、同時出発)
周囲が300mの周回コースを、AとBの2人が一定速度で進んでいる。
① スタートラインから、Aが速度100m/分で、Bが速度50m/分で互いに反対方向に歩くとき、2人が最初に出会うまで何分かかりますか
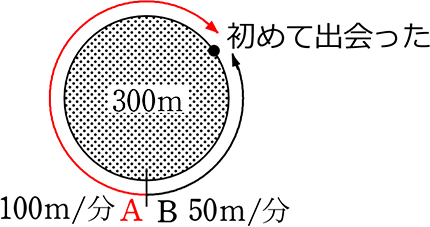
→ 出会う = 2人の合計距離が300m
出会うまでの時間をx分とすると
→ A距離+B距離=300 → 100x+50x=300 → 150x=300 → x = 2 分後
② 2人が①と同じ速度で、同じ方向に進むとき、AがはじめてBに追い越すまで何分かかりますか
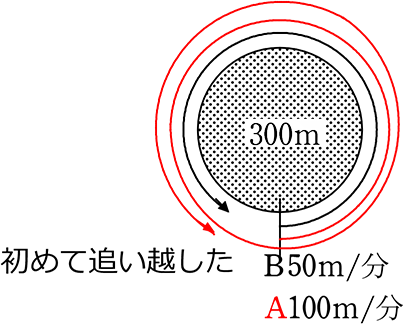
→ 追い越す=2人の距離の差が300m
追い越すまでの時間をx分とすると
→ A距離-B距離=300 → 100x-50x=300 → 50x=300 → x = 6 分後

出会う、追い越す のポイント

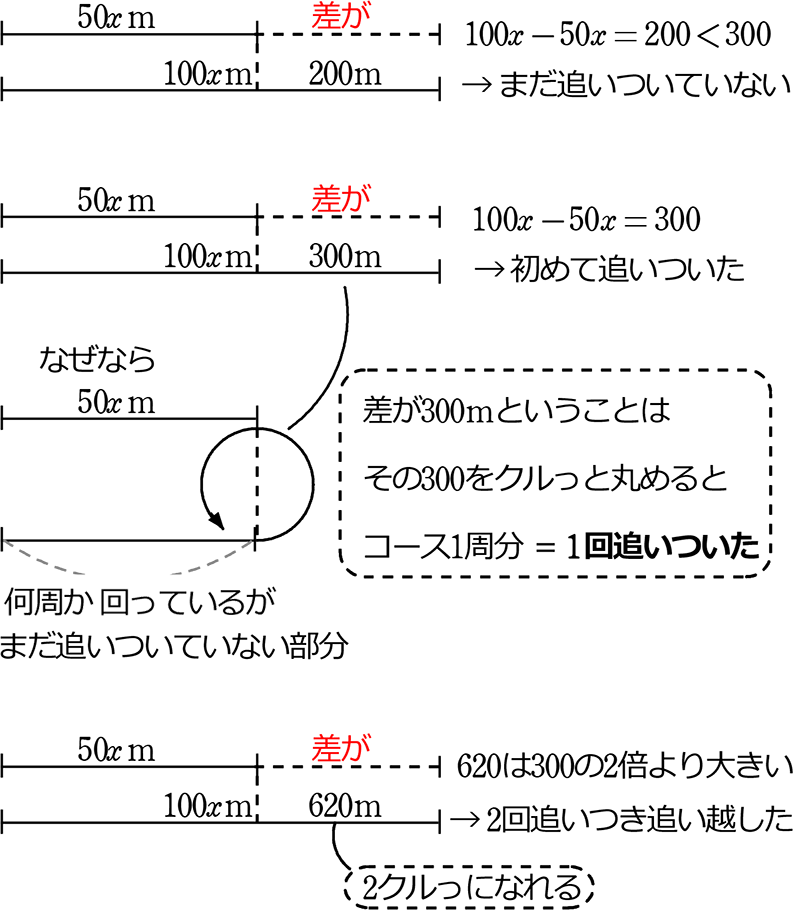
ex. 差が3クルっ分あれば、3回追い越した
まとめ
● 反対方向で初めて出会う
・ 2人の合計距離が 周長
・ 2人の時間は当然同じ
● 同方向で初めて追いつく
・ 2人の距離の差が周長
・ 2人の時間は当然同じ
《 例 》
Aの容器には12%の食塩水、Bの容器には8%の食塩水が入っています
Aの3分の1をBに混ぜると、9%の食塩水が600gできました
A、Bの食塩水は初め何gずつあったのでしょう
「食塩水の問題」ですね → 「距離問題」同様まずは「図」を書いて問題のイメージ化ですね!
割合の基本「マル図」は、 でしたね
でしたね
そして、基本マル図に「食塩水」を当てはめると![中学数学 連立方程式[二元一次] |](../img/2020連立例題②-3b.png)
そして、数学の原則、
「3つのうち2つ(4つのうち3つ)が解れば、残りの1つも必ず解る」ですね!
ではでは、


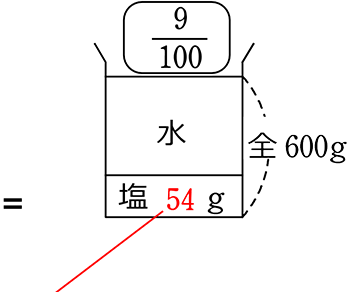
・せっかくですので「3つのうち2つわかっている」右辺の「塩」を先に求めてしまいますね
→ 600×\(\large{\frac{9}{100}}\) = 54 g 
・そして、「\(\large{\frac{1}{3}}\) したもの」→ ややこしいので
「Aが求まったら、それを3倍すればよいですね」
Aの食塩水(Aの全体)をx、Bの食塩水(Bの全体)をyとおいてみます
全体の合計 → x+y = 600 (g)
塩の合計 → \(\large{\frac{12}{100}}\)x+\(\large{\frac{8}{100}}\)y = 54 (g)
\(\small{\begin{cases}
x+y = 600 \\
12x+8y = 5400
\end{cases}}\)
↓
\(\small{\begin{cases}
x+y = 600 \\
3x+2y = 1350
\end{cases}}\)
∴ x = 150, y = 450
xは元を\(\large{\frac{1}{3}}\) されたものなので、元は、150×3 = 450
A. Aは450g、 Bも450g
ちなみに、Aの「
塩の合計 → x+y = 54 (g)
全体の合計 → \(\large{\frac{x}{0.12}}\)+\(\large{\frac{y}{0.08}}\) = 600 (g)
\(\small{\begin{cases}
x+y = 54 \\
\large{\frac{x}{0.12}}\small{+}\large{\frac{y}{0.08}} \small{=} \small{600}
\end{cases}}\)
∴ x = 18 (Aの塩), y = 36 (Bの塩)
∴ 「Aの全体(食塩水)」 = \(\large{\frac{18}{0.12}}\) = 150 (g)
「Bの全体(食塩水)」 = \(\large{\frac{36}{0.08}}\) = 450 (g)
「Aの全体」は元を\(\large{\frac{1}{3}}\)されたものなので、元は、150×3 = 450
A. Aは450g、 Bも450g
計算は大変になってしまいましたが、マル!! ですね!
お疲れ様でした !!
その他の問題は、「問題集」で !!















