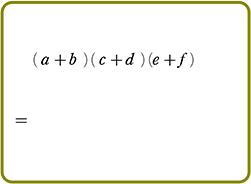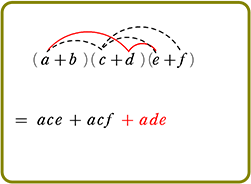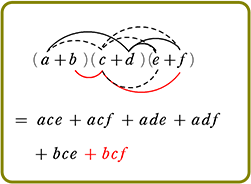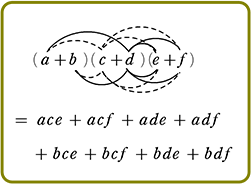| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 文字を用いた式の四則計算 | (2) 連立方程式 |
| ア | 簡単な整式の加法・減法、単項式の乗法・除法 |
|---|---|
| ・ | 単項式・多項式・同類項・定数項とは |
| ・ | 文字式の 加法・減法 |
| ・ | 文字式の 乗法・除法 |
| ・ | 分配法則の手順 |
| ・ | 分配法則のイメージ画像 |
| ・ | 指数法則 |
| ① | 式の値 |
| イ | 文字式の利用 |
| ① | 素数、因数、約数 |
| ・ | 素数とは |
| ・ | 「1」は素数? |
| ・ | 因数とは |
| ・ | 素因数とは |
| ・ | 約数とは |
| ② | 素因数分解 |
| ・ | 3年生の因数分解の先取イメージ |
| ・ | 分解が「×」でつながる理由 |
| ・ | 偶数を文字を使って表す |
| ・ | 奇数を文字を使って表す |
| ・ | 倍数判定 |
| ・ | 平方数 |
| ・ | 2~100までの素因数分解 |
| ③ | 最大公約数・最小公倍数 |
| ・ | 「互いに素」とは |
| ④ | 約数の個数・約数の総和 |
| ・ | 約数の個数 |
| ・ | 約数の総和 |
| ウ | 目的に応じた式の変形 (等式の変形) |
文字を用いた四則計算
ア 簡単な整式の加法・減法、単項式の乗法・除法
まずは、1年生過程の要点の復習です。
① (カッコ)で囲まれたら、それで「1文字扱い」と考えられるようになること
ex. 

 など
など
② ×÷ だけで、つながっている(構成されている)ものは
元(≒項)が「1つ」で、その「元」がどう変形されたのかという問題
ex. \(\large{\frac{x+1}{2}}\) → 1×\(\large{\frac{1}{2}}\)×(x+1) →
→ 元が\(\large{\frac{1}{2}}\)倍されて さらに、 (x+2)倍された
③ +- でつながっているものは、 「元」が複数ある
ex. \(\large{\frac{x+1 }{2}}\)+3x-5y →  +
+ -
- 
単項式・多項式・同類項
それでは、2年生過程に入りますね。
「項」が集まれば、「式」になりますね
・「項」が1つだけ集まったもの・・・単項式 (= 項)
ex. -1, 3, x, xy, 4x, 2x2y などなど
・「項」が複数集まったもの・・・多項式
ex. x+1, x2-1, 2a+3b, 4x2+8x+1などなど
数字として定まってしまっている項を、「定数項」といいます
ex. 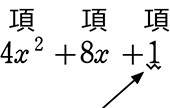
項は項でも、
例えば、xが、2と判明しようが 5と判明しようが
「定数項」はxの値に関わらず 1 ですね
ex. 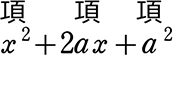 でaは「1」と判明したとします
でaは「1」と判明したとします
→ x2+2・(1)・x+(1)2
→ 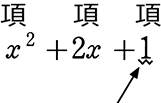
「定数項」に昇格!
項で使用している文字が同じものを、「同類項」といいます
ex. 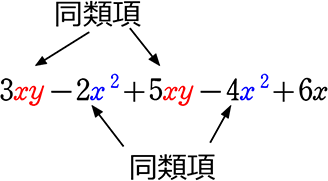
→ 同類項は、まとめることができますので、上の式は 8xy-6x2+6x とできますね!
《 例 》
-b+4ax-3 について次の問いに答えましょう
① 項をいいなさい → -b、4ax、-3
② 単項式か多項式か答えなさい → 多項式
③ 何項式かいいなさい → 3項式
④ 係数をいいなさい →
-bの係数は-1、
4axの係数は4、
-3の係数は-3
↑中学では定数項の係数を
聞いてくることはないですね
⑤ x の係数をいいなさい → 4a(xに注目→xにかかるのは4a)
⑤ 定数項をいいなさい → -3
⑥ 次数をいいなさい → 2 (最高の次数は 2・a・x → 文字の掛け合わせが2回)
⑦ 1次の項をいいなさい → -b
⑧ 何次式かいいなさい → 2次式
⑨ 何元何次式かいいなさい → 3元2次式 (文字の種類3、最高の文字の掛け合わせ2)

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)
文字式の加法・減法
最も簡潔な形にするだけですね!
① (カッコ)を外したり
② 通分したり
③ 同類項をまとめたり するだけです
《 例 》
\(\large{\frac{y^2-1}{2}}\)+\(\large{\frac{x+1}{3}}\)-\(\large{\frac{x+y^2}{6}}\)
= \(\large{\frac{(y^2-1)}{2}}\)+\(\large{\frac{(x+1)}{3}}\)-\(\large{\frac{(x+y^2)}{6}}\) …①凡ミス防止のため(カッコ)をつけた
= \(\large{\frac{3(y^2-1)}{6}}\)+\(\large{\frac{2(x+1)}{6}}\)-\(\large{\frac{(x+y^2)}{6}}\) …②通分をした
= \(\large{\frac{3(y^2-1)+2(x+1)-(x+y^2)}{6}}\) …③分母が同じになったので、分子を同じ土俵に乗せた
= \(\large{\frac{3y^2-3+2x+2-x-y^2}{6}}\) …④分配法則を用いて(カッコ)を外した
= \(\large{\frac{2y^2-1+x}{6}}\) …⑤同類項をまとめた(計算した)
= \(\large{\frac{x+2y^2-1}{6}}\) …⑥アルファベット順に並び替えた //
⑤まででも間違いではありませんが、並びの暗黙のルールは原則、
1. アルファベット順
2. 同じアルファベットの場合は、次数の高いもの順 ですね
慣れてきますと、いきなり②や③や④から始められるようになりますね!
(いきなり⑤は、テストなどで見直しがしにくいのかなと思います)
文字式の乗法・除法
加法・減法と同様に最も簡潔な形にするだけですね!
①分配法則を用いて(カッコ)を外したり
②÷を×にしたり(分数表示にしたり)
③同じ文字をまとめたり するだけです
①分配法則
1年生では、(カッコ)に掛けるものは、「1つ」でしたね。
《 例 》
a(x+y)= 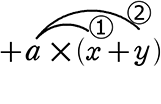 =
= 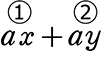 などでしたね
などでしたね
・3(2+3)は、
(1)カッコの中を先に計算すれば、
3(2+3) = 3(5) = 3×5 = 15
(2)分配法則で行うと、
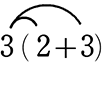 = 6+9 = 15 → (1)と同じ答ですね!
= 6+9 = 15 → (1)と同じ答ですね!
2年生以降では、(カッコ)に複数個掛けていくことになりますが、
「順次掛ける」だけですので、手間なだけで何も変わりませんね! =
= 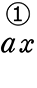 +
+ 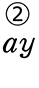 +
+ 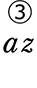 +
+ 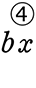 +
+ 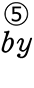 +
+ 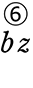 +
+ 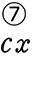 +
+ 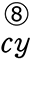 +
+ 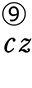 ですね!
ですね!
→ 同類項が無いので、これ以上は、まとめられませんね(計算できませんね)
よって、これが「答え」です
・(2+3+4)(7-3-2) は、
(1)カッコの中を先に計算すれば、
(2+3+4)(7-3-2) = (9)(2) = 18
(2)分配法則で行うと、
14-6-4+21-9-6+28-12-8 = 18 → (1)と同じ答ですね!
展開のしかた
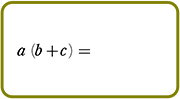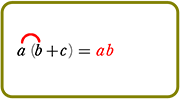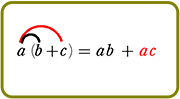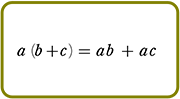
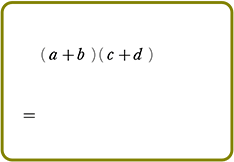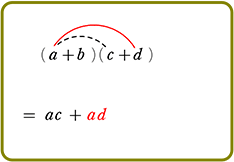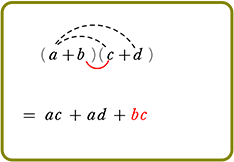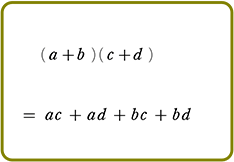
手順は、(カッコ)が増えようが、(カッコ)の中が増えようが、
『おしりを一周させたら、次は手前の一周にとりかかる』
それだけですね!
「計算問題」だけでなく、「組み合わせの問題」にも
役に立つので、忘れないでくださいね!
② ÷を×にする
これは完全に1年生の復習ですね
逆数にするだけでしたね!
《 例 》
(2+3+4)÷(7-3-2)
= (2+3+4)×\(\large{\frac{1}{(7-3-2)}}\) …①逆数にして「×」にした
= \(\large{\frac{(2+3+4)}{(7-3-2)}}\) …②まとめた
= \(\large{\frac{2+3+4}{7-3-2}}\) …③カッコは不要になっている
= \(\large{\frac{9}{2}}\)…④計算をした
慣れれば、いきなり③からできますね!
③ 同じ文字をまとめる
「累乗」で表したり、「約分」したりするだけですね!
《 例 》
2x2y×3xy3÷xy×\(\large{\frac{3}{2xy}}\)
= \(\large{\frac{2x^2y×3xy^3×3}{xy×2xy}}\) …①まとめた …②約分 (斜線でどんどん消していく)
…②約分 (斜線でどんどん消していく)
= x・3・y2・3 …③残ったものを取り出した
= 9xy2 …④まとめの計算をした

指数法則
〈前提ルール〉
① a0 = 1 (0乗が「1」の理由)
② a-m = \(\large{\frac{1}{a^m}}\)
〈指数法則〉
① am×an = am+n
② (am)p = am×p
②’ (ambn)p = am×p bn×p
②’’ \(\left(\large{\frac{a^m}{b^n}}\right )^p\) = \(\large{\frac{a^{m\color{red}{\times} p}}{b^{n\color{red}{\times} p}}}\)
③ am÷an = am-n
《 例 》
① -5x3y2z×\(\large{\frac{1}{2}}\)xy2z3
(方法1)= -\(\large{\frac{5}{2}}\)xxxx・yyyy・zzzz = -\(\large{\frac{5}{2}}\)x4y4z4 (数える)
(方法2)= -\(\large{\frac{5}{2}}\)x3+1y2+2z1+3 = -\(\large{\frac{5}{2}}\)x4y4z4 (指数法則)
② (x2)3
(方法1)= xx・xx・xx = x6 (数える)
(方法2)= x2×3= x6 (指数法則)
②’ (-2x2y3)3
(方法1)= -8xx・xx・xx・yyy・yyy・yyy = -8x6y9 (数える)
(方法2)= (-2)1×3・x2×3・y3×3 = -8x6y9 (指数法則)(指数どうしの分配法則)
②’’ \(\left(\large{\frac{y^3}{x^2}}\right )^3\)
(方法1)= \(\large{\frac{yyy}{xx}}\)・\(\large{\frac{yyy}{xx}}\)・\(\large{\frac{yyy}{xx}}\) = \(\large{\frac{y^9}{x^6}}\) (数える)
(方法2)= \(\large{\frac{y^{3\color{red}{\times} 3}}{x^{2\color{red}{\times} 3}}}\) = \(\large{\frac{y^9}{x^6}}\) (指数法則)
③ -5x3y2z÷\(\large{\frac{1}{2}}\)xy2z3
(方法1)= -5x3y2z×2÷xy2z3
= 
= -\(\large{\frac{10x^2}{z^2}}\) (どんどん約分)
(方法2)= -5x3y2z×2÷xy2z3
= -10x3-1・y2-2・z1-3
= -10x2y0z-2
= -\(\large{\frac{10x^2}{z^2}}\) (指数法則+前提ルール)
2つの方法が 使いこなせたら鬼金棒ですね!
抜け駆け約分の禁 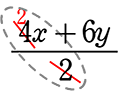 = 2x+6y × 「抜け駆け約分」
= 2x+6y × 「抜け駆け約分」 = 2x+3y 〇
= 2x+3y 〇
\(\large{\frac{4x+6y}{2}}\) は正確には 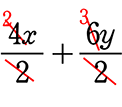 (項が2つ)ですものね
(項が2つ)ですものね
\(\large{\frac{4x+6y}{2}}\) は「通分しましたよ!というアピール表現」ですから
\(\large{\frac{4x+6y}{2}}\) の分母の「2」は「共有状態」であることを忘れない!ですね
\(\large{\frac{1}{2}}\)(4x+6y)と変形するとよくわかりますね(\(\large{\frac{1}{2}}\)を分配法則 = 共有)
この点、
\(\large{\frac{4x\times 6y}{2}}\) は、すべて×÷でできているので、これで1つの項ですね
= \(\large{\frac{4x}{2}}\)・6y = 4x・\(\large{\frac{6y}{2}}\) =  = 2x・6y = 12xy
= 2x・6y = 12xy



① 式の値
式、または、値を、どのように活用すれば 計算が楽か?
それだけですね! (「楽」 = 「ミスが少ない」)
具体的には、
・式または値を、「簡潔な形」にしてみたり、
・式または値を、「展開」してみたり、
・「2乗」してみたり、(←3年生)
ですね。
《 例 》
x = \(\large{\frac{1}{2}}\), y = -1 のとき、3(x+y)-(x+4y) の値は?
(方法①) 先に全てを代入して、
3(x+y)-(x+4y)
= 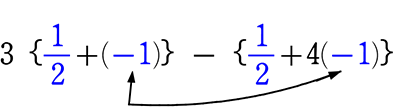
マイナスの値を
代入する時は、
(カッコ)を忘れずに!
…①xに\(\large{\frac{1}{2}}\)、yに-1を代入
= 3\(\left(\large{\frac{1}{2}}\small{-1}\right )\)-\(\left(\large{\frac{1}{2}}\small{-4}\right )\) …②中の(カッコ)を外した
= \(\large{\frac{3}{2}}\)-3 -\(\large{\frac{1}{2}}\)+4 …③分配法則で(カッコ)を外した
= \(\large{\frac{3}{2}}\)-\(\large{\frac{6}{2}}\) -\(\large{\frac{1}{2}}\)+\(\large{\frac{8}{2}}\) …④通分した
= \(\large{\frac{3-6-1+8}{2}}\) …⑤同じ土俵に乗せた
= \(\large{\frac{11-7}{2}}\)
= \(\large{\frac{4}{2}}\)
= 2
と、いうふうに
「ミチミチ」計算してもかまいませんが、
(方法②) 先に計算して、
3(x+y)-(x+4y)
= 3x+3y-x-4y …①分配法則で(カッコ)を外した
= 2x-y …②計算した(同類項をまとめた)
= 2\(\left(\large{\color{blue}{\frac{1}{2}}}\right )\)-(-1) …③xに\(\large{\frac{1}{2}}\) 、yに-1を代入
= 1+1
= 2
と、いうふうに、式を簡潔な形にしてから、代入すれば
(①は合計4か所に代入、②は合計2か所に代入)、
絶対ではありませんが、計算が楽になることが多いですね!
「どうやって解くのか?」から「どうやったら楽か?」を考えだしてきたら、
数学レベルが上級レベルになってきている、といえるのではないでしょうか。
もちろん「ミチミチ計算する」根性も「大切なもの」ですね!!
イ 文字式の利用
文字式を利用して、色々な証明ができていくわけですが、
その前に、
「数の区分方法」を少々
① 素数、因数、約数
素数とは、
① 1と自分でしか割り切れない自然数
または、
② 1と自分しか約数を持たない自然数
または、
③ 約数が2つしかない自然数
どれも同じ意味ですので、自分がしっくりくるもので
理解しておいてくださいね。お父ちゃんは①です。
では本題です。例えば
「2」は、「1」と「2(自分)」でしか割れないですね。よって「2」は素数!
「6」は、「1」と「2」と「3」と「6(自分)」で割れますね。
よって、
①的に言うなら、「自分以外でも割れてしまう」
②的に言うなら、「自分以外の約数(2や3)がある」
③的にいうなら、「約数が2つ以上ある」
すなわち、6は素数ではない!ですね。
「31」は、
…2で割れない、3でもだめ、4も×、5も、・・・
半分くらいの15も×、半分超えてもないということは、
(16×2=32、17×2=34、18×2=36…)
半分より大きいものに最小である「2」を掛けても、
必ず元(31)より大きい!
すなわち・・・半分までに約数がないということは・・・
約数は「ない」ということですので、
「あり」そうで「ない」31は、素数ですね!

『1』は素数?
『1』は素数なのでしょうか?そうではないのでしょうか?
結論から言いますと、
「『1』は素数とはしない」 ですね!
先に出てきた条件①に当てはめると、
「1で割れる、かつ、自分(1)でも割り切れる」
となって、「1」も素数では? となりますが・・・
①の条件を正確を言うと、
「1と、(1以外である場合の)自分でしか割り切れない。」
という意味を予定しているのですね、
だから③の条件「約数が2つしかない自然数」につながるわけですね。
もう一つの証明で言いますと、
「素数の倍数は素数ではない」ですね
(倍と言うからには、必ず約数に「2」が含まれてしまう)
例えば、
素数「2」の倍数は、
(2)、4、6、8、10、12・・・
素数「3」の倍数は、
(3)、6、9、12、15、・・・
上の4、6、8、10、12・・・も、
6、9、12、15、・・・も、素数ではないですね!
ここで、
「1」も素数に入れると、
「1」の倍数、(1)、2、3、4、5、6・・・
「全整数」となって、「1」以外は「素数」ではない!となってしまいますね!
( = 2も3も5も…素数ではないとなってしまいます)
よって、「1」は素の素という感じはしますが、「素数」から外します。
「1」は「数字の1」という意味より、
「そのものが『ある』という意味の1」、英語の「is」のようなものとイメージしておけばよいのではないでしょうか。
因数とは、
その数字を作るための「元(=部品)」ですね。
「因」という文字の意味は、「その、元」ですものね!
原
例えば、「60」という数字を、
60=6×10
と分解すれば、
「6」は、「60」の因数(60の部品)、
「10」も「60」の因数(60の部品)
となります。
素因数とは、
その数字を作るための「元の
例えば、先ほどの「60」という数字を
60=2×30
とすれば、
「2(
「30」は「60」の因数(60の部品)
となりますね。
全て、最小部品にまで分解することを
後で出てくる、素因数分解といいますね!
約数とは、
その数字を割り切れる自然数ですね。
=因数と考えてもいいのですが、
約数は、「1」も「自分」も含む
因数は、「1」を除いてしまいます。
ex. 12を素因数分解すると
12 = 22×3 ですが
12 = 13×22×3や
12 = 14×22×3 とはしませんものね!
60 = 1×60
x = 1×x
これらは、〇×〇の形になっているので、「分解」したように見えますが、
(分解されたもの = 因数なのですが)
60や xを「分解というより、正確に表現しただけ」とも言えますね
60=1×60 → ある、60が → 「60がある」
x=1×x → ある、xが → 「xがある」
「1」は因数としない (数学ルール)
② 素因数分解
素因数分解は、3年生で習うようですが、
難しいものでもないし、数字の基本でもあると思いますので、
(逆に小学生で習ってもよいのでは?とさえ感じますね)
ここ2年でやってしまいますね
では本題、素因数分解とは、
「数字を素数(=最小部品)にまで分解する」ことですね!
《 例 》
60を素因数分解しましょう
60 = 2×2×3×5
∴ 22×3×5 〔22・3・5〕 〔(2)2(3)(5)〕
どれも同じ意味ですが、「素因数分解しましょう」というときの
答えの表現方法は、「×」を使う表現方法が無難ですね。
(方法)
与えられた数字を、素数で割り続ける!それだけですね
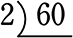 …適当な素数で割る
…適当な素数で割る
↓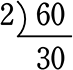 … 30は素数でないから…
… 30は素数でないから…
↓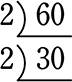 … また素数で割る
… また素数で割る
↓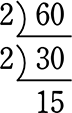 … 15は素数でないから…
… 15は素数でないから…
↓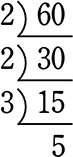 … また素数で割る
… また素数で割る
↓素数(5は素数)になったので終了!
60は、「2、2、3、5 からできている!」ということですね、
60 = 2×2×3×5
↑同じ素数は、「まとめなければ!」いけないので…
= 22×3×5
↑記入は次数の高いものから低いものへ!
慣れてきますと、「面倒」と感じてくると思います
適当に『因数』に分解して、『素因数』にまで分解するようになると思います
ex.
60 = 6×10 = (2×3)(2×5) = 22×3×5 //
10は\(\leftrightarrow\)2×5 8は\(\leftrightarrow\)23 などなど 「繰り返し使う」→「自分のもの」に !!
因数分解
3年生で習いますが、イメージだけ先に・・・
「文字」の入ったものを『(最小の)因数』に分解する。それだけですね。
必要性
| 素因数分解 | → | 約数や倍数など、その「数字」の性質が解る |
| 因数分解 | → | 2次方程式の解を簡単に求められたり、2次関数のx切片を求められたり、その「文字を含んだ数」の性質が解る |
《 例 》
x2-1 = 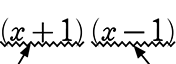
最小部品 最小部品
こんな感じですね!
(かっこ)を「一文字」と見れるようになっていれば、
ちゃんと、素因数分解と同じように「〇×〇」の形になっているのが解るはずですね!
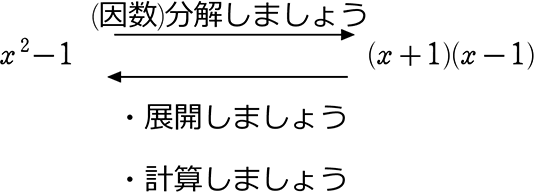
(ちなみに)
文字がない(=自然数だけの)場合なら、
60 = 22×3×5

(イメージするなら)
自転車 = (タイヤ)2・(フレーム) (ハンドル) (ペダル) (サドル)

ですね!

「分解」は、どうして「×」でつながってなければいけないの?
( )÷( )、( )+( )、( )-( )の形ではなく、
( )×( )すなわち( )( )の形なのでしょうか?
まず、( )÷( )は、機械的に ( )×\(\large{\frac{1}{(\ \ )}}\)、すなわち \((\ \ )\)\(\left(\large{\frac{1}{(\ \ )}}\right)\) の形にできますね。
「同じ意味なら、
実際、「÷」という記号は今後、ほとんど出てこなくなりますね。
( )+( )、( )-( ) の形は、「分解しましょう」というより
「ぶっ壊しましょう」という感じでしょうか。
例えば、「60をぶっ壊しましょう」とあったとすると、
60 = 2+58
60 = 2+58-3+3
60 = 2+58-3+3-3+3
・
・
・
人により、無限に答がありますね。
→あまり「意味がない」ということにつながりますね。
先生も
なにより、あまりに細かく壊されると、逆の作業(=組立)が困難ですね¡
イメージするならば、
「×」は「分解」→「ネジ」をゆるめるだけで分解する感じ
・自転車 = (タイヤ)2 ・(フレーム) (ハンドル) (ペダル) (サドル) → 組立が楽
「+-」は「ぶっ壊し」→「金のこぎり」でぶっ壊す感じ
フレームを真っ二つに切る人、ハンドルを真っ二つに切る人・・・
・自転車 = 金属片+ゴム片+アルミ片・・・ → 組立が困難
◎「分解」は、その数字が「どんな部品 からできているか」
を知るために、必要不可欠なものなのですね。
前置きが長くなってしまいましたが、
本題の「文字式の利用」です。
文字式を利用して、問題を解いていきましょう。
《 例 》
偶数を文字を使って表しましょう
0、2、4、6、8…と全て列挙するのは不可能ですね!
文字を使うと、「全ての場面をカバー」できます。
すなわち、「証明した」ということにつながっていきます。
「全ての場面をカバー」=「証明した」 ですね!
偶数とは、「2で割り切れる整数」→「2を約数に持つ整数」ですね!
よって、 2n
以上です!
n に 0、1、2、3…100…どんな整数を入れてみても、確かに偶数ですね
ちなみに、「0」は・・・偶数です!
《 例 》
30は偶数であることを証明しましょう
① 30÷2 = 15、2で割り切れるので偶数である
② 30 = 2×15、偶数は2nで表せる整数、よって偶数である
③ 30 = 2×15、2を約数(または因数でも可)にもっている
よって偶数である //
色々表現方法はありますが、①②③のどれでもOKですね!
《 例 》
奇数を一言で表現しましょう
2n+1
《 例 》
3つの連続する整数の和は、3の倍数であることを証明しましょう。
0、1、2 → 0+1+2=3
1、2、3 → 1+2+3=6
2、3、4 → 2+3+4=9
確かに今のところ3の倍数ですが
全ての場面をあげるのは不可能ですね・・・
よって、文字を使いましょう!
(証明)
最も小さい数字をn、とすると、3つの連続する整数は
n、n+1、n+2 で表すことができる
その和は、(n)+(n+1)+(n+2) = 3n+3 = 3・(n+1)
と表すことができる
(3つの連続する整数の和は、3を約数(または因数でも可)に持つ、)
よって、3つの連続する整数の和は3の倍数である //
文字にxを使ってもかまいませんが、
連続する整数を入れていくような場面では、
「n」や「m」を使うことが多いですね。 number の n?
《 例 》
30は3の倍数であることを証明しましょう。
30=6・5
よって、30は3の倍数である //
↑これは「証明」しきれていないですね!
これで言えることは、30は6の倍数である。
(または、5の倍数である。)ということだけですね。
(解答例)
30を素因数分解すると
30=2・3・5
よって、30は(3を約数にもつので) 3の倍数である // OKですね!
〔 倍数判定 〕
「倍数」とは…その数を整数倍された数
cf
ということは…「0」はすべての倍数?
→ 「0」はすべての数の倍数?と単品で聞かれたときは …「0」はすべての倍数
→ 「2」の倍数に「0」は含まれる?と~の倍数は?と聞かれたときは …「0」は含めない
ex. 3の倍数は? 3, 6, 9, …
2と3の最小公倍数は? 6
《 例 》
下1桁が偶数ならば、2の倍数であることを証明しましょう
例:3506
→ そもそも、偶数とは2で割り切れるものをいうので
下1桁が偶数ならば、2の倍数である
《 例 》
各桁の和が3の倍数ならば、3の倍数であることを証明しましょう
例:1080
→ 4桁の数字の千の位の数字をa、百の位の数字をb、
十の位の数字をc、一の位の数字をd とすると
1000a+100b+10c+d と表すことができる。改造すると
999a+a+99b+b+9c+c+d とできる
= 3(333a+33b+3c)+a+b+c+d
∴ 3(333a+33b+3c) の部分は因数に3を持つので、3の倍数(確定)である
∴ 残りの a+b+c+d が3の倍数であれば、その数は3の倍数となる
∴ 各桁の和が3の倍数ならば、3の倍数
→ 5桁なら 10000a+1000b+100c+10d+e
= 3(3333a+333b+33c+3d)+a+b+c+d+e で
何桁でも「原理」は同じですね
(何桁にでも対応する証明方法はありますが、
文字だらけになって、
「原理」「本質」が逆にわかりにくくなります。
今後の数学学習でもそういった
本質がわかりにくい公式や証明に出会うと思いますが、
基本は「本質の理解」→「文字化(公式、証明)」
の順ですね!)
《 例 》
下二桁が4の倍数ならば、4の倍数であることを証明しましょう
例:5632
→ 百の位の数字をa、十の位の数字をb、一の位の数字をcとすると
100a+10b+c
= 4(25a)+10b+c
(102以上は4で割りきれる)
∴ 4(25a)の部分は因数に4を持つので、4の倍数(確定)である
∴ 残りの 10b+c が4の倍数であれば、その数は4の倍数となる
∴ 下2けたが4の倍数ならば、4の倍数
《 例 》
下一桁が5の倍数ならば、5の倍数であることを証明しましょう
例:3335 6130
→ そもそも本能的に知っていますが・・・105円、1000円・・・念のため
→ 100a+10b+c
= 5(20a+2b)+c
∴ 下一桁が5の倍数ならば、5の倍数
(0は5の倍数?→0はすべての数の倍数です
→0は5の倍数)
《 例 》
2の倍数かつ3の倍数ならば、6の倍数であることを証明しましょう
例 4122
→ 6 = 2×3
→ ただの合わせ技ですね(6は2と3の最小公倍数)
∴ 2の倍数かつ3の倍数ならば、6の倍数
→ 偶数で、しかも各位の数字の和が3の倍数なら6の倍数ということですね
《 例 》
7の倍数かどうかは、7で割り切れるか試すのが1番早いですね
→ 不要
《 例 》
下三桁が8の倍数ならば、8の倍数であることを証明しましょう
例:3184
→ 1000a+100b+10c+d
= 8(125a)+100b+10c+d
(103以上は8で割りきれる)
∴下三桁が8の倍数ならば、8の倍数
《 例 》
各桁の和が9の倍数ならば、9の倍数であることを証明しましょう
例:1080
→ 100a+10b+c
= 9(11a+b)+a+b+c
∴ 各桁の和が9の倍数ならば、9の倍数
(3を出せば、3の倍数証明でしたね)
《 例 》
下一桁が0ならば、10の倍数であることを証明しましょう
例:9990
→ 100a+10b+c
= 10(10a+b)+c
∴ 下一桁が0ならば、10の倍数
《 例 》
各位を一つおきに足したものの差が11の倍数ならば、11の倍数であることを証明しましょう
例:3916
→ 10000a+1000b+100c+10d+e
= 9999a+a+1001b-b+99c+c+11d-d+e
(なぜか偶数桁目は1を足したとき、
奇数桁目は1を引いたときに11の倍数になりますね)
= 11(909a+91b+9c+d)+a-b+c-d+e
∴各位を一つおきに足したものの差が11の倍数ならば、11の倍数
(0はすべての倍数 → 0は11の倍数)
倍数判定
・下一桁が偶数
・各桁の和が3の倍数
・下二桁が4の倍数
・下一桁が5の倍数
・2の倍数かつ3の倍数
・7の倍数:不要
・下三桁が8の倍数
・各桁の和が9の倍数
・下一桁が0
・交互の差が11の倍数
〔 平方数 〕
平方数とは
0以上の整数の2乗で表すことができる整数
ex. 0, 1, 4, 9, 16, 25, 36, 49…121…無限にある
確かに、(0)2, (1)2, (2)2, (3)2…(11)2…で表せますね
一言、『整数の2乗でできている数 (0もOK)』で十分ですね
《 例 》
24にできるだけ小さい自然数をかけて、
その積がある自然数の2乗になるようにしたい。
どんな自然数をかければよいか。
→ 24×△=〇2 な形になるような△は? ということですね
すなわち、素因数分解の結果が
☆2× ▽2× □2 な形になればよいということですね
= ( ☆2×▽2×□2 ) = ( ☆▽□ )2 ですものね (指数法則)
24を素因数分解してみると、
24 = 3×8 = 22×2×3
→ これを、22×22×32 にできれば、(2×2×3)2= 〇2 な形になっていますね
∴ (あと 2×3=) 6 ( をかければ (2・2・3)2= 122 な形)
《 例 》
140をできるだけ小さい自然数nで割って、
その商がある整数の2乗になるようにしたい。
どんな自然数で割ればよいか。
→ \(\large{\frac{140}{n}}\) = 〇2な形になるnは?ということですね
→ 分子の140を素因数分解してみると、
\(\large{\frac{2\ \cdot \ 7\ \cdot \ 10}{n}}\) = \(\large{\frac{2^2×7×5}{n}}\)
→ n が7×5なら〇2な形の22
∴ 35 (で割ればよい)

2~100までの素因数分解
憶える必要はないですが、
1度くらいは、「(自分以外の)何かで割れる」か試しておきたいものですね!
(本来は1×は省略して書きません
「1と自分でしか割り切れない」
という意味で記しています)
2 = 1× 2
3 = 1× 3
4 = 1× 22
5 = 1× 5
6 = 1× 2×3
7 = 1× 7
8 = 1× 23
9 = 1× 32
10 = 1× 2×5
11 = 1× 11
12 = 1× 22×3
13 = 1× 13
14 = 1× 2×7
15 = 1× 3×5
16 = 1× 24
17 = 1× 17
18 = 1× 32×2
19 = 1× 19
20 = 1× 22×5
21 = 1× 3×7
22 = 1× 2×11
23 = 1× 23
24 = 1× 23×3
25 = 1× 52
26 = 1× 2×13
27 = 1× 33
28 = 1× 22×7
29 = 1× 29
30 = 1× 2×3×5
31 = 1× 31
32 = 1× 25
33 = 1× 3×11
34 = 1× 2×17
35 = 1× 5×7
36 = 1× 22×32
37 = 1× 37
38 = 1× 2×19
39 = 1× 3×13
40 = 1× 23×5
41 = 1× 41
42 = 1× 2×3×7
43 = 1× 43
44 = 1× 22×11
45 = 1× 32×5
46 = 1× 2×23
47 = 1× 47
48 = 1× 24×3
49 = 1× 72
50 = 1× 52×2
51 = 1× 51
52 = 1× 22×13
53 = 1× 53
54 = 1× 33×2
55 = 1× 5×11
56 = 1× 23×7
57 = 1× 3×19
58 = 1× 2×29
59 = 1× 59
60 = 1× 22×3×5
61 = 1× 61
62 = 1× 2×31
63 = 1× 32×7
64 = 1× 26
65 = 1× 5×13
66 = 1× 2×3×11
67 = 1× 67
68 = 1× 22×17
69 = 1× 3×23
70 = 1× 2×5×7
71 = 1× 71
72 = 1× 23×32
73 = 1× 73
74 = 1× 2×37
75 = 1× 52×3
76 = 1× 22×19
77 = 1× 7×11
78 = 1× 2×3×13
79 = 1× 79
80 = 1× 24×5
81 = 1× 34
82 = 1× 2×41
83 = 1× 83
84 = 1× 22×3×7
85 = 1× 5×17
86 = 1× 2×43
87 = 1× 3×29
88 = 1× 23×11
89 = 1× 89
90 = 1× 32×2×5
91 = 1× 7×13
92 = 1× 22×23
93 = 1× 3×31
94 = 1× 2×47
95 = 1× 5×19
96 = 1× 25×3
97 = 1× 97
98 = 1× 72×2
99 = 1× 32×11
●大きな数字でも素数がありますね。実は素数は無限にあります。
→ 43×47 = 2021 は計算できますが
2021を素因数分解しなさい なんていわれたら・・・
大丈夫!そんな問題はでません!
●素数と思っていたら、素数でなかった、
逆に、素数ではないと思っていたら、素数だった
というものは、少し注意しておいてくださいね
●一の位が「1、3、7、9」の数字は素数の可能性がありますね
●20くらいまでの素数は、空で言えるようになりたいですね
「2、3、5、7、11、13、17、19・・・」
③ 最大公約数・最小公倍数
最大公約数を
GCD … Greatest Common Divisor や
GCM … Greatest Common Measure と言ったり
最小公倍数を
LCM … Least Common Multiple と言ったりしますね
「文字式の利用」からは外れますが、
せっかく「素因数分解」で「素因数」を学んだのですから、
最大公約数・最小公倍数についてお話させてもらいますね。
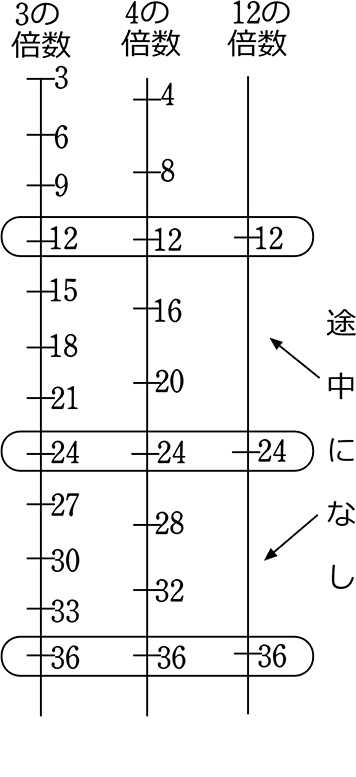
例えば、27と36と54の、最大公約数、最小公倍数は?
27の約数は、1、3、9、27 ですね。
27の倍数は、27、54、81、108、・・・52488・・・ですね。
36の約数は、1、2、3、4、6、9、12、18、36 ですね
36の倍数は、36、72、108、144、・・・52488・・・ですね。
54の約数は、1、2、3、6、9、18、27、54 ですね。
54の倍数は、54、108、162、216、・・・52488・・・ですね。
よって、最大公約数は 9
最小公倍数は 108
3つを簡単に図でイメージすると、
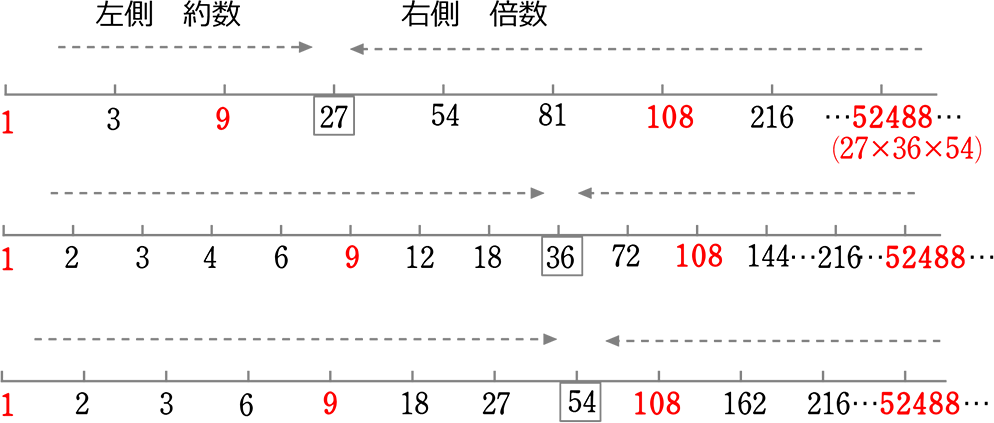
・最大公約数 …共通の約数で最大もの (できる限り右のもの)
(最
・最小公倍数 …共通の倍数で最小のもの (できる限り左のもの)
(最大公倍数は無限。 簡単に公倍数を求める方法は、
そのものどうしの掛け合わせ。27×36×54 計算は大変ですが)
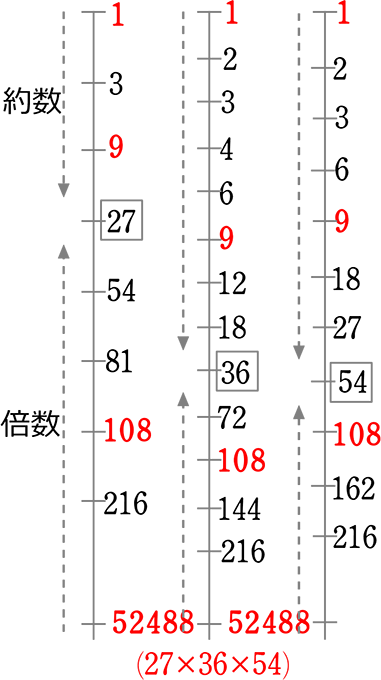
・最大公約数 …共通の約数で最大もの (できる限り下のもの)
(最
・最小公倍数 …共通の倍数で最小のもの (できる限り上のもの)
(最大公倍数は無限。 簡単に公倍数を求める方法は、
そのものどうしの掛け合わせ。27×36×54 計算は大変ですが)
〔素因数分解を利用する解法〕
まずはそれぞれ素因数分解します
27 = 33 = 3・3・3
36 = 32×22 = 3・3・2・2
54 = 33×2 = 3・3・3・2
これを表にすると

・最大公約数 …全てに共通な因数 …3×3 = 9
・最小公倍数… ×(一部に共通な因数) ×(全てに素な因数)
×(一部に共通な因数) ×(全てに素な因数)
= (最大公約数)(一部に共通な因数)(全てに素な因数)
= 9 ×3×2 ×2 = 108
ですね
実は、小学校で習った最大公約数・最小公倍数の求め方と同じことなのです
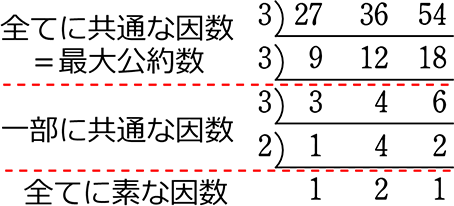
確かに同じ原理ですね!(ちなみに1は因数ではない)
これで、どこまで掛けたら「最大公約数」?、「最小公倍数」?と、
迷うことは無くなりましたね!

「互いに素」とは、どういう関係?
「 互いに素(そ)」とは、共通因数がない数字たちの関係です。
「互いに素数」という意味ではありません。
2つの数字が「互いに素」の関係にあるときは、
2つの最小公倍数は?
→ 2つの数字を掛け合わせるしかありません
途中にはないのです!
《 例 》
15と28の最小公倍数は?
15も28も素数ではありませんね。どちらも自分以外の因数を持ちますね!
15 = 3×5
28 = 2×2×7
ですが、共通の因数は・・・ありませんね。
このような「共通因数のない」関係の数字を「互いに素」といいます
よって、最小公倍数は、 3×5 ×2×2×7 = 15×28 = 420 //
そのもの同士を掛けるしかないのです
(420までの途中にありそうで、ないのです)
これを高校生風にかっこよく言うと、
「15と28は、互いに素なので15と28の最小公倍数は15×28、すなわち420」
逆に、当然、最大公約数は「1」ですね!
他方、「素数」どうしの最小公倍数は、そのものどうしを掛け合わせるしかなかったですね。
これは、体感的にも経験的にもすでに感じていましたね。
3と5の最小公倍数は…15 のように。
上の2つの例は、分数の分母にしてみれば、
イメージしやすいかもわかりませんね。
\(\large{\frac{1}{3}}\)+\(\large{\frac{1}{5}}\) = \(\large{\frac{5}{3\ \cdot \ 5}}\)+\(\large{\frac{3}{5\ \cdot \ 3}}\) = \(\large{\frac{5+3}{15}}\)
「ぱっと見で 通分するためには、3と5を掛け合わせるしかないな!」
\(\large{\frac{1}{15}}\)+\(\large{\frac{1}{28}}\) = \(\large{\frac{28}{15\ \cdot \ 28}}\)+\(\large{\frac{15}{28\ \cdot \ 15}}\) = \(\large{\frac{28+15}{420}}\)
「途中にありそうで…ない!15×28を計算するのかぁ…」
(実際は、15×28には\(\large{\frac{2}{2}}\)という「1」をかけて、
15×\(\large{\frac{2}{1}}\)×28×\(\large{\frac{1}{2}}\) = 30×14 = 14×30で暗算できますね)
以下は、高校生の過程ですので、読むだけでかまいません。
《 例 》
〇〇〇〇な整数nは、12の倍数であることを証明しましょう。
という問題があったとします。
このとき、いきなり12の倍数と証明できそうにないので、
ある2つの数字の倍数であるから、12の倍数である、と証明しよう
とします
A. nは〇〇すると2の倍数、△△すると6の倍数、よって、nは12の倍数である
↑これは証明になっていませんね!
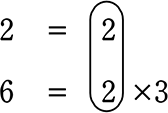
最小公倍数は、2×3=6 すなわち6の倍数ということ
しか言えていません。実際18などは、2と6の倍数ではありますが、
12の倍数ではありませんね!
ということは、最初に選んだ2数、2と6がダメだったのですね
互いに素な3と4を選ぶべきだったということになります。
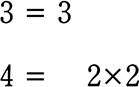
最小公倍数は、3×2×2=12
すなわち12の倍数であると言えてますね!
A. nは〇〇すると3の倍数、△△すると4の倍数、3と4は互いに素であるからnは12の倍数である マルですね!




④ 約数の個数・約数の総和
約数の個数
素因数分解ができると、約数の個数も簡単に求められます。
《 例 》 360の約数の個数を求めましょう。
時間をかけて、個別に列挙するのもありですが、
1、2、3、4、5、6、8、9、10、12、15、18、20、24、30、36、40、45、60、72、90、120、180、360
A. 24 通り
大変すぎですね!
ここで、これらの約数は全て「因数の組み合わせ」ということに注目すると・・・
360 = 23×32×5 = 2・2・2・3・3・5
ex. 上の列挙の
3は「3」を1つ使ったもの
10は「2・5」の2つを使ったもの
12は「2・2・3」の3つを使ったもの
・
・
・
これらの因数の組み合わせ方が、「何通り」あるか?
が分かればよいということですね!
イメージは、クレーンゲームで、2・2・2・3・3・5 という5枚のカードを
とる時の、組み合わせパターンの種類ですね。
1枚も取れないパターン、2枚とれた時の組み合わせパターン、
3枚取れた時のパターン・・・5枚取れた時のパターン
一体、考えられるパターンは何通りあるのでしょうか?
20・30・50 = 1・1・1 =1←最小公約数ですね
20・30・50 = 1・1・1 =1←最小公約数ですね
(何かの 0乗は0ではなく「1」でしたね!)
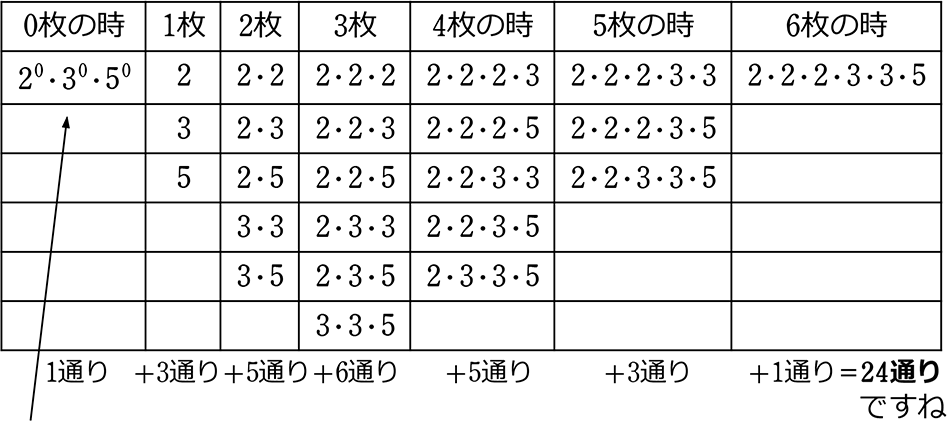
これを図で表すと
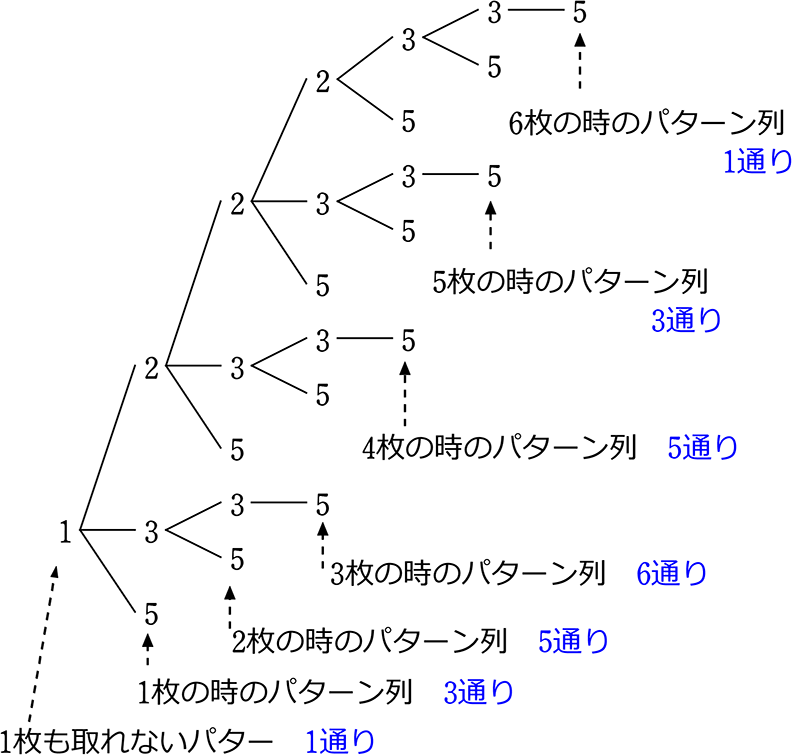
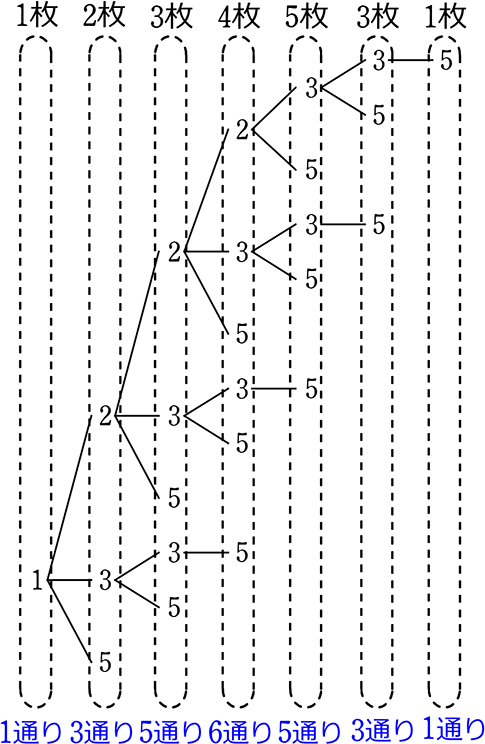
確かに、合計24通りですね!
※ 2年後半で学ぶ「確率」の「組合せ」の樹形図とは異なります
「組合せ」の樹形図は6枚から「3枚」選ぶなど
今回は6枚から「選ばない」「1枚選ぶ」「2枚選ぶ」…「6枚選ぶ」をかぶせて描いたものです
「全部を書き出す」にしても「表」にしても「図」にしても大変ですね!
これは、カードの作り方が良くなかったのです。
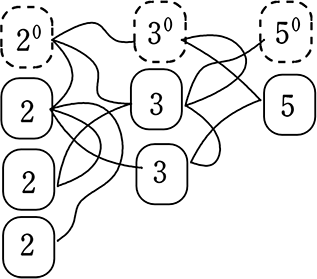
このように作ってしまうと、無数に組合わせが
ある感じがして、混乱していまいますね。
それでは、カードを作り直しますね。
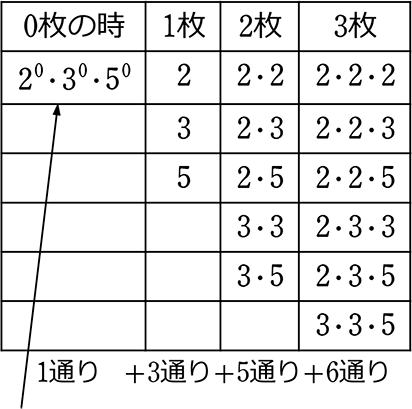
カードの組み合わせ「2の部類」「3の部類」「5の部類」でまとめます。
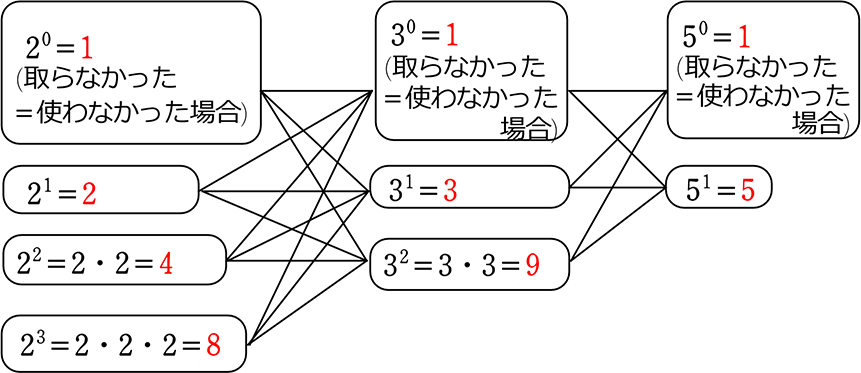
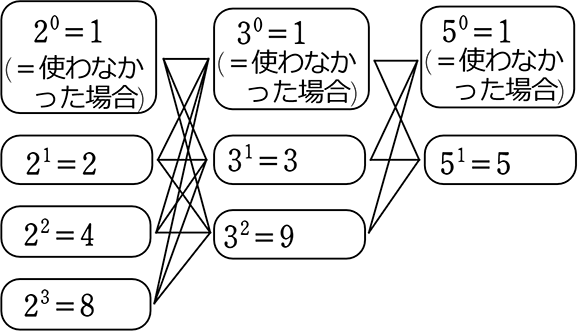
「2」だけの組み合わせなら、4通りしかないとわかりますね
「3」だけなら、3通りしかない
「5」だけなら、2通りしかない
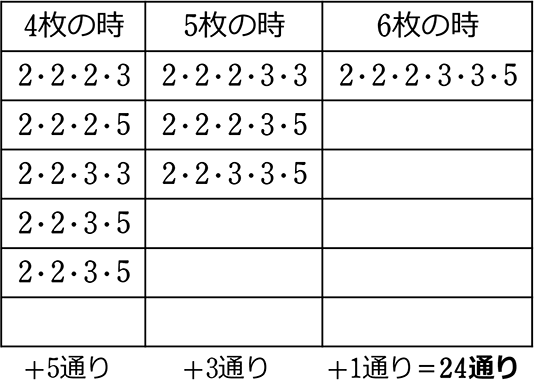
すなわち、 = 4通り×3通り×2通り = 24
= 4通り×3通り×2通り = 24
A. 24 通り ですね!
そして、この「4」「3」「2」は実は、360の素因数分解にヒントが出ています!
360 = 23×32×5 = 23×32×51
「4」「3」「2」と、新しく作ったカードと、素因数分解の指数を見比べて下さい・・・・・・
素因数分解したものの指数にそれぞれ「1を足したもの」ですね!
→「使わなかった場合の0乗」をカードとして含めるための「+1」ですね

約数の個数
まず 素因数分解をして
〇 = 素数指数×素数指数×素数指数 のとき
約数の個数 = (バリエーション数)×(バリエーション数)×(バリエーション数) = (指数+1)(指数+1)(指数+1)
※ バリエーション数 = 使わないという意味の0乗分を忘れない = 指数+1
※ 0乗は「1」
※ 指数しか使わない、素数自体はどうでもよい
※ 素因数分解を間違えない
今後、この問題に出会った時は、計算問題を解くかのように
「公式」に当てはめるだけでいいですね!
《 例 》
300 の約数の個数は?
300 = 52×22×3
∴ 個数 = (バリエーション数)(バリエーション数)(バリエーション数)= (50,51,52)(20,21,22)(30,31) = 3通り×3通り×2通り = 18個
約数の総和
《 例 》 360の約数の総和を求めましょう
どういう意味かと申しますと・・・
「全ての約数」を「足し合わす」、ということですね!
1、2、3、4、5、6、8、9、10、12、15、18、
20、24、30、36、40、45、60、72、90、120、180、360
これらの和は…1170 ですね
しかし、「約数を羅列すること」も「それらを足す計算」も大変すぎますね
ちゃんと便利な公式がありますが、まず公式の原理です
上の 1、2、3、4、5、6、8、9、10、12、15、18、
20、24、30、36、40、45、60、72、90、120、180、360を求めるためには


を全て「たどった」ものでしたね = 全ての組合せ
ex.
1→1→1とたどれば「約数1」、 1→1→5なら約数5
1→3→1なら3、 1→3→5なら15
・
・
・
8→9→1なら72、8→9→5なら360
どれ一つ同じものはないですね!
これを文字に置きかえるてみると
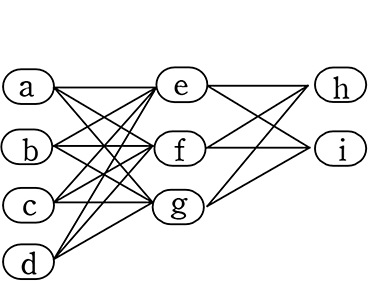
aef, aei, afh, afi, …dgh, dgi の24個(1つ1つが約数にあたる)
これを aef+aei+afh+afi, …+dgh+dgi にすれば「約数の総和」ということですね
そしてこれは2年冒頭で学んだ「分配法則」そのものですね!
すなわち を
を 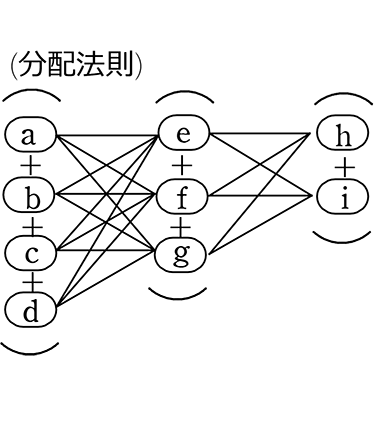 にするということですね
にするということですね
これを「文字」から「数字」に戻すと
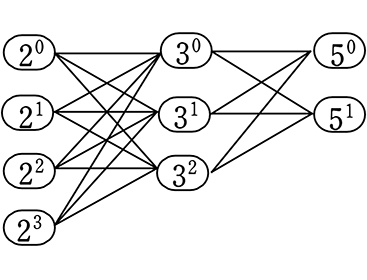 を
を 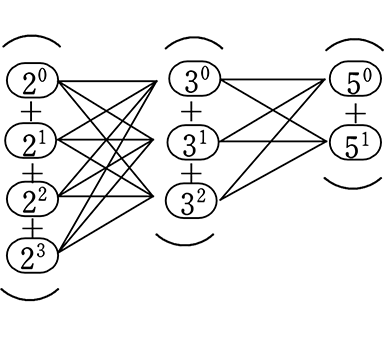 にすれば = 約数の総和 ですね!
にすれば = 約数の総和 ですね!
そして「文字」は(カッコ)の中で計算はできませんが、
「数字」は(カッコ)の中を先に計算してもかまいませんね!
→ (20+21+22+23)(30+31+32)(50+51)
= (1+2+4+8)(1+3+9)(1+5)
= (15)(13)(6)
= 1170
もちろん、分配法則でもかまいませんが・・・
→ (20+21+22+23)(30+31+32)(50+51)
= (1+2+4+8)(1+3+9)(1+5)
= (1・1・1+1・1・5+1・3・1・・・+8・9・5) ←全約数
ですが、せっかく(カッコ)の中が数字だけなのですから
分配法則せずとも
(カッコ)の中から計算する方が全然楽ですね
というわけで

約数の総和
まず 素因数分解をして
〇 = 素数指数×素数指数×素数指数 のとき
約数の総和 = (バリエーションの和)×(バリエーションの和)×(バリエーションの和)
※ バリエーションの和 → 使わないという意味の0乗分を忘れないように
※ 0乗は「1」
※ 素因数分解を間違えない
《 例 》
2400 の約数の総和を求めましょう
2400 = 25・52・3
∴ 約数の総和 =(バリエーションの和)(バリエーションの和)(バリエーションの和) = (20+21+22+23+24+25)(50+51+52)(30+31) = (1+2+4+8+16+32)(1+5+25)(1+3) = (63)(31)(4) = 7812
原理がなんとなくでも解れば
公式も忘れにくくなりますね。
「約数の総和」では、せっかく(カッコ)の中に文字がなくて、
(カッコ)の中から先に計算できる!! のですから、楽しましょうね。
ps. ないとは思いますが、「分配法則」の求め方も
「全ての約数を列挙せよ」という問題には有効ですね!
《 例 》
18の約数を求めましょう(羅列しましょう)
18=2×32
約数=(20, 21)(30, 31, 32)
=(1, 2)(1, 3, 9)
=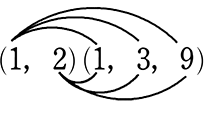 (符号のない分配法則をして)
(符号のない分配法則をして)
=1、3、9、2、6、18
∴ 並び替えて、1、2、3、6、9、18




ウ 目的に応じた式の変形
いわゆる『等式の変形』ですね。
一言で言うと、「左辺を目的の文字だけにする」という「作業」ですね!
使える武器は、1年生の1次方程式と全く同じです。
①移項、全とっかえ、全符号替え
②本体改造(等式の性質3、4)
これだけで、パズルを解くように全て解けてしまいます!
この「作業化」のねらいは、
「式」を「機械的」に解くということですね!
イメージするならば、
例えば買い物中に、ふと「2割引き後の値段が1,600円ということは元値はいくらなんだろう?」と思った時、
「ということは」「2割の金額を引いたものが1600」「ということは…」
この「ということは」が頭の中に何個もあると、頭が混乱しがちです。
そこで、「ということは」をできる限り無くすために、式を思い浮かべるのですね!
「何かに0.8を掛けると、1600」すなわち「0.8x=1600」
すなわち「何か(x)は、1600を0.8で割ったものだ!」
と思考回路がすっきりしますね!
少し違うイメージなら、
アコヤ貝から真珠(x)を取り出す感じでしょうか。
「トンカチでたたいたら、中の真珠まで壊れる・・・ということは、貝を何かで開く・・・」
慣れた職人さんは「ここにナイフを刺して開く → ある袋を破る → 真珠を取り出す → 塩水で洗う」
というふうに、「ということは」が無く、 一連の「作業」で真珠(x )を取り出しているはずですね。
慣れれば「問題」ではなく、「作業」ということですね!
変な話になってしまいましたが、本題に入りますね。
《 例 》
次の等式をxについて解きましょう。(=左辺をxだけにしましょう)
x = \(\large{\frac{3y(x+2y)}{2}}\)
2x = 3y(x+2y) … 分数の形が嫌なので、「両辺に2を掛けた」
↓
2x = 3xy+6y2 …(カッコ)の中にもxがあるので、「展開した」
↓
2x-3xy = 6y2 …xを含む項を左辺に、xを含まない項を右辺に、「移項した」
↓
x(2-3y) = 6y2 …共通因数xでくくり出した (展開の逆)
↓
x = \(\large{\frac{6y^2}{(2-3y)}}\) …両辺を、xの係数(2-3y)で割った。(カッコ)を1文字と見れるように!
↓
x = \(\large{\frac{6y^2}{2-3y}}\) //
分数の形では、(2-3y)の(カッコ)がなくても、
明らかに、6y2 を「2-3y」で割っているという形が
分かるので、(カッコ)を省略した
〈 当然、÷の形では(カッコ)は必要→ 6y2÷(2-3y)〉



お疲れ様でした !!
その他の問題は、「問題集」で !!