| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平面図形と平行線の性質 | (2) 図形の合同・図形の性質 |
| ア | 平行線や角の性質 |
|---|---|
| ① | 平行線と角 |
| ・ | 対頂角 |
| ・ | 同位角 |
| ・ | 錯角 |
| ・ | (逆) 同位角(錯角)が等しい⇒平行 |
| ・ | 同側内角 |
| ② | 三角形と角 (三角形の角) |
| ・ | 三角形の内角の和は、180°の証明 |
| ・ | 三角形の外角とは |
| ・ | 三角形の外角の求め方 |
| ・ | 四角形の外側の角(凸四角形を含む)の求め方 |
| ・ | 三角形の外角の和 |
| ・ | 鋭角三角形、鈍角三角形、直角三角形 |
| ・ | 対角・対辺とは |
| ・ | 三角形の対辺と対角の関係 |
| ・ | 斜辺は重要! |
| ③ | 平行線と面積 (頂点の平行移動)(等積変形) |
| イ | 多角形の角の性質 |
| ・ | 多角形の内角の総和 |
| ・ | 多角形の内角の総和の公式 |
| ・ | 多角形の外角の総和 |
| ・ | 多角形の外角の総和の公式 |
| ・ | 多角形の対角線の本数 |
平面図形と平行線の性質
ア 平行線や角の性質
①平行線と角
それでは、平行線と角の特徴(性質)を見ていきましょう
人は、「特徴」があると「名前」をつけたくなりますね!
口には出さなくても、心の中で「あの『茶髪君』いけてる!」などなど、
名前をつけた、=『特徴がある』 ということですね!
それでは、2本の平行線とそれを横切る直線について、3つほど。
前提として、『 直線は、180° 』ですね!
![]()
あまりに当たり前すぎて(=特徴が無さすぎて)、
つい意識の外に忘れてしまいますね。
常に意識しましょうとは言いませんが、いつでも意識の中に
呼び戻せるように、意識しましょうね!
【 対頂角 (たいちょうかく) 】

・(位置関係) 対(つい)の角ですね
(平行線は関係なかったですね…)
・(性質) 対頂角は等しい
(∠a = ∠b)
・(物理的イメージ)
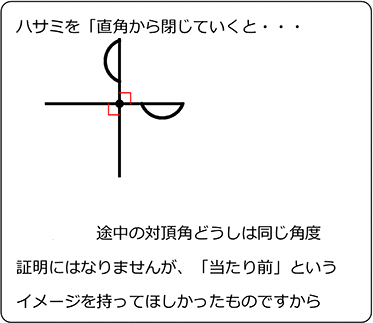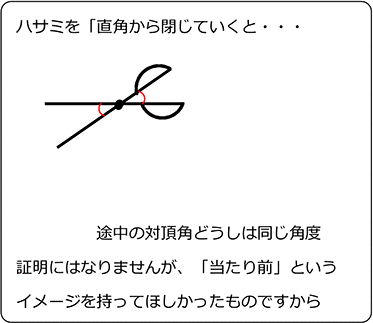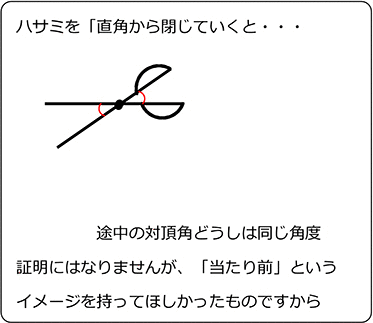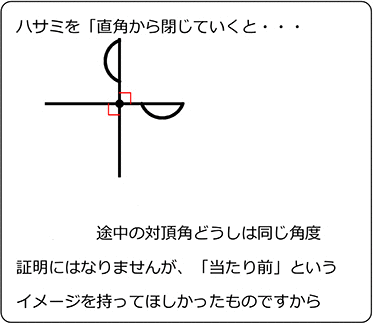
・(数学的証明)

「直線は180°」という意識の呼び戻し
↓
\( \small{\begin{cases}
∠a = 180°-∠c (基準: \color{red}{ 赤線 } ) \\
∠b = 180°-∠c (基準: \color{blue}{ 青線 } )
\end{cases}}\)
(どちらも右辺が同じ、すなわち)
∴ ∠a = ∠b
【 同位角 (どういかく) 】

・(位置関係) 同じような位置関係の角
・(性質) 平行
(平行
・(物理的イメージ)
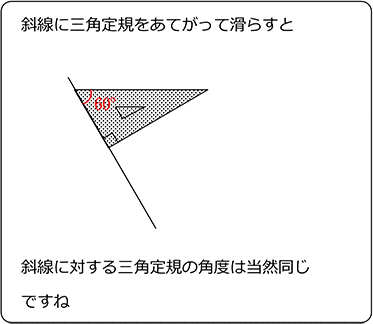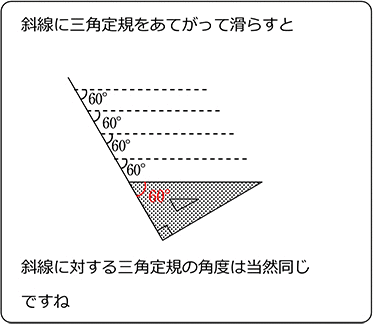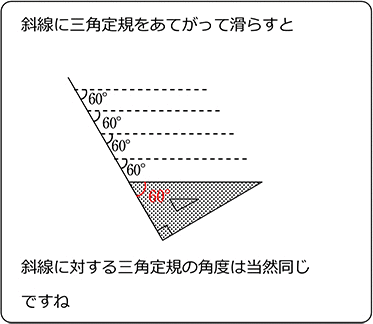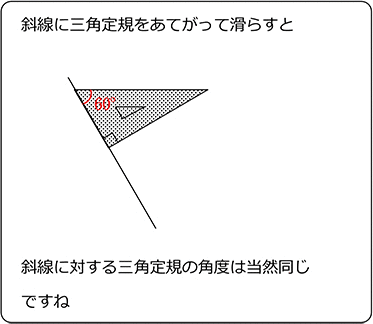
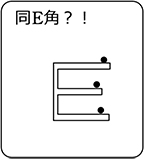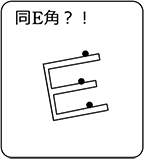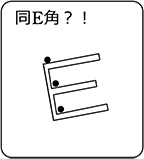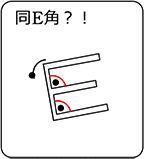
同位角が同じでない場合、
2直線をどちらかに延長し続けると・・・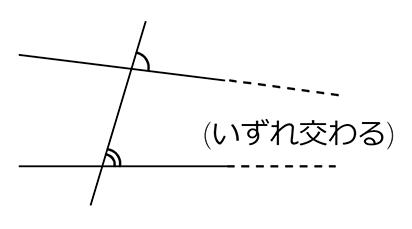
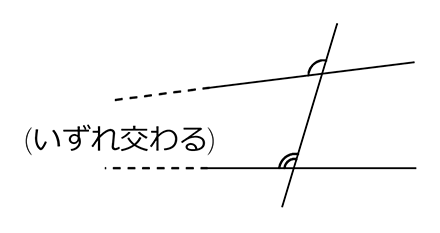
ということですね
平行とは
同一の平面上にあって、
両方向に限りなく延長しても、
いずれの方向においても互いに交わらない直線
・(数学的証明)
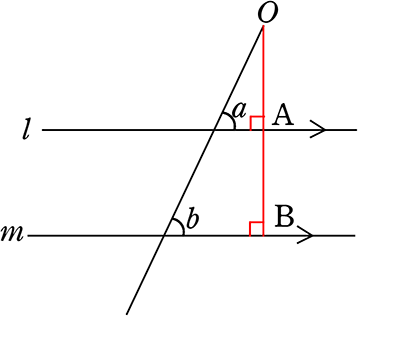
Oから直線lとその平行線mに
垂線を下す
(三角形の内角の和は180°)
\(\small{\begin{cases}
∠a = 180°-90°-∠O (△OaAにおいて) \\
∠b = 180°-90°-∠O (△ObBにおいて)
\end{cases}}\)
(どちらも右辺が同じ、すなわち)
∴ ∠a = ∠b
【 錯角 (さっかく) 】

・(位置関係) 図のような位置関係の角
(強いて言うなら「Z」のような?)
・(性質) 平行
(平行
・(数学的証明)

\(\small{\begin{cases}
∠a = ∠A (対頂角より) \\
∠b = ∠A (同位角より)
\end{cases}}\)
∴ ∠a = ∠b
・(物理的イメージ)は不要ですね!
「楽で便利」というイメージを持つといいと思います
上の証明のように、∠a = ∠A (対頂角)、∠b = ∠A (同位角)
∴ ∠a = ∠b という「2段階」を踏まなくても、
∠a = ∠b (錯角)!! 一言で済みますね!
(昔の数学者が、この角度にも名前をつけたら楽かも?!
といことで『錯角』とか名付けたのかもですね!)
長くなってしまいましたが、「対頂角」「同位角・錯角」は、
『名前』、『位置関係』、
『平行なら、同じ角度。 同じ角度なら、平行』
ということだけおさえておけば、
今後の問題を解くための「使える武器」になりますね!
もちろん、下図のような「平行ではない場合」でも
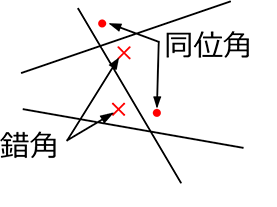
「同位角」、「錯角」と言いますが、
問題では、9分9厘「平行」ですね!
(平行の時に力を発揮しますので)
平行ではないのは、習い初めの「名前確認テスト」「位置確認テスト」
くらいかと思います

クリック・タップで答え (反応が遅い場合があります)

クリック・タップで答え (反応が遅い場合があります)
〔 逆の証明 〕
(逆) 同位角(錯角)が等しい ⇒ 平行
まず証明を求められることはありません
問題では「同位角(または錯角)が等しいので平行!」と当たり前のように使用してOKです!
ですが念のため証明です
・同位角が等しい
交点をそれぞれA、Bとする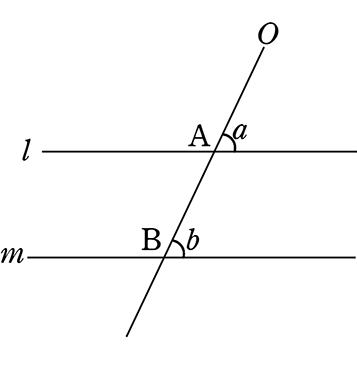
Oから直線mに垂線を下ろしそれぞれの交点をC、Dとする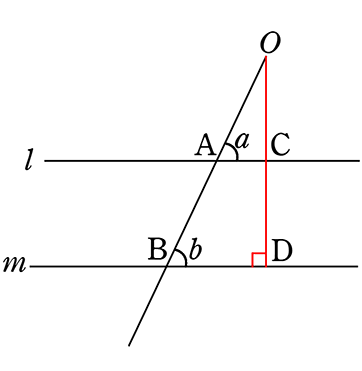
△OACと△OBDにおいて
∠O = ∠O (共通)
∠a = ∠b (仮定より)
よって2つの角が等しいので
△OAC∽△OBD
∴ ∠OCAも90°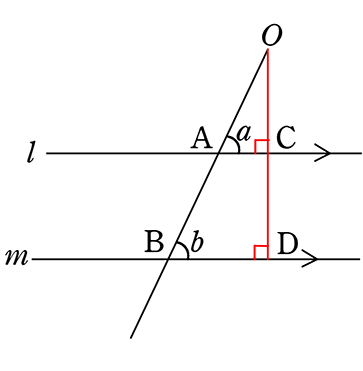
答1 ∴ 2つは相似の位置(3年)にあるので「対応する辺は平行」である
∴ l // m
答2 ∴ lはODの垂線、mもODの垂線
∴ 1つの直線に対する垂線は平行であるので
l // m
答3 CDの外側にmに垂線を引いて交点をEFとする
→すべて90°になる
∴ 四角形CDEFは平行四辺形(長方形)
∴ l // m
同様に
・錯角が等しい
対頂角は等しいので、
1つの錯角の対頂角と他の角で証明してもよい
→以下先ほどの
同位角が等しい
ですので省略しますね
同側内角
「同側内角」とは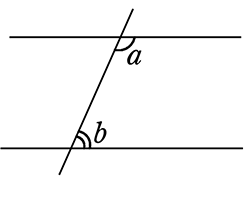 aとbのセットのことをいいます
aとbのセットのことをいいます
・同側内角の和が180°
ですね。
(証明)
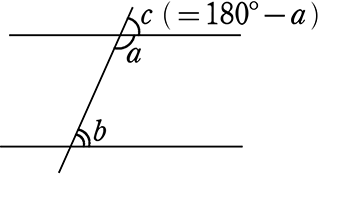
図で、∠c=180°-a
よって、∠b=∠c であれば、
同位角が等しいので、2直線は平行
∠b=∠c
∠b=180°-∠a (cをaで表した)
∠a+∠b=180° (移項した)
∴ 同側内角の和が180°
・同位角が等しい
ex. 次の図は、どのよう図形か調べましょう
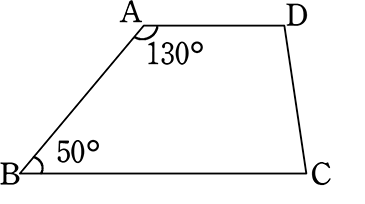
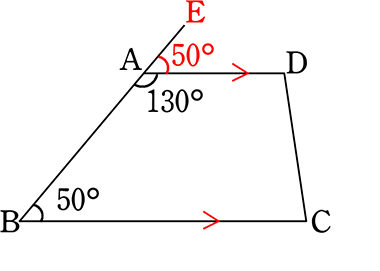
BAの延長上にEをとる
∠EAD=180°-130°=50°
よって、 同位角が等しいのでAD//BC
∴ 台形
→ 証明問題で、点Eを設定するのは面倒ですね
→ 一言、同側内角の和が(130°+50°=)180°
∴ AD//BCな 台形 (少し楽ができましたね)
② 三角形と角
なんといっても、三角形の大特徴は、
『三角形の内角の和は、180°』ですね!
図形の問題は、ほぼ三角形を原点にしてますね!

三角形の内角の和は、180°の証明
(どんな形の三角形であっても) 三角形の
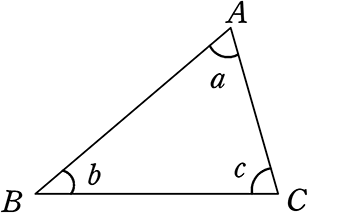
内角とは、三角形の「内側の角」、
図でいえば ∠aや∠bや∠c ですね
三角形の内角の和 = ∠a+∠b+∠c = 180°ということですね
本当に180°か証明は簡単ですね! では、
① BCを延長します
② Cから、ABと平行な直線を伸ばします
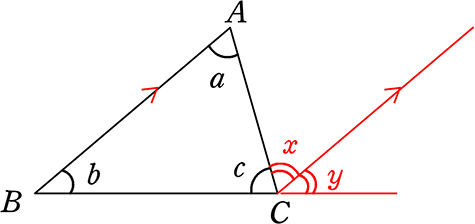
まず、∠c+∠x+∠y = 180° ですね (∵ 一直線)
∵←読み「なぜなら」 ∴←読み「ゆえに」
そして、
\(\small{\begin{cases}
∠x = ∠a (錯角より)\\
∠y = ∠b (同位角より)
\end{cases}}\)
すなわち、∠c+∠x+∠y = ∠c+∠a+∠b = 180°
∴ 三角形の内角の和は180° //
三角形の外角
三角形の『外角』とは、
「三角形の1辺と他の1辺の延長線がつくる角」
ですね
言葉では理解しにくいと思いますので、
下図のような「場所」であるという視覚的理解で十分ですね

・1つのセット は「対頂角」の関係ですので、同じ角度ですね
は「対頂角」の関係ですので、同じ角度ですね
・外角の角度は?という場合、1セットの角度を足しません、
「対頂角」の関係ですし、1つを言えば十分ですね!
ex) 頂点aの外角の角度は? → 直線180°-∠a
ここで、前出の「ポイント『内角の和は180°』」の下図をよく見ていただくと、
x+yはCの外角になっていますね!!
ということは、x+yはa+bでしたので、 a+b = c の外角ですね!!

三角形の外角の求め方
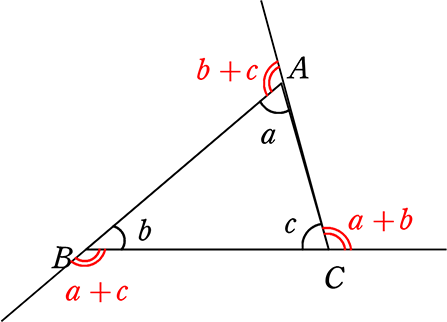
① 外角 = 離れた2つの内角の和 ex) c の外角=a+b
② 外角 =
(当然と言えば当然ですね。
三角形の内角の和は180°、一直線も180°、180°つながりですね!)
ここでは文字で理解ができましたら、略図でイメージ化しますね
(今後の問題では、これ(外角)を計算するのではなく、
複雑な図形にさりげなくひそんでいる「この関係」に、
「気づく」ということの方が大切ですので!)
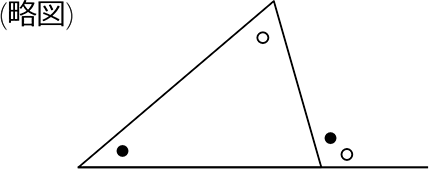
通称『内角と外角の関係』ですね
俗にいう「スリッパの法則」ですね 横から見たスリッパ?
横から見たスリッパ?
《 例 》
xの角度を求めましょう
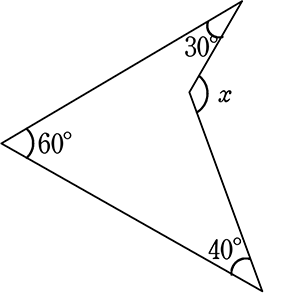
色々な「補助線」の引き方が考えられますね
補助線:元の図にはないが、
問題解決のために自分で引く線
〔補助線1〕
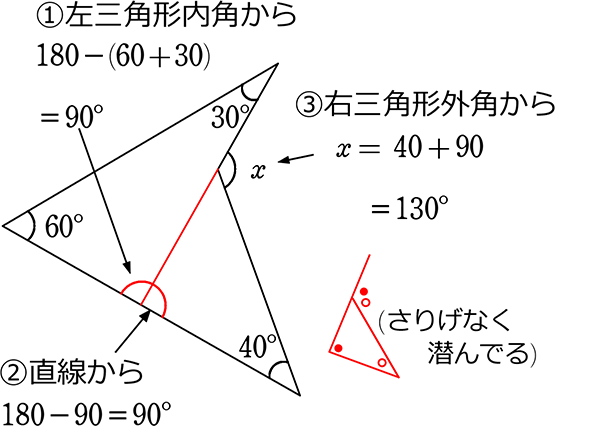
A. x = 130°
〔補助線2〕
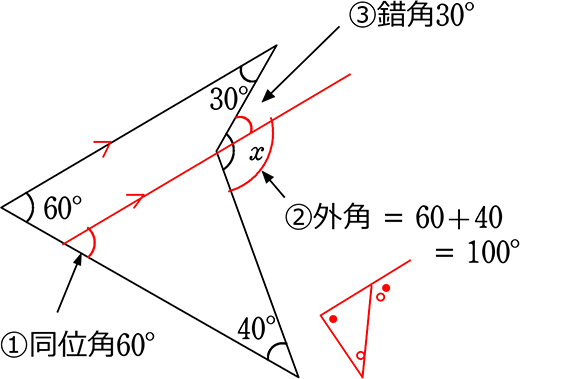
∴ x = ②+③ = 130°
A. x = 130°
〔補助線3〕
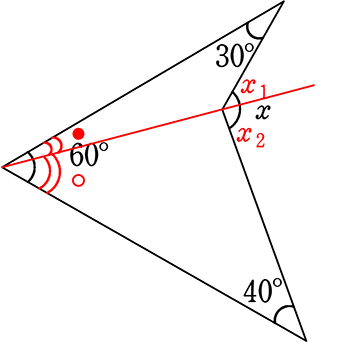
x1 = 30°+●
x2 = 40°+〇
∴ x = x1+x2
= 30°+40°+●+〇
= 30°+40°+60° = 130°
ちなみに、四角形の内角の和は360°でしたね
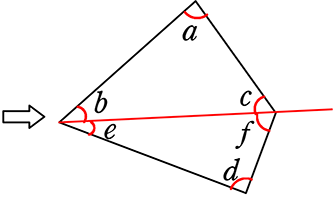
∵ 四角形の内角の和 = a+b+c+d+e+f = 2つの三角形の内角の和(a+b+c)+(d+e+f) = 180°×2 = 360°
同様に、


上の
以上より

【 四角形の外側の角 】
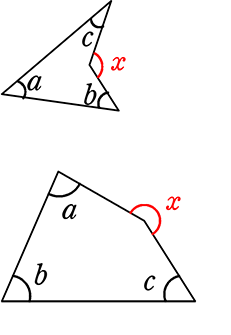
※四角形の『外

四角形の『外角』は
t やs の場所ですね
※注) 実は中学では、凹四角形を四角形として扱いませんので、
ちゃんと補助線を引いてxのような角度を求めてくださいね! 答のみなら… 公式で!
【 三角形の外角の和 】
360° です!
実は、三角形であろうと、四角形であろうと、n角形であろうと
外角の和は全て『360°』です! 後の「多角形と角」でお話しますね。
鋭角三角形、鈍角三角形、直角三角形
・
・直 角とは … 90°の角
・
ちなみに
・
(よって、0°や181°、360°などは上のどれにも当てはまりませんね
→ 固有名詞があるのは180°まで)
・鋭角三角形とは …1番大きい角が 90°未満
・直角三角形とは …1番大きい角が 90°
・鈍角三角形とは …1番大きい角が 90°超
ex) 1番大きい角が・・・

(鋭角三角形)

(直角三角形)

(鈍角三角形)
三角形の内角の和は180°ですので、
90°が2か所存在することは不可能ですね
90°が2か所あれば、それは四角形以上ですね
たとえば、タテの2線を、上に上に延ばしていくと…

いずれ交わる
= 三角形になれる
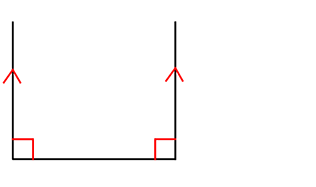
交わらない(平行)
= 四角形以上
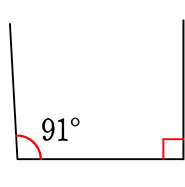
上に延ばす限りは
交わらない
= 四角形以上
割合的に見るならば、



・鈍角三角形 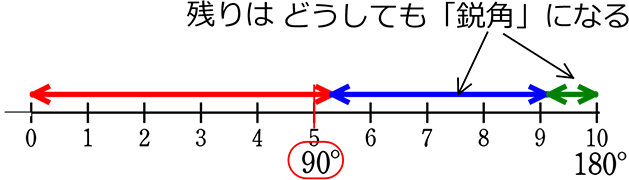
・直角三角形 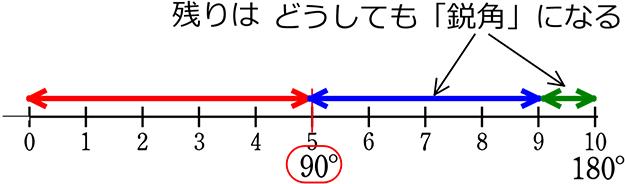
・鋭角三角形 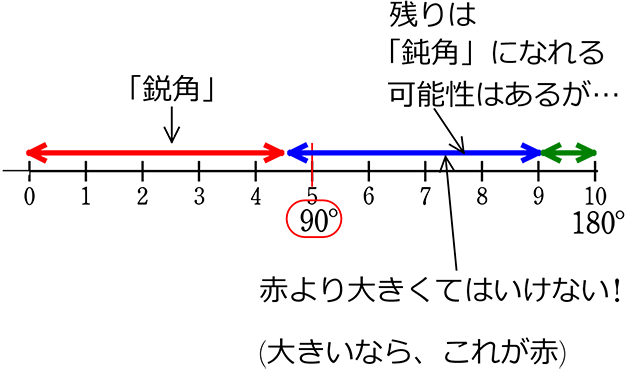
対角・対辺
四角形の場合と三角形の場合で違いますね
・四角形の場合、対応するのは、
角 ⇔ 角
辺 ⇔ 辺 ですね
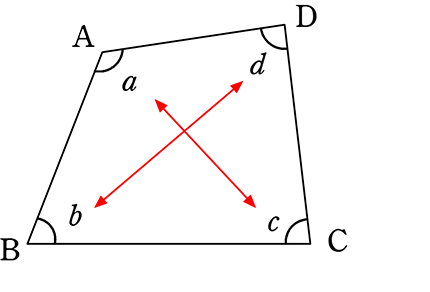
例えば
∠aの対角は、∠c
∠bの対角は、∠d
∠cの対角は、∠a
∠dの対角は、∠b
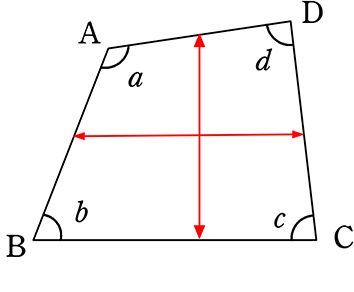
例えば
辺ABの対辺は、辺DC
辺BCの対辺は、辺AD
辺CDの対辺は、辺AB
辺ADの対辺は、辺BC
・三角形の場合、対応するのは・・・
角 ⇔ 辺
辺 ⇔ 角 ですね
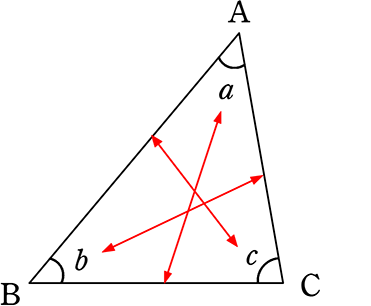
例えば、
∠aの対辺は、辺BC
∠bの対辺は、辺AC
∠cの対辺は、辺AB
辺ABの対角は、∠c
辺BCの対角は、∠a
辺ACの対角は、∠b
ちなみに、三角形の「辺」に名前を付けたいとき、
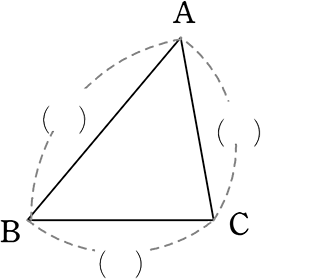
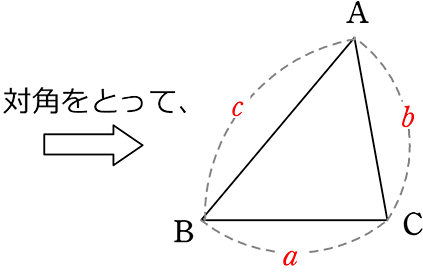
とすることが
多いですね!
もちろん、x, y, z, などを付けても、辺ABのままでもOKです
三角形の対辺と対角の関係
対辺の長さの順位は、対角の大きさの順位に対応しますね!

図では
∠C > ∠A > ∠B
となっていますので、
c > a > b
となりますね!
直角三角形において、「直角」に対する「対辺」を
特別に、『斜辺』といいますね!

自然1番長い辺が「斜辺」になりますね!
・「直角の向かい側」 で理解してもよいですし
・「直角三角形なら1番長い辺」 で理解してもよいですね!
他の鋭角・鈍角三角形で「斜辺」という固有名詞はありませんね
辺AB、辺〇〇、…などと言うしかありませんね

斜辺
『斜辺』は勉強が進むにつれて、結構重要になってきます
そこで、斜辺のイメージを一つ
『斜辺』を「釣り竿」、『高さ』を「釣り糸」、
『底辺』を「海 (自分から浮きまでの距離)」とするとよいですね!
それでは、釣り竿を自分中心に回してみましょう
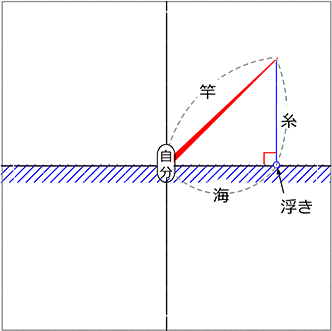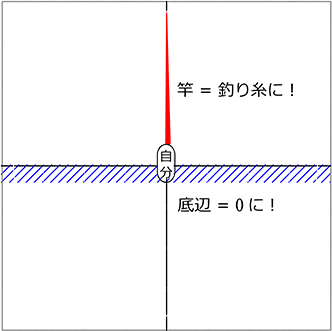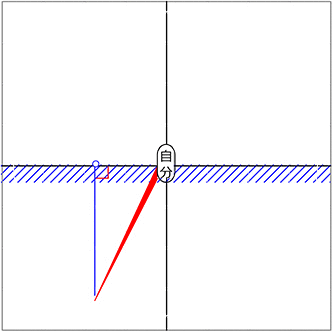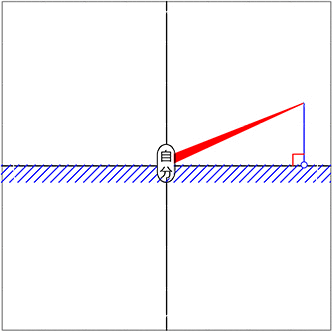
ということで、斜辺(釣り竿)を回すと
「全ての直角三角形を網羅(もうら)するということですね!!」
(釣り竿の角度だけで「形」が決まる)
「浮きの動きが面白いですね!」
「海中に竿を沈めるのは無理がありますが、イメージですので!」
③ 平行線と面積 (頂点の平行移動)

面積は、
△pAB も △p’AB も △p’’AB も △p’’’AB も 同じですね!
なぜなら、
三角形の面積 = \(\large{\frac{1}{2}}\)×底辺×高さ
ですね
形は変われど、「\(\large{\frac{1}{2}}\) 」も「底辺」も「高さ」も変わっていませんものね!
三角形の「頂点」が、「底辺」に「平行に移動」しても面積は変わらない
と、まとめることができますね
当たり前と言えば当たり前なのですが、
「問題」で利用すると、つい見落としがちになる単元ですね!


イ 多角形の角の性質
多角形の内角の総和
四角形の内角の総和は、「360°」ですね!
では、なぜ360°なのでしょうか?
それは、「四角形が三角形2つからできている」からですね!
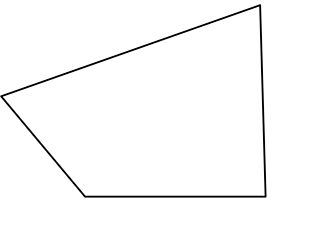

三角形2つからできているのがわかりますね
そして、角度マークを書き足すと、
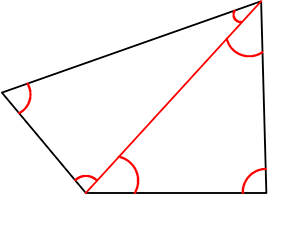 ですね!
ですね!
適当な数字で確認してみると…
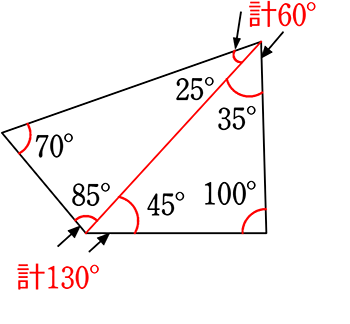
・70°+計130°+100°+計60° = 360°
・左の三角形の内角+右の三角形の内角
= 180°+180° = 360°
よって、「四角形の内角の総和」は、2×180° = 360°
ということがわかりましたね!
では、5角形、6角形、・・・ n角形ではどうでしょうか
(5角形)
= 3・三角形
→ 3・180°
= 540°
(6角形)
= 4・三角形
→ 4・180°
= 720°
(n角形)
=(n-2)・三角形
→ (n-2)・180°

多角形の内角の総和
n角形の内角の
ですが、実は、使う場面があまりない公式ですので、
→ 三角形の数×180°
なんだったら、
→ 三角形の数! でもいいですね!
三角形の個数は?となってしまったら、
1番簡単な「四角形」で思い出せばよいですね

「2個! 」
「四角で2、ということは、 → n角なら n-2個か!」
多角形の外角の総和
多角形の外角の総和は、「三角形の外角の和」で少し触れましたが、
何角形であろうと「360°」になります
例えば、「五角形」で見てみますね
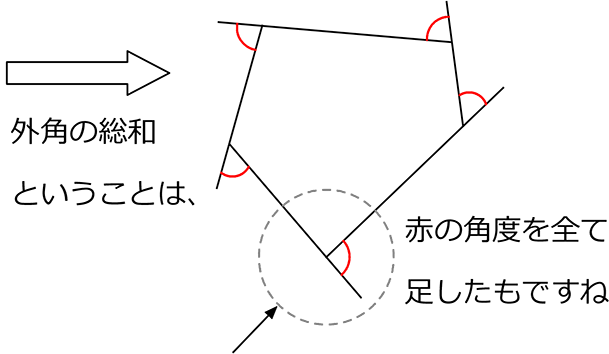
解りやすくするために、1つの角だけを取り出しますね
外角 = 180°-その内角 でしたね、これを図で表現すると、
 ですね
ですね
「総和」ということは、これの「全部バージョン」ということですね!


麦わら帽子の個数 = 5個 (=5角形の5)
=180°×5 = 900°
後は、900°から先ほど学んだ「多角形の内角の総和」を引けば
= 「多角形の
900°- 五角形の内角の総和
= 900°-(5-2)・180°
= 900°-540°
= 360°(本当にやっぱり360°ですね)
これを公式風に表現すると、
n角形の外角の総和
= \(\underbrace{ n・180° }_{ 総麦わら }\)-\(\underbrace{ (n-2)・180° }_{ 総内角 }\)
= 180°{ (n-(n-2) } …180°でくくった
= 180°(2) …nが消えた
= 360° … = nに関係なく360°!

多角形の外角の総和
n角形の外角の総和
= 総麦わら帽子 - 総内角
- 総内角
= 結局 360° で十分ですね!


多角形の対角線の本数
三角形では、対角線は1本も引けませんね
→ 0本
四角形では
→ 2本

五角形では
→ 5本

六角形では
→ 9本
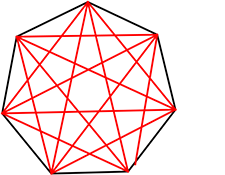
七角形では
→ 14本
では n角形の対角線の本数は?
数字からは 規則性が見つけにくいですが、図をよく見ると・・・
ありますね、規則性が・・・
① どの図も 1つの頂点から、「自分」と「両隣」の3本が引けませんね
ということで、一つの頂点から引ける対角線は、
(n角形-3) 本
② 当然、n角形の頂点の数は
n 個
よって、 (n-3)・(n頂点数) 本?
違いますね 例えば

「AからCへ」と「CからAへ」は
ダブっていますね
1本につき、2回数えていますので…
③ ダブルカウント解消のため、「2」で割ります

・ n角形の1つの頂点から出せる対角線の本数 = (n-3) 本
(意味)
{線を引こうとする頂点数-(自分+両隣)}
・ n角形の対角線の本数 = \(\large{\frac{(n-3)n}{2}}\) 本
(意味)
\(\large{\frac{(自分と両隣を除いた本数)(頂点数)}{2かぶり}}\)
《 例 》
(1) 八角形の対角線の本数は?
\(\large{\frac{(8-3)・8}{2}}\) = 20本 //
(2) 八角形のある1つの頂点から引ける対角線の本数は?
8-3 = 5本 //
(3) 八角形の1つの頂点から引ける対角線によってできる三角形の数は?
・全頂点の数-2 = 8-2 = 6個 //
(・1つの頂点から引ける対角線の本数+1 = 5+1 = 6個 //)
まとめ
・ n角形の頂点の数 = n 個 (当然ですね)
・ n角形の1つの頂点から引ける対角線の本数 = n-3 本
・ n角形の1つの頂点から引ける対角線によってできる三角形の数
= n-2 個  (= 1つの頂点から引ける対角線の本数+1)
(= 1つの頂点から引ける対角線の本数+1)
・ n角形の対角線の本数 = \(\large{\frac{(n-3)n}{2}}\) 本
お疲れ様でした !!
その他の問題は、「問題集」で !!