| 中学1年生課程へ | 中学2年生 | 中学3年生課程へ |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平面図形と平行線の性質 | (2) 図形の合同・図形の性質 |
| ア | 証明の必要性と意味及びその方法 |
|---|---|
| ・ | 「証明」の必要性 |
| ・ | 「証明」のイメージ |
| イ | 三角形の合同条件 |
| ① | 合同とは |
| ② | 三角形の合同条件 |
| ・ | 三角形の合同条件のまとめ |
| ・ | 三角形の合同条件、他にもある? |
| ③ | 仮定と結論 |
| ウ | 三角形や平行四辺形の性質の論証 |
| ① | 二等辺三角形 |
| ・ | 必要条件・十分条件・反例 とは |
| ・ | 定義、定理、性質、特徴、違いは? |
| ・ | 二等辺三角形の条件 のまとめ |
| ② | 正三角形 |
| ・ | 正三角形の条件 のまとめ |
| ③ | 直角三角形の合同条件 |
| ・ | 直角三角形の合同条件 のまとめ |
| ・ | 直角三角形の考え方 |
| ④ | 平行四辺形の条件 |
| ・ | 平行四辺形の条件の証明 |
| ・ | 平行四辺形の条件の逆の証明 |
| ・ | 平行四辺形の条件 のまとめ |
| ⑤ | 特別な平行四辺形 |
| (1) | 長方形の条件 |
| (2) | ひし形の条件 |
| (3) | 正方形の条件 |
| ・ | 他の平行四辺形の条件のまとめ |
| ・ | 典型例題 正三角形の条件+三角形の合同条件 |
図形の合同・図形の性質
ア 証明の必要性と意味及びその方法
「証明」・・・難しいイメージがあるかもしれませんが・・・
大丈夫です! 面白くなってきます!
「証明」の必要性
『証明』・・・数学だけでなく、実社会でも普通によく聞く言葉ですね!
読んで字のごとく、「証拠を示して→明らかにすること」ですね!
(「判定フィルター」が、「その事実」が「証拠になる」か「証拠にならない」か「判定」しますね)
この流れがないと、人は納得できないし、納得させられないですね!
例えば、クラスの給食費がなくなった → いきなり犯人扱いされた。
納得できないですね!
「証拠は?」となりますね。
A「証拠は・・・放課後1人で教室でゴソゴソしていたのを見た」
→判定フィルター(証拠には・・・・・・ならない!) →無罪
B「証拠は・・・防犯ビデオに現場が映っている」
→判定フィルター(証拠に・・・・・・なる!) →有罪
証明とは
「ある事実」 →「判定フィルター」 →「判定」
という「一連の流れ」ですね!
そして、人に納得してもらうためには、この一連の流れ、
すなわち、「証明」が必要!ということになりますね!
「証明」のイメージ
それでは、「証明」の方法(流れ)を、図を使ってイメージ化してみますね
イメージで十分ですので!
【 刑事事件の証明のイメージ】


ここで、A検事が「殺人罪」を証明しようとしているとします


B検事が同じ事案を証明しました

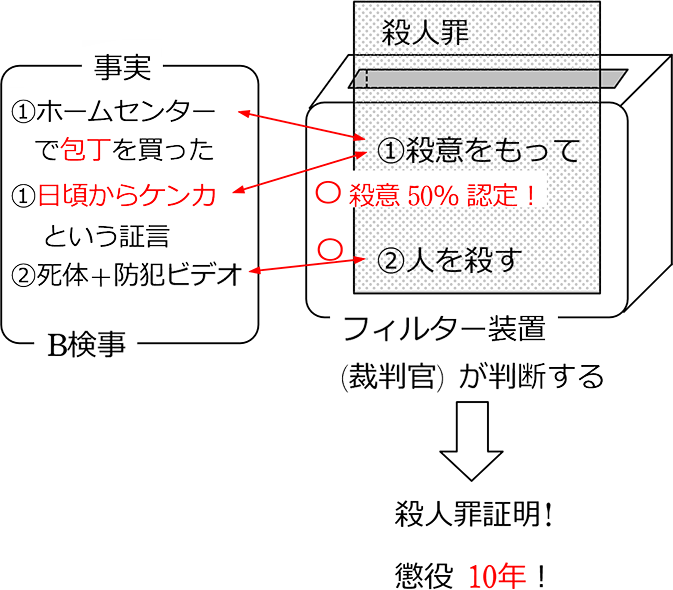
C検事が証明しました
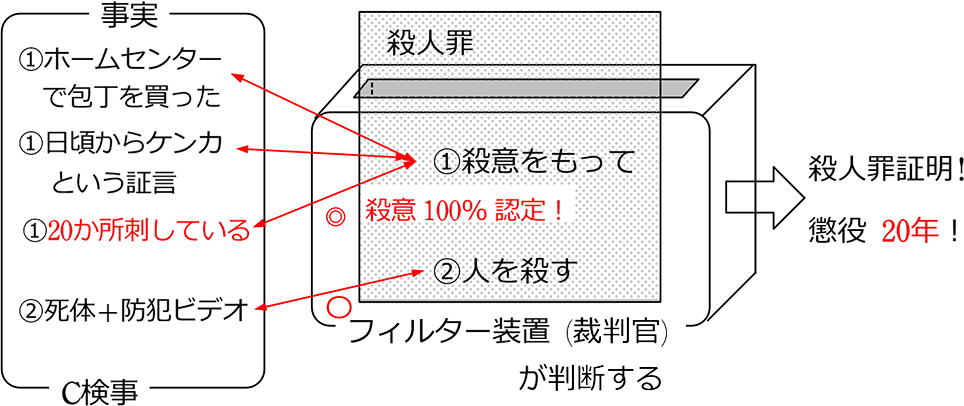
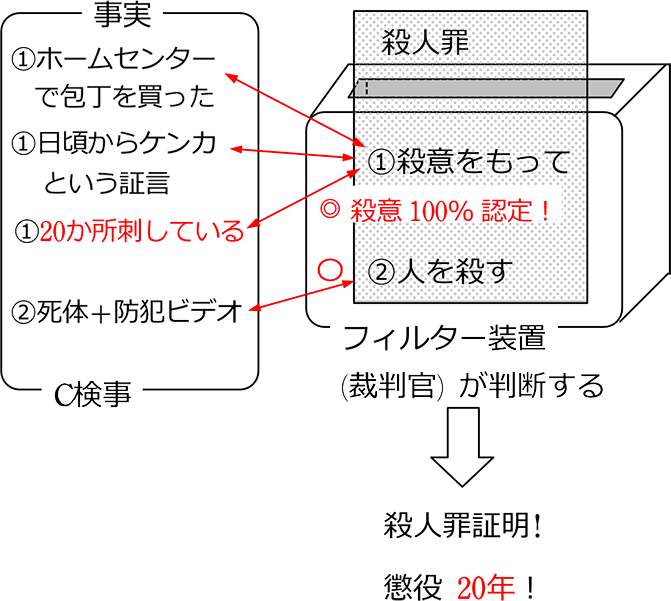
【 数学の証明のイメージ 】


では、A君がある図形を「正三角形である」と証明しようとしています

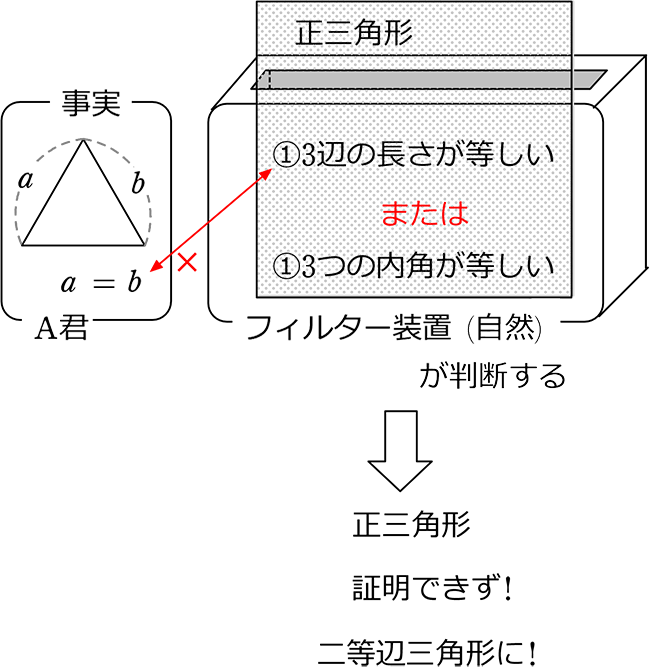
B君が同じ事案を証明しました


C君が同じ事案を証明しました

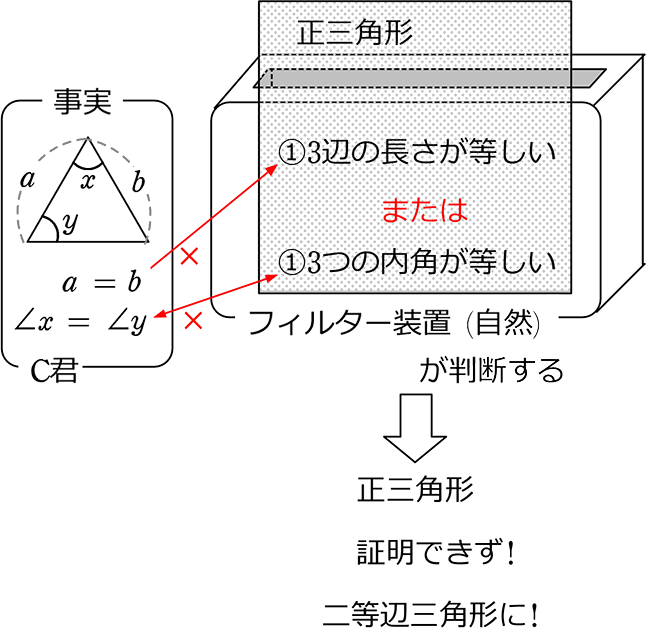
D君が同じ事案を証明しました
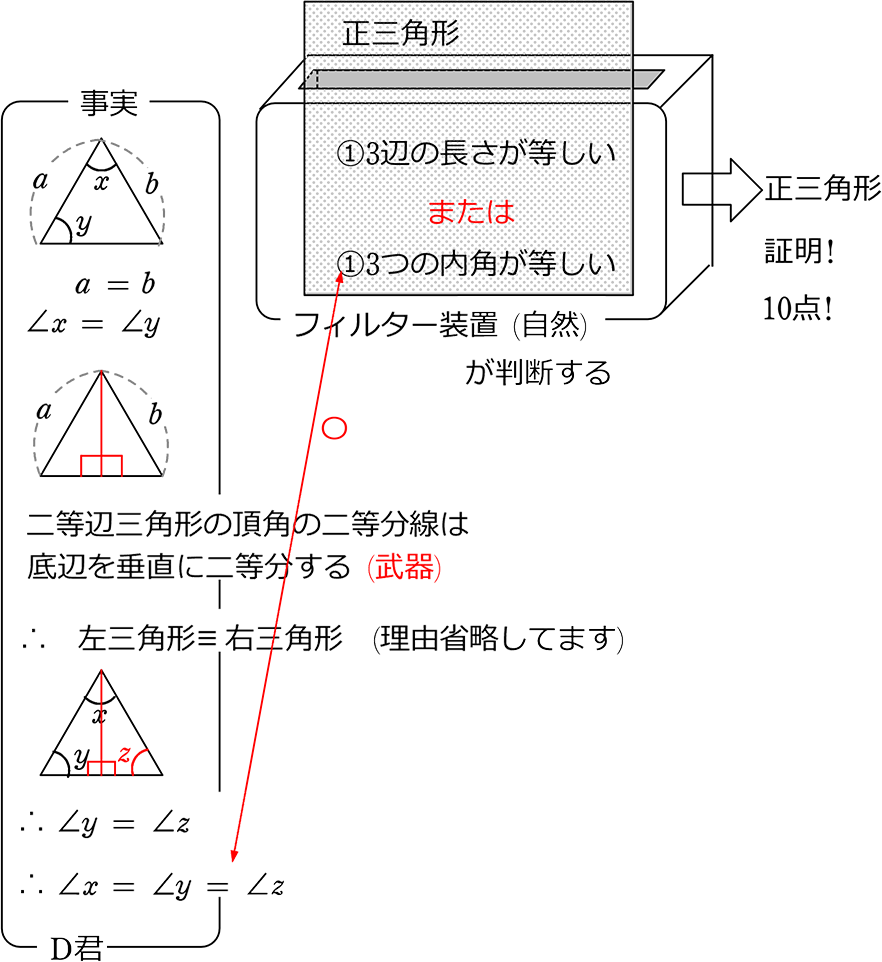
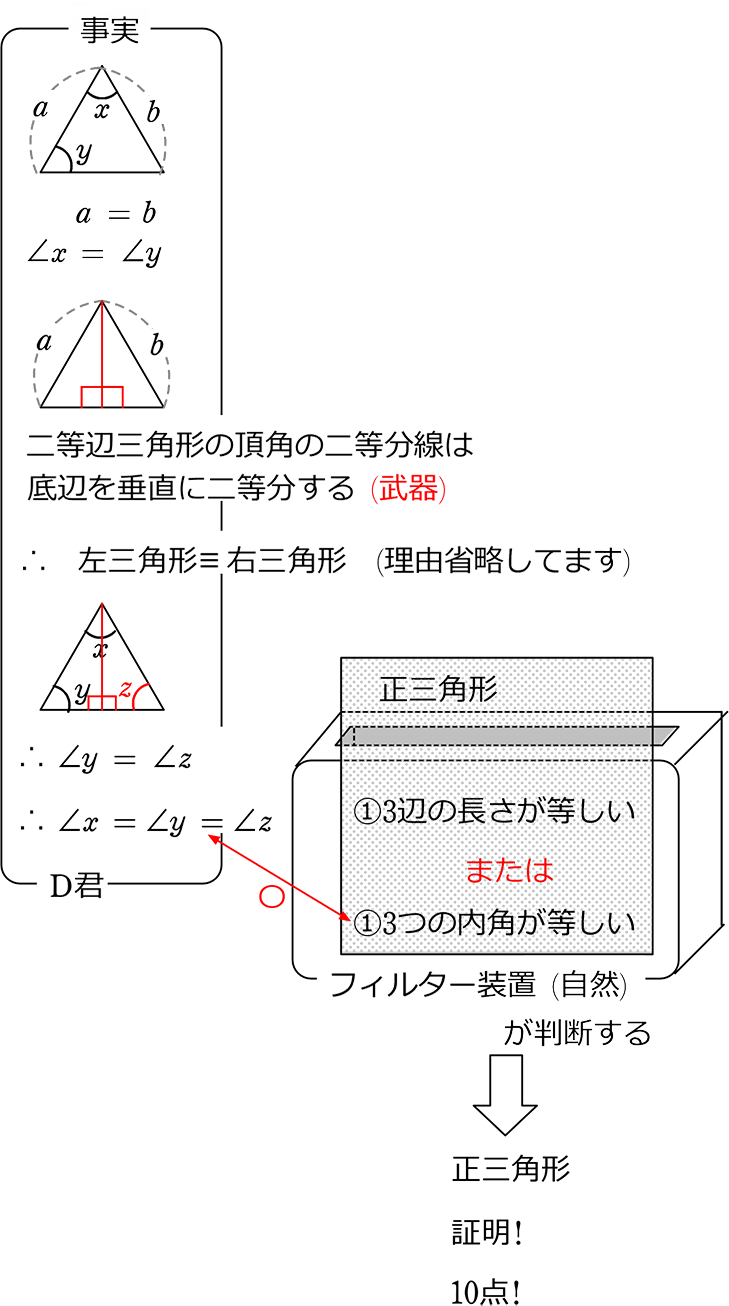
これらのイメージ例から分かることを簡単にまとめますと、
〔要点〕
●フィルターに適した「事実」だけが、『証拠』になれる、適してない「事実」は「ただの事実」
●各フィルターの「要件」(数学では「条件」)を知っていないと、「証拠」と「ただの事実」の区別ができない
●「武器」があれば、「事実」から「新しい事実」を導くことができる
〔違い〕
◎法律は「人の気持ち」の証明があるが、数学にはない
→数学の方が明確!
◎法律は「人(裁判官)」が判断するが、数学は「自然の摂理(=神)」が判断する
→数学は、「判断」に間違いがない (対して「人」は間違えるもの)
→数学の方が明確!
◎法律は「要件」を条文から考え出すが、数学は「要件」を明記してくれている
→数学の方が明確!
〔目標〕
〇各フィルター(各図形)の「要件」の理解。図形は自然の摂理ですので、ほぼ当たり前と思う「要件」ばかりですのでご安心ください
〇「武器」を増やす、使いこなす (新事実発見のために!)
問題の中で、「武器(=一言で済む)」として使ってよいのか、「やはりそれにも証明がいるのか」の線引きが
「時期」によって異なるのが、1番の問題といえますね
ここでは、できる限り「受験時には武器」「定期テストではその武器自体の証明も必要かも」なども指摘していきますね
長くなってしまいましたが、本題に入っていきますね
イ 三角形の合同条件
① 合同とは
合同とは、
『同じ形 で 同じ大きさ』ですね!
それだけです!
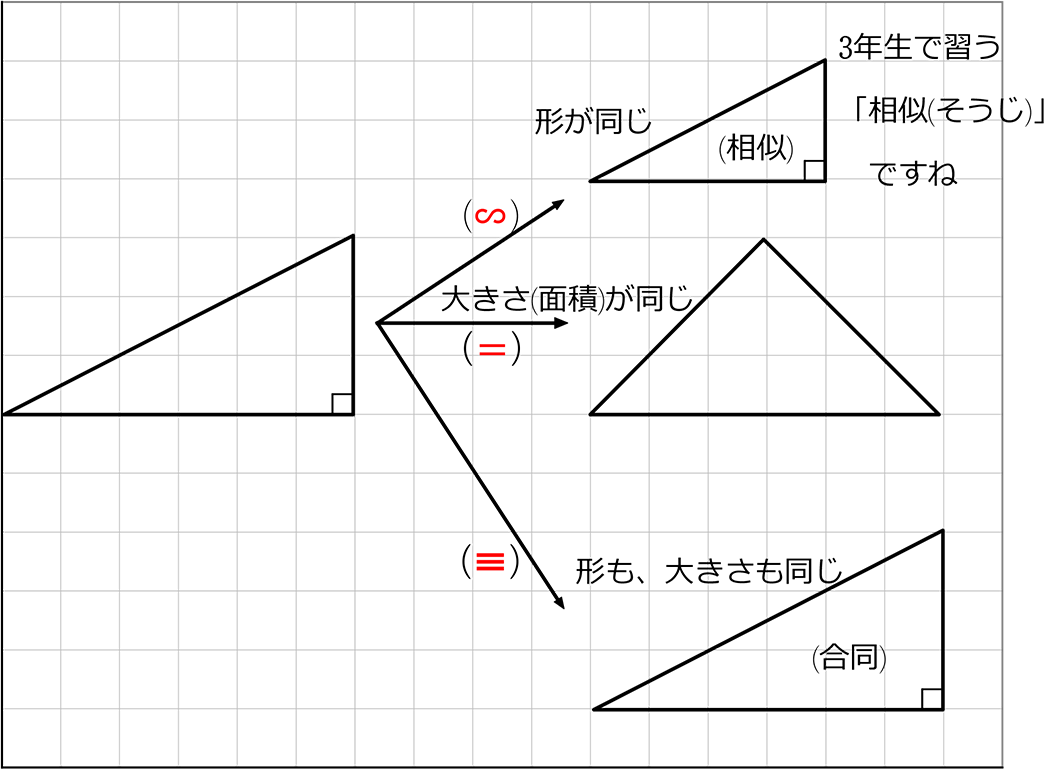
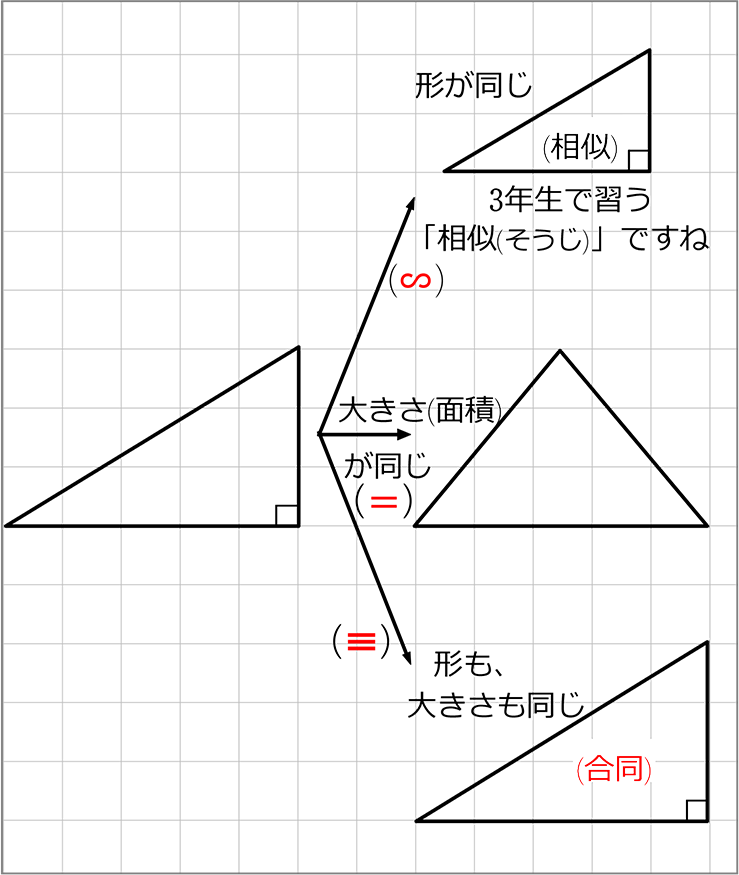
「合同」ということは、

ピッタリ1つに重なるということですね
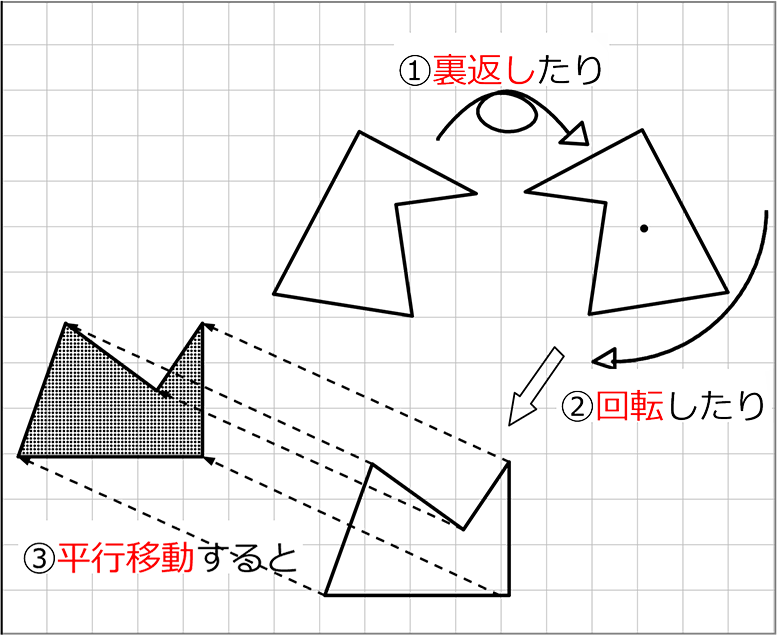
重ねるために使える作用は、
・使える作用 → 「裏返し」「回転」 「平行移動」
・使えない作用 → 「拡大・縮小」「変形」
重ねると一致する「点」「辺」「角」を
「対応する点」「対応する辺」「対応する角」とい言いますね
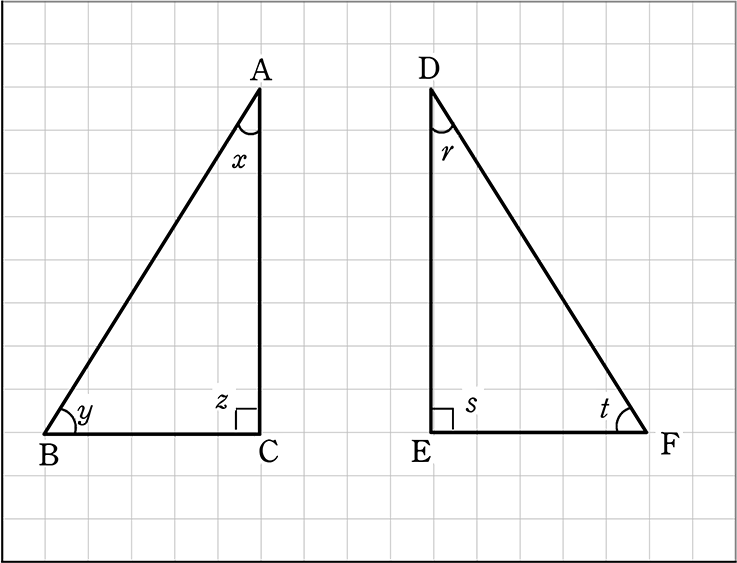

ex.
点Bに対応する点は 点F
点Eに対応する点は 点C
辺ABに対応する辺は 辺DF (アルファベット順に、辺FDでもOKです)
∠tに対応する角は ∠y
そして、△ABC と △DFEが「合同」という意味の記号が
「 ≡ 」 ですね!
ex.
△ABC ≡ △DFE 〇 →対応する点の順番がちゃんと一致
△ABC ≡ △DEF × → 対応する点の順番が一致していない
一致していないと…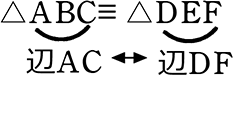 「対応」が おかしくなってしまいますね!
「対応」が おかしくなってしまいますね!
② 三角形の合同条件
※以後は「要件」という言葉を、数学に合わせて「条件」と言いますね
基本、「合同」の条件は、
① 全ての辺の長さが同じ、 かつ
② 全ての角の大きさが同じ
という事実を集められれば、「証明」ですね!
例えば、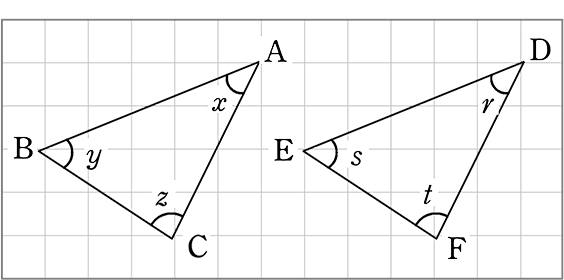
○○なので、 辺AB = 辺DE …①
○○なので、 辺BC = 辺EF …②
○○なので、 辺CA = 辺FD …③
○○なので、 ∠x = ∠r …④
○○なので、 ∠y = ∠s …⑤
○○なので、 ∠z = ∠t …⑥
∴ ①②③④⑤⑥より
「全ての辺の長さが等しく、
全ての角の大きさが等しい」ので、 ←「条件」ですね
△ABC
ではありますがっ !!
「三角形」はある程度の段階で、『形』『大きさ』が決まってしまいますね。(「決まる」とは)
日本語で例えるなら、「皆(みな)まで言うな!」「あとは一本道」「自動的に決まる」
将棋で例えるなら、『詰み』の形で終了! 『玉まで取る』ところまでしないですね
すなわち、
「決まった後の作業」は、言葉は悪いですが『無駄』ということですね
そして、どこまですれば『詰み』なのか、ちゃんと「明記」してくれているのが数学の優しいところですね!
そして、それが…「三角形が1つに決まる条件」ということであり、
2つの三角形が、同じ条件で決まれば「合同」ということですね!
cf. 「決まる」+「同じ条件で」=「合同条件」
三角形はどこまですれば「決まる」かを、イメージだけしておきましょう
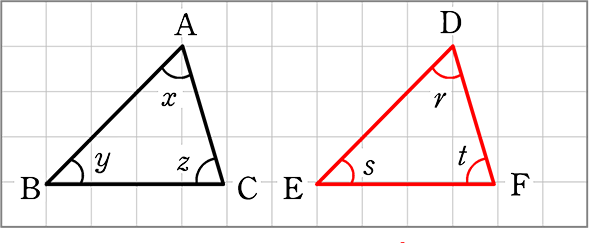
△ABCと△DEFの△ABCについて
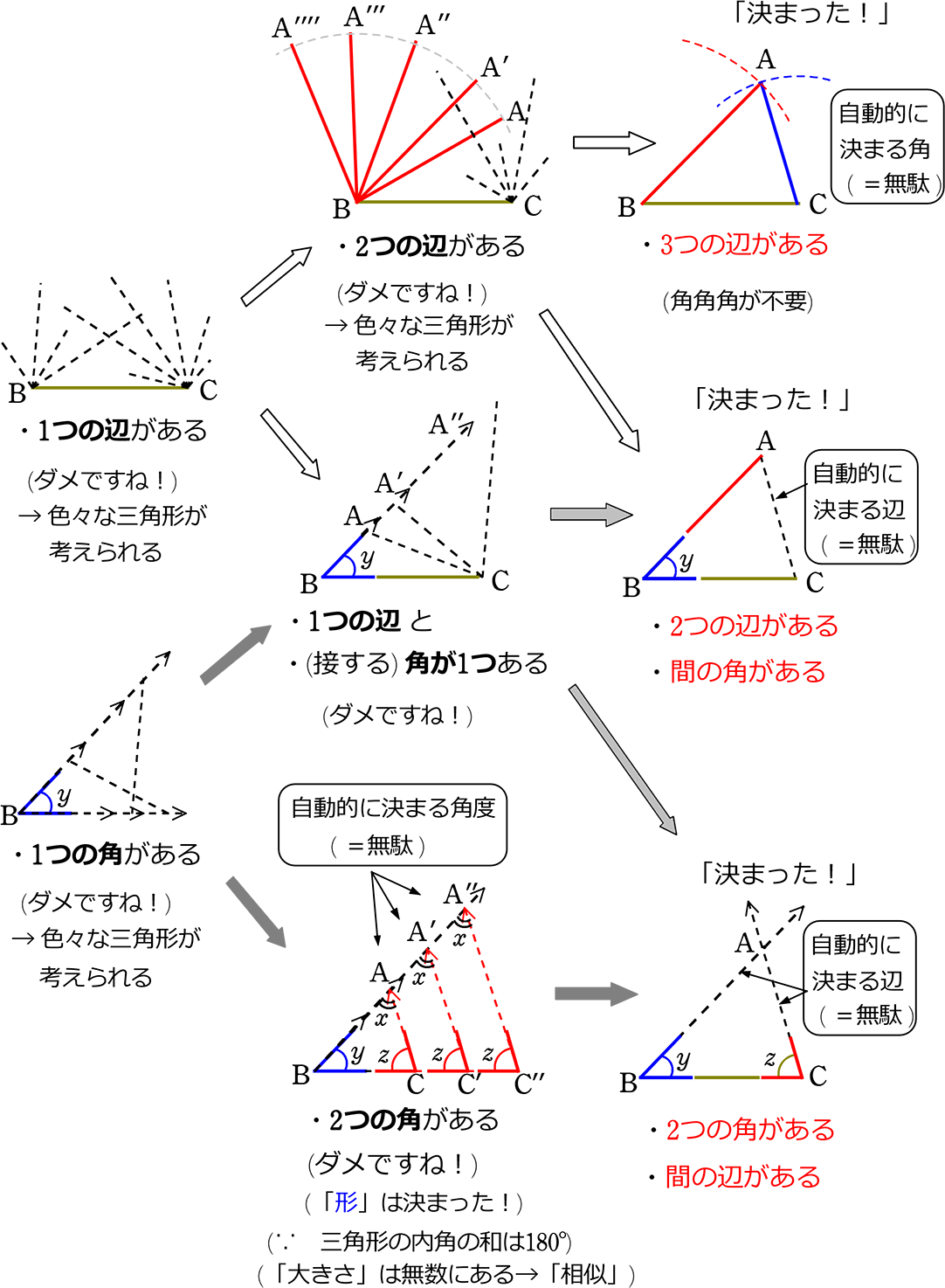
以上をまとめれば、『三角形の合同条件』ですね!
その前に、少し気づいた点があると思います!
(1) 全 辺辺辺角角角のうち、「3つの部分」だけでよい(形、大きさが決まる)
ex.
①辺・辺・辺 ②辺・辺・角 ③辺・角・角
cf.
「3つの部分」が同じということで、
「≡」マークは3本線?
はたまた、面積が同じなら「=(イコール)」
面積だけでなく形まで同じなので「≡」3本線?
(2) 「辺」で「大きさ」が、「決まる」
「角」で「形」が、「決まる」
よって、大きさを決める「辺」が1つは入っていないといけない
ex. 辺・角・角

(2つの) 三角形の合同条件 (フィルター集①)
(1)
(図のイメージ) 
(3イメージ)
辺・辺・辺
(一言条件)
「3辺相等」
(言葉条件)
「3組の辺
がそれぞれ等しい」
(2)
(図のイメージ) 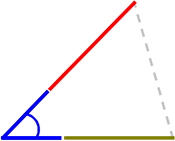
(3イメージ)
辺・辺・角
(一言条件)
「2辺
夾:~にはさまれた
(言葉条件)
「2組の辺とその間の角
がそれぞれ等しい」
(3)
(図のイメージ) 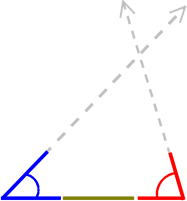
(3イメージ)
辺・角・角
(一言条件)
「2角
(言葉条件)
「1組の辺とその両端の角
がそれぞれ等しい」
図のイメージを憶えてしまえば、
図を思い浮かべながら、「言葉」が出てきますね 図の方が大切 !!

三角形の合同条件、他にもある?
上の「3つの合同条件」の他に、「決まる!」場面はあるのでは?
① こちらの「3部分」でも「決まる!」
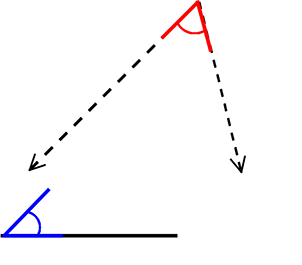
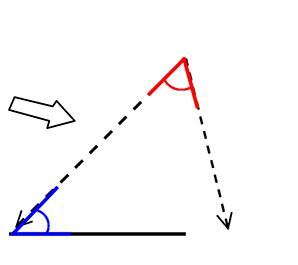
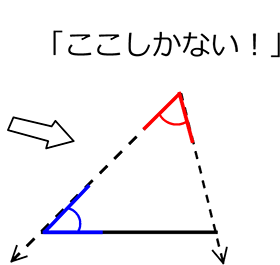
・1辺が同じ
・どこか、2角が同じ (辺の両端でなくてよい?)
しかし、2つの角が解れば、残りの角xも分かる
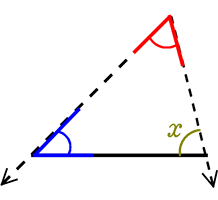
x = 180°-赤-青
ですので、
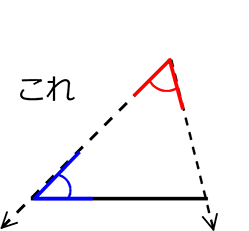
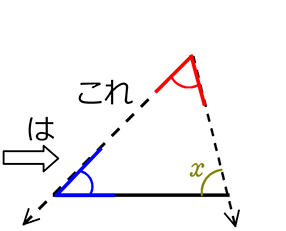
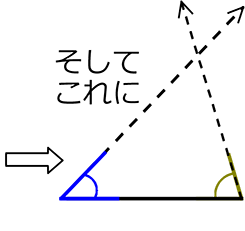
「2角夾辺」に
組み込んで
しまいましょう
「条件」は「同じことである」を除いていきたいですものね
② 次に、こちらの「3部分」は・・・? (斧を振りおろす感じで)

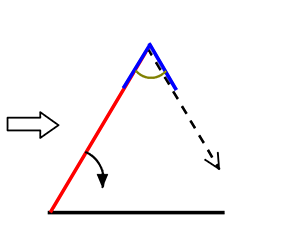
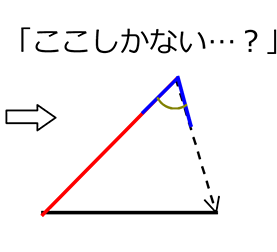
・2辺が同じ
・どこか、1角が同じ(間の角でなくてよい?)
→ ダメですね !!

(折り返せる
→二等辺三角形)

「ここにもあるということ」
「1つに決まらず!」
ただし、「赤<黒」や「青の角が直角」な場合はOKですね!
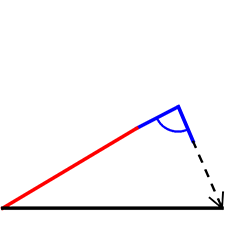

黒>赤のとき、黒を折り返すとただの反転 → 形に変化はないということ → ここしかない、1つに決まる
黒>赤に含まれる直角三角形も同様に、折り返してもただの反転ということですね
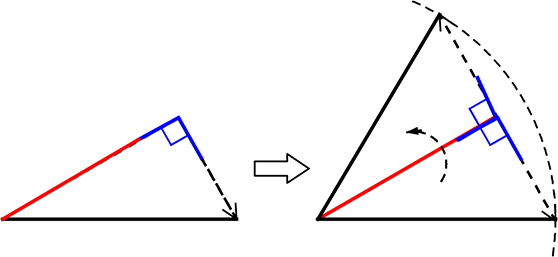
「ただの反転だ!」 |
「黒>赤の場合は間の角でなくてもよい」では、
「条件」としてシンプルさに欠けますね!
除外ですね!(合同条件④としている国もあるらしいですが)
「やはり、間の角で!」
というわけで
「三角形の合同条件」はやはり
① 3辺 相等
② 2辺夾角 相等
③ 2角夾辺 相等
でお願いいたします
《 例 》
図のようなとき、△OABと△ODCが合同であることを証明しましょう
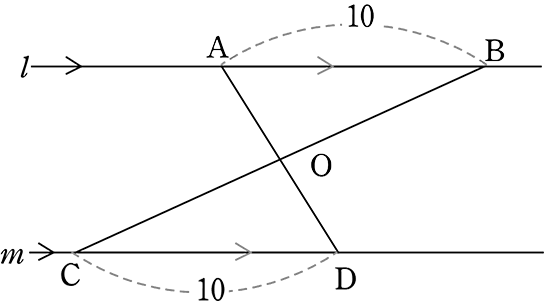
自分の持っている「武器」で、すぐに分かる「新事実」を書き込んでみると…
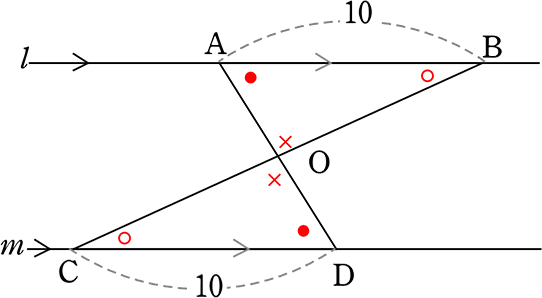
△OABと△ODCにおいて ←書き出しの「決まり文句」
AB = CD (図より) …① ←既成事実
l//m より ←既成前提事実
∠BAD = ∠CDA ←新事実 (錯角) ←武器名…②
∠ABC = ∠DCB ←新事実 (錯角) ←武器名…③
①②③より
一組の辺と、その両端の角が、それぞれ等しい ←三角形の合同条件③ので
△OAB ≡ △ODC //
ちなみに注釈を除くと…
△OABと△ODCにおいて
AB = CD (図より) …①
l//m より
∠BAD = ∠CDA (錯角) …②
∠ABC = ∠DCB (錯角) …③
①②③より
一組の辺と、その両端の角が、それぞれ等しい ので
△OAB ≡ △ODC //
書き方は「ほぼ自由」です!
例えば、
平行線の錯角は等しいので
∠ BAD = ∠ CDA …②
のように日本語を多用してみたり…
上のように、(錯角)と一言で済ませたり…
「表現方法」は自由です
「フィルターに適した事実」 = 「証拠」 を示せばよいだけですね
「既成事実」には「どこに書いてあったか」を添えて下さいね!
ex. (仮定より) (条件より) (図より) など
「新事実」には「使った武器の名前」を添えてくださいね
ex. (錯角) (対頂角) など
問題集の解答例は、解答例を作った人の書式です。違って当然です!
また、「フィルター」内に「複数の条件(「または」でつながるもの)」があるように、
使う「条件」も人により当然異なることがありますが、〇マルですね!
③ 仮定と結論
図形の場面では「仮定と結論」はそれほど気にすることはありませんね!
例えば、次のような問題があったとします
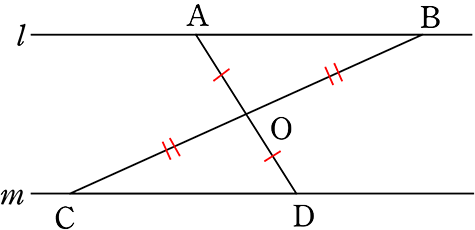
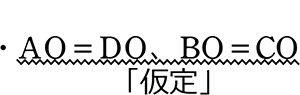 ならば
ならば 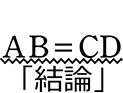 であるとを証明しましょう
であるとを証明しましょう
「~ならば~である」
という形の場合、
「ならば」の部分を「仮定」と言います
「である」の部分を「結論」と言います
ただそれだけですね
よって、証明では「仮定」の部分を ただの「既成事実」として使用してOKです
(「辺の長さ」や「角度」が「同じ」という証明は、
「その辺」や「その角」を含む「三角形」の合同を証明すれば
「その辺」や「その角」は同じということがいえますね)
ex.
AO = DO (仮定より)
BO = CO (仮定より)
∠AOB = ∠DOC (対頂角)
2組の辺とその間の角がそれぞれ等しい ので
∴ △OAB ≡ △ODC
∴ AB = CD //
証拠が離れている場合は …① …②など番号付けをして
最後に①②③より~
と証明したりしますが
各証拠が近いときは番号付けをしなくても十分相手に伝わりますね!
ここで・・・問題レベルが上がってくると、「ならば である」を使わず
「のとき」、「である」、と言う場合もありますね、例えば上の問題では、
 のとき
のとき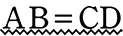 を証明しましょう
を証明しましょう である。
である。 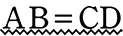 を証明しましょう
を証明しましょう
このような場合の証明では
ex.
AO = DO (条件より)
BO = CO (条件より)
・
・
・
と言ってもよいですね
もちろん、結局同じ意味なので
(仮定より) と言ってもかまいませんね!
ウ 三角形や平行四辺形の性質の論証
ここからは、しばらく図形の「合同条件」ではなく、
図形の「成立条件」のお話ですね
| ・合同条件 | … | 2つ以上の図形が、『同じ大きさ、同じ形』であるというための条件 |
| ・成立条件 | … | ある1つの図形が、『○○角形』(二等辺三角形や平行四辺形だ)であるというための条件 |
① 二等辺三角形
まずは各部名称から、
「特徴があれば名前をつけたくなる」という人間のサガですね
二等辺三角形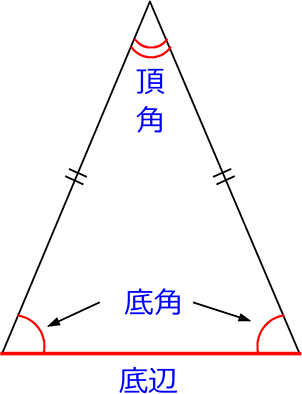
 (武器)
(武器)
二等辺三角形
「定義」はこれだけですね!
そして、実は、角が等しいという意味のちょんちょんマーク ( 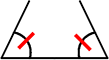 )はまだつけられないのです…
)はまだつけられないのです…
では、それを証明していきましょう!
《 例 1 》
△ABCが、AB = ACならば(二等辺三角形ならば)、 ∠B = ∠Cである ことを証明しましょう

(考え方)
∠Bを含む三角形と∠Cを含む三角形が、「合同」であることを証明すれば、
自然∠B = ∠Cといえますね
では、どういった「補助線」を引いて2つの三角形を作りましょうか
(証明)
∠Aの二等分線とBC(辺BC)の交点をDとする (自分で勝手に設定OK)
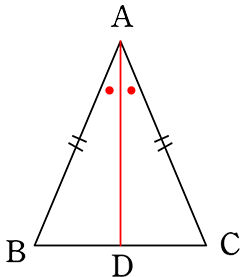
△ABDと△ACDにおいて ←決まり文句
AB = AC (仮定より)
AD = AD (共通) ←「同じもの」を使っているという意味
∠BAD = ∠CAD (∠Aの二等分線より) ←自分でそう設定していた
∴ 二組の辺と その間の角が それぞれ等しい から
△ABD ≡ △ACD
∴ ∠B = ∠C
「証明」しましたので、今後は『定理』となります
(仮定理) (仮武器)
二等辺三角形
「定理」は、今後「証明」せずに「武器」になります
ex. ∠B = ∠C (二等辺三角形より)
ですが、「習い始めの頃」の定期テストでは「定理」そのものの証明がありますね!
教科書で「証明付きの定理」は、証明できるようにしましょうね!
ここで、上の定理の「
「\(\Leftarrow\)」左向きも証明できれば、「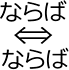 」両矢印となって、より「鋭い武器」になりますね!
」両矢印となって、より「鋭い武器」になりますね!
では、
《例 2 》
底角が等しいならば、二等辺三角形であることを証明しましょう
→実は、まだ「二等辺三角形」であると証明していないのですから、
二等辺三角形の特徴の固有名詞「底角」という単語を使えませんので
正確には…
《 例 2’ 》
2つの角が等しい三角形は、二等辺三角形であることを証明しましょう
ですね!
(証明)
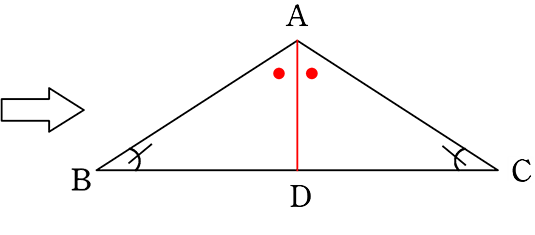
∠Aの二等分線とBC(辺BC)の交点をDとする
△ABDと△ACDにおいて
∠B = ∠C (仮定より) …①
∠BAD = ∠CAD (∠Aの二等分線より) …②
①②より
∠ADB = ∠ADC (三角形の内角の和は180°より) …③
↑∠ADBも∠ADCも、内角180°-(●+ )という意味
)という意味
AD = AD (共通) …④
②③④より
1組の辺と その両端の角が それぞれ等しい から
△ABD ≡ △ACD
∴ AB = AC
∴ 2つの角が等しい三角形は、二等辺三角形である
逆も証明しましたので
 (本武器)
(本武器)
二等辺三角形  2つの角が等しい
2つの角が等しい

必要条件、十分条件、反例
上の《 例 1》で、
「二等辺三角形」
「証明した」ということは
「二等辺三角形」
ということになりますね!
「お題」が「正しい」ということを、数学では
「命題」が「真」といいます
その上で、「なぜ反対方向( \(\Leftarrow\) )も証明が必要なの?」
「当然反対方向も成り立つのではないの?」と思ったかもしれませんね。
実は、命題が真(すなわち、⇒が〇マル)というのは、

悲しいかな
「この関係である」という証明にとどまるのです !!
=仮定は結論に一応納まっていると言っただけ !!
なのです!
ex. 4+2 
「4+2」は一応「6」に納まっている
4+2 = 6の、「=」とはイメージが違いますね!

「=」は重ささえ同じならばよいイメージ
「⇔」は特徴まで同じなイメージ
決して

「この関係」や
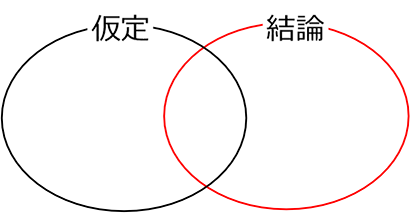
「この関係」では
絶対ありません !!
逆矢印(\(\Leftarrow\))も証明して初めて「この関係 」になれます
」になれます
例えば、今証明した 「二等辺三角形 ⇔ 2つの角が等しい三角形」 などですね
逆も証明したもので、「良く使う」「便利」なものは「定理」に昇格していきますね
仮定 ⇔ 結論の図で
「隙間が無くなったら、他の定義 (二等辺三角形 ⇔ 2辺が等しい)などはどこに入るの?」となりますが、 となります
となります
先に「仮定と結論」で解いた
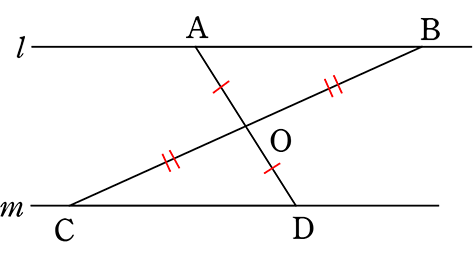
AO = DO、BO = CO ならば
AB = CD であることを証明しましょう
→ 真 でしたね
なども、結論の方が大きい(結論が含む側)ということが分かりますね
また例えば、
xが淳一郎君ならば、xは男子である → 「真」ですね
すなわち  この関係を証明したにすぎないのです!
この関係を証明したにすぎないのです!
ちなみに逆は…
x が男子
いやいやそんなことはないな、貞人君かもしれない → 「偽」
中学の段階では、「~ならば~である」を証明できた時(=真の時)、
それは
① 当然に逆は成り立たない (逆も証明が必要)
②「仮定」は「結論に納まっている」と証明したにすぎない!
すなわち  「目玉焼き」の関係にすぎない!
「目玉焼き」の関係にすぎない!
③ 命題が「偽」のときは「反例」を1つ挙げる
ex.
xy=15 (x>y)
→ 偽 (反例 x=-3, y=-5) 反例が複数あるときも1つ挙げればOK
という、3点だけイメージを持っていただけたら十分です!
【 ここから先は高校のお話です、読み飛ばしてOKです】
先の、xが淳一郎君ならば、xは男子である → 「真」
すなわち  この関係を証明したにすぎない! のですが、
この関係を証明したにすぎない! のですが、
・この関係において、
(↑目玉焼きの関係)
淳一郎君は男子に納まってさえいれば十分なので、
淳一郎君を「十分条件」
・この関係において、
(目玉焼き)
男子は淳一郎君を含んでいる必要があるので、
男子を「必要条件」といいますね
《 例 》
a+b = 0 と a = b =0 (どっちを先に試してもかまいません)
・a+b = 0 ⇒ a = b = 0 …偽! (反例 a = 3、b = -3)
「⇒」を「ならば」ではなく「ということは」や「と言えば」と読むと
なぜか真偽の判断がしやすくなりますね
ex. a+b = 0
「偽」のときは、「このような場合『成り立ちませんよ~』という 反対証拠(反例)を1つ示して相手を納得させます
「偽」ということは
「眼鏡の関係」 →「目玉焼き」発生せず! →「必要・十分」の関係発生せず
では逆
a = b = 0 \(\Rightarrow\) a+b = 0
a+b = 0 \(\Leftarrow\) a = b = 0
どっちでもかまいません同じですので
両方で進めてみますね
!真…
→「ならば」が「真」
→「目玉焼き」発生

「結論」が含む側でしたね(大)
「仮定」が納まる側でしたね(小)
∴ a+b = 0(であること)は、(a = b = 0であるための)必要条件
a = b = 0(であること)は、(a+b = 0であるための)十分条件
《 例 》 3+3 と 7
3+3 ⇒ 7 … 偽 → 眼鏡 
7 ⇒ 3+3 … 偽 → 眼鏡 
∴ 目玉焼き発生せず
3+3(であること)は (7であるための) 必要でも十分でもない条件
7(であること)は (3+3であるための) 必要でも十分でもない条件
正確には  「離れ眼鏡」でしたね
「離れ眼鏡」でしたね
《 例 》 x2 = 0 と x = 0において
x2 = 0 ⇒ x = 0 …真 → 「目玉焼き」発生!!
ですが!
いきなり「真」の時は、「必要・十分」を当てはめる前に
先に「逆」を試すと少し楽ができるかもですね
では、逆
x = 0 ⇒ x2 = 0 …真
両方「真」 → どちらにとっても「必要であり十分でもある」
∴ x2 = 0(であること)は (x = 0であるための)必要十分条件
x = 0(であること)は (x2 = 0であるための)必要十分条件
ですね
「含む側、納まる側を考えなくて済みましたね
余談が過ぎましたね・・・
二等辺三角形の続きです
二等辺三角形の証明は、全て(頂)角の「二等分線」で始まりますね。

そして、どれもちゃんと「△ABD ≡ △ACD」が
証明できましたね、
この証明を、ほんの少し延長すると
かなり使える「武器」が手に入ります
《 例 》
二等辺三角形の頂角の「二等分線」は、
底辺の「垂直二等分線」になることを証明しましょう
(証明)
・
・ (省略)
・
∴ △ADB ≡ △ADC
合同より
BD = CD …① ← 二等分の根拠
∠ADB = ∠ADC
また ∠ADB+∠ADC = 180° ← 一直線なので
∴ ∠ADB = ∠ADC = 90°
∴ AD⊥BC …②
①②より
二等辺三角形の頂角の二等分線は、底辺の垂直二等分線になる //

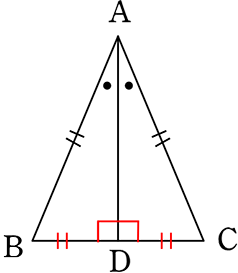
二等辺三角形の頂角の二等分線は、
底辺の垂直二等分線になる
(底辺を垂直に2等分する)
もちろん、「逆」も証明できます
二等辺三角形
\(\Leftarrow\) 1つの角の二等分線が、対辺の垂直二等分線ならば
(1つの辺の垂直二等分線が、対角の二等分線ならば)
ですが、結局、左右の三角形の合同を証明しますので、
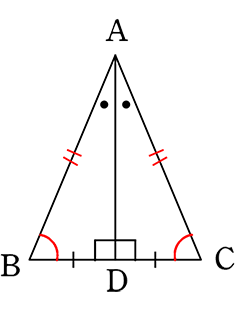
辺AB = 辺AC や ∠ABD = ∠ACD などを
利用して、∴二等辺三角形!
と言う方が全然楽ですね
鋭い武器ではありましたが、
逆は「いまいちな武器」と言えますね!

定義、定理、性質、特徴、違いは?
| 定義 | … | 意味をはっきり述べたもの (証明の根拠である) |
| 定理 | … | 正しいと証明されたもの (証明の根拠になれる) |
| 特徴 | … | 他のものと違って、特色がある |
| 特長 | … | 他のものよりも、特に優れている |
| 性質 | … | もともと持っている特性 |
| 性格 | … | 変わる可能性を含んでいる特性 |
となっていますが
数学のテストで「言葉の意味を述べよ」などは出題されないと思いますので、
| ・定義 | … | 「だから、そういう名前をつけた」 で十分ですね |
ex)
「茶髪....だから茶髪君と名前をつけた」
「二辺が等しい....だから二等辺三角形と名前をつけた」
「茶髪君の髪が茶色であることを証明せよ」
「・・・茶髪だからそう名付けたのですが…」
「二等辺三角形の二辺が等しいことを証明せよ」
「・・・二辺が等しいからそう名付けたのですが…」
→ 証明のしようがない → そういうものを、そう名付けようとみんなで決めた(前提条件のようなもの) → 名づけの「理由」は言えるけど…、名付けの「証明」て… →前提である「名づけ」の証明などありえない → 定義の証明のような問題は出ない
「彼をなぜ二等辺三角形と名付けたのですか?」「まあ…に, 二辺が等しいから…」
「彼を二等辺三角形と名付けたことを証明せよ」「むかーし…みんなで…覚えやすいように…というか日本語おかしくない?」
・定理 ≒ 性質 ≒ 特徴
・武器 = 定義、定理(性質、特徴)
で、定義、定理のイメージはOKですね
図形で、最初に名前を付けた人は
まず「辺」に注目して、次に「角」に注目している人なのかなあ・・・
と、つまらない想像をしてしまいますね
「二等角三角形…かっこいいのに…」

二等辺三角形の条件 (フィルター集②)・二等辺三角形の武器
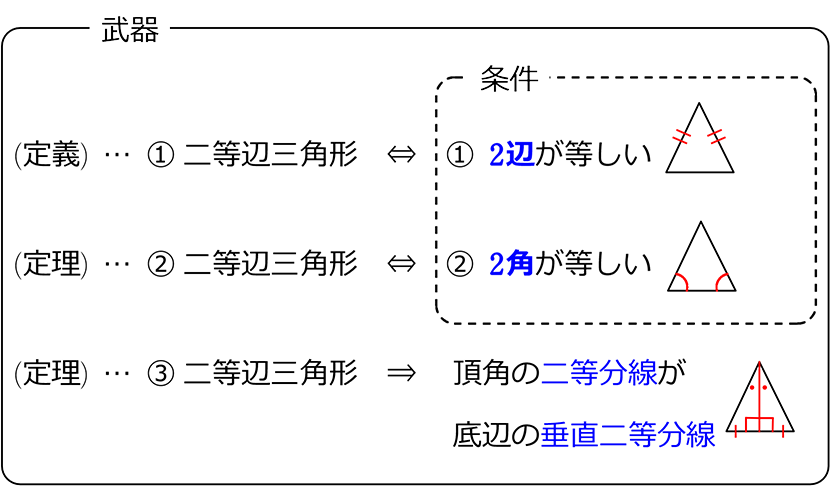
武器
が二等辺三角形の条件
(定義)
① 二等辺三角形 
(定理)
② 二等辺三角形 
(定理)
③ 二等辺三角形
底辺の垂直二等分線 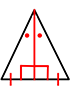
●「条件」に適した「事実」 = 「証拠」を挙げることができれば
⇒ 二等辺三角形である と言えるということですね
●③の逆も「条件」ですが 使いが悪いので
→ あえて外しています
●全てが「武器」になります
ex.
「武器」として使うときは、
→ 二等辺三角形「なので」「より」「であるから」、辺○○ = 辺○○とサラッと言ってよいですね
→ 2つの角が等しいので、△○○○は二等辺三角形、よって辺○○ = △△は等しい」
などなど・・・
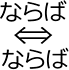 を、「なので」「より」「であるから」とサラッと言い換えて使うということですね
を、「なので」「より」「であるから」とサラッと言い換えて使うということですね
③の「左向きならば(\(\Leftarrow\))」は、使いが悪いので、先述のように外してます
② 正三角形
二等辺三角形の延長版ですね!
人にとって、正三角形は最も単純な形ですが、
正三角形本人にとっては、最も厳しい条件を課せられている三角形ですね!
「髪は耳にかからないように」「ズボンはストレート」「スカートはひざ下5cm」
のように・・・
その分、話があまり膨らまないですね!
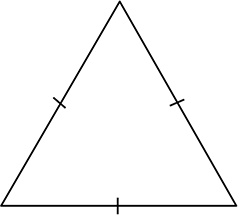
 (武器)
(武器)
正三角形
《 例 》
△ABCが、AB = BC = CA (= 正三角形)ならば、 ∠A = ∠B = ∠Cであることを証明しましょう

(証明)
△ABCを、AB = ACの(またはAを頂角とする)
二等辺三角形と見れば
∠B = ∠C …①
△ABCを、BA =BCの(またはBを頂角とする)
二等辺三角形と見れば
∠C = ∠A …②
①②より
∠B = ∠C = ∠A //
仮定理
正三角形
では、「逆」です
《 例 》
△ABCが、∠A = ∠B = ∠ C ならば、AB = BC = CA であることを証明しましょう

(証明)
△ABCを、∠B = ∠Cの二等辺三角形と見れば
AB = AC …①
△ABCを、∠A = ∠Cの二等辺三角形と見れば
BA = BC …②
①②より
AB = BC = CA //
逆も証明しましたので

| 正三角形 | ∠A = ∠B = ∠C
(全ての角が60°) |

正三角形の条件 (フィルター集③) ・ 正三角形の武器
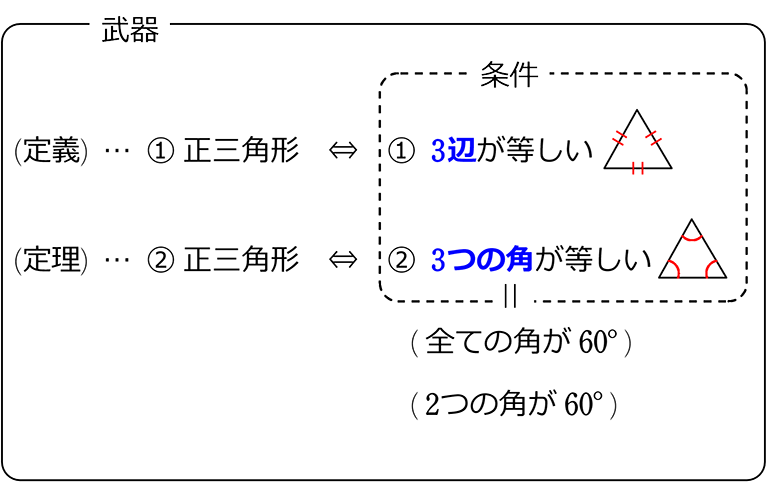
武器
が正三角形の条件
(定義)
① 正三角形 
(定理)
② 正三角形

(= 全ての角が60°)
(= 2つの角が60°)
正三角形は、二等辺三角形の延長ですので
二等辺三角形の性質を全て持ち合わせていますね!
よって、「武器」の時は「二等辺三角形」として扱ってもよいとなります
ex.
二等辺三角形なので(正三角形を指して)、頂角の二等分線が底辺の垂直二等分線!も使用可ですね! 
cf.
正三角形 ⇒ 頂角の二等分線が底辺の垂直二等線

もちろん逆は成り立ちませんので!
(逆は、二等辺三角形であるとしか言えませんね)
(全ての角が60°)と(2つの角が60°)は、「武器」ではありますが、
念のため、「条件」「定義」「定理」から外す方が無難ですね!
ex.
●正三角形の証明が最終目的の場合
→「3つの(全ての)角が等しいので、正三角形」〇
→「2つの角が60°なので、正三角形」×
●正三角形が問題の途中過程の場合
→「△ABCは正三角形、よって全ての角が等しいので、∠C = 60°」と全て書かなくても
「△ABCは正三角形より、∠C = 60°」で十分ですね
基本的に、
正方形にしても、他の図形にしても
定義、定理に60°や90°のような
「具体的な数字」は出てこないですね!
「全て同じ」「2つが同じ」など「同じ系」ですね!
③ 直角三角形の合同条件
「直角三角形」は数学で、最もよく扱われる「三角形」ですね
そこで提案ですが、直角三角形では、自己中心主義ならぬ
「斜辺中心主義」で考えていくとよいのかなと思います
すなわち、直角三角形を考えるときは、
ついつい「直角」に目が行きがちですが、「斜辺」から考える!
「釣り竿のイメージ」も「斜辺」をグルグル回しましたね!
戻りまして、「直角三角形の合同条件」ですが、結論から言いますと

直角三角形の合同条件 (フィルター集④)
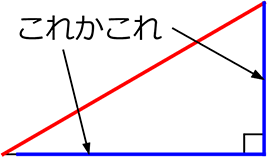
①「斜辺」と「他の1辺」 がそれぞれ等しい

②「斜辺」と「1つの鋭角」 がそれぞれ等しい
ですね!
〈証明〉
直角三角形ABCと直角三角形DEFで、
AB=DE、AC=DF ならば
△ABC ≡ △DEFであることを証明しましょう
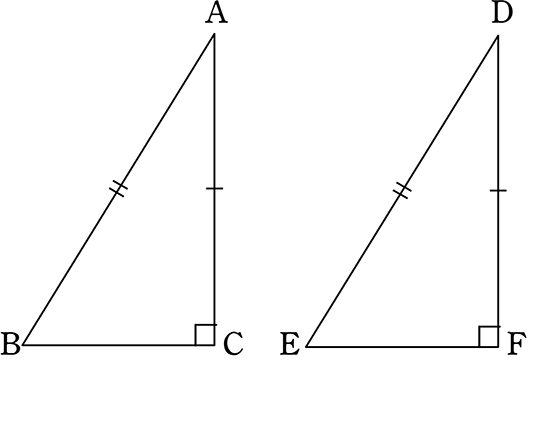
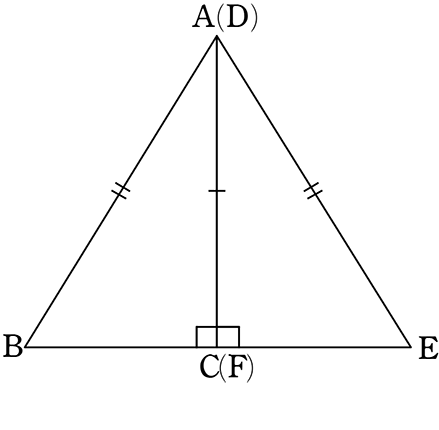
辺ACと辺DFを重ねると
∠ACB+∠ACE=180°より、BCEは一直線なので
△ABEは三角形である (四角形ではない)
次に、△ABEで、
AB=DEより、(二辺が等しいので)△ABEは二等辺三角形である
よって、∠ABC=∠DEF、
また
∠BAC=180°-90°-∠ABC=90°-∠ABC
∠EDF=180°-90°-∠DEF=90°-∠DEF より
∠BAC=∠EDF (残りの角も等しいということ)
∴ (AB=DE、∠BAC=∠EDF、AC=DFより)
2辺とその間の角がそれぞれ等しいので、 △ABC ≡ △DEF
もし、条件がBC=EFならば、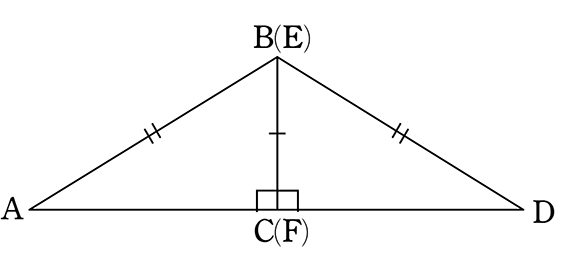 のように くっつければよいですね
のように くっつければよいですね
(直角三角形の合同の考え方)
「直角三角形」は「三角形」の中で最も重要なもの、
「直角三角形」は、この「親子中学」では「斜辺中心主義」で行きましょうと提案していましたね。
そこで、「釣り竿のイメージ」を、0°~90°に絞ったものが次です

イメージはなんとなくでもかまいません!
ただ、押さえてもらいたいことは・・・
「直角三角形」は、「斜辺(釣り竿)」の角度だけで唯一無二の「形」が決まるということです
たとえば、隣の釣り人が「同じ角度」で釣り竿を持っていたら、
自分と全く「同じ形」の「直角三角形」ができているということです
さらにそれが、「同じ長さの竿」であれば「同じ形」+「同じ大きさ」ということになるということですね!

本題に戻りまして 条件をもう一度

①「斜辺」と「他の1辺」 がそれぞれ等しい

②「斜辺」と「1つの鋭角」 がそれぞれ等しい
①の条件は、斜辺中心主義で言うと、
・「斜辺」と「隣接する角(どちらでもよい)」 がそれぞれ等しい
↓
・「斜辺」と「直角以外の角(どちらでもよい)」 がそれぞれ等しい
↓
・「斜辺」と「鋭角(どちらでもよい)」 がそれぞれ等しい
↓
・「斜辺」と「1つの鋭角」 がそれぞれ等しい
というふうに、表現方法を言い換えただけとわかりますね
②の条件は、
ただの①の裏返しですね!
「竿の長さ」と「その角度」で、「大きさ」と「形」が決まる
決まるということは、
「他の角度」、「他の辺の長さ」も「自動的に決まっている」
すなわち、同じ長さの竿ならば、
「角度」だけで「他の辺の長さ」が自動的に決まる ⇔ 「他の辺の長さ」だけで「角度」が自動的に決まる
と言ってもかまいませんね!
よって、
・「斜辺」と「隣接する角(どちらでもよい)」がそれぞれ等しい
↓
(他の辺が同じと言っても同じこと)
↓
・「斜辺」と「他の辺(どちらでもよい)」がそれぞれ等しい
↓
・「斜辺」と「他の1辺」がそれぞれ等しい
というふうに、表現方法を言い換えただけとわかりますね
よって
斜辺中心主義では、②はほとんど①と同じことを言っている となりますね!
よって、「直角三角形の合同条件」は「三角形の合同条件」を
さらに絞ったものと言うことができますね

もちろん、証明できるなら、普通の「三角形の合同条件」で証明しても全く構いませんね
(直角三角形)
・釣り竿の「角度だけ」で、「形」が決まる
・さらに釣り竿の「長さだけ」で、「大きさ」も決まる
《 例 》
∠SOTの二等分線OZ上の点Pから、2辺OS、OTに垂線を引いた交点を
それぞれA、Bとします。このとき、PA = PBであることを証明しましょう
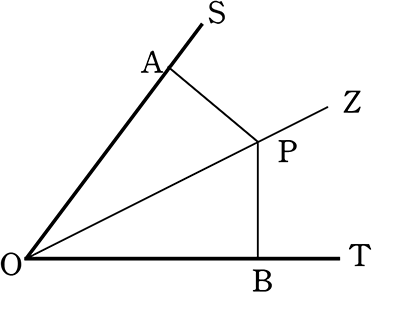
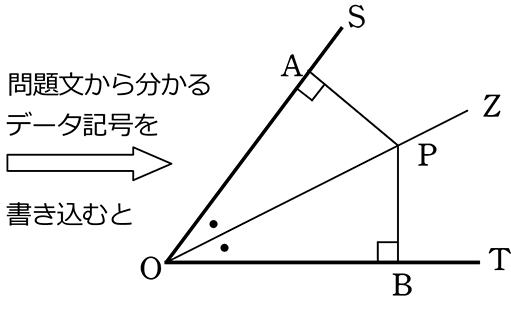
(証明)
△OAPと△OBPにおいて
∠OAP = ∠OBP = 90° (仮定より) …① ←直角三角形という証拠
∠AOP = ∠BOP (仮定より) …② ←二等分線なので、当然
OP = OP (共通) …③
①②③より、直角三角形の 斜辺と 1つの鋭角 がそれぞれ等しいから
△OAP ≡ △OBP
∴ PA = PB //
④ 平行四辺形の条件
平行四辺形は、ただの四角形が「色々な特徴」を持ち始める親玉的存在の四角形ですね(四角形の分類)
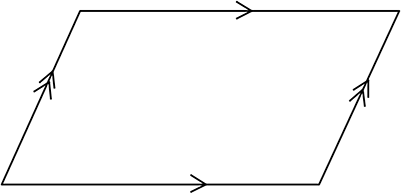
 (武器)
(武器)
平行四辺形
出発点はこれだけなんですね!
ここから、色々な「定理」ができていくのです
《 例 1 》
平行四辺形

△ABDと△CDBにおいて
AD//BC、 AB//DC より
●∠ABD = ∠CDB (錯角) …①
〇∠ADB = ∠CBD (錯角) …②
BD = BD (共通) …③
①②③より
1組の辺と 両端の角が それぞれ等しい ので
△ABD ≡ △CDB
∴ AB = CD、 AD = CB
∴ 平行四辺形
《 例 2 》
平行四辺形

(証明①)
例1の延長となります
△ABDと△CDBにおいて
・
・ (同様なので省略)
・
∴ ∠A = ∠C
同様に対角線ACを引くと
△ABC ≡ △CDA
∴ ∠B = ∠D
← 全く「同じ作業」の場合、
このように、「同様に」+「結論」
でOKです(テストでも)
∴ 平行四辺形
(証明②)
「合同」を使わない証明
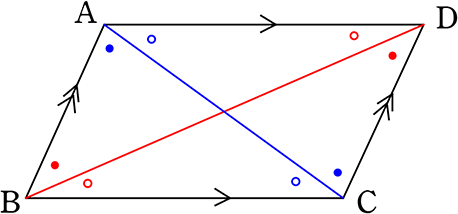
(証明)
AD//BC、AB//DCより
(●) ∠BAC = ∠DCA (錯角) = ∠a
(〇) ∠ACB = ∠CAD (錯角) = ∠b
(●) ∠ABD = ∠CDB (錯角) = ∠c
(〇) ∠ADB = ∠CBD (錯角) = ∠d とする
↑●〇●〇はこんがらないないように書いただけ → 後で消して下さいね
∠A = ∠a+∠b (●+〇)
∠C = ∠a+∠b (●+〇)
∴ ∠A = ∠C
∠B = ∠c+∠d (●+〇)
∠D = ∠c+∠d (●+〇)
∴ ∠B = ∠D
∴ 平行四辺形
《 例 3 》
平行四辺形
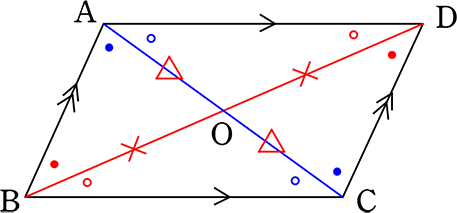
(証明)
△OADと△OCBにおいて (△OABと△OCDでも可ですね)
∠DAC = ∠BCA (錯角) …①
∠ADB = ∠CBD (錯角) …②
 ABCDは平行四辺形なので
ABCDは平行四辺形なので
AD = BC …③
←先ほど証明した「新武器(対辺が等しい)」ですね!
「定理」の証明段階(初期レベル)では、も
しかしたら、ちゃんとAD = BCの証明をす
る方がよいかもですね
①②③より
1組の辺と 両端の角がそれぞれ等しい ので
∴ △OAD ≡ △OCD
∴ OA = OC、OB = OD
∴ 平行四辺形
以上で4つのことが分かりましたね
仮定理
① 平行四辺形
② 平行四辺形
③ 平行四辺形
④ 平行四辺形
平行四辺形の条件の逆の証明
それでは、「逆」の証明です
① 四角形の対辺がそれぞれ平行
…は「定義」ですから、証明は不要ですね!
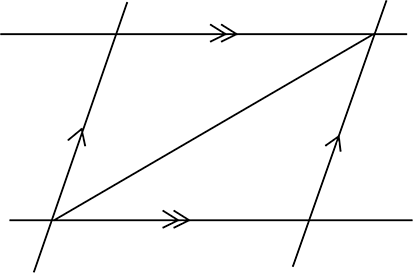
→「だからそういう名前を付けた」
→ 何を証明したら「平行四辺形」?
となってしまいますね!
② 四角形ABCDの対辺がそれぞれ等しい
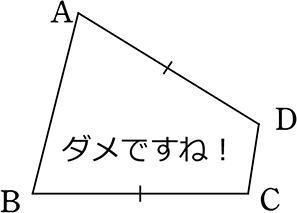
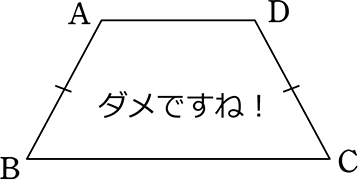
対辺がそれぞれ等しいけど、
平行四辺形でない図は描けない…
よって、平行四辺形!
と言えれば楽なのですが…
それでは、数学的証明です

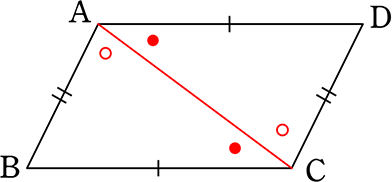
(証明)
△ABCと△CDAにおいて
AB = CD (仮定より) …①
BC = DA (仮定より) …②
AC = AC (共通) …③
①②③より
3組の辺がそれぞれ等しいので
△ABC ≡ △CAD
∴ ∠ACB = ∠CAD (●=●)
∴ 錯角が等しいので AD//BC …④
↑武器:平行線の性質
同様に、∠BAC = ∠DCA (〇=〇)
錯角が等しいので AB//DC …⑤
④⑤より
対辺がそれぞれ平行なので、四角形ABCDは平行四辺形である
∴ 四角形ABCDの対辺がそれぞれ等しい
③ 四角形ABCDの対角がそれぞれ等しい
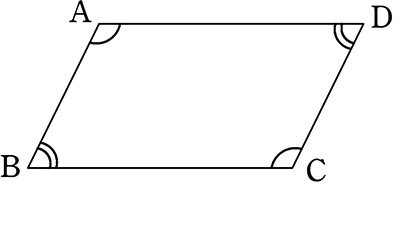

ABの延長上に点Eを、 BCの延長上に点Fをとる
四角形の内角の和は360° …①
仮定 ∠A =∠C、 ∠ABC = ∠D より
∠A+∠ABC = ∠D+∠BCD (=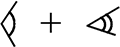 ) …②
) …②
①②より
∠A+∠ABC = ∠D+∠BCD = 180°
∠A = 180°-∠ABC …③ ←∠A+∠ABC=180° を移項
また、 ∠CBE = ∠180°-ABC …④ ←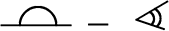
③④より (どちらも右辺が同じなので)
∠A = ∠CBE
∴ 同位角が等しいので AD//BC …⑤
同様に、AB//DC …⑥
⑤⑥より
対辺がそれぞれ平行なので、四角形ABCDは平行四辺形である
∴ 四角形ABCDの対角がそれぞれ等しい
④ 四角形ABCDの対角線がそれぞれの中点で交わる
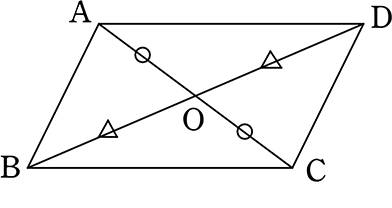
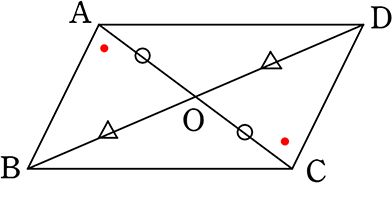
②の「対辺がそれぞれ等しければ…」と同じ手順で
(証明)
△OABと△OCDにおいて (△OADと△OCBでも可ですね)
OA = OC (仮定より) …①
OB = OD (仮定より) …②
∠AOB = ∠COD (対頂角) …③
①②③より
2辺と その間の角が それぞれ等しい ので
△OAB ≡ △OCD
∴ ∠OAB = ∠OCDより錯角が等しいので AB//DC …④
同様に △OAD ≡ OCB より
AD//BC …⑤
④⑤より
対辺がそれぞれ平行なので、四角形ABCDは平行四辺形である
∴ 四角形ABCDの対角線がそれぞれの中点で交わる
そして、もう一つあるのです合わせ技ですね
⑤ 平行四辺形
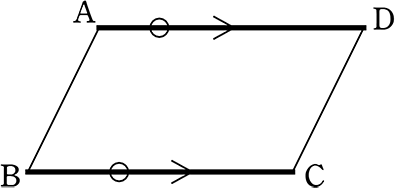
これは証明していないようで、実はすでに証明していますね
下図のように、平行四辺形の次の2つの「定義」と「定理」は、実は
2組が平行
 ですね
ですね
平行四辺形
そして、それよりも小さい
平行四辺形
では本題、その逆は?
⑤’四角形ABCDの1組の対辺が平行でかつ等しい

(証明)
対角線AC、BDを引く
△OADと△OCBにおいて
AD//BCより
∠OAD = ∠OCB (錯角) …①
∠ODA = ∠OBC (錯角) …②
AD = BC (仮定より) …③
①②③より
1組の辺と その両端の角が それぞれ等しい ので
△OAD ≡ △OCB
∴ OA = OC、OD = OB
四角形ABCDの対角線がそれぞれの中点で交わるので平行四辺形である ←学びたての新武器ですね
∴ 四角形ABCDの1組の対辺が平行でかつ等しい
一応 全て証明しましたが
証明方法を全て憶える必要はないですね
「二等辺三角形」が 「頂角の二等分線」を引くように
「平行四辺形」は 「対角線」を引けば、あとは簡単な「証明」ですものね!
定期テスト用ですね!

平行四辺形の条件 (フィルター集⑤) ・ 平行四辺形の武器
武器
(定義) 平行四辺形 ⇔
(定理) 平行四辺形 ⇔
(定理) 平行四辺形 ⇔
(定理) 平行四辺形 ⇔
(定理) 平行四辺形 ⇔
条件
① 2組の対辺がそれぞれ平行
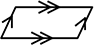
② 2組の対辺がそれぞれ等しい
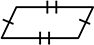
③ 2組の対角がそれぞれ等しい

④ 対角線がそれぞれの中点で交わる
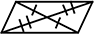
⑤ 1組の対辺が平行で(かつ)等しい
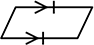 や
や 
武器
が平行四辺形の条件
(定義)
① 平行四辺形 
(定理)
② 平行四辺形 
(定理)
③ 平行四辺形 
(定理)
④ 平行四辺形 
(定理)
⑤ 平行四辺形  や
や 
《 例 》 ABCD←
ABCD← マークは平行四辺形です。「なにか四角形」ではありませんの対辺AB、DCの中点をそれぞれM、Nとします
マークは平行四辺形です。「なにか四角形」ではありませんの対辺AB、DCの中点をそれぞれM、Nとします
四角形MBNDは平行四辺形であることを証明しましょう
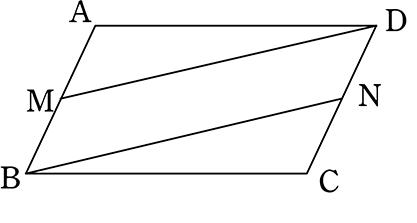
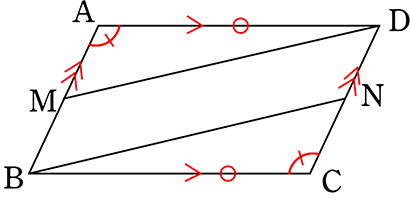
色々な条件が使えそうですね
自分が最も簡単、得意と思う証明方法でよいですね
(証明)
平行四辺形より
AB = DC
M、Nはその中点であるから
AM = MB = DN = NC …①
AB//DCよりMB//DN …②
①②より
1組の対辺が 平行で 等しい ので 四角形MBNDは平行四辺形 //
△AMD ≡ △CNBを証明して「対辺がそれぞれ等しいので」でも
いけそうですね 「対角がそれぞれ等しい」もいけそうですね
⑤ 特別な平行四辺形
平行四辺形5条件に、さらに厳しい条件を加えると
「長方形」や「ひし形」や「正方形」になりますね!
「付け加える」ということは、これら3つの図形は
それぞれ「平行四辺形の条件」を全て備えているということですね
(1) 長方形

 (武器)
(武器)
長方形


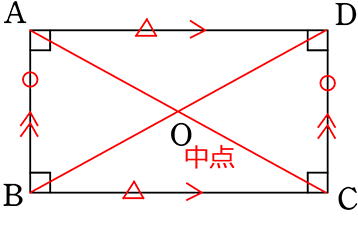
確かに、平行四辺形5条件を全て備えていますね!
対辺、①平行 ②等しい
対角、③等しい
対角線、④中点で交わる
⑤1組 平行かつ等しい
→ 長方形は、③の条件に さらに厳しい条件を加えたものですね
対角 ③等しい → 4つの角 ③’全て等しい
《 例 》
長方形
(証明)
△ABCと△DCBにおいて
・
・ (省略)
・
∴ △ABC ≡ △DCB
∴ AC = DB
∴ 対角線の長さが等しい
∴ 長方形
《 逆 》
四角形の対角線の長さが等しい
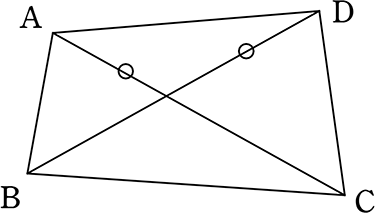
ダメですね !!
対角線の長さが等しいというデータだけでは何も証明できないですね!
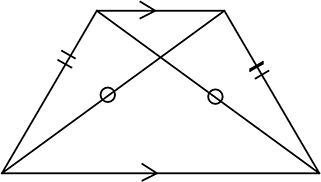
(反例)
等脚台形の対角線の長さも等しいですね!
対角線の長さが等しい平行四辺形
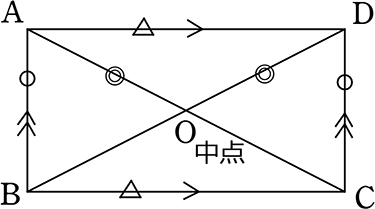
(証明)
△ABC、△DCB、△BAD、△CDAにおいて
AC = DB = BD = CA (仮定より) …①
AB = DC = BA = CD (仮定より) …②
BC = CB = AD = DA (仮定より) …③
3つの辺がそれぞれ等しいので
∴ △ABC ≡ △DCB ≡ △BAD ≡ △CDA
∴ ∠A = ∠B = ∠C = ∠D
∴ 4つの角が等しいので 長方形 である
∴ 対角線の長さが等しい平行四辺形
(2) ひし形
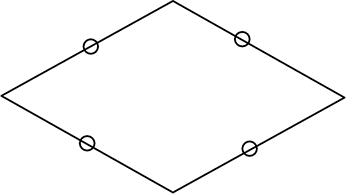
 (武器)
(武器)
ひし形
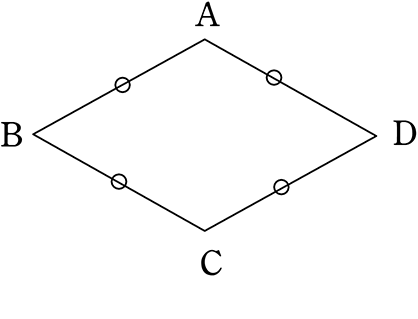

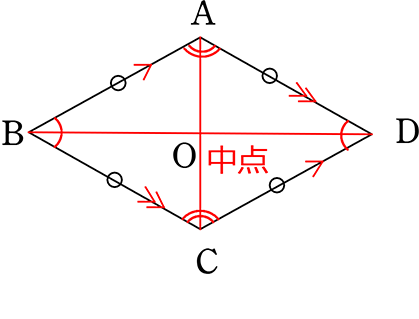
考え方は、「長方形」と同じですね (元々平行四辺形である)
対辺 ①平行 ②等しい
対角 ③等しい
対角線 ④中点で交わる
⑤1組平行かつ等しい
を踏まえた上で
→ ひし形は、②の条件に さらに厳しい条件を加えたものですね
対辺 ② 等しい → 4辺 ②’ 全て等しい
《 例 》
ひし形

△ABOと△ADOにおいて
AB = AD (仮定より) …①
AO = AO (共通) …②
BO = DO (仮定より) …③
①②③より 3つの辺がそれぞれ等しいので
△ABO ≡ △ADO
∴ △ABDは 2辺が等しい ので二等辺三角形
∠BAO = ∠DAOより
頂角の二等分線は底辺の垂直二等分線であるので
∴ AO⊥BD
∴ ひし形
《 逆 》
四角形の対角線が直交する(垂直に交わる)
もうわかりすね!ダメですね !!
「凧型」でアウトですね! 
対角線が直交する(垂直に交わる)平行四辺形
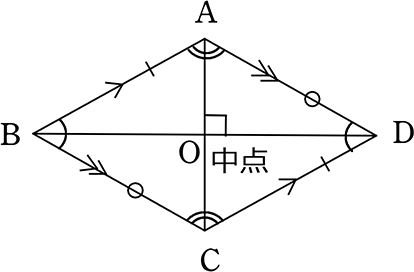
(証明)
△ABOと△CBOと△CDOと△ADOにおいて
・
・ (省略しますね)
・
∴ △ABO ≡ △CBO ≡ △CDO ≡ △ADO
∴ AB = BC = CD = DA
∴ 4つの辺が等しいので ひし形
∴ 対角線が直交する(垂直に交わる)平行四辺形
(3) 正方形
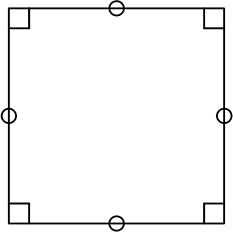
 (武器)
(武器)
正方形
「長方形」+「ひし形」ですね!
対辺 ①平行 ②等しい
対角 ③等しい
対角線 ④中点で交わる
⑤1組平行かつ等しい
を踏まえた上で
→ 正方形は、②と③の条件に さらに厳しい条件を加えたものですね
対辺、②等しい → ②’全て等しい
対角、③等しい → ③’全て等しい
《 例 》
正方形
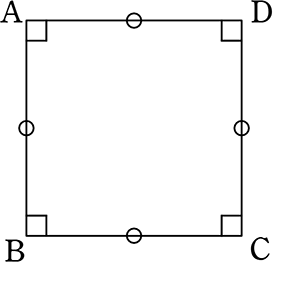


(証明)
△ABCと△DCBにおいて
・
・ (省略)
・
∴ △ABC ≡ △DCB
∴ AC = DB
∴ 対角線の長さが等しい …①
△BAOと△BCO、△DAOと△DCOにおいて
・
・ (省略)
・
∴ △BAO ≡ △BCO ≡ △DAO ≡ △DCO
∴ △BACはBA = BCな二等辺三角形
∠ABO = ∠CBOよりBOは∠Bの二等分線
よって頂角の二等分線は底辺ACの垂直二等分線であるので
BO⊥AC …②
①②より
正方形
《 逆 》
対角線が等しく(かつ)直交する四角形
さすがにOKかと感じますが…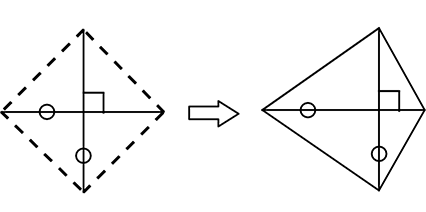 やはりダメですね!
やはりダメですね!
対角線が等しく(かつ)直交する平行四辺形
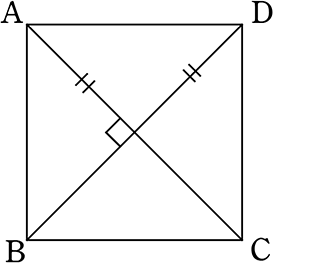

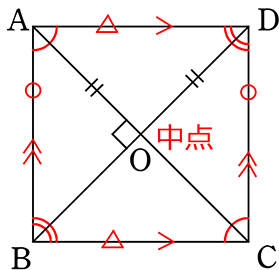
仮定(材料)が多すぎて、逆に何を求めるのだっけ?となりますね
「正方形」である!ですね
→ 「4つの辺、4つの角 が等しい」 ですね
(証明)
△OABと△OBCと△OCDと△ODAにおいて
Oは中点より
OA = OB = OC = OD
仮定より
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
∴ 2つの辺とその間の角が等しいので
△OAB ≡ △OBC ≡ △OCD ≡ △ODAであり
かつ直角二等辺三角形
∴ 4つの辺、(かつ)4つの角が等しいので 正方形
∴ 対角線が等しく(かつ)直交する平行四辺形

他の平行四辺形の条件 (フィルター集⑥) ・ 他の平行四辺形の武器

長方形(武器)
が長方形の条件
(定義)
① 長方形
(定理)
② 長方形
対角線の長さが等しい(単品) 

ひし形(武器)
がひし形の条件
(定義)
① ひし形
(定理)
② ひし形
対角線が直交する(単品) 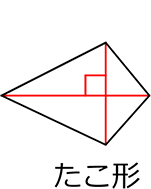

正方形(武器)
が正方形の条件
(定義)
① 正方形
(定理)
② 正方形
対角線が等しく、直交する(単品) 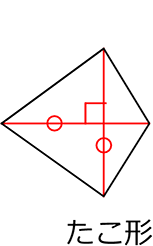
〈 参考 〉
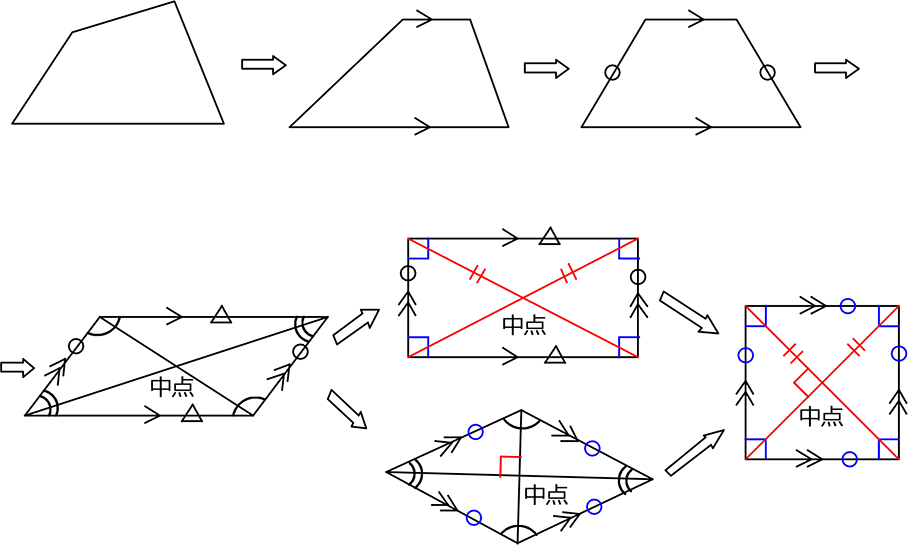
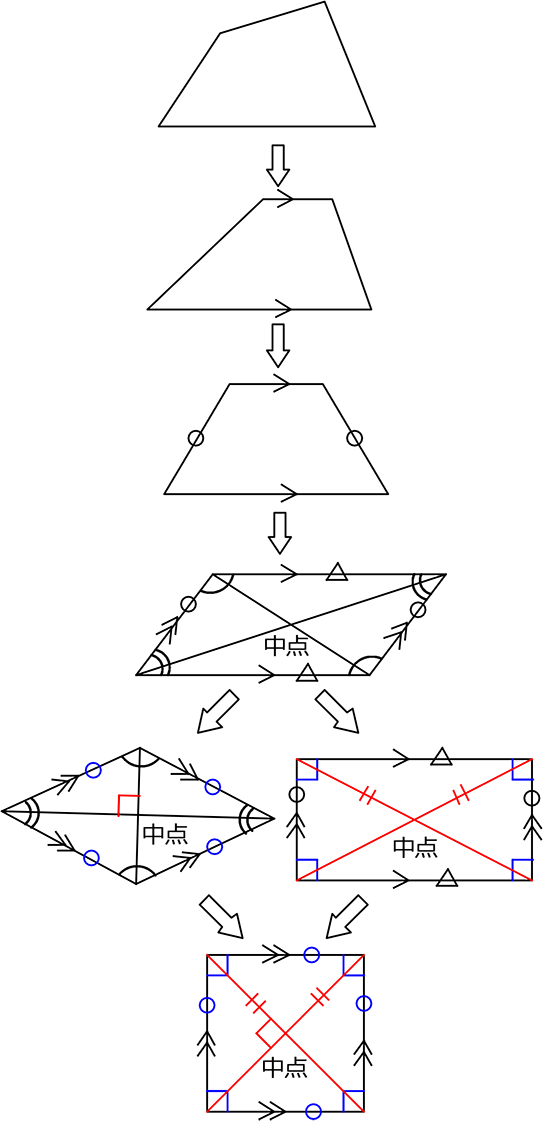

《 例 》
図の平行四辺形において、AD=10cm,
AB=8cm、∠Aの二等分線が辺BCと
交わる点をE,∠Dの二等分線が辺BCと
交わる点をFとするとき、
線分EFの長さを求めましょう
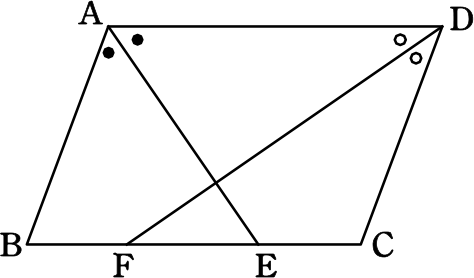
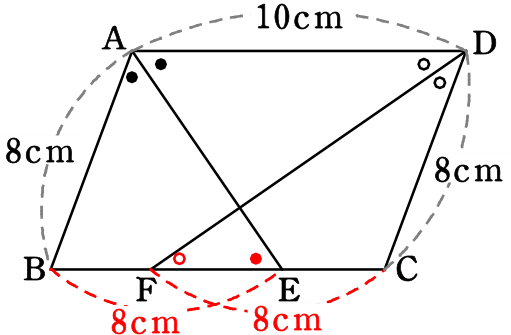
●=●(錯角)より、(二等辺三角形で)
BA=BE=8cm
○=○(錯角)より、(二等辺三角形で)
CD=CF=8cm
∴ EF=8+8-10=6cm
かぶった部分の長さ
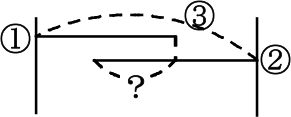
?=①+②-③

太線部分が③ですものね
長々と定理の証明をしてきましたが、
証明方法を憶える必要は、ありません!
憶えるべきは・・・「武器」です
たとえば
・長方形・・・
(図形を思い浮かべながら)
「全ての角が等しい!」
「対角線の長さが等しい平行四辺形」
・平行四辺形・・・
(図形を思い浮かべながら)
「対辺が等しい!」「対角が等しい!」
などですね!
各図形の「定理の証明」くらいなら、
対角線を引いて
→どの三角形の合同を言えば、
辺や角が同じといえるか?
(武器から「同じ長さマーク」「同じ角度マーク」「平行マーク」などのマークを書き込みながら)簡単に導けますね!
あえて言えば、「どの三角形の合同を証明しようか」という所に集中ですね
それには「武器」「条件」を、しっかり頭に入れておくことが前提ですね!
《 例 》
線分AB上に適当に点Cをとり、
AC、CBを1辺とする正三角形ACD、CBEをつくりました
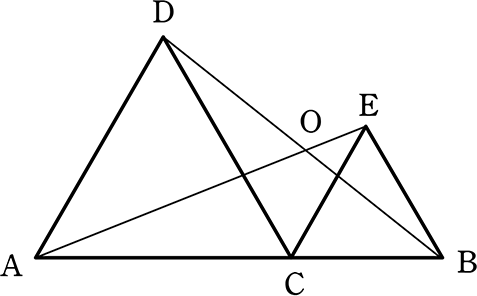
(1) AE = BD を証明しましょう
・「辺」や「角」が「イコール」の証明は、
→ ほぼ それらを含む「三角形の合同」の証明をすればよいですね
・2つの三角形を探す時、
ついつい「離れた、同じような形の三角形( )」が目につきがちですが、
)」が目につきがちですが、
かなりの確率で「一部が重なった三角形( )」を探さなければいけませんね
)」を探さなければいけませんね
「透視」ではありませんが「ぱっと見印象のない三角形も見つけ出せるようにがんばりましょうね」←練習あるのみです
AEを含む三角形 …△AEC、△AEB
BDを含む三角形 …△BDC、△BDA
△AECと△BDCが似ているな!
すぐに始めずに、何と何が「対応」しているか「図を見ながら予想」
2箇所も対応しているのを発見できれば、まずその三角形ですね!
見つけた三角形が、また風景に溶け込まないように「シャーペンでなぞる」
「薄~く塗る」のもよいですね(画像処理で言えば「最前面に移動」ですか)
長くなってしまいましたので、もう一度問題を
AE = BD の証明
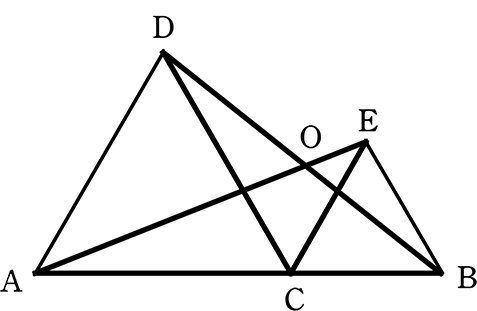
狙いの三角形が見えますか~?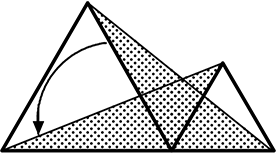
Cを支点にパタンと倒すイメージ
△ACEと△DCBにおいて
CE = CB (△ECBは正三角形より) …① ←正三角形⇔全ての辺が等しい(武器)
AC = DC (△DACは正三角形より …②
∠ACE = 180°-60° …③ ←直線180°ー正三角形の1角∠ECB60°
∠DCB = 180°-60° …④ ←直線180°ー正三角形の1角∠DCA60°
③④より
∠ACE = ∠DCB …⑤
①②⑤より
2辺と 間の角が それぞれ等しい ので ←使用条件
△ACE ≡ △DCB
∴ AE = BD
見直し確認
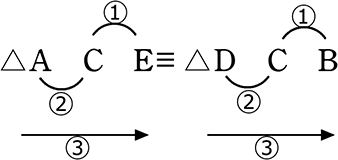
① CE=CB
② AC=DC
③ ∠ACE=∠DCB
→ 対応している!
完全な確認にはなりませんが、
「凡ミス」発見に。
(2) ∠AOBの角度を求めましょう

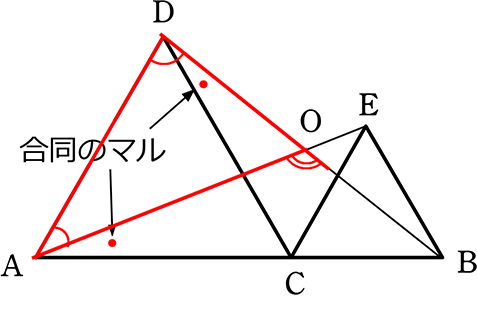
難しいですね!
・∠ODAと∠OADさえ解れば・・・
・図に溶け込んだ  スリッパの発見
スリッパの発見
・図に「同じ角度マーク」の記入
・合同の結果の利用
→ (1)の合同より
∠BDC = ∠EAC (●)
△DACは正三角形より
∠ODA = 60°+ ●
∠OAD = 60°- ●
→ ∠AOB
= ∠ODA+∠OAD スリッパ
= (60°+ ●)+(60°- ●)
= 60°+60°
= 120°
★ ●などの記号の記入が大切ですね (∠アルファベットはややこしい)
★ 結局●の個別の角度は解りませんでしたね! (結構あるパターンです)
「何か解らないけど…」「同じものなら、足しても同じ」「同じものなら、引いても同じ」
「等式の性質」の図形への応用…慣れていきましょうね!
お疲れ様でした !!
その他の問題は、「問題集」で !!















