| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 図形の相似 | (2) 円周角・中心角 | (3) 三平方の定理 |
| ア | 三平方の定理の意味と証明 |
|---|---|
| ① | 三平方の定理 |
| ② | 三平方の定理の証明 |
| ・ | ピタゴラスさんの証明方法 |
| ・ | バスカラさんの証明方法 |
| ・ | ガーフィールドさんの証明方法 |
| ・ | 相似を利用した証明方法 |
| ・ | ユークリッドさんの証明方法 |
| ③ | 三平方の定理の逆 |
| ・ | 三平方の定理の逆の証明①(同一法) |
| ・ | 三平方の定理の逆の証明②(相似の利用) |
| ④ | 特別な角 |
| ・ | 特別な辺 |
| ・ | ピタゴラス数 |
| イ | 三平方の定理の活用 |
| ① | 面積 (1年平面図形への応用問題) |
| ・ | 正三角形の高さと面積 |
| ・ | 例題) テープの折り返し |
| ・ | 内分点、外分点を求める(余談:高校課程) |
| ・ | 座標上の2点間の距離を求める |
| ・ | ヒポクラテスの月 |
| ② | 体積 (1年空間図形への応用問題) |
| ・ | 正四面体に関する頻出問題 |
| ・ | 正四面体の公式集 |
| ・ | 例題) 立体の体積を2通りに求めて高さを求める |
| ・ | 例題) 立体の切断、付け足しを考える |
| ③ | 最短距離 (最短経路) |
| ④ | 立体の切断 |
| ⑤ | 体積比 |
| ⑥ | 立体の対角線 |
三平方の定理
ア 三平方の定理の意味と証明
三平方の定理(ピタゴラスの定理)!一度は聞いたことがあるのではないでしょうか
まさに、『King of 定理』と言えますね!
単純なのにすごく役立つ
経済的に言えば「コストパフォーマンス」がよい、すごくよいですね
ただ、今まで学んできた単元の応用問題をつくりやすくなるので
「三平方の定理」=「難しい」と思いがちになりますね
三平方の定理自体はすごくシンプル!
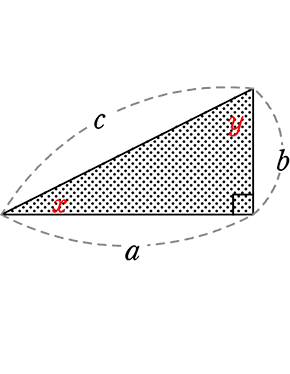
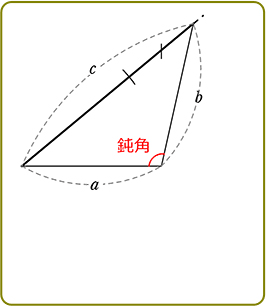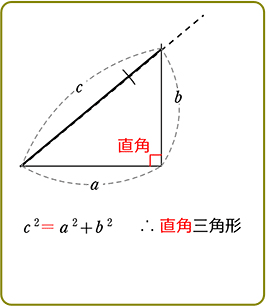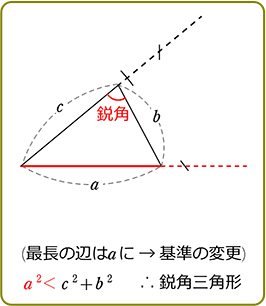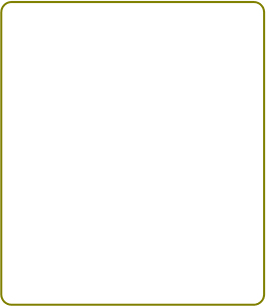
① 三平方の定理

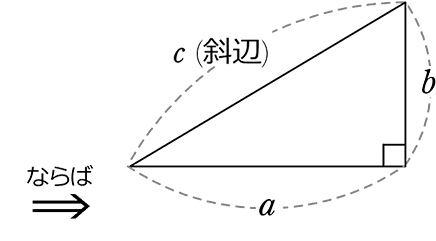
三平方の定理 (ピタゴラスの定理)
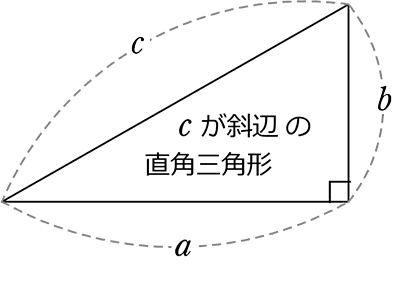
 c2= a2 + b2
c2= a2 + b2
これだけです !!
・直角三角形
・(最大の辺)2 = (他の辺)2+ (他の辺)2
cf.
直角三角形の辺の名前
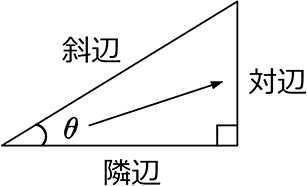
∠θを基準に、
隣にあるのが 隣辺
対面にあるのが 対辺
ですが中学では、「斜辺」と「それ以外」で十分ですね
これだけです!
直角三角形の3辺のうち、2辺が判れば残りの1辺がわかります
三平方の定理を少し変形すると
c2 = a2+b2 → c = \(\small{\sqrt{a^2+b^2}}\)
a2 = c2-b2 → a = \(\small{\sqrt{c^2-b^2}}\)
b2 = c2-a2 → b = \(\small{\sqrt{c^2-a^2}}\)
すなわち
・ 斜辺 = \(\small{\sqrt{(他の辺)^2+(他の辺)^2}}\)
・ 斜辺以外の辺 = \(\small{\sqrt{(斜辺)^2-(他の辺)^2}}\)
斜辺が1番大きい!
「左辺丸々2乗」の左辺の2乗を取るには、右辺丸々に ±√ をつける。 (平方根の掘り下げ利用法)でしたね
よって、二次方程式的には、 解は2つですが、
図形に「マイナス」はありませんので、 「a>0より」を省いている
ということになりますね
《 例 》
xを求めましょう
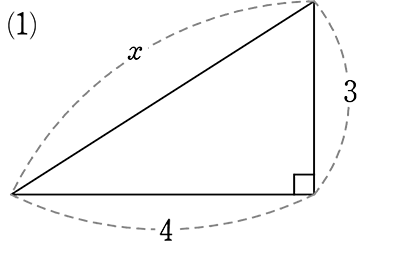
x2 = 32+42
= 9+16
= 25
x = ±5
x>0より A. x = 5
慣れてきますと、変形バージョンで … x = \(\small{\sqrt{4^2+3^2}}\) = \(\small{\sqrt{16+9}}\) = 5 //
さらに慣れてきますと、比から…
5, 4, 3 の三角形だな… 5 //
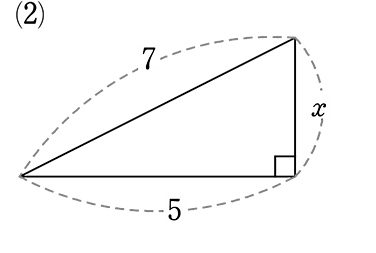
x = \(\small{\sqrt{7^2-5^2}}\)
= \(\small{\sqrt{49-25}}\)
= 2\(\small{\sqrt{6}}\) //
30~40.png)
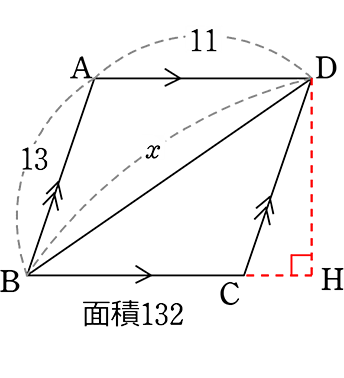
・ ABCD = 底辺11×高さDH → DH = 132÷11 = 12
ABCD = 底辺11×高さDH → DH = 132÷11 = 12
| ・CH | =\(\small{\sqrt{CD^2-DH^2}}\) = \(\small{\sqrt{13^2-12^2}}\) = \(\small{\sqrt{169-144}}\) = \(\small{\sqrt{25}}\) = 5 |
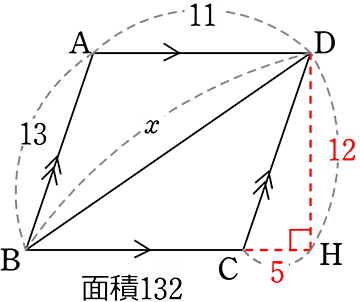
x = \(\small{\sqrt{BH^2+DH^2}}\)
=\(\small{\sqrt{ (11+5)^2+12^2}}\)
= \(\small{\sqrt{16^2+12^2}}\)
= \(\small{\sqrt{256+144}}\)
= \(\small{\sqrt{400}}\)
= 10\(\small{\sqrt{4}}\)
= 20 //
《 例 》
水面に浮いた丸太の直径を求めましょう (図は断面図)
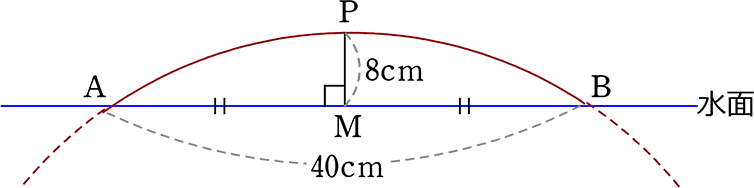
大きな円が書けないので、縮小図を書いてみると

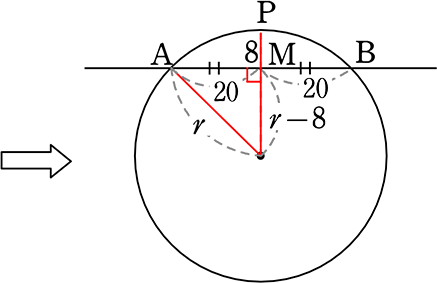
r = \(\small{\sqrt{20^2+(r-8)^2}}\) = \(\small{\sqrt{400+r^2-16r+64}}\) = …
変形バージョンよりも原型の方がよいようですね、もとい
r2 = 202+(r-8)2
r2 = 400+r2-16r+64
r2 = r2-16r+464
16r = 464
r = 29 問いは直径より 58cm //
② 三平方の定理の証明
三平方の定理の定理の証明方法は、300通り以上あるらしいですね!
それだけあると、出題者側も
「三平方の定理を証明せよ」という問題は出しにくいですね
よって、三平方の定理の証明自体の問題は、
出てもメジャーどころの証明の虫食い問題
ということになるのかなと思います
親子中学数学では、5つほど紹介しますが、
理屈さえわかればよいと思います
そして気に入った1つだけは、
「自分の三平方の定理の証明方法」として
「納得」+「表現」ができれば十分 としますね!
基本的にどの証明方法も
流れは・・・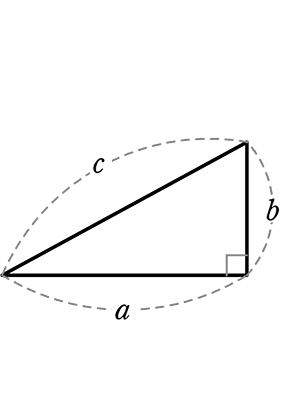
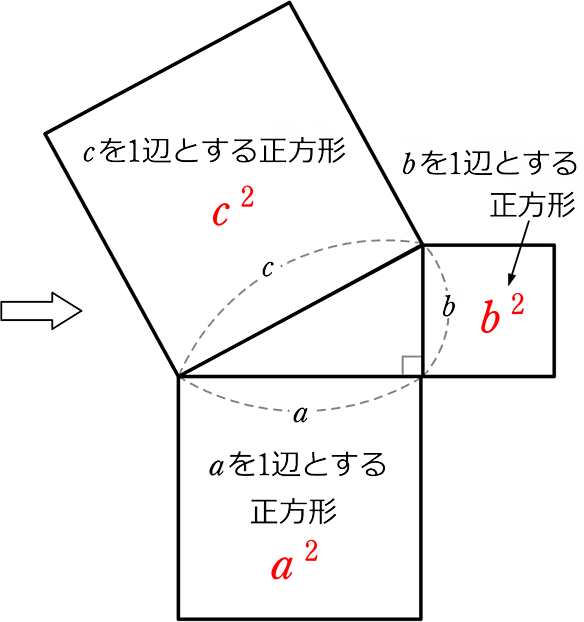
→ a を1辺とする正方形の面積( a2 ) +b を1辺とする正方形の面積( b2)
= c を1辺とする正方形の面積( c2 ) になる!ですね
直角二等辺三角形ならば一目瞭然ですね!
 a2+b2=c2
a2+b2=c2
逆に、直角三角形ではない 正三角形は一目瞭然でOUT! ですね
 a2=b2=c2 になってしまいますね
a2=b2=c2 になってしまいますね
それでは、どのような直角三角形でも成り立つという証明に移りますね
前置き確認として、直角三角形の2つの鋭角どうしの和は どんな時でも90°ですね

x+y = 90°
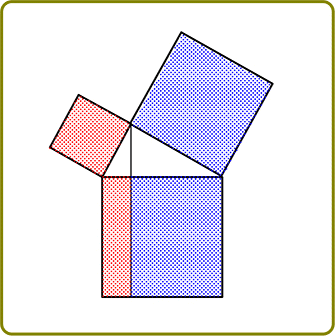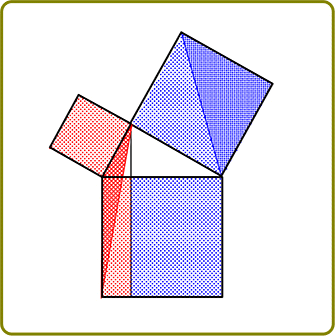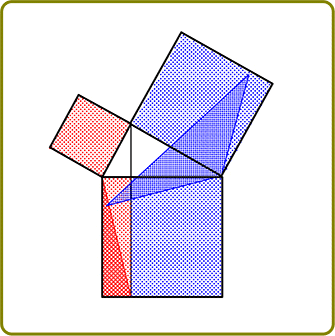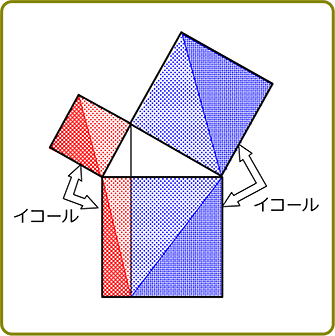
証明① ピタゴラスさんの証明方法 (面積を2通りに計算)
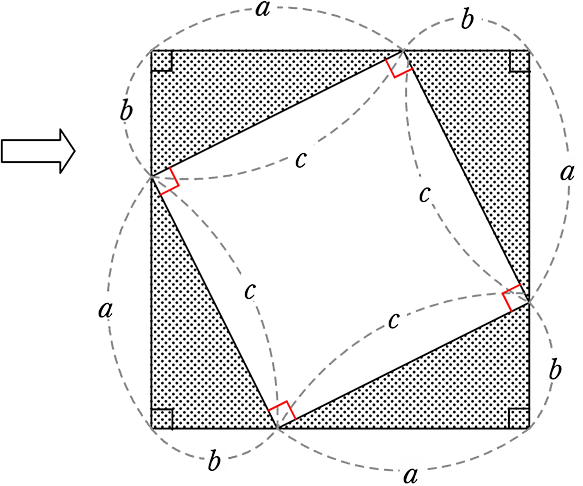
合同な直角三角形を図のように4つ並べると 外と中に2つの正方形ができる
(前提)
・外の正方形の1辺は本当に直線?
| → | (直角になるように配置した)直角+鋭角+他の鋭角 = 180° |
| → | 外側の辺はちゃんと直線!
(中の白四角形は当然に正方形 ← 4辺4角が等しい) |
(本題)
大の正方形の面積を2通りで求めてみると、
① 縦×横 =(a+b)2 = a2+2ab+b2
| ② | 4つの直角三角形の面積 + 内側の正方形面積
= 4コ×\(\large{\frac{1}{2}}\)ab+c2 |
→ 2つは同等であるはずなので
① = ②
→ a2+2ab+b2 = 2ab+c2
→ c2=a2+b2 //
証明② バスカラさんの証明方法 (面積を2通りに計算)
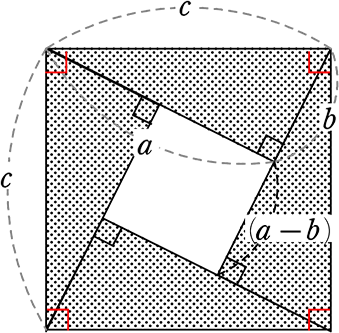
① 縦×横 = c2
| ② | 4つの直角三角形の面積+内側の正方形面積
= 4×\(\large{\frac{1}{2}}\)ab+(a-b)2 |
① = ② → c2 = a2+b2
証明③ ガーフィールドさんの証明方法 (面積を2通りに計算 )
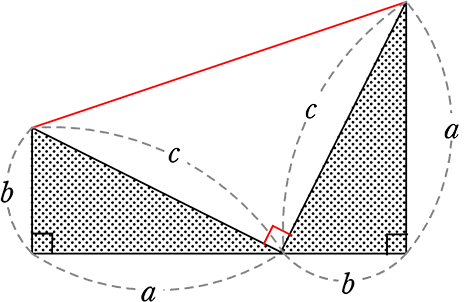
① 台形の面積 =\(\large{\frac{ (上底+下底)高さ}{2}}\) = \(\large{\frac{(a+b)(a+b)}{2}}\) =\(\large{\frac{ a^2+2ab+b^2}{2}}\)
| ② | 2つの直角三角形の面積 + 1つの直角二等辺三角形の面積(白)
= 2×\(\large{\frac{1}{2}}\)ab+\(\large{\frac{1}{2}}\)c2 = ab+\(\large{\frac{c^2}{2}}\) = \(\large{\frac{2ab+c^2}{2}}\) |
① = ②より → \(\large{\frac{a^2+2ab+b^2}{2}}\) = \(\large{\frac{2ab+c^2}{2}}\) → c2 = a2+b2 //
→ 証明①ピタゴラスさんの証明方法の半分バージョン(2つくっつければ正方形)ですね
証明④ 相似を利用した証明方法
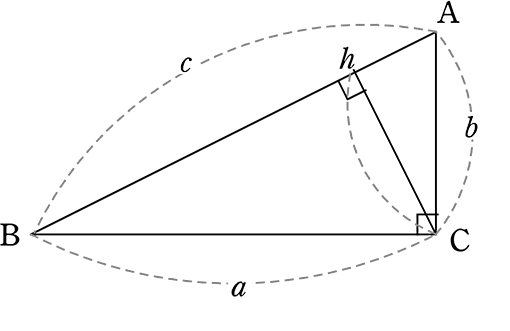
・△BCA∽△BhC (∠B共通、90°共通)
・△BCA∽△ChA (∠A共通、90°共通)
∴ △BCA∽△BhC∽△ChA
∴ △B
△B
①②を 足し合わせてみると
a2 = cBh
+) b2 = cAh
a2+b2 = c(Bh+Ah)
→ Bh+Ah は図より「c」であるので
a2+b2 = c(c)
∴ c2 = a2+b2
証明⑤ ユークリッドさんの証明方法
復習として、2年生の等積変形とは
(等しい面積のまま変形させる) でしたね
頂点を底辺に平行移動させても


(等積変形) △eAd = △eAB
↓
(合同) △eAB ≡ △CAf
| ∵ ① | eA = CA (小正方形の1辺) |
| ② | AB = Af (大正方形の1辺) |
| ③ | ∠eAB = ∠CAf (どちらも90°+∠CAB) |
↓
(等積変形) △CAf = △jAf
∴ △eAd = △jAf
∴ 2△eAd =  ACde = 2△jAf =
ACde = 2△jAf =  Afjk
Afjk

同様に青三角形で
∴ 2△hBi =  BCih = 2△Bjg =
BCih = 2△Bjg =  Bgjk
Bgjk
(→ 同様の作業の場合は 証明部分を省略してもよい)
∴ c2 = a2+b2
③ 三平方の定理の逆
先に「三平方の定理」をお話ししたときに、
当たり前のように「
ここでは、少し+α しつつ「逆の証明」をさせていただきますね!

三平方の定理の逆
三角形で最大の辺を「c」としたとき

c2 = a2+b2
Cを斜辺とする直角三角形
(+αとして)
| c2>a2+b2 | 鈍角三角形  |
| c2<a2+b2 | 鋭角三角形  |
おまけとして
| c2 = a2 = b2 | 正三角形  |
( 2年生 鈍角三角形・鋭角三角形)
《 例 》
次の長さを3辺とする三角形は、どのような三角形でしょう
(1) 3、5、4
| → | 最大の辺の5の2乗は「25」
他の辺の2乗の足し算は 9+16 = 「25」 |
「25」=「25」
∴ (5が斜辺の) 直角三角形
(2) 4、5、6
| → 最大の辺の2乗「36」< | 他の辺の2乗の足し算 16+25 =「41」 |
∴ 鋭角三角形
(3) \(\small{\sqrt{7}}\)、 2\(\small{\sqrt{2}}\)、4
| → | 最大の辺がぱっと見、わからないので、とりあえず順に2乗すると、7、8、16 |
| → 最大の辺の2乗「16」> | 他の辺の2乗の足し算「15」 |
∴ 鈍角三角形
余談として、念のために
「三平方の定理の逆」
・c2= a2+b2
を証明しておきますね
三平方の定理の逆の証明①(同一法)
| c2= a2+b2 | (c を斜辺とする)直角三角形 |
△ABCとは別に、EF =a、FD = b、∠F= ∠90°の△DEFを準備する

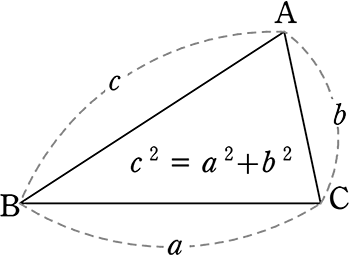
三平方の定理より ED2= a2+b2 …①
仮定より c2 =a2+b2 …②
①②より (右辺が等しいので) ED2= c2
∴ ED>0より ED = c
| ∴ | DE = AB、EF = BC、FD = CA、より3組の辺がそれぞれ等しいので
△DEF ≡ △ABC |
| ∴ | ∠F= ∠C= 90° より △ABCは (cを斜辺とする)直角三角形 // |
この証明で十分ではありますが、
「三平方の定理の逆」を証明するために
「三平方の定理」を使うことに納得がいかない、
またはこの論法ならどんな証明でもできるのでは?
と納得がいかない場合のみ次を…
ですが、「余談」であることに変わりはありません!
三平方の定理の逆の証明②(相似の利用)
その前に、次の(1つの頂点から垂線を下した)三角形には
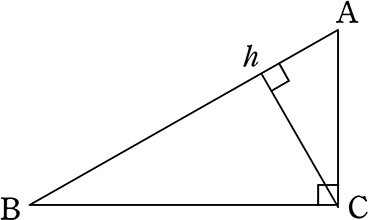

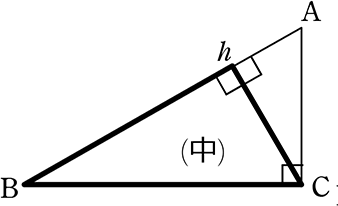

1本の線で 3つとも相似になるのは「直角三角形」だけですね!
→ △大 ∽ △中 ∽ △小
→ △BCA ∽ △BhC ∽ △ChA
(2角が等しいので相似)
他の三角形はどんなに頑張っても、2つまでですね
ex)

△大 ∽ △中 で2つの相似までですね

正三角形 (二等辺三角形)でさえ、2つの相似ですね
→ △中 ∽ △小 ( 正確には合同 )
〔 証明② 相似の利用 〕
( 証明②は、「三平方の定理」の証明の「相似を利用した証明」の逆バージョンですね
| → | 大中小3つの三角形が相似でないと成り立たないという証明になります |
| → | 逆を言えば、3つが相似なら直角三角形ということですね |
(仮定) a2+b2= c2
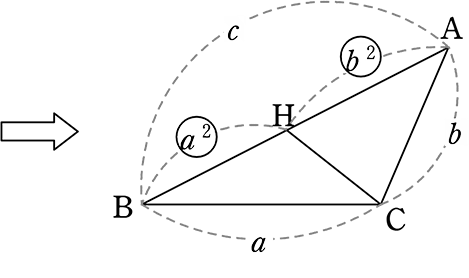
△BCAの線分BAを a2:b2 に内分する点をHとすると
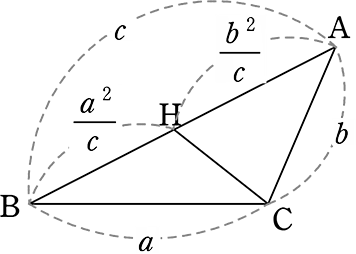
| ・ | BH = \(\large{\frac{c}{a^2+b^2}}\)×a2 = (仮定より) \(\large{\frac{ca^2}{c^2}}\) = \(\large{\frac{a^2}{c}}\) |
| ・ | AH = \(\large{\frac{c}{a^2+b^2}}\)×b2 = (仮定より) \(\large{\frac{cb^2}{c^2}}\) = \(\large{\frac{b^2}{c}}\) |
● △BAC(大)と△BCH(中)において
BA:BC=c:a
BC:BH = a:\(\large{\frac{a^2}{c}}\) → ca:a2
∴ BA:BC = BC:BH …①
∠B = ∠B (共通) …②
①②より
「2組の辺の比 と その間の角がそれぞれ等しい」ので
△BAC(大) ∽ △BCH(中)
∴ ∠BCA = ∠BHC …③
● △BAC(大) と △CAH(小)において、(同様に)
BA:AC =c:b
CA:AH = b:\(\large{\frac{b^2}{c}}\) → cb:b2 → c:b
∴ BA:AC = CA:AH …④
∠A = ∠A(共通) …⑤
④⑤より「2組の辺の比 と その間の角がそれぞれ等しい」ので
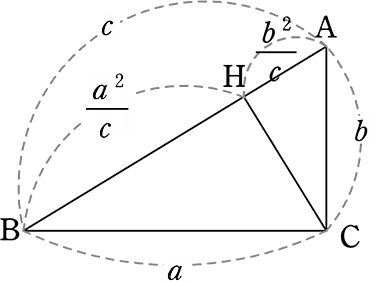
△BAC(大) ∽ △CAH(小)
∴ ∠BCA = ∠CAH …⑥
③⑥より ∠BCA = ∠BHC = ∠CHA …⑦
∠BHC+∠CHA = 180° …⑧ であるので
⑦⑧より ∠BCA = ∠BHC = ∠CHA = 90°
∴ a2+b2 =c2 ならば、△ABCはcを斜辺とする直角三角形である //
④ 特別な角
これは、絶対に憶えないといけない・・・式(公式)・・・ではなく、
…『比』ですね!
最も代表的な2つの『直角三角形の辺の比の値』となります!

特別な角
● 正三角形の半分である…
【30° 60° 90°の直角三角形】通称?『サブローキュー』の三角の辺の比は
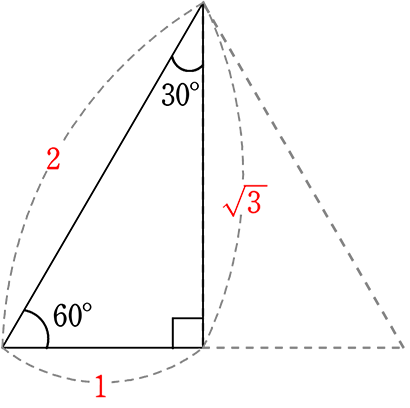
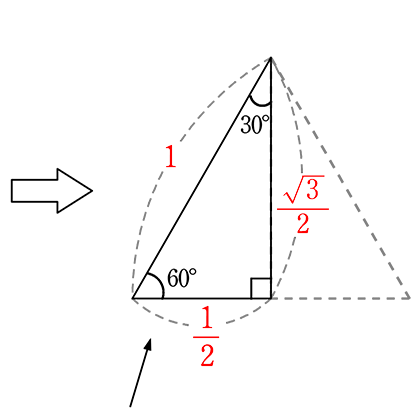
とことん「斜辺中心主義」で、
斜辺を基準である数字の「1」
にしている
1は、正三角形の一辺
\(\large{\frac{1}{2}}\)は、正三角形の1辺の「半分」
だから当然の\(\large{\frac{1}{2}}\)ですね!
新たに憶えるのは
正三角形の高さ、\(\large{\frac{\sqrt{3}}{2}}\)!
言葉のリズム的に「1対2~対\(\small{\sqrt{3}}\) 」と憶えてしまいがちですが、
親子中学では、「斜辺中心主義」で行きましょう!としていますので、
「1対2~対\(\small{\sqrt{3}}\) 」ではなく、「斜辺」から出発
「
または
「
大小中、大中小どちらでも構いませんので、憶え初めということもありますので
是非、この順番で憶えてほしいと思います (後々必ず役に立ちますので!)
できる限り「ついでにもう1周」も毎回言ってほしいと思います!
(背景に正三角形もイメージしながら!)
cf. \(\small{\sqrt{3}}\) = 1.732…
● 正方形の半分である…
【 45° 45° 90°の直角三角形 】通称?『ヨンゴー』の辺の比は
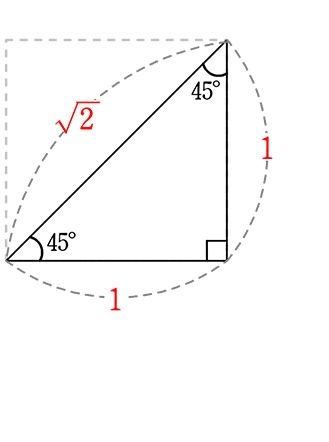
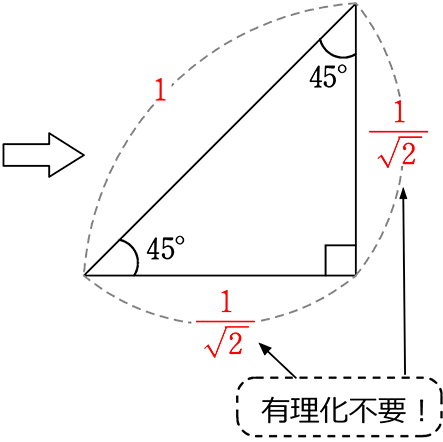
「
で お願いします
cf. \(\small{\sqrt{2}}\) = 1.414…

クリック・タップで答え (反応が遅い場合があります)
《 例 》
(1) 面積を求めましょう
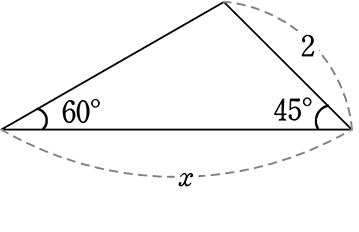
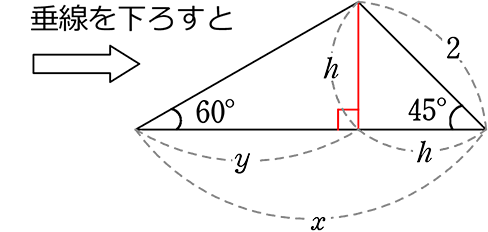
・右三角形は「ヨンゴー」で 2:h = 1:\(\large{\frac{1}{\sqrt{2}}}\)
→
・左は「サブローキュー」で y: h = \(\small{\sqrt{3}}\): 1
→ y:(\(\small{\sqrt{2}}\)) = \(\small{\sqrt{3}}\):1
→ y = \(\small{\sqrt{6}}\)
∴ x = y+h = \(\small{\sqrt{6}}\)+\(\small{\sqrt{2}}\)
| ∴ 面積 | = \(\large{\frac{1}{2}}\)・x・h
= \(\large{\frac{1}{2}}\)・(\(\small{\sqrt{6}}\)+\(\small{\sqrt{2}}\))・\(\small{\sqrt{2}}\) |
(2) 正三角形ABCの内部の線 x を求めましょう
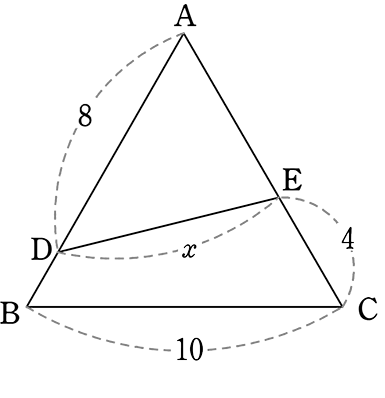
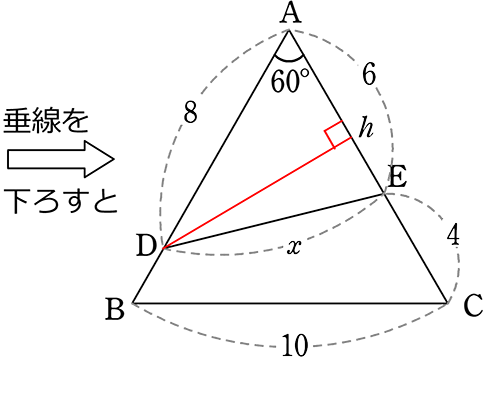
・ 8:Dh = 1:\(\large{\frac{\sqrt{3}}{2}}\) → Dh = 4\(\small{\sqrt{3}}\)
・ 8:Ah = 1:\(\large{\frac{1}{2}}\) → Ah = 4
∴ hE = 6-Ah = 6-(4) = 2
∴ 三平方の定理で
x = \(\small{\sqrt{(Dh)^2+(hE)^2}}\) = \(\small{\sqrt{(4\small{\sqrt{3}})^2+2^2}}\) = \(\small{\sqrt{48+4}}\) = \(\small{\sqrt{52}}\) = 2\(\small{\sqrt{13}}\) //

特別な角② (角度には注目しませんので正確には「特別な辺」)
「サブローキュー」、「ヨンゴー」には敵いませんが、
直角三角形の比で重要なものの2つです
【 5・4・3 の直角三角形 】
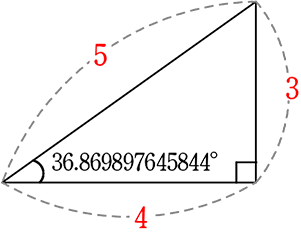
5:4:3
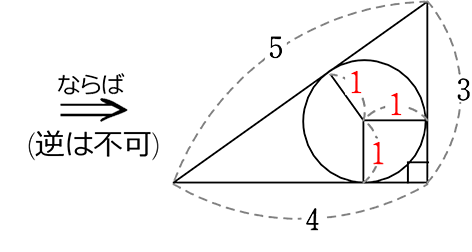
内接円の半径 r は「1」
【 15・14・13 の三角形 】 ←直角三角形ではありませんが、
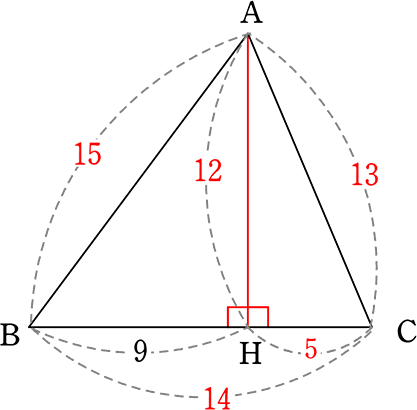
(憶え方:偶数のセット)
△ABHの「15:12:9」は実は「5・4・3の直角三角形」を3倍したものですね!
【 15・14・13 の片割れの直角三角形 】かなり細い三角形ですね
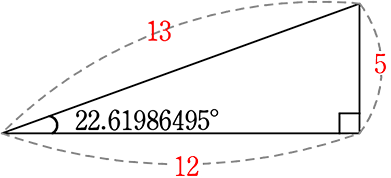
「13」は上の「15・14・13」の「13」ですね
「12」は上の「AH」ですね
《 例 》
図のようなとき、内接円の半径 r を求めましょう
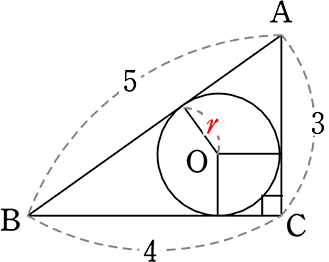
→ 面積を2通りに求めればよいですね
| ① | △ABC = \(\large{\frac{1}{2}}\)・4・3 = 6 |
| ② | △ABC = △OAB+△OBC+△OCA ←「r」がちょうど共通な「高さ」になりますね |
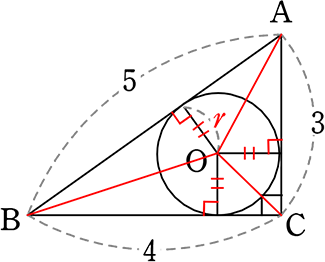
= \(\large{\frac{1}{2}}\)・5・r+\(\large{\frac{1}{2}}\)・4・r+\(\large{\frac{1}{2}}\)・3・r
= \(\large{\frac{(5+4+3)r}{2}}\) (←底辺共有2三角形の考え方)
= 6r
① = ②より
6 = 6r
A. r = 1
知っていれば、一言、「1」で済みますね!
《 例 》
図のようなとき、内接円の半径rを求めましょう
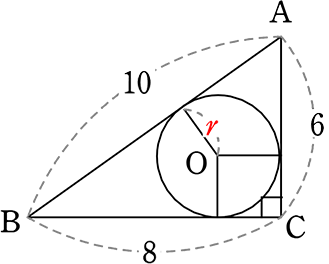
① 10:8:6 の直角三角形 = 2×( 5:4:3 の直角三角形) → 相似比 2
∴ r は「1」と知っているので、 1×(相似比)2 = 2 A. r = 2
② 地道に、 \(\large{\frac{(10+8+6)r}{2}}\) = 24
→ 12r = 24 → r = 2 でもOKですね
《 例 》
図のようなとき、次の問いに答えましょう
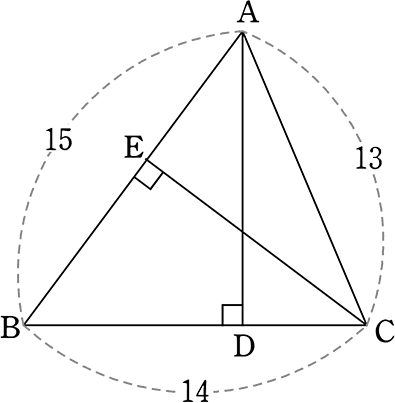
(1) ADを求めましょう
→ BDをxとすると、DCは 14-x
△ABDで、AD2 = 152-x2
△ACDで、AD2 = 132-(14-x)2
∴ ADは同じ長さなので
| 152-x2 | = | 132-(14-x)2 |
| 225-x2 | = | 169-196+28x-x2 |
| 28x | = | 252 |
| 7x | = | 63 |
| x | = | 9 (=BD) |
∴ △ABDで、AD = \(\small{\sqrt{15^2-9^2}}\) = \(\small{\sqrt{225-81}}\) = \(\small{\sqrt{144}}\) = 12
| A. | AD = 12 |
(2) △ABCの内接円の半径r は?
→ (1)より、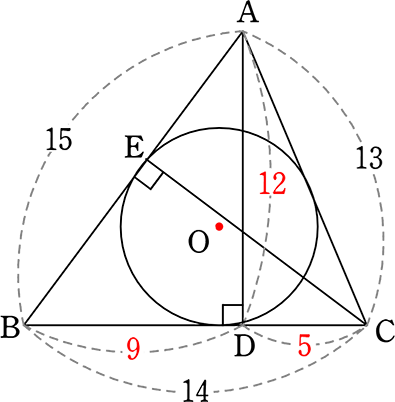
→ △ABC = \(\large{\frac{1}{2}}\)・14・12 = 7・12 = 84
→ △ABC = △OAB+△OBC+△OCA
= \(\large{\frac{(15+14+13)r}{2}}\) = \(\large{\frac{42r}{2}}\) = 21r
∴ 21r = 84 A. r = 4
(3) CEを求めましょう
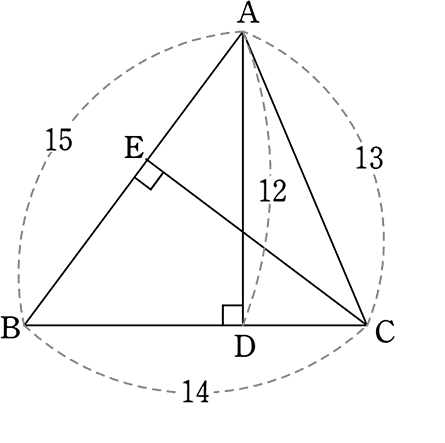
(1)よりAD = 12なので
△ABC = \(\large{\frac{1}{2}}\)・14・12 = 7・12
(ABを底辺、CEを高さと見て)
△CAB = \(\large{\frac{1}{2}}\)・15・CE = 7・12
→ CE = \(\large{\frac{7\cdot12\cdot2}{15}}\)
| A. | CE = \(\large{\frac{56}{5}}\) |
もちろん、AE = x とおいて (1)のように解いてもかまいませんが、同じことをするのは面倒ですね!

ピタゴラス数
ピタゴラス数とは、
c2 =a2+b2 を自然数(正の整数)で成り立たせる組 のことですね
例えば、( 5, 4, 3 ) ( 13, 12, 5 )の直角三角形などですね
そして、ピタゴラス数は次の式で見つけることができます
2つの自然数 m , n (m>n) で
大:斜辺 c = m2+n2
小:辺 a = m2-n2
中:辺 b = 2mn
ex) 適当に2つの数字を用意して
例えば、m = 2 , n = 1 なら
c = 22+11= 4+1 = 5
a = 22-11= 4-1 = 3
b = 2・2・1 = 4
∴ ( 5, 4, 3 ) の直角三角形が発見できましたね
例えば、m = 3 , n = 2 を用意すれば
c = 9+4 = 13
a = 9-4 = 5
b = 2・3・2 = 12
∴ ( 13, 12, 5 ) の直角三角形が発見できましたね
そして、ex)のような 最大公約数が「1」である組合せを「原始ピタゴラス数」
( 実は無数にある。 ) それ以外は ただのピタゴラス数ですね
例えば、( 10, 8, 6 )などはただのピタゴラス数ですね
∵ 原始 ( 5, 4, 3 ) の相似ですものね
《 例 》
△ABCの3辺が、
AB = m2+n2 , BC = 2mn , CA = m2-n2 (m>n)
ならば、△ABCは ∠C = 90°の直角三角形であることを証明しましょう
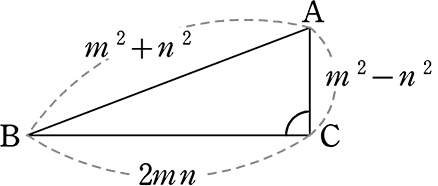
→ ただ ABの 2乗が、 = BC2+CA2 になればよいだけですね
(証明)
| ・AB2 | = (m2+n2)2 = m4+2m2n2+n4 …① |
・BC2+CA2
= (2mn)2+(m2-n2)2
= 4m2n2+m4-2m2n2+n4
= m4+2m2n2+n4 …②
∴ ①=②より ∠C = 90°の直角三角形である //
イ 三平方の定理の活用
① 面積 (1年平面図形への応用問題)
面積に応用という訳ではありませんが、
面積を求める時に、「三平方の定理」はよく役立ちますね!
ですが、あくまで「面積」の問題であって、「三平方」の問題ではないですね!
《 例 》
1辺 6cmの正三角形の「高さ」と「面積」を求めましょう
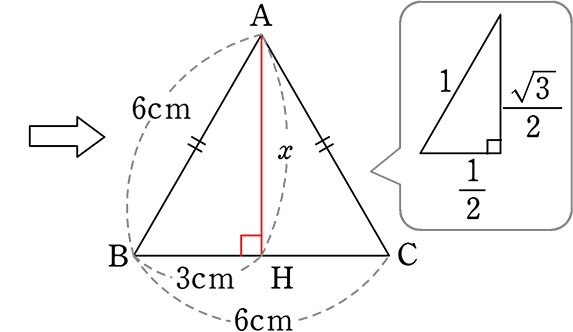
→ 皆まで言うなという感じですが、念のため
(AB:x=) 6:x = 1:\(\large{\frac{\sqrt{3}}{2}}\) → x = 3\(\small{\sqrt{3}}\)
(もちろん、AH = \(\small{\sqrt{6^2-3^2}}\) = 3\(\small{\sqrt{3}}\)でもOK)
∴ 高さ 3\(\small{\sqrt{3}}\) cm //
→ 面積 = \(\large{\frac{1}{2}}\)・6・3\(\small{\sqrt{3}}\) = 9\(\small{\sqrt{3}}\)
∴ 面積 9\(\small{\sqrt{3}}\) cm2 //
《 例 》
1辺 acmの正三角形の「高さ」と「面積」を求めましょう
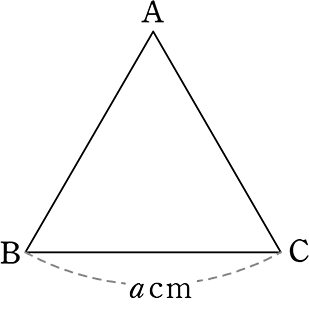
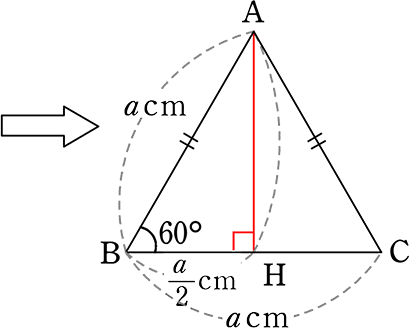
高さ → (AB:AH=) a:AH = 1:\(\large{\frac{\sqrt{3}}{2}}\)
∴ AH = \(\large{\frac{\sqrt{3}}{2}}\)a

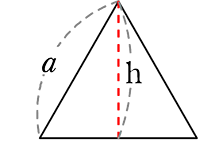
1辺aの正三角形の
| 高さ h = \(\boldsymbol{\large{\frac{\sqrt{3}}{2}}}\)a |
height:高さ
ここで、「正三角形の高さ h = \(\large{\frac{\sqrt{3}}{2}}\)a = \(\large{\frac{\sqrt{3}}{2}}\)(斜辺) 」と暗記的に憶えるよりは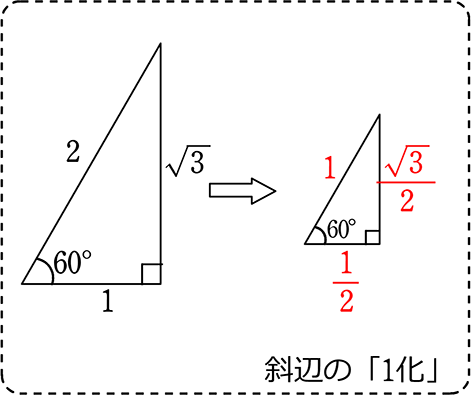
「割合」だから「\(\large{\frac{\sqrt{3}}{2}}\)a」と理解できれば、
「今後のため」にもなりますし、
この公式を公式ではなく、
「当たり前のもの」と思うことができますね
すなわち・・・
| ① | 2時間で120km進む。6時間なら? a時間なら? |
| → | 1時間あたり60km(←\(\large{\frac{120km}{2時間}}\)=\(\large{\frac{60km}{1時間}}\))×6時間= 360km 進む |
| → | 1時間あたり60km(←\(\large{\frac{120km}{2時間}}\)=\(\large{\frac{60km}{1時間}}\))×a時間= 60akm 進む |
⇒「1時間あたり60km」
「a 時間なら 60akm」
分母(時間)を「1化」すると「暗算が楽」になりましたね
(1化する→暗算が楽、1化しない→計算が楽)
| ② | 同様に、1000円の消費税は80円、6000円なら? a円なら? |
| → | 1円あたり0.08円(\(\large{\frac{80円}{1000円}}\)=\(\large{\frac{0.08円}{1円}}\))×6000円= 480円 |
| → | 1円あたり0.08円(\(\large{\frac{80円}{1000円}}\)=\(\large{\frac{0.08円}{1円}}\))×a円= 0.08a円 |
⇒「1円あたり0.08円」
「a円なら 0.08a円」
| ③ | 同様に、斜辺2のとき高さは\(\small{\sqrt{3}}\) 、斜辺6なら? aなら? |
| → | 1斜辺あたり\(\large{\frac{\sqrt{3}}{2}}\)高さ(\(\large{\frac{\sqrt{3}高さ}{2斜辺}}\)=\(\large{\frac{\large{\frac{\sqrt{3}}{2}}高さ}{1斜辺}}\))×6= 3\(\small{\sqrt{3}}\)高さ |
| → | 1斜辺あたり\(\large{\frac{\sqrt{3}}{2}}\)高さ(\(\large{\frac{\sqrt{3}高さ}{2斜辺}}\)=\(\large{\frac{\large{\frac{\sqrt{3}}{2}}高さ}{1斜辺}}\))×a= \(\large{\frac{\sqrt{3}}{2}}\)a高さ |
⇒「1斜辺あたり\(\large{\frac{\sqrt{3}}{2}}\)高さ」
「a斜辺なら \(\large{\frac{\sqrt{3}}{2}}\)a高さ」
| ④ | 同様に、斜辺2のとき底辺は1、斜辺6のときは? aのときは? |
| → | 1斜辺あたり\(\large{\frac{1}{2}}\)底辺(\(\large{\frac{1底辺}{2斜辺}}\)=\(\large{\frac{\large{\frac{1}{2}}底辺}{1斜辺}}\))×6= 3底辺 |
| → | 1斜辺あたり\(\large{\frac{1}{2}}\)底辺(\(\large{\frac{1底辺}{2斜辺}}\)=\(\large{\frac{\large{\frac{1}{2}}底辺}{1斜辺}}\))×a= \(\large{\frac{1}{2}}\)a底辺 |
⇒「1斜辺あたり\(\large{\frac{1}{2}}\)底辺」
「a斜辺なら \(\large{\frac{1}{2}}\)a底辺」
(イメージ)
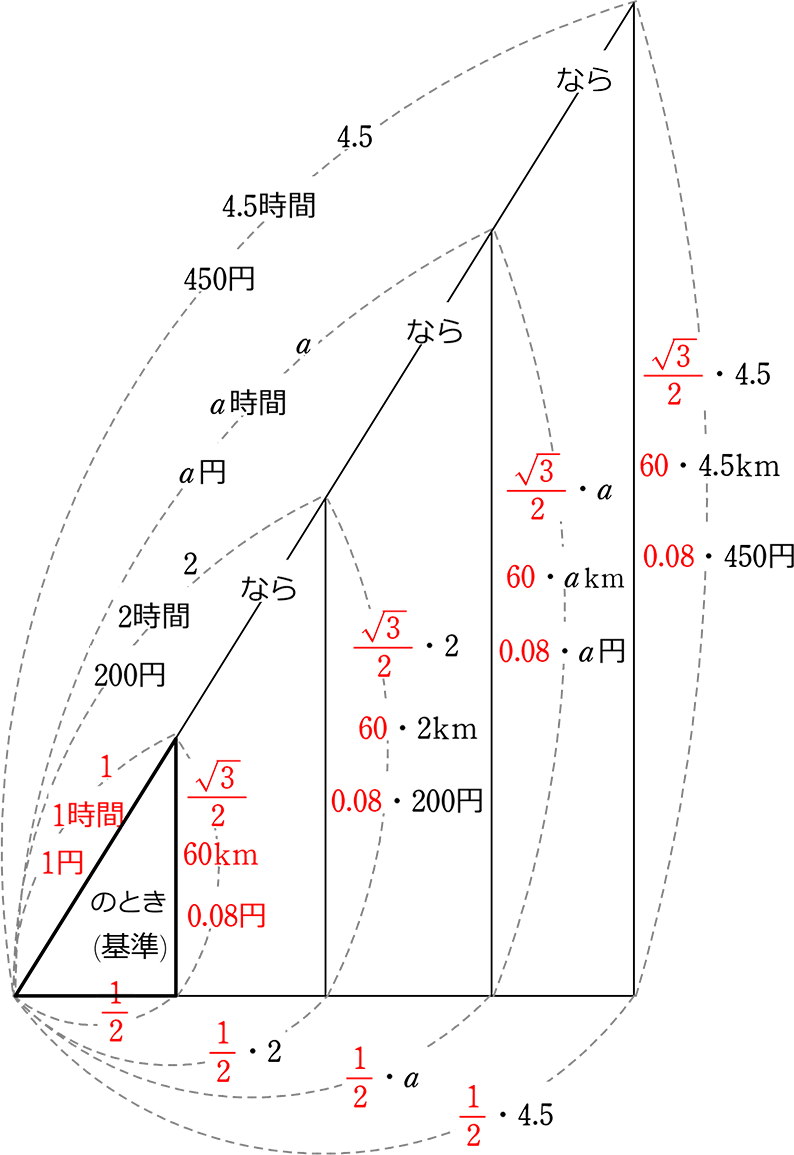
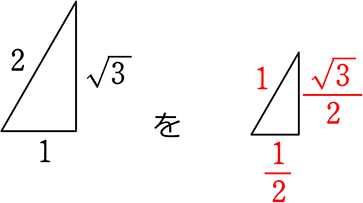
で憶えることは、「1時間あたり」「1円あたり」
のように「1斜辺あたりの高さ、底辺」という「基準」で憶えるということですね
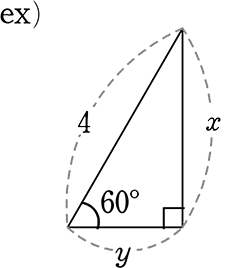
( 2:\(\small{\sqrt{3}}\):1 で憶えている場合)
4:x = 2:\(\small{\sqrt{3}}\) → 2x = 4\(\small{\sqrt{3}}\) → x = 2\(\small{\sqrt{3}}\)
4:y = 2:1 → 2y = 4 → y = 2
( 1:\(\large{\frac{\sqrt{3}}{2}}\):\(\large{\frac{1}{2}}\) で憶えている場合)
x = \(\large{\frac{\sqrt{3}}{2}}\)・4 = 2\(\small{\sqrt{3}}\)
y = \(\large{\frac{1}{2}}\)・4 = 2
もちろん
4:x = 1:\(\large{\frac{\sqrt{3}}{2}}\) → x = 2\(\small{\sqrt{3}}\)
4:y = 1:\(\large{\frac{1}{2}}\) → y = 2
でも十分 2:\(\small{\sqrt{3}}\):1 だけで憶えている場合より楽ですね!
上のことが理解できれば、
1辺aの「正三角形の面積」の公式も当たり前のことに思えますね
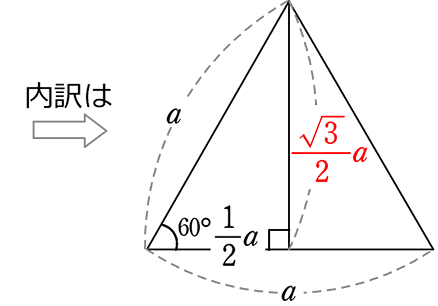
面積 = \(\large{\frac{1}{2}}\)・a・\(\large{\frac{\sqrt{3}}{2}}\)a


1辺aの
| 正三角形の面積 = \(\boldsymbol{\large{\frac{\sqrt{3}}{4}}}\)a2 |
(= \(\large{\frac{1}{2}}\)・a・\(\large{\frac{\sqrt{3}}{2}}\)a)
\(\boldsymbol{\large{\frac{\sqrt{3}}{4}}}\)a2 は忘れても
\(\large{\frac{1}{2}}\)・a・\(\large{\frac{\sqrt{3}}{2}}\)a はすぐに考えつきますね!
《 例 》
幅3cmの紙テープを図のように線分ABで折り返した時
ABが5cmであった、△ABCの面積を求めましょう
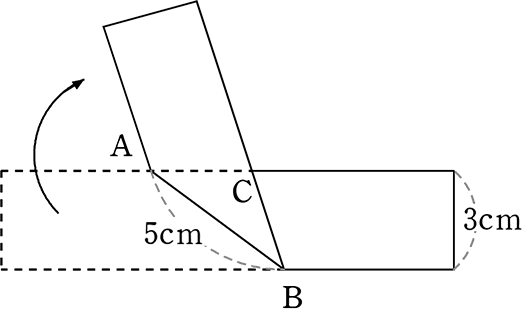
その前に、前提として
| テープの折り返しで「重なった部分の三角形」は、どのような角度で折り返しても、
自然現象的に「二等辺三角形」ですね |
(証明)
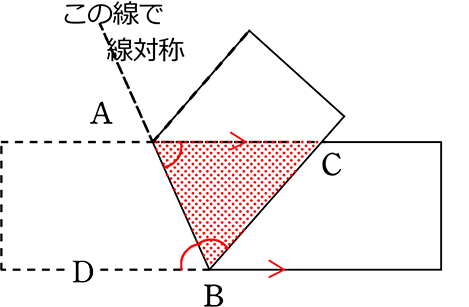
∠CBA = ∠DBA (線対称より)
∠DBA = ∠CAB (錯角より)
∴ ∠CBA = ∠CAB より
2角が等しいので
△CABは二等辺三角形
⇒ 重なった部分は二等辺三角形
それでは、本題に戻って、
△CABの面積は?
→ \(\large{\frac{1}{2}}\)×ACまたはBC×3cm
→ ACまたはBCがわかればいいんだな
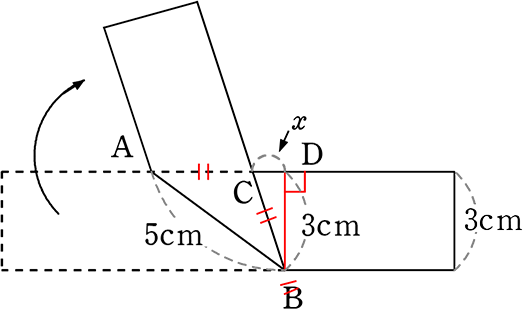
AD = \(\small{\sqrt{5^2-3^2}}\) = \(\small{\sqrt{25-9}}\) = \(\small{\sqrt{16}}\) = 4cm
↑「5,4,3 の三角形だな」→ 4 でもOK
| ∴ | CDをxとすると、AC = 4-x = BC (二等辺三角形より) |
△BCDにおいて、BC2 = CD2+BD2
| (4-x)2 | = | x2+32 |
| 16-8x+x2 | = | x2+32 |
| -8x | = | -7 |
| x | = | \(\large{\frac{7}{8}}\) |
∴ AC = 4-\(\large{\frac{7}{8}}\) = \(\large{\frac{32-7 }{8}}\) = \(\large{\frac{25}{8}}\)
∴ △ABC = \(\large{\frac{1}{2}}\)・AC・高さ = \(\large{\frac{1}{2}}\)・\(\large{\frac{25}{8}}\)・3 = \(\large{\frac{75}{16}}\)
| A. | \(\large{\frac{75}{16}}\) | cm2 |
《 例 》
「関数」の問題
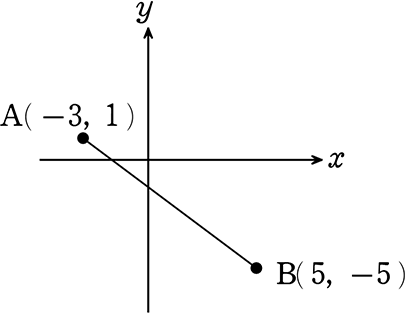
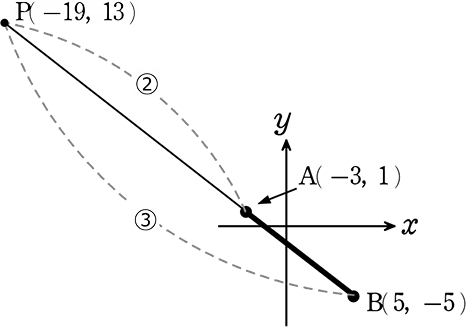
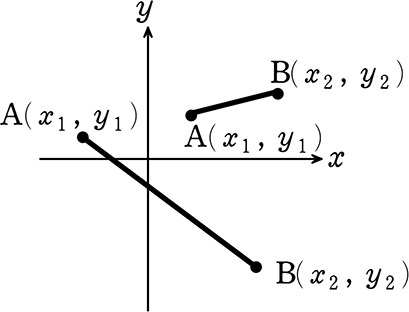
(1) ABの中点の座標を求めましょう (復習ですね) (座標の中点の求め方)
→ ( \(\large{\frac{5\color{red}{+}(-3)}{2}}\) , \(\large{\frac{-5\color{red}{+}1}{2}}\) ) = ( \(\large{\frac{2}{2}}\) , \(\large{\frac{-4}{2}}\) ) = ( 1, -2 ) //
cf.
完全な余談問題です (高校の課程)
(2) ABを3:2に内分する点Pの座標を求めましょう

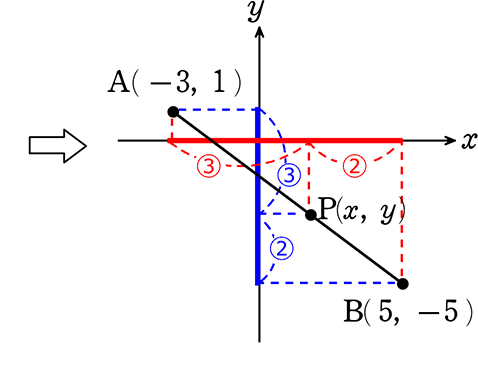
→ まずx方向だけを考えると
AB間の距離は、5-(-3) = 8 →「引き算!」
ということは
・AP間の距離は、x-(-3) = x+3
・PB間の距離は、5-(x) = 5-x
| ∴ (x+3):(5-x) | = | ③:② |
| ②(x+3) | = | ③(5-x) |
| 2x+6 | = | 15-3x |
| 5x | = | 9 |
| x | = | \(\large{\frac{9}{5}}\) (\(\large{\frac{9}{5}}\), ?) |
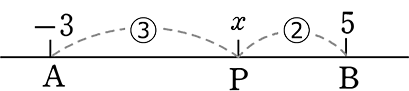
→ 同様にyだけを考えると
どちらでもOK
「ABを 3:2」とは
↑Aが始点で、3:2
・AP間の距離は、y-(1) = y-1 (下なら 1-(y) = 1-y)
・BP間の距離は、-5-(y) = -5-y (下なら y-(-5) = y+5)
| ∴ (y-1):(-5-y) | = | ③:② |
| 2y-2 | = | -15-3y |
| 5y | = | -13 |
| y | = | -\(\large{\frac{13}{5}}\) |
(下なら)
| (y+5):(1-y) | = | ②:③ |
| 3y+15 | = | 2-2y |
| 5y | = | -13 |
| y | = | -\(\large{\frac{13}{5}}\) |
∴ P\(\left(\large{\frac{9}{5}},-\large{\frac{13}{5}}\right )\)
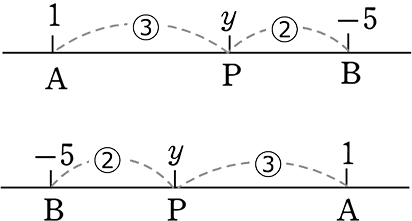
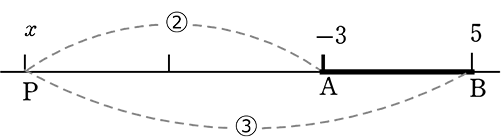
(3) ABを 3:2 に外分する点Pの座標を求めましょう

→ xだけを考えると
AP間の距離は、x-(-3) = x+3
PB間の距離は、x-(5) = x-5
| ∴ (x+3):(x-5) | = | 3:2 |
| 2(x+3) | = | 3(x-5) |
| 2x+6 | = | 3x-15 |
| x | = | 21 (21, ?) |
→ 同様に y だけを考えると
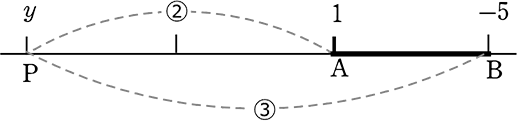
AP間の距離は、y-(1) = y-1
PB間の距離は、y-(-5) = y+5
| ∴ (y-1):(y+5) | = | 3:2 |
| 2y-2 | = | 3y+15 |
| y | = | -17 |
∴ P(21, -17)
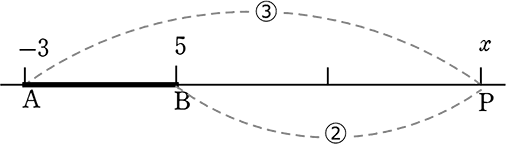
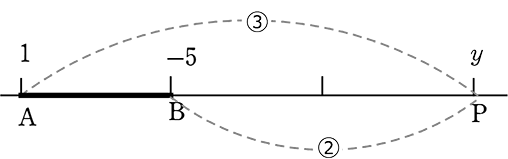
(4) ABを 2:3 に外分する点Pの座標を求めましょう
→ xだけを考えると
AP間の距離は、-3-(x) = -3-x
PB間の距離は、5-(x) = 5-x
| ∴ (-3-x):(5-x) | = | 2:3 |
| -9-3x | = | 10-2x |
| x | = | -19 (-19, ?) |
→ 同様に y だけを考えると
AP間の距離は、1-(y) = 1-y
PB間の距離は、-5-(y) = -5-y
| ∴ (1-y):(-5-y) | = | 2:3 |
| 3-3y | = | -10-2y |
| y | = | 13 |
∴ P(-19, 13)
◎ 公式にするために、文字で同じようにやってみましょう
● ABを m:n に内分する点P(xp, yp)の座標は?
→ xだけを考えると
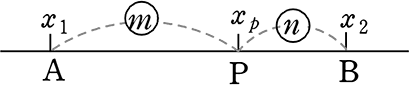
AP間の距離は、xp-x1
PB間の距離は、x2-xp
| ∴ xp-x1:x2-xp | = | m:n |
| nxp-nx1 | = | mx2-mxp |
| nxp+mxp | = | mx2+nx1 |
| (n+m)xp | = | mx2+nx1 |
| xp | = | \(\large{\frac{mx_2+nx_1}{m+n}}\) |
→ yだけを考えると

AP間の距離は、yp-y1
PB間の距離は、y2-yp
| ∴ yp-y1:y2-yp | = | m:n |
| nyp-ny1 | = | my2-myp |
| nyp+myp | = | my2+ny1 |
| (n+m)yp | = | my2+ny1 |
| yp | = | \(\large{\frac{my_2+ny_1}{m+n}}\) |

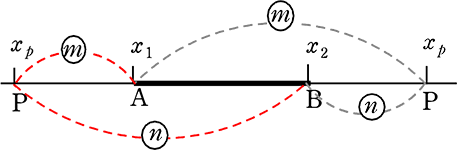
m:n に「内分」するPの座標
P(xp, yp) = 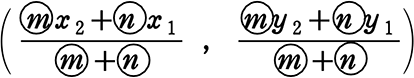
| 公式の注意点 … | mは終点に掛ける。nは始点に掛ける。(クロスな感じ) |
【 試し確認 】
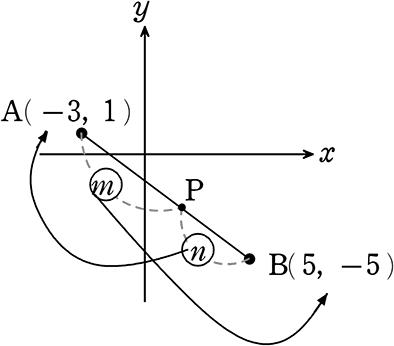
↑クロスな感じ
●「ABを3:2」に内分する点Pの座標は?
Aが始発で3, 2
P = ( \(\large{\frac{3\ \cdot \ 5+2\cdot(-3) }{3+2}}\), \(\large{\frac{3\cdot(-5)+2\ \cdot \ 1}{3+2}}\))
= (\(\large{\frac{15-6}{5}}\), \(\large{\frac{-15+2}{5}}\))
= (\(\large{\frac{9}{5}}\), -\(\large{\frac{13}{5}}\)) 同じですね
●「ABを1:1(中点)に内分する点Pの座標は?
Aが始発で1,1
P = \(\large{\frac{(1\ \cdot \ 5+1\cdot(-3)}{1+1}}\), \(\large{\frac{1\cdot(-5)+1\ \cdot \ 1}{1+1}}\))
= (\(\large{\frac{5+(-3)}{2}}\), \(\large{\frac{-5+1}{2}}\)) ←まさに中点の公式ですね
= (1, -2)
●「ABを3:2」に内分する点Pの座標は?
Aが始発で3, 2
P = (\(\large{\frac{18+4}{5}}\), \(\large{\frac{9+4}{5}}\))
= (\(\large{\frac{22}{5}}\), \(\large{\frac{13}{5}}\))
よって、直線の(右肩上がり、右肩下がり)傾きは関係のない公式ですね
ABを〇:△なら「Aが始発で〇:~」
BAを〇:△なら「Bが始発で○:~」
ということだけ忘れなければよいですね
● ABを m:n に外分する点P(xp, yp)の座標は?
→ xだけを考えると
( m>n のとき、mは相手を越えて、戻って相手に着地)
( m<n のとき、上のようだと相手に着地できないのでmは相手の反対側に行く)
同時に行きますね
・AP間の距離は、越xp-x1 外x1-xp
・PB間の距離は、越xp-x2 外x2-xp
| ∴ xp-x1:xp-x2 | = | m:n |
| nxp-nx1 | = | mxp-mx2 |
| nxp-mxp | = | -mx2+nx1 |
| (n-m)xp | = | -mx2+nx1 |
| xp | = | \(\large{\frac{-mx_2+nx_1}{-m+n}}\) |
| = | \(\large{\frac{mx_2-nx_1}{m-n}}\) |
| ∴ x1-xp:x2-xp | = | m:n |
| nx1-nxp | = | mx2-mxp |
| -nxp+mxp | = | mx2-nx1 |
| (-n+m)xp | = | mx2-nx1 |
| xp | = | \(\large{\frac{mx_2-nx_1}{m-n}}\) |
越も外も全く同じですね!
( yも同様なので省略しますね)

m:nに「外分」するPの座標
P(xp, yp) = (\(\large{\frac{mx_2-nx_1}{m-n}}\), \(\large{\frac{my_2-ny_1}{m-n}}\))
【 試し確認 】
越「ABを3:2」に外分する点Pの座標は?
P = (\(\large{\frac{3\ \cdot \ 5-2\cdot(-3)}{3-2}}\), \(\large{\frac{3\cdot(-5)-2\ \cdot \ 1}{3-2}}\))
= (15+6, -15-2)
= (21, -17) ←先と同じですね
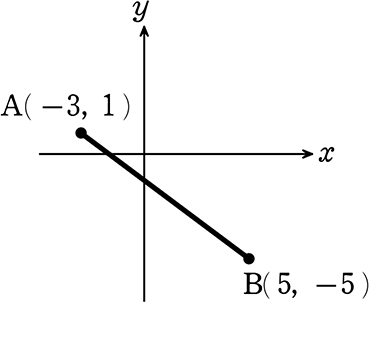
外「ABを2:3」に外分する点Pの座標は?
P = (\(\large{\frac{2\ \cdot \ 5-3\cdot(-3)}{2-3}}\), \(\large{\frac{2\cdot(-5)-3\ \cdot \ 1}{2-3}}\))
= (\(\large{\frac{10+9}{-1}}\), \(\large{\frac{-10-3}{-1}}\))
= (-19, 13) ←先と同じですね!
どっちに出るか自動判別してくれていますね!
前にある方が始点 だけ気を付ける
だけ気を付ける
m:n の順を間違わない
| ◎ | 公式の当てはめに不安がある場合は、
最初のように「距離」と「比」から計算してもよいですね |
かなり横道にそれてしまいましたが、本題に戻りますね
(5) AB間の距離を求めましょう
再度図です
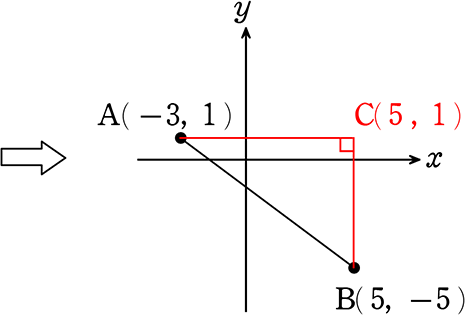
→ AB = \(\small{\sqrt{(AC)^2+(BC)^2}}\)
・AC = 5-(-3) = 8
・BC = 1-(-5) = 6
∴ AB = \(\small{\sqrt{8^2+6^2}}\) = \(\small{\sqrt{64+36}}\) = \(\small{\sqrt{100}}\) = 10 //
→ これが「座標上の2点間の距離」の公式の原理ですね
《 例 》
図のようなとき、接点A接点Bの長さを求めましょう
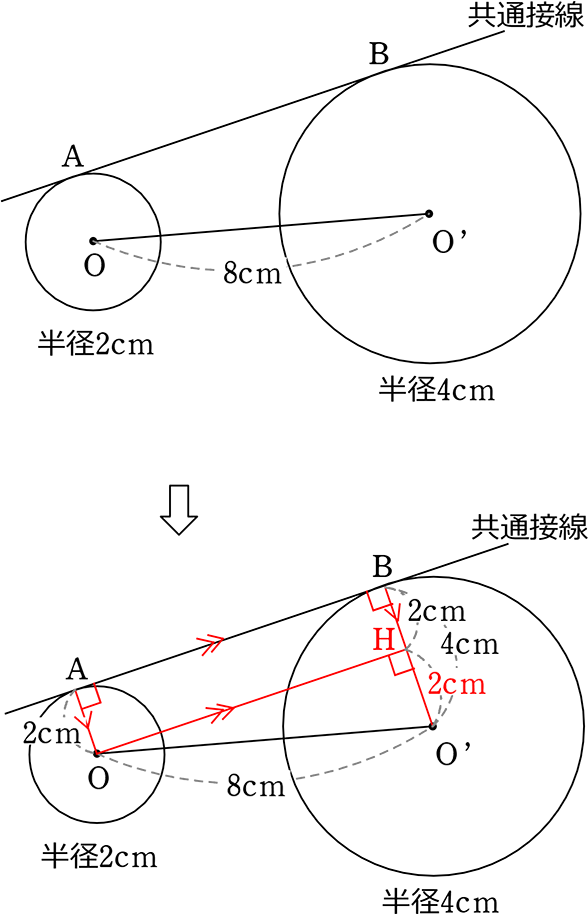
AO、BO’は接線に垂直 → ∴ AO//BO’
OからABに平行なOHをひくと → AO = BH
ここまでデータを書き込めたら、後は簡単ですね
→ AB = OH
OH = \(\small{\sqrt{8^2-2^2}}\) = \(\small{\sqrt{64-4}}\) = \(\small{\sqrt{60}}\) = 2\(\small{\sqrt{15}}\)
| A. | 2\(\small{\sqrt{15}}\) cm |
《 例 》
三辺を直径とする半円を3つ書いたとき、赤い部分の面積を求めましょう
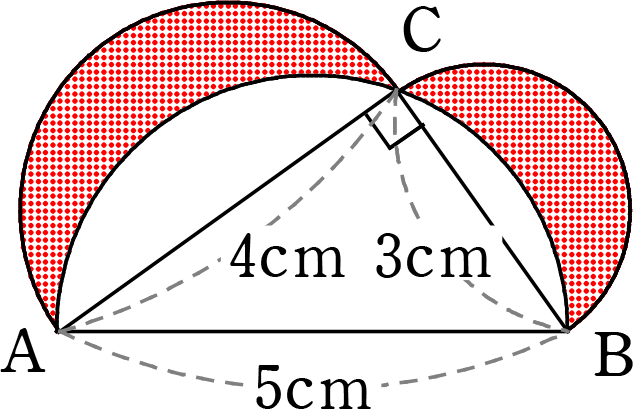
いわゆる「ヒポクラテスの月」と言われるものですね
→ 『 赤い部分の面積 = 直角三角形の面積になる』というものですね
ということは、赤面積 = \(\large{\frac{1}{2}}\)・3・4 = 6cm2??
では、地道に確認
| 赤面積 | = | 全部-直径ABの半円 (円周角が直角なら弦は直径) |
| = | △ABC+直径ACの半円+直径BCの半円-直径ABの半円 ですね | |
| = | \(\large{\frac{1}{2}}\)・3・4 +\(\large{\frac{1}{2}}\)・22π +\(\large{\frac{1}{2}}\)・1.52π -\(\large{\frac{1}{2}}\)・2.52π | |
| = | 6+2π+1.125π-3.125π | |
| = | 6 |
| A. | (確かに) 6cm2 |
《 例 》
斜線部の面積を求めましょう
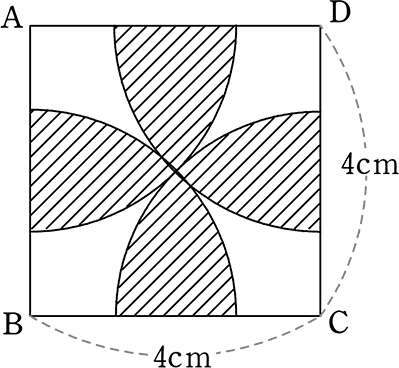
この手の「模様問題」は
何から何をどういう順番で削っていくのか
どこが求めやすいのか、直線を足して分析したり
パズル感覚の練習ですね
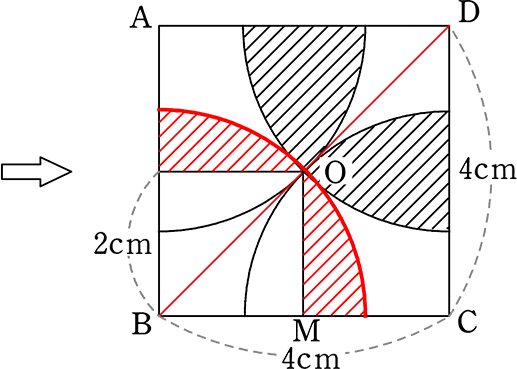
| → | 赤斜線面積 = \(\large{\frac{1}{4}}\)赤円-2cm正方形
それ(赤斜線部分)が4つで黒斜線部分ですね |
| → | BO(赤円半径):OM →「ヨンゴーの直角三角形」 |
| ∴ BO:2 | = | \(\small{\sqrt{2}}\):1 |
| BO | = | 2\(\small{\sqrt{2}}\) |
| ∴ 赤斜線面積 | = | \(\large{\frac{1}{4}}\)赤円- 2cm正方形 |
| = | \(\large{\frac{1}{4}}\)・(2\(\small{\sqrt{2}}\))2π-22 | |
| = | 2π-4 |
→ 黒斜線部分 = 4赤斜線部分 = 4(2π-4)
| A. | 8π-16 (cm2) |
② 体積 (1年空間図形への応用問題)
《 例 》
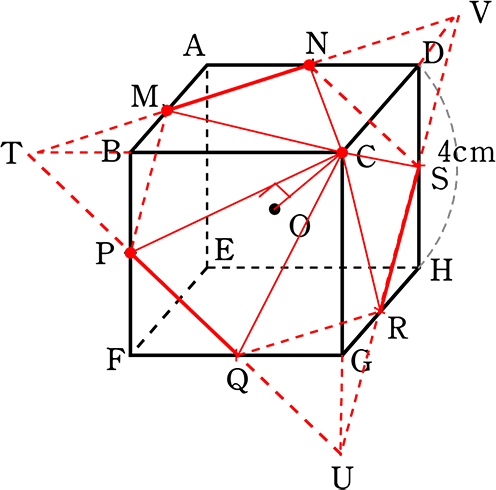
1辺3の正四面体ABCDについて、以下の問いに答えましょう
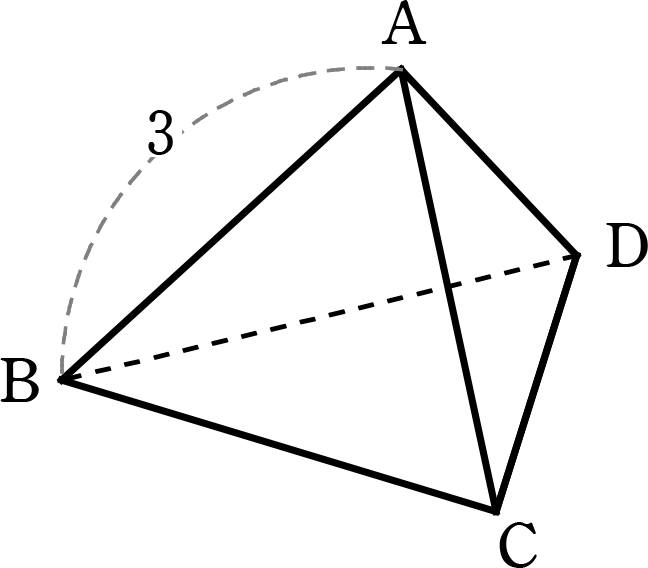
(正四面体 = 4面全てが正三角形)
(1) 表面積は?
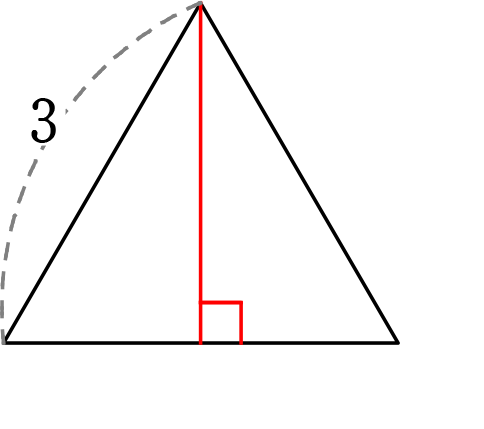
| ↓1面(正三角形)の高さ | = \(\large{\frac{\sqrt{3}}{2}}\)a = \(\large{\frac{\sqrt{3}}{2}}\)・(3) = \(\large{\frac{3\sqrt{3}}{2}}\) |
(または、
| ↓1面(正三角形)の面積 | = \(\large{\frac{1}{2}}\)・底辺・高さ = \(\large{\frac{1}{2}}\)・3・\(\large{\frac{3\sqrt{3}}{2}}\) = \(\large{\frac{9\sqrt{3}}{4}}\) |
→ ∴ 表面積
(2) 点Aから△BCDに下した垂線の長さは?
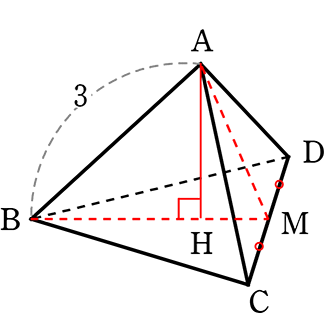
(紙に描いた立体の内部の図形は「ただのイメージ」ですが、
面倒でも別に書き出して、数値を書き込むと「具体的なイメージ」となって、
新たな「値」などを発見することが結構ありますね)
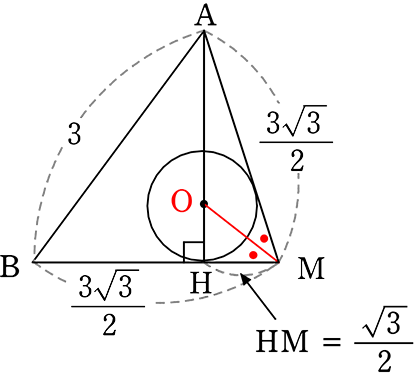
ここで、Aからの垂線 点Hは「△ACDの重心である」と知っていれば、
「BH:HM = 2:1」ですね! (重心とは)
∴ BH = \(\large{\frac{3\sqrt{3}}{2}}\)×\(\large{\frac{2}{3}}\) = \(\small{\sqrt{3}}\)
| ∴ AH | = \(\small{\sqrt{AB^2-BH^2}}\) = \(\small{\sqrt{3^2-(\sqrt{3})^2}}\) = \(\small{\sqrt{9-3}}\) = \(\small{\sqrt{6}}\) という流れですね |
(Hが△BCDの重心という理由)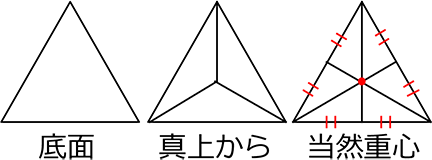
∴ 正四面体の頂点から底面に落とした垂線は底面の重心に当たる
cf.
正三角形の場合は、「重心(対辺の中点への線の交点)」であり、「内心(角の二等分線の交点)」であり、「外心(辺の垂直二等分線の交点) でもありますね

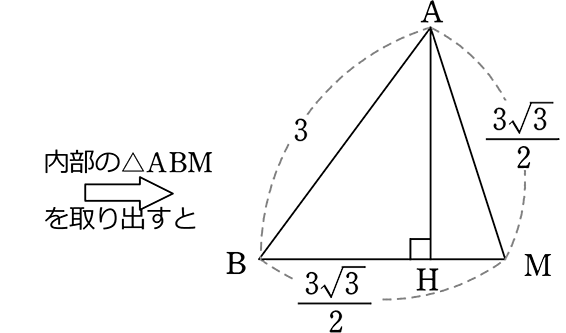
「重心」と「知らない場合」で進めますね、「15, 14, 13, の三角形」の要領で…
→ HM = x とすると、 BH = \(\large{\frac{3\sqrt{3}}{2}}\)-x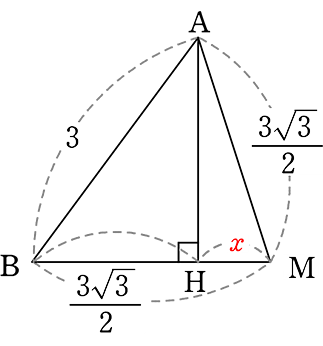
| ・ | △ABHで、AH2 = 32-\(\left(\large{\frac{3\sqrt{3}}{2}}\small{-x}\right )^2\) = 9-\(\left(\large{\frac{ 27 }{ 4 }}\small{-3\sqrt{3}}x+x^2\right )\) = -x2+3\(\small{\sqrt{3}}\)x+\(\large{\frac{9}{4}}\) |
| ・ | △AMHで、AH2 = \(\left(\large{\frac{3\sqrt{3}}{2}}\right )^2\)-x2 = -x2+\(\large{\frac{27}{4}}\) |
| ∴ -x2+3\(\small{\sqrt{3}}\)x+\(\large{\frac{9}{4}}\) | = | -x2+\(\large{\frac{27}{4}}\) |
| 3\(\small{\sqrt{3}}\)x | = | \(\large{\frac{18}{4}}\) = \(\large{\frac{9}{2}}\) |
| x | = | \(\large{\frac{9}{2\ \cdot \ 3\sqrt{3}}}\) |
| = | \(\large{\frac{3}{2\sqrt{3}}}\) | |
| = | \(\large{\frac{3\sqrt{3}}{6}}\) | |
| = | \(\large{\frac{\sqrt{3}}{2}}\) ←HM |
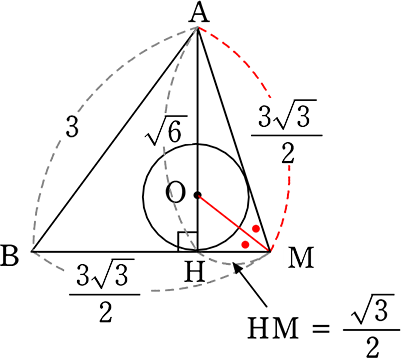
∴ △AMHで AH = \(\small{\sqrt{\left( \large{\frac{3\sqrt{3}}{2}}\right )^2-\left( \large{\frac{\sqrt{3}}{2}} \right )^2}}\) = \(\small{\sqrt{\large{\frac{27-3}{4}}}}\) = \(\small{\sqrt{6}}\) // ←重心と知っている場合と同じ答えですね
(3) 四面体ABCDの体積は?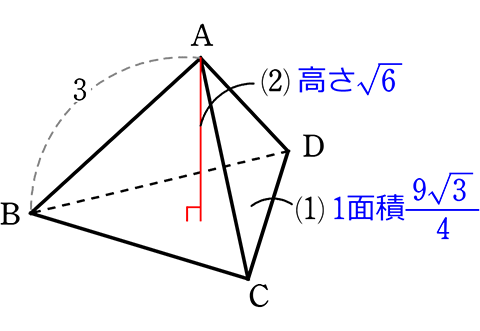
四面体の体積 = \(\large{\frac{1}{3}}\)・底面積・高さ = \(\large{\frac{1}{3}}\)・\(\large{\frac{9\sqrt{3}}{4}}\)・\(\small{\sqrt{6}}\) = \(\large{\frac{3\sqrt{3\ \cdot \ 3\ \cdot \ 2}}{4}}\) = \(\large{\frac{9\sqrt{2}}{4}}\) //
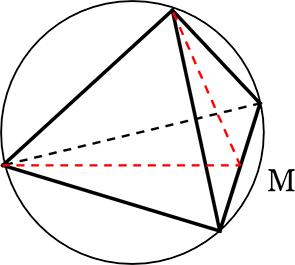
(4) 四面体ABCDの内接球の半径は?
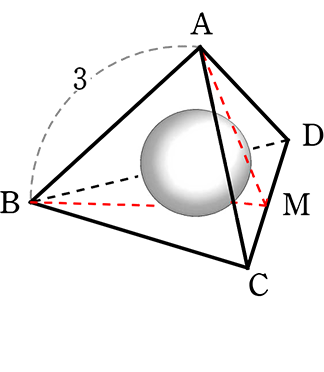

球はABには接しませんね(届きませんね)
なぜなら、BM、AMは「面」、 ABは「谷」ですものね
球の中心はAH上のどこかですね
なぜなら正四面体を真上からみると…

…AH上ですね
ついでに、Hは△BCDの重心ということも
納得できます → ∴ BH:HM = 2:1
→ OHを求めれば、それが内接球の半径ですね
| → AO:OH | = | \(\large{\frac{3\sqrt{3}}{2}}\):\(\large{\frac{\sqrt{3}}{2}}\) (角の二等分線と辺の比より) |
| = | 3\(\small{\sqrt{3}}\):\(\small{\sqrt{3}}\) | |
| = | 3:1 |
∴ AH = \(\small{\sqrt{6}}\)、AO:OH = 3:1 より
OH = \(\large{\frac{\sqrt{6}}{3+1}}\)・1 =\(\large{\frac{\sqrt{6}}{4}}\) = 内接球の半径 //
(5) 外接球の半径は?
→ 内接球の中心と外接球の中心は一致します!
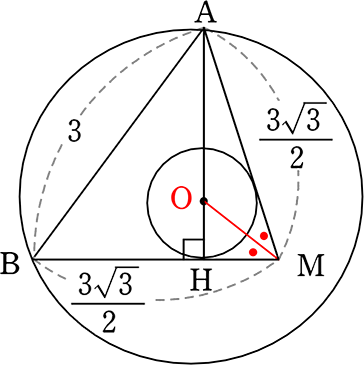
図が正確でないので
きれいな二重丸には
なりませんでしたが…
→ 外接球半径 = OA ですね!
∴ AH-OH = \(\small{\sqrt{6}}\)-\(\large{\frac{\sqrt{6}}{4}}\) = \(\large{\frac{3\sqrt{6}}{4}}\) //
正四面体に関して、たった「1辺」のデータから
ここまで求まるのも すごいことですね
今回は1辺「3」で行いましたが、これを1辺「a」で行うと
たくさんの公式ができあがりますね!

正四面体のデータ

正三角形の高さ = \(\large{\frac{\sqrt{3}}{2}}\)a
正三角形の面積 = \(\large{\frac{\sqrt{3}}{4}}\)a2
正四面体の高さ = \(\large{\frac{\sqrt{6}}{3}}\)a
正四面体の体積 = \(\large{\frac{\sqrt{2}}{12}}\)a3
正四面体の内接球の半径 = \(\large{\frac{\sqrt{6}}{12}}\)a (高さの = \(\large{\frac{1}{4}}\))
正四面体の外接球の半径 = \(\large{\frac{\sqrt{6}}{4}}\)a (高さの = \(\large{\frac{3}{4}}\))
(頂点Aからの垂線と △BCDの交点は「重心」!)
立体図形のイメージ練習にもってこいですので、
是非「a」で練習してみてくださいね!
立体図形のイメージ(空間認識力?)は前頭葉が熱くなりますが、
鍛えられれば、日常生活でも必ず役立ちますね!
ex)
| ・ | 10tトラックに18t の荷物を積むことができます!違反ですが! |
| ・ | 部屋のお片付けも「始めれば」、スッキリできるように!
→「始め」なければ、散らかりっぱなしですが、やればできる人のはずです! |
《 例 》
1辺8cmの正方形ABCDの辺BC、CDの中点をそれぞれE、Fとしたとき、
以下の問いに答えましょう
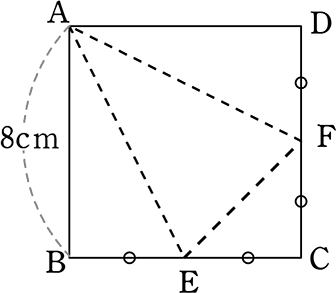
(1) BCDが1点で集まるように点線で折り曲げたときにできる
三角錐の体積を求めましょう
イメージ図はこんな感じでしょうか
イメージ図はできる限り正確に書けますように!
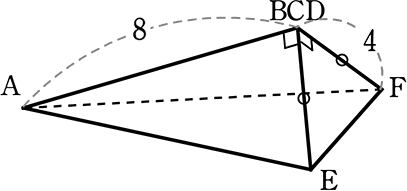
| 三角錐の体積 | = | \(\large{\frac{1}{3}}\)・底面積・高さ |
| = | \(\large{\frac{1}{3}}\)・△CEF・AB | |
| = | \(\large{\frac{1}{3}}\)・\(\left( \large{\frac{1}{2}}\cdot\small{4}\cdot\small{4} \right )\)・8 | |
| = | \(\large{\frac{1}{3}}\)・(8)・8 | |
| = | \(\large{\frac{64}{3}}\) cm2 |
(2) △AEFを底面としたときの三角錐の高さを求めましょう
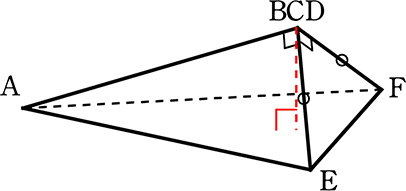
→ (1)で求めた体積に変わりはありませんので
三角錐の体積\(\large{\frac{64}{3}}\) = \(\large{\frac{1}{3}}\)・△AEF・高さ
△AEF =  ABCD-△ABE-△ECF-△FDA = 64-16-8-16 = 24
ABCD-△ABE-△ECF-△FDA = 64-16-8-16 = 24

三平方を学んだところなので、△AEFを見て、
思わず EF = \(\small{\sqrt{EC^2+FC^2}}\) …AE=…△AEFの高さは…と難しく考えがちに
なりますが、基本に戻って「1番楽な方法探し」を忘れずに!
| ∴ \(\large{\frac{1}{3}}\)・△AEF・高さ | = | \(\large{\frac{64}{3}}\) |
| \(\large{\frac{1}{3}}\)・24・高さ | = | \(\large{\frac{64}{3}}\) |
| 8・高さ | = | \(\large{\frac{64}{3}}\) |
| 高さ | = | \(\large{\frac{8}{3}}\) cm |

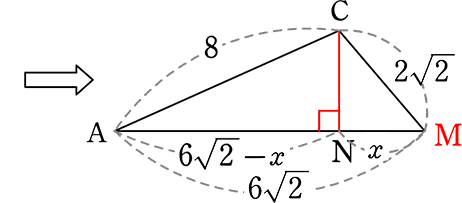
もちろん、「15, 14, 13の三角形」のように、断面図→CMの値→AMの値→x の値→高さCN と求めてもOKです
少し時間はかかりますが、いい勉強になりますね!
《 類問 》
1辺4cmの立方体ABCD_EFGHの辺BCの中点をMとするとき、
頂点Bから△AFMに下ろした垂線の長さを求めましょう
立方体:全面正方形、直方体:長方形の面もある
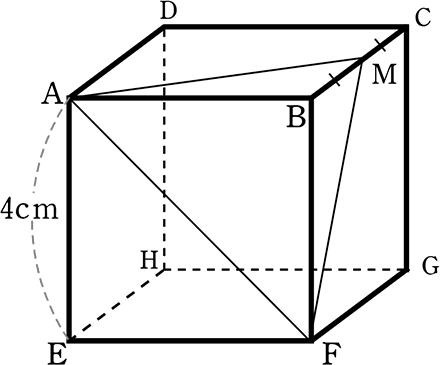
| → | 「頂点Bから△AFMに下ろした垂線の長さ」 = 「三角錐B_AFMの高さ」 |
(流れ)
| ① | 三角錐の体積をできる限り簡単に求めておく(底面BFMなど) |
| ② | 三角錐の体積を△AFMを底面とした求め方で求めれば高さ(垂線の長さ)がわかる (別方向からの体積) |
| ③ | ということは△AFMの面積も必要だな |
では
| ① 三角錐の体積 | = | \(\large{\frac{1}{3}}\)・(△AFB)・BM |
| = | \(\large{\frac{1}{3}}\)・(\(\large{\frac{1}{2}}\)・4・4)・2 | |
| = | \(\large{\frac{1}{3}}\)・8.・2 | |
| = | \(\large{\frac{16}{3}}\) cm3 |
② △AFMの面積
→ 図の切り出しでイメージ
底辺AF = 4\(\small{\sqrt{2}}\) はすぐ判明
(1:\(\small{\sqrt{2}}\) = 4:AF)

高さMNのためにMFをイメージ図で
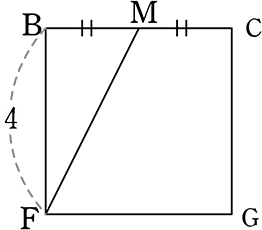
| MF | = \(\small{\sqrt{BF^2+BM^2}}\) |
| = \(\small{\sqrt{16+4}}\) = \(\small{\sqrt{20}}\) | |
| = 2\(\small{\sqrt{5}}\) |
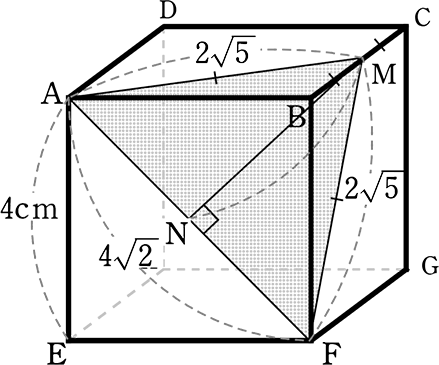
| ∴ 高さMN | = \(\small{\sqrt{MF^2-NF^2}}\) = \(\small{\sqrt{(2\sqrt{5})^2-(2\sqrt{2})^2}}\) = \(\small{\sqrt{20-8}}\) = 2\(\small{\sqrt{3}}\) |
∴ △AFM = \(\large{\frac{1}{2}}\)・4\(\small{\sqrt{2}}\)・2\(\small{\sqrt{3}}\) = 4\(\small{\sqrt{6}}\) cm2
| ③ 三角錐の体積\(\large{\frac{16}{3}}\) | = | \(\large{\frac{1}{3}}\)・4\(\small{\sqrt{6}}\)・高さ |
| \(\large{\frac{4\sqrt{6}}{3}}\)・高さ | = | \(\large{\frac{16}{3}}\) |
| 4\(\small{\sqrt{6}}\)・高さ | = | 16 |
| 高さ | = | \(\large{\frac{4}{\sqrt{6}}}\) = \(\large{\frac{4\sqrt{6}}{6}}\) = \(\large{\frac{2}{3}}\)\(\small{\sqrt{6}}\) |
| A. | (垂直に下ろした線=) \(\large{\frac{2}{3}}\)\(\small{\sqrt{6}}\) cm |
《 例 》
1辺6cmの立方体ABCD_EFGHの辺EF、FGの中点をそれぞれI、Jとするとき、
立体ABC_IFJの体積を求めましょう

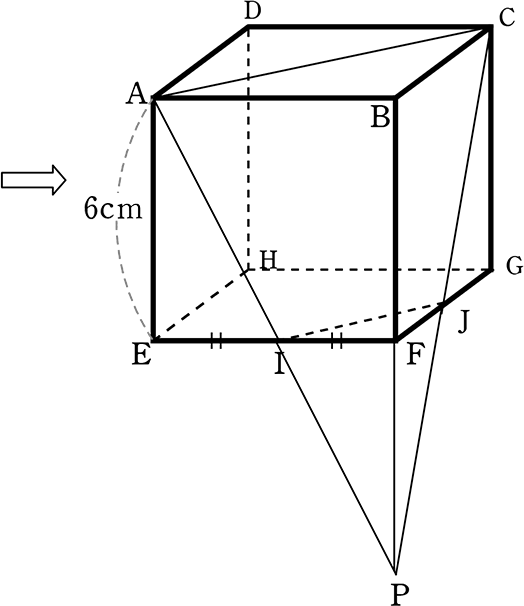
| → | 三角錐の体積 を求める公式はありますが、
頂点のない途中までの公式はありませんね |
| → | ということは、
立体ABC_IFJ = 三角錐P_BAC-三角錐P_FIJ ですね |
では、
まず大三角錐P_BACの体積
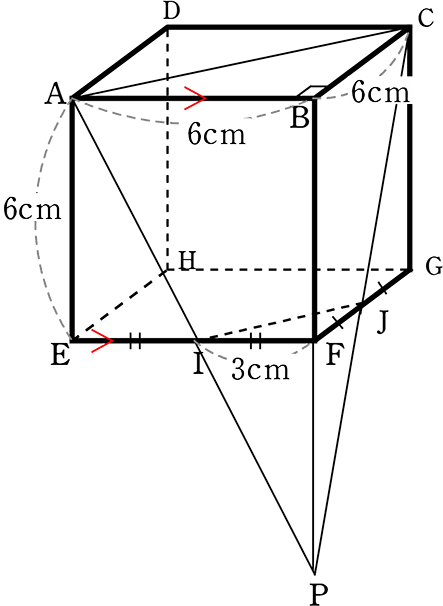
・底面積△BAC = \(\large{\frac{1}{2}}\)・6・6 = 18
・高さBPは・・・
 IF= \(\large{\frac{1}{2}}\)AB ですね
IF= \(\large{\frac{1}{2}}\)AB ですね
中点連結定理の逆 (AB//IFかつIF=\(\large{\frac{1}{2}}\)AB
∴ FP = BF = 6cm → BP = 12cm
∴ 大三角錐P_BAC = \(\large{\frac{1}{3}}\)・18・12 = 72cm3
次に、小三角錐P_FIJの体積
・△FIJ = \(\large{\frac{1}{2}}\)・3・3 = \(\large{\frac{9}{2}}\)
・高さPF = 6
→ \(\large{\frac{1}{3}}\)・\(\large{\frac{9}{2}}\)・6 = 9cm3
よって、
立体ABC_IFJ = 三角錐P_BAC-三角錐P_FJI = 72-9 = 63cm3
cf.
もちろん、「あたるもの」や「相似比」で体積を求めてもOK
・小三角錐 = \(\large{\frac{1}{3}}\)・\(\large{\frac{9}{2}}\)・6 = 9cm3
・小三角錐:大三角錐 = 1・1・1:2・2・2 = 1:8
∴ 大三角錐 = 9cm3×8 = 72cm3
∴ 立体 = 大-小 = 72-9 = 63cm3
《 例 》
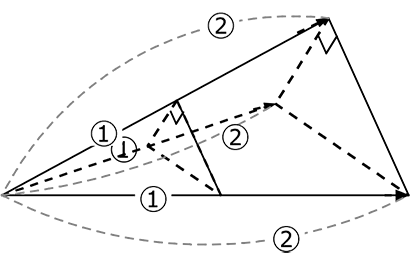
次のような、各辺の長さが1である2つの正三角柱でできた立体について
以下の問いに答えましょう
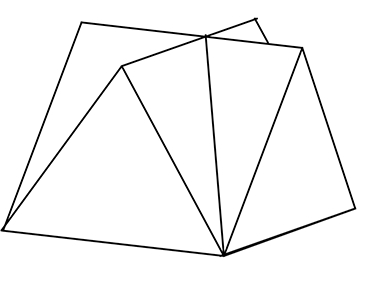
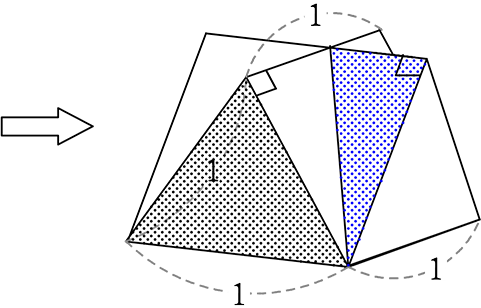
(1) 表面積を求めましょう
| → | 表面積 =  ×4+ ×4+ ×8+ 底の正方形 ですね ×8+ 底の正方形 ですね |
| ・ |  正三角形の面積 = \(\large{\frac{\sqrt{3}}{4}}\) が4面で、\(\large{\frac{\sqrt{3}}{4}}\)×4 = \(\small{\sqrt{3}}\) 正三角形の面積 = \(\large{\frac{\sqrt{3}}{4}}\) が4面で、\(\large{\frac{\sqrt{3}}{4}}\)×4 = \(\small{\sqrt{3}}\) |
・  側面三角形の面積 =
側面三角形の面積 = 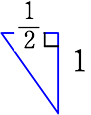 → \(\large{\frac{1}{2}}\)・\(\large{\frac{1}{2}}\)・1 = \(\large{\frac{1}{4}}\)
→ \(\large{\frac{1}{2}}\)・\(\large{\frac{1}{2}}\)・1 = \(\large{\frac{1}{4}}\)
\(\large{\frac{1}{4}}\) が8面で、2
・ 底面正方形 = 1・1 = 1
∴ \(\small{\sqrt{3}}\)+2+1 = \(\small{\sqrt{3}}\)+3
| A. | \(\small{\sqrt{3}}\)+3 |
(2) 体積を求めましょう

または

→ 上で行きますね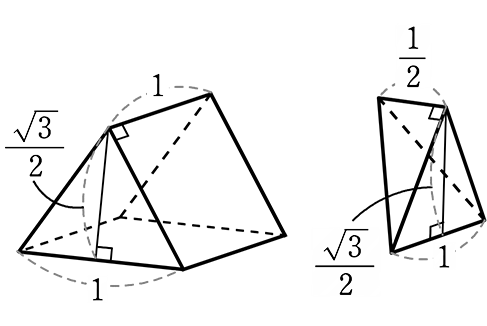
| ・三角柱の体積 | = 底面積・高さ = \(\large{\frac{\sqrt{3}}{4}}\)×1 = \(\large{\frac{\sqrt{3}}{4}}\) |
| ・三角錐の体積 | = \(\large{\frac{1}{3}}\)・底面積・高さ = \(\large{\frac{1}{3}}\)・\(\large{\frac{\sqrt{3}}{4}}\)・\(\large{\frac{1}{2}}\) が2つ = \(\large{\frac{\sqrt{3}}{12}}\) |
| ∴ 立体の体積 | = \(\large{\frac{\sqrt{3}}{4}}\)+\(\large{\frac{\sqrt{3}}{12}}\) =\(\large{\frac{ 3\sqrt{3}+\sqrt{3}}{12}}\) = \(\large{\frac{4\sqrt{3}}{12}}\) = \(\large{\frac{\sqrt{3}}{3}}\) // |
複雑な立体の計算は
| ① | イメージ化 |
| ② | どのような立体が付け加えられているのか、または引かれているのか
→ 練習あるのみですね! |
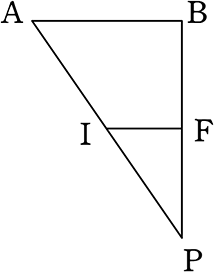
③ 最短距離 ( 最短経路 )

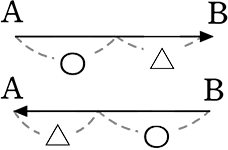
点Aと点Bの最短距離を表すものは、「イ」ですね
という訳で、「最短距離を求めよ」という問題でのポイントは

最短距離 → どうすれば「
これだけです!
《 例 》
y軸上にA、x軸上にBがあるとき、PABQの長さが最小になるような A, Bの座標を求めましょう
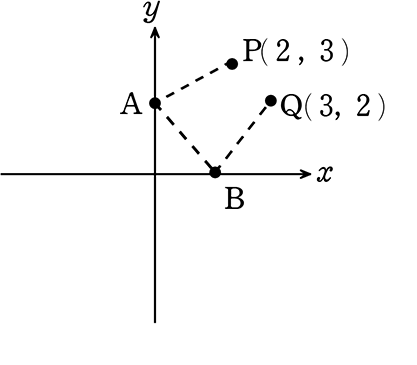

| → | Aはy軸上を、Bはx軸上を自由に動けます |
| → | y軸についてPと対称な点P’をとれば、点Aがy軸上をどんなに動いても
「APの距離」 = 「AP’の距離」ですね! |
| → | 同様に、x軸についてQと対称な点Q’とします |
| → | P’ABQ’が一直線 = 最短距離 |
| → | あとは、2点P’(-2, 3)、Q’(3, -2)を通る直線の y切片とx切片を求めるだけですね |
y = \(\large{\frac{-2-(3)}{3-(-2)}}\)(x+2)+3 (2点から直線を求める)
= \(\large{\frac{-5}{5}}\)(x+2)+3
= -x-2+3
= -x+1
・y切片 → y = -(0)+1 = 1
・x切片 → 0 = -x+1 → x = 1
| A. | A(0, 1) B(1, 0) のとき最短 |
《 例 》
図のように半径3cm、高さ6cmの円柱の母線をABとしたとき、
Aから側面を1周してBにいたる最短距離は何cm?

立体をとりまく
ですね!
(展開図)
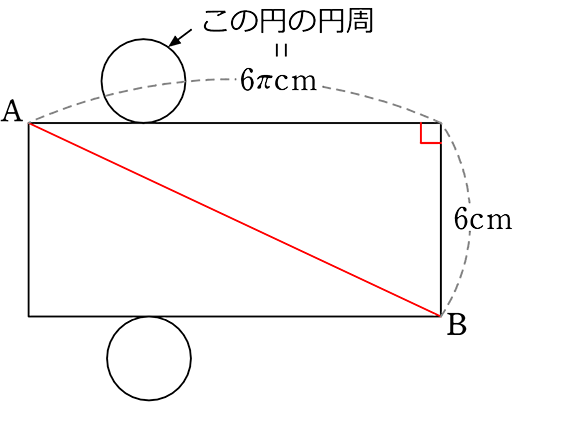
AB = \(\small{\sqrt{(6\pi)^2+6^2}}\)
= \(\small{\sqrt{36\pi^2+36}}\)
= \(\small{\sqrt{36(\pi^2+1)}}\)
= 6\(\small{\sqrt{\pi^2+1}}\) cm //
cf. 2周してBにいたる場合は何cm?
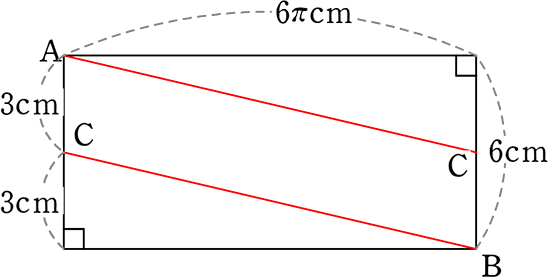
A~B = AC+CB = 2AC (または 2BC)
AC = \(\small{\sqrt{(6\pi)^2+3^2}}\)
= \(\small{\sqrt{36\pi^2+9}}\)
= \(\small{\sqrt{9(4\pi^2+1)}}\)
= 3\(\small{\sqrt{4\pi^2+1}}\)
∴ A~C~B = 2AC = 6\(\small{\sqrt{4\pi^2+1\ }}\) cm //
《 例 》
図のような直方体で、辺AB、BCと交わるように EからGに紐をかける場合で
紐が最も短くなるのは何cm?
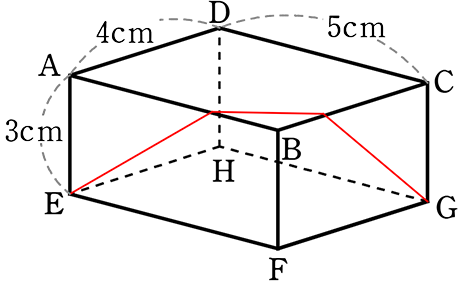
→ 展開図ですね
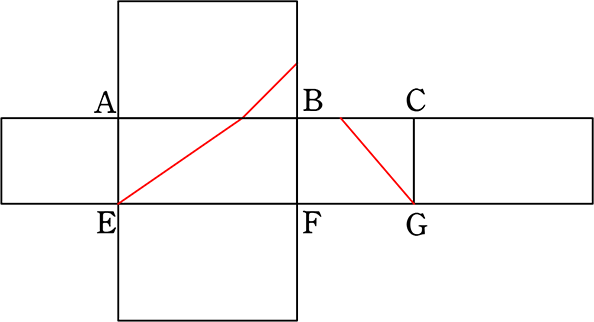
→ 一直線になっていない → 展開の仕方が悪い
→ 一直線になりましたね!
一直線であれば
どんな展開図でもOK
・ EP = EF+BF = 5+3 = 8
・ GP = GF+BF = 4+3 = 7
∴ EG = \(\small{\sqrt{8^2+7^2}}\) = \(\small{\sqrt{64+49}}\) = \(\small{\sqrt{113}}\)
| A. | \(\small{\sqrt{113}}\) cm |
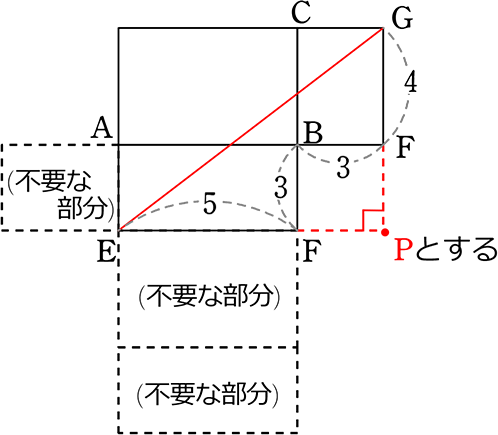
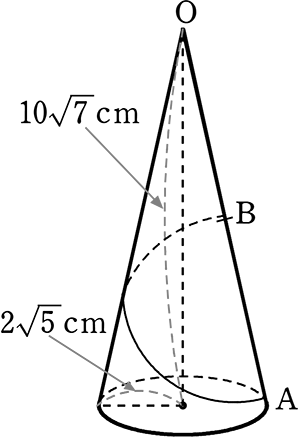
《 例 》
図のような三角錐の1つの母線OAの中点をBとするとき、
BからAまで紐を1周巻く最短の長さを求めましょう
| → | まずは「展開図」ですね |
| → | 正しいイメージで考えるために、展開イメージ図はできる限り正確がよい |
| → | という訳で、「円錐の形」と展開図の「扇形の形」の関係は・・・ |
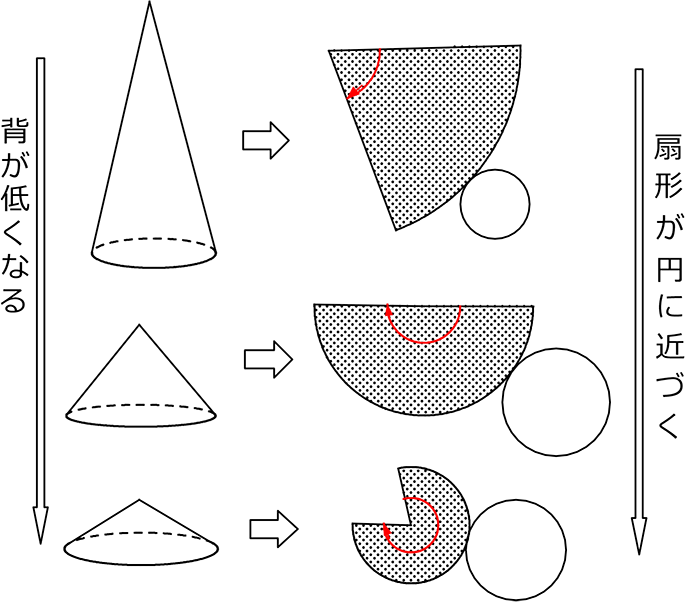
(展開図) けっこう背が高いのでこんな感じ?
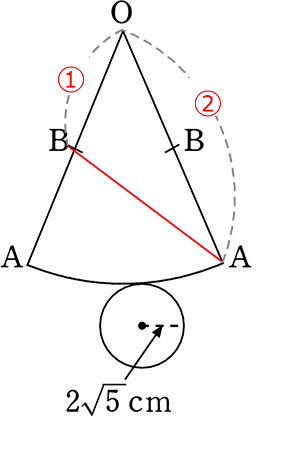
→ 最短距離は赤線BA
→ 『△OBAはどのような三角形か』 ですね
(データ集め)
→ 弧AA = 小円の円周 = 2・2\(\small{\sqrt{5}}\) ・π = 4\(\small{\sqrt{5}}\)π cm
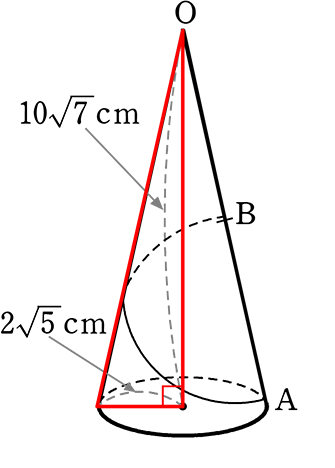
| → 母線OA | =\(\small{\sqrt{ (2\sqrt{5})^2+(10\sqrt{7})^2}}\) = \(\small{\sqrt{20+700}}\)
= \(\small{\sqrt{720}}\) = \(\small{\sqrt{8\cdot9\cdot10}}\) = 12\(\small{\sqrt{5}}\) cm |
| → 展開図の∠O | = 割合×360° (扇形の割合) |
| = \(\large{\frac{大円の弧}{大円の完全円周}}\)×360° | |
| = \(\large{\frac{4\sqrt{5}π}{2 \ \cdot \ 12\sqrt{5} \ \cdot \ π}}\)・360° | |
| = \(\large{\frac{1}{6}}\)・360° = 60° |
→ 半母線OB = \(\large{\frac{OA}{2}}\) = 6\(\small{\sqrt{5}}\) cm
OB:OA = 1:2 で∠O = 60° ということは・・・「サブローキュー」ですね
→ ∴ ∠OBA = 90°
ちなみに正確な展開図は・・・
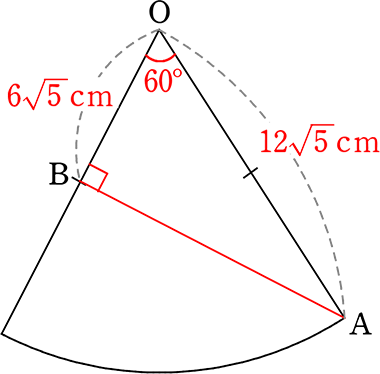
∴ 紐AB = \(\large{\frac{\sqrt{3}}{2}}\)×12\(\small{\sqrt{5}}\)
= 6\(\small{\sqrt{15}}\) cm //
(もちろん、AB:12\(\small{\sqrt{5}}\) = \(\large{\frac{\sqrt{3}}{2}}\):1 でも、AB = \(\small{\sqrt{(12\small{\sqrt{5}})^2-(6\small{\sqrt{5}})^2 }}\) で 求めてもOKですね)
この手の問題で、∠Oは 30°、45°、60°、90°、120°(= 60°×2) など
「特別な角」になるように作られていますね
④ 立体の切断
《 例 》
図のように透明な「直方体」に水が深さ4cmで入っています
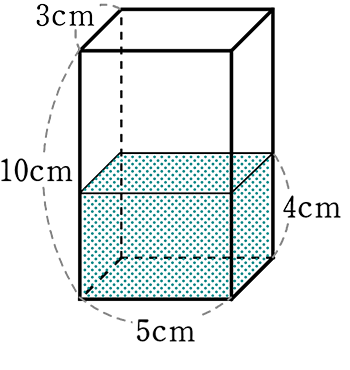
適当に傾けると
図のようになりました
xを求めましょう
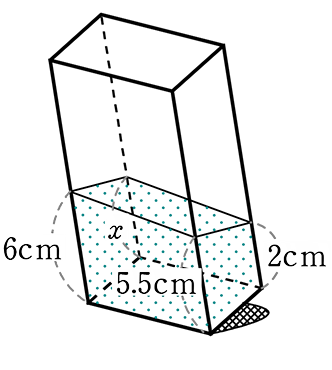
→ 自然現象的に、「対辺な関係にある辺の長さの和は同じ」ですので、
6+2 = 5.5+x
x = 8-5.5 = 2.5 A. 2.5cm
《 例 》
1辺4cmの立方体を以下の図の3点を通るように切ったとき、
「切り口の形」と「切り口の面積」を求めましょう
(1) 3点B, D, F を通る平面で切るとき
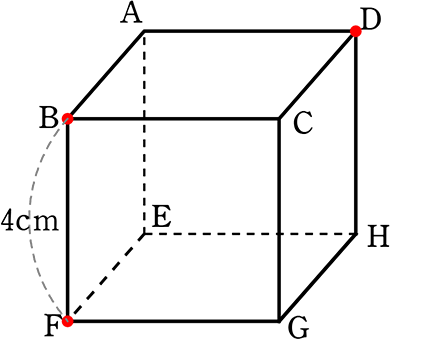
(基本) 平面は3点で「決まる」
(形) →三角形BFDではないですね
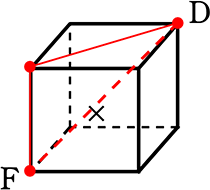
豆腐を中華包丁 か
か
下敷きで切るイメージで!
→ 点Hも通りますね!
すなわち、「切り口」を形作る線(平面図形の
「立体の内部にはありません」 (上図ならFDのような線はない)
再度、(形)

∴ (形) → 四角形BFHD → 長方形
(確かに縁線は立体の表面上)
(面積) = BF×BD = 4×4\(\small{\sqrt{2}}\) = 16\(\small{\sqrt{2}}\) cm2 //
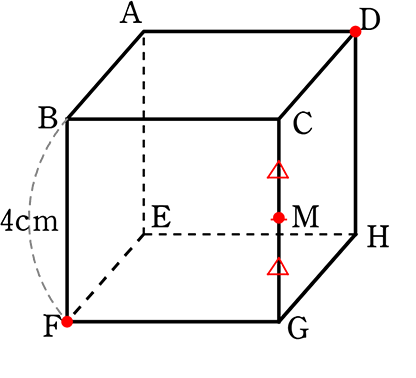
(2) CDの中点MとD, F の3点を通る平面で切るとき
まずはすぐに
わかる
表面上の線
「対面が平行なら切り口も平行」ですので
直方体 → 面BFGC//面AEHD
| → | DからMFと平行な線
→ AEの中点を通るはず |
| → | 同様に、FからMDと平行な線
→ AEの中点を通るはず |
(形) 平行四辺形× → (FD>MNな)ひし形〇
(より厳しい条件をクリアした方で!)
| (面積) ひし形 | = \(\large{\frac{1}{2}}\)・対角線・対角線
= \(\large{\frac{1}{2}}\)・FD・MN |
・FD = \(\small{\sqrt{(FH)^2+(HD)^2}}\)
(FH = \(\small{\sqrt{2}}\)・4 = 4\(\small{\sqrt{2}}\) )
= \(\small{\sqrt{(4\sqrt{2})^2+(4)^2}}\) = \(\small{\sqrt{32+16}}\)
= \(\small{\sqrt{48}}\) = \(\small{\sqrt{16\cdot3}}\) = 4\(\small{\sqrt{3}}\)
・MN = AC = FH = 4\(\small{\sqrt{2}}\)
∴ 面積 = \(\large{\frac{1}{2}}\)・4\(\small{\sqrt{3}}\)・4\(\small{\sqrt{2}}\) = 8\(\small{\sqrt{6}}\) cm2 //
(3) ABの中点M、ADの中点N、点Gの3点を通る平面で切るとき
まずはすぐに
わかる
表面上の線
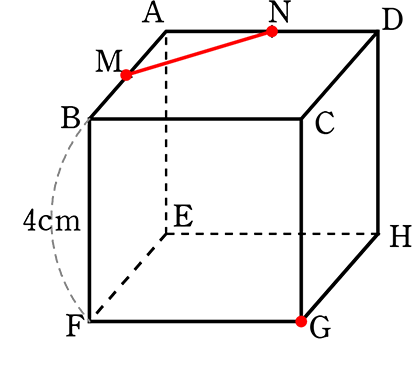
点M、N、G、を通る平面レベルにあるのは確か

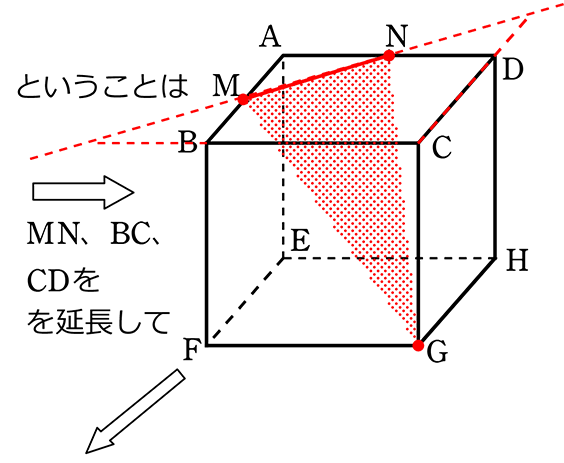
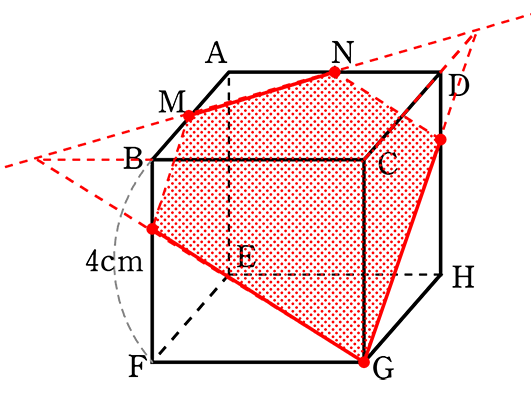
→ MNに包丁の刃を当てて
角度はGに向けるイメージ
(形) 5角形
(面積) 難しいですね
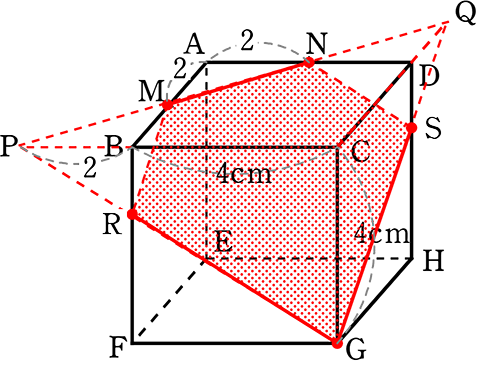
(流れ) △GQP-△PRM-△QNS
PB = 2 (△NAMと△PBMの「ちょう」より)
BR = \(\large{\frac{4}{3}}\) (△PBRと△PCGの「山」より)
PM = MN = 2\(\small{\sqrt{2}}\)
RM = \(\small{\sqrt{(BM)^2+(BR)^2}}\) = \(\small{\sqrt{2^2+\large{(\frac{4}{3})}^2}}\)
= \(\small{\sqrt{4+\large{\frac{16}{9}}}}\) = \(\small{\sqrt{\large{\frac{52}{9}}}}\) = \(\large{\frac{2\sqrt{13}}{3}}\)
PG = \(\small{\sqrt{(PC)^2+(CG)^2}}\) = \(\small{\sqrt{6^2+4^2}}\)
= \(\small{\sqrt{52}}\) = 2\(\small{\sqrt{13}}\)
PR = \(\large{\frac{2}{6}}\)・PG = \(\large{\frac{2\sqrt{13}}{3}}\)
(DQ側も全く同じですので省略しますね)
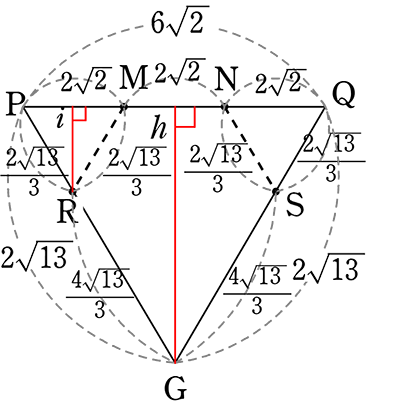
Gh = \(\small{\sqrt{(2\sqrt{13})^2-(3\sqrt{2})^2}}\)
= \(\small{\sqrt{52-18}}\) = \(\small{\sqrt{34}}\)
∴ △GQP = \(\large{\frac{1}{2}}\)・6\(\small{\sqrt{2}}\)・\(\small{\sqrt{34}}\)
= 3\(\small{\sqrt{2\cdot2\cdot17}}\) = 6\(\small{\sqrt{17}}\)
Ri = \(\small{\sqrt{(\frac{2\sqrt{13}}{3})^2-(\sqrt{2})^2}}\) = \(\small{\sqrt{\frac{52}{9}-2}}\) = \(\small{\sqrt{\frac{52-18}{9}}}\) = \(\large{\frac{\sqrt{34}}{3}}\)
∴ △RMP = \(\large{\frac{1}{2}}\)・2\(\small{\sqrt{2}}\)・\(\large{\frac{\sqrt{34}}{3}}\) = \(\large{\frac{\sqrt{2\cdot2\cdot17}}{3}}\) = \(\large{\frac{2\sqrt{17}}{3}}\)
∴ 五角形GSNMR = 6\(\small{\sqrt{17}}\)-2・\(\large{\frac{2\sqrt{17}}{3}}\) = \(\large{\frac{18\sqrt{17}-4\sqrt{17}}{3}}\)
= \(\large{\frac{14\sqrt{17}}{3}}\) cm2 //
(4) ABの中点M、ADの中点N、BFの中点Pの3点を通る平面で切るとき
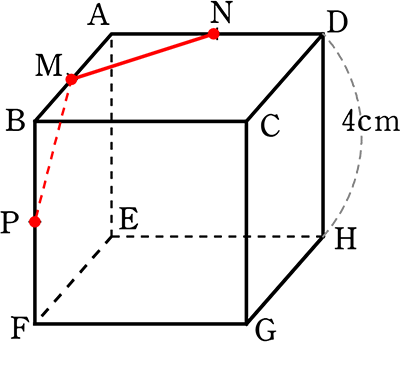
(形) 正六角形
(面積) 正六角形の中心をOとする
MN = 2\(\small{\sqrt{2}}\) (AN = 2のヨンゴーより)
正六角形は正三角形が6つ集まったもの
(1辺aの正三角形の面積公式)
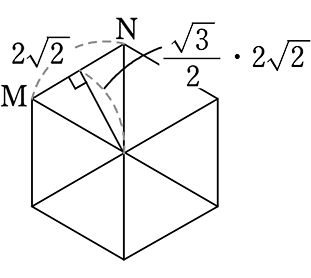
△OMN = \(\large{\frac{1}{2}}\)・2\(\small{\sqrt{2}}\)・\(\small{\sqrt{6}}\) = 2\(\small{\sqrt{3}}\)
∴ 正六角形MPQRSN = 6・2\(\small{\sqrt{3}}\) = 12\(\small{\sqrt{3}}\) cm2
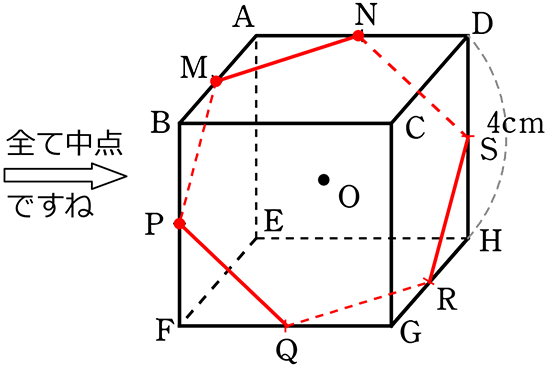
余談としての
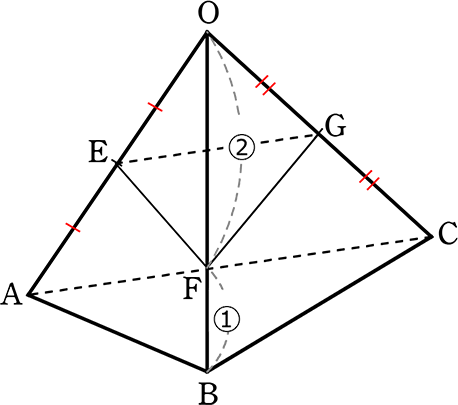
(追加問題1) 正六角錐C‐MPQRSNの体積を求めましょう
(方法1) \(\large{\frac{1}{3}}\) ・底面積MPQRSN・高さCO
(方法2) (三角錐V‐CTU)-3(三角錐C‐BPM)-3三角錐T‐BPM)
(方法1) 底面積12\(\small{\sqrt{3}}\)cm2 は(4)で求めていますので、あとは高さCOですね
△COMからCOを求めてみますね(Oは対角線CEの中点かはわからないので)

MO = MN = 2\(\small{\sqrt{2}}\) (正三角形の1辺より)
= \(\small{\sqrt{2^2+4^2}}\) = \(\small{\sqrt{4+16}}\) = 2\(\small{\sqrt{5}}\)
| ∴ | CO = \(\small{\sqrt{(2\sqrt{5})^2-(2\sqrt{2})^2}}\) = \(\small{\sqrt{20-8}}\) = \(\small{\sqrt{12}}\) = 2\(\small{\sqrt{3}}\) cm (OはCEの中点でしたね) |
| ∴ | 正六角錐C‐MPQRSN = \(\large{\frac{1}{3}}\)・12\(\small{\sqrt{3}}\)・2\(\small{\sqrt{3}}\) = 8・3 = 24 cm3 // |
(方法2) 正六角錐C_MPQRSNの体積、2種類の三角錐(C_MBP、T_BPM)の切り落とし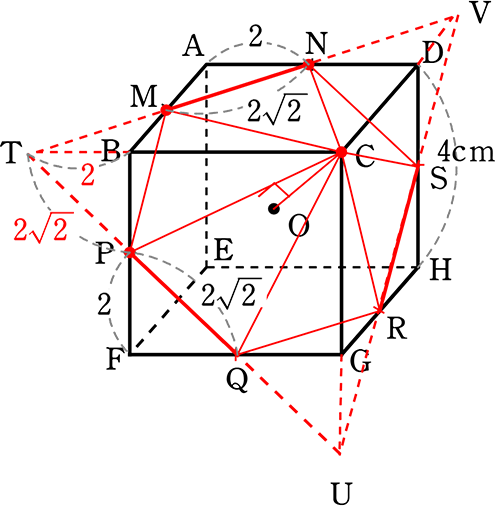
| → | MN = TM 、 PQ = TP= 2\(\small{\sqrt{2}}\) (△AMNと△BMT、 △FPQと△BPTで1:1の「ちょう」より) |
| → | AN = TB = 2 (1:1の「ちょう」より) |
同様にすると
・三角錐C‐BMP = 三角錐C‐GQR = 三角錐C‐DNS
・三角錐T‐BMP = 三角錐U‐GQR = 三角錐V‐DNS
・大三角錐V‐CTU = \(\large{\frac{1}{3}}\)・底面積△CTU・高さVC
= \(\large{\frac{1}{3}}\)・(\(\large{\frac{1}{2}}\)・6・6)・6 = 36cm3 …①
・三角錐C‐BMP = \(\large{\frac{1}{3}}\)・(\(\large{\frac{1}{2}}\)・2・2)・4 = \(\large{\frac{8}{3}}\) cm3 …②
・三角錐T‐BPM = \(\large{\frac{1}{3}}\)・(\(\large{\frac{1}{2}}\)・2・2)・2 = \(\large{\frac{4}{3}}\)cm3 …③
∴ 正六角錐C‐MPQRSN = ①-3×②-3×③ = 36-8-4 = 24cm3 //
(追加問題2) 6点MPQRSNで切った時、Cを含む側の体積を求めましょう
(正六角錐C‐MPQRSNの体積との違いに注意してくださいね!
→ 三角錐C‐BMP、C‐DNS、C-GQRを、含むか含まないかの違い)

(考え方1) 正六角錐C‐MPQRSN +3( 三角錐C‐BMP)
= 24+3(\(\large{\frac{8}{3}}\)) = 32 cm3 //
(考え方2) 三角錐V‐CTU - 3(三角錐T‐BPM)
= 36-3(\(\large{\frac{4}{3}}\)) = 32 cm3 //
⑤ 体積比
図形の「体積比」は、相似の場面で学んだ図形の「面積比」と
全く同じように考えることができましたね!
図形の『体積比』は
基準が同じ (底面積が同一平面や平行、高さの線が同じ角度) 場合
(横にあたるもの)(縦にあたるもの)(高さにあたるもの):(横にあたるもの)(縦にあたるもの)(高さにあたるもの)
\(\Updownarrow\)
(底面積にあたるもの)(高さにあたるもの):(底面積にあたるもの)(高さにあたるもの)
「比」であるから、
「正真正銘の底面積」も「正真正銘の高さ」も必要ないですね!
(イメージ)

↑
そして、これに関しては元の図形と「相似」
→ 高さが2倍×(底面積が4倍)
= 高さが2倍×(縦が2倍×横が2倍)
→「体積比は、相似比(1辺)の
3乗に等しい」につながるのでしたね
相似比1:2
上のイメージは「正真正銘な高さ」ですが、これらが
「高さに
そして、「三角錐」であろうが「円錐」であろうが「同様」であることはもう理解できますね
《 例 》
OA = OB = OCの三角錐で、OAの中点がE、OCの中点がG、
OF:FB = 2:1のとき、三角錐の体積比O‐ABC:O‐EFGを求めましょう
どこが「底面積にあたるもの」「高さにあたるもの」かは、
もう判っているとは思いますが、念のため三角錐を倒してみますね
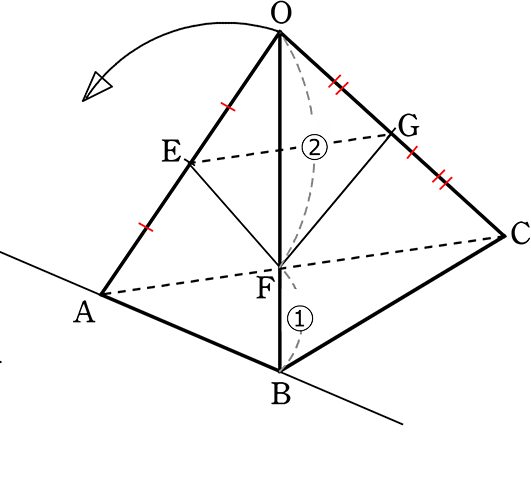
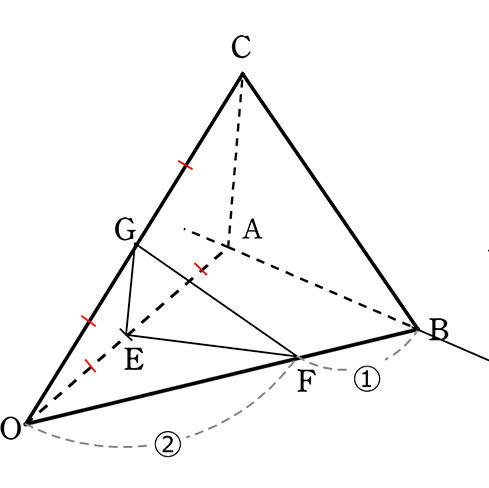
→ 「底面積にあたるもの」 = 「(面積の)横にあたるもの」×「(面積の)縦にあたるもの」
∴ △OAB:△OEF = (OB・OA):(OF・OE) = 3×2:2×1 = 6:2 = ③:①
→ 三角錐O‐ABCの「(体積の)高さにあたるもの」 = OC = 2
三角錐O‐EFGの「(体積の)高さにあたるもの」 = OG = 1
∴ 三角錐O‐ABC:三角錐O‐EFG
= 「底面積にあたるもの」×「高さにあたるもの」:「底面積にあたるもの」×「高さにあたるもの」
= △OAB×OC:△OEF×OG = ③× 2 :①× 1 = 6:1
A. 三角錐O‐ABC:三角錐O‐EFG = 6:1
| ・ | もちろん、△OBCや△OACを底面積と考えてもOKです
△ABCだけはダメですね! |
| ・ | もちろん、横・縦 = 底面積 → 底面積・高さ と段階を踏まずに
横・縦・高さ:横・縦・高さ でもOKですね |
《 例 》
各辺の長さが全て6cmの正四面体O‐ABCDにおいて、
OB、ODの中点L、Mと頂点Aの3点で正四面体を切るとき
辺OCとの交点をNとして、以下の問いに答えましょう
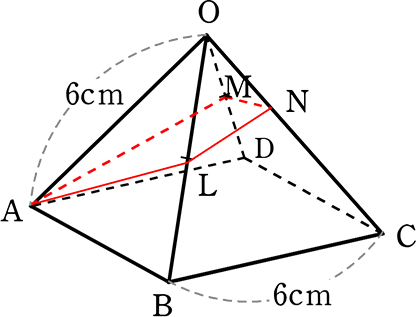
(1) ONの長さを求めましょう
→ 図をBの方から見ると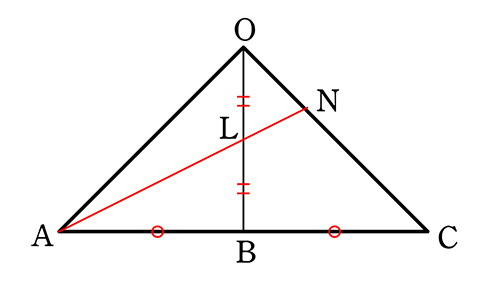
→ BからANに平行な補助線を引くと
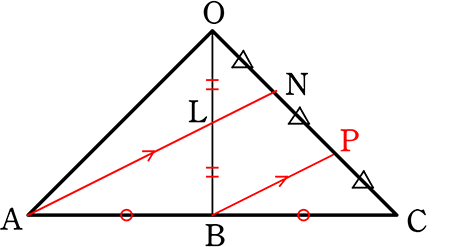
△CANの「山」より CP:PN = 1:1
△OBPの「山」より ON:NP = 1:1
∴ ON = NP = PC
∴ OC = 6cmより、より、 ON = 2cm //
(2) 切り口の四角形ALNMの面積を求めましょう
→ 正四角錐を真上から見ると
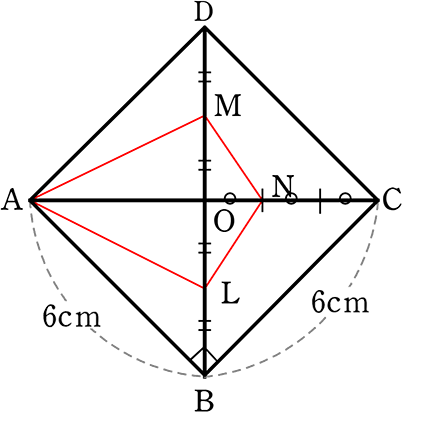
四角形ALNMは「凧型」とわかる
→ 凧型の面積 = \(\large{\frac{1}{2}}\) ・対角線・対角線
= \(\large{\frac{1}{2}}\) ・AN・ML (底辺共有2三角形)
→ AC = \(\small{\sqrt{AB^2+BC^2}}\) = \(\small{\sqrt{6^2+6^2}}\)
= 6\(\small{\sqrt{2}}\) (= DBでもある)
OA:OC:AC = 6:6:6\(\small{\sqrt{2}}\)
= 1:1:\(\small{\sqrt{2}}\)
∴ ∠AOC = 90°(ヨンゴーの直角三角形)

辺がすべて等しい正四角錐の頂角は 90°
| ∴ AN | = \(\small{\sqrt{OA^2+ON^2}}\) = \(\small{\sqrt{6^2+2^2}}\) = \(\small{\sqrt{40}}\) = 2\(\small{\sqrt{10}}\) cm ←たこ形の長い方の対角線 |
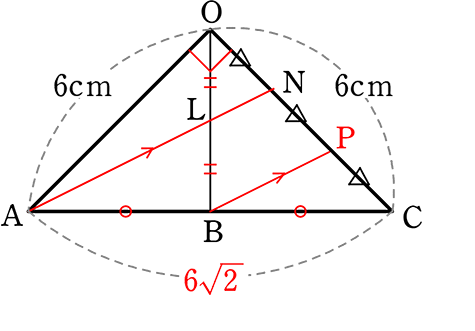
次にML
△OBDで
DB = 6\(\small{\sqrt{2}}\) より
・LM = 3\(\small{\sqrt{2}}\) cm ←短い方の対角線
(中点連結定理)
∴ 四角形ALNM = \(\large{\frac{1}{2}}\)・2\(\small{\sqrt{10}}\)・3\(\small{\sqrt{2}}\) = 3\(\small{\sqrt{2\cdot5\cdot2}}\) = 6\(\small{\sqrt{5}}\) cm2 //
(3) 四角錐O‐ALNMを切り取ったとき、残りの立体の体積を求めましょう
| → | 四角錐では体積比「底面積にあたるもの」「高さにあたるもの」が使えないので真上からOACを通る包丁で2等分した三角錐O‐ABCとO‐ALNで考えると、三角錐になって「あたるもの」で考えることができる |

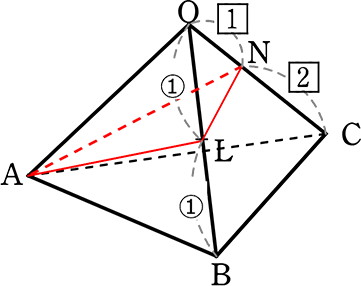
→ 三角錐A‐OLN:A‐OBC = (底面積にあたるもの)(高さにあたるもの):(底面積にあたるもの)(高さにあたるもの) = (①×1)(AO):(②×3)(AO) = 1:6
| ∴ | 四角錐O‐ALNM:O‐ABCD = 2:12 = 1:6 (当然結局1:6) |
| ∴ | 四角錐O‐ABCDをVとすると、 O‐ALNM = \(\large{\frac{1}{6}}\)V |
では、四角錐O‐ABCDの正確な体積は・・・
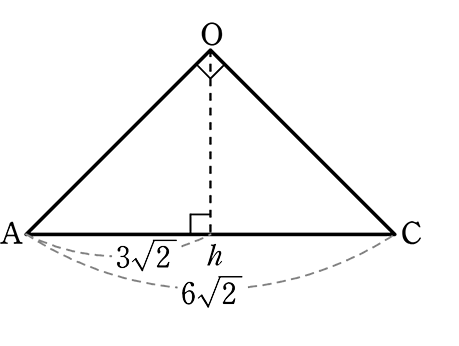
△OACは二等辺三角形
→ Ah = Ch
∴ Ah = 3\(\small{\sqrt{2}}\)
∠OAh = 45° より
∴ △hAOもヨンゴー
∴ 高さOh = 3\(\small{\sqrt{2}}\)
∴ 四角錐O‐ABCD = \(\large{\frac{1}{3}}\)・36・3\(\small{\sqrt{2}}\) = 36\(\small{\sqrt{2}}\) cm3
∴ 四角錐O‐ALNM = 36\(\small{\sqrt{2}}\)×\(\large{\frac{1}{6}}\) = 6\(\small{\sqrt{2}}\) cm3
∴ 残りの立体の体積 = 36\(\small{\sqrt{2}}\)-6\(\small{\sqrt{2}}\) = 30\(\small{\sqrt{2}}\) cm3//
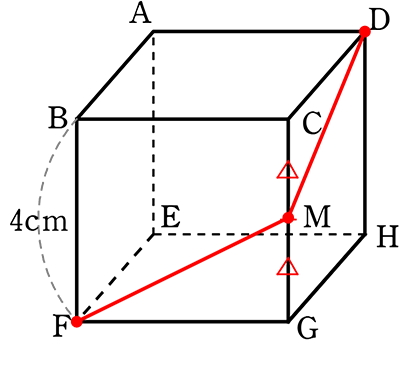
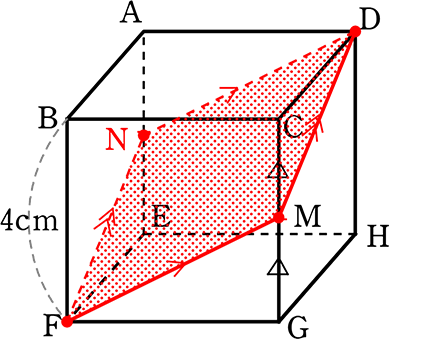
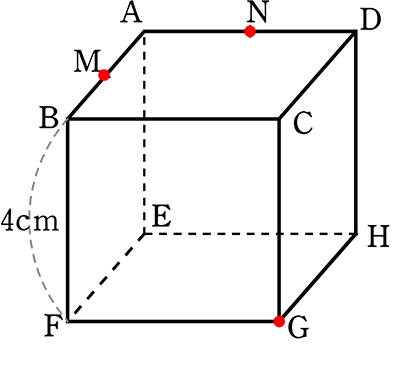
⑥ 立体の対角線
《 例 》
図のような直方体ABCD‐EFGHの辺AEの中点をPとし、
点P、頂点F、Hの3点を通る平面と対角線CEの交点をQとします
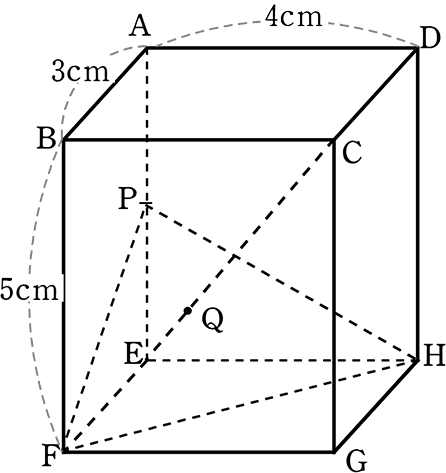
(1) 対角線CEの長さを求めましょう
→ CEGの平面を切り出すと
EGがわかればCEがわかりますね
EG = \(\small{\sqrt{(GH)^2+(HE)^2}}\)
= \(\small{\sqrt{3^2+4^2}}\) = \(\small{\sqrt{9+16}}\) = 5 cm
5, 4, 3 だな…「5」でもOK
∴ CE = \(\small{\sqrt{25+25}}\) = \(\small{\sqrt{50}}\) = 5\(\small{\sqrt{2}}\) cm //
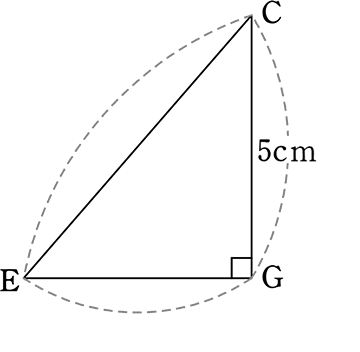
(2) CQの長さを求めましょう

→ AEGCの平面を切り出すと
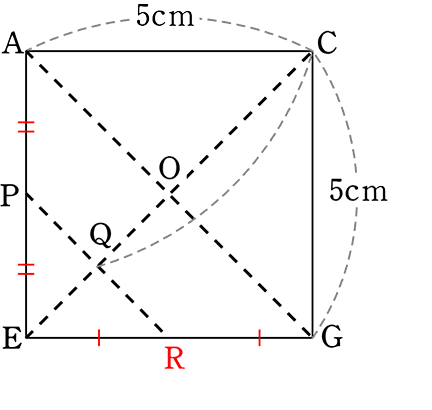
・EG = 5cmより正方形とわかる
↑△HGEは「5, 4, 3の直角三角形」
・底面EFGHの
対角線EGと対角線FHの交点を
Rとすると、RはEG、FHの中点
(平行四辺形系の対角線は中点で交わる)
よって、図より
CQは\(\large{\frac{3}{4}}\)CEですね!(△CAG≡△EAG、△ERP∽△EGA相似比2)
∴ CQ = \(\large{\frac{3}{4}}\)×5\(\small{\sqrt{2}}\) = \(\large{\frac{15\sqrt{2}}{4}}\) cm //
(3) 頂点F、Gから対角線CEにおろした垂線の交点をそれぞれS、Tとするとき
CT:TS:SE を求めましょう
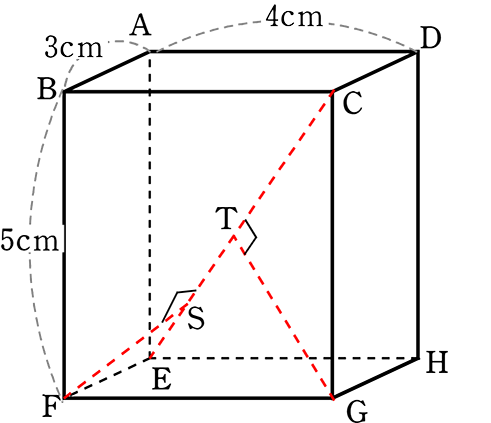
かなりイメージ力が鍛えられますね!
→ CE = 5\(\small{\sqrt{2}}\) cm でしたね
あとは、
CT、ESがわかればいけそうですね
ETに注目すると、直角三角形TEGの1辺が四角形EFGHの対角線になっている
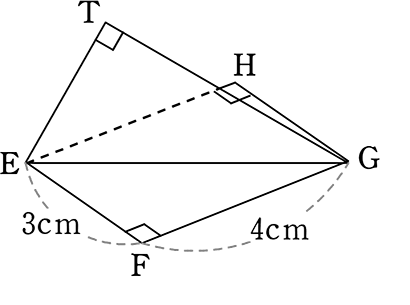
→ △EFGは「5,4,3の直角三角形」より
EG = 5 cm
(もちろん、EG = \(\small{\sqrt{3^2+4^2}}\) でもOK)
→ ET、TG はわかりませんね
→ 他の材料探し
→ EG = 5cm、CGも5cm…ということは△GECは「ヨンゴーの直角三角形」

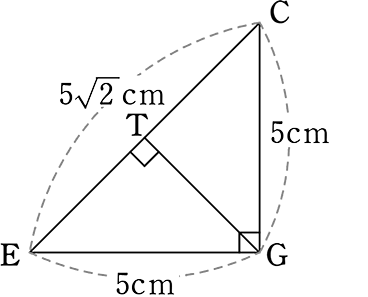
∴ CT = ET = \(\large{\frac{5\sqrt{2}}{2}}\)
(二等辺三角形⇒頂角からの垂線は 底辺を2分する)
あとはESですね
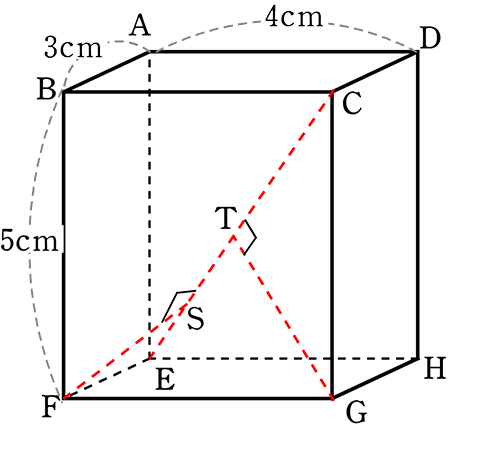
コツはつかんだので同様に
△FECに注目して・・・
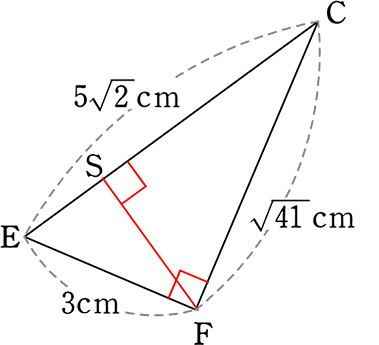
FC = \(\small{\sqrt{5^2+4^2}}\) = \(\small{\sqrt{25+16}}\) = \(\small{\sqrt{41}}\)
かなりイメージが難しいですが
∠EFC = 90°ですね
(∠EFC = 90° が見つけられない場合は「15,14,13のAHの求め方」でESが求められますね)
∠EFC = 90°が見つけられたら、相似で楽できますね
3:ES = 5\(\small{\sqrt{2}}\):3
ES = \(\large{\frac{9}{5\sqrt{2}}}\) = \(\large{\frac{9\sqrt{2}}{10}}\)
∴ 対角線 CE = 5\(\small{\sqrt{2}}\) 、 CT = \(\large{\frac{5\sqrt{2}}{2}}\) (←中点)、 ES = \(\large{\frac{9\sqrt{2}}{10}}\)
最後の間違い防止のため、CTとESの長さを比較しますね
(図が悪くて実は、①ではなく・・・
②だったらもったいないですから!)
CT2 = \(\large{\frac{50}{4}}\) = \(\large{\frac{1250}{100}}\) 、 ES2 = \(\large{\frac{162}{100}}\) ∴ CT>ES ∴ ①でOK
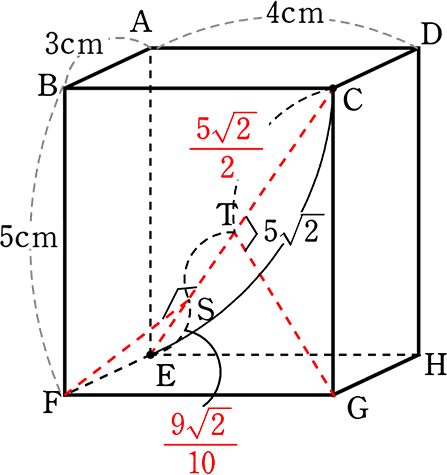
あとは、TS。 TS = ET-ES = \(\large{\frac{5\sqrt{2}}{2}}\)-\(\large{\frac{9\sqrt{2}}{10}}\) = \(\large{\frac{25\sqrt{2}-9\sqrt{2}}{10}}\) = \(\large{\frac{16\sqrt{2}}{10}}\)
∴ CT:TS:SE = \(\large{\frac{5\sqrt{2}}{2}}\):\(\large{\frac{16\sqrt{2}}{10}}\):\(\large{\frac{9\sqrt{2}}{10}}\) = \(\large{\frac{5}{2}}\):\(\large{\frac{16}{10}}\):\(\large{\frac{9}{10}}\) = 25:16:9 //
かなり「一筋縄ではいかない」難しい問題でしたね!
ここまでの例題は、あくまで『図形』の問題(長さ、角度、面積、体積、比など)であって、
「三平方の定理」、「特別な角」はあくまでそれらを解くための道具ですね!
「三平方の定理」自体が難し訳ではないですね!
2次元の平面に描かれた3次元の図形をイメージすることはなかなか大変ですね!
集中力もいりますし、何より練習が大切だと思います!
あと少し!
頑張っていきましょう!!
お疲れ様でした!
その他の問題は、「問題集」で !!















