| 中学1年生課程へ | 中学2年生課程へ | 中学3年生課程 |
| A 数と式 | B 図形 | C 関数 | D 資料の活用 |
| (1) 平方根 | (2) 式の展開・因数分解 | (3) 二次方程式 |
平方根
ア 数の平方根の必要性
ついに3年生過程ですね!
頑張っていきましょう!
まずは、√ですね
√の簡単なイメージは、「正方形の1辺」ですね
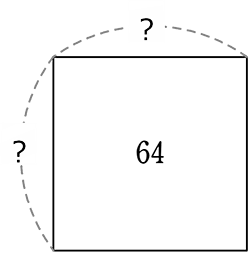

① 解らないものは、
文字(xなど)にしていましたね!
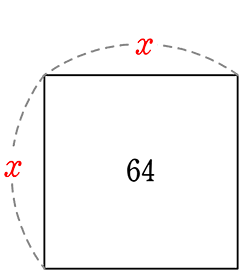
ですが! ② せっかく「2乗したら64」というヒントがあるのですから、
ただ「x」とおくのは、もったいないですね! そこで・・・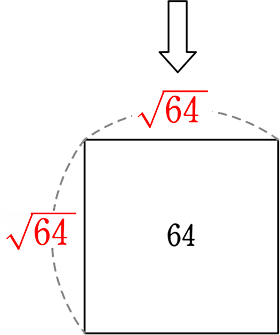
とおこう!というだけですね!
√ は「根号(こんごう)」といって、\(\small{\sqrt{64 }}\) は「ルート64」と読みますね
\(\small{\sqrt{64}}\)×\(\small{\sqrt{64}}\) = (\(\small{\sqrt{64}}\))2 = 64 となります (2乗すれば√ の中の数字になりますよ~)

《 例 》
xの値を0.5秒で答えましょう






そして、これらは実は、例えば、
「60kmの道のりを行くのに、2時間かかった、速さは?」の
「\(\large{\frac{60}{2}}\)km/h !」 と0.5秒で言ったのと同じようなものですね!
そうです! できる限り簡単な形にするのが「数学ルール」でしたね!
√を簡単な形にする方法
「2乗すれば中の数字」より
↓
中の数字が、2乗の形(\(\small{\sqrt{( )^2}}\) ) なら√が不要
↓
中の数字が、2乗の形(\(\small{\sqrt{( )^2}}\) ) なら√の前に出せる
||
中の数字が、2乗の形(\(\small{\sqrt{〇^2・□^2・☆^1}}\) ) なら、2乗の形のものは√の前に出せる
《 例 》
次の値はいくらですか = 簡単な形にしましょうましょう = a\(\small{\sqrt{b}}\)の形のしましょう
\(\small{\sqrt{1}}\) = \(\small{\sqrt{1×1}}\) = \(\small{\sqrt{1^2}}\) = 1
√ の中を「素因数分解」すれば、「2乗なもの」を発見できますね!
(素因数分解のしかた)
\(\small{\sqrt{3}}\) = \(\small{\sqrt{3}}\)(←これ以上どうしようもないですね、よって これが「最も簡潔な形」です)

\(\small{\sqrt{100}}\) = \(\small{\sqrt{2・2・5・5}}\) = \(\small{\sqrt{2^2・5^2}}\) = 2・5√ = 10
\(\small{\sqrt{121}}\) = \(\small{\sqrt{11^2}}\) = 11
\(\small{\sqrt{20}}\) = \(\small{\sqrt{2^2・5}}\) = 2\(\small{\sqrt{5}}\)
\(\small{\sqrt{40}}\) = \(\small{\sqrt{2・2・2・5}}\) = \(\small{\sqrt{2^2・2・5}}\) = 2\(\small{\sqrt{10}}\)
\(\small{\sqrt{216}}\) = \(\small{\sqrt{2・2・2・3・3・3}}\) = \(\small{\sqrt{2^2・2・3^2・3}}\) = 2・3\(\small{\sqrt{2・3}}\)=6\(\small{\sqrt{6}}\)
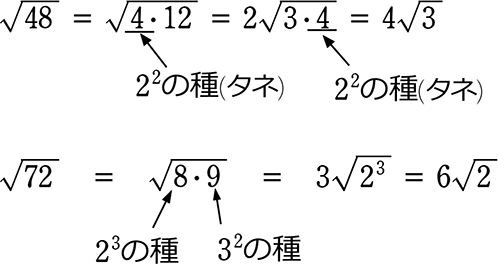
慣れてきますと、細かく素因数分解せず
平方数で割っていくと楽 と思うようになりますね
4 = 22 → 「4で割れたら22 get!」
9 = 32 → 「9で割れたら32 get!」
\(\small{\sqrt{20}}\)=\(\small{\sqrt{\color{red}{4}\ \cdot \ 5}}\)=2\(\small{\sqrt{5}}\)
\(\small{\sqrt{27}}\)=\(\small{\sqrt{\color{red}{9}\ \cdot \ 3}}\)=3\(\small{\sqrt{3}}\)
\(\small{\sqrt{50}}\)=\(\small{\sqrt{\color{red}{25}\ \cdot \ 2}}\)=5\(\small{\sqrt{2}}\)
よく出てくるものは
\(\small{\sqrt{8}}\) = 2\(\small{\sqrt{2}}\)!
など、勝手に憶えてしまいますね
√の前に出す(〇√)ことは値が具体的になっていくということですね
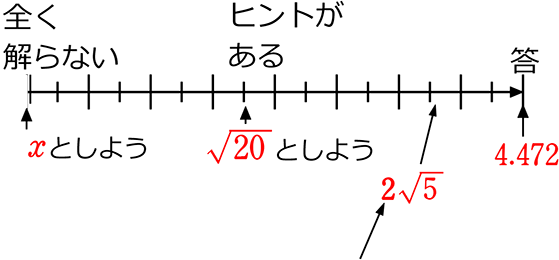
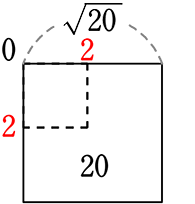
前に出た「2」の意味は、1辺は最低「2」
よりは大きいと解明したことと同じ!
問題に\(\small{\sqrt{5}}\) の値(2.236)がない場合は、
2\(\small{\sqrt{5}}\)が最終の形になります
これら正方形の1辺を
①とりあえず「√ 」で表そう
②それから簡単な形に近づけよう
というのが、「√ 」の大まかな基本イメージですね!
ただし、これらは「正方形」という「プラスだけ」を扱う「図形」の場合のお話となります!
例えば、正方形の図形がない場合は…
ex) x を求めましょう
・x2 = 9 A. ±3 確かに (-3)2=(-3)×(-3)=9
・x2 = 3 A. ±\(\small{\sqrt{3}}\) 確かに (-\(\small{\sqrt{3}}\))2=(-\(\small{\sqrt{3}}\))×(-\(\small{\sqrt{3}}\))=3
・x2 = 20 A. ±2\(\small{\sqrt{5}}\) 確かに (-2\(\small{\sqrt{5}}\))2=(-2\(\small{\sqrt{5}}\))×(-2\(\small{\sqrt{5}}\))=4×5=20
というふうに「
(イメージ)
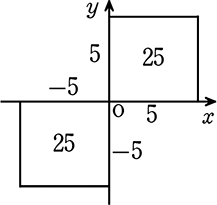
1辺が-5の正方形など
自然界には存在しませんが
0を基準とした人間には
1辺が-(マイナス)の正方形を
考えることができますね
そして、この x の値のことを平方根(へいほうこん)と言います
ex)
・9の平方根は A. ±3
・3の平方根は A. ±\(\small{\sqrt{3}}\)
・20の平方根は A. ±2\(\small{\sqrt{5}}\)
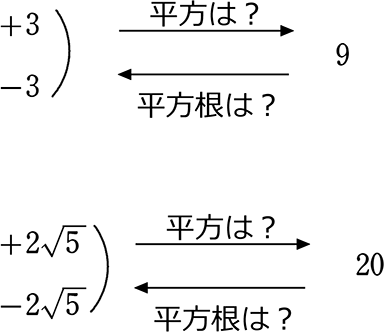
「平方」は? = 「2乗しましょう」
「平方根」は? = 「±√をつけましょう」

\(\small{\sqrt{64}}\) = ±8 ???
これは慣れてきたころによく起こる小混乱ですね
\(\small{\sqrt{64}}\)は、すでに√がついているので、64の平方根で
-がついていないので、+の方の平方根ということですね
その+の方の平方根である\(\small{\sqrt{64}}\)を簡潔な形にせよ という問題ですね
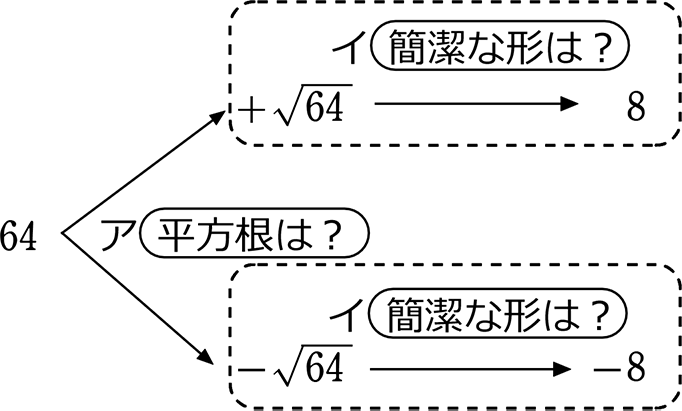
\(\small{\sqrt{64}}\)を見たときに
→ √がついている → 「64の平方根は?ということか」というアとイをごちゃまぜにした読み方 → 小混乱
\(\small{\sqrt{64}}\)を見たときは
→ √がついている → 「これは64の平方根!(プラスの方の)」と読めば → 「(イ)簡単な形は?」ということか
《 例 》
\(\small{\sqrt{64}}\)の値を求めよ
この問いをくどく言いなおすと
(64の平方根の
∴ \(\small{\sqrt{64}}\)=+\(\small{\sqrt{64}}\)=\(\small{\sqrt{8^2}}\)=8
他に考えられる小混乱は、
\(\small{\sqrt{64}}\)は\(\small{\sqrt{(+8)^2}}\)とも\(\small{\sqrt{(-8)^2}}\) とも変形できるし…
2乗の形のものは前に出せるから、±8?
→ ダメです!
「2乗の形のものは√の前に出せる」 → 正確には「2乗の形のものの絶対値が前に出せる」ですね (後述)
\(\small{\sqrt{(-8)^2}}\) → |-8| → -(-8) =8 (絶対値の外し方)
・ アとイをごちゃまぜにしない!
・ 前に出れるのは絶対値
● この後に学ぶ「二次方程式」のために、もう少し掘り下げますね!
「x2の平方根は、右辺の値に±√をつけたもの」
ex) x2 = 4 → x = ±\(\small{\sqrt{4}}\)
x2 = y → x = ±\(\small{\sqrt{y}}\)
\(\Downarrow\) もっと言えば
「x2の平方根は、右辺丸々に±√をつける」
ex) x2 = y-3 → x = ±\(\small{\sqrt{y-3}}\)
x2 = a+b+c → x = ±\(\small{\sqrt{a+b+c}}\)
\(\Downarrow\) もっと言えば
「左辺丸々を2乗の形ならば、右辺丸々に±√をつければ、左辺の2乗がとれる」
ex)
・ (x+3)2 = \(\large{\frac{3}{5}}\) → x+3 = ±\(\small{\sqrt{\large{\frac{3}{5}}}}\)
・(x-4)2 = y-2 → x-4 = ±\(\small{\sqrt{y-2}}\)
・(a+b+c)2 = d+e+f → a+b+c = ±\(\small{\sqrt{d+e+f}}\) ですね!

「左辺丸々2乗」なら、「右辺丸々に±√」
(をつければ、左辺の2乗がとれる)
cf. (x+1)2-1 = \(\large{\frac{5}{4}}\) などは-1を右辺に移項すれば、
「左辺丸々2乗」の形になりますね!

とりあえず置く √ と log
「とりあえず置いてしまおう!」
それから「ルールに基づいて、簡潔な形に近づけていこう!」というものが
数学には結構ありますね!
中学では「√ 」、高校では「log」などでしょうか
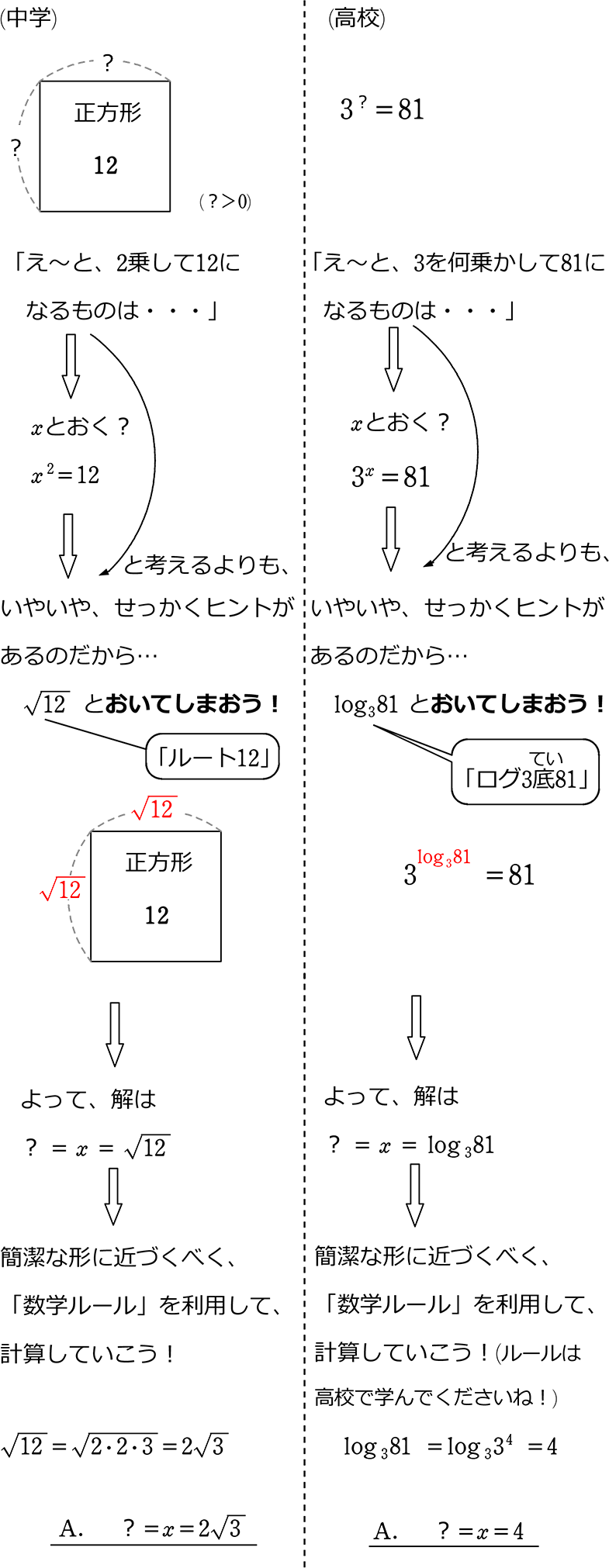
変に「え~と」と考えるより、「0.5秒でおいてしまう(実はそれが解)!」というのも
「あり」かと思います
そして、慣れてきたら
「え~と・・・±2\(\small{\sqrt{3}}\) や 4 」と頭の中で簡潔な形にできるように
なればよいのかなと思います
① 平方根の大小
整数の大小は、例えば
-6<-2<0<1<3<7 で、これを数直線上に表せば、

で、右にあればあるほど、大きくなりますね
そこでこれらを、単純に「2乗」してみると
(-6)2= 36、(-2)2= 4、 02= 0、 12= 1、 32= 9、 72= 49 で
マイナスの値がプラスになって
先ほどと順序が変わってしまいますね!
2乗しても位置関係が変わらないようにするには
どのように2乗すればよいのでしょうか? 簡単ですね
→マイナス側は、マイナスを外して2乗して、またマイナスを付ける
→ すなわち、数字だけを2乗すれば、 大小関係は元と同じですね!
これで、√ のついたものの大小も
はっきりしてきますね!

√付きの大小関係
・ 「2乗」してみる
・ マイナスの時は、数字だけ2乗する
または
・ 逆に全部√の中に入れる(全部\(\small{\sqrt{a}}\)の形にする)
ただそれだけですね
《 例 》
不等号を入れましょう
・\(\small{\sqrt{12}}\) □ \(\small{\sqrt{15}}\) 2乗すると、12と15 ∴ \(\small{\sqrt{12}}\) <\(\small{\sqrt{15}}\)
・6 □ \(\small{\sqrt{34}}\) 2乗すると、36と34 ∴ 6 >\(\small{\sqrt{34}}\)
・-\(\small{\sqrt{5}}\) □ 2.236 プラスとマイナスは当然に ∴ -\(\small{\sqrt{5}}\) < 2.236
・-2\(\small{\sqrt{3}}\) □ -\(\small{\sqrt{15}}\) 数字だけ2乗すると、-12と-15 ∴ -2\(\small{\sqrt{3}}\) >-\(\small{\sqrt{15}}\)
② 有理数・無理数
(数の分類)
有理数・・・分数で表せる数
無理数・・・分数で表せない数
これは、一体どういう意味なのでしょうか?
まず、「分数」は「比」でしたね!
例えば、下の三角形の小三角形と大三角形の辺の「比」は、1:2 ですね
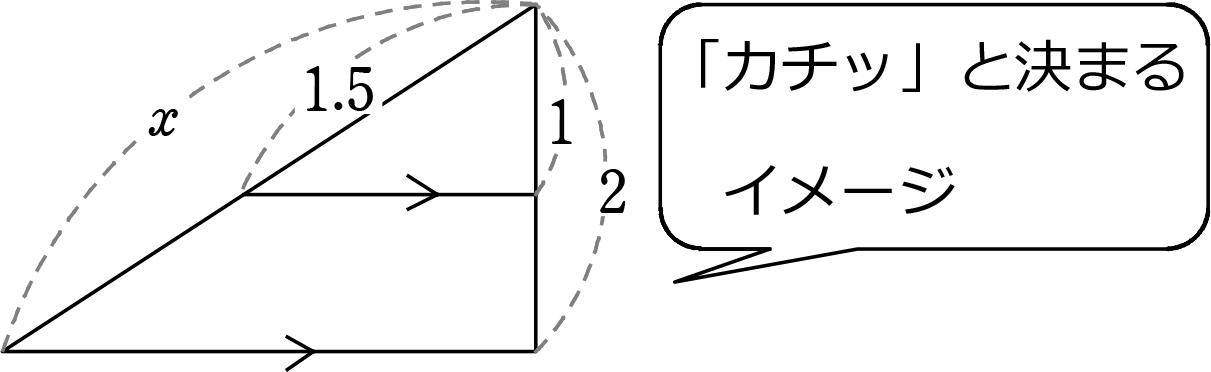
これを、「分数」で表すと、
小を基準にすれば、 大は\(\large{\frac{2}{1}}\)(倍)、または 大(と小)の比は 2:1
大を基準にすれば、 小は\(\large{\frac{1}{2}}\)(倍)、または 小(と大)の比は 1:2 (比の値)
\(\large{\frac{△}{〇}}\)、△:〇 を「分の」「対」読まずに、どちらも
〇「につき」△と読めば、どちらも同じものとわかりますね
確かに、\(\small{\begin{cases}
1:2 \small{=} 1.5:x \\
1:1.5 \small{=} 2:x \\
\large{\frac{2}{1}} \small{=} \large{\frac{x}{1.5}} \\
\large{\frac{1}{2}} \small{=} \large{\frac{1.5}{x}}
\end{cases}}\) どれで求めても、x = 3 ですね ∴ 分数は「比」
よって、分数の分子分母、比の左右は同じ数なら何をかけてもよいので
→ 整数比で表せる
ex. \(\large{\frac{1.2}{1.3}}\) → \(\large{\frac{12}{13}}\)、1.2:1.3→ 12:13
∴ 分数で表せる → 整数比で表せる → 有理数は整数比で表せる → 有比数 ←造語です
対して、無理数は分数で表せない → 整数比で表せない → 無比数←造語です
無理数のイメージ図は
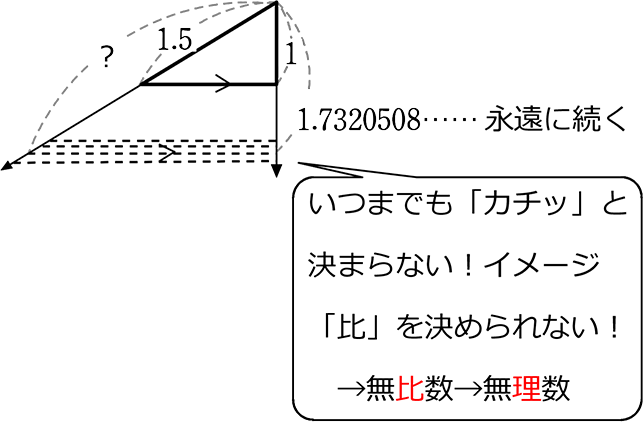
具体的には、無理数とは「循環しない無限小数」でしたね、
「π」と「√ の残るもの」ということですね
《 例 》
●「整数」は、当然全て分数で表せるので「有理数」ですね
ex) 1 → \(\large{\frac{1}{1}}\) 0 → \(\large{\frac{0}{3}}\) -5 → -\(\large{\frac{5}{1}}\)
●「分数」は、分数と言うぐらいだから「有理数」ですね
●「有限小数(…と続かずにピシッと終わる)」も分数で表せるので「有理数」ですね
ex) 0.35 → \(\large{\frac{35}{100}}\) 0.00006 → \(\large{\frac{6}{100000}}\) -0.08 → -\(\large{\frac{8}{100}}\)
cf. 有限小数になる分数は、分母が「2」か「5」の素因数のみでできている
(他の素因数があると「(循環する)無限小数」になる)
\(\large{\frac{1}{\color{red}{ 2}}}\) = 0.5 (有限)
\(\large{\frac{1}{3}}\) = 0.333・・・
\(\large{\frac{1}{4}}\) = \(\large{\frac{1}{\color{red}{ 2}^2}}\) = 0.25 (有限)
\(\large{\frac{1}{\color{red}{ 5}}}\) = 0.2 (有限)
\(\large{\frac{1}{6}}\) = \(\large{\frac{1}{\color{red}{ 2}\ \cdot \ 3}}\) = 0.1666・・・
\(\large{\frac{1}{7}}\) = 0.142857・・・
\(\large{\frac{1}{8}}\) = \(\large{\frac{1}{\color{red}{ 2}^3}}\) = 0.125 (有限)
\(\large{\frac{1}{9}}\) = \(\large{\frac{1}{3^2}}\) = 0.111・・・
\(\large{\frac{1}{10}}\) = \(\large{\frac{1}{\color{red}{2}\ \cdot \ \color{red}{5}}}\) = 0.1 (有限)
●「循環する無限小数」も、分数で表せますね→「有理数」
ex) 0.
0.
両辺を10倍すると → 10x = 3.3333…
(後の引き算で、小数点以下が消えるように、(小数第1位を合わせて) 10の何乗かをする)
引き算をしてみると
10x = 3.3333…
-) x = 0.3333…
9x = 3
∴ x = \(\large{\frac{3}{9}}\) = \(\large{\frac{1}{3}}\) 確かに 1÷3 = 0.3333…
ex) \(0.\dot{5}7142\dot{8}\) → 「点をたくさん打つのは大変なので、スパンの始まりと終わりにだけに点を打ちます(数学ルール)
0.
x = 0.571428…とおくと、1000000x = 571428.571428…
1000000x = 571428.571428…
-) x = 0.571428…
999999x = 571428
∴ x = \(\large{\frac{571428}{999999}}\) = \(\large{\frac{4}{7}}\)
●「循環しない無限小数」は、「引き算技」も使えず → 分数表示不可 → 無理数
\(\small{\sqrt{4}}\) = 2 → 有理数
\(\small{\sqrt{3}}\) = \(\small{\sqrt{3}}\) → 無理数(最終的に√が残れば「無理数」)
\(\small{\sqrt{8}}\) = 2\(\small{\sqrt{2}}\) → 無理数 (√が残ったので無理数)
そして、円周率π (3.14141356…)も循環しない無限小数 → 無理数ですね!
イ 数の平方根を含む式の計算
① 有理化
有理化とは、分数の分母に √ がこないようにすることですね!
数字は、「どのような 1」を掛けても、元の数字に変化はありませんね!
例えば、「3」という数字に、
「1という1」を掛けても、
「\(\large{\frac{2}{2}}\) という1」を掛けても、
「\(\large{\frac{\sqrt{5}}{\sqrt{5}}}\)という1」を掛けても、
「\(\large{\frac{0.33}{0.33}}\) という1」を掛けても、「3」ですね!
これを利用して、分母の√ をとる作業が、「有理化」ですね!
《 例-パターン① 》
・ \(\large{\frac{3}{\sqrt{2}}}\) を有理化しましょう
\(\large{\frac{3}{\sqrt{2}}}\) には「どのような1」を掛ければ、分母にある√ がとれるのでしょうか?
→ 「\(\large{\frac{\sqrt{2}}{\sqrt{2}}}\)という1」ですね!
∴ \(\large{\frac{3}{\sqrt{2}}}\)×\(\large{\frac{\sqrt{2}}{\sqrt{2}}}\) = \(\large{\frac{3\times\sqrt{2}}{\sqrt{2^2}}}\) = \(\large{\frac{3\sqrt{2}}{2}}\)
・ \(\large{\frac{\sqrt{6}}{\sqrt{3}}}\) を有理化しましょう
\(\large{\frac{\sqrt{6}}{\sqrt{3}}}\)×\(\large{\frac{\sqrt{3}}{\sqrt{3}}}\) = \(\large{\frac{\sqrt{3\cdot2×3}}{3}}\) = \(\large{\frac{3\sqrt{2}}{3}}\) = \(\small{\sqrt{2}}\)
これは実は、次に学ぶ \(\large{\frac{\sqrt{a}}{\sqrt{b}}}\) = \(\small{\sqrt{\large{\frac{a}{b}}}}\) でもOKなのですが、あまりにも有理化の経験回数の方が増えていくと思いますので、忘れがちになりますね!
逆を言えば、「有理化さえできれば間違いなし!」ですね
《 例-パターン② 》
\(\large{\frac{\sqrt{7}-\sqrt{2}}{\sqrt{7}+\sqrt{2}}}\) を有理化しましょう
どのような「1」をかけましょうか
→ 展開公式 (a+b)(a-b) = a2-b2 を利用した
分母の真ん中の符号を逆にした「1」をかければ、いい感じに√がなくなりますね
→ \(\large{\frac{\sqrt{7}-\sqrt{2}}{\sqrt{7}-\sqrt{2}}}\) という「1」をかけて
= \(\large{\frac{(\sqrt{7}-\sqrt{2})(\sqrt{7}-\sqrt{2})}{(\sqrt{7}+\sqrt{2})(\sqrt{7}-\sqrt{2})}}\)
= \(\large{\frac{7-2\sqrt{14}+2}{7-2}}\) 分子は(a-b)2=a2-2ab+b2 を利用
= \(\large{\frac{9-2\sqrt{14}}{5}}\)
「有理化」は数学ルールですので、「約分」と同じように、最後の答えは
必ず「有理化」してくださいね!
(ただし、高校の「三角関数」の場面では有理化は、ほぼ不要ですね)
② 乗法・除法

根号の乗法・除法
大前提として、

でなければいけません (数学ルール)
なぜなら、根号は、

という意味ですから、
2乗して「-(マイナス)」になる数字はありませんね!
ex) (+1)×(+1) = +1
(-1)×(-1) = +1
それを踏まえて、公式というほどではありませんが、
・ a×\(\small{\sqrt{b}}\) = a\(\small{\sqrt{b}}\)
・ \(\small{\sqrt{a}}\)×\(\small{\sqrt{b}}\) = \(\small{\sqrt{ab}}\)
・ \(\small{\sqrt{a}}\)÷\(\small{\sqrt{b}}\) = \(\large{\frac{\sqrt{a}}{\sqrt{b}}}\) = \(\small{\sqrt{\large{\frac{a}{b}}}}\) = \(\small{\sqrt{a÷b}}\)
《 例 》 計算しましょう
・ \(\small{\sqrt{2}}\)×\(\small{\sqrt{5}}\) = \(\small{\sqrt{10}}\)
・ 2×\(\small{\sqrt{6}}\) = 2\(\small{\sqrt{6}}\)
・ 4\(\small{\sqrt{5}}\)×2\(\small{\sqrt{10}}\) = 8\(\small{\sqrt{5×5\cdot2}}\) = 40\(\small{\sqrt{2}}\)
・ \(\large{\frac{\sqrt{6}}{\sqrt{3}}}\) = \(\small{\sqrt{\large{\frac{6}{3}}}}\) = \(\small{\sqrt{2}}\)
・ \(\large{\frac{\sqrt{24}}{2\sqrt{3}}}\) \(\small{\begin{cases}
\scriptsize{=} \large{\frac{\sqrt{3\cdot8}}{2\sqrt{3}}} \scriptsize{=} \large{\frac{2\sqrt{3\cdot2}}{2\sqrt{3}}} \scriptsize{=} \small{\sqrt{\large{\frac{3\cdot2}{3}}}} \scriptsize{=} \small{\sqrt{2}} …先に分子スッキリ \\
\scriptsize{=} \large{\frac{\sqrt{3\cdot2^3}×\sqrt{3}}{2\sqrt{3}×\sqrt{3}}} \scriptsize{=} \large{\frac{6\sqrt{2}}{6}} \scriptsize{=} \small{\sqrt{2}} …先に分母スッキリ
\end{cases}}\)
(√ の計算問題で、どのように解けば楽かを考えることは大切ではありますが、
まずは有理化がおすすめかなと思います
もちろん自分が1番得意な思考回路で解くことが1番ですが!)
《 例 》 逆に全て√ の中に収めましょう( \(\small{\sqrt{a}}\) の形)
・ 2\(\small{\sqrt{3}}\) = \(\small{\sqrt{2^2×3}}\) = \(\small{\sqrt{12}}\)
・ 3\(\small{\sqrt{2}}\) = \(\small{\sqrt{3^2×2}}\) = \(\small{\sqrt{18}}\)

平方根の近似値の求め方
12m2の土地の広さを想像する時、おそらく

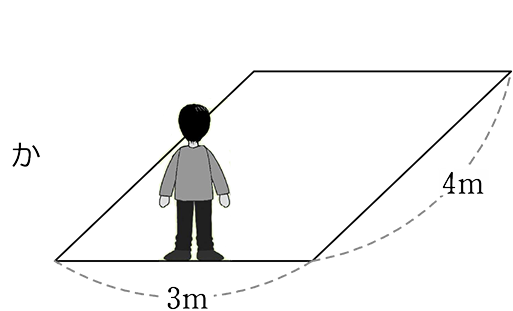
などの長方形で、広さをイメージするのではないでしょうか
そして、正方形でイメージするためには、1辺は「小数」になりそうだと
諦めたこともあるのではないでしょうか
そうです、正方形で1辺の長さを求めるには、地道な作業が必要なのですです
面積12の1辺は? \(\small{\sqrt{12}}\) !なら本当に楽なのですが、
今は「近似値」を求めようとしているのでしたね
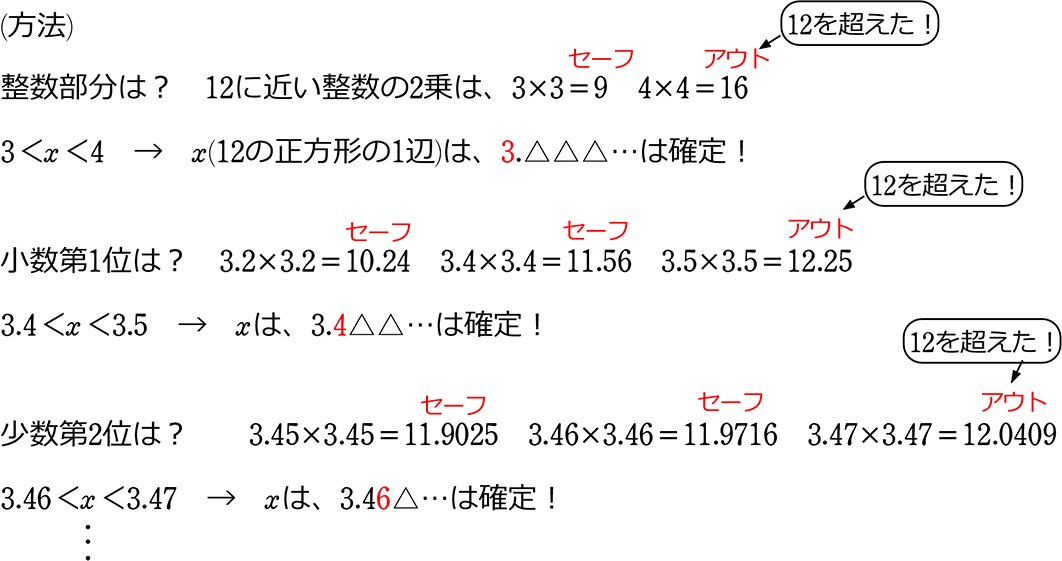
(方法)
整数部分は? 12に近い整数の2乗は、 3×3=
4×4=
3<x<4 → x(12の正方形の1辺)は、 3.△△△…は確定!
小数第1位は? 3.2×3.2=
3.5×3.5=
3.4<x<3.5 → xは、 3.4△△…は確定!
少数第2位は? 3.45×3.45=
3.47×3.47=
3.46<x<3.47 → xは、 3.46△…は確定!
・
・
・
このように地道に「あたり」を探しながら求めていくことになります・・・
ですが安心して下さいね、
試験では、小数第1位まで求める知識があれば十分ですので!
(4桁×4桁のような掛け算をさせられることはありません)
ちなみに、
32 = 9
(3.4)2 = 11.56
(3.46)2 = 11.9716
・
・
・
これを続けると、11.99999…というふうに「12」に近づいていきますね
「12」になることはありませんが!
以下は近似値の有名なゴロ合わせです
\(\small{\sqrt{2}}\) = 1.414 21356… (ヒトヨヒトヨ ニヒトミゴロ) (一夜一夜に人見ごろ)
\(\small{\sqrt{3}}\) = 1.732 0508… (ヒトナミニ オゴレヤ) (人並みにおごれや!)
\(\small{\sqrt{5}}\) = 2.236 0679… (フジサンロク オウムナク) (富士山麓 オウム鳴く)
30年で人や街並みは変われど、√の近似値は変わらないのですね…当然ですね
『自然の摂理』が決める「数学」は、変わりませんが、
『人間』が決める「社会科」は、変わりますね!
「いい国造ろう(1192)鎌倉幕府」が「いい箱(1185)作ろう鎌倉幕府」という教科書もあるみたいですね!
③ 加法・減法
根号を含む加法・減法は、√を「文字」と同じように扱えばよいだけですね!
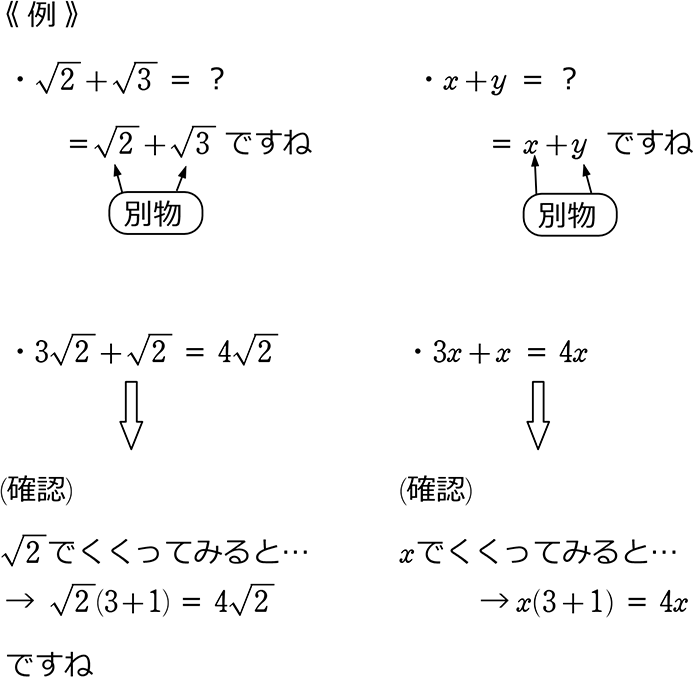
《 例 》
\(\large{\frac{36}{\sqrt{24}}}\)-\(\small{\sqrt{\large{\frac{3}{2}}}}\)-\(\large{\frac{\sqrt{64}}{3}}\)
=\(\large{\frac{36\sqrt{24}}{24}}\)-\(\large{\frac{\sqrt{6}}{2}}\)-\(\large{\frac{8}{3}}\) …有理化など
=\(\large{\frac{3\sqrt{24}}{2}}\)-\(\large{\frac{\sqrt{6}}{2}}\)-\(\large{\frac{8}{3}}\) …約分
=\(\large{\frac{3・2\sqrt{6}}{2}}\)-\(\large{\frac{\sqrt{6}}{2}}\)-\(\large{\frac{8}{3}}\) …前出し
=3\(\small{\sqrt{6}}\)-\(\large{\frac{\sqrt{6}}{2}}\)-\(\large{\frac{8}{3}}\) …約分
=\(\large{\frac{18\sqrt{6}-3\sqrt{6}-16}{6}}\) …通分
=\(\large{\frac{15\sqrt{6}-16}{6}}\) …分子の計算
=\(\large{\frac{5\sqrt{6}}{2}}\)-\(\large{\frac{8}{3}}\) //
ウ 具体的な場面での平方根を用いた処理
《 例 》
1辺の長さが1の正方形の対角線の長さは? (三平方の定理を使わない)
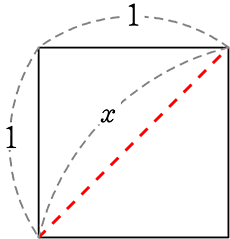
同じものを4枚くっつけると見えてきますね!
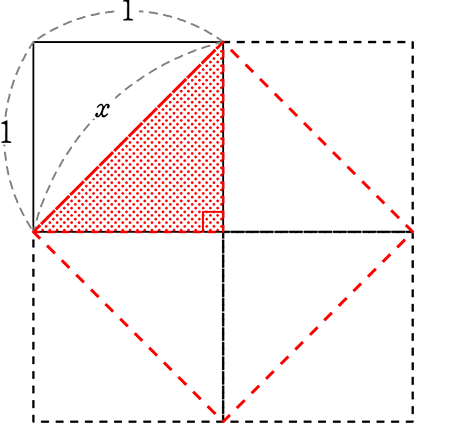

→ \(\large{\frac{1}{2}}\)・1・1 = \(\large{\frac{1}{2}}\)
→ \(\large{\frac{1}{2}}\)・4個 = 2
は4つの辺、4つの角が
等しいので正方形
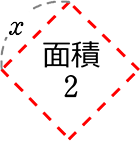
∴ x = \(\small{\sqrt{2}}\) //
√に関する文章問題はあまりないですね!
やはり、√に関する問題は、計算問題、パズルチックな問題がほとんどとなりますね
〔 √の中は絶対にプラス 〕
《 例 》 計算しましょう
・ (-\(\small{\sqrt{2}}\))2 = 2
・-(\(\small{\sqrt{2}}\))2 = -2
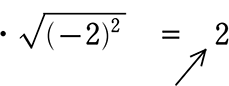
-2 ではありません!

大鉄則がありましたね!
よって、これの正体は、 「2乗したら4」
すなわち 「4の平方根(\(\small{\sqrt{4}}\))」ですね!
問題作者が、4が√ の中にいることをいいことに
(-2)2 といういたずら変形を加えたものですね
プラス は 、 「 いったん √ 内で計算」を…省けるから →「2個あれば出られる」
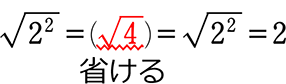
マイナスは、「いったん √ 内で計算」を省けない
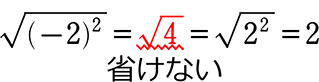
《 例 》
・\(\small{\sqrt{(3-\pi)^2}}\) = \(\small{\sqrt{(3-3.14…)^2}}\) = \(\small{\sqrt{(-0.14…)^2}}\) = \(\small{\sqrt{(-1)^2\cdot(0.14…)^2}}\) = \(\small{\sqrt{(0.14…)^2}}\) = 0.14… = π-3
ちょっと不思議ですね!この原理は
①数字は2乗すれば必ずプラス (-3)×(-3)= 9
②√の中は必ずプラス この2つの条件から
→√の中で2乗なものは『その絶対値』を√の前に出せる ということにつながりますね
→上の「マイナスの場合 (\(\small{\sqrt{(-2)^2}}\) = \(\small{\sqrt{4}}\) = \(\small{\sqrt{2^2}}\) = 2)において いったん√の中で計算を省けない」というものなどは、「絶対値を前に出す」の簡易バージョンということになりますね
・\(\small{\sqrt{(5-3)^2}}\) ←プラスとわかればそのまま出してもよいですね = (5-3) = 2 もちろん先に中を計算してもよい \(\small{\sqrt{2^2}}\) = 2 ですね
・\(\small{\sqrt{(3-5)^2}}\) = マイナスの場合の絶対値を前に出すと = -(3-5) = 2 または = \(\small{\sqrt{(-2)^2}}\) = 絶対値を前に出す → 2
もちろん「簡易バージョン」で「いったん中で計算」 → \(\small{\sqrt{4}}\) = 2 でもかまいません
・\(\small{\sqrt{(3-\pi)^2}}\) の「3-π」は…「-」! → ∴ -(3-π) = π-3
先に出てきた
√を簡単な形にする方法
「2乗すれば中の数字」より
↓
中の数字が、2乗の形(\(\small{\sqrt{( )^2}}\) ) なら√が不要
↓
中の数字が、2乗の形(\(\small{\sqrt{( )^2}}\) ) なら√の前に出せる
||
中の数字が、2乗の形(\(\small{\sqrt{〇^2・□^2・☆^1}}\) ) なら、2乗の形のものは√の前に出せる
↓
\(\small{\sqrt{( )^2}}\)は、
( )>0のとき、|( )|=( )
( )<0のとき、|( )|=-1( )
(絶対値の外し方)
ですね
① 整数部分・小数部分
《 例 》 「整数部分」を答えましょう
・ \(\small{\sqrt{2}}\) → 1×1=
∴ \(\small{\sqrt{2}}\) =1.△△△
かっこよく言えば、
1<\(\small{\sqrt{2}}\)<2 A. 1
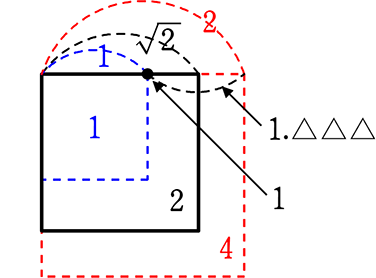
・ \(\small{\sqrt{15}}\) → 3×3=
∴ \(\small{\sqrt{15}}\) =3.△△△
かっこよく言えば、3<\(\small{\sqrt{15}}\)<4 A. 3
・ \(\small{\sqrt{27}}\) → 5×5=
∴ \(\small{\sqrt{27}}\) =5.△△△
かっこよく言えば、5<\(\small{\sqrt{27}}\)<6 A. 5
・ 2\(\small{\sqrt{6}}\) ←外の2は「整数部分」ではありません!「最低2はある」という意味にとどまります → \(\small{\sqrt{24}}\) ←中に入れる → 4×4=
∴ \(\small{\sqrt{24}}\) =4.△△△
かっこよく言えば、4<\(\small{\sqrt{24}}\)<5 A. 4
↑「2」を中に入れずに、「\(\small{\sqrt{6}}\)」の整数部分「2」をもとめて、
(外の2) ×(\(\small{\sqrt{6}}\)の整数部分の2) =4でもよいのでは?
→ ダメです!たまたまです!必ず中に入れてください!
次の問題で確認ですね
・ 3\(\small{\sqrt{7}}\) → \(\small{\sqrt{63}}\) → 7×7=
∴ \(\small{\sqrt{63}}\) =7.△△△ A. 7
中に入れずに行うと… (外の3) ×(\(\small{\sqrt{7}}\)の整数部分2) = 6
→ 中に入れると、限界に大きいものを探すことができる!
・ 4+\(\small{\sqrt{5}}\) → \(\small{\sqrt{5}}\) 単体の整数部分は → 2×2=
∴ \(\small{\sqrt{5}}\) = 2.△△△ → 4+2.△△△ = 6.△△△ A. 6
・ 4-\(\small{\sqrt{5}}\) ←-の時は注意! → \(\small{\sqrt{5}}\) 単体の整数部分は → 2×2 =
∴ \(\small{\sqrt{5}}\) = 2.△△△ → 4-2.△△△ = 1.△△△ A. 1
ex. 4-2.2 = 1.8 A. 1
ということで
整数部分 ⇒ 暗算で求まる
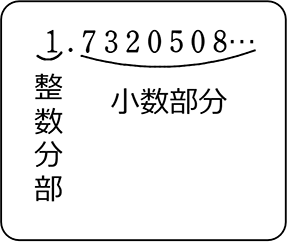
《 例 》 「小数部分」を答えましょう
まずは「整数部分」を求めることになりますね!
→ 「全部」-「整数部分」 = 「小数部分」
2.6457513…(全部)
-) 2 (整数部分)
0.6457513…(小数部分)
・ \(\small{\sqrt{8}}\) → 2×2=
∴ 整数部分は 2 ∴ 小数部分は \(\small{\sqrt{8}}\)-2
・ 2\(\small{\sqrt{7}}\) → \(\small{\sqrt{28}}\) → 5×5=
∴ 整数部分は 5 ∴ 小数部分は 2\(\small{\sqrt{7}}\)-5
・ 6+\(\small{\sqrt{3}}\) → \(\small{\sqrt{3}}\) 単体の整数部分は → 1×1=
∴ \(\small{\sqrt{3}}\) =1.△△△ ∴ 全体の整数部分は 6+1.△△△ → 7
∴ 全体の小数部分 = 全体-全体の整数部分 = 6+\(\small{\sqrt{3}}\)-7 = -1+\(\small{\sqrt{3}}\)
・ 6-\(\small{\sqrt{3}}\) ←-の時は注意! → \(\small{\sqrt{3}}\) 単体の整数部分は → 1×1=
∴ \(\small{\sqrt{3}}\)= 1.△△△ ∴ 全体の整数部分は 6-1.△△△ = 4.△△△ → 4
∴ 小数部分は 6-\(\small{\sqrt{3}}\)-4 = 2-\(\small{\sqrt{3}}\)
② 根号を無くす自然数m
根号がなくなる数字は、平方数(自然数2)ということですね
ex. 0, 1, 4, 9, 16, 25, 36, 49, 64, 91, 100, 121・・・ (0×0も含めて構いません)
→ 64 = 82 → 64は平方数
→ 64 = 2×4×8 → 4は平方数(いろんなところに平方数はつくれますね)
《 例 》
\(\small{\sqrt{24m}}\) が自然数になるための、自然数mの最小の値を求めましょう
1番簡単なのは、 m = 24 の時ですね! → \(\small{\sqrt{24\cdot\color{red}{24}}}\) = 24
ですが、24より小さい数字でも√ がとれそうですね
→ \(\small{\sqrt{24m}}\) = \(\small{\sqrt{2^2\cdot6\cdot m}}\) ∴ 最小の自然数 m = 6 ですね
この手の問題は、
「どうすれば、√の中身が全て2乗になりますか?」ということですね!
すなわち、√の中身が、
\(\small{\sqrt{〇\color{red}{^2}\cdot\color{red}{1^2}\cdot△\color{red}{^2}\cdot□\color{red}{^2}\cdot\color{red}{1^2}}}\) のように「全て2乗」な形、
すなわち、もっと極端にいうと、√の中が

「全てが、偶数乗か、 1( = 12)」になればよいということですね!
● \(\small{\sqrt{8m}}\) が
→ \(\small{\sqrt{8m}}\) = \(\small{\sqrt{2^2\cdot2\cdot\color{red}{m}}}\) ←22は前に出られますが、出さずに√ の中の先頭にでも置いておいて下さいね!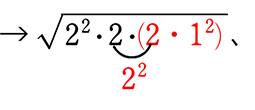
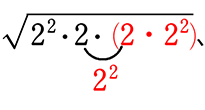
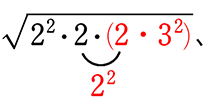
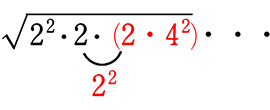
∴ m = 2、8、18、32、… A. 無限にある
● \(\small{\sqrt{8m}}\) が
→ (上の問より) A. m = 2
・自然数(=正の整数) 1,2,3,4…
「マイナス」「0」 不可
・整数 … -1,0,1,2…
「マイナス」「0」 OK
● \(\small{\sqrt{8m}}\) が
→ 「√の中はプラス」よりm≧0、m = 0の時、 \(\small{\sqrt{8m}}\) = \(\small{\sqrt{8\cdot0}}\) = \(\small{\sqrt{0}}\) = 0
A. m = 0
整数
・・・ -2,-1,0,1,2・・・
ですが、√ の中が「-(マイナス)」はあり得ないので、
この問題では、0,1 2 3 4・・・
● \(\small{\sqrt{8m}}\) が
→ m = 0 の時、 \(\small{\sqrt{8m}}\) = \(\small{\sqrt{8\cdot0}}\) = \(\small{\sqrt{0}}\) = 0 ←自然数ではない!OUT
∴ \(\small{\sqrt{8m}}\) = \(\small{\sqrt{2^2\cdot2\cdot m}}\) より A. m = 2
● \(\small{\sqrt{5(60-m)}}\)
↑mが最小ではなく、√が最小ですね
→ ( )が「0」の時、\(\small{\sqrt{5\cdot0}}\) = \(\small{\sqrt{0}}\) = 0
∴ ( ) = 0 → (60-m)が0 → 60-m = 0 → m = 60 の時
A. m = 60
● \(\small{\sqrt{5(60-m)}}\) が最小の
√が最小の自然数ですね
→ √が自然数なので0はダメ = (60-m)が0はダメ
∴ \(\small{\sqrt{5\cdot\color{red}{5}}}\) の時が最小の自然数ですね!
→ 60-m = 5 → m = 55 A. 55
● \(\small{\sqrt{5(60-m)}}\) が
mが最小の整数
→ √ の中が全て2乗になるために、考えられる(60-m)は…
(5・12) ← \(\small{\sqrt{5\cdot(5・1^2)}}\) ∴ 60-m=5・12 → m=55
(5・22) ← \(\small{\sqrt{5\cdot(5・2^2)}}\) ∴ 60-m=5・22 → m=40
(5・32) ← \(\small{\sqrt{5\cdot(5・3^2)}}\) ∴ 60-m=5・32 → m=15
(5・42) ← \(\small{\sqrt{5\cdot(5・4^2)}}\) ∴ 60-m=5・42 → m=-20
・
・
・
∴ mは整数より「マイナス」もOK → 永遠に続く!
A. 解なし
● \(\small{\sqrt{5(60-m)}}\) が
→ 上と同じであるが、mが
(上の問題より) A. 15
● \(\small{\sqrt{\large{\frac{8}{m}}}}\) が最小の自然数になるような、自然数mの値は?
→ \(\small{\sqrt{\large{\frac{8}{m}}}}\) = \(\small{\sqrt{\large{\frac{2^2\cdot2}{m}}}}\) = 2\(\small{\sqrt{\large{\frac{2}{m}}}}\) ∴ m =2 ではダメですね! \(\small{\sqrt{\large{\frac{8}{2}}}}\) = 2
→ 普通に、m = 8 のときですね! \(\small{\sqrt{\large{\frac{8}{8}}}}\) = \(\small{\sqrt{1}}\) = 1 A. m = 8
これは、22 を√の前に出してしまったからのミスですね!
→ 先に出たきた「出さずに√の中の先頭にでも置いておいて下さいね!」
ですね、実は√の中が「掛け算だけ」の時は、前出しOKなのですが、
「割り算」の時は、前出しは危険ですね!
よって、そのような「場合分け」は面倒ですので、いつでも
「出さずに√ の中の先頭にでも置いておいて下さいね!」ですね!
● \(\small{\sqrt{\large{\frac{8}{m}}}}\) が自然数になるような、最小の自然数mの値は?
mが最小
→ \(\small{\sqrt{\large{\frac{8}{m}}}}\) = \(\small{\sqrt{\large{\frac{2^2\cdot2}{m}}}}\) A. m = 2
● \(\small{\sqrt{\large{\frac{8}{m}}}}\) が自然数になるような、最大の自然数mの値は?
mが最
→ \(\small{\sqrt{\large{\frac{8}{m}}}}\) = \(\small{\sqrt{\large{\frac{2^2\cdot2}{m}}}}\)
∴ m = 22・2のとき A. m = 8
ちなみに、
m = 22・2・22 → \(\small{\sqrt{\large{\frac{2^2\cdot2}{2^2\cdot2\cdot\color{red}{2^2}}}}}\) = \(\small{\sqrt{\large{\frac{1}{2^2}}}}\) = \(\small{\sqrt{\large{\frac{1^2}{2^2}}}}\) = \(\small{\sqrt{\left( \large{\frac{ 1 }{ 2 }} \right )^2}}\) = \(\large{\frac{1}{2}}\)
m = 22・2・32 → \(\small{\sqrt{\large{\frac{2^2\cdot2}{2^2\cdot2\cdot\color{red}{3^2}}}}}\) = \(\small{\sqrt{\large{\frac{1}{3^2}}}}\) = \(\large{\frac{1}{3}}\)
m = 22・2・42 → \(\small{\sqrt{\large{\frac{2^2\cdot2}{2^2\cdot2\cdot\color{red}{4^2}}}}}\) = \(\small{\sqrt{\large{\frac{1}{4^2}}}}\) = \(\large{\frac{1}{4}}\)
・
・
・
と、mの値はいくらでも大きくできますが、
\(\large{\frac{1}{2}}\)、\(\large{\frac{1}{3}}\)、\(\large{\frac{1}{4}}\)は自然数ではないですから… OUT!ですね!

・どうすれば、\(\small{\sqrt{〇^2}}\) や \(\small{\sqrt{1^2}}\) の形になるか
・前出しはしない
・「自然数」、「整数」 の違い
・どっちの最小を求めよと言っているのか?
(√の値なのか、mの値なのか)
√は、計算問題・パズルチックな問題がメインになりますね!
お疲れ様でした !!
その他の問題は、「問題集」で !!















